Prediction of Potential Evapotranspiration Using Temperature-Based Heuristic Approaches
Abstract
1. Introduction
2. Materials and Methods
2.1. Case Study
2.2. Group Method of Data Handling Type Neural Network
2.3. Multivariate Adaptive Regression Splines
2.4. M5 Model Tree
2.5. Stephens-Stewart Model
2.6. Hargreaves and Samani Model
2.7. Model Development by Heuristic Methods
- Tmin, Tmax, Ra
- Tmin, Tmax, Ra, α.
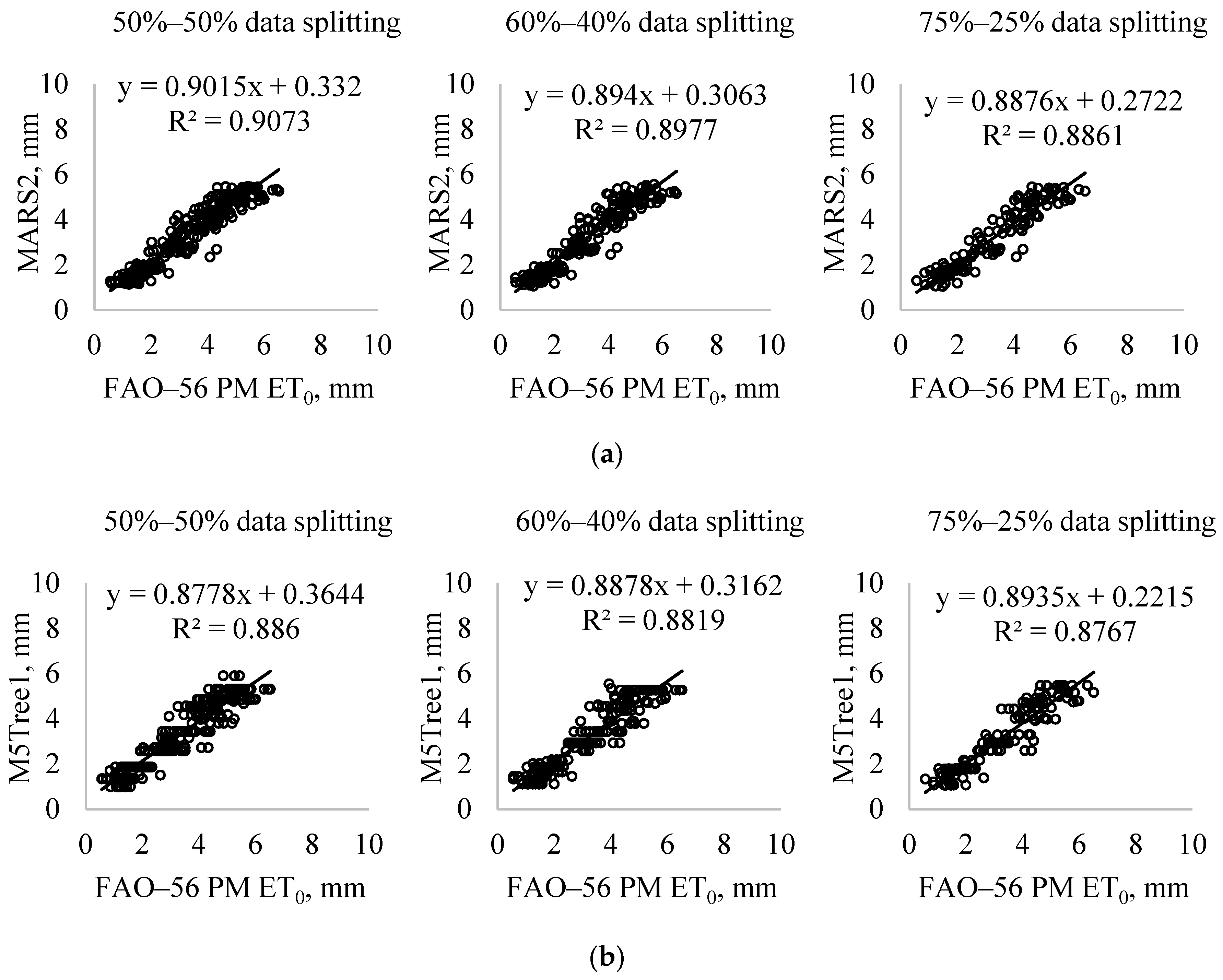
3. Application and Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jing, W.; Yaseen, Z.M.; Shahid, S.; Saggi, M.K.; Tao, H.; Kisi, O.; Salih, S.Q.; Al-Ansari, N.; Chau, K.W. Implementation of evolutionary computing models for reference evapotranspiration modeling: Short review, assessment and possible future research directions. Eng. Appl. Comput. Fluid Mech. 2019, 13, 811–823. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Howell, T.A.; Jensen, M.E. Evapotranspiration information reporting: I. Factors governing measurement accuracy. Agric. Water Manag. 2011, 98, 899–920. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Howell, T.A.; Jensen, M.E. Evapotranspiration information reporting: II. Recommended documentation. Agric. Water Manag. 2011, 98, 921–929. [Google Scholar] [CrossRef]
- Ren, X.; Qu, Z.; Martins, D.S.; Paredes, P.; Pereira, L.S. Daily reference evapotranspiration for hyper-arid to moist sub-humid climates in inner mongolia, China: I. Assessing temperature methods and spatial variability. Water Resour. Manag. 2016, 30, 3769–3791. [Google Scholar] [CrossRef]
- Xing, W.; Wang, W.; Shao, Q.; Peng, S.; Yu, Z.; Yong, B.; Taylor, J. Changes of reference evapotranspiration in the Haihe River Basin: Present observations and future projection from climatic variables through multi-model ensemble. Glob. Planet. Chang. 2014, 115, 1–15. [Google Scholar] [CrossRef]
- Valiantzas, J.D. Temperature-and humidity-based simplified Penman’s ET0 formulae. Comparisons with temperature-based Hargreaves-Samani and other methodologies. Agric. Water Manag. 2018, 208, 326–334. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop evapotranspiration-Guidelines for computing crop water requirements-FAO Irrigation and drainage paper 56. FAO Rome 1998, 300, D05109. [Google Scholar]
- Yaseen, Z.M.; Sulaiman, S.O.; Deo, R.C.; Chau, K.-W. An enhanced extreme learning machine model for river flow forecasting: State-of-the-art, practical applications in water resource engineering area and future research direction. J. Hydrol. 2018, 569, 387–408. [Google Scholar] [CrossRef]
- Khosravinia, P.; Nikpour, M.R.; Kisi, O.; Yaseen, Z.M. Application of novel data mining algorithms in prediction of discharge and end depth in trapezoidal sections. Comput. Electron. Agric. 2020, 170, 105283. [Google Scholar] [CrossRef]
- Zhu, S.; Ptak, M.; Yaseen, Z.M.; Dai, J.; Sivakumar, B. Forecasting surface water temperature in lakes: A comparison of approaches. J. Hydrol. 2020, 585, 124809. [Google Scholar] [CrossRef]
- Yuan, X.; Chen, C.; Lei, X.; Yuan, Y.; Adnan, R.M. Monthly runoff forecasting based on LSTM–ALO model. Stoch. Environ. Res. Risk Assess. 2018, 32, 2199–2212. [Google Scholar] [CrossRef]
- Adnan, R.M.; Liang, Z.; Yuan, X.; Kisi, O.; Akhlaq, M.; Li, B. Comparison of LSSVR, M5RT, NF-GP, and NF-SC models for predictions of hourly wind speed and wind power based on cross-validation. Energies 2019, 12, 329. [Google Scholar] [CrossRef]
- Kisi, O.; Shiri, J.; Karimi, S.; Adnan, R.M. Three different adaptive neuro fuzzy computing techniques for forecasting long-period daily streamflows. In Big Data in Engineering Applications; Springer: Singapore, 2018; pp. 303–321. [Google Scholar]
- Alizamir, M.; Kisi, O.; Muhammad Adnan, R.; Kuriqi, A. Modelling reference evapotranspiration by combining neuro-fuzzy and evolutionary strategies. Acta Geophys. 2020, 68, 1113–1126. [Google Scholar] [CrossRef]
- Petković, B.; Petković, D.; Kuzman, B.; Milovančević, M.; Wakil, K.; Ho, L.S.; Jermsittiparsert, K. Neuro-fuzzy estimation of reference crop evapotranspiration by neuro fuzzy logic based on weather conditions. Comput. Electron. Agric. 2020, 173, 105358. [Google Scholar] [CrossRef]
- Zhu, B.; Feng, Y.; Gong, D.; Jiang, S.; Zhao, L.; Cui, N. Hybrid particle swarm optimization with extreme learning machine for daily reference evapotranspiration prediction from limited climatic data. Comput. Electron. Agric. 2020, 173, 105430. [Google Scholar] [CrossRef]
- Jovic, S.; Nedeljkovic, B.; Golubovic, Z.; Kostic, N. Evolutionary algorithm for reference evapotranspiration analysis. Comput. Electron. Agric. 2018, 150, 1–4. [Google Scholar] [CrossRef]
- Adnan, R.M.; Chen, Z.; Yuan, X.; Kisi, O.; El-Shafie, A.; Kuriqi, A.; Ikram, M. Reference Evapotranspiration Modeling Using New Heuristic Methods. Entropy 2020, 22, 547. [Google Scholar] [CrossRef]
- Khoshravesh, M.; Sefidkouhi, M.A.G.; Valipour, M. Estimation of reference evapotranspiration using multivariate fractional polynomial, Bayesian regression, and robust regression models in three arid environments. Appl. Water Sci. 2015, 7, 1911–1922. [Google Scholar] [CrossRef]
- Mattar, M.A. Using gene expression programming in monthly reference evapotranspiration modeling: A case study in Egypt. Agric. Water Manag. 2018, 198, 28–38. [Google Scholar] [CrossRef]
- Mehdizadeh, S. Estimation of daily reference evapotranspiration (ETo) using artificial intelligence methods: Offering a new approach for lagged ETo data-based modeling. J. Hydrol. 2018, 559, 794–812. [Google Scholar] [CrossRef]
- Mehdizadeh, S.; Behmanesh, J.; Khalili, K. Comprehensive modeling of monthly mean soil temperature using multivariate adaptive regression splines and support vector machine. Theor. Appl. Climatol. 2017, 133, 911–924. [Google Scholar] [CrossRef]
- Sanikhani, H.; Kisi, O.; Maroufpoor, E.; Yaseen, Z.M. Temperature-based modeling of reference evapotranspiration using several artificial intelligence models: Application of different modeling scenarios. Theor. Appl. Climatol. 2018. [Google Scholar] [CrossRef]
- Shiri, J. Improving the performance of the mass transfer-based reference evapotranspiration estimation approaches through a coupled wavelet-random forest methodology. J. Hydrol. 2018, 561, 737–750. [Google Scholar] [CrossRef]
- Tao, H.; Diop, L.; Bodian, A.; Djaman, K.; Ndiaye, P.M.; Yaseen, Z.M. Reference evapotranspiration prediction using hybridized fuzzy model with firefly algorithm: Regional case study in Burkina Faso. Agric. Water Manag. 2018, 208, 140–151. [Google Scholar] [CrossRef]
- Yin, Z.; Wen, X.; Feng, Q.; He, Z.; Zou, S.; Yang, L. Integrating genetic algorithm and support vector machine for modeling daily reference evapotranspiration in a semi-arid mountain area. Hydrol. Res. 2016, 48, 1177–1191. [Google Scholar] [CrossRef]
- Adamala, S. Temperature based generalized wavelet-neural network models to estimate evapotranspiration in India. Inf. Process. Agric. 2018, 5, 149–155. [Google Scholar] [CrossRef]
- Gavili, S.; Sanikhani, H.; Kisi, O.; Mahmoudi, M.H. Evaluation of several soft computing methods in monthly evapotranspiration modelling. Meteorol. Appl. 2017, 25, 128–138. [Google Scholar] [CrossRef]
- Karbasi, M. Forecasting of multi-step ahead reference evapotranspiration using wavelet- gaussian process regression model. Water Resour. Manag. 2017, 32, 1035–1052. [Google Scholar] [CrossRef]
- Farlow, S.J. The GMDH algorithm of Ivakhnenko. Am. Stat. 1981, 35, 210–215. [Google Scholar]
- Adnan, R.M.; Khosravinia, P.; Karimi, B.; Kisi, O. Prediction of hydraulics performance in drain envelopes using Kmeans based multivariate adaptive regression spline. Appl. Soft Comput. 2020, 100, 107008. [Google Scholar] [CrossRef]
- Nasir, V.; Nourian, S.; Avramidis, S.; Cool, J. Prediction of physical and mechanical properties of thermally modified wood based on color change evaluated by means of “group method of data handling”(GMDH) neural network. Holzforschung 2019, 73, 381–392. [Google Scholar] [CrossRef]
- Adnan, R.M.; Liang, Z.; Parmar, K.S.; Soni, K.; Kisi, O. Modeling monthly streamflow in mountainous basin by MARS, GMDH-NN and DENFIS using hydroclimatic data. Neural Comput. Appl. 2020. [Google Scholar] [CrossRef]
- Nkurlu, B.M.; Shen, C.; Asante-Okyere, S.; Mulashani, A.K.; Chungu, J.; Wang, L. Prediction of permeability using group method of data handling (GMDH) neural network from well log data. Energies 2020, 13, 551. [Google Scholar] [CrossRef]
- Najafzadeh, M.; Barani, G.-A.; Kermani, M.R.H. Estimation of pipeline scour due to waves by GMDH. J. Pipeline Syst. Eng. Pract. 2014, 5, 06014002. [Google Scholar] [CrossRef]
- Najafzadeh, M.; Barani, G.-A.; Hessami-Kermani, M.-R. Evaluation of GMDH networks for prediction of local scour depth at bridge abutments in coarse sediments with thinly armored beds. Ocean Eng. 2015, 104, 387–396. [Google Scholar] [CrossRef]
- Najafzadeh, M.; Zahiri, A. Neuro-fuzzy GMDH-based evolutionary algorithms to predict flow discharge in straight compound channels. J. Hydrol. Eng. 2015, 20, 4015035. [Google Scholar] [CrossRef]
- Shahabi, S.; Khanjani, M.-J.; Kermani, M.H. Hybrid wavelet-GMDH model to forecast significant wave height. Water Supply 2015, 16, 453–459. [Google Scholar] [CrossRef]
- Tsai, T.-M.; Yen, P.-H. GMDH algorithms applied to turbidity forecasting. Appl. Water Sci. 2016, 7, 1151–1160. [Google Scholar] [CrossRef]
- Parsaie, A.; Haghiabi, A.H. Improving modelling of discharge coefficient of triangular labyrinth lateral weirs using SVM, GMDH and MARS techniques. Irrig. Drain. 2017, 66, 636–654. [Google Scholar] [CrossRef]
- Alitaleshi, F.; Daghbandan, A. Using a multi-objective optimal design of GMDH type neural networks to evaluate the quality of treated water in a water treatment plant. Desalination Water Treat. 2019, 139, 123–132. [Google Scholar] [CrossRef]
- Daghbandan, A.; Khalatbari, S.; Abbasi, M.M. Applying GMDH-type neural network for modeling and prediction of turbidity and free residual aluminium in drinking water. Desalination Water Treat. 2019, 140, 118–131. [Google Scholar] [CrossRef]
- Da Silva Carvalho, R.L.; Delgado, A.R.S. Estimativas da evapotranspiração de referência do município de Ariquemes (RO) utilizando os métodos Penman-Monteith-FAO e Hargreaves-Samani. Rev. Bras. De Agric. Irrig. 2016, 10, 1038–1048. [Google Scholar]
- Friedman, J.H. Multivariate adaptive regression splines. Ann. Stat. 1991, 19, 1–67. [Google Scholar] [CrossRef]
- Quinlan, J.R. Learning with Continuous Classes. In Proceedings of the 5th Australian Joint Conference on Artificial Intelligence, Hobart, Tasmania, 16–18 November 1992; pp. 343–348. [Google Scholar]
- Adnan, R.M.; Liang, Z.; Trajkovic, S.; Zounemat-Kermani, M.; Li, B.; Kisi, O. Daily streamflow prediction using optimally pruned extreme learning machine. J. Hydrol. 2019, 577, 123981. [Google Scholar] [CrossRef]
- Kisi, O.; Parmar, K.S. Application of least square support vector machine and multivariate adaptive regression spline models in long term prediction of river water pollution. J. Hydrol. 2016. [Google Scholar] [CrossRef]
- Adnan, R.M.; Liang, Z.; El-Shafie, A.; Zounemat-Kermani, M.; Kisi, O. Prediction of suspended sediment load using data-driven models. Water 2019, 11, 2060. [Google Scholar] [CrossRef]
- Yin, Z.; Feng, Q.; Wen, X.; Deo, R.C.; Yang, L.; Si, J.; He, Z. Design and evaluation of SVR, MARS and M5Tree models for 1, 2 and 3-day lead time forecasting of river flow data in a semiarid mountainous catchment. Stoch. Environ. Res. Risk Assess. 2018, 32, 2457–2476. [Google Scholar] [CrossRef]
- Ghaemi, A.; Rezaie-Balf, M.; Adamowski, J.; Kisi, O.; Quilty, J. On the applicability of maximum overlap discrete wavelet transform integrated with MARS and M5 model tree for monthly pan evaporation prediction. Agric. For. Meteorol. 2019, 278, 107647. [Google Scholar] [CrossRef]
- Adnan, R.M.; Yuan, X.; Kisi, O.; Anam, R. Improving accuracy of river flow forecasting using LSSVR with gravitational search algorithm. Adv. Meteorol. 2017, 2017, 1–23. [Google Scholar] [CrossRef]
- Kisi, Ö.; Yildirim, G. Discussion of “Forecasting of reference evapotranspiration by artificial neural networks” by Slavisa Trajkovic, Branimir Todorovic, and Miomir Stankovic. J. Irrig. Drain. Eng. 2005, 131, 390–391. [Google Scholar] [CrossRef]
- Mehdizadeh, S.; Behmanesh, J.; Khalili, K. Using MARS, SVM, GEP and empirical equations for estimation of monthly mean reference evapotranspiration. Comput. Electron. Agric. 2017, 139, 103–114. [Google Scholar] [CrossRef]
- Kisi, O. Modeling reference evapotranspiration using three different heuristic regression approaches. Agric. Water Manag. 2016, 169, 162–172. [Google Scholar] [CrossRef]
- Keshtegar, B.; Mert, C.; Kisi, O. Comparison of four heuristic regression techniques in solar radiation modeling: Kriging method vs RSM, MARS and M5 model tree. Renew. Sustain. Energy Rev. 2018, 81, 330–341. [Google Scholar] [CrossRef]
- Keshtegar, B.; Kisi, O. RM5Tree: Radial basis M5 model tree for accurate structural reliability analysis. Reliab. Eng. Syst. Saf. 2018, 180, 49–61. [Google Scholar] [CrossRef]
- Kisi, O.; Kilic, Y. An investigation on generalization ability of artificial neural networks and M5 model tree in modeling reference evapotranspiration. Theor. Appl. Climatol. 2015, 126, 413–425. [Google Scholar] [CrossRef]
- Rahimikhoob, A. Comparison between M5 model tree and neural networks for estimating reference evapotranspiration in an arid environment. Water Resour. Manag. 2014, 28, 657–669. [Google Scholar] [CrossRef]
- Amanifard, N.; Nariman-Zadeh, N.; Farahani, M.H.; Khalkhali, A. Modelling of multiple short-length-scale stall cells in an axial compressor using evolved GMDH neural networks. Energy Convers. Manag. 2008, 49, 2588–2594. [Google Scholar] [CrossRef]
- Ivakhnenko, A.G. Polynomial theory of complex systems. IEEE Trans. Syst. ManCybern. 1971, SMC-1, 364–378. [Google Scholar] [CrossRef]
- Ivakhnenko, A.G.; Ivakhnenko, G.A. Problems of further development of the group method of data handling algorithms. Part I. Pattern Recognit. Image Anal. C/C Raspoznavaniye Obraz. I Anal. Izobr. 2000, 10, 187–194. [Google Scholar]
- Adnan, R.M.; Liang, Z.; Heddam, S.; Zounemat-Kermani, M.; Kisi, O.; Li, B. Least square support vector machine and multivariate adaptive regression splines for streamflow prediction in mountainous basin using hydro-meteorological data as inputs. J. Hydrol. 2020, 586, 124371. [Google Scholar] [CrossRef]
- Roy, S.S.; Roy, R.; Balas, V.E. Estimating heating load in buildings using multivariate adaptive regression splines, extreme learning machine, a hybrid model of MARS and ELM. Renew. Sustain. Energy Rev. 2018, 82, 4256–4268. [Google Scholar] [CrossRef]
- García Nieto, P.J.; García-Gonzalo, E.; Álvarez Antón, J.C.; Suárez, V.M.G.; Bayón, R.M.; Martín, F.M. A comparison of several machine learning techniques for the centerline segregation prediction in continuous cast steel slabs and evaluation of its performance. J. Comput. Appl. Math. 2018, 330, 877–895. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Rahmati, O. Prediction of the landslide susceptibility: Which algorithm, which precision? CATENA 2018, 162, 177–192. [Google Scholar] [CrossRef]
- Kuter, S.; Akyurek, Z.; Weber, G.-W. Retrieval of fractional snow covered area from MODIS data by multivariate adaptive regression splines. Remote Sens. Environ. 2018, 205, 236–252. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, R.; Goh, A.T.C. Multivariate adaptive regression splines approach to estimate lateral wall deflection profiles caused by braced excavations in clays. Geotech. Geol. Eng. 2017. [Google Scholar] [CrossRef]
- Jekabsons, G. ARESLab: Adaptive Regression Splines Toolbox for Matlab/Octave Ver. 1.13.0; Riga Technical University: Riga, Latvia, 2016. [Google Scholar]
- Afsarian, F.; Saber, A.; Pourzangbar, A.; Olabi, A.G.; Khanmohammadi, M.A. Analysis of recycled aggregates effect on energy conservation using M5′ model tree algorithm. Energy 2018, 156, 264–277. [Google Scholar] [CrossRef]
- García Nieto, P.J.; García-Gonzalo, E.; Sánchez, A.B.; Miranda, A.A.R. Air quality modeling using the PSO-SVM-based approach, MLP neural network, and M5 model tree in the metropolitan area of oviedo (Northern Spain). Environ. Modeling Assess. 2017, 23, 229–247. [Google Scholar] [CrossRef]
- Avval, Y.J.; Derakhshani, A. New formulas for predicting liquefaction-induced lateral spreading: Model tree approach. Bull. Eng. Geol. Environ. 2018, 78, 3649–3661. [Google Scholar] [CrossRef]
- Deo, R.C.; Downs, N.; Parisi, A.V.; Adamowski, J.F.; Quilty, J.M. Very short-term reactive forecasting of the solar ultraviolet index using an extreme learning machine integrated with the solar zenith angle. Environ. Res. 2017, 155, 141–166. [Google Scholar] [CrossRef]
- Pham, H.T.; Marshall, L.; Johnson, F.; Sharma, A. Deriving daily water levels from satellite altimetry and land surface temperature for sparsely gauged catchments: A case study for the Mekong River. Remote Sens. Environ. 2018, 212, 31–46. [Google Scholar] [CrossRef]
- Lin, L.; Wang, Q.; Sadek, A.W. A combined M5P tree and hazard-based duration model for predicting urban freeway traffic accident durations. Accid. Anal. Prev. 2016, 91, 114–126. [Google Scholar] [CrossRef] [PubMed]
- Singh, G.; Sachdeva, S.N.; Pal, M. M5 model tree based predictive modeling of road accidents on non-urban sections of highways in India. Accid. Anal. Prev. 2016, 96, 108–117. [Google Scholar] [CrossRef] [PubMed]
- Jekabsons, G. M5PrimeLab: M5′Regression Tree and Model Tree Ensemble Toolbox for Matlab/Octave Ver. 1.7.0.; Institute of Applied Computer Systems Riga Technical University: Riga, Latvia, 2016; Available online: http://www.cs.rtu.lv/jekabsons/Files/M5PrimeLab.pdf (accessed on 20 December 2019).
- Stephens, J.C.; Stewart, E.H. A comparison of procedures for computing evaporation and evapotranspiration. Publication 1963, 62, 123–133. [Google Scholar]
- Hargreaves, G.H.; Samani, Z.A. Estimating potential evapotranspiration. J. Irrig. Drain. Div. 1982, 108, 225–230. [Google Scholar]
- Hargreaves, G.H.; Samani, Z.A. Reference crop evapotranspiration from temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Tiyasha, T.; Tung, M.; Yaseen, Z.M. A survey on river water quality modelling using artificial intelligence models: 2000–2020. J. Hydrol. 2020, 585, 124670. [Google Scholar] [CrossRef]
- Adnan, R.M.; Yuan, X.; Kisi, O.; Yuan, Y.; Tayyab, M.; Lei, X. Application of soft computing models in streamflow forecasting. In Proceedings of the Institution of Civil Engineers-Water Management; Thomas Telford Ltd.: London, UK, 2019; Volume 172, No. 3; pp. 123–134. [Google Scholar]
- Bhagat, S.K.; Tung, T.M.; Yaseen, Z.M. Development of artificial intelligence for modeling wastewater heavy metal removal: State of the art, application assessment and possible future research. J. Clean. Prod. 2019, 250, 119473. [Google Scholar] [CrossRef]










| Station | Variable | xmin | xmax | xmean | Sx | Csx | Correlation with ET0 |
|---|---|---|---|---|---|---|---|
| Adana | Tmin (°C) | −3.4 | 23.4 | 9.33 | 7.70 | 0.08 | 0.828 |
| Tmax (°C) | 17.0 | 44.0 | 31.3 | 7.02 | −0.41 | 0.850 | |
| Ra (MJ/m2) | 15.5 | 41.7 | 29.4 | 9.35 | −0.14 | 0.920 | |
| ET0 (mm) | 0.57 | 6.52 | 3.32 | 1.52 | 0.04 | 1.000 | |
| Antakya | Tmin (°C) | −4.6 | 24.8 | 9.18 | 8.16 | 0.22 | 0.860 |
| Tmax (°C) | 14.4 | 42.6 | 28.8 | 7.64 | −0.32 | 0.878 | |
| Ra (MJ/m2) | 16.0 | 41.6 | 29.5 | 9.16 | −0.11 | 0.926 | |
| ET0 (mm) | 0.28 | 7.20 | 3.39 | 1.86 | 0.06 | 1.000 |
| Model | Input | Training | Test | ||||
|---|---|---|---|---|---|---|---|
| RMSE (mm) | MAE (mm) | NSE | RMSE (mm) | MAE (mm) | NSE | ||
| 50% training and 50% test | |||||||
| MARS1 | Tmin, Tmax, Ra | 0.454 | 0.363 | 0.908 | 0.467 | 0.359 | 0.907 |
| MARS2 | Tmin, Tmax, Ra, α | 0.461 | 0.356 | 0.905 | 0.466 | 0.357 | 0.907 |
| M5Tree1 | Tmin, Tmax, Ra | 0.408 | 0.301 | 0.926 | 0.518 | 0.406 | 0.885 |
| M5Tree2 | Tmin, Tmax, Ra, α | 0.408 | 0.301 | 0.926 | 0.518 | 0.406 | 0.885 |
| HS | Tmin, Tmax, Ra | 2.021 | 1.777 | −0.82 | 2.006 | 1.782 | −0.72 |
| CHS | Tmin, Tmax, Ra | 0.523 | 0.407 | 0.878 | 0.510 | 0.383 | 0.889 |
| SS | Tmin, Tmax, Ra | 0.501 | 0.390 | 0.888 | 0.463 | 0.355 | 0.909 |
| GMDHNN1 | Tmin, Tmax, Ra | 0.448 | 0.353 | 0.898 | 0.456 | 0.347 | 0.895 |
| GMDHNN2 | Tmin, Tmax, Ra, α | 0.443 | 0.347 | 0.901 | 0.453 | 0.343 | 0.898 |
| 60% training and 40% test | |||||||
| MARS1 | Tmin, Tmax, Ra | 0.435 | 0.344 | 0.916 | 0.510 | 0.389 | 0.889 |
| MARS2 | Tmin, Tmax, Ra, α | 0.447 | 0.347 | 0.912 | 0.492 | 0.376 | 0.898 |
| M5Tree1 | Tmin, Tmax, Ra | 0.402 | 0.288 | 0.929 | 0.529 | 0.406 | 0.881 |
| M5Tree2 | Tmin, Tmax, Ra, α | 0.402 | 0.288 | 0.929 | 0.529 | 0.406 | 0.881 |
| HS | Tmin, Tmax, Ra | 2.048 | 1.809 | −0.86 | 1.960 | 1.734 | −0.63 |
| CHS | Tmin, Tmax, Ra | 0.509 | 0.396 | 0.885 | 0.527 | 0.395 | 0.882 |
| SS | Tmin, Tmax, Ra | 0.482 | 0.376 | 0.897 | 0.482 | 0.368 | 0.901 |
| GMDHNN1 | Tmin, Tmax, Ra | 0.428 | 0.331 | 0.909 | 0.480 | 0.368 | 0.902 |
| GMDHNN2 | Tmin, Tmax, Ra, α | 0.424 | 0.327 | 0.910 | 0.478 | 0.366 | 0.903 |
| 75% training and 25% test | |||||||
| MARS1 | Tmin, Tmax, Ra | 0.438 | 0.339 | 0.916 | 0.516 | 0.408 | 0.884 |
| MARS2 | Tmin, Tmax, Ra, α | 0.437 | 0.336 | 0.917 | 0.522 | 0.405 | 0.882 |
| M5Tree1 | Tmin, Tmax, Ra | 0.385 | 0.279 | 0.935 | 0.550 | 0.424 | 0.869 |
| M5Tree2 | Tmin, Tmax, Ra, α | 0.385 | 0.279 | 0.935 | 0.550 | 0.424 | 0.869 |
| HS | Tmin, Tmax, Ra | 2.053 | 1.821 | −0.841 | 1.894 | 1.659 | −0.556 |
| CHS | Tmin, Tmax, Ra | 0.504 | 0.388 | 0.889 | 0.552 | 0.414 | 0.868 |
| SS | Tmin, Tmax, Ra | 0.479 | 0.370 | 0.900 | 0.491 | 0.382 | 0.896 |
| GMDHNN1 | Tmin, Tmax, Ra | 0.421 | 0.322 | 0.914 | 0.497 | 0.385 | 0.881 |
| GMDHNN2 | Tmin, Tmax, Ra, α | 0.420 | 0.320 | 0.915 | 0.495 | 0.384 | 0.883 |
| Average | |||||||
| MARS1 | Tmin, Tmax, Ra | 0.442 | 0.349 | 0.913 | 0.498 | 0.385 | 0.893 |
| MARS2 | Tmin, Tmax, Ra, α | 0.448 | 0.346 | 0.911 | 0.493 | 0.379 | 0.896 |
| M5Tree1 | Tmin, Tmax, Ra | 0.398 | 0.289 | 0.930 | 0.532 | 0.412 | 0.878 |
| M5Tree2 | Tmin, Tmax, Ra, α | 0.398 | 0.289 | 0.930 | 0.532 | 0.412 | 0.878 |
| HS | Tmin, Tmax, Ra | 2.041 | 1.802 | −0.840 | 1.953 | 1.725 | −0.635 |
| CHS | Tmin, Tmax, Ra | 0.512 | 0.397 | 0.884 | 0.530 | 0.397 | 0.880 |
| SS | Tmin, Tmax, Ra | 0.487 | 0.379 | 0.895 | 0.479 | 0.368 | 0.902 |
| GMDHNN1 | Tmin, Tmax, Ra | 0.432 | 0.335 | 0.907 | 0.478 | 0.367 | 0.893 |
| GMDHNN2 | Tmin, Tmax, Ra, α | 0.429 | 0.331 | 0.909 | 0.475 | 0.364 | 0.895 |
| Model | Input | Training | Test | ||||
|---|---|---|---|---|---|---|---|
| RMSE (mm) | MAE (mm) | NSE | RMSE (mm) | MAE (mm) | NSE | ||
| 50% training and 50% test | |||||||
| MARS1 | Tmin, Tmax, Ra | 0.383 | 0.290 | 0.959 | 0.635 | 0.521 | 0.872 |
| MARS2 | Tmin, Tmax, Ra, α | 0.369 | 0.286 | 0.962 | 0.566 | 0.460 | 0.963 |
| M5Tree1 | Tmin, Tmax, Ra | 0.341 | 0.257 | 0.968 | 0.639 | 0.527 | 0.870 |
| M5Tree2 | Tmin, Tmax, Ra, α | 0.335 | 0.256 | 0.969 | 0.598 | 0.489 | 0.886 |
| HS | Tmin, Tmax, Ra | 1.513 | 1.316 | 0.367 | 1.781 | 1.613 | 0.065 |
| CHS | Tmin, Tmax, Ra | 0.641 | 0.456 | 0.886 | 0.718 | 0.603 | 0.848 |
| SS | Tmin, Tmax, Ra | 0.438 | 0.339 | 0.947 | 0.678 | 0.572 | 0.864 |
| GMDHNN1 | Tmin, Tmax, Ra | 0.350 | 0.268 | 0.963 | 0.552 | 0.436 | 0.912 |
| GMDHNN2 | Tmin, Tmax, Ra, α | 0.345 | 0.263 | 0.965 | 0.550 | 0.433 | 0.913 |
| 60% training and 40% test | |||||||
| MARS1 | Tmin, Tmax, Ra | 0.464 | 0.359 | 0.938 | 0.468 | 0.370 | 0.933 |
| MARS2 | Tmin, Tmax, Ra, α | 0.454 | 0.345 | 0.941 | 0.453 | 0.373 | 0.966 |
| M5Tree1 | Tmin, Tmax, Ra | 0.406 | 0.305 | 0.953 | 0.478 | 0.380 | 0.930 |
| M5Tree2 | Tmin, Tmax, Ra, α | 0.439 | 0.326 | 0.945 | 0.441 | 0.348 | 0.941 |
| HS | Tmin, Tmax, Ra | 1.612 | 1.402 | 0.256 | 1.722 | 1.569 | 0.127 |
| CHS | Tmin, Tmax, Ra | 0.676 | 0.487 | 0.869 | 0.647 | 0.538 | 0.877 |
| SS | Tmin, Tmax, Ra | 0.526 | 0.400 | 0.921 | 0.510 | 0.436 | 0.923 |
| GMDHNN1 | Tmin, Tmax, Ra | 0.441 | 0.339 | 0.939 | 0.426 | 0.345 | 0.943 |
| GMDHNN2 | Tmin, Tmax, Ra, α | 0.430 | 0.335 | 0.941 | 0.424 | 0.342 | 0.945 |
| 75% training and 25% test | |||||||
| MARS1 | Tmin, Tmax, Ra | 0.455 | 0.351 | 0.941 | 0.368 | 0.276 | 0.957 |
| MARS2 | Tmin, Tmax, Ra, α | 0.443 | 0.349 | 0.944 | 0.335 | 0.269 | 0.971 |
| M5Tree1 | Tmin, Tmax, Ra | 0.390 | 0.291 | 0.957 | 0.373 | 0.304 | 0.963 |
| M5Tree2 | Tmin, Tmax, Ra, α | 0.406 | 0.299 | 0.953 | 0.367 | 0.292 | 0.958 |
| HS | Tmin, Tmax, Ra | 1.663 | 1.463 | 0.211 | 1.641 | 1.489 | 0.168 |
| CHS | Tmin, Tmax, Ra | 0.677 | 0.497 | 0.869 | 0.601 | 0.481 | 0.888 |
| SS | Tmin, Tmax, Ra | 0.526 | 0.416 | 0.621 | 0.410 | 0.327 | 0.648 |
| GMDHNN1 | Tmin, Tmax, Ra | 0.439 | 0.347 | 0.940 | 0.318 | 0.248 | 0.968 |
| GMDHNN2 | Tmin, Tmax, Ra, α | 0.426 | 0.337 | 0.944 | 0.304 | 0.247 | 0.969 |
| Average | |||||||
| MARS1 | Tmin, Tmax, Ra | 0.434 | 0.333 | 0.946 | 0.490 | 0.389 | 0.921 |
| MARS2 | Tmin, Tmax, Ra, α | 0.422 | 0.327 | 0.949 | 0.451 | 0.367 | 0.967 |
| M5Tree1 | Tmin, Tmax, Ra | 0.379 | 0.284 | 0.959 | 0.497 | 0.404 | 0.921 |
| M5Tree2 | Tmin, Tmax, Ra, α | 0.393 | 0.294 | 0.956 | 0.469 | 0.376 | 0.928 |
| HS | Tmin, Tmax, Ra | 1.596 | 1.394 | 0.278 | 1.715 | 1.557 | 0.120 |
| CHS | Tmin, Tmax, Ra | 0.665 | 0.480 | 0.875 | 0.655 | 0.541 | 0.871 |
| SS | Tmin, Tmax, Ra | 0.497 | 0.385 | 0.830 | 0.533 | 0.445 | 0.812 |
| GMDHNN1 | Tmin, Tmax, Ra | 0.410 | 0.318 | 0.947 | 0.432 | 0.343 | 0.941 |
| GMDHNN2 | Tmin, Tmax, Ra, α | 0.401 | 0.312 | 0.950 | 0.426 | 0.341 | 0.942 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adnan, R.M.; Heddam, S.; Yaseen, Z.M.; Shahid, S.; Kisi, O.; Li, B. Prediction of Potential Evapotranspiration Using Temperature-Based Heuristic Approaches. Sustainability 2021, 13, 297. https://doi.org/10.3390/su13010297
Adnan RM, Heddam S, Yaseen ZM, Shahid S, Kisi O, Li B. Prediction of Potential Evapotranspiration Using Temperature-Based Heuristic Approaches. Sustainability. 2021; 13(1):297. https://doi.org/10.3390/su13010297
Chicago/Turabian StyleAdnan, Rana Muhammad, Salim Heddam, Zaher Mundher Yaseen, Shamsuddin Shahid, Ozgur Kisi, and Binquan Li. 2021. "Prediction of Potential Evapotranspiration Using Temperature-Based Heuristic Approaches" Sustainability 13, no. 1: 297. https://doi.org/10.3390/su13010297
APA StyleAdnan, R. M., Heddam, S., Yaseen, Z. M., Shahid, S., Kisi, O., & Li, B. (2021). Prediction of Potential Evapotranspiration Using Temperature-Based Heuristic Approaches. Sustainability, 13(1), 297. https://doi.org/10.3390/su13010297










