An Adapted Version of the Water Wave Optimization Algorithm for the Capacitated Vehicle Routing Problem with Time Windows with Application to a Real Case Using Probe Data
Abstract
1. Introduction
2. Background: The Water Wave Optimization Algorithm
- Step 1, Initialization. A population of N solutions (i.e., waves) for the problem under examination is randomly generated; each wave has an initial h set at .
- Step 2. The fitness value f(x) is determined and the wave having the best value is identified.
- Step 3, Propagation. Propagation is the operation by which the solutions of the problem change at each iteration of the algorithm. It is therefore carried out on all waves of the population; anytime a wave is propagated, it gets a new position, which is obtained by applying the following formula:where represents the original wave, is a uniformly distributed random number in the range [−1;1], (1 d ) is a generic dimension of the problem, is the length of the d dimension of the search space. The fitness value of the new solution is calculated and then compared to the corresponding fitness value before the propagation; to choose whether to maintain or replace it with , the following set of inequalities is applied (for a maximization problem):The wavelength is thus updated according to the following formula:where and are respectively the maximum and the minimum fitness values among the current population, is the wavelength reduction coefficient and is a very small positive number, to avoid division-by-zero.The propagation is repeated once for each iteration of the algorithm.
- Step 4, Refraction. After some iterations, it is possible that some waves reach . This means that, despite their propagation for times, these waves were not able to identify an effective solution for the problem under examination; the logical consequence would be their removal from the set of problem solutions. Refraction is performed exactly on those waves that are expected to disappear, and consists in identifying a new wave, determined as a Gaussian random number with mean and standard deviation :where is the best solution found so far; hence, the aim of refraction is to replace the ineffective solution of the problem with a good new one. The height of the new wave is also restored to , as previously done in the propagation phase when better solutions were obtained, and the wavelength is updated as follows:
- Step 5, Breaking. Breaking is a procedure that mimics the real behavior of waves when moving to a position where the water depth is low, i.e., their breaking into a train of solitary waves. This procedure is only applied to those waves that returned the best solutions to the problem in question, i.e., on waves that became after propagation. By breaking, a local search is performed around this best solution by taking k random dimensions (with 1 ≤ k ≤ , being a predefined number) and generating a solitary wave for each dimension d, as follows:where is the breaking coefficient.If there are no solitary waves better than , is maintained; otherwise it is replaced by the fittest one among the solitary waves.
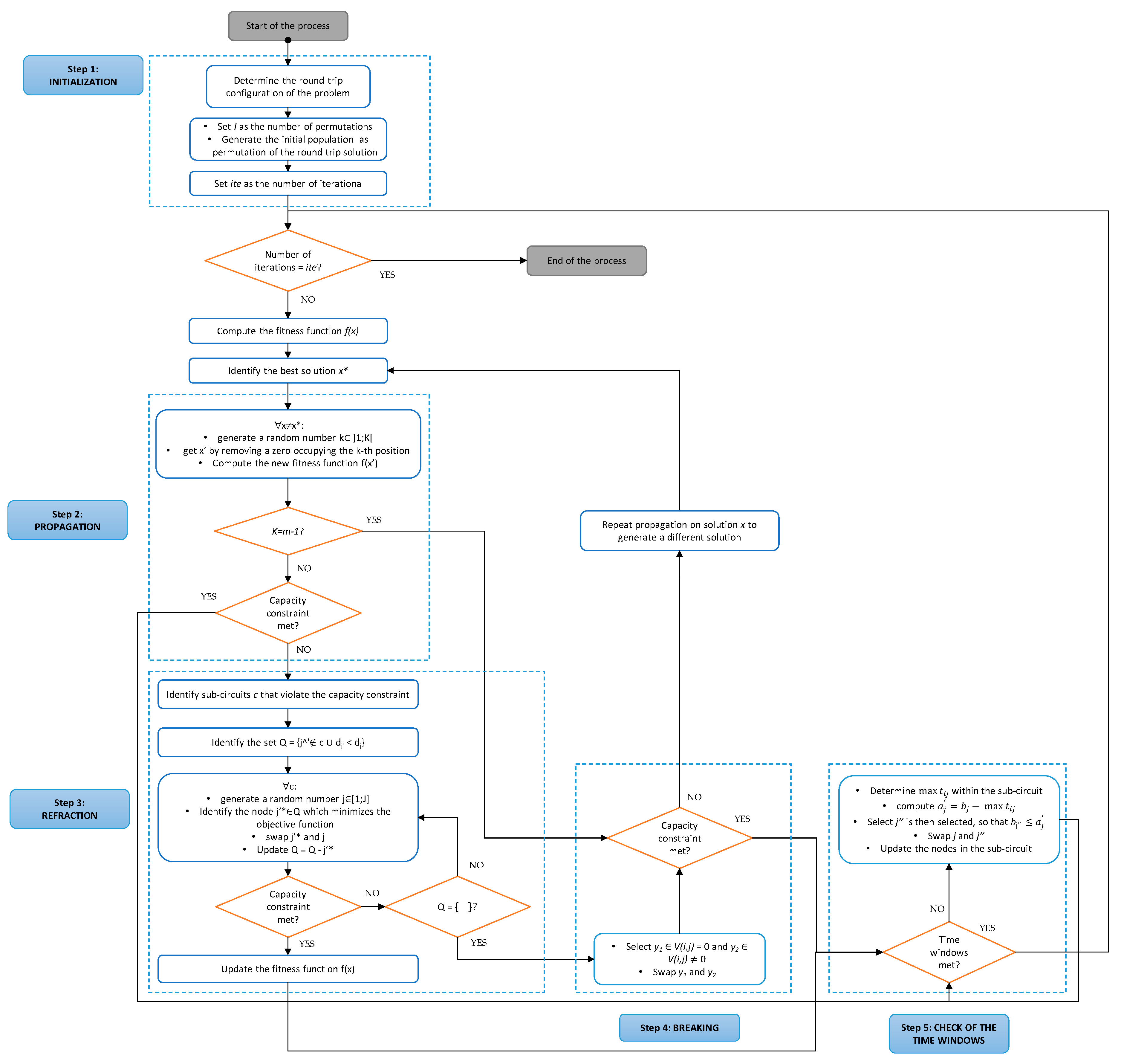
3. The Adapted Water Wave Optimization to the CVRPTW
- the number of solutions corresponds to the number of permutations;
- all solutions have the same size (2N+1) and the same value of the objective function, i.e., the same fitness value (the journey time for each route is steady, as each node is always included between two zeros);
- all solutions are possible and realistic.
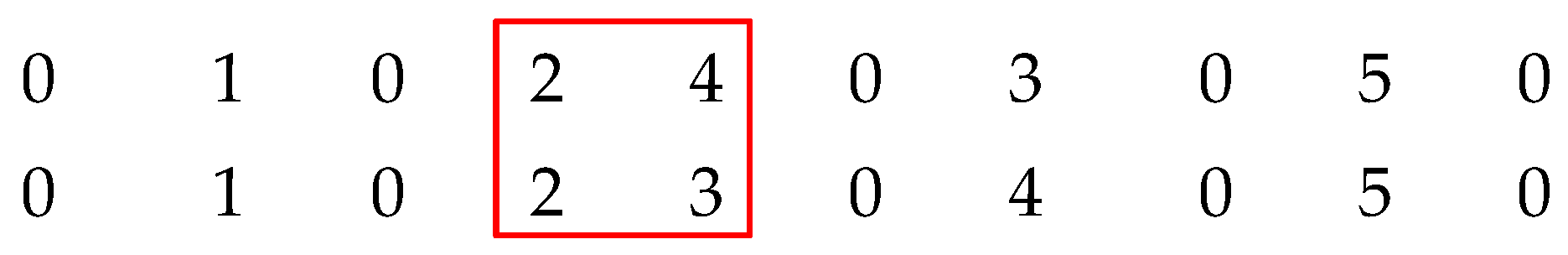 |
4. Case Study
5. Conclusions
- for minimizing cost instead of travelling time;
- for modelling and solving a simple CVRP without time windows, by removing step 5 (i.e., the check on time constraints) from the algorithm structure.
Author Contributions
Funding
Conflicts of Interest
References
- Singh, R.K.; Murty, H.R.; Gupta, S.K.; Dikshit, A.K. An overview of sustainability assessment methodologies. Ecol. Indic. 2012, 15, 281–299. [Google Scholar] [CrossRef]
- Litman, T.; Burwell, D. Issues in sustainable transportation. Int. J. Glob. Environ. Issues 2006, 6, 331–347. [Google Scholar] [CrossRef]
- Banister, D.; Anderton, K.; Bonilla, D.; Givoni, M.; Schwanen, T. Transportation and the. Environment. Annu. Rev. Environ. Resour. 2011, 36, 247–270. [Google Scholar] [CrossRef]
- Baldacci, R.; Mingozzi, A.; Roberti, R. Recent exact algorithms for solving the vehicle routing problem under capacity and time window constraints. Eur. J. Oper. Res. 2012, 218, 1–6. [Google Scholar] [CrossRef]
- Dantzig, G.B.; Ramser, J.H. The Truck Dispatching Problem. Manag. Sci. 1959, 6, 80–91. [Google Scholar] [CrossRef]
- Abbatecola, L.; Fanti, M.P.; Ukovich, W. A Review of New Approaches for Dynamic Vehicle Routing Problem. In Proceedings of the 2016 IEEE International Conference on Automation Science and Engineering (CASE), Fort Worth, TX, USA, 21–25 August 2016. [Google Scholar]
- Drexl, M. Rich Vehicle Routing in Theory and Practice. In Fraunhofer Centre for Applied Research on Supply Chain Services; Technical Report LM-2011-04; Mainz, Johannes Gutenberg University and SCS: Nuremberg, Germany, 2011. [Google Scholar]
- Solomon, M.M. Algorithms for the vehicle routing and scheduling problem with time window constraints. Oper. Res. 1987, 35, 234–265. [Google Scholar] [CrossRef]
- Kallehauge, B. Formulations and exact algorithms for the vehicle routing problem with time windows. Comput. Oper. Res. 2008, 35, 2307–2330. [Google Scholar] [CrossRef]
- El-Sherbeny, N.A. Vehicle routing with time windows: An overview of exact, heuristic and metaheuristic methods. J. King Saud Univ. 2010, 22, 123–131. [Google Scholar] [CrossRef]
- Morganti, E.; Seidel, S.; Blanquart, C.; Dablanc, L.; Lenz, B. The impact of e-commerce on final deliveries: Alternative parcel delivery services in France and Germany. Transp. Res. Procedia 2014, 4, 178–190. [Google Scholar] [CrossRef]
- dos Santos Coelho, L.; Maidl, G.; Pierezan, J.; Mariani, V.C.; da Luz MV, F.; Leite, J.V. Ant Lion Approach Based on Lozi Map for Multiobjective Transformer Design Optimization. In Proceedings of the International Symposium on Power Electronics, Electrical Drives, Automation and Motion, Amalfi, Italy, 20–22 June 2018. [Google Scholar]
- Glover, F. Future paths for integer programming and links to artificial intelligence. Comput. Oper. Res. 1986, 13, 533–549. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Dorigo, M.; Maniezzo, V.; Colorni, A. Ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man Cybern. Part B 1996, 26, 29–41. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.-S. Nature-Inspired Metaheuristic Algorithms; University of Cambridge, UNIVER PRESS: Cambridge, UK, 2010. [Google Scholar]
- Arockia Panimalar, S. Nature Inspired Metaheuristic Algorithms. Int. Res. J. Eng. Technol. 2017, 4, 306–309. [Google Scholar]
- Kozan, E. and Preston, P. Genetic algorithms to schedule container transfers at multimodal terminals. Int. Trans. Oper. Res. 1999, 6, 311–329. [Google Scholar] [CrossRef]
- Zheng, Y.-J. Water wave optimization: A new nature-inspired metaheuristic. Comput. Oper. Res. 2015, 55, 1–11. [Google Scholar] [CrossRef]
- Wu, X.-B.; Liao, J.; Wang, Z.-C. Water Wave Optimization for the Traveling Salesman Problem. In Intelligent Computing Theories and Methodologies; Huang, D.S., Bevilacqua, V., Premaratne, P., Eds.; ICIC: Mumbai, India, 2015; Volume 9225. [Google Scholar]
- Bottani, E.; Rinaldi, M.; Montanari, R.; Murino, T.; Centobelli, P. An adapted water wave optimization for routing order pickers in manual warehouses. In Proceedings of the XXI Summer School “Francesco Turco”—Industrial Systems Engineering, Palermo, Italy, 13–15 September 2016. [Google Scholar]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Layeb, A.; Ammi, M. A GRASP algorithm based on new randomized heuristic for vehicle routing problem. J. Comput. Inf. Technol. 2013, 1, 35–46. [Google Scholar] [CrossRef]
- Li, Y.H.; Mao, H.J.; Qin, Y.M. Vehicle Routing Problem with Multiple Time Windows and Batch Splitting Based on Inferior First Bidirectional Search Algorithm. J. Phys.:Conf. Ser. 2019, 1314, 012116. [Google Scholar] [CrossRef]
- Liu, J.; Liu, D.; Liu, M.; He, Y. An improved multiple ant colony system for the collection vehicle routing problems with intermediate facilities. In Proceedings of the 8th World Congress on Intelligent Control and Automation, Jinan, China, 7–9 July 2010. [Google Scholar]
- Soltanian, A.; Derakhshan, F.; Soleimanpour-Moghadam, M. MWWO: Modified Water Wave Optimization. In Proceedings of the 3rd Conference on Swarm Intelligence and Evolutionary Computation (CSIEC2018), Bam, Iran, 6–8 March 2018. [Google Scholar]
- Sathyanarayanan, S.; Suresh, J.; Jayakumar, S.K.V. A hybrid population seeding technique based genetic algorithm for stochastic multiple depot vehicle routing problem. In Proceedings of the International Conference of Computing and Communications Technologies, Liverpool, UK, 26–28 October 2015; pp. 119–127. [Google Scholar]
- Braekers, K.; Ramaekers, K.; Van Nieuwenhuyse, I. The vehicle routing problem: State of the art classification and review. Comput. Ind. Eng. 2016, 99, 300–313. [Google Scholar] [CrossRef]
| Symbol | Description | Symbol | Description |
|---|---|---|---|
| N | Number of customers (i.e., number of nodes) | J*’ | Node belonging to Q which minimizes |
| M | Number of vehicles | Demand of each customer, non-negative, integer | |
| Travel time from node to node , positive, integer | G | Demand vector | |
| Travel time from node to node of the same k-th route traveled by one specific vehicle | c | Node set constituting a sub-circuit | |
| I | Number permutations | Load capacity of each vehicle, non-negative, integer | |
| V(i,j) | Initial matrix (each line represents a vector, i.e., a solution) | J | Nodes belonging to c for which the capacity constraint is not observed |
| ite | Number of iterations | j | Random number [1; J] corresponding to the node subjected to shift |
| K | Number of zeros in each string | Demand associated to node j | |
| k | Random number [1; K] | Q | Set of elements not belonging to c, for which |
| j* | Position of the k-th zero within the i-th string | j’ | Nodes belonging to Q |
| Time window. |
| Scenario Characteristics | |
|---|---|
| Number of stops on the route | Known (deterministic) |
| Customer service demand quantity | Deterministic |
| Onsite services/waiting times | Deterministic |
| Time windows structure | Strict time windows |
| Node/Arc covering constraints | Precedence + Subset covering constraints |
| Physical Characteristics | |
|---|---|
| Transportation network design | Direct network |
| Location of addresses (customers) | Customers on nodes |
| Number of points of origin | Single origin |
| Number of points of loading/unloading facilities (depot) | Multiple depots |
| Time window type | Restriction on customers + vehicle |
| Number of vehicles | Limited number of vehicles |
| Capacity consideration | Capacitated vehicles |
| Vehicle homogeneity (Capacity) | Similar vehicles |
| Travel Time | Deterministic |
| Objective | Travel time + distance + vehicle + lateness dependent |
| Vehicle 1 | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 (9) | 49 (8) | 32 (7) | 22 (9) | 51 (2) | 53 (1) | 10 (9) | 6 (9) | 60 (3) | 37 (1) | 39 (5) | 40 (5) | 65 (3) | 20 (2) | 29 (6) | 24 (4) |
| 21 (8) | 63 (4) | 1 (8) | 25 (4) | 64 (4) | 62 (3) | 3 (9) | 27 (1) | 17 (9) | 16 (1) | 13 (3) | 46 (7) | 26 (2) | 56 (6) | 0 | |
| Vehicle 2 | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 (8) | 30 (3) | 43 (4) | 66 (7) | 61 (5) | 34 (5) | 55 (5) | 45 (3) | 58 (3) | 18 (5) | 2 (5) | 4 (7) | 31 (3) | 15 (7) | 57 (10) | 33 (6) |
| 54 (11) | 35 (3) | 42 (9) | 28 (11) | 48 (3) | 67 (5) | 7 (7) | 36 (1) | 23 (4) | 5 (7) | 8 (5) | 52 (3) | 38 (10) | 50 (5) | 47 (5) | 11 (5) |
| 59 (6) | 12 (4) | 14 (7) | 9 (3) | 19 (8) | 41 (9) | 44 (9) | 0 | ||||||||
| Vehicle 1 | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 (3) | 12 (1) | 15 (1) | 19 (1) | 23 (1) | 24 (1) | 36 (2) | 2 (1) | 9 (9) | 44 (10) | 32 (9) | 65 (9) | 57 (9) | 61 (5) | 58 (5) | 59 (6) |
| 64 (7) | 60 (6) | 55 (10) | 56 (8) | 62 (5) | 67 (7) | 66 (6) | 50 (6) | 63 (3) | 42 (4) | 34 (5) | 46 (6) | 39 (3) | 47 (4) | 48 (3) | 51 (1) |
| 52 (1) | 16 (1) | 20 (7) | 0 | ||||||||||||
| Vehicle 2 | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 (10) | 11 (12) | 4 (8) | 22 (5) | 28 (4) | 21 (10) | 25 (11) | 17 (12) | 10 (12) | 5 (9) | 7 (11) | 6 (12) | 8 (13) | 27 (12) | 29 (10) | 40 (9) |
| 13 (9) | 43 (5) | 31 (10) | 30 (10) | 38 (11) | 26 (12) | 53 (11) | 14 (8) | 37 (10) | 1 (11) | 41 (9) | 49 (10) | 33 (6) | 54 (5) | 35 (13) | 18 (13) |
| 3 (6) | 45 (10) | 0 | |||||||||||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tebaldi, L.; Murino, T.; Bottani, E. An Adapted Version of the Water Wave Optimization Algorithm for the Capacitated Vehicle Routing Problem with Time Windows with Application to a Real Case Using Probe Data. Sustainability 2020, 12, 3666. https://doi.org/10.3390/su12093666
Tebaldi L, Murino T, Bottani E. An Adapted Version of the Water Wave Optimization Algorithm for the Capacitated Vehicle Routing Problem with Time Windows with Application to a Real Case Using Probe Data. Sustainability. 2020; 12(9):3666. https://doi.org/10.3390/su12093666
Chicago/Turabian StyleTebaldi, Letizia, Teresa Murino, and Eleonora Bottani. 2020. "An Adapted Version of the Water Wave Optimization Algorithm for the Capacitated Vehicle Routing Problem with Time Windows with Application to a Real Case Using Probe Data" Sustainability 12, no. 9: 3666. https://doi.org/10.3390/su12093666
APA StyleTebaldi, L., Murino, T., & Bottani, E. (2020). An Adapted Version of the Water Wave Optimization Algorithm for the Capacitated Vehicle Routing Problem with Time Windows with Application to a Real Case Using Probe Data. Sustainability, 12(9), 3666. https://doi.org/10.3390/su12093666







