Abstract
Energy systems planning commonly involves the study of supply and demand of power, forecasting the trends of parameters established on economics and technical criteria of models. Numerous measures are needed for the fulfillment of energy system assessment and the investment plans. The higher energy prices which call for diversification of energy systems and managing the resolution of conflicts are the results of high energy demand for growing economies. Due to some challenging problems of fossil fuels, energy production and distribution from alternative sources are getting more attention. This study aimed to reveal the most proper energy systems in Saudi Arabia for investment. Hence, integrated fuzzy AHP (Analytic Hierarchy Process), fuzzy VIKOR (Vlse Kriterijumska Optimizacija Kompromisno Resenje) and TOPSIS (Technique for Order Preferences by Similarity to Idle Solution) methodologies were employed to determine the most eligible energy systems for investment. Eight alternative energy systems were assessed against nine criteria—power generation capacity, efficiency, storability, safety, air pollution, being depletable, net present value, enhanced local economic development, and government support. Data were collected using the Delphi method, a team of three decision-makers (DMs) was established in a heterogeneous manner with the addition of nine domain experts to carry out the analysis. The fuzzy AHP approach was used for clarifying the weight of criteria and fuzzy VIKOR and TOPSIS were utilized for ordering the alternative energy systems according to their investment priority. On the other hand, sensitivity analysis was carried out to determine the priority of investment for energy systems and comparison of them using the weight of group utility and fuzzy DEA (Data Envelopment Analysis) approaches. The results and findings suggested that solar photovoltaic (PV) is the paramount renewable energy system for investment, according to both fuzzy VIKOR and fuzzy TOPSIS approaches. In this context our findings were compared with other works comprehensively.
1. Introduction
Energy generation, transmission, and distribution are important subjects due to rising energy consumption linked to the population and industrial growth [1]. Many people still do not have access to electricity, about 2.7 billion people are still using conventional energy sources [2] that have adverse effects on the environment, human health [3], global deforestation, and greenhouse gas emissions [4]. On the other hand, energy planning systems comprise conflicting issues that have moved from single and restricted goals to multiple and more complex objectives due to the presence of several parameters, benchmarks, investors, and shareholders. The world energy is currently 81% from fossil fuels, 5% from nuclear, and 14% from renewable energy sources. The nuclear sources are considered dangerous, the fossil fuels are counted consumable, significantly hazardous, and unsafe, mainly due to their irreversible environmental impact on human, animals, plants, and climate change [5]. Developing alternative energy sources to fossil fuels has several challenges. These alternative sources are mainly solar, wind power, biomass, nuclear, ocean waves, and hydroelectric power [6]. In the long-term, predicting the most beneficial energy alternatives is very important, many factors such as population, geographic restrictions, societal needs, and politics are involved in decision-making. More importantly, the investors usually have limited resources and cannot devote them all to alternative sources simultaneously. On the other hand, an alternative energy appropriate for one country may be not a good choice for another one. There are many other measures, such as political preferences, security, and costs, influencing the selection of alternative energy sources. Although several disadvantages of alternative energy sources are counted in the literature [7], such as negative effects on public health [7], diminishing water quality [8], and life-cycle global warming emissions [9], the advantages [10] still mitigate the downsides, and the renewable energy sources are inexhaustible, cheaper, and their production technologies are not harmful.
Saudi Arabia is still extensively dependent on fossil fuels, the energy consumption will jump from 40 GW to 120 GW per hour until 2028, which will accelerate global warming [11] and diminish the environmental systems [12]. The energy security problem, the rising energy prices, and the other important factors require sustainable development of power generation systems. The application of multi-criteria decision-making (MCDM) approaches [13] can prioritize the importance of the energy systems. On the other hand, the economic growth and social needs will increase the hydrocarbon consumption from 3.4 million BOE (barrels of oil equivalent) to 8.3 million BOE per day shortly. High energy demand necessitates intensive investments for protecting the environment, advancing the gas emission reduction technologies [8] to obtain clean and cheap energy sources and reduce the negative impacts caused by reliance on fossil fuels [14]. Therefore, reliability, suitability, sustainability, and diversification of energy sources are of great interest to many nations for determining the most appropriate energy sources for investment to meet challenging and unfavorable attributes that might include both quantitative and qualitative factors [15]. Several decision-makers (DMs) may be involved in the decision-making process for determining the attributes, sources, and the selection of the location and technologies. Both energy sources planning and technologies selection, are multi-criteria group decision-making (GDM) problems. Several people, such as the individuals, regional residents, politicians, managers, experts, government and civil organizations, could be involved in the decision-making process. Hence, numerous conflicting parameters must be considered and evaluated by DMs to reach a consensus for the selection of the best alternative energy sources. These conflicting parameters need to reach a consensus for accomplishing a common agreement between the decision-makers to select the best alternative energy systems. The agreement and/or consensus aims to reduce the discussions [16] and facilitate GDM faster for processing with minimum amendments [17] to develop energy strategies and investment opportunities for renewable energy sources using ELECTRE (ELimination Et Choix Traduisant la REalité) [18] and new consensus models with non-homogeneous experts [19].
In light of these complications, fuzzy set theory might be useful for undertaking challenging assessment and consensus problems of energy systems, when the linguistic variables and terms are employed for decision-making to solve the ambiguity, vagueness, and subjectivity of human judgments [20]. Although fuzzy AHP (Analytic Hierarchy Process) handles both measurable and qualitative multi-criteria GDM problems, it has the ability to handle DMs’ vague and imprecise judgments using soft computing techniques for clarification. Fuzzy AHP is employed mainly for pairwise comparisons of multi-criteria GDM problems. Pairwise comparison uses solicited input data obtained from DMs that offer maximum awareness for evaluating the consistency of DMs’ judgments. This background makes fuzzy AHP an ideal approach for investigating the renewable energy systems. Similarly, VIKOR (Vlse Kriterijumska Optimizacija Kompromisno Resenje) is the modest computational technique for solving multi-criteria GDM problems, coinciding the closeness to ideal and anti-ideal alternatives over conflicting aspects. A detailed comparison of fuzzy VIKOR with PROMETHEE (Preference Ranking Organization Method for Enrichment Evaluation), ELECTRE, and TOPSIS (Technique for Order Preferences by Similarity to Idle Solution) has been presented in many papers [21,22,23]. The GDM methods for applicability and adaptability using the ELECTRE approach for location planning and selection are presented in [18]. The aim of this study is to integrate fuzzy AHP, fuzzy VIKOR, and TOPSIS methodologies to determine the best alternative energy sources for future investment in Saudi Arabia.
Fuzzy AHP is used to rank the weights of the criteria, fuzzy VIKOR and fuzzy TOPSIS approaches are employed to select the best options of energy sources. This study will also consider and focus on the main conflicting criteria of the assessment and comparisons. Hence, the rest of paper is organized as follows. Section 2 describes the literature review for both energy systems investigation and MCDM approaches. Method and methodologies are given in Section 3, in this context, fuzzy AHP, fuzzy VIKOR, and fuzzy TOPSIS approaches are employed for determining criteria weights and analyzing the energy systems assessment. This section also shows the details of calculations. Section 4 presents the results and findings of the integrated fuzzy AHP, fuzzy VIKOR, and fuzzy TOPSIS methodologies for prioritizing the energy systems investments. Section 5 gives the sensitivity analysis for the energy systems. Finally, our conclusions are presented in Section 6.
2. Literature Review
Recently, the energy demand has increased, and the utilization of technologies for renewable energy has expanded significantly; thus, previous works have examined the role of these technologies in different perspectives of energy research problems, employing various MADM (multi attribute decision making) approaches. Renewable energy has become an integral component of sustainable economic development; hence several studies have been carried out to determine the investment strategies in renewable energy alternatives. For instance, the AHP method was used for solar energy [24] investigation and the selection of locations for thermal power plants [25] in India, solar farm sites determination in Turkey [26], biofuels and fossil fuels comparison [27], and wind observation station location selection [28] in different countries. On the other hand, many novel techniques and MADM approaches, such as ANP (Analytic Network Process), AHP, VIKOR, ELECTRE, and TOPSIS were developed to rank the alternative systems and to optimize the energy systems. The MADM approaches have been employed to reduce uncertainties in energy growth, wherever different investors are involved in the decision-making, considering a broad range of economic, social, technical, and environmental aspects [29]. The world primary energy need is increasing due to the rapid economic development [30]. Sustainability in energy resources and prioritizing the renewable energy system are therefore important mechanisms. In this context, Vishnupriyan and Manoharan [31] presented sustainability in limited energy resources by integrating a renewable energy system with a grid to meet energy demand using AHP and stochastic multi-attribute acceptability analysis. The decision-makers selected the important criteria using fuzzy AHP based type 2 fuzzy sets, and fuzzy multi attribute decision-making approaches for energy resources prioritization. Siksnelyte et al. [32] reviewed sustainable decision-making to solve energy problems and determine the contradictory effects using MADM approaches. In this perspective, Mardani et al. [29,32] carried out detailed analyses of MADM methods and applications in energy systems. They labeled MADM and fuzzy MADM approaches into the following groupings: AHP, VIKOR, TOPSIS, PROMETHEE, fuzzy sets, and system and ANP are mostly used for impact analysis, energy technology evaluation, and for the selection of the best place for energy generation. Krishankumar et al. [33] discussed the framework of ranking the alternatives utilizing the developed interval-valued probabilistic linguistic term set (IVPLTS)-based classical VIKOR approach. Alizadeh et al. [34] combined two models—Benefit, Opportunity, Cost, Risk, and ANP models—to determine the solar energy as the preferential renewable energy source for Iran. In decision-making, the DMs should not only consider the costs of energy systems, but also the energy systems’ efficiency and their environment protection abilities [35]. Therefore, DEA (Data Envelopment Analysis), TOPSIS, and COPRAS (Complex Proportional Assessment of alternatives) were employed to investigate the priority of energy systems investment and sensitivity analysis under different scenarios. Ilbahar et al. [36] reviewed the utilization and evaluation of renewable energy sources using MADM for several determinations, particularly energy policies and criteria used for geographic distribution and the determination of application areas [37]. Krishankumar et al. [38] proposed a new decision framework of MADM to extend the COPRAS method to q-ROFS for the prioritization of objects and aggregate preference matrix by prioritizing the renewable energy source in India. Shmelev and Bergh [39] verified the selection of the most suitable renewable energy source for electricity generation, optimal site identification [40], and the selection of the best alternative energy options [40,41]. For instance, Yazdani-Chamzini et al. [42] applied integrated AHP-COPRAS and novel approaches [43] to select the best alternative renewable energy projects. Acar and Dincer [44] used five main measures for the selection of hydrogen production methods using hesitant fuzzy AHP. An integrated fuzzy [45] and comparative analysis of hybrid decision-making with balanced scorecard-based [46] approaches were used for investment analysis of renewable energy alternatives. Carrico et al. [47] investigated the optimal energy-efficient options in water systems using Ant Colony and ELECTRE-III to solve the multi-criteria GDM problems. Bhowmik et al. [48] used TOPSIS to find the optimal green energy source. Rani et al. [49] proposed a new divergence measure for ranking and choosing the renewable energy sources in MCDM problems based on the fuzzy TOPSIS approach to compare some existing methods. Lee and Chang [41] employed PROMETHEE to evaluate five different energy sources. Celikbilek and Tuysuz [50] used fuzzy multi-attribute GDM to make pairwise comparison energy systems to find the best alternatives. Energy source selection is a complex problem, many criteria and sub criteria, such as technical, environmental, social, and economic needs, must be considered. The technological maturity, reliability, safety, the impact on ecosystems, social benefits, and social acceptability are good examples of immeasurable sub-criteria of energy systems [51]. These criteria and sub-criteria sets are naturally vague and imprecise, and need the domain experts’ judgments for clarification. Therefore, fuzzy set theory-based approaches were integrated with AHP, ANP, VIKOR, TOPSIS, and the other decision-making methods for the evaluation of renewable energy systems and elimination of imprecision. For instance, fuzzy AHP, fuzzy ANP, fuzzy DEMATEL (decision-making trial and evaluation laboratory), fuzzy TOPSIS [52], and fuzzy ELECTRE approaches were uncovered with the aim of determining the priority of energy systems. Colak and Kaya [53] employed the integrated fuzzy approaches for criteria prioritization and decision-making. Ren [54] established a novel multi-attribute GDM method and combined with the interval AHP intuitionistic fuzzy distance-based method to prioritize energy storage technologies. In this context, Siksnelyte et al. [32] and Ilbahar et al. [36] carried out extensive works on MADM approaches and fuzzy sets theory and determined that about 27% of total publications are about sustainable energy systems. On the other hand, they found that the distribution of methods by application areas of energy systems are as follows: 16.67% are AHP and ANP applications, 8.33% are fuzzy applications, 5.36% of VIKOR are about energy policy and energy project selection. Additionally, the distribution of application areas by method are as follows: in 15.76% of energy policy papers AHP and ANP were used, in 10.35% fuzzy sets, and in 28.57% of energy systems papers VIKOR was employed. The MADM and fuzzy MADM approaches are labeled into the following methods: AHP, VIKOR, TOPSIS, PROMETHEE, and ANP, that are mostly used for impact analysis. The fuzzy sets and system, AHP, TOPSIS, ANP, and PROMETHEE methods are mainly applied for energy technology evaluation. The AHP and fuzzy sets are applied for the selection of the best place for energy generation. Although the costs of energy systems are important criteria, the energy systems’ efficiency, its environment protection ability, abundancy, and availability are more important criteria for several countries. Therefore, AHP, DEA, TOPSIS, and COPRAS were employed to evaluate and investigate the energy system priority and sensitivity under different decision-making scenarios. The utilization and evaluation of renewable energy sources particularly using MADM for several determinations, such as energy policies, criteria evaluation, geographic distribution, and the application areas, are very common lately. It was also determined that fuzzy AHP has serious application in energy systems research. Hence, Kahraman et al. [55] performed a comparison analysis using fuzzy AHP and found that wind energy was the best alternative in Turkey. Lee et al. [56] determined that the hydrogen energy technologies are the best choice for implementation. Sánchez-Lozano et al. [57] integrated the GIS (provided the database containing the alternatives), and fuzzy AHP and fuzzy TOPSIS methods to identify the optimal places for solar PV (photovoltaic) power plants in southeast Spain. Yunna and Geng [58] examined the best location for solar thermoelectric power plants. Fuzzy sets-based linguistic interval preferences modeling was also used with these integrated MADM approaches to better handle uncertainty of the decision-making processes in energy systems research. It was also determined that ELECTRE was the second MADM approach, followed by TOPSIS and VIKOR; ANP and DEMATEL (decision-making trial and evaluation laboratory) are the third most preferred methods for site selection and alternative location evaluation [32,52,55,56,57,58]. Similarly, our results and findings show that solar photovoltaic energy is the best choice for the Kingdom.
3. Method and Methodologies
3.1. Fuzzy AHP Methodology for Determining Experts’ Weights for Criteria
Fuzzy AHP is a well-organized approach for determining the criteria weights and for the justification of multi-criteria GDM problems using fuzzy set theory. DMs specify choices in the form of ordinary language and allocate them to the attribute chosen for the assessment of decision problem. Rezaei and Ortt [59] employed AHP to solve complex multi-criteria GDM problems by breaking the hierarchical structure to simpler compositions. Fuzzy AHP overcomes the limitation of qualitative criteria, and solves the subjectivity, imprecision, and vagueness that are present in the decision problem, to formulate the uncertainties associated with perceptions and preferences. The fuzzy linguistic and numerical preferences are normalized via these structural models in uncertain systems when DMs lack the necessary data. In the fuzzy AHP method, a judgmental matrix is established for pair-wise comparison of criteria, then fuzzy arithmetic and aggregation operators are used to carry out the procedural calculations for determining the weights. In this study, triangular fuzzy numbers were employed in order to enhance the degree of judgment and bring flexibility in decision-making. DMs specified their preferences in the form of natural language expressions instead of numerical values, which brought a large cogitation to specify the preferences and identify the thoughts in a more systematic way. Figure 1 shows the flow chart of this study and decision-making procedure for energy systems selection. The determination of weights was carried out in the following steps: (1) the decision problem was hierarchically modeled containing the goals, (2) the priorities for the weights of criteria was established by judging the pairwise comparisons, (3) the outcomes were synthesized by judging the overall priorities for the hierarchy, and (4) the consistency of the judgments was examined.
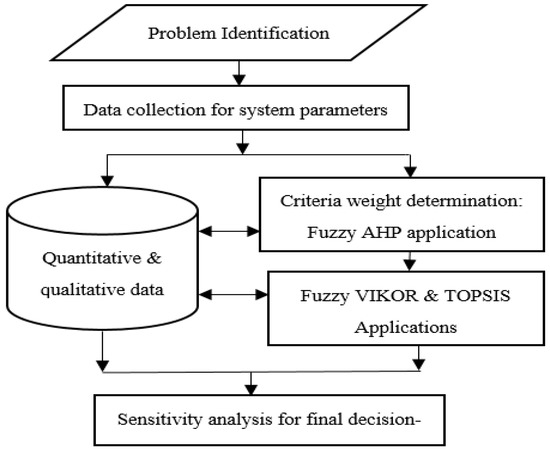
Figure 1.
Flow chart for the energy systems selection decision procedure.
The criteria set used for multi criteria GDM, conducted for selection of energy systems [6,13,15,18,22,24,26,29,32,36,40] in different countries, is given in Table 1.

Table 1.
The criteria list used for the selection of energy systems in different countries.
Table 2 shows the scores used for the assessment of fuzzy linguistic terms. The experts utilized these fuzzy linguistic terms to assess the importance of criteria.

Table 2.
Evaluation of fuzzy linguistic terms with fuzzy scores.
The energy systems were assessed by the following criteria in the Kingdom, based on experts’ judgments. A pairwise comparison was carried out. The experts were informed about how to use fuzzy linguistic terms in pairwise comparison. A group consensus was sought for the pairwise comparison; in the case of conflicts, the decision of the majority was considered and/or an average of the decisions was used for the assessment. Averaging the decision and/or max-min compositional rule of inference are the most common approaches used for consensus. The benefit of averaging the decision is that the idea of all DMs was considered for the assessment of the problem. The criteria considered were as follows—c1: power generation capacity, c2: efficiency, c3: storability, c4: safety, c5: air pollution, c6: depletable, c7: net present value, c8: enhanced local economic development, and c9: government support.
Each criteria weight was calculated by summing the allocated weights given in Table 3. Experts’ opinions were found and then divided by the number of the experts. The opinions of twelve domain experts were categorized under the main three DMs’ perspectives. The fuzzy extent analysis presented by Chang [28] was employed for determining the triangular fuzzy number. The DMs were the experts of energy systems from different domains; hence, the decision was made in a non-homogeneous environment. Equation (1) was employed for the calculations of weights:
where shows the weight allocated by the Kth expert’s decision. Table 4 shows the fuzzy evaluation matrix of criteria for the weights obtained from the linguistic values are presented in Table 3.

Table 3.
The pairwise comparisons of criteria for energy systems assessment.

Table 4.
Fuzzy evaluation matrix of criteria for the numerical weights.
In order to describe the membership functions, triangular fuzzy numbers (TFNs) are well-defined by three real tuple, (l, m, u) to designate the lowest value, mean value, and maximum value of the membership degrees. Some Algebraic operations on TFNs can be presented using fuzzy sets; essentially, the inverse operation can be presented as in Equation (2).
Let A be a set of triangular fuzzy numbers and , the inverse of this set can be presented as follows:
3.2. FAHP Algorithm of Fuzzy Synthetic Extent
Let be an object set, and be a goal set. According to Chang’s [28] synthetic extent analysis, we can get extent analysis for each goal. Thus, ‘m’ extent analysis values were obtained for each object, with the following parameters:
where M jgi (j = 1, 2,…,m) are triangular fuzzy numbers. Chang’s [28] extent analysis is given below:
Step 1: The fuzzy synthetic extent value with respect to the ith object is demarcated in this step, the fuzzy operation ‘m’ values are obtained from for a specific matrix given in Equation (3):
Equation (3) was applied to obtain the fuzzy synthetic extent analysis outcomes; the results are presented in Table 5.

Table 5.
The fuzzy synthetic extent analysis values.
In order to obtain the inverse matrix the values of M jgi (j = 1, 2,...,m) are added such that the lowest values are indicated by , the middle values by and the upper values by that are all summed to the decision criteria of the consecutive value. Hence, the total values presented in Equation (3) are obtained:
and then, the inverse of the previous vector is obtained for the total values using Equation (4):
The inverse vector was used as given in Equation (5) to obtain the fuzzy criteria weights of energy systems. The findings are presented in Table 6.

Table 6.
Fuzzy criteria weights of energy systems.
Step 2: Let us assume and are two TFNs, the degree of possibility of can be defined as given in Equation (6):
As seen in Equation (7), the lower, middle, and upper fuzzy values of degree of possibility can be presented. Some sample calculations are presented below. Table 7 shows the degree possibility for convex fuzzy numbers in this study.

Table 7.
Degree possibility of convex fuzzy numbers for alternative energy systems.
Step 3: The possibility degree for a convex fuzzy number bigger than k convex fuzzy Mi (i = 1, 2, k) number is calculated by Equation (8):
Suppose that for . Then, the vector of weight can be presented by , where are alternative energy systems.
Figure 2 shows the details of Equation (6), and ‘d’ is the highest intersection point between the membership degrees, and , to compare M1 and M2. Both values of and must be determined for the comparison of alternative energy systems.
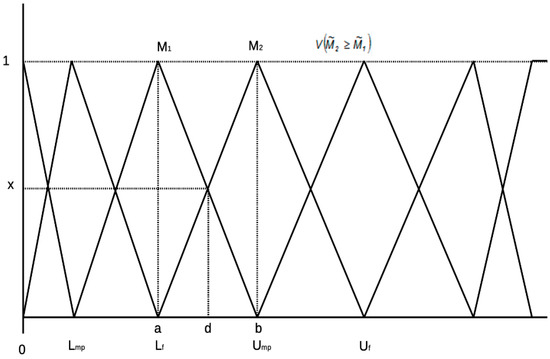
Figure 2.
The intersection between M1 and M2 convex fuzzy numbers.
Min (1, 0. 635, 0.389, 0, 0, 0, 0, 0, 0) = 0
Min (0.635, 1, 1, 0.793, 1, 1, 1, 1, 1, 0.635) = 0.635
Min (0.389, 0.739, 1, 0.531, 1, 1, 1, 1, 1, 0.389) = 0.389
Step 4: A normalization process is carried out, the normalized weight vectors, , are obtained using Equation (9), where Ws are non-fuzzy numbers.
The set of normalized weights were as follows; 0.3502, 02223, 0.1362, 0.2914, 0, 0, 0, 0, 0.
3.3. Fuzzy VIKOR Method
Fuzzy VIKOR is a tangible method for multi-criteria GDM problems, when DMs are not able to present their opinions at the beginning stage of the decision process. In order to achieve the highest group utility value of the “majority” (, given in Equation (11)) and the distinct regret of the “opponent” ( given by Equation (12)), the compromise solution can be obtained by DMs. Involving the preferences of DMs by weighting the criteria by fuzzy AHP, the resolutions will be based on the negotiations and compromise of DMs. In this study, heterogeneous fuzzy information was employed to carry out the conversion of operations to homogenize the decision structure using the extended VIKOR approach [60]. The fuzzy VIKOR ranking is based on the ideal solution of merit function Q, with v values selected which will be applied only for a given set of alternative criteria. The fuzzy VIKOR is a more useful method for solving multi-criteria GDM problems, which is a robust approach in evaluating the alternatives over conflicting criteria. Fuzzy GDM approaches play an important role using intuitionistic fuzzy information [61], Pythagorean fuzzy sets [62,63], and hesitant linguistic information [64] in different areas. A group of DMs determines the fixed ideal solution by the best (positive ideal) and the worst (negative ideal) values of entire criterion ratings using Equation (10), sequentially. In this approach, DMs evaluate every alternative and a compromise ranking is conducted by averaging the decisions to consider the opinions and ideas close to the ideal solution f*.
Now, the maximum group utility value of the majority and the distinct regret of the opponent are computed as given in Equations (11) and (12):
where symbolizes the weights of criteria and shows the DMs’ preferences for relative importance of the criteria. The value of merit function ) for each alternative is calculated by Equation (13):
where S* is the minimum and is the maximum value of Si, respectively, R* is the minimum and is the maximum value of Ri, respectively, and v is the weight for the strategy of maximum group utility, whereas (1−v) is employed for the weight of specific regrets. The result is attained by the majority rule with a maximum group utility decision, where the minimum individual regret of the pretender solution is obtained by . In general, 0.5 is used for the value of v, however it can be any value between the range of 0 to 1. Presently, ranking the order of S, R, and Q for alternatives in increasing order will give the evaluation of criteria; therefore, three ranking lists will be obtained. Let us suppose that a compromise solution of the alternative Al ranks the best by the minimum value of merit function Q, and satisfies the given conditions, hence a compromise solution of alternative A1 can be proposed as the best ranked alternative by the measure of merit function Q (minimum), if the following conditions are satisfied: firstly, evaluating each alternative with each criteria; secondly, ranking the comparisons with the measure of closeness to fuzzy VIKOR for solving incompatible decision-making problems with different units of criteria. The fuzzy linguistic terms and related fuzzy numbers used in the fuzzy VIKOR analysis are presented in Table 8.

Table 8.
Fuzzy linguistic terms and corresponding fuzzy numbers.
The energy systems used in this study were hydrogen (E1), fossil fuels (E2), hydropower (E3), wind (E4), solar PV (E5), geothermal (E6), nuclear (E7), and biomass (E8). The criteria set considered for the evaluation of energy systems is presented in Table 9.

Table 9.
The criteria considered for the evaluation of energy systems.
3.4. Fuzzy TOPSIS Method
Yazdani and Payam [65] presented the basic idea of the TOPSIS model. Taylan et al. [66] used the fuzzy TOPSIS method for solving the GDM problems under the fuzzy environment for construction project risk assessment and compressor selection in the petrochemical industry [67]. In this study, the opinions of DMs regarding the energy systems were aggregated and deemed to be equally important for judgment. Eight alternative energy systems were evaluated based on nine criteria. Fuzzy TOPSIS approach was applied using the following steps.
Step 1: Fuzzy linguistic terms presented in Table 8 were used for the aggregation of values. Equation (14) was used for averaging the fuzzy crisp values. Let us assume that N = {n1, n2,…,n9} are the set of energy systems for assessment. Initially, the DMs used fuzzy numerical values to evaluate the energy systems regarding the criteria, and a rating order was obtained by multiplying the matrix of ratings with each criteria weight and summing them all:
where are fuzzy crisp values assigned by k-th DM for energy system regarding the related criteria, (+) indicates the fuzzy arithmetic sum function. Hence, X = ()nxm is the fuzzy decision matrix described by fuzzy numerical values. The criteria set were considered as the decision parameters, including the linguistic terms (xi) and the related outcomes. Similarly, represents the membership function to associate each value of criteria to its fuzzy equivalences.
Step 2: The normalization of data can guarantee the decision matrix presents the range of normalized TFNs data in the interval of [0, 1]. The fuzzy decision matrix normalized, is presented in Equations (15) and (16) for energy systems related to the corresponding criteria. In these two equations, B and C represents the benefit criteria and cost criteria set, respectively.
Equation (17) was employed to determine the maximum numerical value of (cj*) for each energy system given by DMs. Equation (18) shows the normalized weighted fuzzy decision matrix ), which can be used to transform the crisp conclusions of decision criteria in the range of FTNs, between [0, 1].
Hence, the fuzzy positive ideal solution (FPIS) and the fuzzy negative ideal solution (FNIS) can be symbolized by A* and , as given in Equations (19) and (20), respectively.
The normalization is a defuzzification procedure of decision matrix to define the distance of each energy system to the ideal solution. As is well known, the distance to ideal solution may be on both sides of the ideal value. If we define FPIS as Alternative energy system (A(i)*), and FNIS as Alternative energy system (A(i)−), the vertex method can be used to determine the distance between two TFNs. Hence, the fuzzy positive-ideal (FPI) distance ( and fuzzy negative-ideal (FNI) distances ( of alternative energy systems were calculated by Equations (21) and (22), respectively.
Alternative energy system , Alternative energy system
where and , j = 1, 2,…,n.
Alternative energy system (1,…,9)* = [(1, 1, 1), (1, 1, 1),…, (1, 1, 1), (1, 1, 1)]
Alternative energy system (1,…,9)− = [(0, 0, 0), (0, 0, 0),…, (0, 0, 0), (0, 0, 0)]
The term measures the distance between two fuzzy values to compute the closeness coefficient (CCi). This measure was employed to determine the ranking order of energy systems. Equation (23) was employed to calculate the closeness coefficient of each alternative energy system. The FPI distances of energy systems(i)* and FNI distances, energy systems(i)− of alternatives were used to calculate the total distances from the ideal solution. Thus, the closeness coefficient and the ranking order of all energy systems were calculated. The most optimal energy system was determined among nine alternatives for investment.
4. Results and Findings
The data collection was carried out with the Delphi method, which was used to obtain the experts’ opinions, including three carefully selected members from the university and energy sectors. These three experts were core people from the domain, and they were requested to choose three experts each, hence the total twelve carefully selected participants from the universities and the energy sector worked together to establish the main criteria and sub criteria presented in Table 1 and the type of energy systems given in Table 9. The members worked together initially, and then they were divided into three groups who had strong expertise in the field of energy technologies, business, and energy market. The process of the Delphi approach took about two months to shape the domain experts’ opinion-based vision of the energy systems alternatives selection in the Kingdom. A panel work was made, and the panelists were informed about the fuzzy scores used for the assessment of fuzzy linguistic terms given in Table 2 and Table 8. The experts utilized these fuzzy linguistic terms to assess the importance of criteria before sending the first questionnaire, so that they could participate actively in the whole research process. The commitments of the panelists were ensured for the criteria set, the energy systems, and the fuzzy linguistic terms before sending the first questionnaire, so that the experts could participate actively in the whole research process. Then, the questionnaire sets were distributed to the experts.
The response time was set at about four weeks per cycle. It took three cycles to complete the decision-making process. Hence, the data of fuzzy approaches-related energy systems with respect to the criteria set were obtained and presented in Table 8 and Table 10. As appears in Table 8, the fuzzy linguistic terms and their corresponding numerical values were identified. The domain experts explained the importance of alternative energy systems with criteria easily by linguistic terms which were more identical than the numerical values for them and for those who were not familiar with these systems. Table 10 shows the relationship matrix of these two parameters by linguistic terms. Then, we used these linguistic terms for the assessment of the alternative energy systems.

Table 10.
Fuzzy relationships of energy systems with respect to criteria using fuzzy linguistic terms.
As shown in Table 10, the data obtained from the designed questionnaire were linguistic terms produced by the domain experts. As those experts had different backgrounds and areas of specialization in energy systems, a consensus was sought on their decisions for possible energy system, criteria set, and fuzzy terms. Table 11 presents the average of triangular fuzzy numbers (TFNs) established for each energy system about the criteria set. Hence, the heterogeneous opinions based on fuzzy numbers were obtained and unified. The experts’ opinions were aggregated and presented in Table 11, using Equations (5)–(9), (5)–(10), (5)–(11), and (5)–(12).

Table 11.
Aggregated fuzzy linguistic assessments of pairwise comparison.
The DMs arrayed fuzzy linguistic terms to regulate the importance of each criteria and analyzed each energy system with respect to the selected criteria. The results of fuzzy AHP method were determined in Section 3.1 and Section 3.2, based on the fuzzy linguistic terms and numbers presented in Table 1 and Table 2. Table 4 depicts the fuzzy evaluation matrix of criteria for the weights obtained from the linguistic values presented in Table 3. Equation (3) was employed for the calculation of fuzzy synthetic extent analysis, and the findings are presented in Table 5. The inverse vector was calculated using Equation (5) and the fuzzy criteria weights for energy systems were obtained. The complete sets of findings for Fuzzy AHP are presented in Table 6.
4.1. Results and Findings by the Fuzzy VIKOR Approach
As was presented, fuzzy VIKOR extent analysis was used to rank the criteria. Hence, the uij matrix presented in Table 11 and Table 12 shows the experts’ opinions to achieve the fuzzy ratings and comparison of alternative energy systems with respect to each criterion.

Table 12.
Fuzzy evaluation of experts’ aggregated opinions for fuzzy ratings of the alternatives with respect to the criteria.
In Table 13, the indices minimum Si and Ri show maximum majority rule, and a minimum specific regret of an opponent strategy, respectively. Similarly, v represents the weight of a maximum group utility, which is generally assumed to be 0.5. In Table 13 the relationships of alternative energy systems in terms of indices are shown. Table 14 shows the S*, , R*, and values calculated using Equations (11) and (12). These TFNs were determined by merit function Qi (see Equation (13)), which is the rankings obtained for alternative energy systems.

Table 13.
The TFNs (Triangular fuzzy numbers) to measure alternatives.

Table 14.
The fuzzy values for the grading of alternatives.
The calculations in Table 14 need defuzzification. Several defuzzification strategies are suggested by the researchers; the graded mean integration approach was employed in this study. In these strategies, TFNs are defined as A= (li, mi, ui) and defuzzified to transform into crisp numbers by using Equation (24).
Hence, the fuzzy best value and fuzzy worst value of each criterion function were determined and presented in Table 13, which shows the separation measures Si and Ri that were calculated using Equations (11) and (12). The findings are summarized in Table 14 with the defuzzified merit function Qi for each alternative presented in Table 15 for ranking the energy systems.

Table 15.
The ranking order of energy systems of fuzzy VIKOR using the weight of group utility.
The energy supply and demand in Saudi Arabia need revision due to population growth, rapid expansion of the industrial sector, and high air conditioning during summer months. The energy consumption is still low compared to similar-sized countries. The main source of energy generation is oil and gas, to date 240 terawatt hours of electricity is generated, and the predictions depict that the country’s demand will reach 736 terawatt hours by 2022. The national transformation program, called Vision 2030, aims for less dependency on energy from oil production and expands it to alternative energy sources. The critical question is what these energy systems should be and sources for investment priority. Table 15 and Figure 3 show the results and findings after technical, economic, environmental, and social criteria assessment—the rankings depict that the alternative energy systems for investment should be solar PV (E5), geothermal (E6), fossil fuels (E2), biomass (E8), wind (E4), hydrogen (E1), nuclear (E7), and hydropower (E3) in the Kingdom of Saudi Arabia.
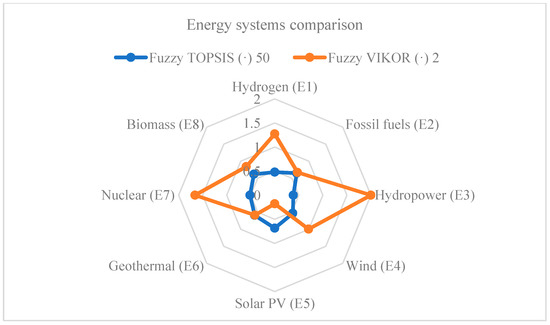
Figure 3.
Energy systems investment ranking by fuzzy VIKOR and TOPSIS approaches.
4.2. Results and Findings By Fuzzy TOPSIS Approach
Table 10 and Table 11 present the fuzzy linguistic terms and averaged TFNs for each energy system regarding the criteria set, respectively. The experts’ opinions were aggregated and presented in Table 11, using the fuzzy numerical values. In order to carry out the steps of the fuzzy TOPSIS method, initially, the DMs’ opinions for energy systems regarding criteria set were averaged using Equations (14) and (17), the maximum values of the closeness coefficient (cj*) were determined; consequently, they were as follows, , , and . Additionally, Equation (18) was used to find the normalized weighted fuzzy decision matrix ) to transform the crisp conclusions of decision criteria in the TFNs between [0, 1]. Due to the availability of several numerical values, a part results and findings is given in Table 16.

Table 16.
The weighted fuzzy decision matrix of energy systems regarding the criteria.
A defuzzification procedure was used for the decision matrix given in Table 16 in order to define the distance of each energy system to the ideal solution for decision-making. The distance might be on both sides of the fuzzy positive ideal solution and fuzzy negative ideal solution. The vertex method was used to determine the distance between the TFNs. Equations (21) and (22) were employed to determine the fuzzy positive-ideal (FPI) distance and fuzzy negative-ideal (FNI) distances of alternative energy systems, respectively. The results are presented in Table 17. As is well known, the closeness coefficients (CCi) are measured by , which shows the distance between two fuzzy numbers. Thus, in Table 17, ( shows the fuzzy positive-ideal (FPI) distance and ( shows fuzzy negative-ideal (FNI) distances of alternative energy systems. This measure was used to calculate the ranking order of energy systems by the fuzzy TOPSIS approach. Consequently, the CCi of all energy systems was determined and presented in Table 17. Equation (23) was employed for the calculations of closeness coefficient of each alternative energy system for the investment priority. As is clearly seen in Table 17, solar PV (E5) had the highest closeness coefficient value for the investment, that is, 0.01368314. It was followed by biomass (E8), and fossil fuels (E2). The remaining energy systems were ordered as follows: geothermal (E6), wind (E4), nuclear (E7), hydrogen (E1), and hydropower (E3).

Table 17.
The closeness coefficient of energy systems for investment priority by the fuzzy TOPSIS method.
4.3. Comparison with Existing Methods
In this work, PV solar (E5) was found to be the optimal alternative energy system for investment by the application of both fuzzy VIKOR and fuzzy TOPSIS approaches. However, the technical, economic, environmental, and social criteria showed that the ranking was changed for the fuzzy VIKOR, and occurred as follows: geothermal (E6), fossil fuels (E2), biomass (E8), wind (E4), hydrogen (E1), nuclear (E7), and hydropower (E3). On the other hand, our findings of fuzzy TOPSIS application depicted that biomass (E8), and fossil fuels (E2) followed the solar PV (E5) investment, and they were followed by geothermal (E6), wind (E4), nuclear (E7), hydrogen (E1), and hydropower (E3). Figure 3 shows the comparison of fuzzy VIKOR and TOPSIS methods based on normalized data for energy systems investment.
Figure 3 also shows the negative ideal values of the entire criterion ratings of the fuzzy VIKOR approach. The value of merit function ) for each alternative was calculated, using v equal to 0.5. The FNI distances of alternative energy systems were calculated, and the FNI for solar PV was found to be 0.08895, the closest value to 0.
Similarly, Equations (15) and (16) were employed to determine the fuzzy decision matrix by the fuzzy TOPSIS approach for energy systems, B the benefit criteria set was employed and Equation (17) was used to determine the maximum numerical value of (cj*) for each energy system. The distance to ideal solution was calculated for both sides of the ideal value. As seen in Figure 3, the FNI distance values were calculated and found to be 0.01368314, the closest value to 0. On the other hand, the FPI distances of alternative energy systems were also calculated by the fuzzy TOPSIS approach, and solar PV was found to be 0.986716, the most ideal value and closest to 1.
Subsequently, a comparison was carried out between our proposed methods and some existing methods proposed previously in [40,68,69,70]. The comparative results and findings are presented in Table 18. To the best of our knowledge, although some criteria were similar, the comparisons were made based on different criteria in these studies. Although multicollinearity and correlation are available to some extent, the needs and expectations of countries are different. Our ranking orders were for the important criteria considered in the Kingdom.

Table 18.
Comparison of energy system alternatives under different available methods.
The Kingdom is now concentrating on evolving the renewable energy resources that were not exploited previously due to the existence of enormous oil and natural gas resources [71]. Large potential of unutilized geothermal resources is also available in Saudi Arabia in Khaybar city. The surface temperatures of the thermal springs in these provinces vary from 31 °C to 96 °C, with a flow rate of 5 to 20 L per minute. The investigation of geothermal reservoir characteristics, the volcanic flows, flow rates, heat flow, and geothermal gradients of the geothermal provinces, showed that the wet geothermal systems of the country can produce about 23–109 kWh of power. Energy generation and consumption is one of the key indicators of quality improvement of life that displays the economic and social development of countries. The mutual demands of industrialization and urbanization increase the requirements of alternative energy systems. According to the energy planning studies given in the Statistical Review of World Energy 2017, Saudi Arabia generated 330.5 billion kWh of electricity during 2016 [71]. The country prepared the largest expansion plan for electric power generation with policies to raise the power generating capacity to 120 GW by 2032. Al-sasi et al. [72] studied the state-of-the-art available tools for determining oil demand using economic models and demand strategies for various petroleum products consumed by different sectors in the Kingdom. For instance, Saudi Arabia’s natural gas reserves have been proven to be 303 trillion cubic feet, according to the investigation made in January 2017. These natural gas reserves are the fourth-largest reserves in the world behind Russia, Qatar, and Iran. The natural gas reserves of the country exist within petroleum deposits and are discovered in the same wells of the crude oil. Demirbas et al. [73] studied the anaerobic digestion of biomass using the microorganism. Biogas is obtained from organic materials of municipal solid waste (MSW). The Kingdom is rich in biomass and fuel can be produced from the bio-wastes to produce energy. Taylan and Demirbas [74] investigated the possible usage of biofuels instead of fossil fuels to produce electricity, heat, some chemicals which will propose a reproducible alternative streamlining the economic and social improvement in the Kingdom. Biofuels are significant sources which suggest numerous benefits for lessening greenhouse gas emissions and sustainable renewable energy systems. The wind energy potential of Saudi Arabia is predicted to be 400 billion kWh and the technical potential is estimated to be 120 billion kWh per year. For future energy demand of the country, the King Abdullah City for Atomic and Renewable Energy suggests a further 41 GW more solar power investment, 17.6 GW nuclear power investment, and 9 GW of wind power investment until 2032.
5. Sensitivity Analysis
In this work, two approaches were used for sensitivity analysis. Initially, the sensitivity analysis was carried out using v, the weight of maximum group utility, which is generally assumed to be 0.5. However, when different values of v are tested, the investment priority of energy systems can be compared. For instance, when v is equal to 0.2, the geothermal (E6) energy investment can take priority for investment, solar PV (E5) takes the second order, fossil fuels (E2) take the third order for investment, and so on. However, when v is equal to 0.5, solar PV (E5) takes the priority for investment, geothermal (E6) energy takes the second order, fossil fuels (E2) take the third order for investment, and so on. Table 15 shows the ranking order of energy systems investment based on the defuzzified merit function Qi using different rates of v. The findings presented in Table 15 and Figure 4 show the ranking order of energy systems with the weight for the strategy of maximum group utility, and the minimum regret obtained. We determined the priority of energy systems using different values of v selected arbitrarily for v = 0.2, 0.5, 0.7, and 0.9. In general, although v is usually equal to 0.5 for calculations of merit function, it can be any value between the range of 0 to 1. Thus, the minimum regret will be achieved based on the ranking obtained in Figure 4. The fuzzy VIKOR-based ranking of energy systems is based on the ideal solution of merit function Q with v values which will be applied only for a given set of alternative criteria.
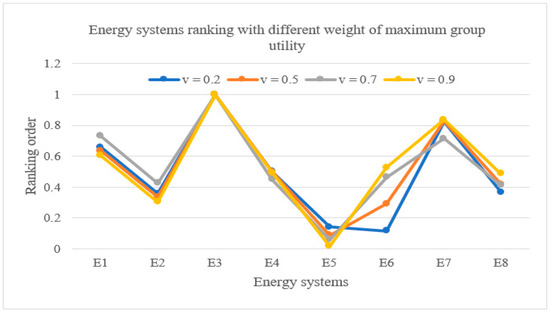
Figure 4.
Comparison of energy system alternatives under different minimum regret cases of v.
As a second approach, fuzzy Data Envelopment Analysis (DEA) was employed for carrying out the sensitivity analysis. During the collection of the data set and application process, fuzzy triangular numbers were used; as a rule of thumb, these data set were unified, and their averaged values were used for analysis. The output-oriented DEA model can be written as given in Equation (25):
where for a set of n energy systems, each energy system (decision-making unit) is identified by m inputs and s outputs, where the inputs and outputs are fuzzy [75].
i = 1, 2, 3, …, m
r = 1, 2, 3, …, s
j = 1, 2, 3, …, n.
yrj is the amount of output r produced by energy system j, yrjo is the amount of output r produced by energy system jo, (i.e., the energy system that is being assessed), xij is the amount of input i used by energy system j, xijo is the amount of input i used by energy system jo, λj is the weight given to energy system j [76].
, represent the slack for input i and the surplus for output r, respectively, for energy system jo. Note that ε is an arbitrarily selected small positive number added to ensure that slacks for all considered inputs and outputs are positive. In this case, the technical efficiency was achieved for each energy system if and only if, both of the following conditions were satisfied: all slacks are equal to 0, and efficiency score is 1/θ and equal to 1. In this paper, an output-oriented DEA model was developed. The idea behind incorporating DEA within the fuzzy VIKOR was to examine the extent to which each energy system can convert their inputs into the outputs. The criteria set was considered in two parts: the net present value (c7), and government support (c9) were considered as the cost criteria (inputs), and the remaining criteria set (c1, c2, c3, c4, c5, c6, and c8) were considered as the benefit criteria set (outputs). Table 19 shows the efficiency of energy systems (Ei) in a sense to evaluate the extent to which to utilize the inputs; the net present value (c7), and government support (c9) in order to get maximum outputs of power generation capacity (c1), efficiency (c2), storability (c3), safety (c4), air pollution (c5), depletable (c6), and local economic development (c8). As the cost and benefit criteria were considered, the final scores were obtained by the minimum regret of the energy systems. Table 19 presents the optimal ranking for the energy alternatives using fuzzy VIKOR over fuzzy DEA (Data Envelopment Analysis). The optimal ranking shows that solar PV (E5) takes priority for the investment, fossil fuels (E2) are the second in order, and biomass (E8) is the third most important energy system for investment. Table 19 shows the remaining energy systems’ investment order.

Table 19.
The ranking of energy systems using fuzzy VIKOR and Data Envelopment Analysis.
6. Conclusions
This paper aimed to use integrated MADM approaches, fuzzy AHP, fuzzy VIKOR, and fuzzy TOPSIS, to determine the priority of energy system investment in Saudi Arabia. Eight different energy systems—Solar PV, Geothermal, Fossil fuels, Biomass, Wind, Hydrogen, Nuclear, and Hydropower—were studied under nine perspectives, such as “power generation—capacity, efficiency, storability, safety, air pollution, depletable, net present value, enhanced local economic development, and government support for the investment”. Solar PV was identified as the most attractive energy system for investment in the Kingdom according to the experts’ opinions. On the other hand, the results of observation for a period of two years showed that the daylight in the Kingdom is 12 h 8 min and 48 s on average per day. This high daylight time is longer than many countries using solar PV systems extensively.
The works of energy systems were categorized for application areas, such as energy policy/project, selection, impact analysis, evaluation of power generation, technologies, regional planning, place selection, national planning, and method selection. They were also categorized by used methods, such as ANP, fuzzy sets, TOPSIS, WASPAS (Weighted Aggregates Sum Product Assessment), WASPAS-G, PROMETHEE, PROMETHEE II, ELECTRE, ELECTRE III, ASPID (synthesis of parameters under information deficiency), and MULTIMOORA (multi-objective optimization by a ratio analysis). This study also revealed that ANP (Analytic Network Process), AHP (Analytical Hierarchical Process), fuzzy sets and system, VIKOR (VIseKriterijumska Optimizacija I Kompromisno Resenje), and PROMETHEE methods are commonly used for energy sector planning at the nationwide level. In this context, Rojas-Zerpa and Yusta [77] integrated the AHP and VIKOR methods for the assessment of electricity supply in rural and remote regions. There are many MADM approaches such as pairwise comparison matrix in multiple criteria decision making, DEA, TOPSIS [78], PROMETHEE, and fuzzy sets and system for energy technologies selection, energy project selection, energy policy and planning. Fuzzy set theory is mainly used in combination with the AHP and TOPSIS methods for the energy policy/project selection issues. Chatterjeea and Chakraborty [79] ranked and analyzed the performance of the original VIKOR method and its five variants based on two expressive examples. It was remarked that when the information in a decision problem is vague and imprecise, the fuzzy VIKOR technique must always be preferred. Hence, we integrated the fuzzy AHP, fuzzy VIKOR, and TOPSIS approaches to manage non-cooperative ideas. We used the Delphi method for data collection. The suggested approach can be effectively applied for decision-making problems. The upcoming studies suggest that similar studies can be conducted based on different multi-attribute GDM techniques, such as fuzzy PROMETHEE, and fuzzy ELECTRE, for comparative purposes of determining the location of investment and the type of energy alternatives on regional bases. Sensitivity analysis was carried out for energy system’s criteria evaluation and verification. Future studies can be carried out for site selection, project, and policy selection in Saudi Arabia.
As natural resources are used for energy generation, energy investment projects have confirmed that they are able to create substantial contributions to the economy in developing countries by providing new employment and creating new business opportunities. Energy generation is one of the most important indicators for economic growth, industrialization, and agricultural development in a country. Moreover, energy generation technologies, diversification of sources, and projects make direct and indirect contributions to economic development, social life, and provide improvements in education, manufacturing, heating, and lighting. Although Saudi Arabia has been implementing several incentives, such as government tax subsidies, price discounts, partial payment schemes for low income people, and encouraging investors for investing renewable energy sources, the country is still extensively dependent on fossil fuels. The investment in renewable energy sources is very limited and low compared to the other G20 countries.
Author Contributions
The individual contribution of the authors was as follows: O.T., R.A. and M.K. together designed research, provided extensive advice throughout the study regarding to research design, research methodology, data collection, assessment of the results and findings and revise the manuscript. A.A., F.R., and E.H.-V. helped to draft, calculation, edit, and revise the manuscript. All authors have read and approved the final manuscript.
Acknowledgments
This research was funded by the Deanship of Scientific Research (DSR) at King Abdulaziz University, Jeddah, under grant no. (RG-7-135-38). The authors, therefore, acknowledge with thanks DSR technical and financial support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sarkodie, S.A.; Strezov, V.; Weldekidan, H.; Asamoah, E.F.; Owusu, P.A.; Doyi, I.N.Y. Environmental sustainability assessment using dynamic autoregressive-distributed lag simulations-nexus between greenhouse gas emissions, biomass energy, food and economic growth. Sci. Total Environ. 2019, 668, 318–332. [Google Scholar] [CrossRef] [PubMed]
- Kulkarni, M.B.; Ghanegaonkar, P.M. Biogas generation from floral waste using different techniques. Glob. J. Environ. Sci. Manag.-GJESM 2019, 5, 17–30. [Google Scholar]
- Li, Y.; Chiu, Y.H.; Lin, T.Y. Research on new and traditional energy sources in OECD countries. Int. J. Environ. Res. Public Health 2019, 16, 1122. [Google Scholar] [CrossRef] [PubMed]
- Cederberg, C.; Persson, U.M.; Schmidt, S.; Hedenus, F.; Wood, R. Beyond the borders-burdens of Swedish food consumption due to agrochemicals, greenhouse gases and land -use change. J. Clean. Prod. 2018, 214, 644–652. [Google Scholar] [CrossRef]
- Perera, F.P. Pollution from fossil-fuel combustion is the leading environmental threat to global pediatric health and equity: Solutions exist. Int. J. Environ. Res. Public Health 2017, 15, 16. [Google Scholar] [CrossRef]
- Budak, G.; Chen, X.; Celik, S.; Ozturk, B. A systematic approach for assessment of renewable energy using analytic hierarchy process. Energy Sustain. Soc. 2019, 9, 37. [Google Scholar] [CrossRef]
- Seyfried, C.; Palko, H.; Dubbs, L. Potential local environmental impacts of salinity gradient energy: A review. Renew. Sustain. Energy Rev. 2019, 102, 111–120. [Google Scholar] [CrossRef]
- Demirbas, A.; Taylan, O.; Kaya, D. Biogas production from municipal sewage sludge (MSS). Energy Sources Part A Recovery Util. Environ. Eff. 2016, 38, 3027–3033. [Google Scholar] [CrossRef]
- Taylan, O.; Kaya, D.; Bakhsh, A.A.; Demirbas, A. Bioenergy life cycle assessment and management in energy generation. Energy Explor. Exploit. 2018, 36, 166–181. [Google Scholar] [CrossRef]
- Ahmed, S.; Abdelgader, A. Renewable energy advantages and disadvantages. Int. J. Res. Sci. Manag. 2016, 3, 7–9. [Google Scholar]
- Rahman, S.M.; Khondaker, A.N. Mitigation measures to reduce greenhouse gas emissions and enhance carbon capture and storage in Saudi Arabia. Renew. Sustain. Energy Rev. 2012, 16, 2446–2460. [Google Scholar] [CrossRef]
- Olabemiwo, F.A.; Danmaliki, G.I.; Oyehan, T.A.; Tawabini, B.S. Forecasting CO2 emissions in the Persian Gulf States. Glob. J. Environ. Sci. Manag.-GJESM 2017, 3, 1–10. [Google Scholar]
- Dong, J.; Liu, D.; Wang, D.; Zhang, Q. Identification of key influencing factors of sustainable development for traditional power generation groups in a market by applying an extended MCDM model. Sustainability 2019, 11, 1754. [Google Scholar] [CrossRef]
- Chapman, A.J.; McLellan, B.C.; Tezuka, T. Prioritizing mitigation efforts considering co-benefits, equity and energy justice: Fossil fuel to renewable energy transition pathways. Appl. Energy 2018, 219, 187–198. [Google Scholar] [CrossRef]
- Hhurlimann, C.; Bengoa, D.S. Valuating renewable energy investments within transactions: A comparative review among practitioners. In Proceedings of the Global and National Business Theories and Practice: Bridging the Past with the Future. Euromed Academy of Business Conference Book of Proceedings, Rome, Italy, 13–15 September 2017; pp. 720–739. [Google Scholar]
- Perez, I.J.; Cabrerizo, F.J.; Alonso, S.; Dong, C.; Chiclana, F.; Herrera Viedma, E. On dynamic consensus processes in group decision making problems. Inf. Sci. 2018, 459, 20–35. [Google Scholar] [CrossRef]
- Lin, C.; Kou, G.; Peng, Y.; Alsaadi, F.E. Aggregation of the nearest consistency matrices with the acceptable consensus in AHP-GDM. Ann. Oper. Res. 2020. [Google Scholar] [CrossRef]
- Erdin, C.; Ozkaya, G. Turkey’s 2023 energy strategies and investment opportunities for renewable energy sources: Site selection based on ELECTRE. Sustainability 2019, 11, 2136. [Google Scholar] [CrossRef]
- Perez, I.J.; Cabrerizo, F.J.; Alonso, S.; Herrera-Viedma, E. A new consensus model for group decision making problems with non-homogeneous experts. IEEE Trans. Syst. Man Cybern. 2014, 44, 494–498. [Google Scholar] [CrossRef]
- Cabrerizo, F.J.; Chiclana, F.; Al-Hmouz, R.; Morfeq, A.; Balamash, A.S.; Herrera-Viedma, E. Fuzzy decision making and consensus: Challenges. J. Intell. Fuzzy Syst. 2015, 29, 1109–1118. [Google Scholar] [CrossRef]
- Opricovic, S.; Tzeng, G.H. Compromise solution by MCDM methods: A comparative analysis of VIKOR and TOPSIS. Eur. J. Oper. Res. 2004, 156, 445–455. [Google Scholar] [CrossRef]
- Abu Taha, R.; Daim, T. Multi-criteria applications in renewable energy analysis, a literature review. Res. Technol. Manag. 2013, 2, 17–30. [Google Scholar]
- Mousavi-Nasab, S.H.; Sotoudeh-Anvari, A. A comprehensive MCDM-based approach using TOPSIS. COPRAS and DEA as an auxiliary tool for material selection problems. Mater. Des. 2017, 121, 237–253. [Google Scholar] [CrossRef]
- Sindhu, S.P.; Nehra, V.; Luthra, S. Recognition and prioritization of challenges in growth of solar energy using analytical hierarchy process: Indian outlook. Energy 2016, 100, 332–348. [Google Scholar]
- Choudhary, D.; Shankar, R. An STEEP-fuzzy AHP-TOPSIS framework for evaluation and selection of thermal power plant location: A case study from India. Energy 2012, 42, 510–521. [Google Scholar] [CrossRef]
- Uyan, M. GIS-based solar farms site selection using analytic hierarchy process (AHP) in Karapinar region, Konya/Turkey. Renew. Sust. Energy Rev. 2013, 28, 11–17. [Google Scholar] [CrossRef]
- Papalexandrou, M.A.; Pilavachi, P.A.; Chatzimouratidis, A.I. Evaluation of liquid bio-fuels using the analytic hierarchy process. Process Saf. Environ. Prot. 2008, 86, 360–374. [Google Scholar] [CrossRef]
- Chang, D. Applications of the extent analysis method on fuzzy AHP. Eur. J. Oper. Res. 1996, 95, 649–655. [Google Scholar] [CrossRef]
- Mardani, A.; Jusoh, A.; Zavadskas, E.K.; Cavallaro, F.; Khalifah, Z. Sustainable and renewable energy: An overview of the application of multiple criteria decision making techniques and approaches. Sustainability 2015, 7, 13947–13984. [Google Scholar] [CrossRef]
- Balin, A.; Baracli, H. A fuzzy multi-criteria decision making methodology based upon the interval type-2 fuzzy sets for evaluating renewable energy alternatives in Turkey. Technol. Econ. Dev. Econ. 2017, 23, 742–763. [Google Scholar] [CrossRef]
- Vishnupriyan, J.; Manoharan, P.S. Multi-criteria decision analysis for renewable energy integration: A southern India focus. Renew. Energy 2018, 121, 474–488. [Google Scholar] [CrossRef]
- Siksnelyte, I.; Zavadskas, E.K.; Streimikiene, D.; Sharma, D. An overview of multi-criteria decision-making methods in dealing with sustainable energy development issues. Energies 2018, 11, 2754. [Google Scholar] [CrossRef]
- Krishankumar, R.; Mishra, A.R.; Ravichandran, K.S.; Peng, X.; Zavadskas, E.K.; Cavallaro, F.; Mardani, A. A group decision framework for renewable energy source selection under interval-valued probabilistic linguistic term set. Energies 2020, 13, 986. [Google Scholar] [CrossRef]
- Alizadeh, R.; Soltanisehat, L.; Lund, P.D.; Zamanisabzi, H. Improving renewable energy policy planning and decision-making through a hybrid MCDM method. Energy Policy 2020, 137, 111174. [Google Scholar] [CrossRef]
- Zhang, H.; Kou, G.; Peng, Y. Soft consensus cost models for group decision making and economic interpretations. Eur. J. Oper. Res. 2019, 277, 964–980. [Google Scholar] [CrossRef]
- Ilbahar, E.; Cebi, S.; Kahraman, C. A state-of-the-art review on multi-attribute renewable energy decision making. Energy Strategy Rev. 2019, 25, 18–33. [Google Scholar] [CrossRef]
- Strantzali, E.; Aravossis, K. Decision making in renewable energy investments: A review. Renew. Sustain. Energy Rev. 2016, 55, 885–898. [Google Scholar] [CrossRef]
- Krishankumar, R.; Ravichandran, K.S.; Kar, S.; Cavallaro, F.; Zavadskas, E.K.; Mardani, A. Scientific decision framework for evaluation of renewable energy sources under q-rung orthopair fuzzy set with partially known weight information. Sustainability 2019, 11, 4202. [Google Scholar] [CrossRef]
- Shmelev, S.E.; Bergh, J.C. Optimal diversity of renewable energy alternatives under multiple criteria: An application to the UK. Renew. Sustain. Energy Rev. 2016, 60, 679–691. [Google Scholar] [CrossRef]
- Kaya, T.; Kahraman, C. Multicriteria renewable energy planning using an integrated fuzzy VIKOR & AHP methodology: The case of Istanbul. Energy 2010, 35, 2517–2527. [Google Scholar]
- Lee, H.; Chang, C. Comparative analysis of MCDM methods for ranking renewable energy sources in Taiwan. Renew. Sustain. Energy Rev. 2018, 92, 883–896. [Google Scholar] [CrossRef]
- Yazdani-Chamzini, A.Y.; Fouladgar, M.M.; Zavadskas, E.K.; Moini, S.H.H. Selecting the optimal renewable energy using multi criteria decision making. J. Bus. Econ. Manag. 2013, 14, 957–978. [Google Scholar] [CrossRef]
- Yazdani, M.; Chatterjee, P.; Zavadskas, E.K.; Streimikiene, D. A novel integrated decision-making approach for the evaluation and selection of renewable energy technologies. Clean Technol. Environ. Policy 2018, 20, 403–420. [Google Scholar] [CrossRef]
- Acar, C.; Dincer, I. Review and evaluation of hydrogen production options for better environment. J. Clean. Prod. 2018, 218, 835–849. [Google Scholar] [CrossRef]
- Dincer, H.; Yuksel, S. Multidimensional evaluation of global investments on the renewable energy with the integrated fuzzy decision-making model under the hesitancy. Int. J. Energy Res. 2019, 43, 1775–1784. [Google Scholar] [CrossRef]
- Dincer, H.; Yuksel, S. Balanced scorecard-based analysis of investment decisions for the renewable energy alternatives: A comparative analysis based on the hybrid fuzzy decision-making approach. Energy 2019, 175, 1259–1270. [Google Scholar] [CrossRef]
- Carrico, N.J.G.; Goncalves, F.V.; Covas, D.I.C.; do Ceu Almeida, M.; Alegre, H. Multi-criteria analysis for the selection of the best energy efficient option in urban water systems. Procedia Eng. 2014, 70, 292–301. [Google Scholar] [CrossRef][Green Version]
- Bhowmik, C.; Baruah, A.; Bhowmik, S.; Ray, A. Green energy sources selection for sustainable energy planning using multi-criteria decision-making approach. In Proceedings of the International Conference on Mechanical, Materials and Renewable Energy, Sikkim, India, 8–10 December 2017; pp. 1–8. [Google Scholar]
- Rani, P.; Mishra, A.R.; Mardani, A.; Cavallaro, F.; Alrasheedi, M.; Alrashidi, A. A novel approach to extended fuzzy TOPSIS based on new divergence measures for renewable energy sources selection. J. Clean. Prod. 2020, 257, 120352. [Google Scholar] [CrossRef]
- Celikbilek, Y.; Tuysuz, F. A fuzzy multi criteria decision making approach for evaluating renewable energy sources. In Proceedings of the 4th International Fuzzy Systems Symposium, Istanbul, Turkey, 5–6 November 2015. [Google Scholar]
- Cristobal, J.R.S. Contractor selection using multicriteria decision making methods. J. Constr. Eng. Manag. 2011, 138, 751–758. [Google Scholar] [CrossRef]
- Solangi, Y.A.; Tan, Q.; Mirjat, N.Y.; Valasai, G.D.; Ali Khan, M.W.; Ikram, M. An integrated delphi-AHP and fuzzy TOPSIS approach toward ranking and selection of renewable energy resources in Pakistan. Processes 2019, 7, 118. [Google Scholar] [CrossRef]
- Colak, M.; Kaya, I. Prioritization of renewable energy alternatives by using an integrated fuzzy MCDM model: A real case application for Turkey. Renew. Sustain. Energy Rev. 2017, 80, 840–853. [Google Scholar] [CrossRef]
- Ren, J.Z. Selection of sustainable prime mover for combined cooling, heat, and power technologies under uncertainties: An interval multicriteria decision making approach. Int. J. Energy Res. 2018, 42, 2655–2669. [Google Scholar] [CrossRef]
- Kahraman, C.; Kaya, I.; Cebi, S. A comparative analysis for multi attribute selection among renewable energy alternatives using fuzzy axiomatic design and fuzzy analytic hierarchy process. Energy 2009, 34, 1603–1616. [Google Scholar] [CrossRef]
- Lee, S.K.; Mogi, G.; Li, Z.; Hui, K.S.; Lee, S.K.; Hui, K.; Park, S.Y.; Ha, Y.J.; Kim, J.W. Measuring the relative efficiency of hydrogen energy technologies for implementing the hydrogen economy: An integrated fuzzy AHP/DEA approach. Int. J. Hydrog. Energy 2011, 36, 12655–12663. [Google Scholar] [CrossRef]
- Sánchez-Lozano, J.M.; Teruel-Solano, J.; Soto-Elvira, P.L.; García-Cascales, M.S. Geographical information systems (GIS) and multi-criteria decision making (MCDM) methods for the evaluation of solar farms locations: Case study in southeastern Spain. Renew. Sustain. Energy Rev. 2013, 24, 544–556. [Google Scholar] [CrossRef]
- Yunna, W.; Geng, S. Multi-criteria decision making on selection of solar–wind hybrid power station location: A case of China. Energy Convers. Manag. 2014, 81, 527–533. [Google Scholar] [CrossRef]
- Rezaei, J.; Ortt, R. Multi-criteria supplier segmentation using a fuzzy preference relations based AHP. Eur. J. Oper. Res. 2013, 225, 75–84. [Google Scholar] [CrossRef]
- Kim, J.H.; Ahn, B.S. Extended VIKOR method using incomplete criteria weights. Expert Syst. Appl. 2019, 126, 124–132. [Google Scholar] [CrossRef]
- Dong, Y.C.; Li, C.C.; Xu, Y.F.; Gu, X. Consensus-based group decision making under multi-granular unbalanced 2-tuple linguistic preference relations. Group Decis. Negot. 2015, 24, 217–242. [Google Scholar] [CrossRef]
- Rani, P.; Mishra, A.R.; Pardasani, K.R.; Mardani, A.; Liao, H.; Streimikienef, D. A novel VIKOR approach based on entropy and divergence measures of Pythagorean fuzzy sets to evaluate renewable energy technologies in India. J. Clean. Prod. 2019, 238, 117936. [Google Scholar] [CrossRef]
- Cui, F.B.; You, X.Y.; Hua, S.; Liu, H.C. Optimal siting of electric vehicle charging stations using pythagorean fuzzy VIKOR approach. Math. Probl. Eng. 2018, 2018, 9262067. [Google Scholar] [CrossRef]
- Liao, H.C.; Xu, Z.S.; Zeng, X.J. Hesitant fuzzy linguistic VIKOR method and its application in qualitative multiple criteria decision making. IEEE Trans. Fuzzy Syst. 2015, 23, 1343–1355. [Google Scholar] [CrossRef]
- Yazdani, M.; Payam, A.F. A comparative study on material selection of microelectromechanical systems electrostatic actuators using Ashby, VIKOR and TOPSIS. Mater. Des. 2015, 65, 328–334. [Google Scholar] [CrossRef]
- Taylan, O.; Bafail, A.O.; Abdulaal, R.M.S.; Kabli, M.R. Construction projects selection and risk assessment by fuzzy AHP and fuzzy TOPSIS methodologies. Appl. Soft Comput. J. 2014, 17, 105–116. [Google Scholar] [CrossRef]
- Taylan, O.; Kaya, D.; Demirbas, A. An integrated multi attribute decision model for compressor selection in petrochemical industry applying fuzzy set theory. Energy Convers. Manag. Energy 2016, 117, 501–512. [Google Scholar] [CrossRef]
- Taylan, O.; Alidrisi, H.; Kabli, M. A multi-criteria decision-making approach that combines fuzzy TOPSIS and DEA methodologies. S. Afr. J. Ind. Eng. 2014, 25, 39–56. [Google Scholar] [CrossRef][Green Version]
- Mousavi, M.; Gitinavard, H.; Mousavi, S. A soft computing based-modified ELECTRE model for renewable energy policy selection with unknown information. Renew. Sustain. Energy Rev. 2017, 68, 774–787. [Google Scholar] [CrossRef]
- Kaya, T.; Kahraman, C. Multicriteria decision making in energy planning using a modified fuzzy TOPSIS methodology. Expert Syst. Appl. 2011, 38, 6577–6585. [Google Scholar] [CrossRef]
- Aramco, S. Saudi Aramco, Annual Review 2016; Saudi Aramco: Dhahran, Saudi Arabia, 2017. [Google Scholar]
- Al-sasi, B.; Taylan, O.; Demirbas, A. The impact of oil price volatility on economic growth. Energy Sources Part B Econ. Plan. Policy 2017, 12, 847–852. [Google Scholar] [CrossRef]
- Demirbas, A.; Coban, V.; Taylan, O.; Kabli, M.R. Aerobic digestion of sewage sludge for waste treatment. Energy Sources Part A Recovery Util. Environ. Eff. 2017, 39, 1056–1062. [Google Scholar] [CrossRef]
- Taylan, O.; Demirbas, A. Forecasting and Analysis of Energy Consumption for Transportation in Kingdom of Saudi Arabia. Energy Sources Part B Econ. Plan. Policy 2016, 11, 1150–1157. [Google Scholar] [CrossRef]
- Wen, M.; Li, H. Fuzzy data envelopment analysis (DEA): Model and ranking method. J. Comput. Appl. Math. 2009, 223, 872–878. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision-making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Rojas-Zerpa, J.C.; Yusta, J.M. Application of multicriteria decision methods for electric supply planning rural and remote areas. Renew. Sustain. Energy Rev. 2015, 52, 557–571. [Google Scholar] [CrossRef]
- Kou, G.; Ergu, D.; Lin, C.; Chen, Y. Pairwise comparison matrix in multiple criteria decision making. Technol. Econ. Dev. Econ. 2016, 22, 738–765. [Google Scholar] [CrossRef]
- Chatterjeea, P.; Chakraborty, S. A comparative analysis of VIKOR method and its variants. Decis. Sci. Lett. 2016, 5, 469–486. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).