Multivariable Analysis of Transport Network Seismic Performance: Mexico City
Abstract
1. Introduction
2. Methodology
- Definition of input and output variables to define the TSP index for the network
- Characterization of the urban area and selection of scenarios to be analyzed
- Seismic hazard and structural seismic vulnerability assessment, including site response analyses.
- Obtaining spatial distribution of damage and road closures scenarios, using geographic information systems techniques (GIS).
- Modeling post-earthquake traffic behavior
- Evaluation of network performance, through the TSP index, and development of SPM maps and SPB curves.
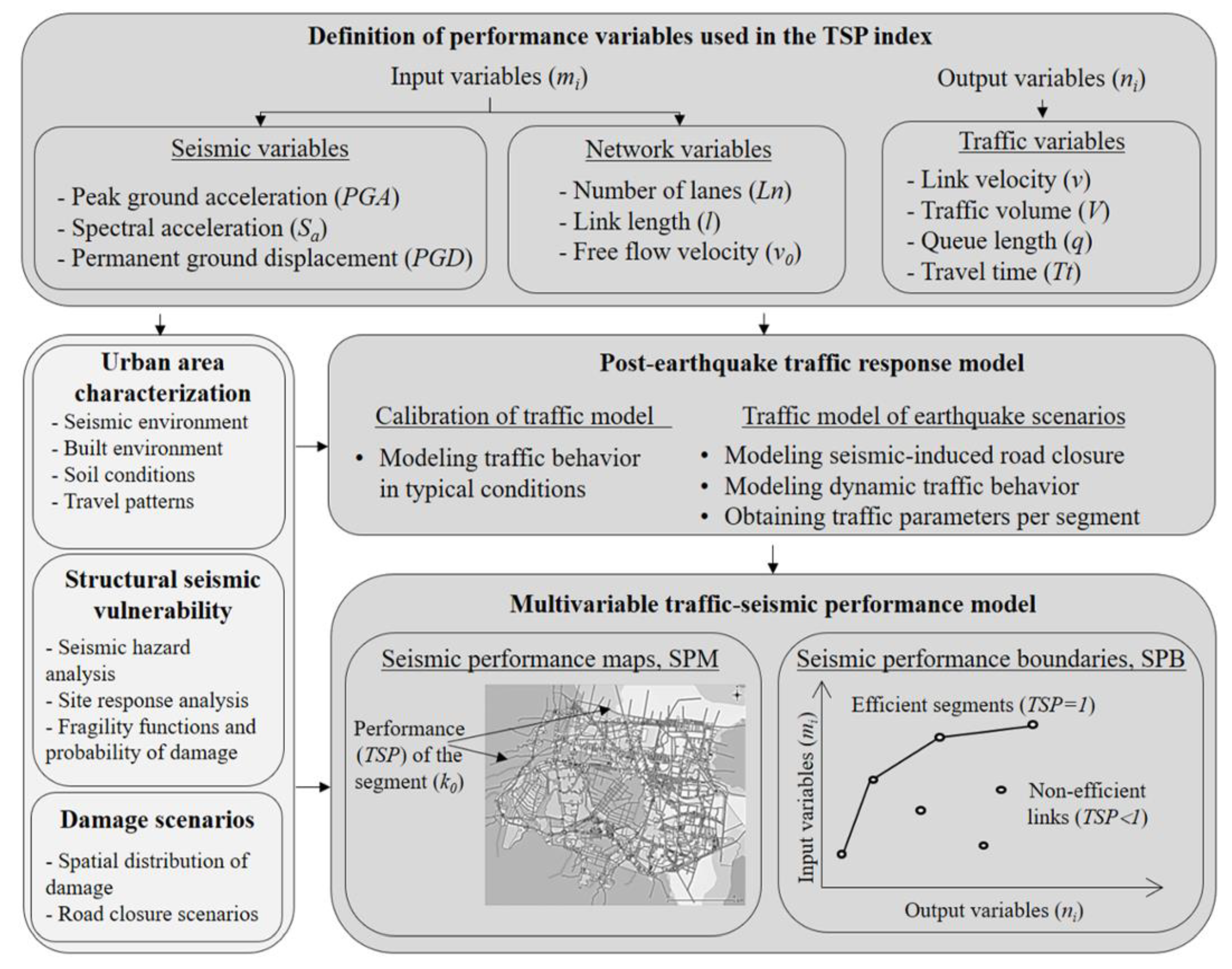
2.1. Definition of Variables for the Multivariable Performance Model and TSP Index
Data Envelopment Analysis
2.2. Characterization of the Urban Area
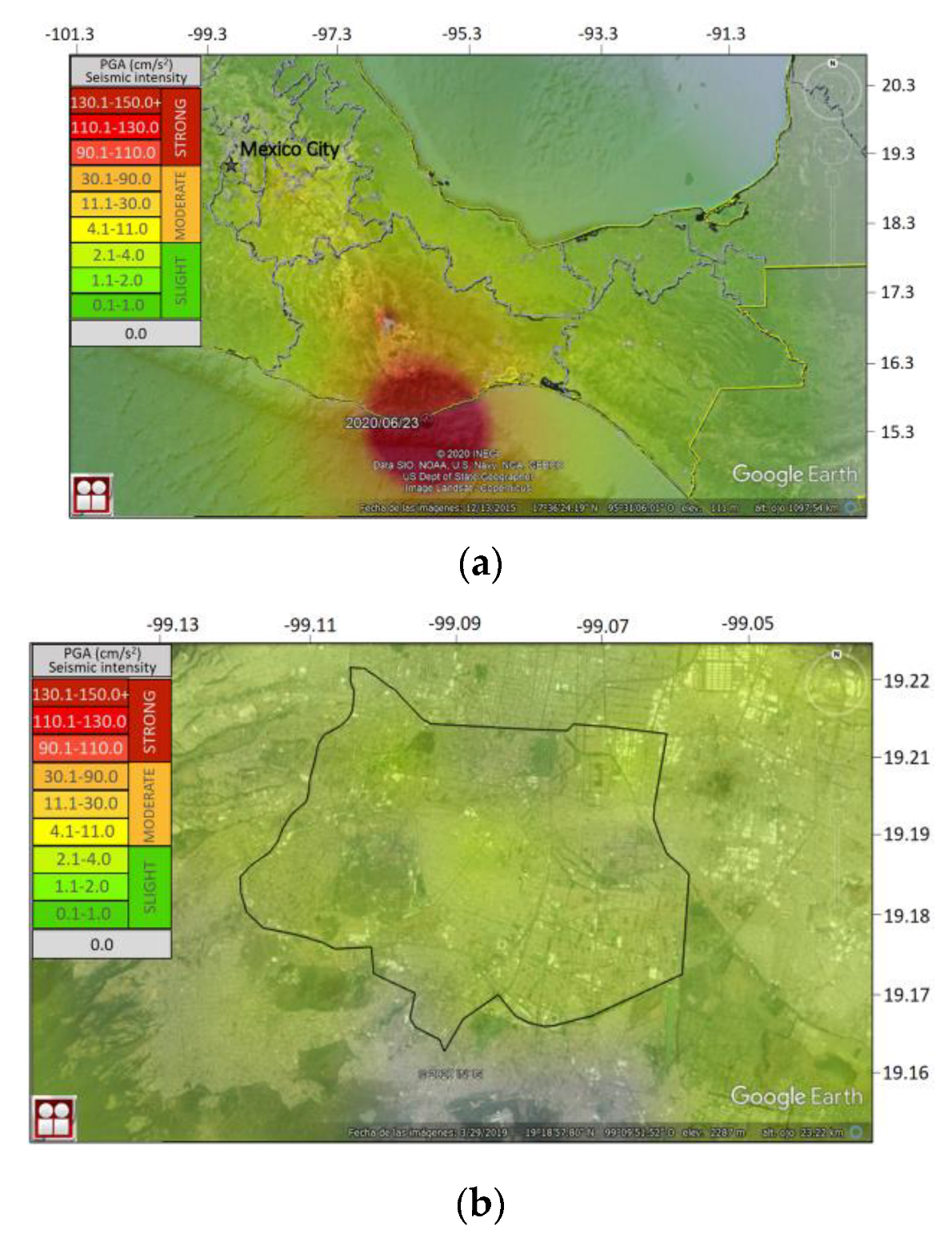
2.2.1. The Seismic Environment
2.2.2. The Built Environment
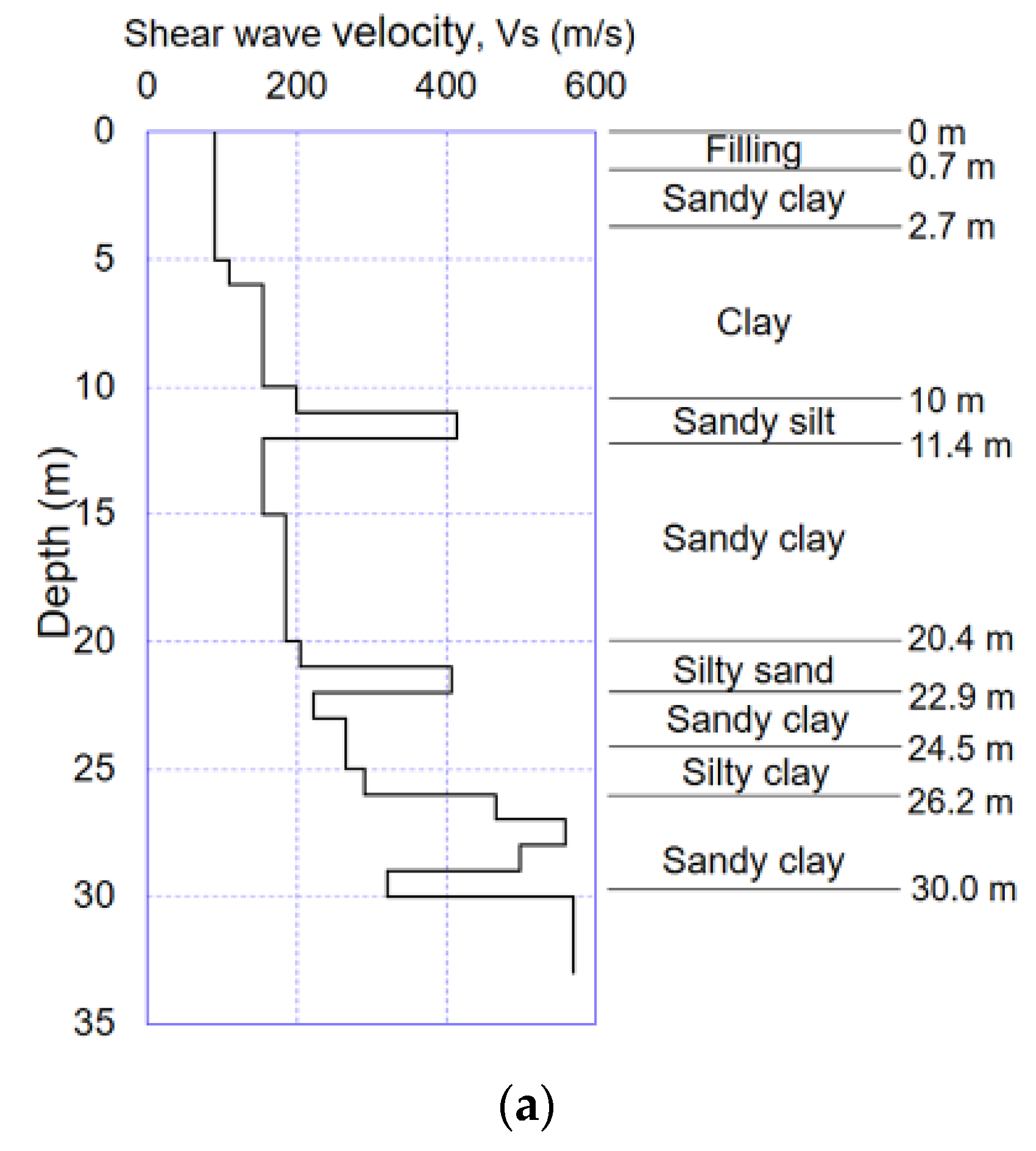
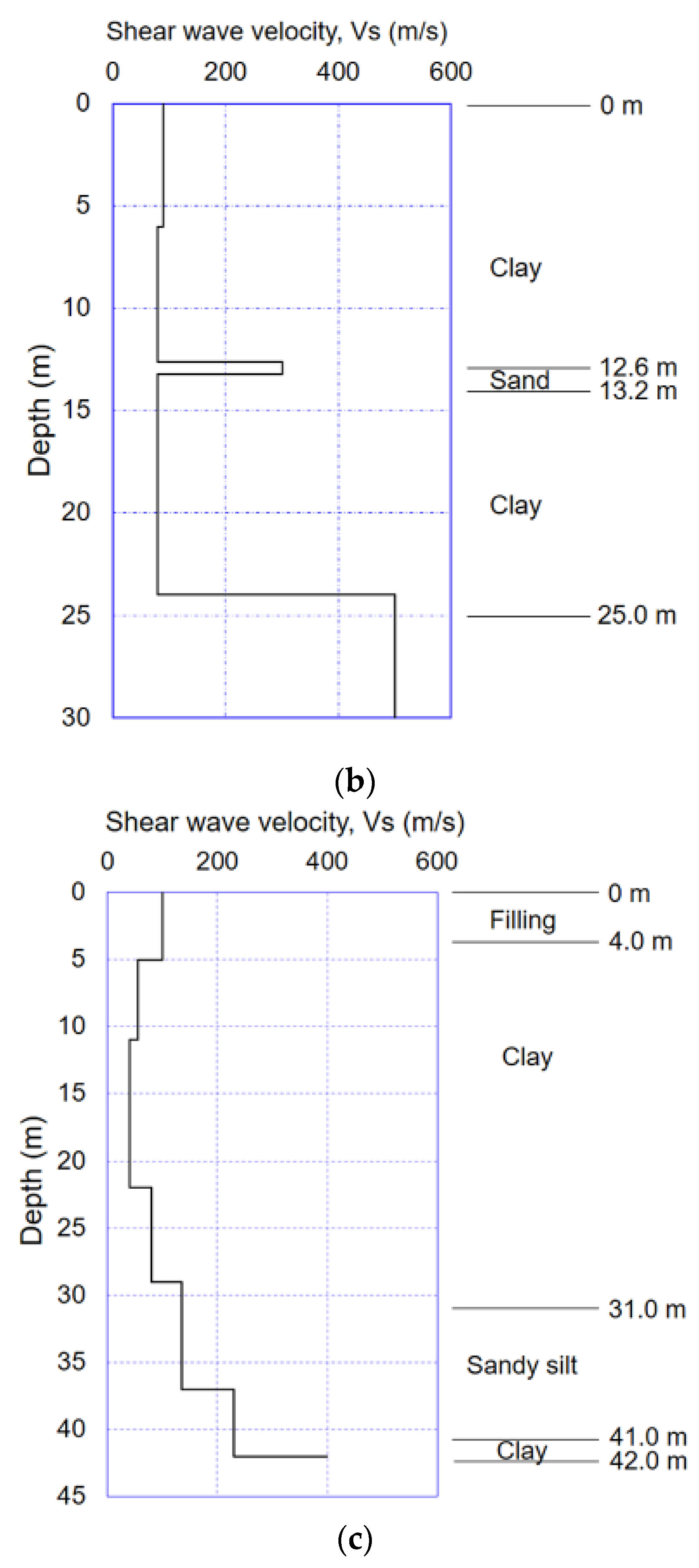
2.2.3. Soil Conditions
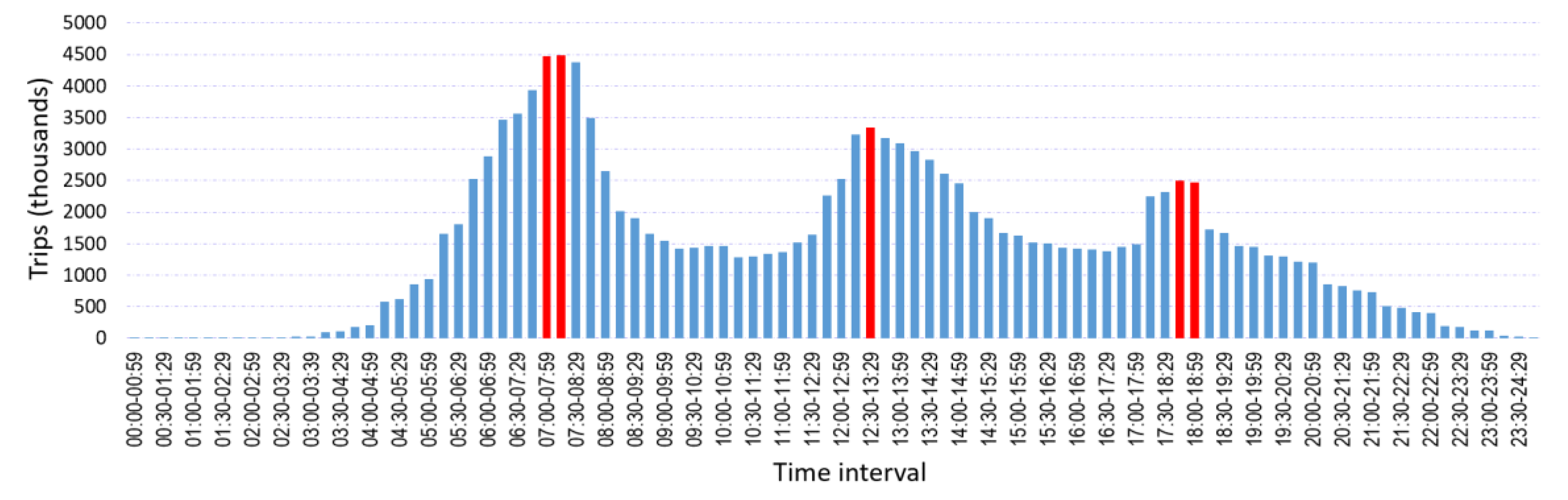
2.2.4. Travel Patterns
2.2.5. Scenarios Selection
2.3. Structural Seismic Vulnerability
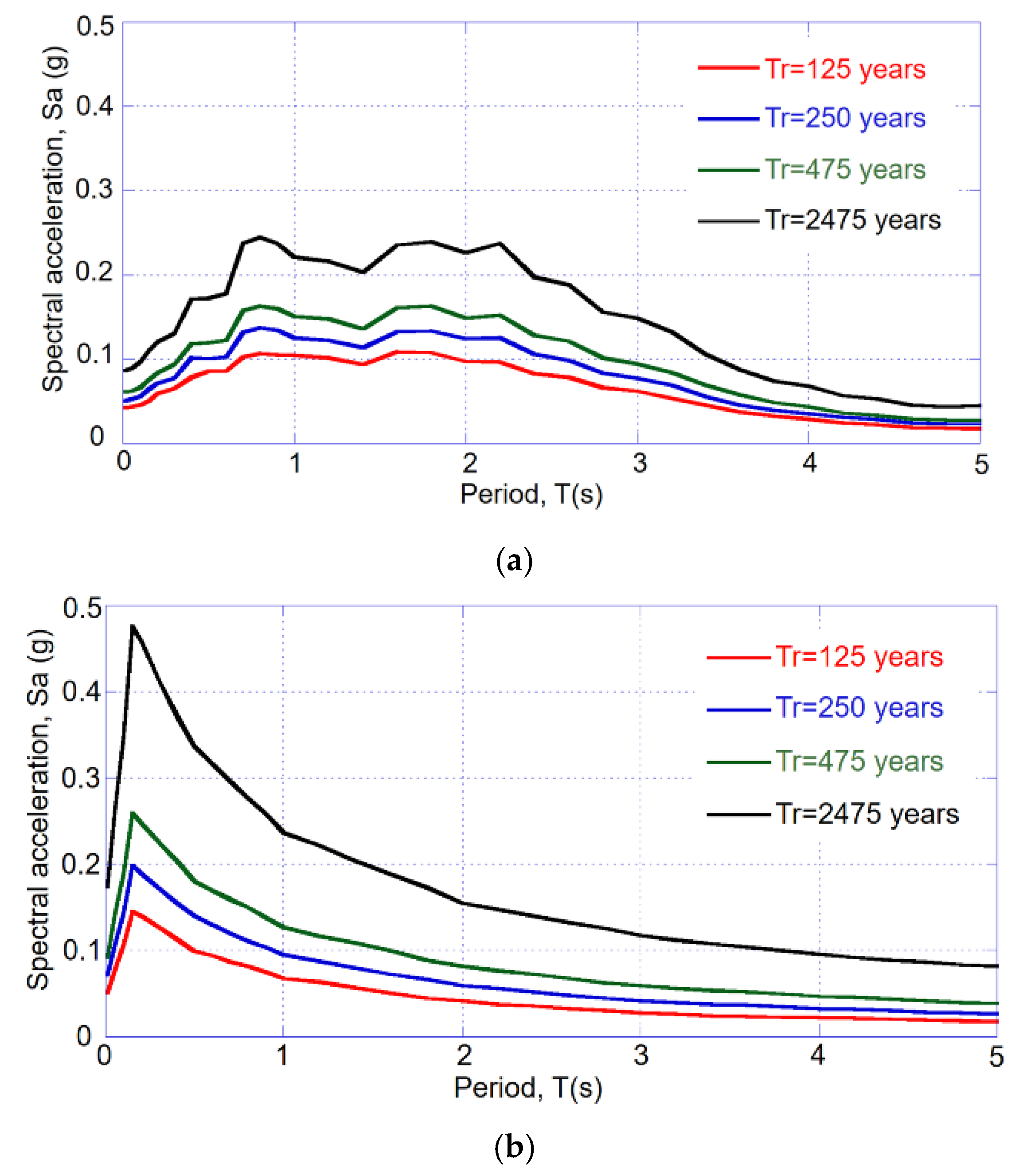
2.3.1. Seismic Hazard
- Characterization of all seismic sources in terms of their probability of occurrence;
- Selection, or development, of appropriate recurrence models, based on historical seismicity and available records, to estimate the rate at which a given event will be exceeded, for each seism genic zone;
- Election of attenuation relationships, to estimate a set of seismic intensity parameters for the site;
- Generation of seismic hazard curves;
- Development of a UHS from the hazard curves for a given return period.
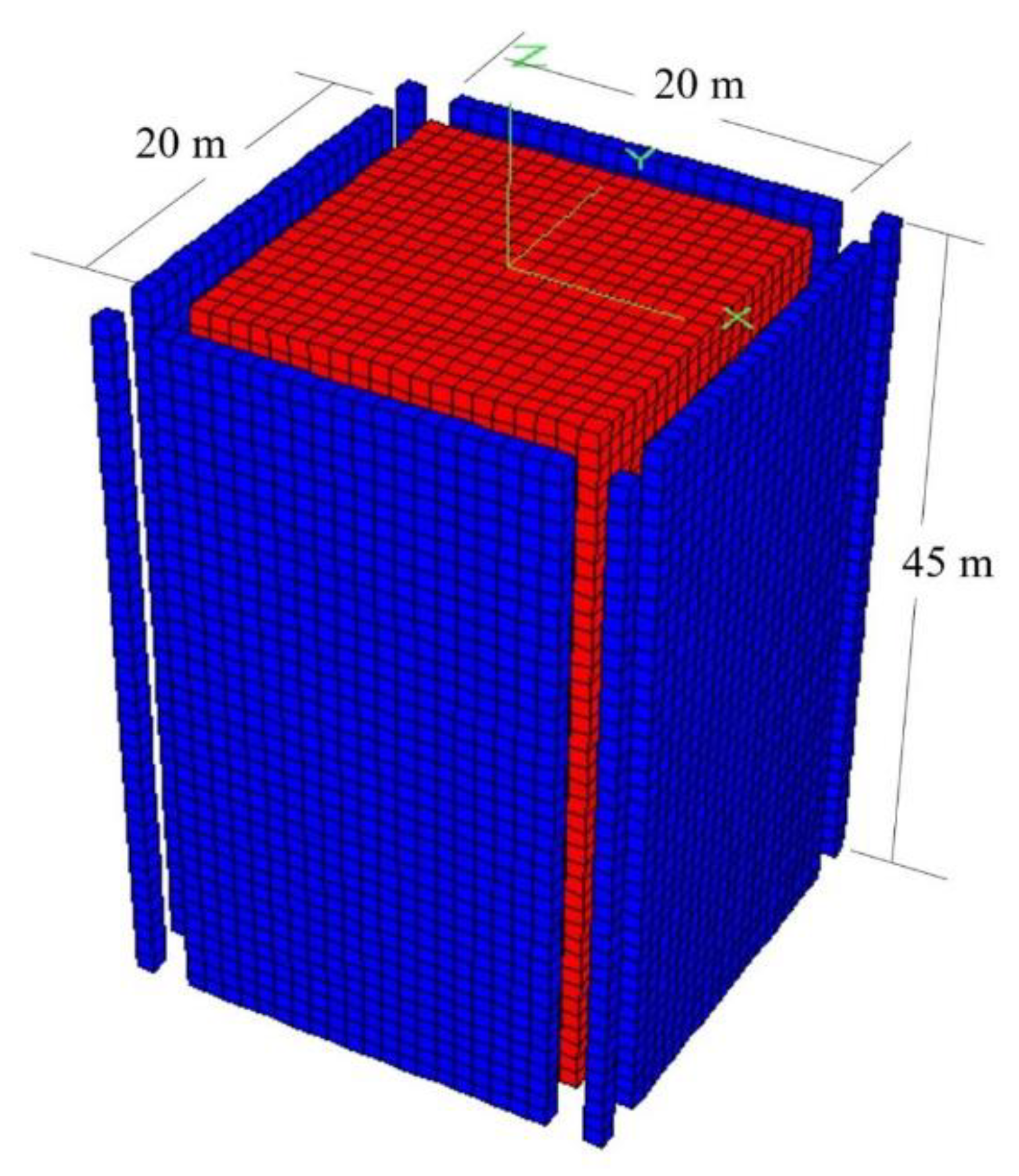
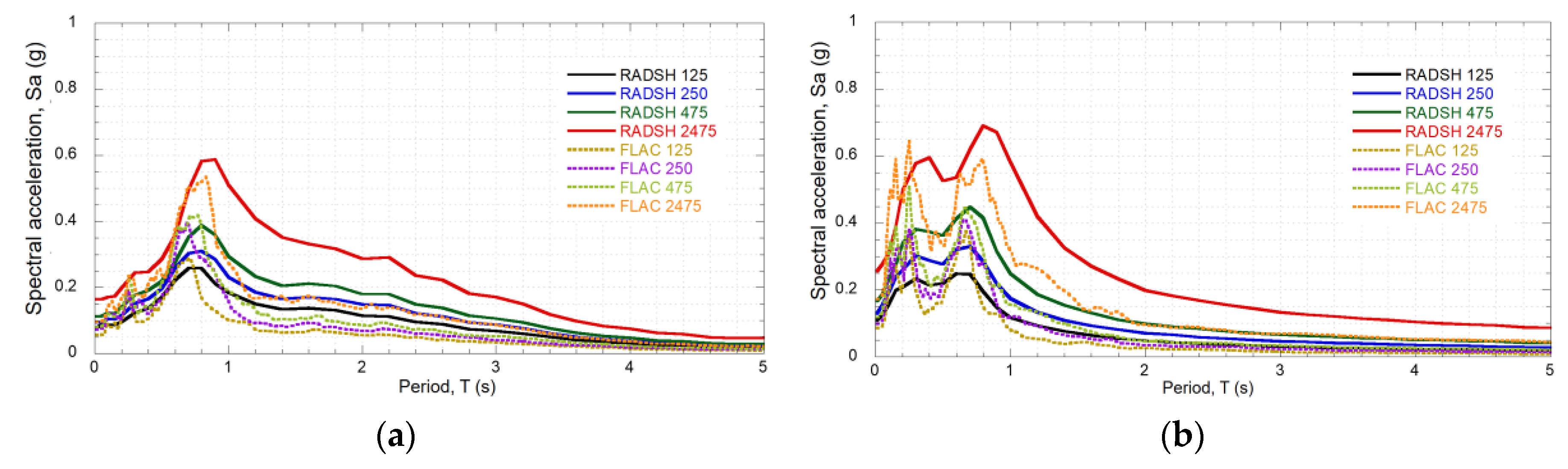
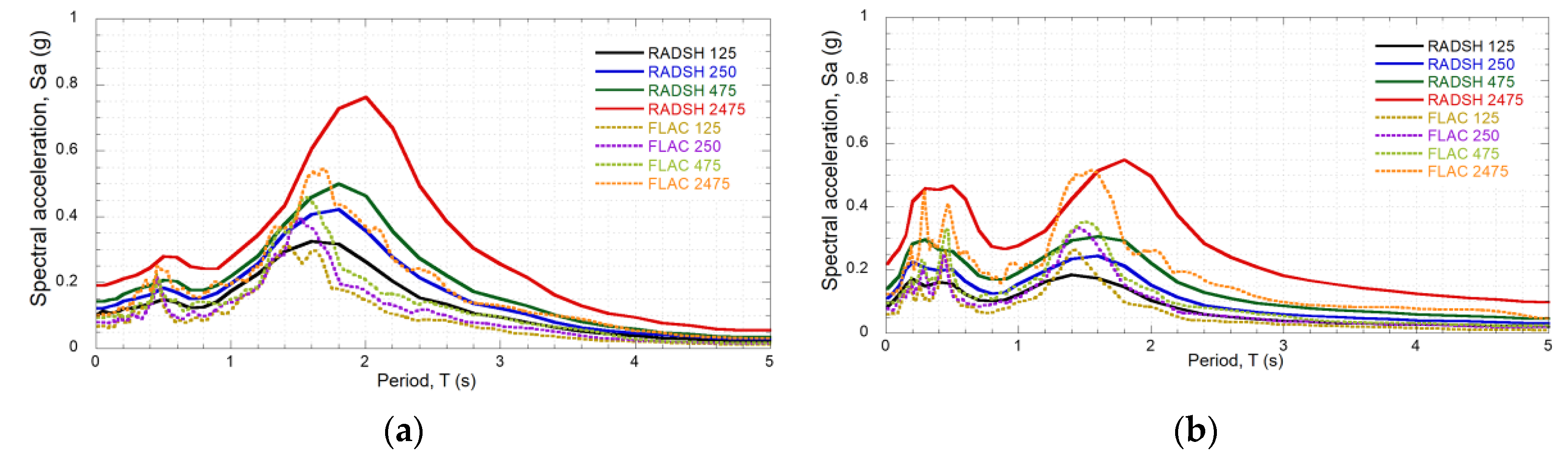
2.3.2. Site Response Analysis
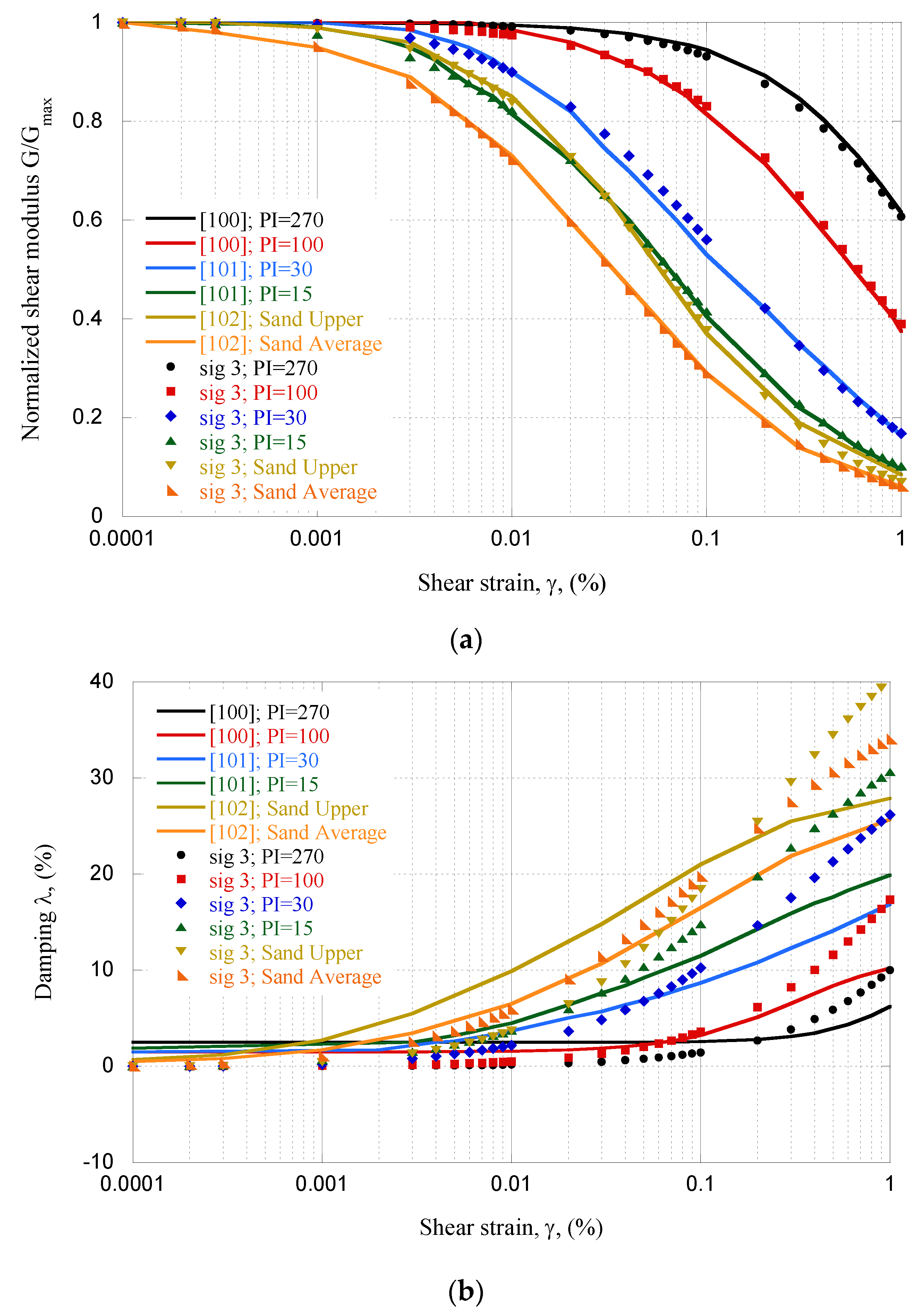
2.3.3. Fragility Curves
2.3.4. Damage Probabilities
2.4. Damage Distribution
2.4.1. Spatial Distribution of Damage
2.4.2. Segments Closure Criteria
2.5. Post-Earthquake Traffic Model
2.5.1. Traffic Model
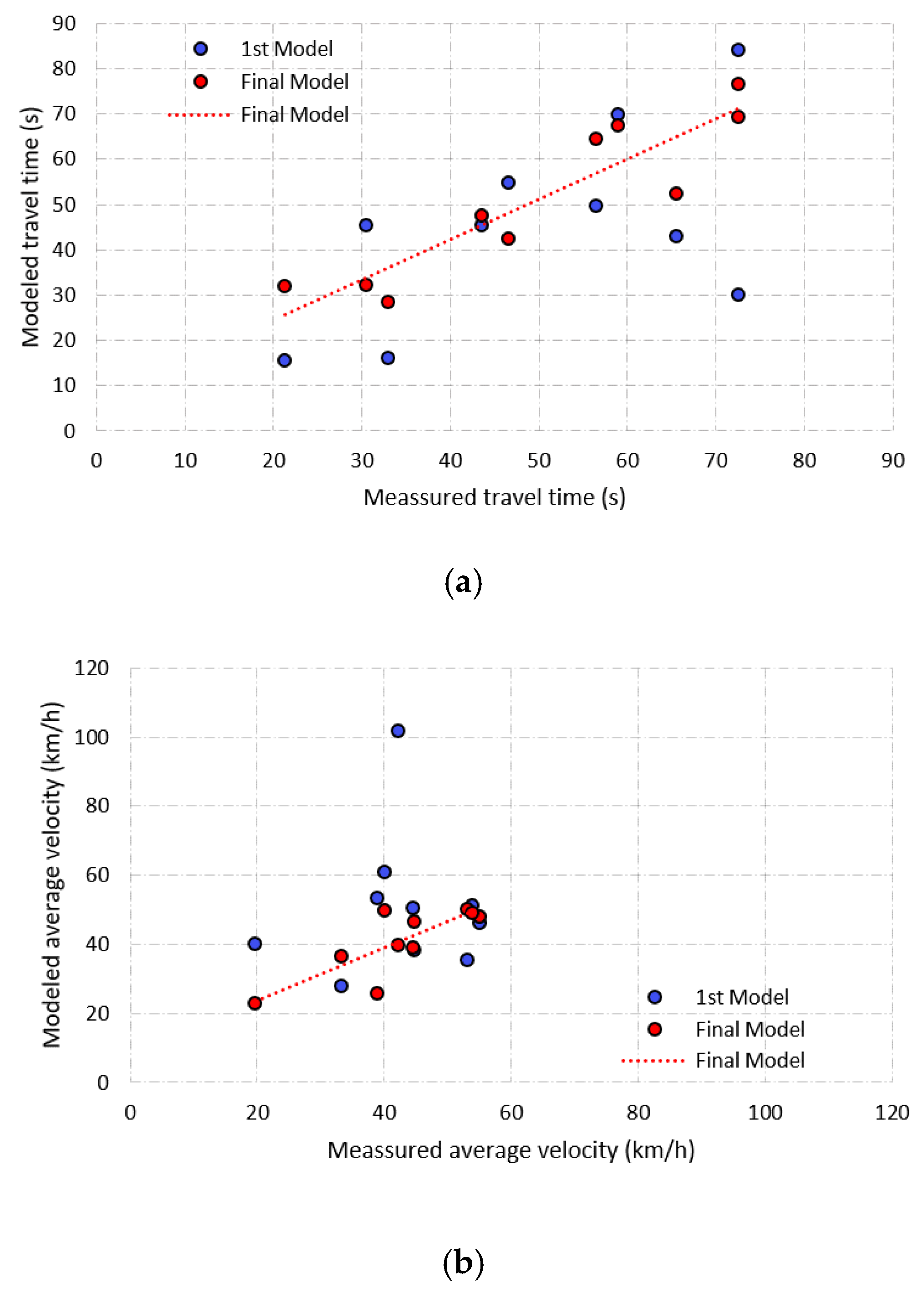
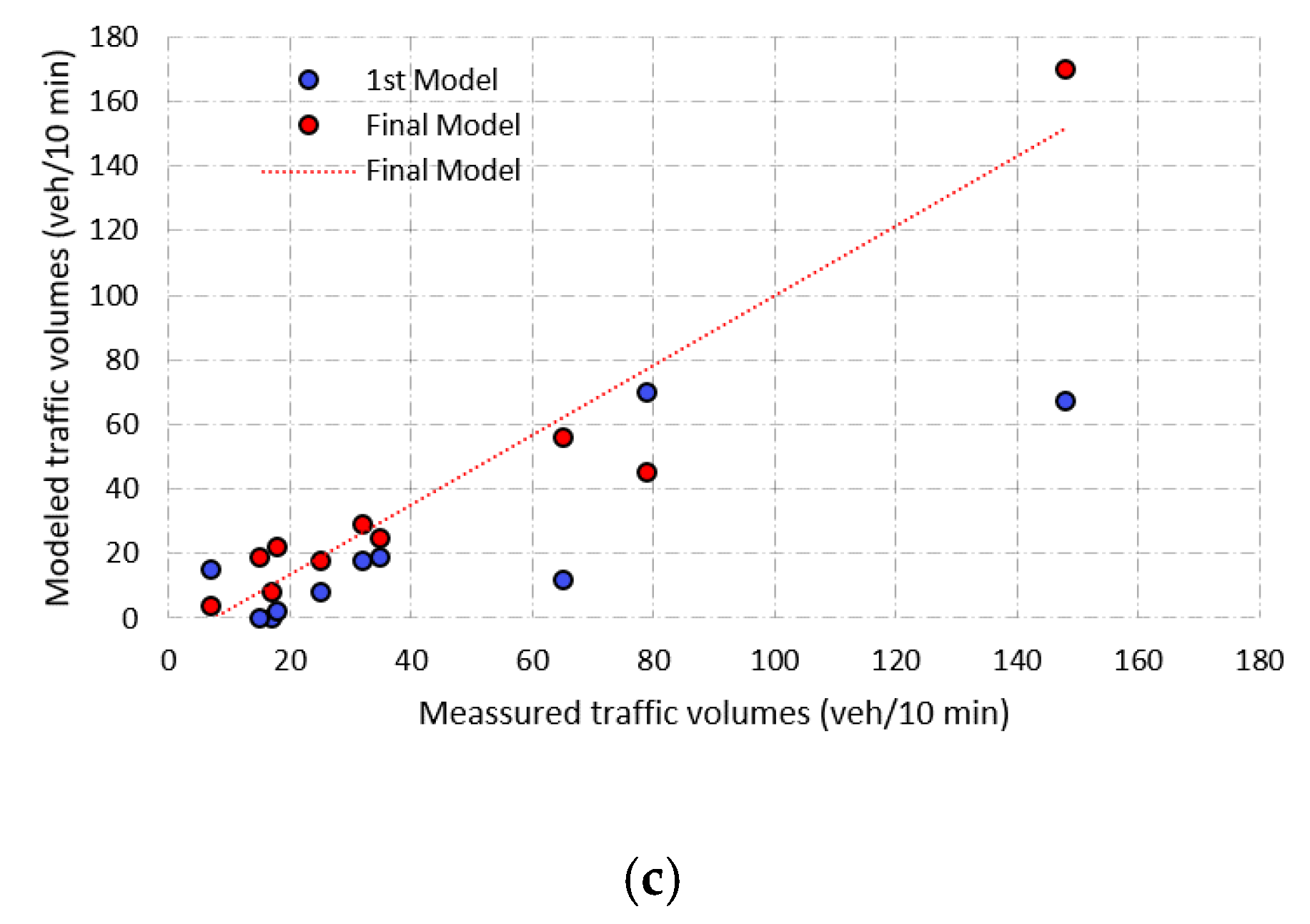
2.5.2. Calibration of Traffic Model
2.5.3. Traffic Modelling of Earthquake Scenarios
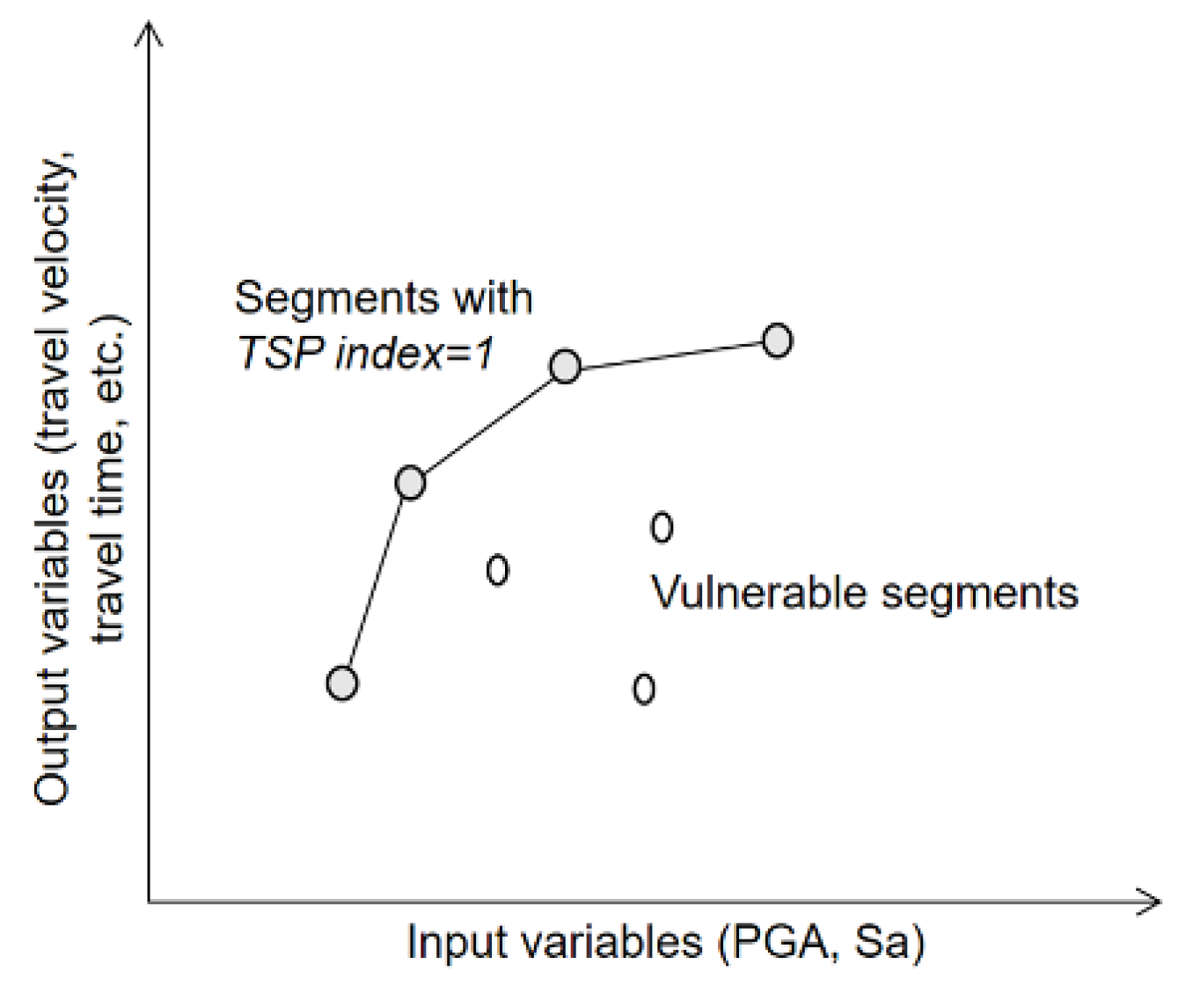
2.6. Multivariable Network Performance Model
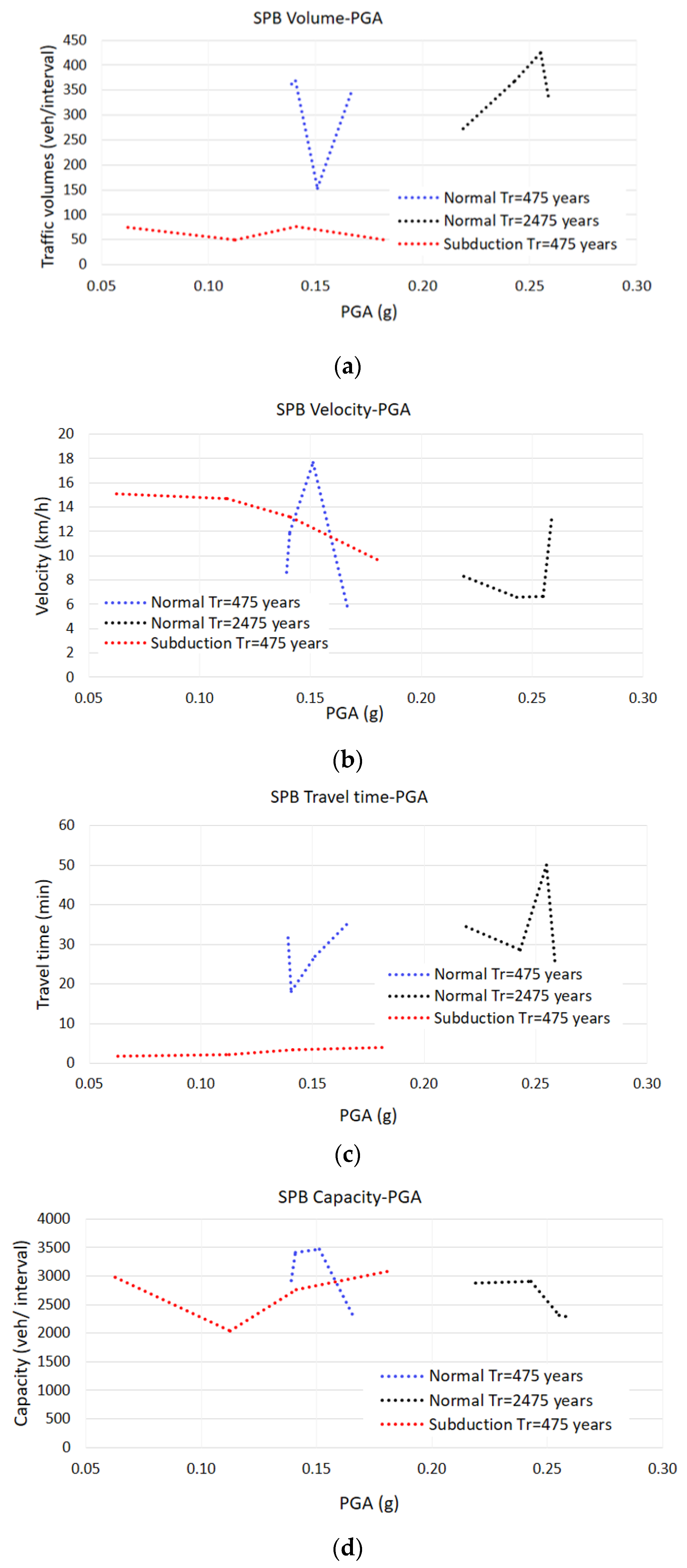
Seismic Performance Boundaries
3. Case Study: Mexico City Road Network
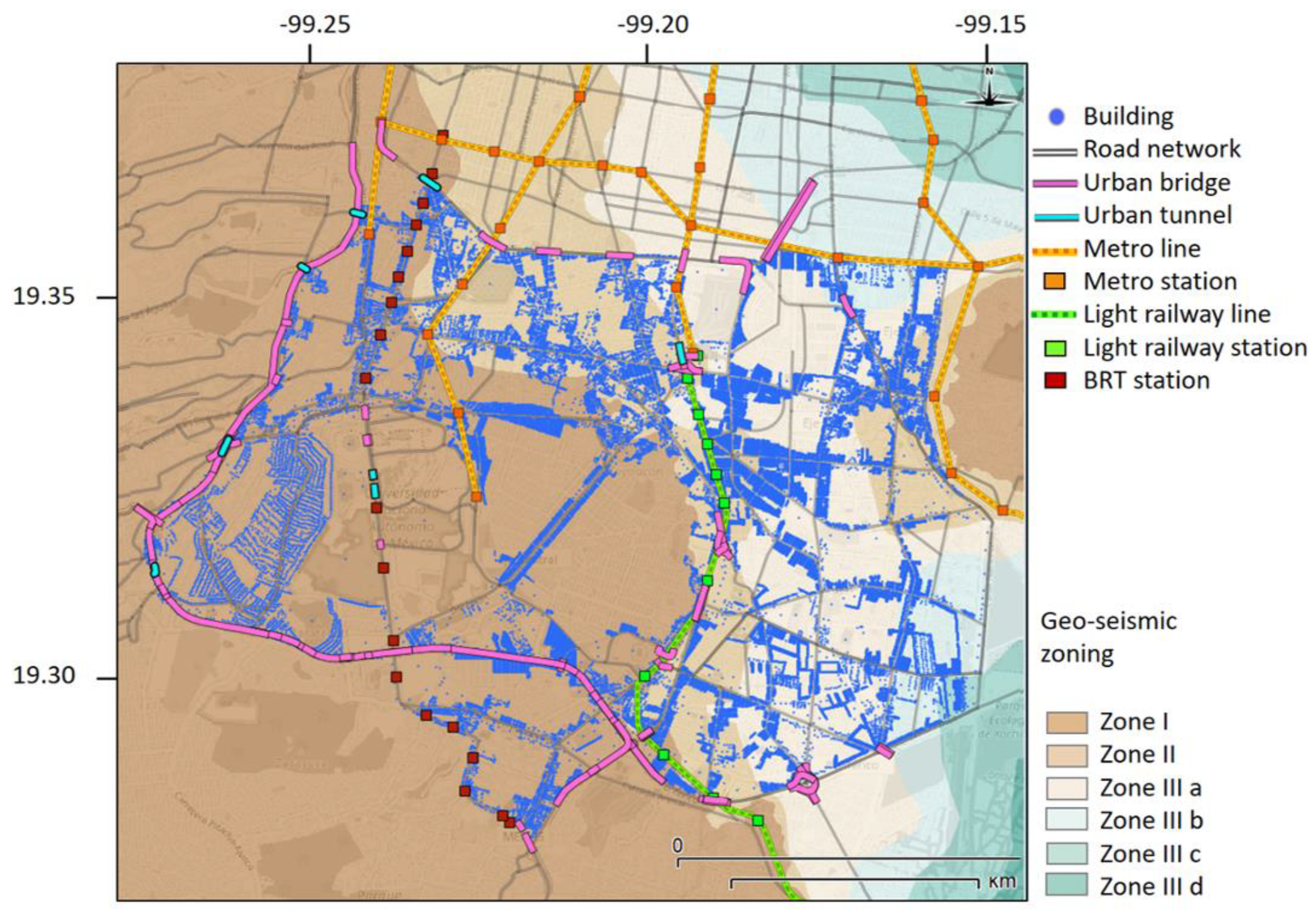
3.1. Characterization of the Urban Area
3.1.1. Seismic Environment
3.1.2. Built Environment
3.1.3. Subsoil Conditions
3.1.4. Travel Patterns
3.2. Structural Seismic Vulnerability
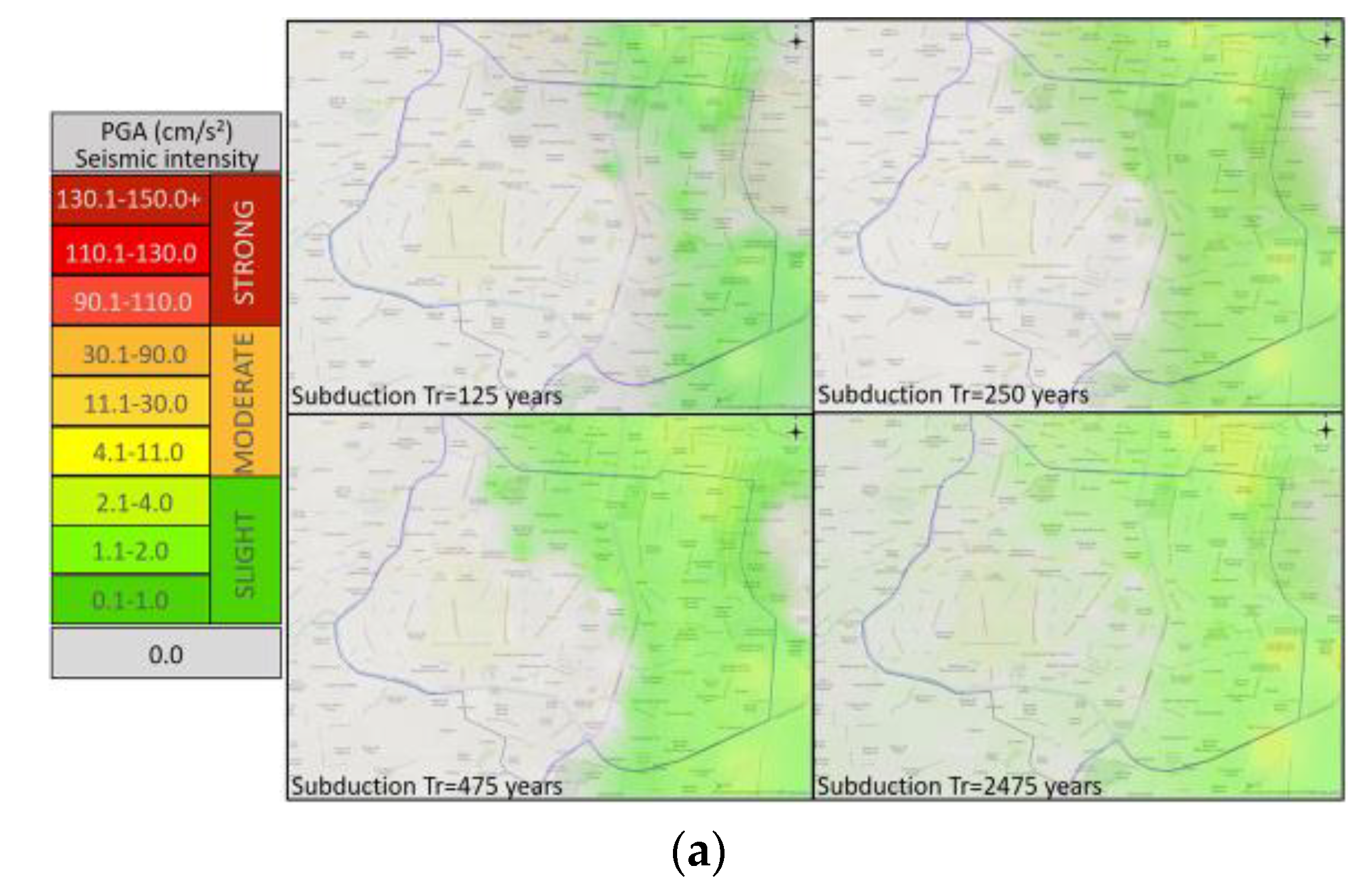
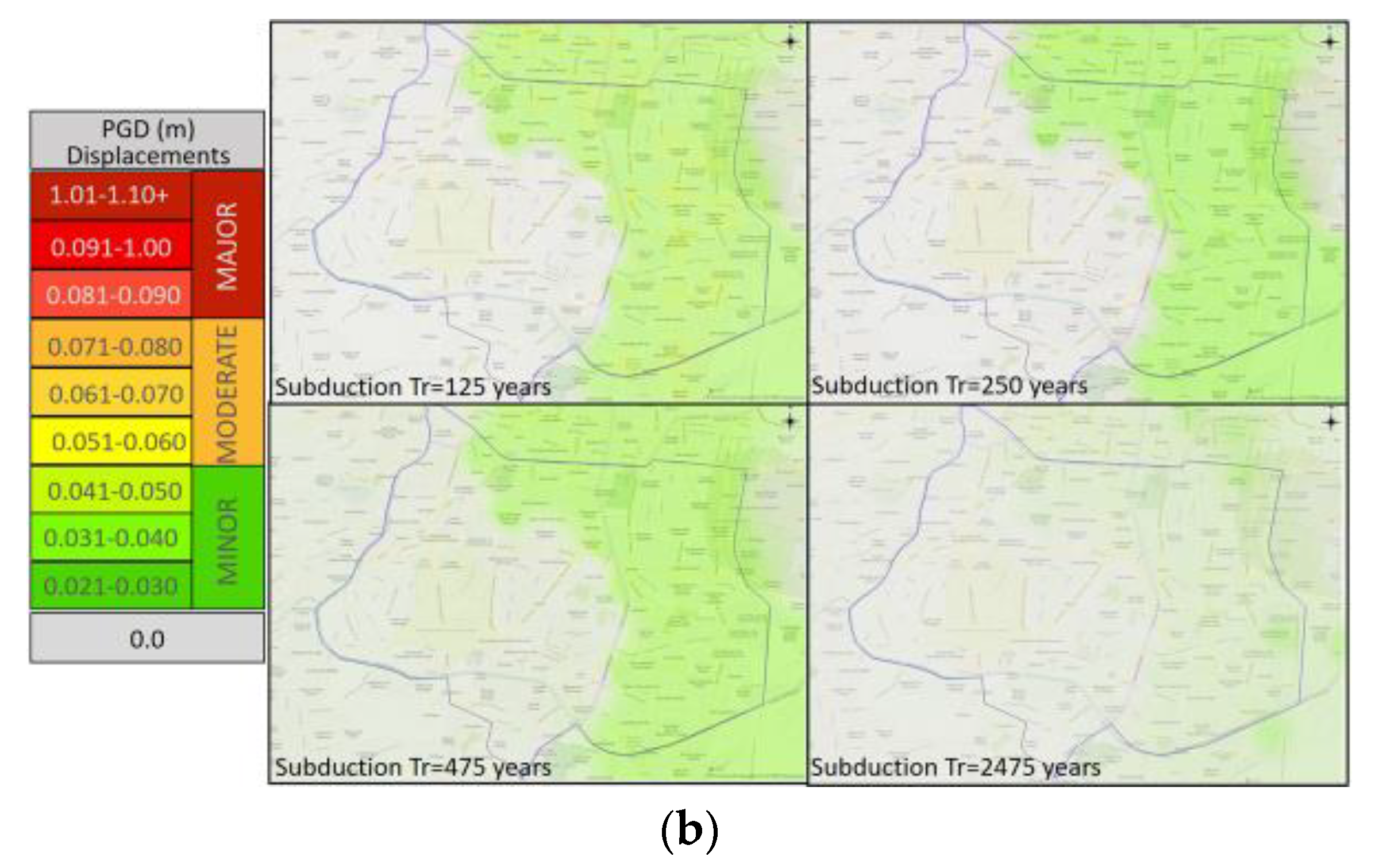
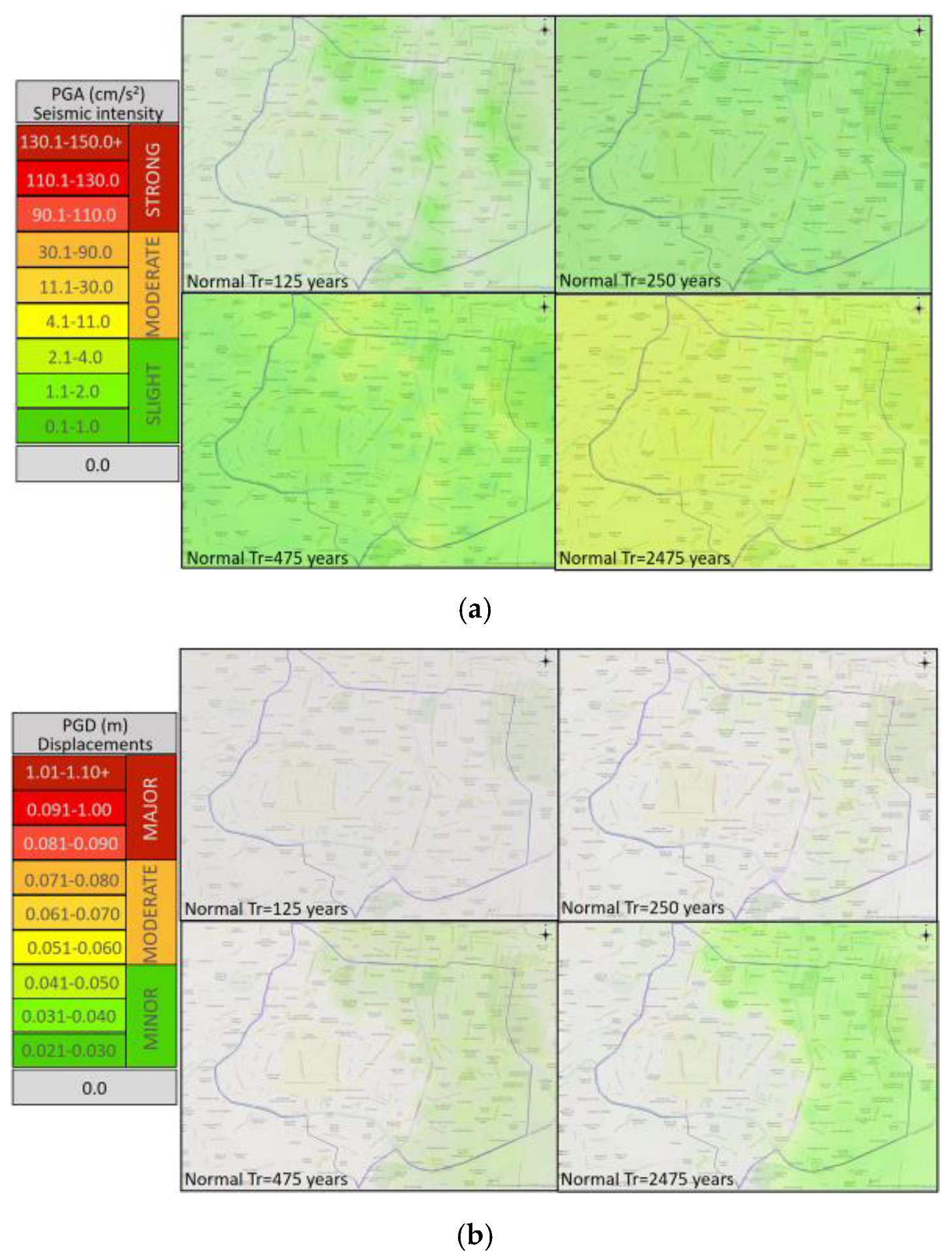
3.2.1. Seismic Hazard
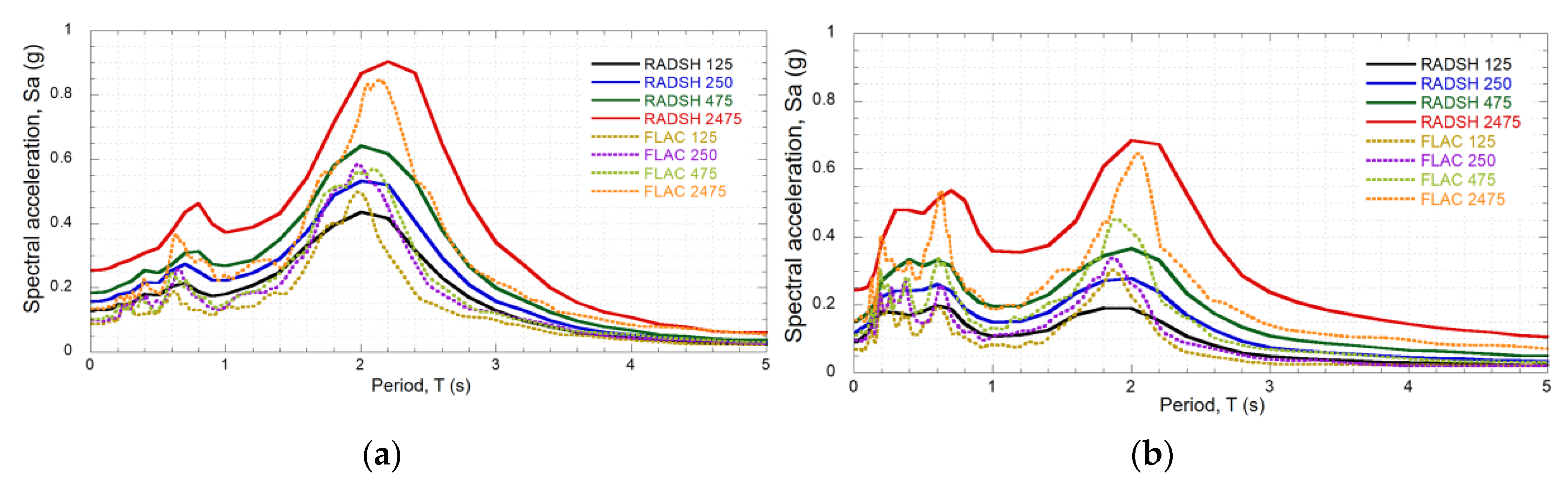
3.2.2. Site Response Analysis
3.2.3. Fragility Curves
3.2.4. Damage Probabilities
3.3. Damage Scenarios
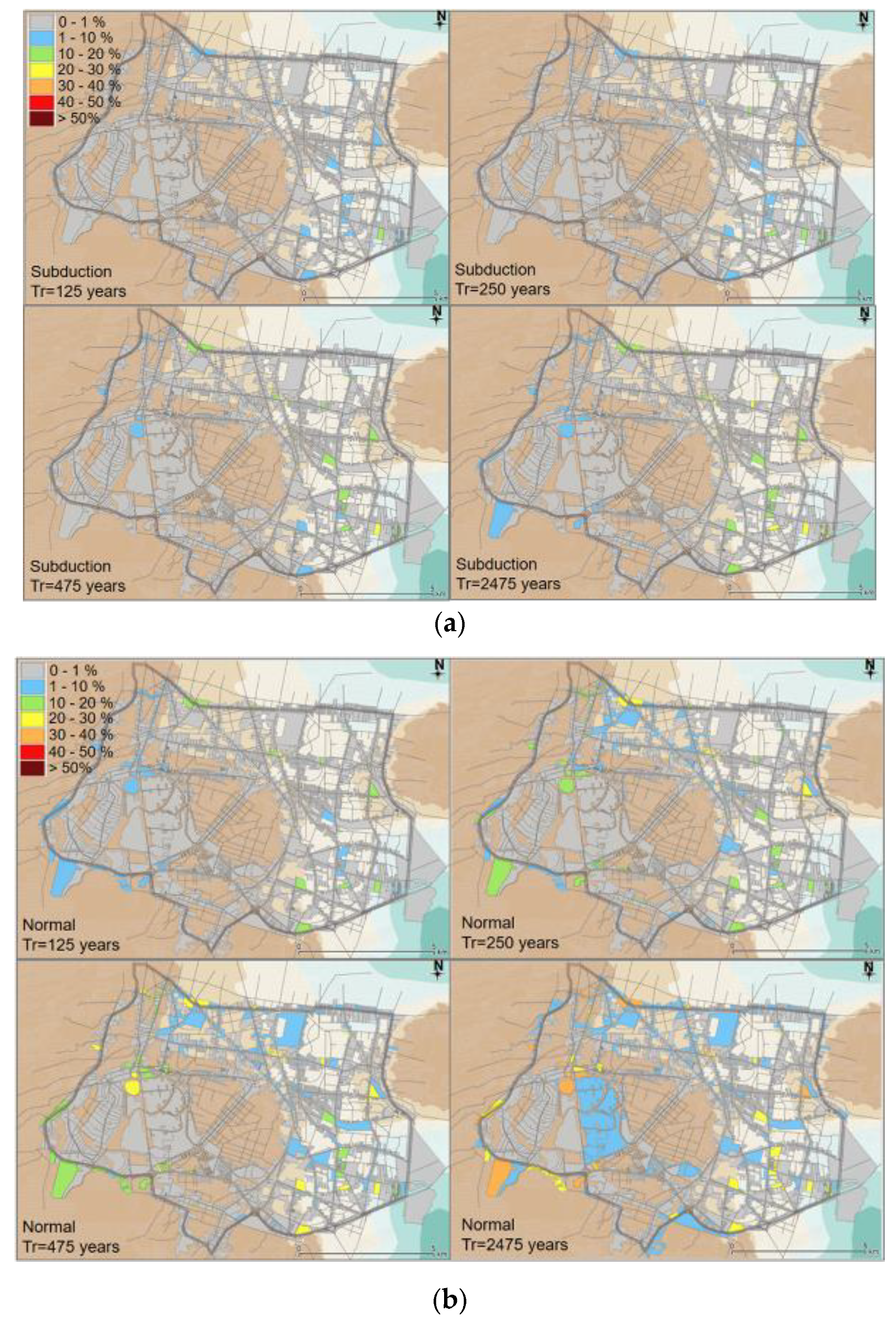
3.3.1. Spatial Distribution of Damage States
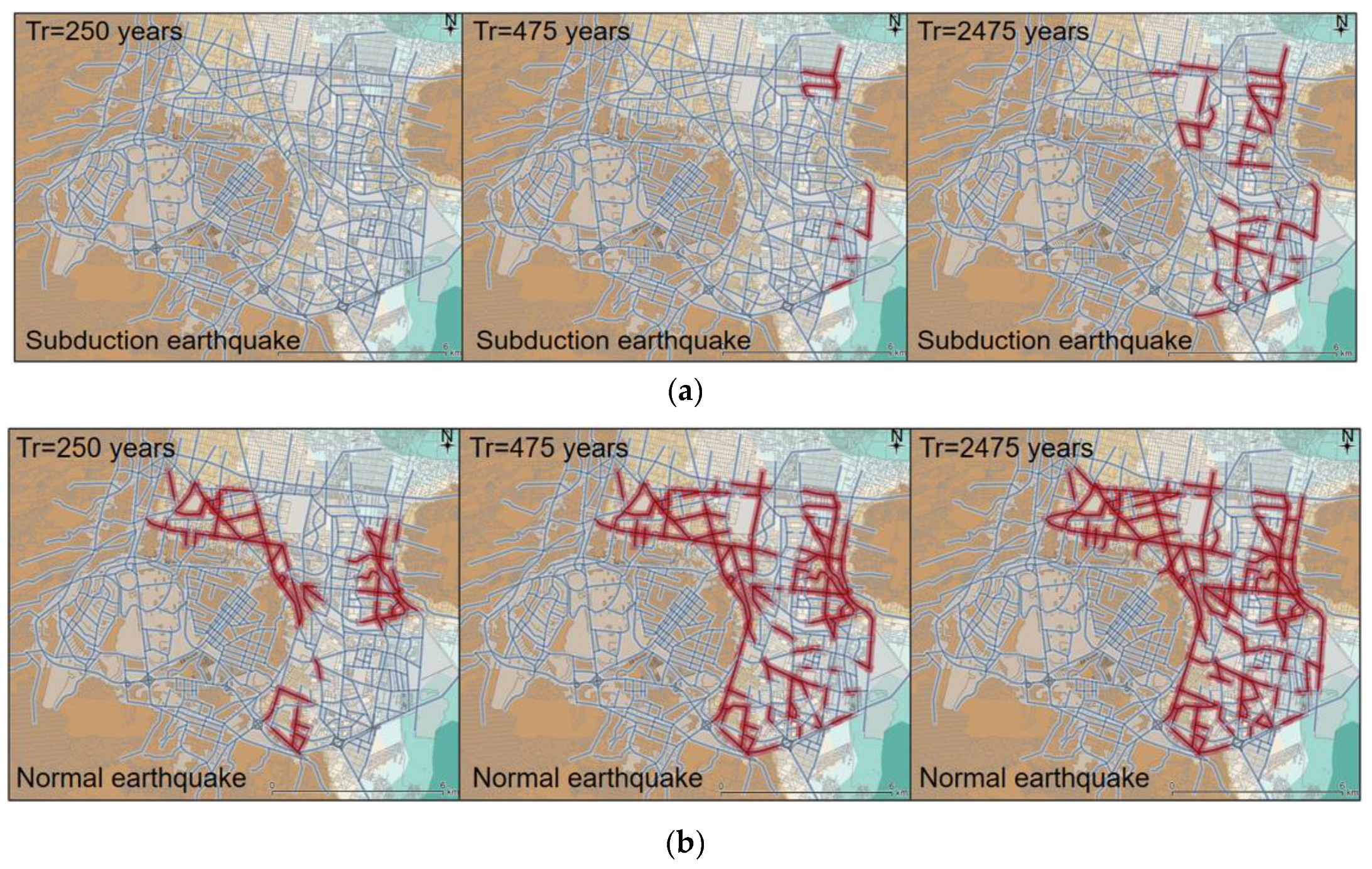
3.3.2. Road Closure Criteria
3.4. Dynamic Traffic Modelling
3.4.1. Calibration of Traffic Model
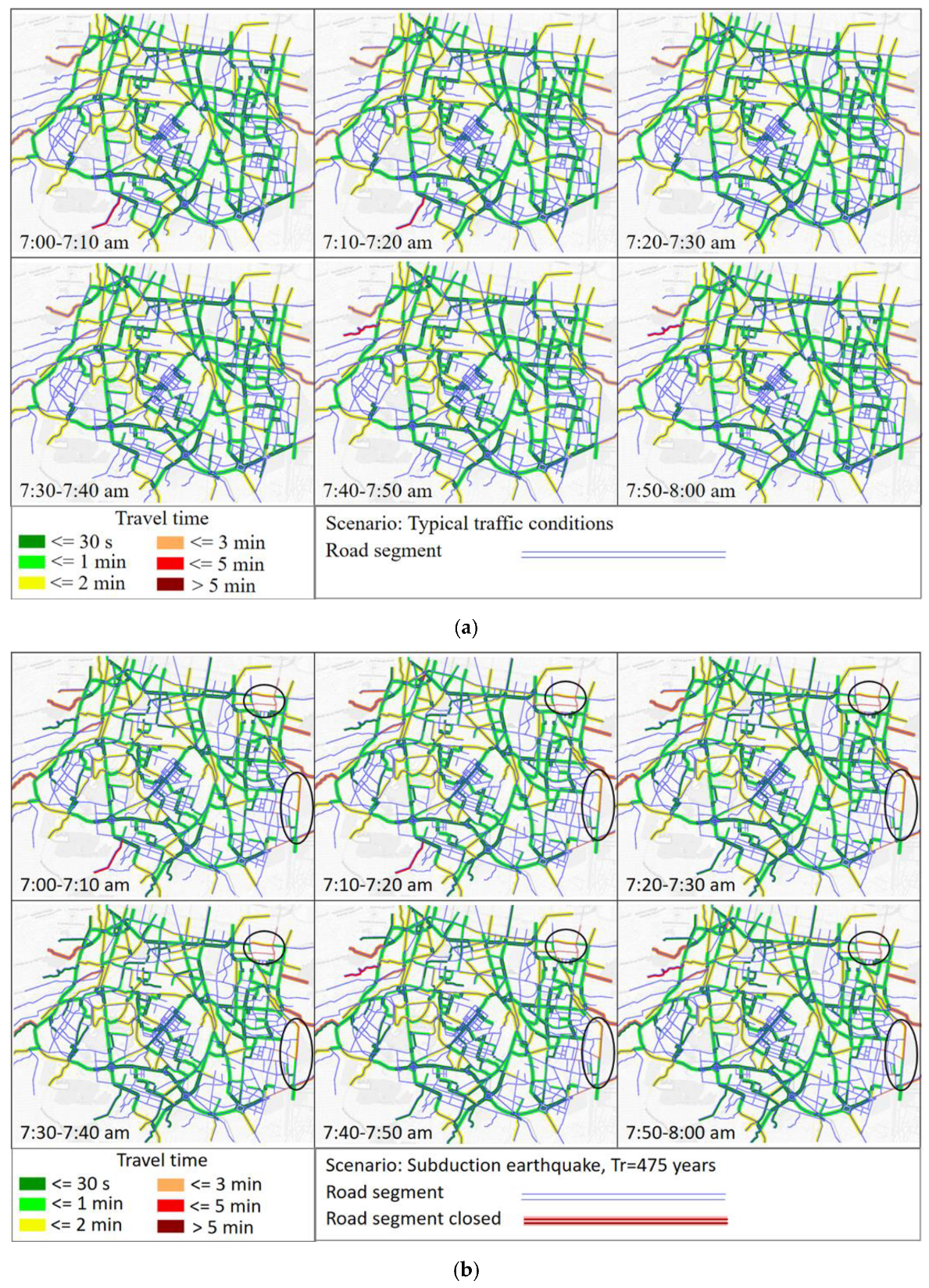
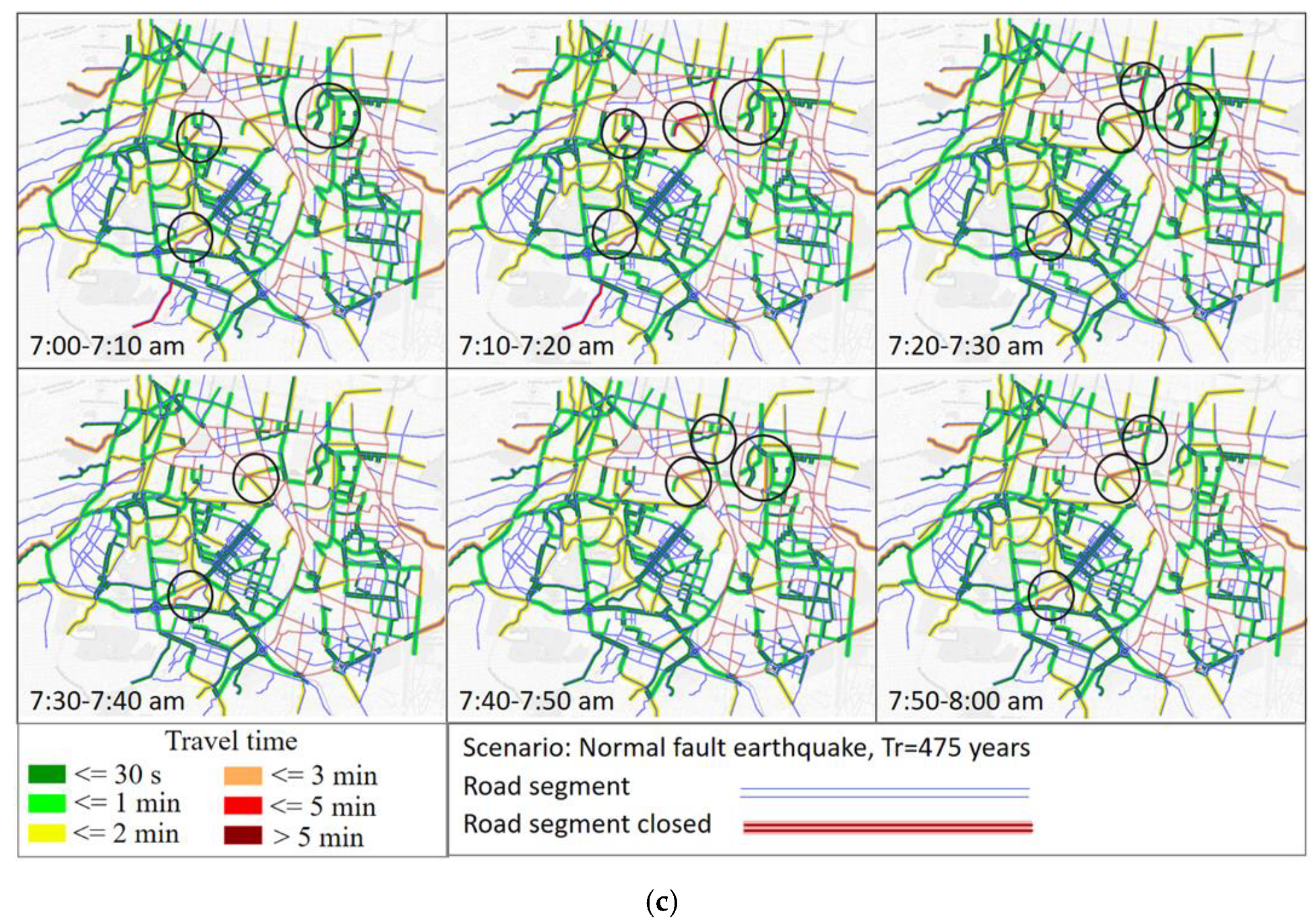
3.4.2. Earthquake Scenario Modelling
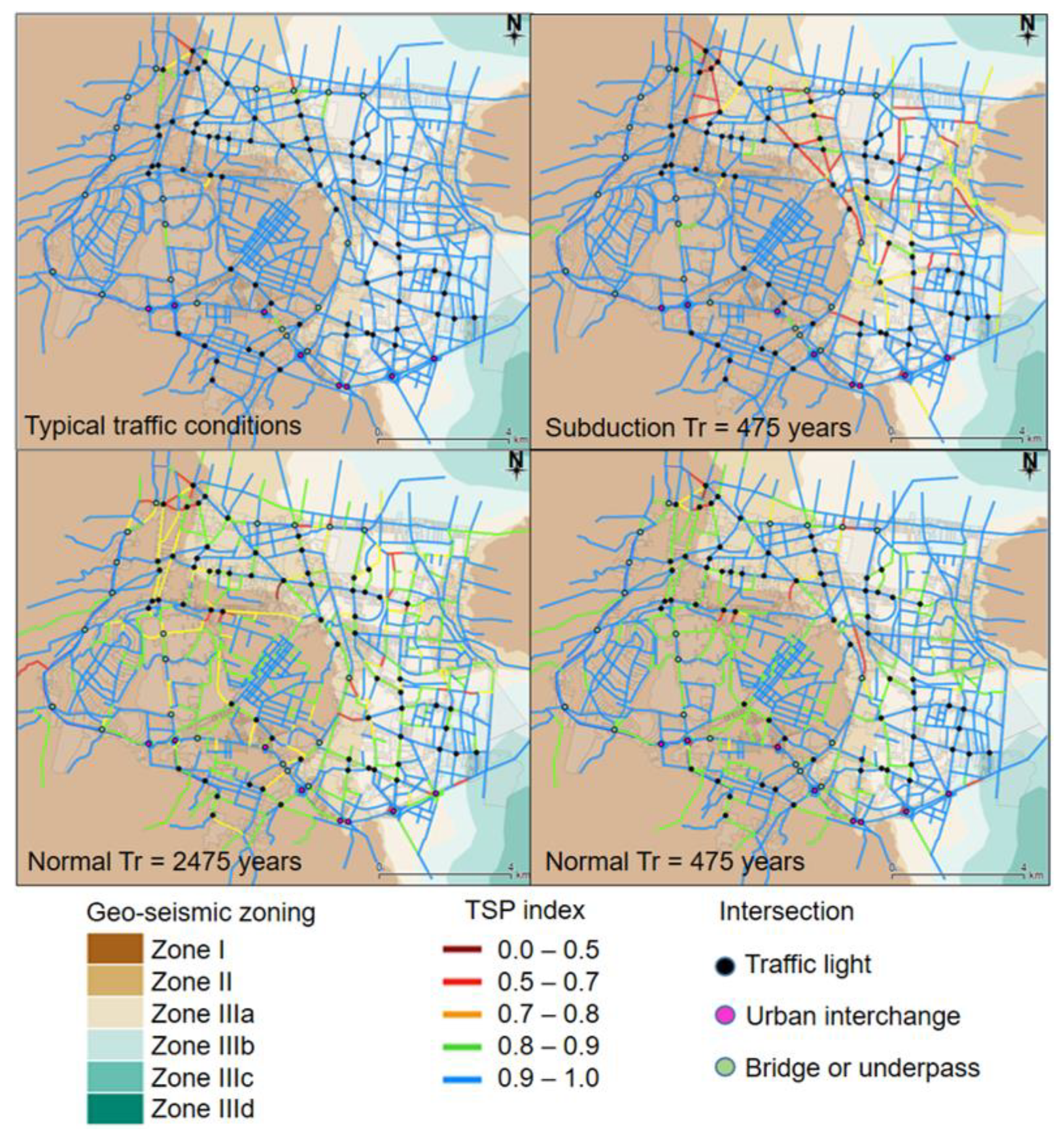
3.5. Multivariable Performance Evaluation and TSP Index
3.5.1. Seismic Performance Maps, SPM
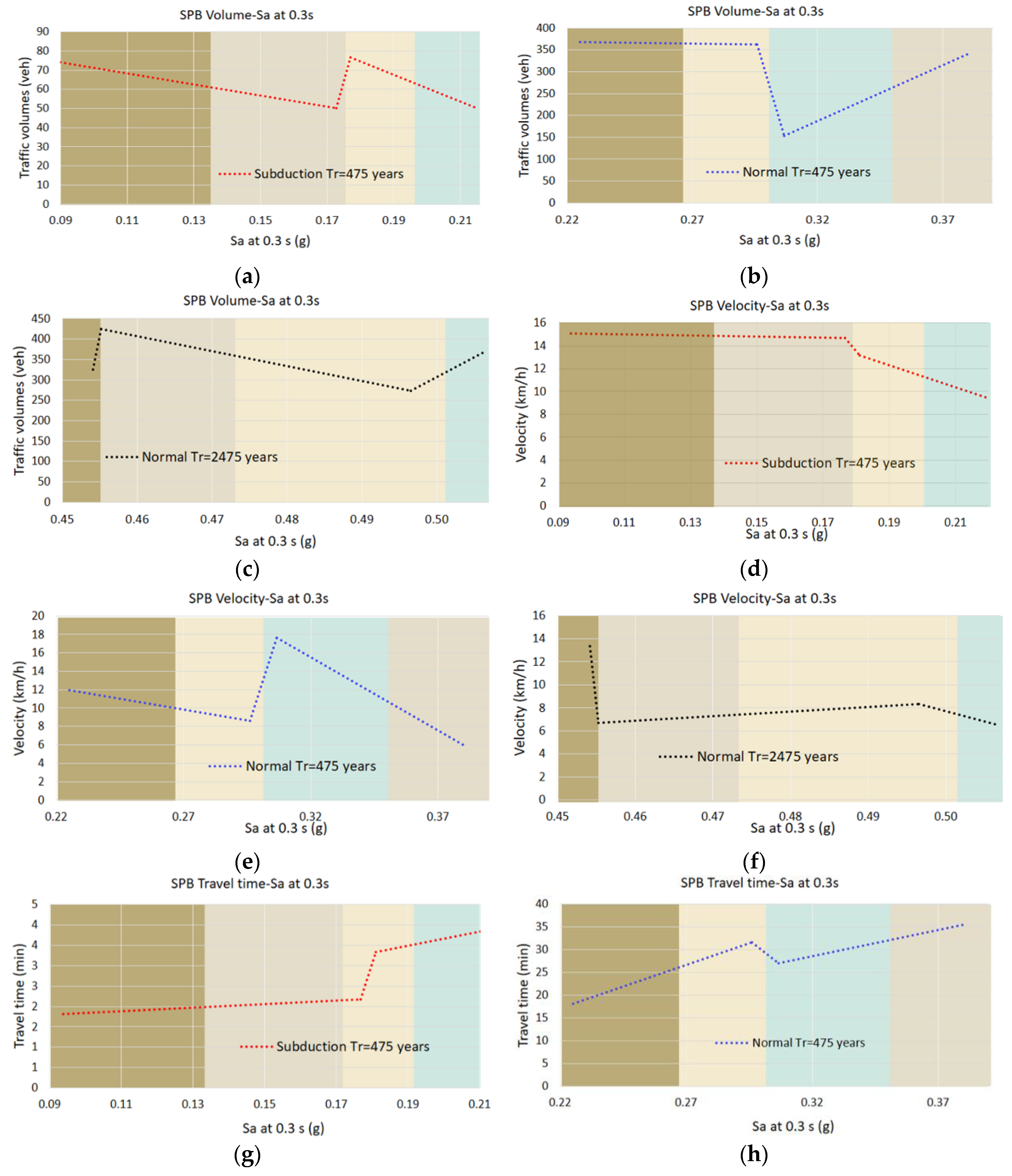
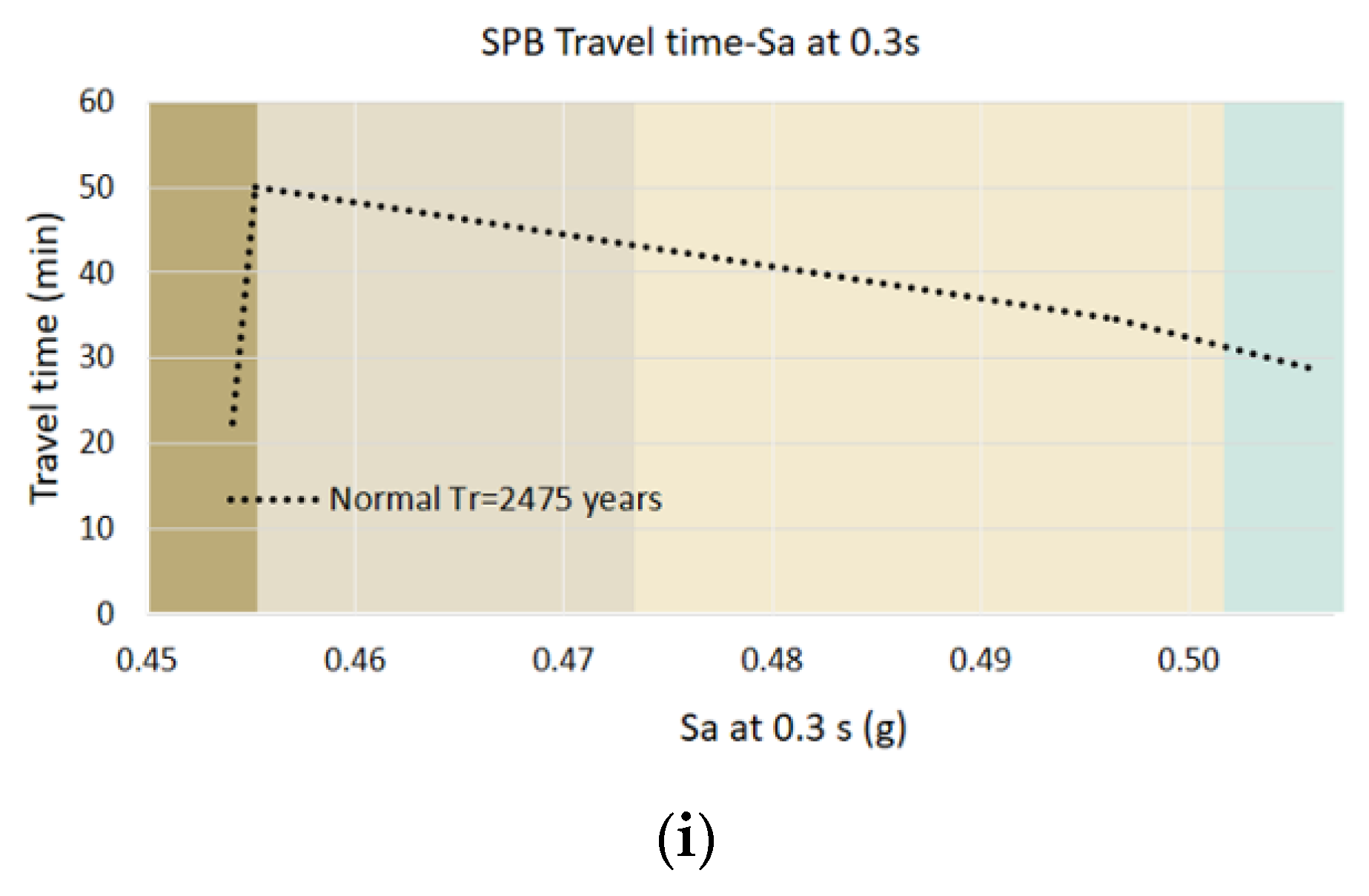
3.5.2. Seismic Performance Boundaries, SPB
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Amirsardari, A.; Sofi, M.; Lumantarna, E.; Imran, I.; Duffield, C. Impact of Earthquakes on the Transportation Infrastructure of Indonesia: A Preliminary Study. Civ. Eng. Dimens. 2019, 21, 19–28. [Google Scholar] [CrossRef]
- Sarkis, A.I.; Palermo, A.; Kammouh, O.; Cimellaro, G.P. Seismic resilience of road bridges: Lessons learned from the 14 November 2016 Kaikōura Earthquake. In Proceedings of the 9th International Conference on Bridge Maintenance, Safety, Melbourne, Australia, 9–13 July 2018; p. 588. [Google Scholar]
- Düzgün, Ş.; Yücemen, M.S.; Kalaycioglu, H.S.; Celik, K.; Kemeç, S.; Ertugay, K.; Deniz, A. An integrated earthquake vulnerability assessment framework for urban areas. Nat. Hazards 2011, 59, 917–947. [Google Scholar] [CrossRef]
- Cubrinovski, M.; Hughes, M.; Bradley, B.A.; Noonan, J.; Hopkins, R.; McNeill, S.; English, G. Performance of Horizontal Infrastructure in Christchurch City through the 2010–2011 Canterbury Earthquake Sequence; University of Canterbury: Christchurch, New Zealand, 2014. [Google Scholar]
- Durante, M.G.; Di Sarno, L.; Zimmaro, P.; Stewart, J.P. Damage to Roadway Infrastructure from 2016 Central Italy Earthquake Sequence. Earthq. Spectra 2018, 34, 1721–1737. [Google Scholar] [CrossRef]
- Romeo, S.; Di Matteo, L.; Melelli, L.; Cencetti, C.; Dragoni, W.; Fredduzzi, A. Seismic-induced rockfalls and landslide dam following the October 30, 2016 earthquake in Central Italy. Landslides 2017, 14, 1457–1465. [Google Scholar] [CrossRef]
- Martino, S.; Bozzano, F.; Caporossi, P.; D’Angiò, D.; Della Seta, M.; Esposito, C.; Marmoni, G.M. Impact of landslides on transportation routes during the 2016–2017 Central Italy seismic sequence. Landslides 2019, 16, 1221–1241. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Hyodo, M.; Nikitas, G.; Ismael, B.; Suzuki, H.; Lombardi, D.; Egami, S.; Watanabe, G.; Goda, K. Geotechnical and infrastructural damage due to the 2016 Kumamoto earthquake sequence. Soil Dyn. Earthq. Eng. 2018, 104, 390–394. [Google Scholar] [CrossRef]
- Kazama, M.; Noda, T. Damage statistics (Summary of the 2011 off the Pacific Coast of Tohoku Earthquake damage). Soils Found. 2012, 52, 780–792. [Google Scholar] [CrossRef]
- Nakanishi, H.; Black, J.; Matsuo, K. Disaster resilience in transportation: Japan earthquake and tsunami 2011. Int. J. Disaster Resil. Built Environ. 2014, 5, 341–361. [Google Scholar] [CrossRef]
- Kawashima, K. Damage of bridges due to the 2011 great east japan earthquake. J. Jpn. Assoc. Earthq. Eng. 2012, 12, 4. [Google Scholar] [CrossRef]
- Yasuda, S.; Towhata, I.; Ishii, I.; Sato, S.; Uchimura, T. Liquefaction-induced damage to structures during the 2011 great east japan earthquake. J. JSCE 2013, 1, 181–193. [Google Scholar] [CrossRef]
- Choi, E.; Desroches, R.; Nielson, B.G. Seismic fragility of typical bridges in moderate seismic zones. Eng. Struct. 2004, 26, 187–199. [Google Scholar] [CrossRef]
- Nielson, B.G.; Desroches, R. Seismic fragility methodology for highway bridges using a component level approach. Earthq. Eng. Struct. Dyn. 2007, 36, 823–839. [Google Scholar] [CrossRef]
- Misra, S.; Padgett, J.E. Seismic Fragility of Railway Bridge Classes: Methods, Models, and Comparison with the State of the Art. J. Bridg. Eng. 2019, 24, 04019116. [Google Scholar] [CrossRef]
- NIBS. Users’s manual and technical manuals. In Report Prepared for the Federal Emergency Management Agency; National Institute of Building Sciences (NIBS): Washington, DC, USA, 2004. [Google Scholar]
- Salmon, M.; Wang, J.; Jones, D.; Wu, C. Fragility Formulations for the BART System. In Advancing Mitigation Technologies and Disaster Response for Lifeline Systems; American Society of Civil Engineers (ASCE): Reston, VA, USA, 2003; pp. 183–192. [Google Scholar]
- Mayoral, J.M.; Argyroudis, S.; Castañon, E.; Argyroudis, S. Vulnerability of floating tunnel shafts for increasing earthquake loading. Soil Dyn. Earthq. Eng. 2016, 80, 1–10. [Google Scholar] [CrossRef]
- Maruyama, Y.; Yamazaki, F.; Mizuno, K.; Yogai, H.; Tsuchiya, Y. Development of fragility curves for highway embankment based on damage data from recent earthquakes in Japan. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008. [Google Scholar]
- Maruyama, Y.; Yamazaki, F.; Mizuno, K.; Tsuchiya, Y.; Yogai, H. Fragility curves for expressway embankments based on damage datasets after recent earthquakes in Japan. Soil Dyn. Earthq. Eng. 2010, 30, 1158–1167. [Google Scholar] [CrossRef]
- Argyroudis, S.; Kaynia, A.M. Analytical seismic fragility functions for highway and railway embankments and cuts. Earthq. Eng. Struct. Dyn. 2015, 44, 1863–1879. [Google Scholar] [CrossRef]
- Werner, S.D.; Taylor, C.E.; Cho, S.; Lavoie, J.P.; Huyck, C.K.; Eitzel, C.; Eguchi, R.T. Redars 2 Methodology and Software for Seismic Risk Analysis of Highway Systems; University of Buffalo: Buffalo, NY, USA, 2006. [Google Scholar]
- Pitilakis, K.; Crowley, H.; Kaynia, A.M. SYNER-G: Typology definition and fragility functions for physical elements at seismic risk. Geotech. Geol. Earthq. Eng. 2014, 27, 1–28. [Google Scholar]
- Anelli, A.; Mori, F.; Vona, M. Fragility Curves of the Urban Road Network Based on the Debris Distributions of Interfering Buildings. Appl. Sci. 2020, 10, 1289. [Google Scholar] [CrossRef]
- Ko, Y.Y.; Yang, H.H.; Chen, C.H. Seismic Fragility Analysis for Sheet Pile Wharves—Case Study of the Hualien harbor in Taiwan; Missouri University of Science and Technology: Rolla, MO, USA, 2010. [Google Scholar]
- Na, U.J.; Chaudhuri, S.R.; Shinozuka, M. Probabilistic assessment for seismic performance of port structures. Soil Dyn. Earthq. Eng. 2008, 28, 147–158. [Google Scholar] [CrossRef]
- Kakderi, K.; Pitilakis, K. Seismic Analysis and Fragility Curves of Gravity Waterfront Structures; Missouri University of Science and Technology: Rolla, MO, USA, 2010. [Google Scholar]
- Fäh, D.; Kind, F.; Lang, K.; Giardini, D. Earthquake scenarios for the city of Basel. Soil Dyn. Earthq. Eng. 2001, 21, 405–413. [Google Scholar] [CrossRef]
- Veneziano, D.; Sussman, J.M.; Gupta, U.; Kunnumkal, S.M. Earthquake loss under limited transportation capacity: Assessment, sensitivity and remediation. In Proceedings of the Seventh US National Conference on Earthquake Engineering, Boston, MA, USA, 21–25 July 2002. [Google Scholar]
- Singhal, A.; Kiremidjian, A.S. Method for Probabilistic Evaluation of Seismic Structural Damage. J. Struct. Eng. 1996, 122, 1459–1467. [Google Scholar] [CrossRef]
- Rossetto, T.; Elnashai, A. A new analytical procedure for the derivation of displacement-based vulnerability curves for populations of RC structures. Eng. Struct. 2005, 27, 397–409. [Google Scholar] [CrossRef]
- Lee, Y.J.; Song, J.; Gardoni, P.; Lim, H.-W. Post-hazard flow capacity of bridge transportation network considering structural deterioration of bridges. Struct. Infrastruct. Eng. 2011, 7, 509–521. [Google Scholar] [CrossRef]
- Nagurney, A.; Qiang, Q. A network efficiency measure for congested networks. EPL Europhys. Lett. 2007, 79, 38005. [Google Scholar] [CrossRef]
- Bocchini, P.; Frangopol, D.M. Connectivity-Based Optimal Scheduling for Maintenance of Bridge Networks. J. Eng. Mech. 2013, 139, 760–769. [Google Scholar] [CrossRef]
- Kurtz, N.; Song, J.; Gardoni, P. Seismic Reliability Analysis of Deteriorating Representative U.S. West Coast Bridge Transportation Networks. J. Struct. Eng. 2016, 142, C4015010. [Google Scholar] [CrossRef]
- Guikema, S.D.; Gardoni, P. Reliability Estimation for Networks of Reinforced Concrete Bridges. J. Infrastruct. Syst. 2009, 15, 61–69. [Google Scholar] [CrossRef]
- Chen, A.; Yang, C.; Kongsomsaksakul, S.; Lee, M. Network-based Accessibility Measures for Vulnerability Analysis of Degradable Transportation Networks. Netw. Spat. Econ. 2007, 7, 241–256. [Google Scholar] [CrossRef]
- Gomez, C.; Baker, J.W. An optimization-based decision support framework for coupled pre- and post-earthquake infrastructure risk management. Struct. Saf. 2019, 77, 1–9. [Google Scholar] [CrossRef]
- Liao, T.-Y.; Hu, T.-Y.; Ko, Y.-N. A resilience optimization model for transportation networks under disasters. Nat. Hazards 2018, 93, 469–489. [Google Scholar] [CrossRef]
- Fan, L.; Tangqing, L. Study on Optimization of Earthquake Transportation Emergency Management System. In Proceedings of the 7th International Conference on Innovation and Management, Tokyo, Japan, 7–10 February 2010; pp. 1851–1863. [Google Scholar]
- Üstün, A.K. Evaluating İstanbul’s disaster resilience capacity by data envelopment analysis. Nat. Hazards 2015, 80, 1603–1623. [Google Scholar] [CrossRef]
- El-Rashidy, R.A.; Grant-Muller, S.M. An assessment method for highway network vulnerability. J. Transp. Geogr. 2014, 34, 34–43. [Google Scholar] [CrossRef]
- Chang, L.; Elnashai, A.S., Jr. Post-earthquake modelling of transportation networks. Struct. Infrastruct. Eng. 2011, 8, 1–19. [Google Scholar] [CrossRef]
- Kilanitis, I.; Sextos, A. Integrated seismic risk and resilience assessment of roadway networks in earthquake prone areas. Bull. Earthq. Eng. 2018, 17, 181–210. [Google Scholar] [CrossRef]
- Feng, K.; Li, Q.; Ellingwood, B.R. Post-earthquake modelling of transportation networks using an agent-based model. Struct. Infrastruct. Eng. 2020, 1–15. [Google Scholar] [CrossRef]
- Taylor, M.A.P. Critical Transport Infrastructure in Urban Areas: Impacts of Traffic Incidents Assessed Using Accessibility-Based Network Vulnerability Analysis. Growth Chang. 2008, 39, 593–616. [Google Scholar] [CrossRef]
- Chen, A.; Kim, J.; Zhou, Z.; Chootinan, P. Alpha Reliable Network Design Problem. Transp. Res. Rec. J. Transp. Res. Board 2007, 2029, 49–57. [Google Scholar] [CrossRef]
- Argyroudis, S.A.; Mitoulis, S.A.; Hofer, L.; Zanini, M.A.; Tubaldi, E.; Frangopol, D.M. Resilience assessment framework for critical infrastructure in a multi-hazard environment: Case study on transport assets. Sci. Total. Environ. 2020, 714, 136854. [Google Scholar] [CrossRef]
- Argyroudis, S.A.; Mitoulis, S.A.; Winter, M.G.; Kaynia, A.M. Fragility of transport assets exposed to multiple hazards: State-of-the-art review toward infrastructural resilience. Reliab. Eng. Syst. Saf. 2019, 191, 106567. [Google Scholar] [CrossRef]
- Kermanshah, A.; Derrible, S. A geographical and multi-criteria vulnerability assessment of transportation networks against extreme earthquakes. Reliab. Eng. Syst. Saf. 2016, 153, 39–49. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, N. Resilience-based risk mitigation for road networks. Struct. Saf. 2016, 62, 57–65. [Google Scholar] [CrossRef]
- Khademi, N.; Balaei, B.; Shahri, M.; Mirzaei, M.; Sarrafi, B.; Zahabiun, M.; Mohaymany, A.S. Transportation network vulnerability analysis for the case of a catastrophic earthquake. Int. J. Disaster Risk Reduct. 2015, 12, 234–254. [Google Scholar] [CrossRef]
- Dizhur, D.; Giaretton, M.; Ingham, J.M. Damage Observations Following the M w 7.8 2016 Kaikoura Earthquake. In Proceedings of the International Conference on Earthquake Engineering and Structural Dynamics, Reykjavík, Iceland, 12–14 June 2017; pp. 249–261. [Google Scholar]
- Marcianò, F.A.; Musolino, G.; Vitetta, A. Signal setting optimization on urban road transport networks: The case of emergency evacuation. Saf. Sci. 2015, 72, 209–220. [Google Scholar] [CrossRef]
- Musolino, G.; Vitetta, A. Short-term forecasting in road evacuation: Calibration of a travel time function. Urban Transport XVII 2011, 116, 615–626. [Google Scholar] [CrossRef]
- Marcianò, F.A.; Musolino, G.; Vitetta, A. Within-day traffic assignment and signal setting in road evacuation: A procedure with explicit path enumeration. WIT Trans. Built Environ. 2011, 117, 403–414. [Google Scholar] [CrossRef]
- Chilá, G.; Musolino, G.; Polimeni, A.; Rindone, C.; Russo, F.; Vitetta, A. Transport models and intelligent transportation system to support urban evacuation planning process. IET Intell. Transp. Syst. 2016, 10, 279–286. [Google Scholar]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Cornell, C.A. Engineering seismic risk analysis. Bull. Seismol. Soc. Am. 1968, 58, 1583–1606. [Google Scholar]
- Porter, K.R. A Beginner’s Guide to Fragility, Vulnerability, and Risk. Encycl. Earthq. Eng. 2015, 1–29. [Google Scholar] [CrossRef]
- Hirokawa, N.; Osaragi, T. Earthquake Disaster Simulation System: Integration of Models for Building Collapse, Road Blockage, and Fire Spread. J. Disaster Res. 2016, 11, 175–187. [Google Scholar] [CrossRef]
- Argyroudis, S.; Selva, J.; Gehl, P.; Pitilakis, K. Systemic Seismic Risk Assessment of Road Networks Considering Interactions with the Built Environment. Comput. Civ. Infrastruct. Eng. 2015, 30, 524–540. [Google Scholar] [CrossRef]
- Galvis, F.; Miranda, E.; Heresi, P.; Dávalos, H.; Silos, J.R. Preliminary statistics of collapsed buildings in Mexico City in the September 19, 2017 Puebla-Morelos Earthquake; Blume Earthquake Engineering Center; Department of Civil and Environmental Engineering Stanford University: Stanford, CA, USA, 2017. [Google Scholar]
- GEER. Geotechnical Engineering Reconnaissance of the 19 September 2017 Mw 7.1 Puebla-Mexico City Earthquake, Version 2.0; Geotechnical Extreme Events Reconnaissance Association: VA, USA, 2017; Available online: http://www.geerassociation.org/administrator/components/com_geer_reports/geerfiles/UNAM_GEER_Sept2017_v2_Final.pdf (accessed on 19 November 2020).
- Román-de la Sancha, A.; Mayoral, J.M.; Hutchinson, T.; Candia, G.; Montgomery, J.; Tepalcapa, S. Assessment of fragility models based on the Sept 19th, 2017 earthquake observed damage. Soil Dyn. Earthq. Eng. 2019, 125, 105707. [Google Scholar] [CrossRef]
- Lighthill, M.J.; Whitham, G.B. On kinematic waves II. A theory of traffic flow on long crowded roads. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1955, 229, 317–345. [Google Scholar] [CrossRef]
- Gazis, D.C.; Herman, R.; Potts, R.B. Car-Following Theory of Steady-State Traffic Flow. Oper. Res. 1959, 7, 499–505. [Google Scholar] [CrossRef]
- Pipes, L.A. An Operational Analysis of Traffic Dynamics. J. Appl. Phys. 1953, 24, 274–281. [Google Scholar] [CrossRef]
- Wang, Y.; Szeto, W.; Han, K.; Friesz, T.L. Dynamic traffic assignment: A review of the methodological advances for environmentally sustainable road transportation applications. Transp. Res. Part B: Methodol. 2018, 111, 370–394. [Google Scholar] [CrossRef]
- Pi, X.; Ma, W.; Qian, Z. (Sean) A general formulation for multi-modal dynamic traffic assignment considering multi-class vehicles, public transit and parking. Transp. Res. Part C Emerg. Technol. 2019, 104, 369–389. [Google Scholar] [CrossRef]
- Zhang, Y.; Atasoy, B.; Akkinepally, A.; Ben-Akiva, M. Dynamic Toll Pricing using Dynamic Traffic Assignment System with Online Calibration. Transp. Res. Rec. J. Transp. Res. Board 2019, 2673, 532–546. [Google Scholar] [CrossRef]
- Wardrop, J.G. Road paper. some theoretical aspects of road traffic research. Proc. Inst. Civ. Eng. 1952, 1, 325–362. [Google Scholar] [CrossRef]
- Ortúzar, J.D.; Willumsen, L.G. Modelling Transport; John Wiley & Sons: New York, NY, USA, 2011. [Google Scholar]
- Kamga, C.N.; Mouskos, K.C.; Paaswell, R.E. A methodology to estimate travel time using dynamic traffic assignment (DTA) under incident conditions. Transp. Res. Part C Emerg. Technol. 2011, 19, 1215–1224. [Google Scholar] [CrossRef]
- Peeta, S.; Ziliaskopoulos, A.K. Foundations of Dynamic Traffic Assignment: The Past, the Present and the Future. Netw. Spat. Econ. 2001, 1, 233–265. [Google Scholar] [CrossRef]
- Sisiopiku, V.P.; Li, X. Overview of dynamic traffic assignment options. In Proceedings of the 2006 Transportation Simulation Symposium, Huntsville, AL, USA, 2–6 April 2006. [Google Scholar]
- Mahut, M.; Florian, M.; Tremblay, N.; Campbell, M.; Patman, D.; McDaniel, Z.K. Calibration and Application of a Simulation-Based Dynamic Traffic Assignment Model. Transp. Res. Rec. J. Transp. Res. Board 2004, 1876, 101–111. [Google Scholar] [CrossRef]
- Instituto Nacional de Estadística y Geografía (INEGI). Encuesta Origen-Destino en hogares de la Zona Metropolitana del Valle de México; Instituto Nacional de Estadística Geografía e Informática: Mexico City, México, 2017. [Google Scholar]
- Mayoral, J.M.; Asimaki, D.; Tepalcapa, S.; Wood, C.; Román-de la Sancha, A.; Hutchinson, T.; Franke, K.; Montalva, G. Site effects in Mexico City basin: Past and present. Soil Dyn. Earthq. Eng. 2019, 121, 369–382. [Google Scholar] [CrossRef]
- Government of Mexico City. RCDF 2004 NTCDS-RCDF Normas Técnicas Complementarias para el Diseño por Sismo; Government of Mexico City: Mexico City, Mexico, 2004. (In Spanish)
- Mayoral, J.M.; Romo, M.P. Seismic response of bridges with massive foundations. Soil Dyn. Earthq. Eng. 2015, 71, 88–99. [Google Scholar] [CrossRef]
- Mayoral, J.; Tepalcapa, S.; Román-de la Sancha, A.; El Mohtar, C.; Rivas, R. Ground subsidence and its implication on building seismic performance. Soil Dyn. Earthq. Eng. 2019, 126, 105766. [Google Scholar] [CrossRef]
- Seed, H.B.; Romo, M.P.; Sun, J.I.; Jaime, A.; Lysmer, J. The Mexico Earthquake of September 19, 1985—Relationships between Soil Conditions and Earthquake Ground Motions. Earthq. Spectra 1988, 4, 687–729. [Google Scholar] [CrossRef]
- Romo, M.P. Clay behavior, ground response and soil-structure interaction studies in Mexico City. In Proceedings of the 3rd International Conference on Recent Advances in Geotechnical Earthquake Engineering and Soil Dynamics, St. Louis, MI, USA, 6–12 April 1995. [Google Scholar]
- Servicio Sismológico Nacional, SSN 2020. Available online: http://www2.ssn.unam.mx:8080/mapas-de-intensidades/ (accessed on 1 September 2020).
- Government of Mexico City. RCDF 2017 NTCDS-RCDF Normas Técnicas Complementarias para el Diseño por Sismo; Government of Mexico City: Mexico City, Mexico, 2017. (In Spanish)
- Bárcena, A.; Romo, M.P. RADSH: Programa de Computadora Para Analizar Depósitos de Suelo Estratificados Horizontalmente Sujetos a Excitaciones Dinámicas Aleatorias; Informe del Instituto de Ingeniería, Universidad Nacional Autónoma de México: Mexico City, Mexico, 1994. (In Spanish) [Google Scholar]
- Osorio, L.; Mayoral, J.M. Seismic microzonation for the northeast Texcoco lake area, Mexico. Soil Dyn. Earthq. Eng. 2013, 48, 252–266. [Google Scholar] [CrossRef]
- Itasca Consulting Group. FLAC, Fast Lagragian Analysis of Continua, User׳s Guide; Itasca Consulting Group: Minnesota, MN, USA, 2005. [Google Scholar]
- Lilhanand, K.; Tseng, W.S. Development and application of realistic earthquake time histories compatible with multiple-damping design spectra. In Proceedings of the 9th World Conference on Earthquake Engineering, Tokyo-Kyoto, Japan, 2–6 August 1988; pp. 819–824. [Google Scholar]
- Abrahamson, N.A. Non-Stationary Spectral Matching Program RSPMATCH; Pacific Gas & Electric Company: San Francisco, CA, USA, 1998. [Google Scholar]
- Mayoral, J.M.; De La Rosa, D.; Tepalcapa, S. Topographic effects during the September 19, 2017 Mexico city earthquake. Soil Dyn. Earthq. Eng. 2019, 125, 105732. [Google Scholar] [CrossRef]
- Schnabel, P.B. SHAKE: A Computer Program for Earthquake Response Analysis of Horizontally Layered Sites; EERC Report 72-12; University of California: Berkeley, CA, USA, 1972. [Google Scholar]
- Chong, S.-H. Soil Dynamic Constitutive Model for Characterizing the Nonlinear-Hysteretic Response. Appl. Sci. 2017, 7, 1110. [Google Scholar] [CrossRef]
- Liu, X.; Cheng, X.; Scarpas, A.; Blaauwendraad, J. Numerical modelling of nonlinear response of soil. Part 1: Constitutive model. Int. J. Solids Struct. 2005, 42, 1849–1881. [Google Scholar] [CrossRef]
- Groholski, D.R.; Hashash, Y.M.; Kim, B.; Musgrove, M.; Harmon, J.A.; Stewart, J.P. Simplified Model for Small-Strain Nonlinearity and Strength in 1D Seismic Site Response Analysis. J. Geotech. Geoenviron. Eng. 2016, 142, 04016042. [Google Scholar] [CrossRef]
- Mayoral, J.M.; Romo, M.P.; Osorio, L. Seismic parameters characterization at Texcoco lake, Mexico. Soil Dyn. Earthq. Eng. 2008, 28, 507–521. [Google Scholar] [CrossRef]
- Mayoral, J.M.; Castañon, E.; Alcantara, L.; Tepalcapa, S. Seismic response characterization of high plasticity clays. Soil Dyn. Earthq. Eng. 2016, 84, 174–189. [Google Scholar] [CrossRef]
- Mayoral, J.M.; Ramírez, J. Site response effects on an urban overpass. Soil Dyn. Earthq. Eng. 2011, 31, 849–855. [Google Scholar] [CrossRef]
- González, C.M.; Romo, M.P. Estimación de Propiedades Dinámicas de Arcillas. Ing. Sísmica 2011, 84, 1–23. (In Spanish) [Google Scholar] [CrossRef]
- Vucetic, M.; Dobry, R. Effect of Soil Plasticity on Cyclic Response. J. Geotech. Eng. 1991, 117, 89–107. [Google Scholar] [CrossRef]
- Seed, H.B.; Idriss, I.M. Soil Moduli and Damping Factors for Dynamics Response Analysis; Calif. Report No. EERC 70–10; University of California: Berkeley, CA, USA, 1970. [Google Scholar]
- Mayoral, J.M.; Badillo, A.; Alcaraz, M. Vulnerability and recovery time evaluation of an enhanced urban overpass foundation. Soil Dyn. Earthq. Eng. 2017, 100, 1–15. [Google Scholar] [CrossRef]
- Ruiz-García, J.; Negrete, M. Drift-based fragility assessment of confined masonry walls in seismic zones. Eng. Struct. 2009, 31, 170–181. [Google Scholar] [CrossRef]
- Villar-Vega, M.; Silva, V.; Crowley, H.; Yepes, C.; Tarque, N.; Acevedo, A.B.; Hube, M.A.; Gustavo, C.D.; María, H.S. Development of a Fragility Model for the Residential Building Stock in South America. Earthq. Spectra 2017, 33, 581–604. [Google Scholar] [CrossRef]
- Jara, J.M.; Olmos, B.A.; Martínez, G. Dynamic properties and seismic vulnerability of typical RC bridges located in México. Procedia Eng. 2017, 199, 2973–2978. [Google Scholar] [CrossRef]
- Díaz, S.A.; Pujades, L.G.; Barbat, A.H.; Hidalgo-Leiva, D.; Vargas-Alzate, Y.F. Capacity, damage and fragility models for steel buildings: A probabilistic approach. Bull. Earthq. Eng. 2017, 16, 1209–1243. [Google Scholar] [CrossRef]
- NIBS. Users’s manual and technical manuals. In Report Prepared for the Federal Emergency Management Agency; National Institute of Building Sciences: Washington, DC, USA, 2012. [Google Scholar]
- PTV. 2006. Available online: http://www.english.ptv.de/cgi-bin/traffic/traf-vision.pl (accessed on 5 December 2018).
- Mahut, M. A multi-lane link model of traffic dynamics based on the “space-time” queue. In Proceedings of the ITSC 2001, 2001 IEEE Intelligent Transportation Systems, Oakland, CA, USA, 25–29 August 2002; pp. 122–126. [Google Scholar]
- Florian, M.; Mahut, M.; Tremblay, N. Application of a simulation-based dynamic traffic assignment model. Eur. J. Oper. Res. 2008, 189, 1381–1392. [Google Scholar] [CrossRef]
- MaxDEA. Basic [Computer Program]; Version 5.0; Beijing Realworld Research & Consultation Company Ltd.: Beijing, China, 2014. [Google Scholar]




| Model | Input | Output |
|---|---|---|
| Output oriented | Link length (l) (m) Number of lanes (Ln) Free flow velocity (v0) (km/h) Peak ground acceleration (PGA) (g) 1 Spectral acceleration at 0.1 s (Sa0.1) (g) 1 Spectral acceleration at 0.3 s (Sa0.3) (g) 1 | Current velocity (v) (km/h) Traffic volume (V) (veh/time interval) Queue length (q) (1/m) 1 Travel time (Tt) (1/s) 1 |
| Classification | Abbreviation | Description | |
|---|---|---|---|
| Buildings | 1 story masonry building | 1 MB | Confined masonry buildings |
| 2 story masonry building | 2 MB | Confined masonry buildings | |
| 3 story masonry building | 3 MB | Confined masonry buildings | |
| 4 story concrete building | 4 CB | Reinforced concrete infilled frame ductile buildings | |
| 5 story concrete building | 5 CB | Reinforced infilled frame ductile concrete buildings | |
| 6 story concrete building | 6 CB | Reinforced infilled frame ductile concrete buildings | |
| 7 story concrete building | 7 CB | Reinforced infilled frame ductile concrete buildings | |
| 8 story concrete building | 8 CB | Reinforced concrete wall system buildings | |
| 9 story concrete building | 9 CB | Reinforced concrete wall system buildings | |
| 10 story concrete building | 10 CB | Reinforced concrete wall system buildings | |
| Transport infrastructure | Single span bridges | SP B | All single-span bridges |
| Concrete, multi-column bent, simple support (seismic design) bridge | CSS B | Concrete slab, multi-beam or girder, box beam bridge. | |
| Continuous concrete, single column, box girder (seismic design) bridge | CCSC B | Concrete box beam bridge | |
| Continuous concrete (seismic design) bridge | CC1 B | Concrete slab, multi-beam or girder, box beam bridge | |
| Steel, multi-column bent, simple support (seismic design) bridge | SSS B | Steel slab, multi-beam or girder, box beam bridge | |
| PS concrete, multi-column bent, simple support (seismic design) bridge | PS SS B | PS concrete slab, multi-beam or girder, box beam bridge | |
| PS concrete, single column, box girder (seismic design) bridge | PS B | PS concrete box beam bridge | |
| Continuous concrete, (seismic design) bridge | CC2 B | Concrete slab, multi-beam or girder, box beam, frame bridge | |
| Bored and drilled tunnel | BD T | Bored and drilled tunnel | |
| Cut and cover tunnel | CC T | Cut and cover tunnel | |
| Metro station | MS | 2 and 3 stories reinforced concrete walls buildings. Ductile behavior. | |
| Metro and light railway tracks | MT | Embankment | |
| Main roads | MR | Up to 2 lanes | |
| Urban roads | UR | More than 2 lanes |
| Event | Station | Magnitude | Epicentral Distance (km) | Focal Depth (km) | PGA (g) |
|---|---|---|---|---|---|
| 19/09/2017 | C.U. | Mw = 7.1 | 114 | 57 | 0.059 |
| 19/09/1985 | C.U. | Mw = 8.1 | 398 | 5 | 0.033 |
| Return Period, Tr (Years) | Zone I | Zone II | Zone IIIa | Zone IIIb | |
|---|---|---|---|---|---|
| Subduction earthquake | 125 | 0.0438 | 0.0772 | 0.1000 | 0.1260 |
| 250 | 0.0530 | 0.0942 | 0.1210 | 0.1570 | |
| 475 | 0.0625 | 0.1127 | 0.1410 | 0.1830 | |
| 2475 | 0.0892 | 0.1637 | 0.1910 | 0.2540 | |
| Normal fault earthquake | 125 | 0.0764 | 0.1099 | 0.0840 | 0.0900 |
| 250 | 0.1055 | 0.1299 | 0.1100 | 0.1180 | |
| 475 | 0.1406 | 0.1665 | 0.1390 | 0.1510 | |
| 2475 | 0.2599 | 0.2558 | 0.2190 | 0.2430 |
| Return Period, Tr (Years) | Zone I | Zone II | Zone IIIa | Zone IIIb | |
|---|---|---|---|---|---|
| Subduction earthquake | 125 | 0.0458 | 0.0866 | 0.1073 | 0.1301 |
| 250 | 0.0560 | 0.1051 | 0.1274 | 0.1600 | |
| 475 | 0.0662 | 0.1230 | 0.1480 | 0.1861 | |
| 2475 | 0.0968 | 0.1716 | 0.1964 | 0.2559 | |
| Normal fault earthquake | 125 | 0.1060 | 0.1580 | 0.1224 | 0.1193 |
| 250 | 0.1427 | 0.1941 | 0.1505 | 0.1430 | |
| 475 | 0.1885 | 0.2341 | 0.1805 | 0.1760 | |
| 2475 | 0.3465 | 0.3110 | 0.2662 | 0.2537 |
| Return Period, Tr (Years) | Zone I | Zone II | Zone IIIa | Zone IIIb | |
|---|---|---|---|---|---|
| Subduction earthquake | 125 | 0.0652 | 0.1238 | 0.1244 | 0.1511 |
| 250 | 0.0774 | 0.1526 | 0.1521 | 0.1868 | |
| 475 | 0.0937 | 0.1772 | 0.1809 | 0.2198 | |
| 2475 | 0.1304 | 0.2453 | 0.2221 | 0.2874 | |
| Normal fault earthquake | 125 | 0.1264 | 0.2343 | 0.1485 | 0.1770 |
| 250 | 0.1722 | 0.3025 | 0.2062 | 0.2408 | |
| 475 | 0.2252 | 0.3815 | 0.2960 | 0.3067 | |
| 2475 | 0.4128 | 0.5779 | 0.4580 | 0.4800 |
| Return Period, Tr (Years) | Zone I | Zone II | Zone IIIa | Zone IIIb | |
|---|---|---|---|---|---|
| Subduction earthquake | 125 | 0.000 | 0.036 | 0.035 | 0.034 |
| 250 | 0.000 | 0.034 | 0.034 | 0.031 | |
| 475 | 0.000 | 0.050 | 0.048 | 0.048 | |
| 2475 | 0.000 | 0.012 | 0.013 | 0.019 | |
| Normal fault earthquake | 125 | 0.000 | 0.001 | 0.001 | 0.000 |
| 250 | 0.000 | 0.005 | 0.005 | 0.004 | |
| 475 | 0.000 | 0.015 | 0.016 | 0.015 | |
| 2475 | 0.000 | 0.038 | 0.038 | 0.038 |
| Infrastructure | Reference | Intensity Measure |
|---|---|---|
| Reinforced concrete buildings (4, 5, 6, 7, 8, 9, 10 stories) | [105] | PGA and Sa |
| Confined masonry buildings (1, 2, 3 stories) | [105] | PGA and Sa |
| Bridges | [108] | PGA |
| Tunnels | [23] | PGD |
| Metro stations | [105] | PGA and Sa |
| Railway systems | [23] | PGD |
| Motorways | [23] | PGD |
| Urban roads | [23] | PGD |
| Average Travel Time | Average Velocity | Traffic Volume | |
|---|---|---|---|
| R2 First model (5 control segments) | 0.3433 | 0.0070 | 0.7153 |
| R2 Final model (10 control segments) | 0.8368 | 0.6529 | 0.9196 |
| Scenario | Average Travel Velocity (km/h) | Average Travel Time (s) | Maximum Queue Length (m) | |
|---|---|---|---|---|
| Pre-earthquake conditions | 49.42 | 15.40 | 56.23 | |
| Subduction earthquake | Tr = 475 years | 22.10 | 33.62 | 61.24 |
| Normal earthquake | Tr = 475 years | 44.19 | 827.89 | 156.03 |
| Tr = 2475 years | 41.07 | 1304.01 | 145.93 | |
| Normal Fault, Tr = 475 Years | Normal Fault, Tr = 2475 Years | Subduction, Tr = 475 Years | |||||||
|---|---|---|---|---|---|---|---|---|---|
| PGA | Sa0.1 | Sa0.3 | PGA | Sa0.1 | Sa0.3 | PGA | Sa0.1 | Sa0.3 | |
| Capacity | 0.429 | 0.681 | 0.687 | 0.008 | 0.011 | 0.785 | 0.456 | 0.426 | 0.402 |
| v | 0.413 | 0.642 | 0.699 | 0.000 | 0.002 | 0.769 | 0.692 | 0.631 | 0.455 |
| Tt | 0.552 | 0.633 | 0.856 | 0.035 | 0.010 | 0.882 | 0.334 | 0.277 | 0.109 |
| q | 0.113 | 0.036 | 0.015 | 0.062 | 0.122 | 0.010 | 0.315 | 0.256 | 0.098 |
| V | 0.481 | 0.036 | 0.490 | 0.007 | 0.245 | 0.680 | 0.769 | 0.716 | 0.565 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Román-de la Sancha, A.; Silva, R. Multivariable Analysis of Transport Network Seismic Performance: Mexico City. Sustainability 2020, 12, 9726. https://doi.org/10.3390/su12229726
Román-de la Sancha A, Silva R. Multivariable Analysis of Transport Network Seismic Performance: Mexico City. Sustainability. 2020; 12(22):9726. https://doi.org/10.3390/su12229726
Chicago/Turabian StyleRomán-de la Sancha, Azucena, and Rodolfo Silva. 2020. "Multivariable Analysis of Transport Network Seismic Performance: Mexico City" Sustainability 12, no. 22: 9726. https://doi.org/10.3390/su12229726
APA StyleRomán-de la Sancha, A., & Silva, R. (2020). Multivariable Analysis of Transport Network Seismic Performance: Mexico City. Sustainability, 12(22), 9726. https://doi.org/10.3390/su12229726