Standalone Photovoltaic Direct Pumping in Urban Water Pressurized Networks with Energy Storage in Tanks or Batteries
Abstract
1. Introduction
2. Materials and Methods
2.1. Monthly Variation in Energy Produced in Photovoltaic Arrays
2.2. Energy Storage in Tanks
2.3. Non-Renewable Energy Savings
2.4. Economic Prioritization of the Alternatives
3. Optimization Problem
3.1. Input Data
3.1.1. Irradiance Data
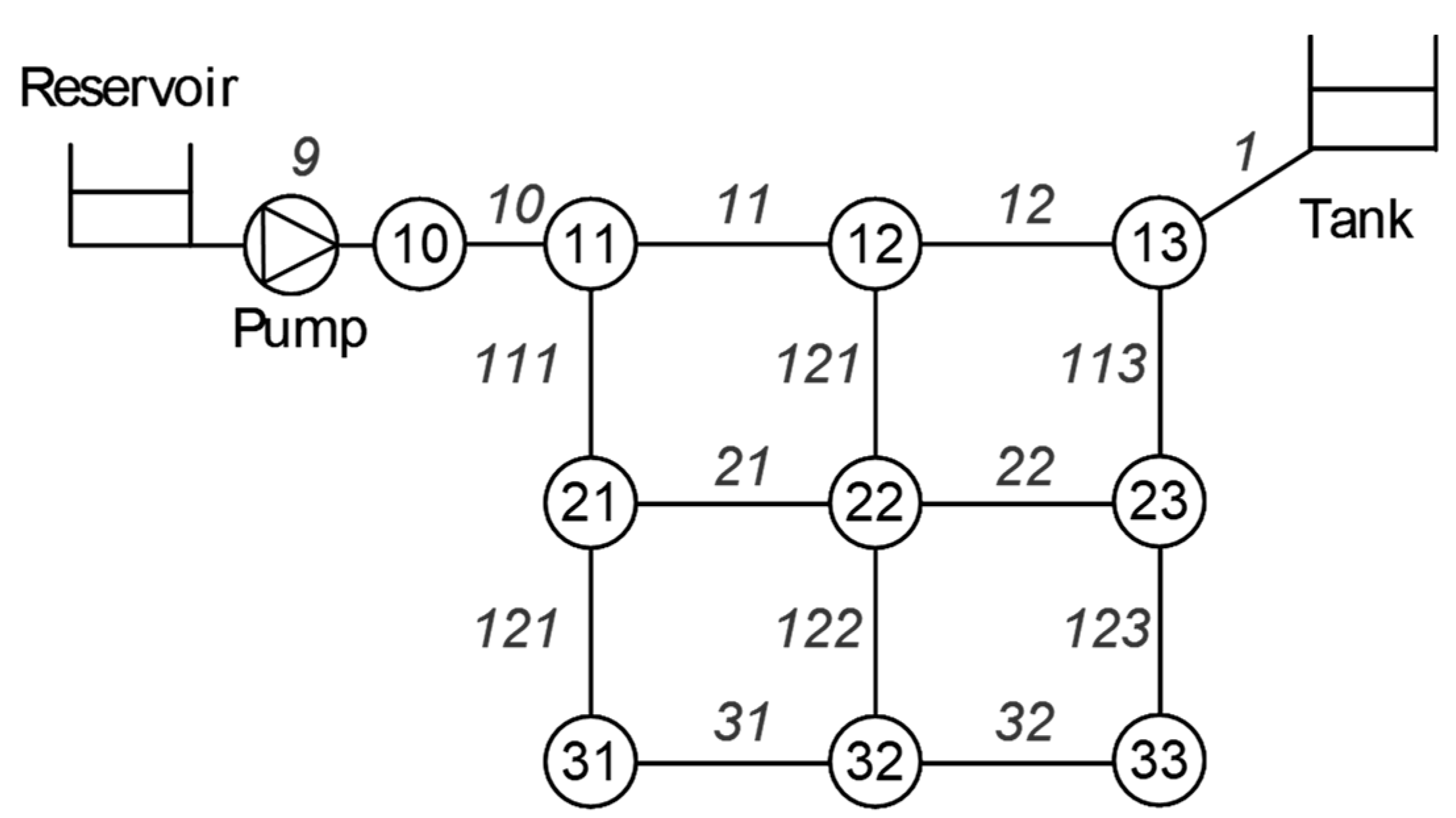
3.1.2. Hydraulic Data
- The hydraulic model of the network. This is the calibrated and operative model that accurately represents the hydraulic behavior of the WPN; no errors should appear when running it. This file must contain the elevation, base demands, and temporal variation in nodes, and the roughness, diameter, and lengths in pipes. It should also consider the pump curves and size of the tanks.
- Pump efficiency (). We highlight this parameter since its use produces a closer approach to reality.
- Monthly water demand variation (K). We should obtain this parameter by dividing each monthly water demand into the average water demand. Their values should be close to 1.
3.1.3. Economic Data
- Equivalent continuous discount rate (r).
- Current investment (I0). This value is different depending on the alternative analyzed, but any of them represent the proper characteristics of every case analyzed. Although the PV arrays costs are similar for every alternative considered, if the battery is operating, we included this cost in the calculations and if tanks are the device selected for storing energy, we incorporated the cost of increasing the tank capacity, new pumps, and pipelines and any other devices to meet the hydraulic demands.
- Economic savings (Si) for every alternative in comparison with the current case (Case 0). To calculate the energy consumption costs, we used the Spanish tariff (which involves calculating power, energy, and reactive energy with different hourly values and the seasonal variation).
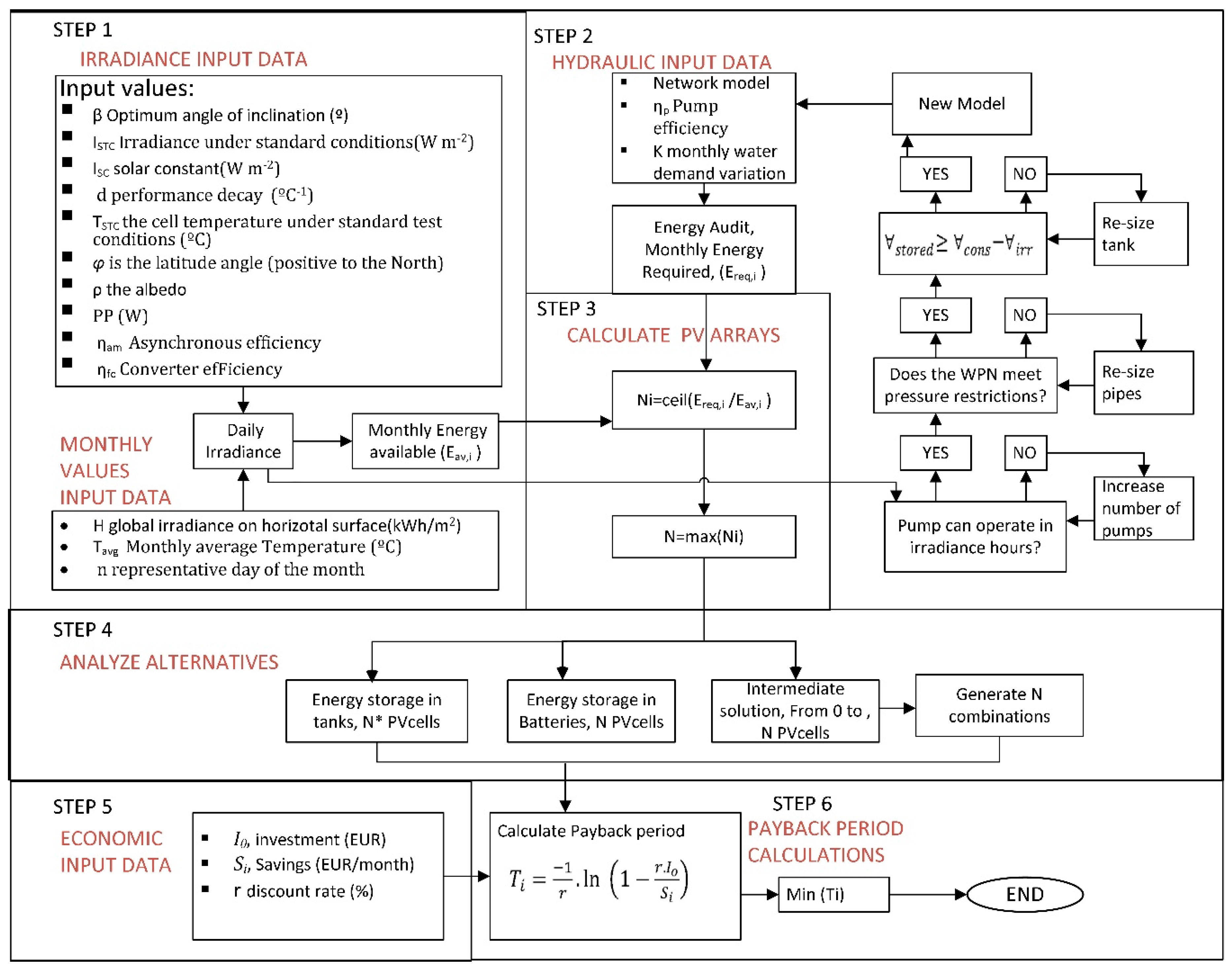
3.2. Calculation Process
4. Case Study
4.1. Input Data for the Case Study
4.1.1. Irradiance Input Data
4.1.2. Hydraulic Input Data
4.1.3. Economic Input Data
4.2. Results
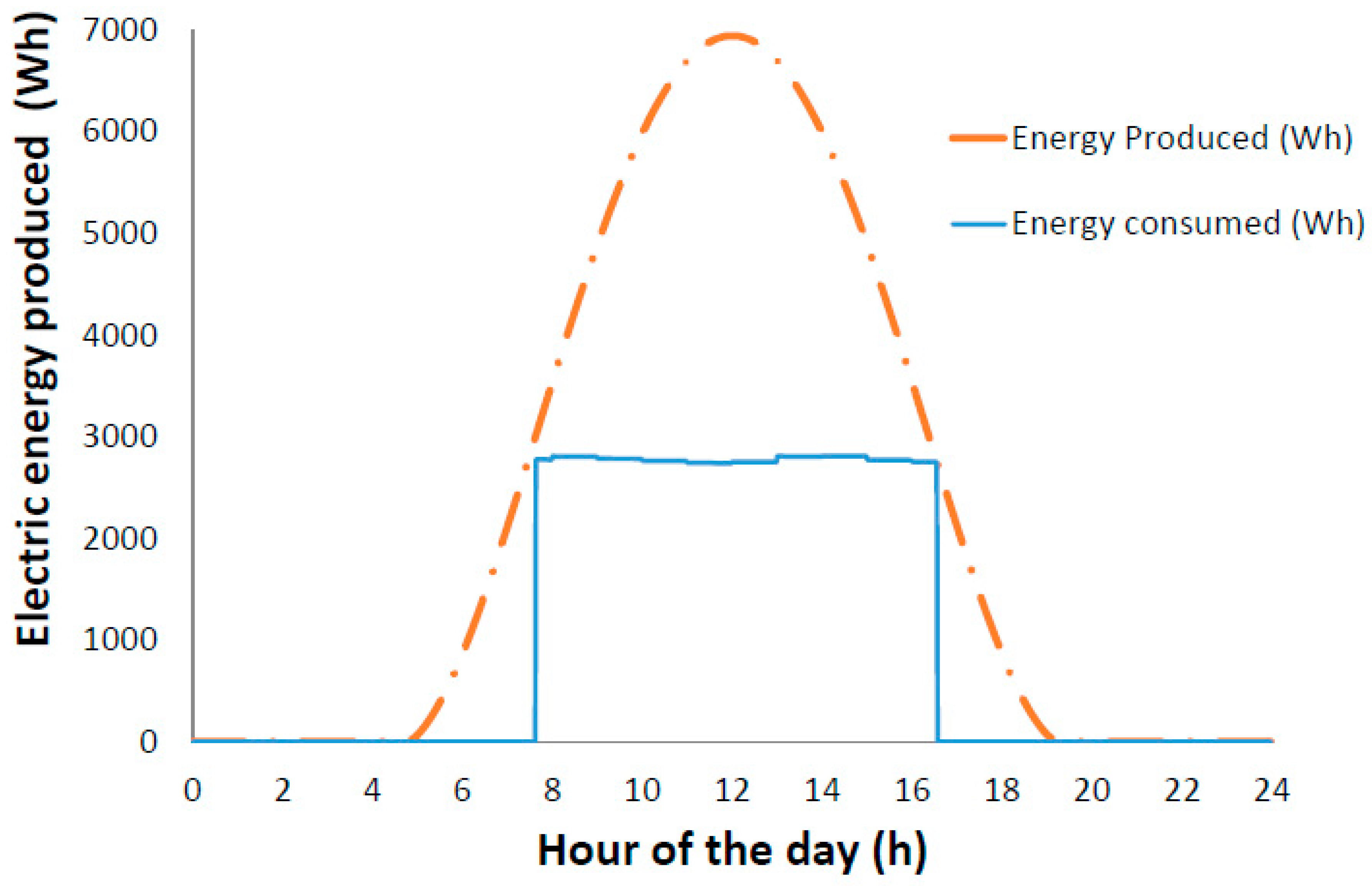
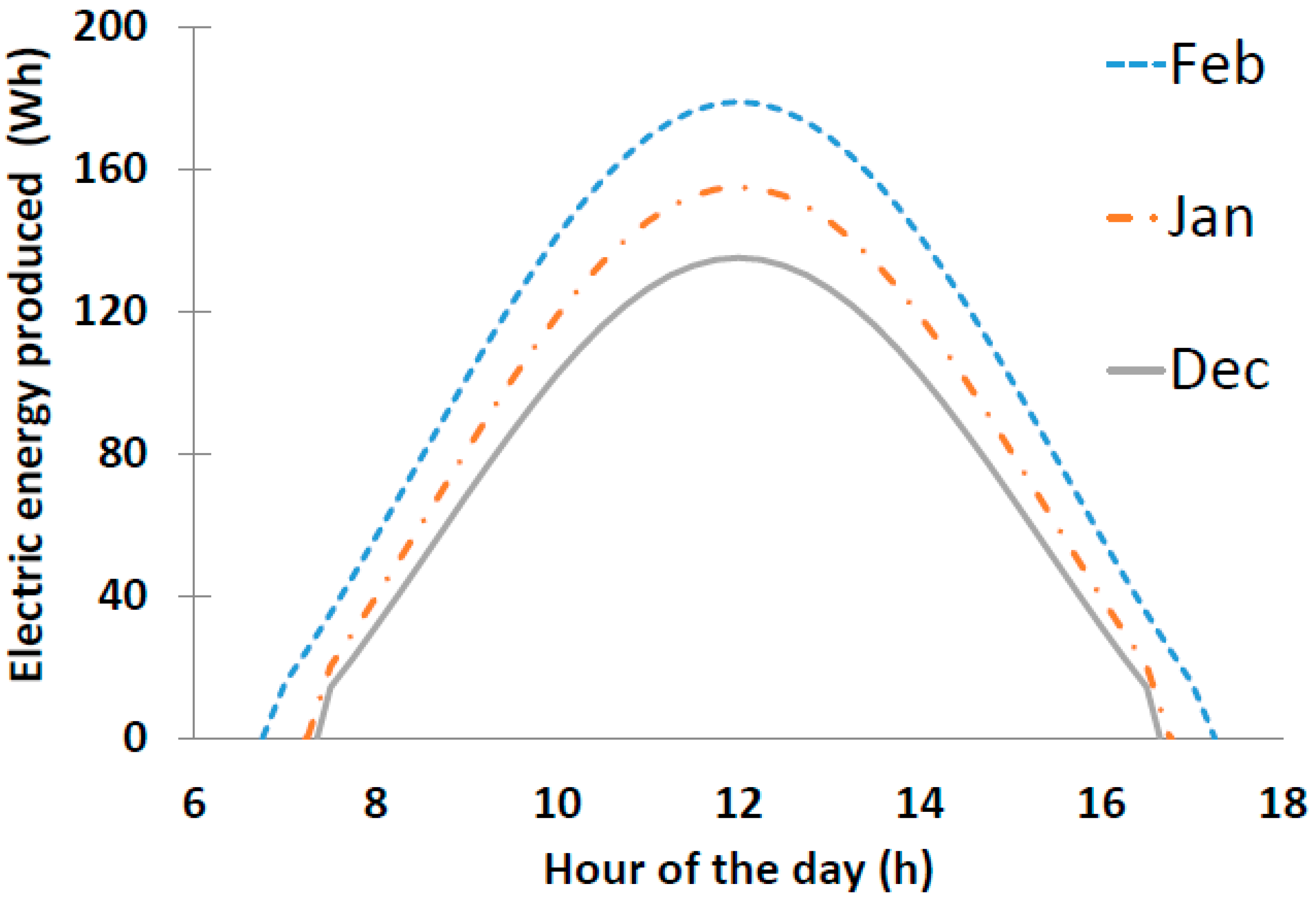
4.2.1. Monthly Energy Production by PV Arrays
4.2.2. New Model Generation for Energy Storage in Tanks (Case II)
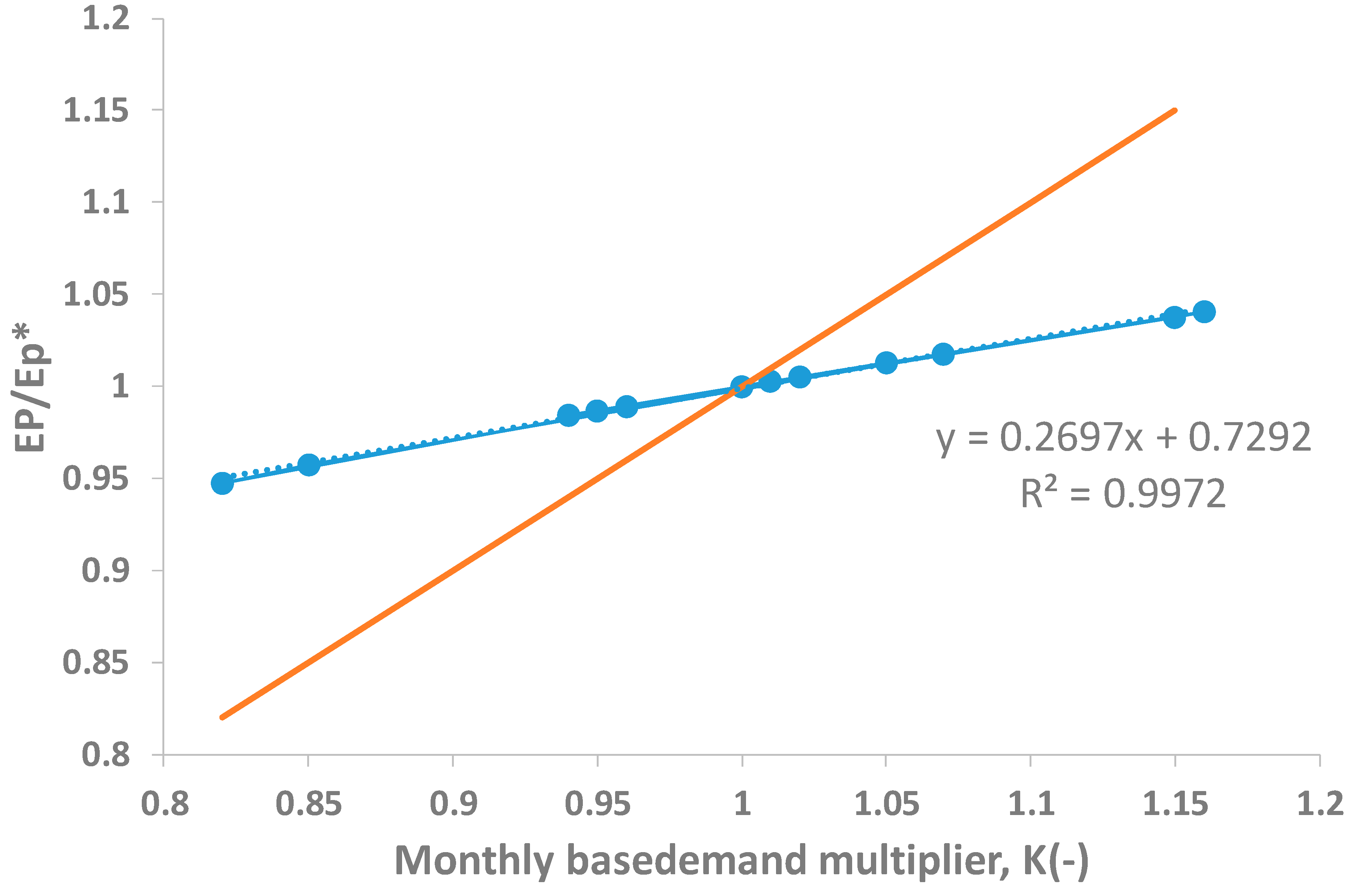
4.2.3. Monthly Energy Consumption and PV Arrays Calculation
4.2.4. Investments and Energy Savings for the Analyzed Cases
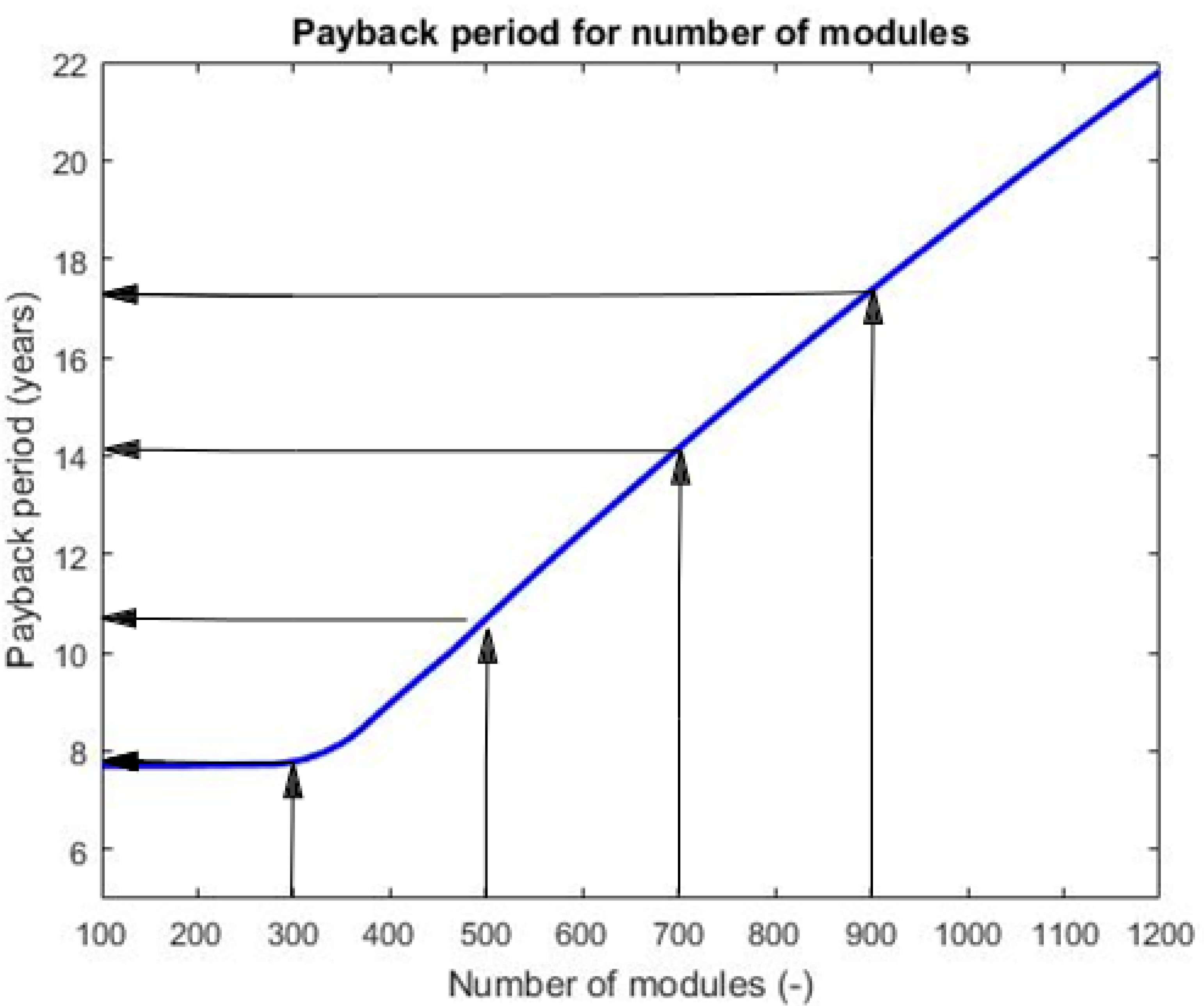
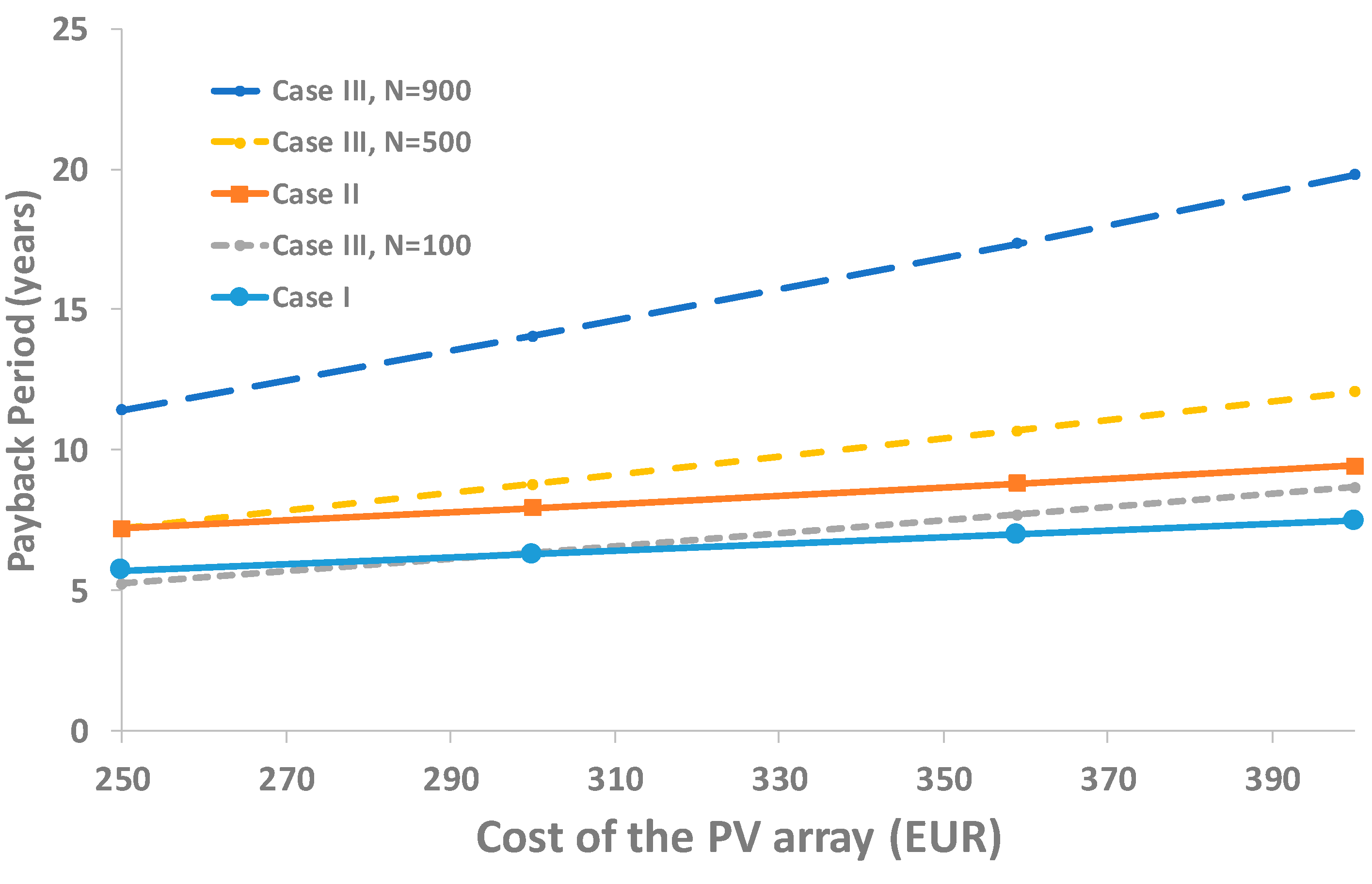
4.2.5. Payback Period Calculations
4.3. Discussion
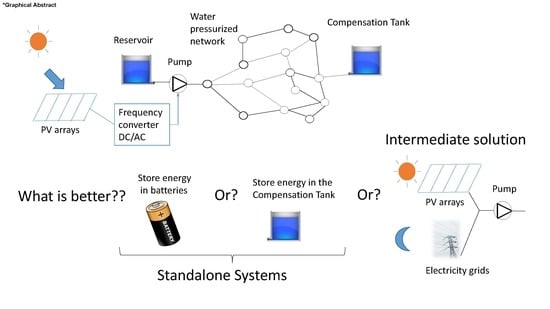
- Case 0 (current): Direct electric supply from the grid (non-renewable energy).
- Case I: Full electricity supply through PV (renewable energy) and energy storage in batteries of the surplus electricity during peak production hours.
- Case II: Full electricity supply by PV (renewable energy) and energy storage in a compensation tank (as potential energy) of the surplus electricity during peak production hours.
- Case III: Electricity supply combining PV (renewable energy) at sunlight hours and direct from the grid (non-renewable energy) at night.
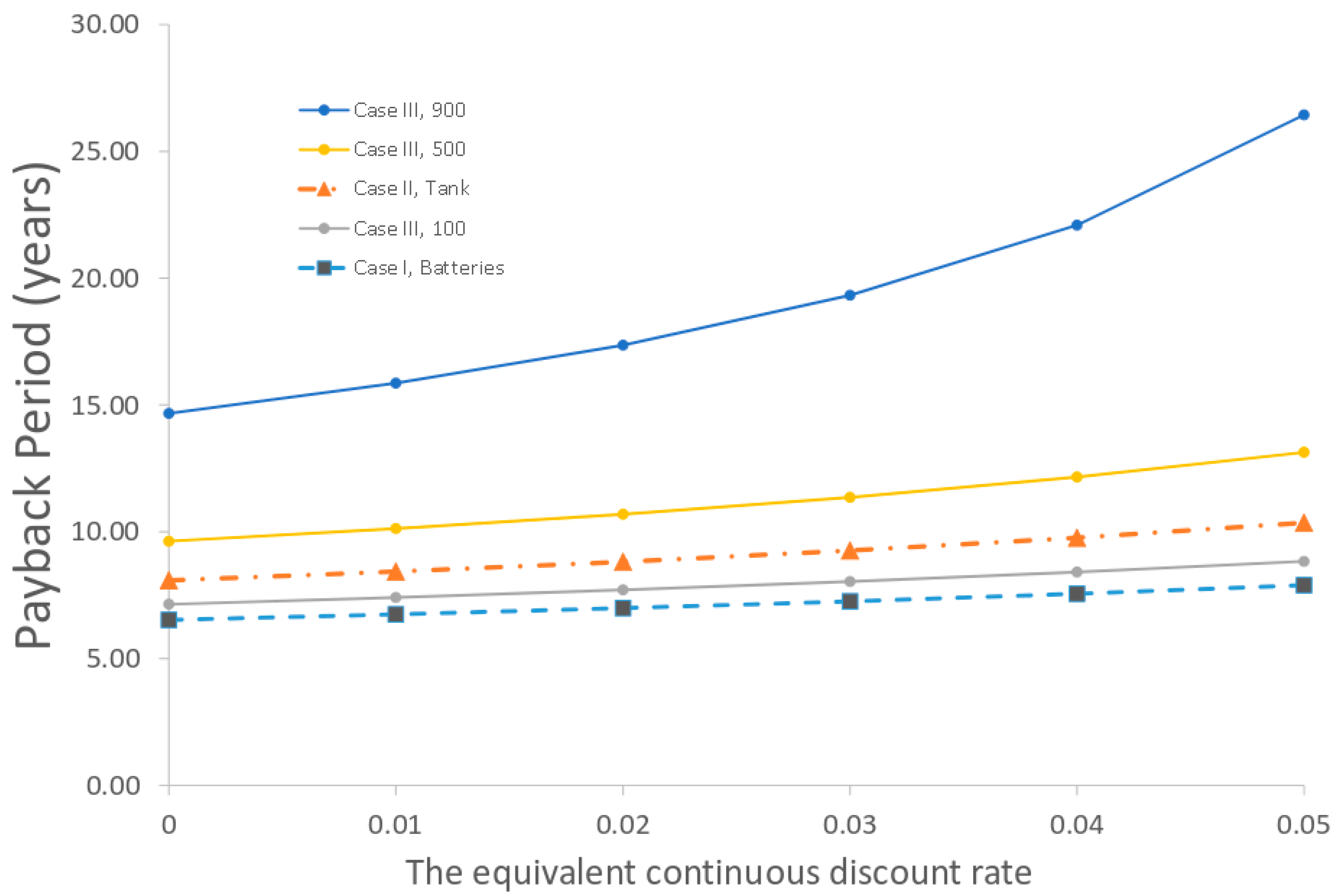
4.4. Sensitivity Analysis
4.5. Future Developments
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Alexandratos, N.; Bruinsma, J. World Agriculture Towards 2030/2050: The 2012 Revision; Food and Agriculture Organization of the United Nations: Rome, Italy, 2012. [Google Scholar]
- International Energy Agency (IEA) Water Energy Nexus. Excerpt from the World Energy Outlook 2016; International Energy Agency: Paris, France, 2016. [Google Scholar]
- Bijl, D.L.; Bogaart, P.W.; Kram, T.; de Vries, B.J.M.; van Vuuren, D.P. Long-term water demand for electricity, industry and households. Environ. Sci. Policy 2016, 55, 75–86. [Google Scholar] [CrossRef]
- Breadsell, J.K.; Byrne, J.J.; Morrison, G.M. Household energy and water practices change post-occupancy in an australian low-carbon development. Sustainability 2019, 11, 5559. [Google Scholar] [CrossRef]
- Watson, K.J. Understanding the role of building management in the low-energy performance of passive sustainable design: Practices of natural ventilation in a UK office building. Indoor Built Environ. 2015, 24, 999–1009. [Google Scholar] [CrossRef]
- Berry, S.; Davidson, K. Zero energy homes—Are they economically viable? Energy Policy 2015, 85, 12–21. [Google Scholar] [CrossRef]
- Wittenberg, I.; Matthies, E. Solar policy and practice in Germany: How do residential households with solar panels use electricity? Energy Res. Soc. Sci. 2016, 21, 199–211. [Google Scholar] [CrossRef]
- Alghamdi, A.; Haider, H.; Hewage, K.; Sadiq, R. Inter-University sustainability benchmarking for Canadian higher education institutions: Water, energy, and carbon flows for technical-level decision-making. Sustainability 2019, 11, 2599. [Google Scholar] [CrossRef]
- Hardy, L.; Garrido, A.; Juana, L. Evaluation of Spain’s water-energy nexus. Int. J. Water Resour. Dev. 2012, 28, 151–170. [Google Scholar] [CrossRef]
- Cucchiella, F.; D’Adamo, I.; Gastaldi, M.; Stornelli, V. Solar photovoltaic panels combined with energy storage in a residential building: An economic analysis. Sustainability 2018, 10, 3117. [Google Scholar] [CrossRef]
- Zsiborács, H.; Baranyai, N.H.; Vincze, A.; Háber, I.; Pintér, G. Economic and Technical Aspects of Flexible Storage Photovoltaic Systems in Europe. Energies 2018, 11. [Google Scholar] [CrossRef]
- Roncero-Sánchez, P.; Parreño Torres, A.; Vázquez, J. Control scheme of a concentration photovoltaic plant with a hybrid energy storage system connected to the grid. Energies 2018, 11, 301. [Google Scholar] [CrossRef]
- Chen, J.; Li, J.; Zhang, Y.; Bao, G.; Ge, X.; Li, P. A hierarchical optimal operation strategy of hybrid energy storage system in distribution networks with high photovoltaic penetration. Energies 2018, 11, 389. [Google Scholar] [CrossRef]
- Reca, J.; Torrente, C.; López-Luque, R.; Martínez, J. Feasibility analysis of a standalone direct pumping photovoltaic system for irrigation in Mediterranean greenhouses. Renew. Energy 2016, 85, 1143–1154. [Google Scholar] [CrossRef]
- Senol, R. An analysis of solar energy and irrigation systems in Turkey. Energy Policy 2012, 47, 478–486. [Google Scholar] [CrossRef]
- Tarjuelo, J.M.; Rodriguez-Diaz, J.A.; Abadía, R.; Camacho, E.; Rocamora, C.; Moreno, M.A. Efficient water and energy use in irrigation modernization: Lessons from Spanish case studies. Agric. Water Manag. 2015, 162, 67–77. [Google Scholar] [CrossRef]
- Chandel, S.S.; Naik, M.N.; Chandel, R. Review of solar photovoltaic water pumping system technology for irrigation and community drinking water supplies. Renew. Sustain. Energy Rev. 2015, 49, 1084–1099. [Google Scholar] [CrossRef]
- Córcoles, J.I.; Gonzalez Perea, R.; Izquiel, A.; Moreno, M.Á. Decision support system tool to reduce the energy consumption of water abstraction from aquifers for irrigation. Water 2019, 11, 323. [Google Scholar] [CrossRef]
- Betka, A.; Attali, A. Optimization of a photovoltaic pumping system based on the optimal control theory. Sol. Energy 2010, 84, 1273–1283. [Google Scholar] [CrossRef]
- Elkholy, M.M.; Fathy, A. Optimization of a PV fed water pumping system without storage based on teaching-learning-based optimization algorithm and artificial neural network. Sol. Energy 2016, 139, 199–212. [Google Scholar] [CrossRef]
- Narvarte, L.; Fernández-Ramos, J.; Martínez-Moreno, F.; Carrasco, L.M.; Almeida, R.H.; Carrêlo, I.B. Solutions for adapting photovoltaics to large power irrigation systems for agriculture. Sustain. Energy Technol. Assess. 2018, 29, 119–130. [Google Scholar] [CrossRef]
- Mohanty, A.; Ray, P.K.; Viswavandya, M.; Mohanty, S.; Mohanty, P.P. Experimental analysis of a standalone solar photo voltaic cell for improved power quality. Optik 2018, 171, 876–885. [Google Scholar] [CrossRef]
- Mérida García, A.; Fernández García, I.; Camacho Poyato, E.; Montesinos Barrios, P.; Rodríguez Díaz, J.A. Coupling irrigation scheduling with solar energy production in a smart irrigation management system. J. Clean. Prod. 2018, 175, 670–682. [Google Scholar] [CrossRef]
- Pardo, M.Á.; Juárez, J.M.; García-Márquez, D. Energy consumption optimization in irrigation networks supplied by a standalone direct pumping photovoltaic system. Sustainability 2018, 10, 4203. [Google Scholar] [CrossRef]
- González Perea, R.; Mérida García, A.; Fernández García, I.; Camacho Poyato, E.; Montesinos, P.; Rodríguez Díaz, J.A. Middleware to operate smart photovoltaic irrigation systems in real time. Water 2019, 11, 1508. [Google Scholar] [CrossRef]
- Wetzel, T.; Borchers, S. Update of energy payback time and greenhouse gas emission data for crystalline silicon photovoltaic modules. Prog. Photovolt. Res. Appl. 2015, 23, 1429–1435. [Google Scholar] [CrossRef]
- Kou, Q.; Klein, S.A.; Beckman, W.A. A method for estimating the long-term performance of direct-coupled PV pumping systems. Sol. Energy 1998, 64, 33–40. [Google Scholar] [CrossRef]
- Meah, K.; Fletcher, S.; Ula, S. Solar photovoltaic water pumping for remote locations. Renew. Sustain. Energy Rev. 2008, 12, 472–487. [Google Scholar] [CrossRef]
- Reddy, P.P.K.K.; Reddy, J.N. Photovoltaic energy conversion system for water pumping application. Int. J. Emerg. Trends Electr. Electron. IJETEE 2014, 10, 22–29. [Google Scholar]
- Child, M.; Haukkala, T.; Breyer, C. The role of solar photovoltaics and energy storage solutions in a 100% renewable energy system for Finland in 2050. Sustainability 2017, 9, 1358. [Google Scholar] [CrossRef]
- Holdermann, C.; Kissel, J.; Beigel, J. Distributed photovoltaic generation in Brazil: An economic viability analysis of small-scale photovoltaic systems in the residential and commercial sectors. Energy Policy 2014, 67, 612–617. [Google Scholar] [CrossRef]
- Wong, J.; Lim, Y.S.; Tang, J.H.; Morris, E. Grid-connected photovoltaic system in Malaysia: A review on voltage issues. Renew. Sustain. Energy Rev. 2014, 29, 535–545. [Google Scholar] [CrossRef]
- Arab, A.H.; Chenlo, F.; Mukadam, K.; Balenzategui, J.L. Performance of PV water pumping systems. Renew. Energy 1999, 18, 191–204. [Google Scholar] [CrossRef]
- Muhsen, D.H.; Khatib, T.; Abdulabbas, T.E. Sizing of a standalone photovoltaic water pumping system using hybrid multi-criteria decision making methods. Sol. Energy 2018, 159, 1003–1015. [Google Scholar] [CrossRef]
- Khatib, T.; Ibrahim, I.A.; Mohamed, A. A review on sizing methodologies of photovoltaic array and storage battery in a standalone photovoltaic system. Energy Convers. Manag. 2016, 120, 430–448. [Google Scholar] [CrossRef]
- Li, C.H.; Zhu, X.J.; Cao, G.Y.; Sui, S.; Hu, M.R. Dynamic modeling and sizing optimization of stand-alone photovoltaic power systems using hybrid energy storage technology. Renew. Energy 2009, 34, 815–826. [Google Scholar] [CrossRef]
- Ru, Y.; Kleissl, J.; Martinez, S. Storage size determination for grid-connected photovoltaic systems. IEEE Trans. Sustain. Energy 2013, 4, 68–81. [Google Scholar] [CrossRef]
- Narvarte, L.; Almeida, R.H.; Carrêlo, I.B.; Rodríguez, L.; Carrasco, L.M.; Martinez-Moreno, F. On the number of PV modules in series for large-power irrigation systems. Energy Convers. Manag. 2019, 186, 516–525. [Google Scholar] [CrossRef]
- Yu, C.; Khoo, Y.S.; Chai, J.; Han, S.; Yao, J. Optimal orientation and tilt angle for maximizing in-plane solar irradiation for PV applications in Japan. Sustainability 2019, 11, 2016. [Google Scholar] [CrossRef]
- Hailu, G.; Fung, A.S. Optimum tilt angle and orientation of photovoltaic thermal system for application in greater Toronto area, Canada. Sustainability 2019, 11, 6443. [Google Scholar] [CrossRef]
- Mérida García, A.; Gallagher, J.; McNabola, A.; Camacho Poyato, E.; Montesinos Barrios, P.; Rodríguez Díaz, J.A. Comparing the environmental and economic impacts of on-or off-grid solar photovoltaics with traditional energy sources for rural irrigation systems. Renew. Energy 2019, 140, 895–904. [Google Scholar] [CrossRef]
- Seme, S.; Lukač, N.; Štumberger, B.; Hadžiselimović, M. Power quality experimental analysis of grid-connected photovoltaic systems in urban distribution networks. Energy 2017, 139, 1261–1266. [Google Scholar] [CrossRef]
- Sugihara, H.; Yokoyama, K.; Saeki, O.; Tsuji, K.; Funaki, T. Economic and efficient voltage management using customer-owned energy storage systems in a distribution network with high penetration of photovoltaic systems. IEEE Trans. Power Syst. 2012, 28, 102–111. [Google Scholar] [CrossRef]
- Pardo, M.A.; Manzano, J.; Valdés-Abellán, J.; Cobacho, R. Standalone direct pumping photovoltaic system or energy storage in batteries for supplying irrigation networks. Cost analysis. Sci. Total Environ. 2019, 673, 821–830. [Google Scholar] [CrossRef] [PubMed]
- Batchabani, E.; Fuamba, M. Optimal tank design in water distribution networks: Review of literature and perspectives. J. Water Resour. Plan. Manag. 2012, 140, 136–145. [Google Scholar] [CrossRef]
- Kurek, W.; Ostfeld, A. Multi-objective optimization of water quality, pumps operation, and storage sizing of water distribution systems. J. Environ. Manag. 2013, 115, 189–197. [Google Scholar] [CrossRef]
- Ahmad, R. Hydraulic design of water distribution storage tanks. In Water Encyclopedia; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2005. [Google Scholar]
- Sarbu, I. A study of energy optimisation of urban water distribution systems using potential elements. Water 2016, 8, 593. [Google Scholar] [CrossRef]
- Gómez, E.; Cabrera, E.; Balaguer, M.; Soriano, J. Direct and indirect water supply: An energy assessment. Proced. Eng. 2015, 119, 1088–1097. [Google Scholar] [CrossRef]
- Hamidat, A.; Benyoucef, B. Systematic procedures for sizing photovoltaic pumping system, using water tank storage. Energy Policy 2009, 37, 1489–1501. [Google Scholar] [CrossRef]
- Spiers, D. Chapter IIB-2—Batteries in PV systems. In Practical Handbook of Photovoltaics, 2nd ed.; McEvoy, A., Markvart, T., Castañer, L., Eds.; Academic Press: Boston, MA, USA, 2012; pp. 721–776. ISBN 978-0-12-385934-1. [Google Scholar]
- Amrouche, S.O.; Rekioua, D.; Rekioua, T.; Bacha, S. Overview of energy storage in renewable energy systems. Int. J. Hydrogen Energy 2016, 41, 20914–20927. [Google Scholar] [CrossRef]
- Wagner, L. Future Energy Improved Sustainable and Clean Options for our Planet; Overview of Energy Storage Technologies; Elsevier: Amsterdam, The Netherlands, 2013; pp. 613–631. [Google Scholar]
- Üçtug, F.G.; Azapagic, A. Environmental impacts of small-scale hybrid energy systems: Coupling solar photovoltaics and lithium-ion batteries. Sci. Total Environ. 2018, 643, 1579–1589. [Google Scholar] [CrossRef]
- Rydh, C.J.; Sandén, B.A. Energy analysis of batteries in photovoltaic systems. Part I: Performance and energy requirements. Energy Convers. Manag. 2005, 46, 1957–1979. [Google Scholar] [CrossRef]
- Todde, G.; Murgia, L.; Deligios, P.A.; Hogan, R.; Carrelo, I.; Moreira, M.; Pazzona, A.; Ledda, L.; Narvarte, L. Energy and environmental performances of hybrid photovoltaic irrigation systems in Mediterranean intensive and super-intensive olive orchards. Sci. Total Environ. 2019, 651, 2514–2523. [Google Scholar] [CrossRef] [PubMed]
- Ghorbanian, V.; Karney, B.; Guo, Y. Pressure standards in water distribution systems: Reflection on current practice with consideration of some unresolved issues. J. Water Resour. Plan. Manag. 2016, 142, 04016023. [Google Scholar] [CrossRef]
- Rossman, L.A. EPANET 2: Users Manual; Environmental Protection Agency: Washington, DC, USA, 2000.
- Giustolisi, O.; Savic, D.; Kapelan, Z. Pressure-driven demand and leakage simulation for water distribution networks. J. Hydraul. Eng. 2008, 134, 626–635. [Google Scholar] [CrossRef]
- Pardo, M.A.; Riquelme, A.; Melgarejo, J. A tool for calculating energy audits in water pressurized networks. AIMS Environ. Sci. 2019, 6, 94–108. [Google Scholar]
- Cabrera, E.; Pardo, M.A.; Cabrera, E., Jr.; Arregui, F.J. Tap water costs and service sustainability, a close relationship. Water Resour. Manag. 2013, 27, 239–253. [Google Scholar] [CrossRef]
- Vindel, J.M.; Polo, J.; Zarzalejo, L.F. Modeling monthly mean variation of the solar global irradiation. J. Atmos. Sol. Terr. Phys. 2015, 122, 108–118. [Google Scholar] [CrossRef]
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes, 4th ed.; Wiley: Hoboken, NJ, USA, 2013; ISBN 978-0-470-87366-3. [Google Scholar]
- Balling, R.C., Jr.; Gober, P.; Jones, N. Sensitivity of residential water consumption to variations in climate: An intraurban analysis of Phoenix, Arizona. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Hoekstra, A.Y.; Mekonnen, M.M.; Chapagain, A.K.; Mathews, R.E.; Richter, B.D. Global monthly water scarcity: Blue water footprints versus blue water availability. PLoS ONE 2012, 7, e32688. [Google Scholar] [CrossRef]
- Kleiner, Y.; Rajani, B. Comprehensive review of structural deterioration of water mains: Statistical models. Urban. Water 2001, 3, 131–150. [Google Scholar] [CrossRef]
- Cabrera, E.; Pardo, M.A.; Cobacho, R.; Cabrera, E. Energy audit of water networks. J. Water Resour. Plan. Manag. 2010, 136. [Google Scholar] [CrossRef]
- Ebara Grupos de Presión Automáticos. Available online: http://www.ebara.es (accessed on 11 November 2019).
| β = 15° | = 1367 W m−2 | = 25 °C |
| ρ = 0.2 | = 1000 Wm−2 | PP = 250 W |
| d = 0.004 °C−1 | = 0.95 | = 0.8 |
| Month | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | 17 | 47 | 75 | 105 | 135 | 162 | 198 | 228 | 258 | 288 | 318 | 344 |
| Tavg (°C) | 11.5 | 12.6 | 13.9 | 15.5 | 18.4 | 22.1 | 24.9 | 25.5 | 23.1 | 19.1 | 14.9 | 12.4 |
| Havg (kWh m−2) | 2.6 | 3.5 | 4.7 | 6.7 | 7.4 | 7.8 | 8 | 6.5 | 5.4 | 3.7 | 2.6 | 2.2 |
| K | 1.01 | 0.82 | 0.85 | 1.07 | 0.95 | 1.02 | 1.16 | 1.15 | 0.95 | 1.00 | 1.05 | 0.94 |
| Components | Investment |
|---|---|
| PV array | 359 (EUR/unit) |
| Batteries | 65,789 (EUR) |
| Pipelines DN350 | 39.52 (EUR/m) |
| Pipelines DN300 | 32.06 (EUR/m) |
| Pump | 5068 (EUR) |
| Oversizing tank | 100 (EUR/m3) |
| Winter | Summer | Power (EUR/kW) | Energy Cons. (EUR/kWh) | Reactive Energy (EUR/kVArh) | |
|---|---|---|---|---|---|
| Peak | 18–22 h | 11–15 h | 59.173 | 0.095 | 0.062 |
| Plain | 8–18 h 22–24 h | 8–11 h 15–24 h | 36.491 | 0.086 | 0.062 |
| Low | 0–8 h | 0–8 h | 8.368 | 0.065 | 0.000 |
| Case I | Case II | ||||
|---|---|---|---|---|---|
| Month | E produced (Wh) | Econs (kwh) | No. of Panels | Econs (kwh) | No. of Panels |
| January | 923.96 | 816.30 | 884 | 962.07 | 1042 |
| February | 1137.69 | 734.94 | 646 | 941.86 | 828 |
| March | 1376.70 | 751.44 | 546 | 945.10 | 687 |
| April | 1637.28 | 845.21 | 517 | 968.31 | 592 |
| May | 1913.57 | 790.24 | 413 | 955.76 | 500 |
| June | 1947.39 | 821.60 | 422 | 963.11 | 495 |
| July | 1990.96 | 886.16 | 446 | 977.55 | 491 |
| August | 1669.27 | 881.69 | 529 | 976.53 | 586 |
| September | 1480.98 | 790.24 | 534 | 955.76 | 646 |
| October | 1098.68 | 813.56 | 741 | 961.02 | 875 |
| November | 864.77 | 835.90 | 967 | 966.24 | 1118 |
| December | 791.49 | 791.09 | 1000 | 954.70 | 1207 |
| Month | Cases I and II | Case III (No. of PV Panels) | ||||
|---|---|---|---|---|---|---|
| 100 | 300 | 500 | 700 | 900 | ||
| January | 8470.64 | 15.70 | 47.11 | 78.51 | 109.92 | 141.33 |
| February | 6858.39 | 31.23 | 93.70 | 156.16 | 218.62 | 281.09 |
| March | 7082.79 | 66.17 | 198.52 | 330.87 | 463.22 | 595.57 |
| April | 8698.96 | 677.82 | 2033.46 | 2575.76 | 2726.41 | 2877.05 |
| May | 7643.50 | 813.58 | 2331.29 | 2631.31 | 2931.33 | 3231.35 |
| June | 8486.69 | 799.38 | 2348.58 | 2777.16 | 3013.05 | 3248.94 |
| July | 8787.34 | 845.36 | 2536.07 | 2934.01 | 3233.68 | 3473.41 |
| August | 8793.44 | 711.72 | 2135.15 | 2713.78 | 2952.72 | 3154.96 |
| September | 7614.53 | 616.72 | 1850.15 | 2281.90 | 2442.15 | 2602.41 |
| October | 8204.18 | 480.06 | 1440.18 | 2238.76 | 2323.26 | 2407.76 |
| November | 8619.18 | 19.91 | 59.73 | 99.55 | 139.37 | 179.18 |
| December | 7545.45 | 12.64 | 37.91 | 63.18 | 88.45 | 113.72 |
| Standalone PV Direct Pumping | Electricity Supply Combining PV Panels and Electricity Grids | ||||||
|---|---|---|---|---|---|---|---|
| Case I | Case II | Case III | |||||
| Actions (Purchase and installation) | Panels and batteries. | Panels, compensation tank, new pumps, sizing pipelines | Panels and batteries. Number of Panels range from 0 to N (minimum number of panels for Case I and II, here N = 1000) | ||||
| No. of Panels (Table 5) | 1000 | 1207 | 100 | 300 | 500 | 700 | 900 |
| Total Investment (Section 4.2.4) | 631,509 | 782,529 | 35,948 | 107,844 | 179,740 | 251,636 | 323,532 |
| Savings (EUR/year) (Table 6) | 96,805 | 96,805 | 5033 | 14,943 | 18,668 | 20,410 | 22,058 |
| Payback Period (Section 4.2.5) | 6.99 | 8.82 | 7.71 | 7.79 | 10.69 | 14.16 | 17.36 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pardo, M.Á.; Cobacho, R.; Bañón, L. Standalone Photovoltaic Direct Pumping in Urban Water Pressurized Networks with Energy Storage in Tanks or Batteries. Sustainability 2020, 12, 738. https://doi.org/10.3390/su12020738
Pardo MÁ, Cobacho R, Bañón L. Standalone Photovoltaic Direct Pumping in Urban Water Pressurized Networks with Energy Storage in Tanks or Batteries. Sustainability. 2020; 12(2):738. https://doi.org/10.3390/su12020738
Chicago/Turabian StylePardo, Miguel Ángel, Ricardo Cobacho, and Luis Bañón. 2020. "Standalone Photovoltaic Direct Pumping in Urban Water Pressurized Networks with Energy Storage in Tanks or Batteries" Sustainability 12, no. 2: 738. https://doi.org/10.3390/su12020738
APA StylePardo, M. Á., Cobacho, R., & Bañón, L. (2020). Standalone Photovoltaic Direct Pumping in Urban Water Pressurized Networks with Energy Storage in Tanks or Batteries. Sustainability, 12(2), 738. https://doi.org/10.3390/su12020738