Classification of Urban Street Networks Based on Tree-Like Network Features
Abstract
1. Introduction
2. Methodology
2.1. The Topological Features of the Tree-Like Street Network
- (1)
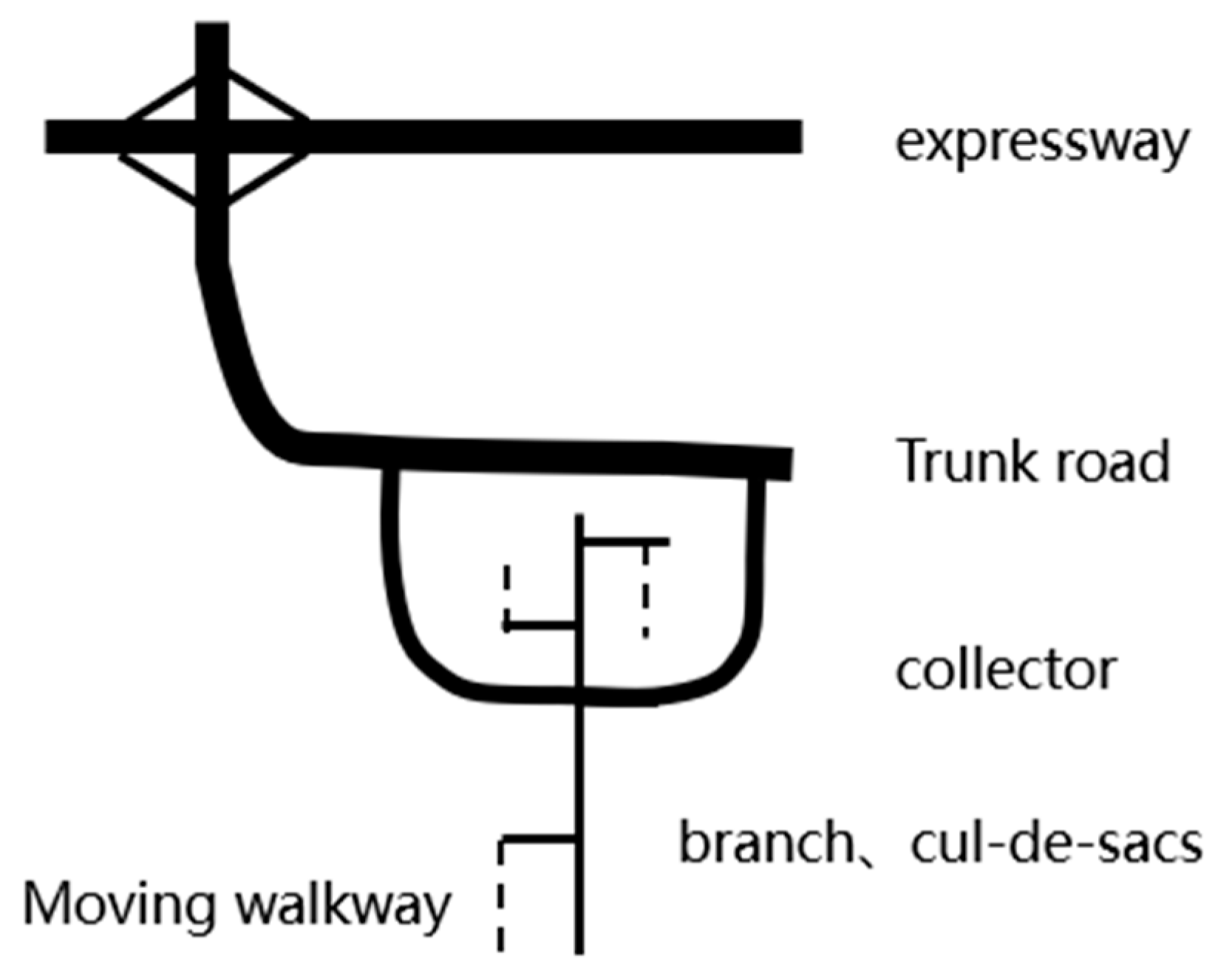
- As is usually obvious by inspection, tree-like street networks have a clearer and more defined hierarchical structure than grids. This condition is necessary for a network to be tree-like; in traffic engineering terms, the artery road runs through the entire area, while the branch road clearly serves a smaller one. A road is only allowed to connect with roads of the same grade or next grade roads. For example, expressway could connect with another expressway or an artery street, but not a local branch.
- (2)
- There exist only a few route switches of different length between any two interior points of a tree-like network. This is an essential difference from the grid street network; it is a necessary and sufficient condition for a network to be a tree network. In most cases, fewer loop routes are found in tree-like street networks. The scarcity of cycles alone, however, is not enough to judge whether a network is tree-like. It is also necessary to confirm if these cycles can provide multipath like a grid network.
- (3)
- There are more T-type intersections and broken roads in the tree-like street system. Undoubtedly, these T-type intersections and broken roads reduce alternative paths for traffic flow, but they provide a more secure environment and the typical appearance characteristics of a tree-like road network.
2.2. Abstracted Expression of Tree-Like Structure in the Street Network
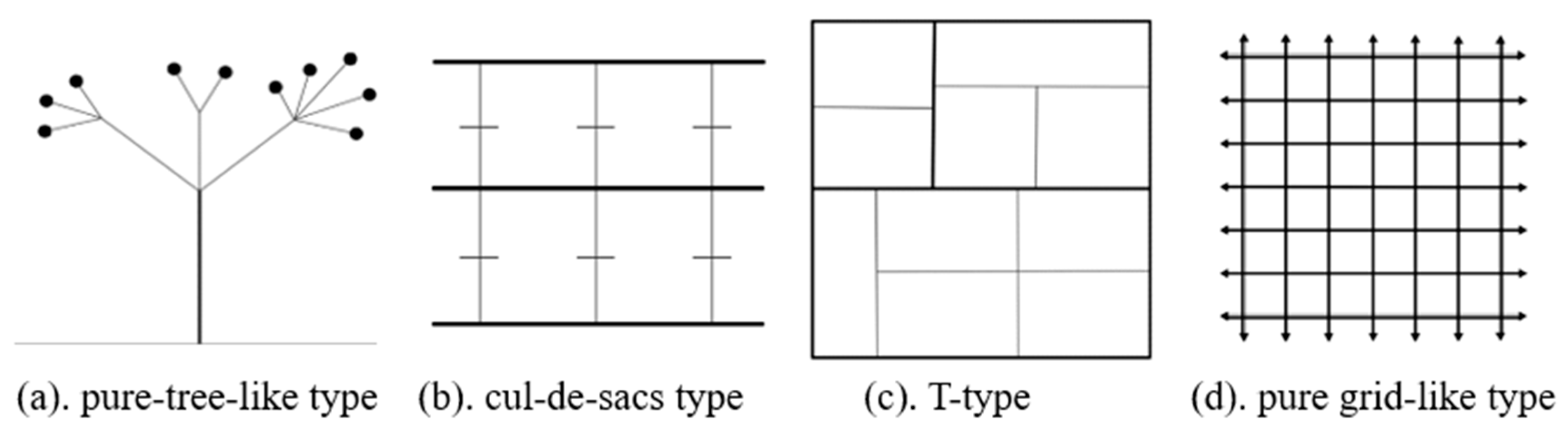
- (1)
- Pure tree-like network pattern (Figure 2a). There are obvious backbone roads through the region, while T-type cross and end-roads are also often adopted, forming a low-connected level network structure. This type of street network helps to protect the privacy of the residents and the stability of the traffic but may be less robust than the others.
- (2)
- The cul-de-sacs network pattern (Figure 2b). There are several trunks passing through a region with many end-roads. This type of network has good accessibility, but might be weaker on interior connectivity than the others.
- (3)
- T-type network pattern (Figure 2c). This street network is similar to a pure grid-shaped network, but the T-type intersections, while possibly reducing the connectivity, may improve the efficiency of trunk transportation.
- (4)
- Pure grid-like network pattern (Figure 2d). The connectivity within this network is higher than in the others; however, due to the excessive number of intersections and the short distance between them, transportation efficiency is usually lower.
2.3. Differences between the Basic Patterns of the Road Network
3. Parameters Describing the Network Pattern
3.1. T-Type and X-Type Intersection Ratios
3.2. Penetrating Street Ratio
3.3. Cul-De-Sac and Cell Ratios
4. Sample Analysis
4.1. Principles of Sample Selection
- (1)
- Most of the street network samples come from historic Chinese cities, such as Nanjing and Suzhou. Others were taken from a classic scholarly work on streets and patterns [2].
- (2)
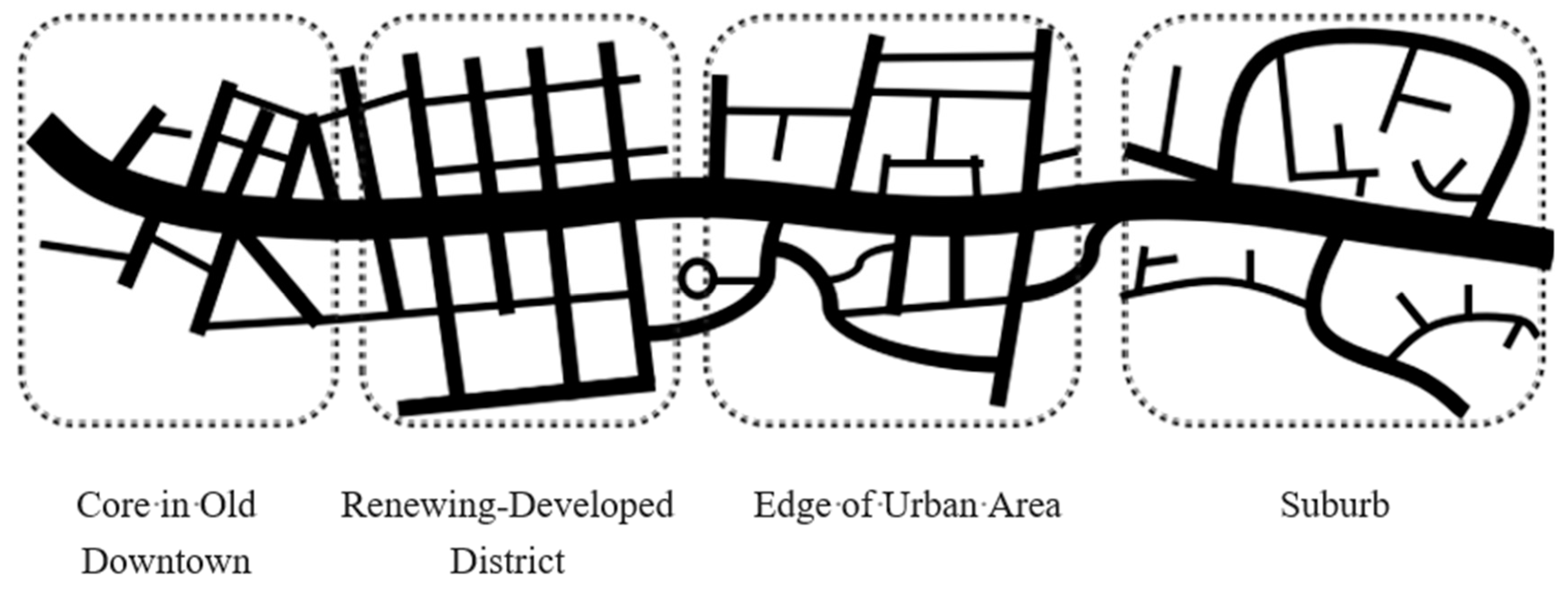
- The samples represent different parts of urban areas: new development zones, cores of downtown districts, ring areas around the city, and outer suburban residential areas.
- (3)
- For convenience of comparison, each sample’s area was limited to four square kilometers (2 km × 2 km). Considering the influence of ground facilities or terrain features, such as railways and rivers, an irregular boundary was also acceptable when the sample had an obvious shape feature. Figure 5 shows two different examples of urban areas from the sample set.
4.2. Data Collection and Analysis
4.3. Data Analysis and Interpretation
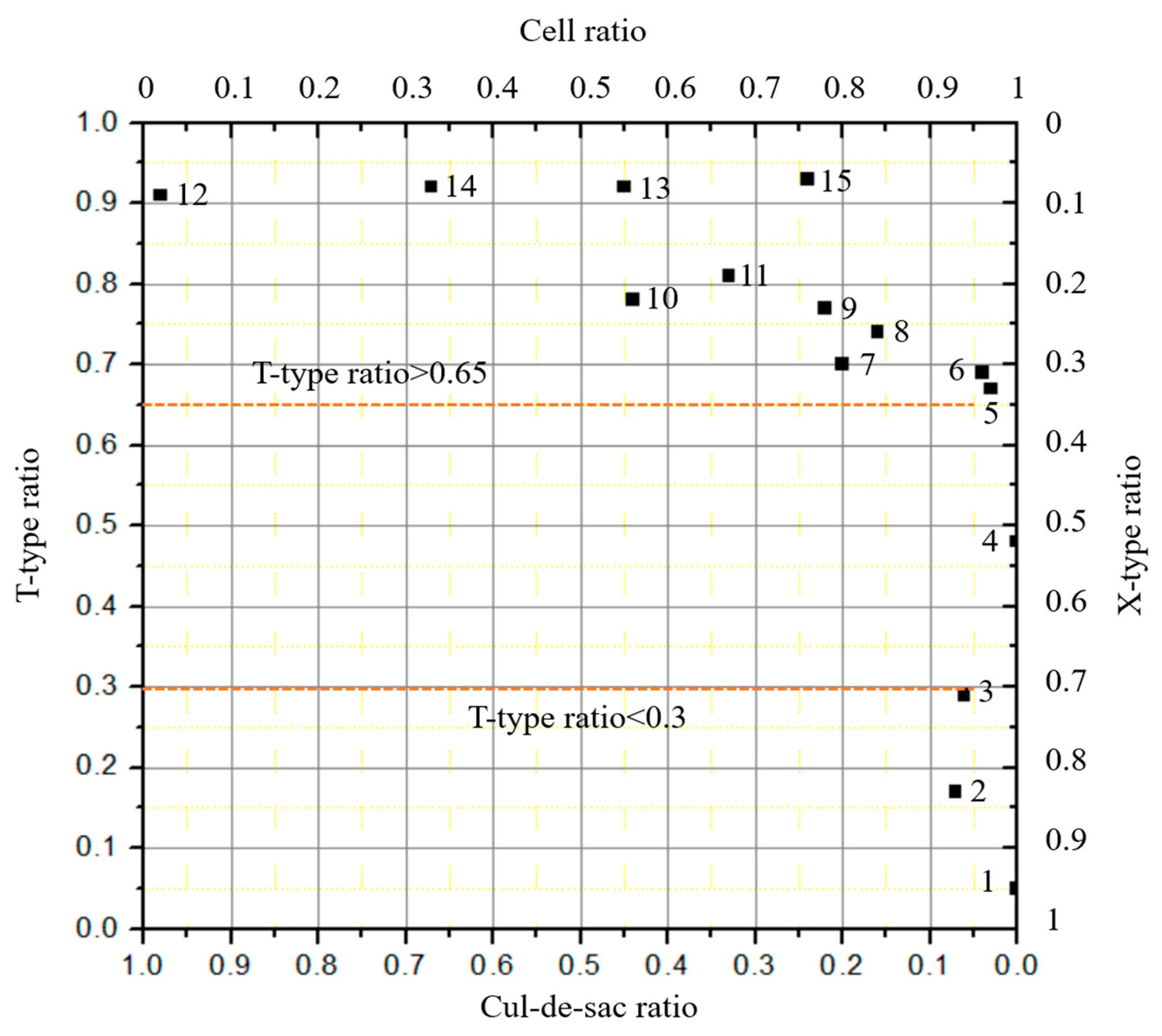
- From Figure 8a, it is obvious that, when the samples are listed in order of monotonically increasing T-type ratio, three distinct regimes emerge, namely T-type ratio ∈ [0,0.3), [0.3,0.9), [0.9,1.0]. These three parts respectively correspond to a pure grid-like network, a transitional state network, and a pure tree-like network. This method can clearly define the boundary between pure tree- and pure grid-like road networks. However, because the indicator values in the transitional region are very close together, it is hard to distinguish any finer divisions in that regime.
- It can be seen from Figure 8b that the penetrating street ratio and the X-type ratio are highly coincident and have almost the same general tendencies in the figure. When the value of either is more than 0.3, it can be used to distinguish a pure grid road network from a rectangular-type street network. However, when the value is less than 0.3, a pure tree-like road network and a T-shaped road network cannot be accurately identified from these indicators alone.
- From Figure 8b, the trend of the cul-de-sac ratio seems to be nearly opposite that of the X-type ratio, but it might be more active (i.e., have more discriminating power) when it is close to the area of the tree-like network pattern. When the cul-de-sac ratio ∈ [0,0.3), the network could be predicted to be either grid-shaped or T-type. When the cul-de-sac ratio ∈ [0.3,0.5), the network could be of the cul-de-sacs type. Finally, when the cul-de-sacs ratio ∈ [0.5,1.0], the network might be purely tree-like.
- The penetrating street ratio is an important and effective indicator for objectively measuring the similarity of a general network to a tree-like network. It has not received enough attention in previous analyses.
5. Conclusions and Further Research
- (1)
- The main point of this paper is to recognize that all urban road networks, instead of being classified as grids or trees, may be arranged on a spectrum between these extremes. Subdividing the geometric structure of the road network further can be effective for research and engineering technology, improvements in land use, road safety, and transportation efficiency in the future.
- (2)
- Through statistical analysis of road samples in different cities or regions, it has been found that the differences in geometric and topological characteristics between the networks mainly come from the number and the type of intersections, the density and hierarchical structure of the road networks, the proportion of broken roads, and the number and proportion of through-roads. Therefore, a road network can be classified according to how closely it resembles a tree-like network in terms of these various parameters.
- (3)
- This study initially divides road networks into four types (pure tree-like networks, cul-de-sac networks, T-shaped networks, and grid-shaped networks) based on properties such as non-circular traffic, number of end roads, and number of alternative paths.
- (4)
- The research proves that it is possible to use different indicators in a certain order (X-type/T-type ratio, cul-de-sac ratio, and penetrating street ratio) to classify road networks. Four specific, quantitative, well-defined indicators for classifying the small-scale structure of street networks are proposed.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Boeing, G. A multi-scale analysis of 27,000 urban street networks: Every US city, town, urbanized area, and Zillow neighborhood. Environ. Plan. B Urban Anal. City Sci. 2018, 8, 1–19. [Google Scholar] [CrossRef]
- Brindle, R.E. Road Hierarchy and Functional Classification. Spec. Rep. 1996, 53, 99–109. [Google Scholar]
- Ye, P.Y.; Chen, X.H. Reviews of Radburn Idea’s Road and Traffic Planning. Urban Plan. Int. 2009, 24, 69–73. [Google Scholar]
- Southworth, M.; Eran, B.J. Streets and the Shaping of Towns and Cities, 2nd ed.; Island Press: Washington, DC, USA, 2003; ISBN 1-55963-916-4. [Google Scholar]
- Strano, E.; Luciano da Fontoura Costa, M.V.; Cardillo, A.; Porta, S.; Latora, V. Urban street networks, a comparative analysis of ten European cities. Environ. Plan. B Plan. Des. 2013, 40, 1071–1086. [Google Scholar] [CrossRef]
- Von, V.; Jaber, S. Urban Streets: Towards Sustainable Mobility in Arabic Cities; University at Stuttgart: Stuttgart, Germany, 2013. [Google Scholar] [CrossRef]
- Cai, J. Urban Road Network System Planning; China Construction Industry Press: Beijing, China, 2013; ISBN 978-7-112-15824-9. [Google Scholar]
- Jiang, B. Street Hierarchies: A Minority of Streets Account for a Majority of Traffic Flow. Int. J. Geogr. Inf. Sci. 2009, 23, 1033–1048. [Google Scholar] [CrossRef]
- Buhl, J.; Gautrais, J.; Reeves, N.; Sole, R.V.; Valverde, S.; Kuntz, P.; Theraulaz, G. Topological Patterns in Street Networks of Self-Organized Urban Settlements. Eur. Phys. J. 2006, 49, 513–522. [Google Scholar] [CrossRef]
- Marshall, S. Streets & Patterns, 1st ed.; China Architecture & Building Press: Beijing, China, 2011; pp. 35–37. ISBN 978-7-112-12724-5. [Google Scholar]
- Xie, F.; Levinson, D. Measuring the structure of road networks. Geogr. Anal. 2007, 39, 336–356. [Google Scholar] [CrossRef]
- Barthelemy, M.; Flammini, A. Modeling Urban Street Patterns. Phys. Rev. Lett. 2008, 4, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Sreelekha, M.G.; Krishnamurthy, K.; Anjaneyulu, M.V.L.R.C. Interaction between Road Network Connectivity and Spatial Pattern. Procedia Technol. 2016, 24, 131–139. [Google Scholar] [CrossRef]
- Marshall, W.E.; Lennard, H.L. Street Network Types and Road Safety: A Study of 24 California Cities. Urban Des. Int. 2010, 15, 133–147. [Google Scholar] [CrossRef]
- Southworth, M.; Ben-Joseph, E. Reconsidering the Cul -de-sac. ACCESS Mag. 2004, 1, 28–33. [Google Scholar]
- Lovegrove, G.R.; Sun, J. Using Community-Based Macro level Collision Prediction Models to Evaluate Safety Level of Neighborhood Road Network Patterns. In Proceedings of the 89th Annual Meeting of the Transportation Research Board, Washington, DC, USA, 10–14 January 2010. [Google Scholar]
- Derrible, S.; Kennedy, C. The Complexity and Robustness of Metro Networks. Phys. A-Stat. Mech. Its Appl. 2010, 389, 3678–3691. [Google Scholar] [CrossRef]
- Marshall, S.; Gil, J.; Kropf, K.; Tomko, M.; Figueiredo, L. Street Network Studies: From Networks to Models and their Representations. Netw. Spat. Econ. 2018, 18, 735–749. [Google Scholar] [CrossRef]
- Boeing, G. Urban spatial order: Street network orientation, configuration, and entropy. Boeing Appl. Netw. Sci. 2019, 4, 67. [Google Scholar] [CrossRef]
- Shi, F.; Wang, W. Urban Road Network Structure Analysis. City Plan. Rev. 2007, 31, 68–73. [Google Scholar]
- Porta, S.; Crucitti, P. The network analysis of urban streets: A primal approach. Environ. Plan. B Plan. Des. 2006, 33, 705–725. [Google Scholar] [CrossRef]
- Mocnik, F.B. The Polynomial Volume Law of Complex Networks in the Context of Local and Global Optimization. Sci. Rep. 2018. [Google Scholar] [CrossRef] [PubMed]
- Mocnik, F.B. Dimension as an Invariant of Street Networks. In Proceedings of the 7th International Conference on Complex Networks and Their Applications, Cambridge, UK, 11–13 December 2018; pp. 455–457. [Google Scholar]
- Tian, F.; Zhang, Y.Q. Graph. and Network Flow Theory, 2nd ed.; Science Press: Beijing, China, 2015; pp. 47–50. ISBN 978-7-03-042688-8. [Google Scholar]
- Chan, S.H.Y.; Donner, R.V.; Lämmer, S. Urban road networks-spatial networks with universal geometric features? Eur. Phys. J. B 2011, 84, 563–578. [Google Scholar] [CrossRef]
- Lima, M. The Book of Trees: Visualizing Branches of Knowledge; China Machine Press: Beijing, China, 2015; pp. 5–9. ISBN 978-7-111-51518-0. [Google Scholar]
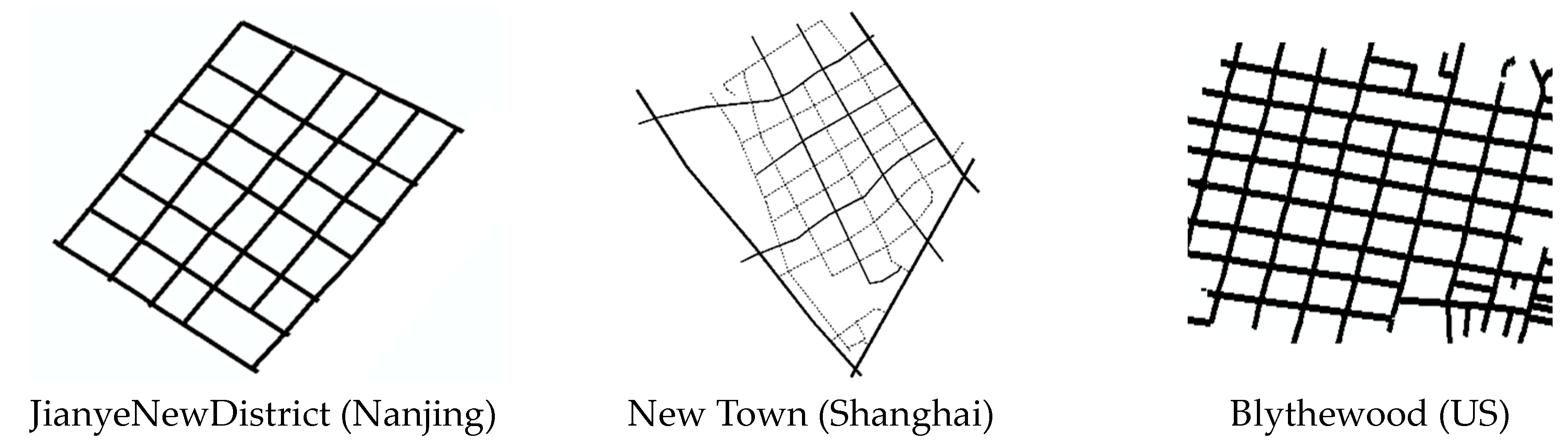
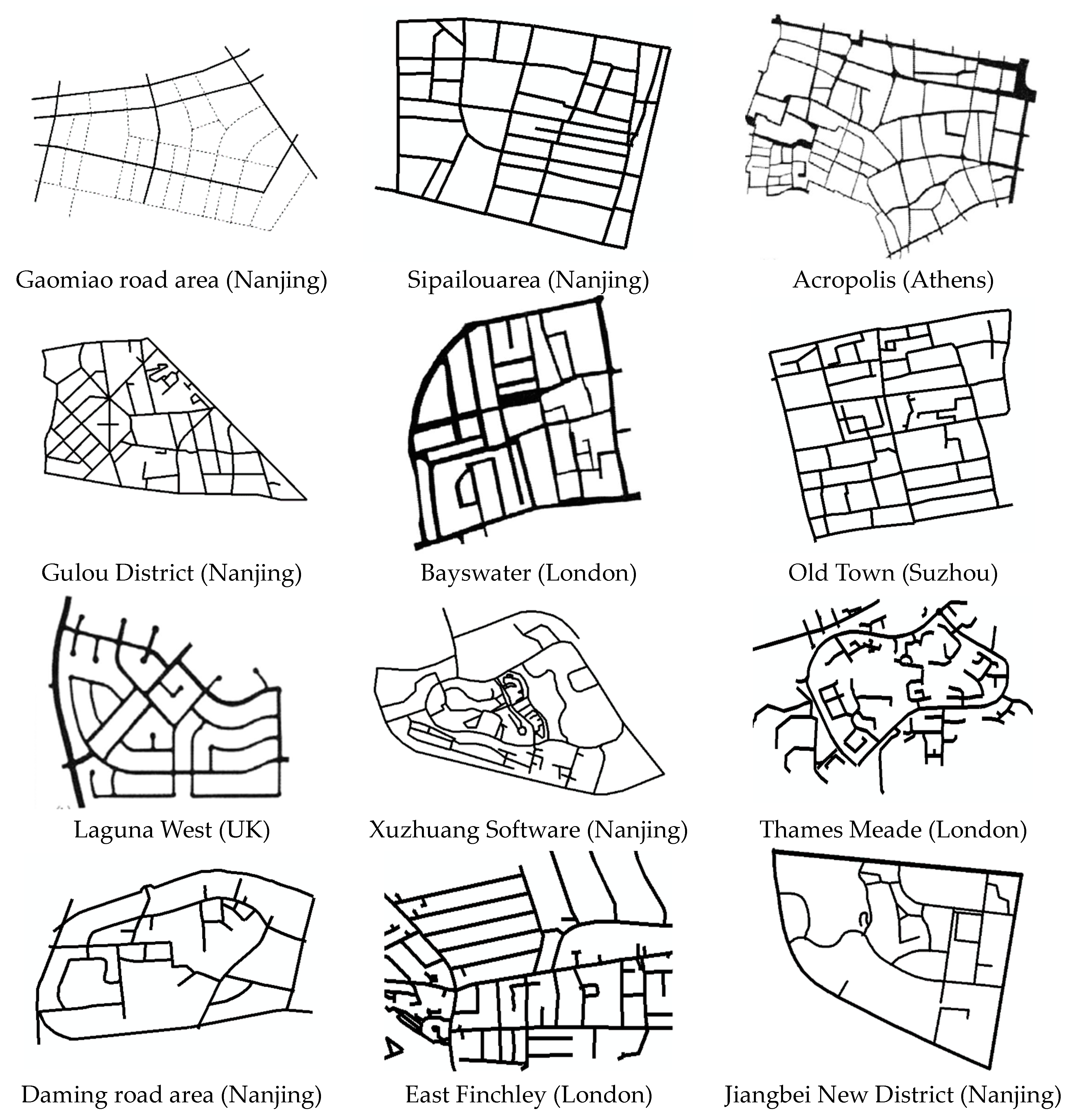
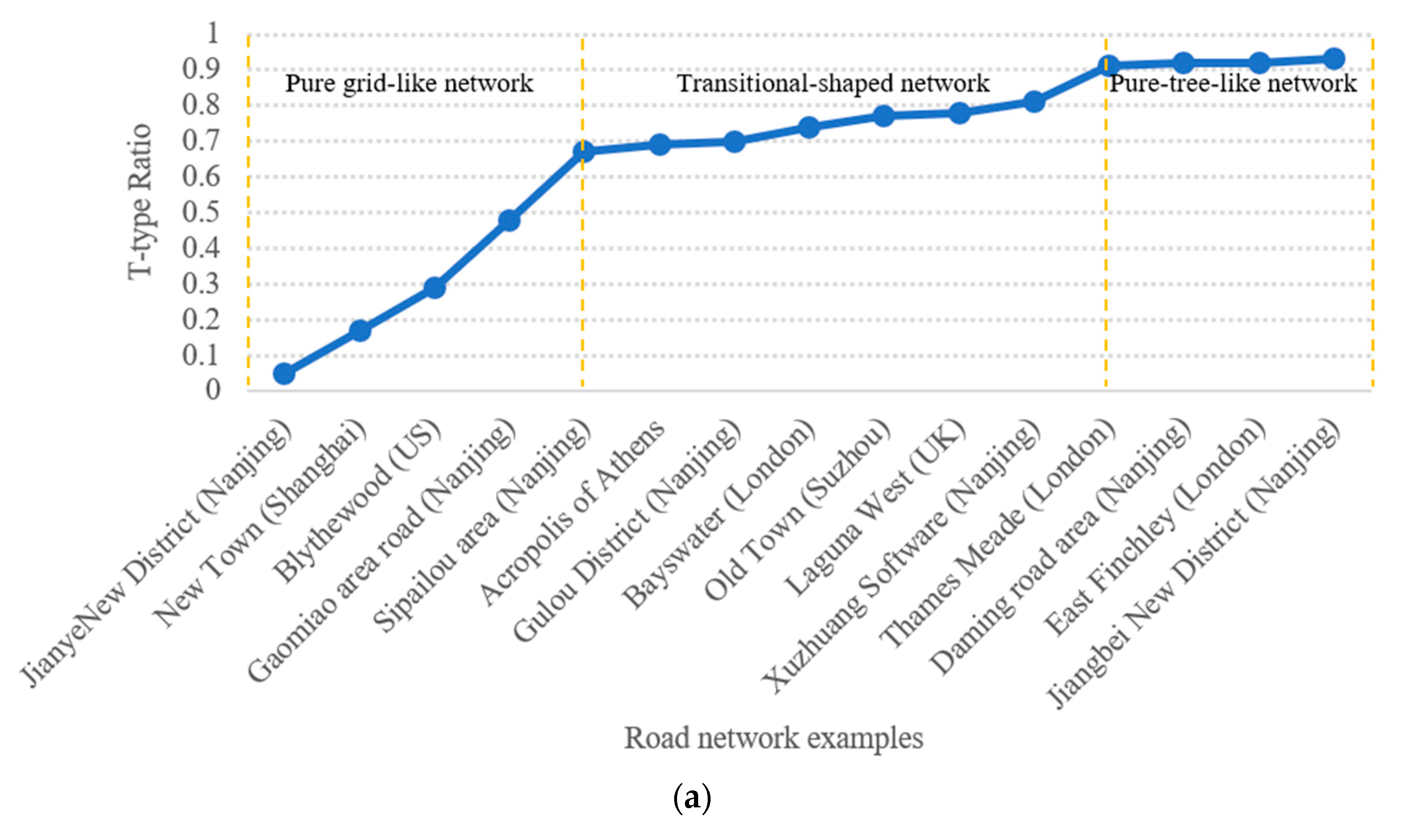
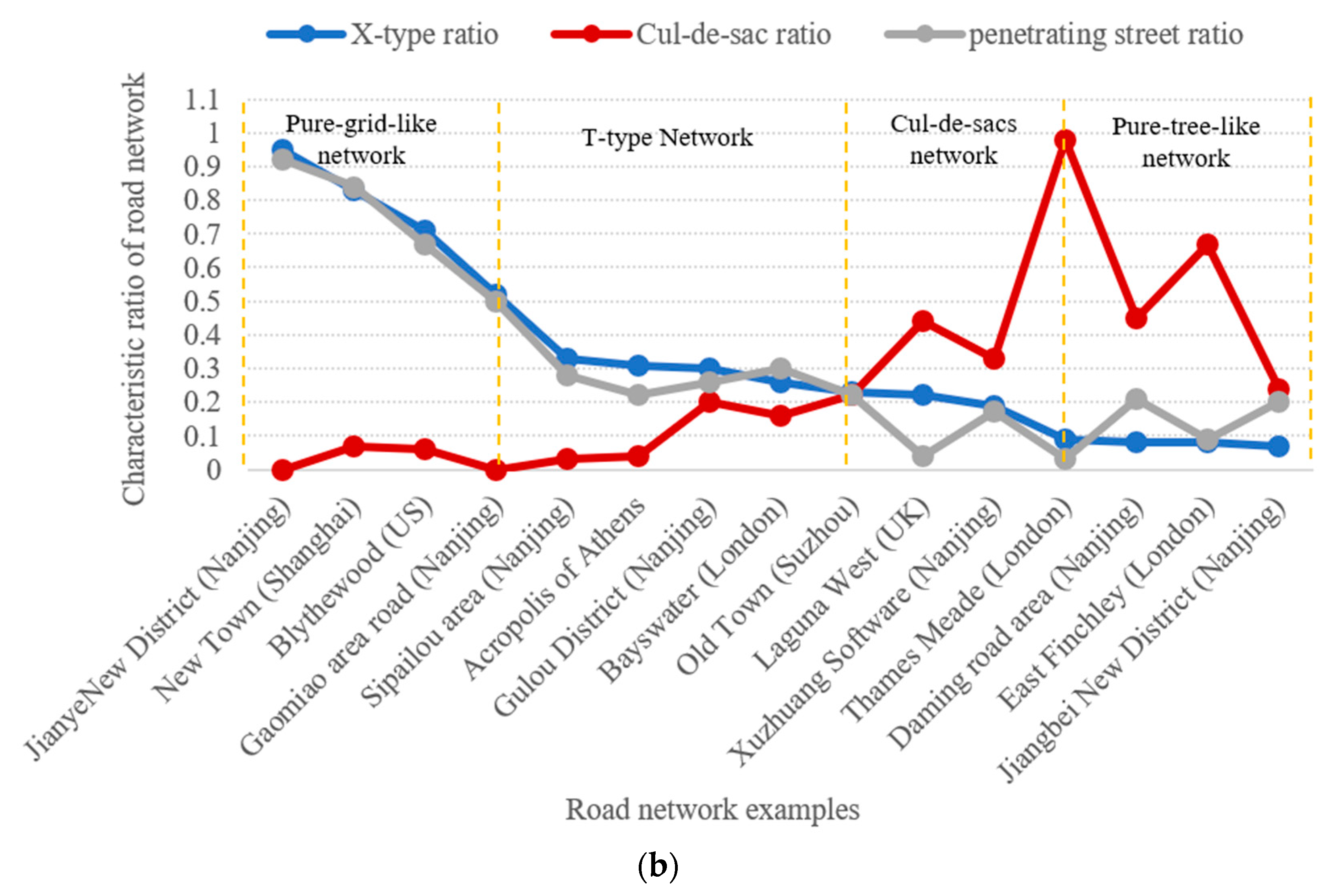
| Serial Number | Network Location | X-Type Ratio | T-TypeRatio | Cul-de-Sac Ratio | Penetrating Street Ratio | Types of Image |
|---|---|---|---|---|---|---|
| 1 | JianyeNewDistrict (Nanjing) | 0.95 | 0.05 | 0 | 0.92 | A |
| 2 | New Town (Shanghai) | 0.83 | 0.17 | 0.07 | 0.84 | A |
| 3 | Blythewood (US) | 0.71 | 0.29 | 0.06 | 0.67 | A |
| 4 | Gaomiao area (Nanjing) | 0.52 | 0.48 | 0 | 0.50 | B |
| 5 | Sipailouarea (Nanjing) | 0.33 | 0.67 | 0.03 | 0.28 | B |
| 6 | Acropolis (Athens) | 0.31 | 0.69 | 0.04 | 0.22 | B |
| 7 | GulouDistrict (Nanjing) | 0.30 | 0.70 | 0.2 | 0.26 | B |
| 8 | Bayswater (London) | 0.26 | 0.74 | 0.16 | 0.30 | B |
| 9 | Old Town (Suzhou) | 0.23 | 0.77 | 0.22 | 0.22 | B |
| 10 | Laguna West (UK) | 0.22 | 0.78 | 0.44 | 0.04 | C |
| 11 | XuzhuangSoftware (Nanjing) | 0.19 | 0.81 | 0.33 | 0.17 | C |
| 12 | Thames Meade (London) | 0.09 | 0.91 | 0.98 | 0.03 | C/D |
| 13 | Daming road area (Nanjing) | 0.08 | 0.92 | 0.45 | 0.21 | D |
| 14 | East Finchley (London) | 0.08 | 0.92 | 0.67 | 0.09 | D |
| 15 | Jiangbei New District (Nanjing) | 0.07 | 0.93 | 0.24 | 0.20 | D |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, B.; Sun, D.; Yu, X.; Song, W.; Ding, L. Classification of Urban Street Networks Based on Tree-Like Network Features. Sustainability 2020, 12, 628. https://doi.org/10.3390/su12020628
Han B, Sun D, Yu X, Song W, Ding L. Classification of Urban Street Networks Based on Tree-Like Network Features. Sustainability. 2020; 12(2):628. https://doi.org/10.3390/su12020628
Chicago/Turabian StyleHan, Baorui, Dazhi Sun, Xiaomei Yu, Wanlu Song, and Lisha Ding. 2020. "Classification of Urban Street Networks Based on Tree-Like Network Features" Sustainability 12, no. 2: 628. https://doi.org/10.3390/su12020628
APA StyleHan, B., Sun, D., Yu, X., Song, W., & Ding, L. (2020). Classification of Urban Street Networks Based on Tree-Like Network Features. Sustainability, 12(2), 628. https://doi.org/10.3390/su12020628





