Visualized Co-Simulation of Adaptive Human Behavior and Dynamic Building Performance: An Agent-Based Model (ABM) and Artificial Intelligence (AI) Approach for Smart Architectural Design
Abstract
1. Motivation and Background
1.1. Performance-Based Design and Challenges
1.2. Co-Simulation: Design-Oriented BPS Platform
1.3. Agent-Based Model (ABM) for PBD
2. Simulation of Human Behavior and Adaptive Geometry
2.1. Simulation of Human Behavior in PBD
2.2. Visualized Simulation of Adaptive Building Geometry, Design Automation, and Optimization
3. Materials and Methods
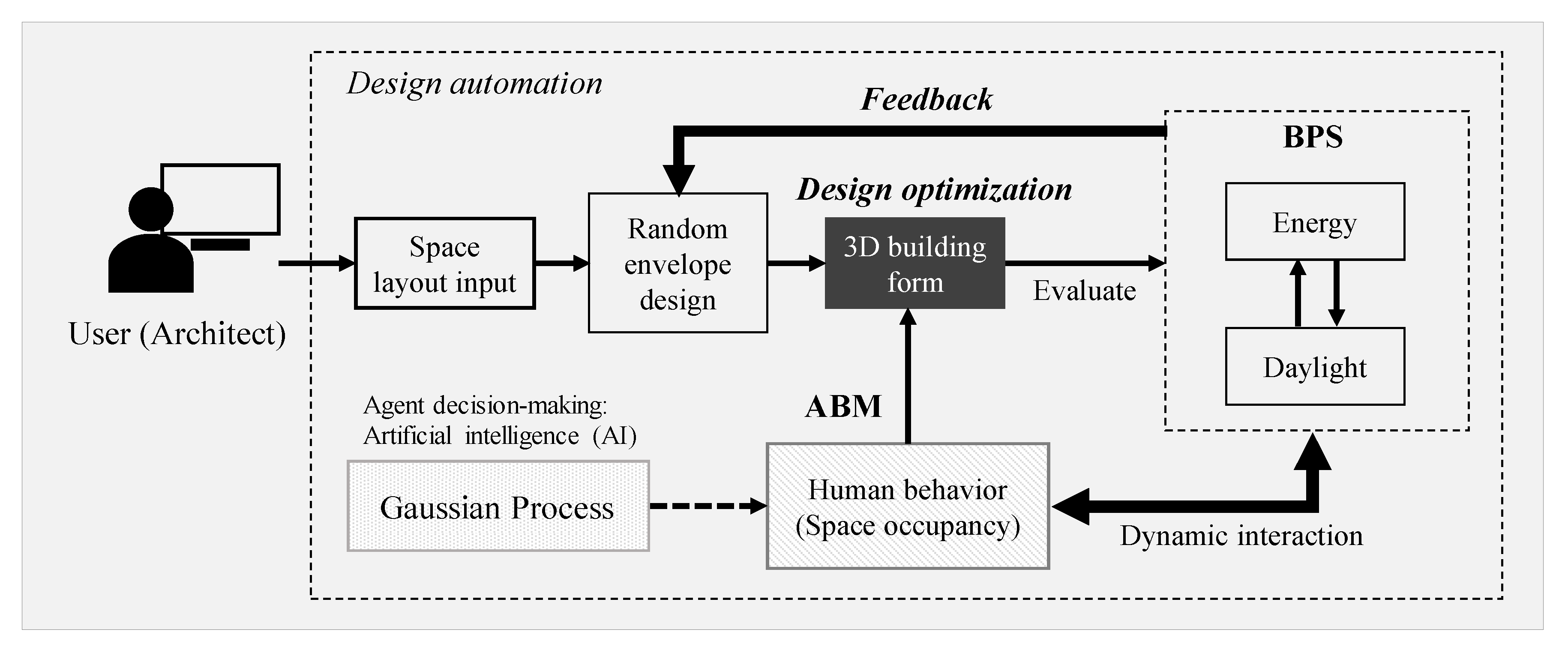
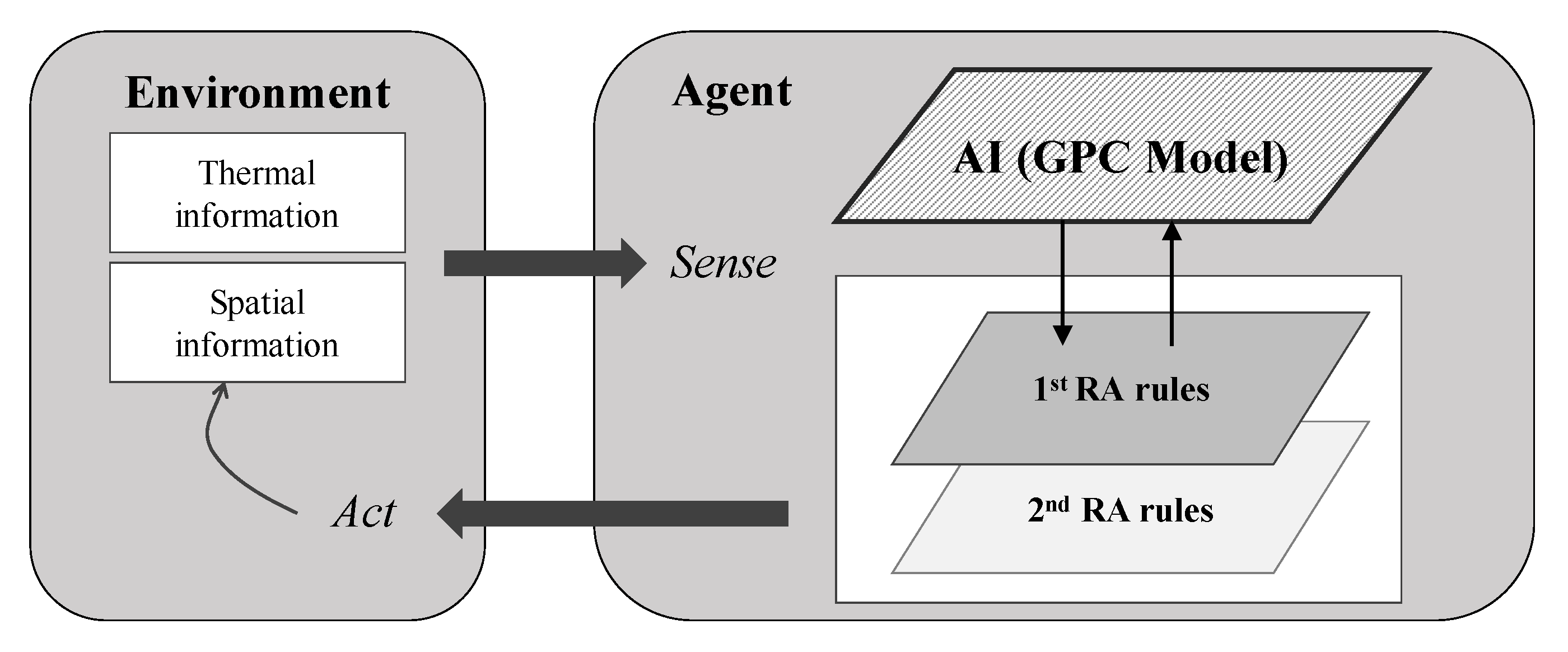
3.1. Scheme of PBD Automation
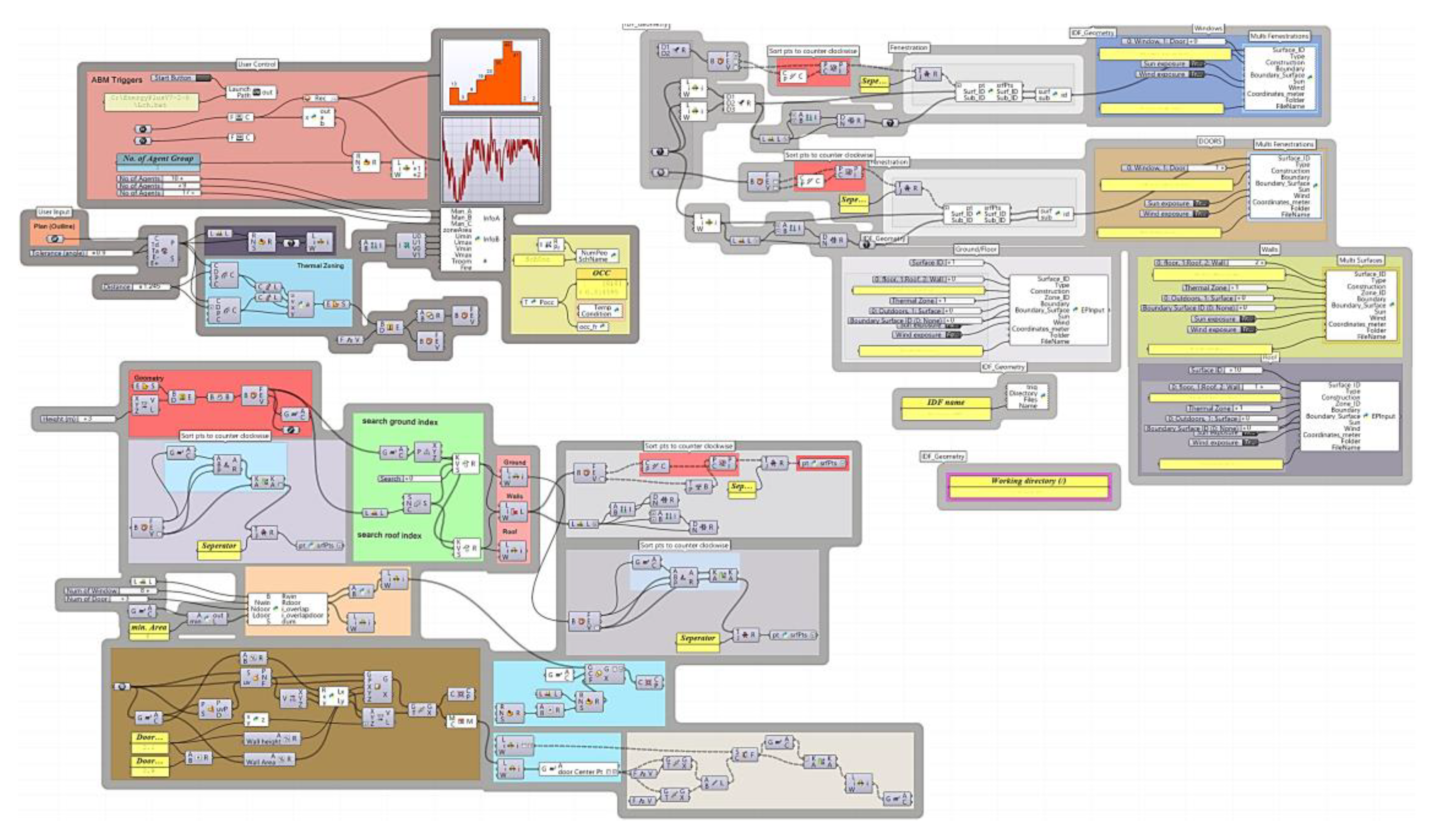
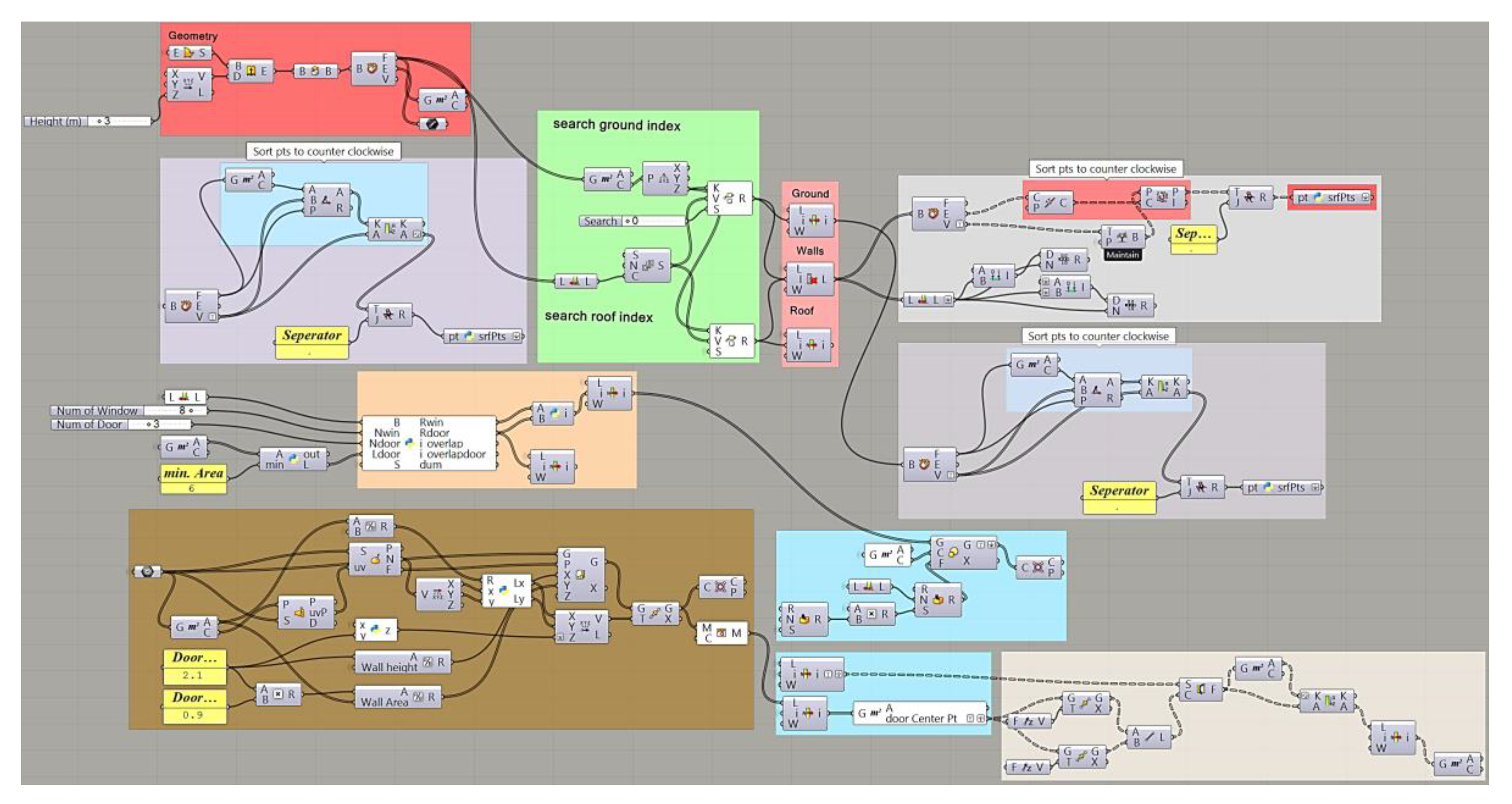
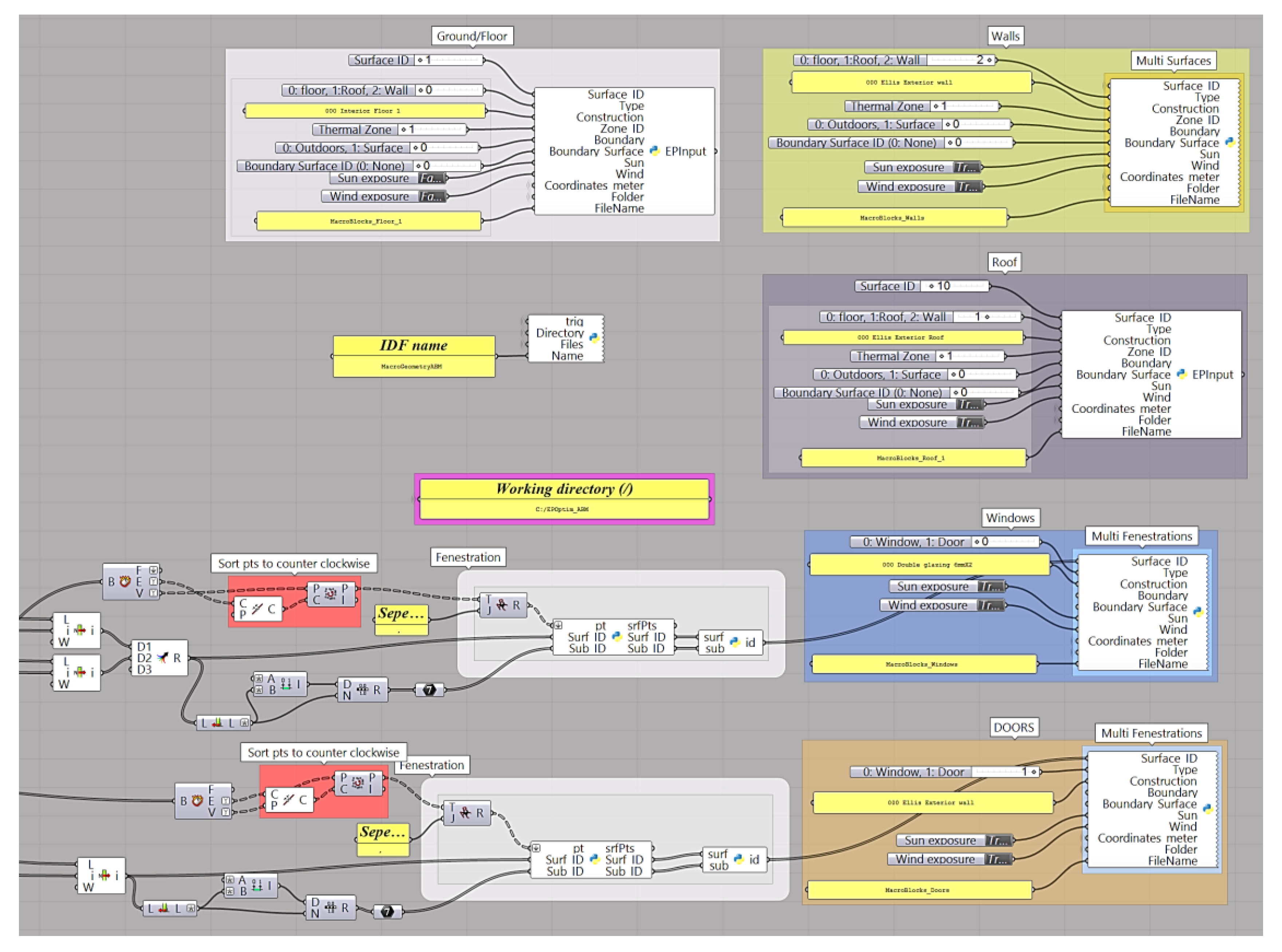
3.2. Development of a Visual User Interface (VUI)
3.3. ABM Development for Space Occupancy and Cognitive Agent Behavior
- (R.1)
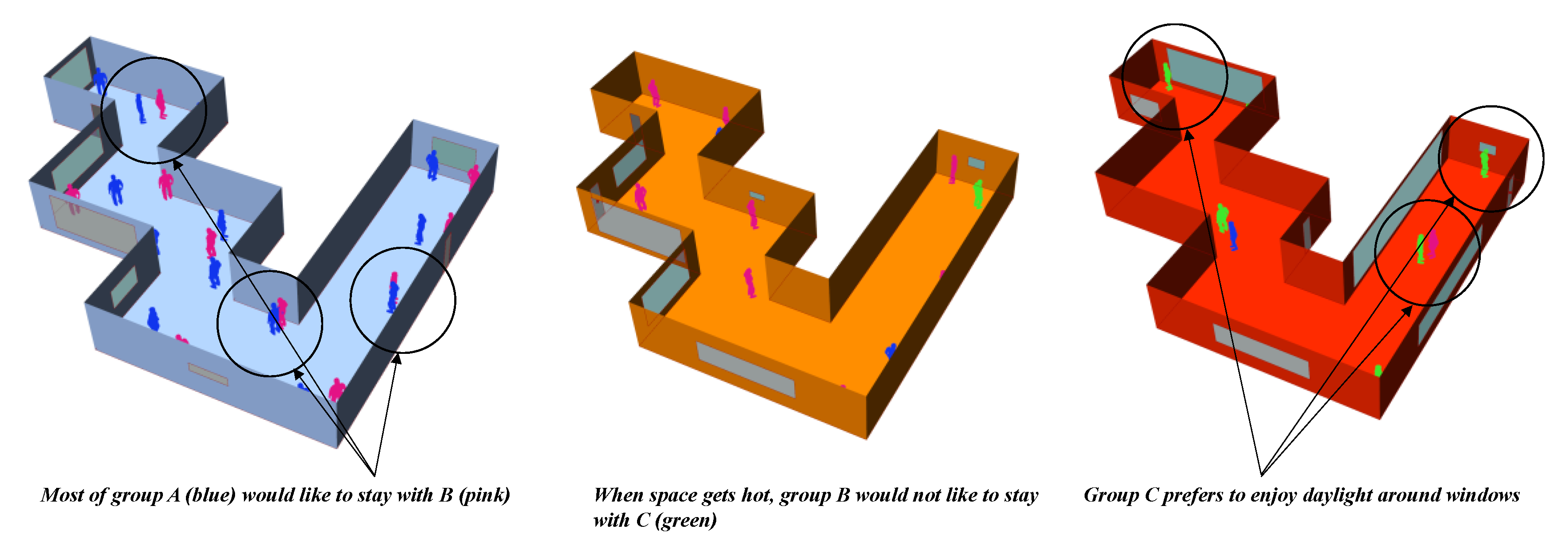
- Most agents in Group A like to stay around corners.
- (R.2)
- Group A and B have an affinity with each other. Agents in these groups would stay around together.
- (R.3)
- Group B would not like to stay with C.
- (R.4)
- Most agents in Group A prefer to stay inside in the morning (7 a.m. to 12 p.m.).
- (R.5)
- Most agents in Group B do not like to stay around doors.
- (R.6)
- Most agents in Group C prefer to stay around windows.
- (S.1)
- Air-conditioning systems operate from 8 a.m. to 6 p.m. During operation, building users have full access to thermostat control. The systems are designed to have dual set points for heating and cooling.
- (S.2)
- Group A is sensitive to slight over-heating. If their skin temperature increases above 33°C, and the ratio of the number of Group A agents to total occupants is greater than 0.5, the agents will change the set point temperature of the cooling equipment to 28°C.
- (S.3)
- Group C is sensitive to over-cooling. If their skin temperature drops below 32°C, the cooling equipment will be turned off.
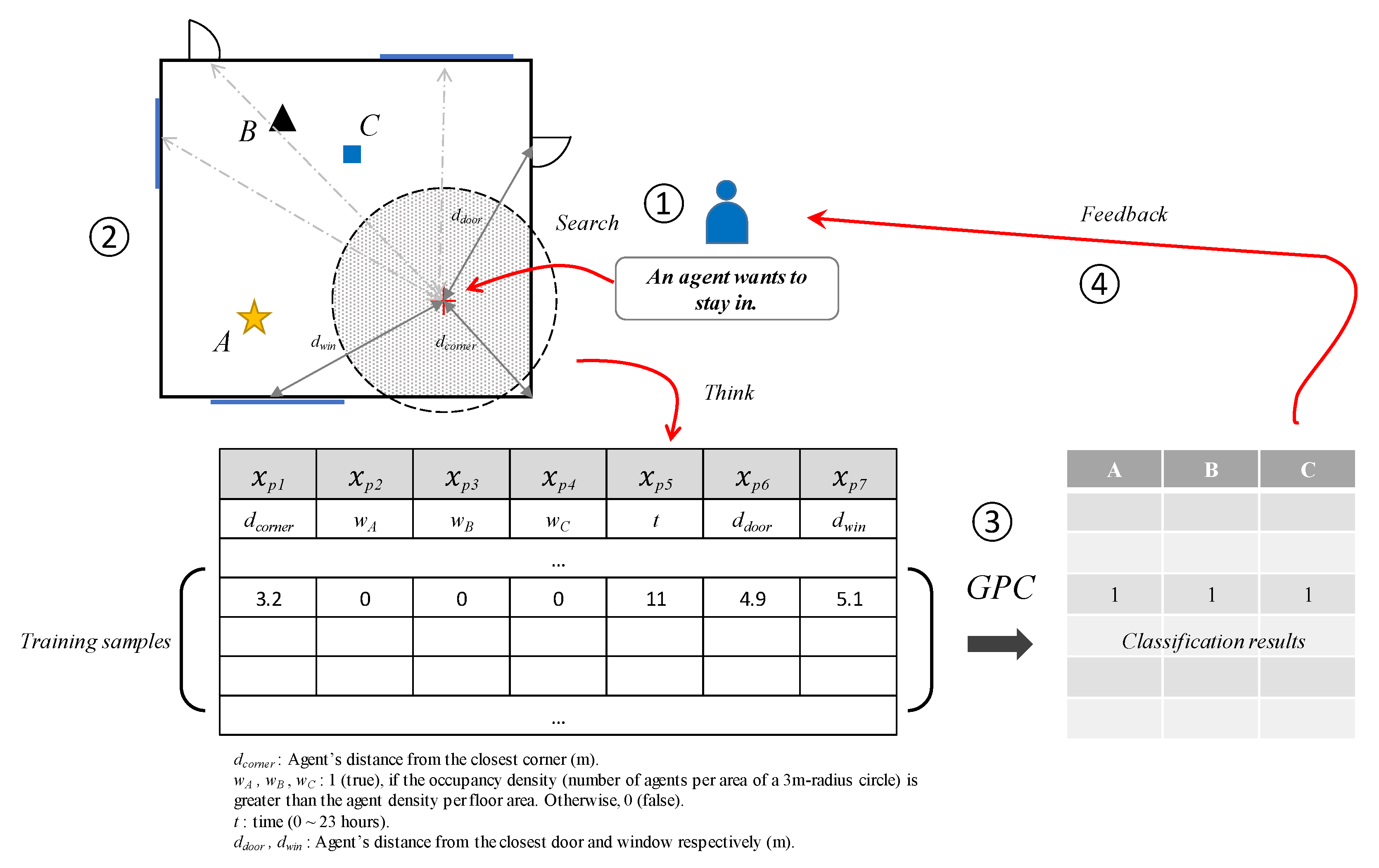
3.4. Agent Positioning Model: Gaussian Process Classifier
4. Test Simulation Results and Discussion
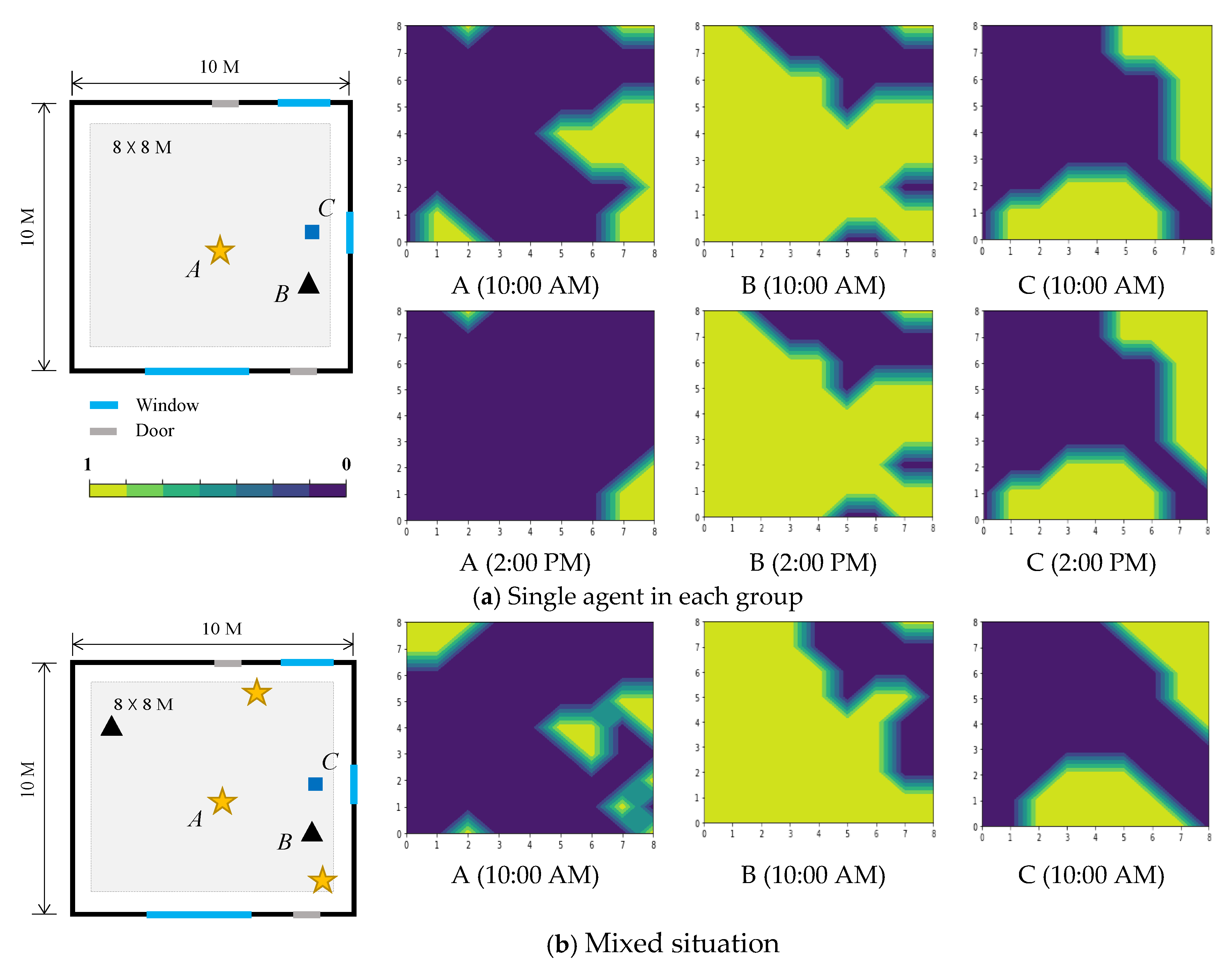
4.1. Gaussian Process Prediction Results
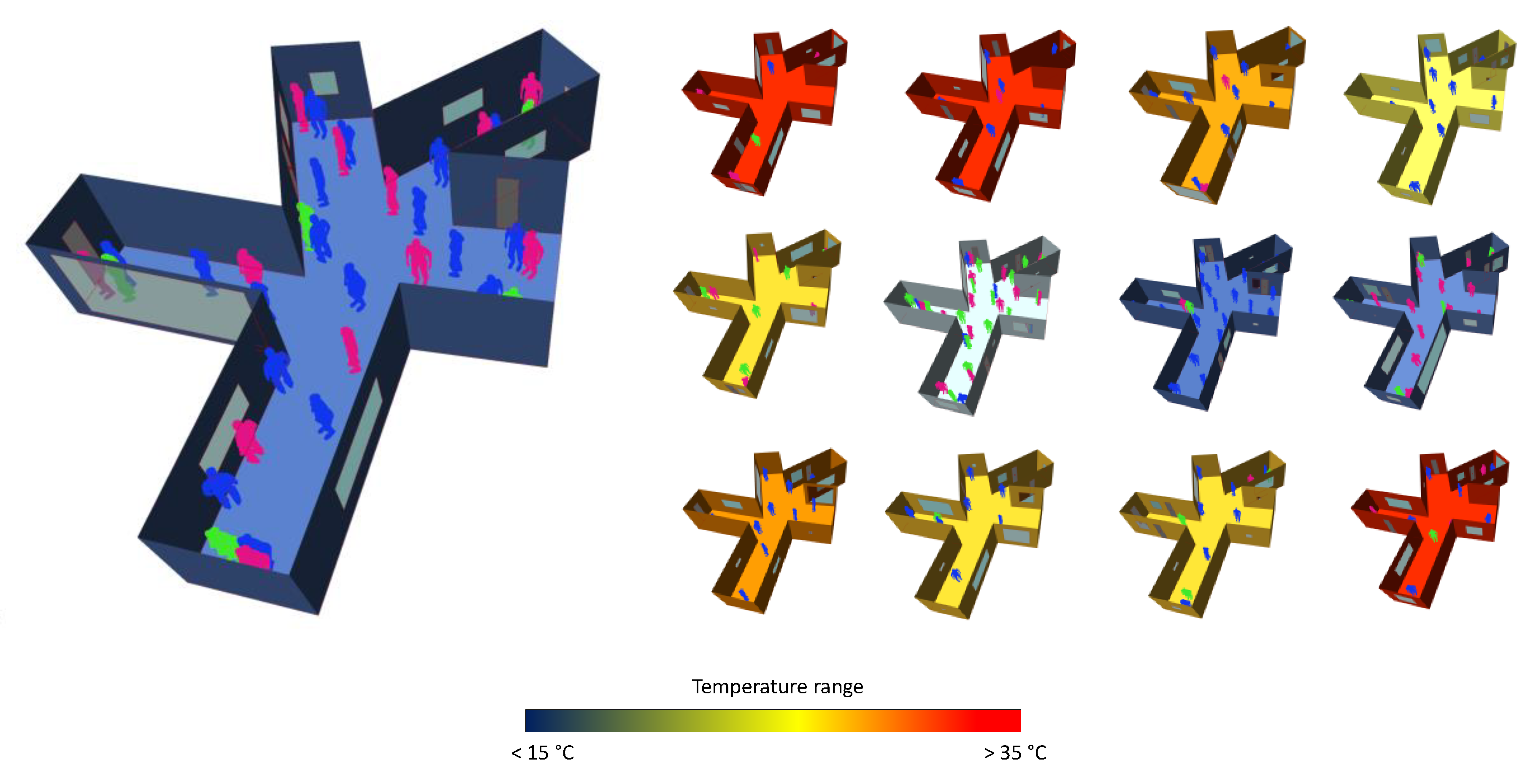
4.2. Visualized Model Outcome: Generation of Building Form and Space Occupancy
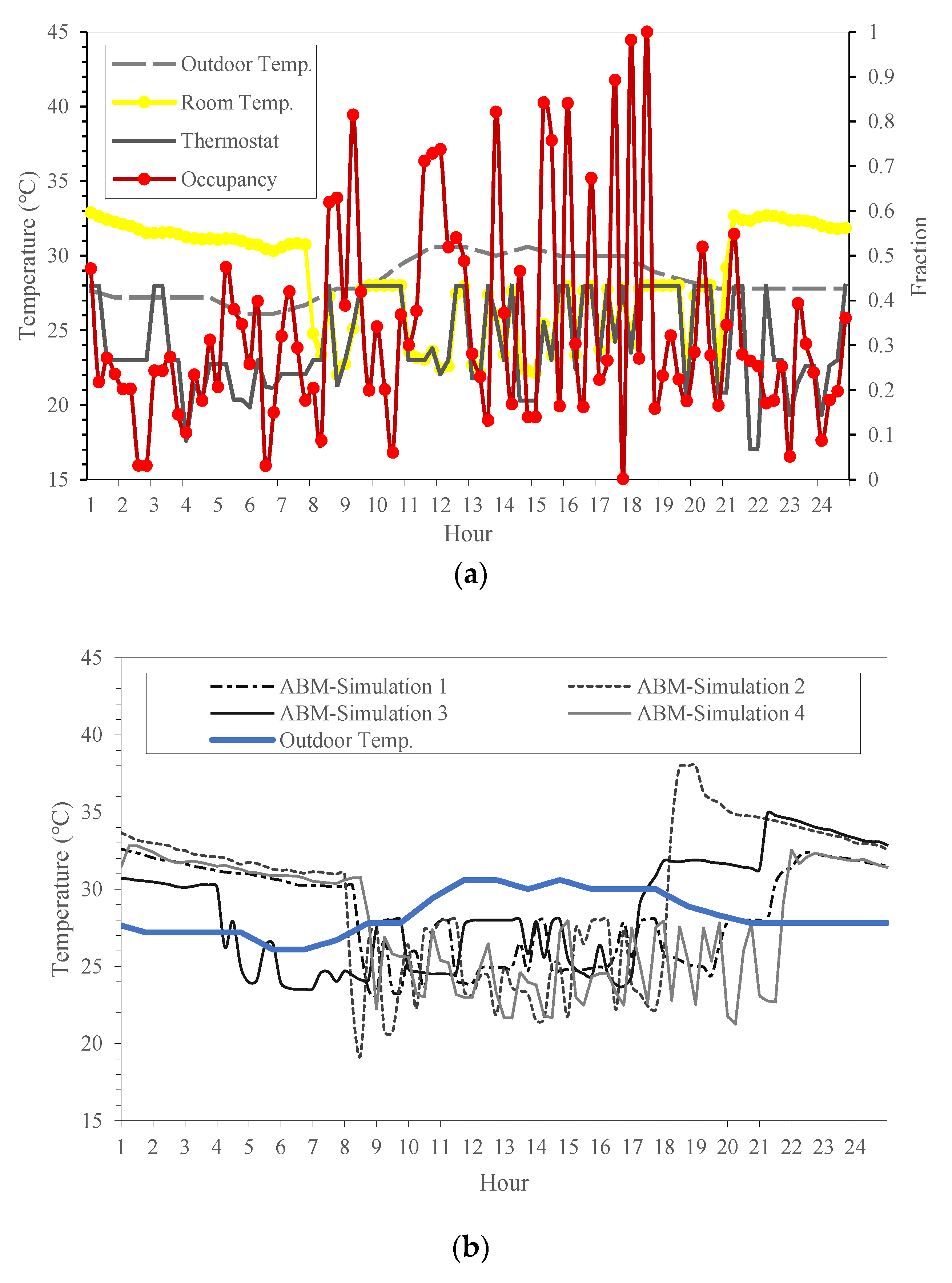
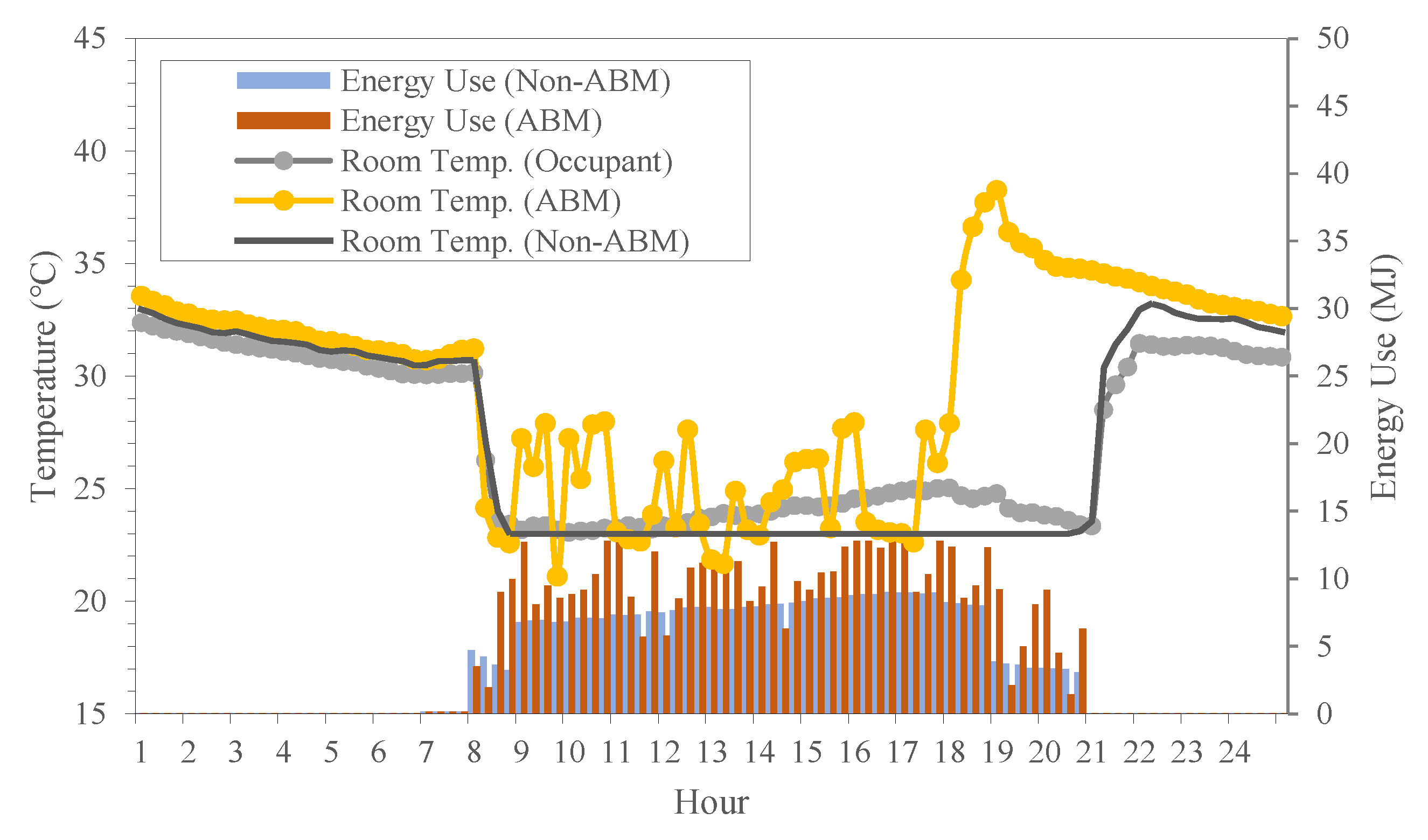
4.3. Analysis of BPS Results
5. Concluding Remarks
Funding
Conflicts of Interest
References
- Solmaz, A.S. A Critical Review on Building Performance Simulation Tools. Int. J. Sustain. Trop. Des. Res. Prac. 2019, 12, 7–20. [Google Scholar]
- Brause, C.; Ford, C.F.; Olsen, C.; Ripple, J.; Uihlein, M.S.; Zarzycki, A.; Vonier, P. Simulations: Modeling, Measuring, and Disrupting Design, TAD; Taylor & Francis Group, LLC.: New York, NY, USA, 2017. [Google Scholar]
- Yi, H.; Yi, Y.K. Performance Based Architectural design optimization: Automated 3D space Layout using simulated annealing. In Proceedings of the 2014 ASHRAE-IBPSA Building Simulation Conference, Atlanta, GA, USA, 25 August 2014; pp. 292–299. [Google Scholar]
- Lin, S.E.; Gerber, D.J. Designing-in performance: A framework for evolutionary energy performance feedback in early stage design. Autom. Constr. 2014, 38, 59–73. [Google Scholar] [CrossRef]
- Lee, E.A. Heterogeneous Modeling. In System Design, Modeling, and Simulation Using Ptolemy II, 1st ed.; Ptolemaeus, C., Ed.; Ptolemy: Berkeley, CA, USA, 2014. [Google Scholar]
- Sebastian, R. Changing roles of the clients, architects and contractors through BIM. Eng. Constr. Arch. Manag. 2011, 18, 176–187. [Google Scholar] [CrossRef]
- Macdonald, I.; Strachan, P. Practical application of uncertainty analysis. Energy Build. 2001, 33, 219–227. [Google Scholar] [CrossRef]
- de Wit, S. Uncertainty in building simulation. In Advanced Building Simulation; Malkawi, A., Augenbroe, G., Eds.; Spon Press: New York, NY, USA, 2003. [Google Scholar]
- Yi, H. User-driven automation for optimal thermal-zone layout during space programming phases. Arch. Sci. Rev. 2016, 59, 279–306. [Google Scholar] [CrossRef]
- Gomes, C.; Thule, C.; Broman, D.; Larsen, P.G.; Vangheluwe, H. Co-simulation: State of the art. arXiv 2017, arXiv:abs/1702.00686. [Google Scholar]
- Hansen, J. Integrated building airflow simulation. In Advanced Building Simulation; Malkawi, A., Augenbroe, G., Eds.; Spon Press: New York, NY, USA, 2003; pp. 87–118. [Google Scholar]
- Wetter, M. Co-simulation of building energy and control systems with the Building Controls Virtual Test Bed. J. Build. Perform. Simul. 2011, 4, 185–203. [Google Scholar] [CrossRef]
- Hong, T.; Sun, H.; Chen, Y.; Taylor-Lange, S.C.; Yan, D. An occupant behavior modeling tool for co-simulation. Energy Build. 2016, 117, 272–281. [Google Scholar] [CrossRef]
- Kensek, K.M. Teaching Visual Scripting in BIM: A case study using a panel controlled by solar angles. J. Green Build. 2018, 13, 113–138. [Google Scholar] [CrossRef]
- Aksamija, A. BIM-Based Building Performance Analysis: Evaluation and simulation of design decisions. In Proceedings of the 17th Biennial ACEEE Conference on Energy Efficiency in Buildings, Pacific Grove, CA, USA, 12 August 2012. [Google Scholar]
- Jeong, W.; Kim, J.B.; Clayton, M.J.; Haberl, J.S.; Yan, W. A framework to integrate object-oriented physical modelling with building information modelling for building thermal simulation. J. Build. Perform. Simul. 2016, 9, 50–69. [Google Scholar] [CrossRef]
- Russell, S.; Norvig, P. Artificial Intelligence: A Modern Approach; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1995. [Google Scholar]
- Wilensky, U.; Rand, W. An Introduction to Agent-Based Modeling: Modeling Natural, Social, and Engineered Complex Systems with NetLogo; MIT Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Epstein, J.M.; Axtell, R. Growing Artificial Societies: Social Science from the Bottom Up; MIT Press: Cambridge, MA, USA, 1996. [Google Scholar]
- Bonabeau, E. Agent-based modeling: Methods and techniques for simulating human systems. Proc. Natl. Acad. Sci. USA 2002, 99, 7280–7287. [Google Scholar] [CrossRef] [PubMed]
- Micolier, A.; Taillandier, F.; Taillandier, P.; Bos, F. Li-BIM, an agent-based approach to simulate occupant-building interaction from the Building-Information Modelling. Eng. Appl. Artif. Intell. 2019, 82, 44–59. [Google Scholar] [CrossRef]
- Lee, Y.S.; Malkawi, A.M. Simulating multiple occupant behaviors in buildings: An agent-based modeling approach. Energy Build. 2014, 69, 407–416. [Google Scholar] [CrossRef]
- Penn, A.; Turner, A. Space syntax based agent simulation. In Pedestrian and Evacuation Dynamics; Schreckenberg, M., Sharma, S.D., Eds.; Springer: Berlin, Germany, 2002; pp. 99–114. [Google Scholar]
- Cheliotis, K. An agent-based model of public space use. Comput. Environ. Urban Syst. 2020, 81, 101476. [Google Scholar] [CrossRef]
- Gao, Y.; Gu, N. Complexity, Human Agents, and Architectural Design: A Computational Framework. Des. Princ. Pract. 2009, 3, 115–126. [Google Scholar] [CrossRef]
- Andrews, C.J.; Yi, D.; Krogmann, U.; Senick, J.A.; Wener, R.E. Designing Buildings for Real Occupants: An Agent-Based Approach. IEEE Trans. 2011, 41, 1077–1091. [Google Scholar] [CrossRef]
- Koutsolampros, P.; Sailer, K.; Varoudis, T. Partitioning indoor space using visibility graphs: Investigating user behavior in office spaces. In Proceedings of the 4th International Symposium Formal Methods in Architecture, Porto, Portugal, 2 April 2018. [Google Scholar]
- Chen, L. Agent-based modeling in urban and architectural research: A brief literature review. Front. Archit. Res. 2012, 1, 166–177. [Google Scholar] [CrossRef]
- Breslav, S.; Goldstein, R.; Tessier, A.; Khan, A. Towards Visualization of Simulated Occupants and their Interactions with Buildings at Multiple Time Scales. In Proceedings of the Symposium on Simulation for Architecture and Urban Design (SimAUD 2014), Tampa, FL, USA, 14 April 2014. [Google Scholar]
- Nagy, D.; Villagi, L.; Stoddart, J.; Benjamin, D. The Buzz Metric: A Graph-based Method for Quantifying Productive Congestion in Generative Space Planning for Architecture. TAD 2017, 1, 186–195. [Google Scholar] [CrossRef]
- Figueroa, M.; Putra, H.C.; Andrews, C.J. Preliminary Report: Incorporating Information on Occupant Behavior into Building Energy Models; The Center for Green Building at Rutgers University for the Energy Efficient Buildings Hub: Philadelphia, PA, USA, 2014. [Google Scholar]
- Hong, T.; Taylor-Lange, S.C.; D’Oca, S.; Yan, D.; Corgnati, S.P. Advances in research and applications of energy-related occupant behavior in buildings. Energy Build. 2016, 116, 694–702. [Google Scholar] [CrossRef]
- D’Oca, S.; Hong, T.; Langevin, J. The human dimensions of energy use in buildings: A review. Renew. Sustain. Energy Rev. 2018, 81, 731–742. [Google Scholar] [CrossRef]
- Janda, K. Buildings Don’t Use Energy: People Do. Archit. Sci. Rev. 2011, 54, 15–22. [Google Scholar] [CrossRef]
- Yi, H. A biophysical approach to the performance diagnosis of human–building energy interaction: Information (bits) modeling, algorithm, and indicators of energy flow complexity. Environ. Impact Assess. Rev. 2018, 72, 108–125. [Google Scholar] [CrossRef]
- Gophikrishnan, S.; Topkar, V.M. Attributes and descriptors for building performance evaluation. HBRC J. 2017, 13, 291–296. [Google Scholar] [CrossRef]
- Yi, H. Rapid simulation of optimally responsive façade during schematic design phases: Use of a new hybrid metaheuristic algorithm. Sustainability 2019, 11, 2681. [Google Scholar] [CrossRef]
- Sakoi, T.; Tsuzuki, K.; Kato, S.; Ooka, R.; Song, D.; Zhu, S. Thermal comfort, skin temperature distribution, and sensible heat loss distribution in the sitting posture in various asymmetric radiant fields. Build. Environ. 2007, 42, 3984–3999. [Google Scholar] [CrossRef]
- Çengel, Y.A.; Ghajar, A.J. Heat and Mass Transfer: Fundamentals & Applications, 4th ed.; McGraw-Hill: New York, NY, USA, 2011. [Google Scholar]
- Oğulata, R.T. The Effect of Thermal Insulation of Clothing on Human Thermal Comfort. Fibres Text. East. Eur. 2007, 15, 67–72. [Google Scholar]

| Clothing Insulation Level(clo) | |||
| μ | σ | ||
| Summer: day | 0.32 | 0.08 | |
| Summer: night | 0.15 | 0.05 | |
| Winter: day | 0.9 | 0.09 | |
| Winter: night | 1.38 | 0.11 | |
| Auxiliary Parameters | |||
| Base | Min. | Max. | |
| Lighting power: general (W/m2) | 13 | 11 | 15 |
| Lighting power: intense (W/m2) | 15 | 11 | 19 |
| Appliance density (W/m2) | 15 | 12 | 22 |
| Occupant metabolic rate (W) | 80 | 70 | 130 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yi, H. Visualized Co-Simulation of Adaptive Human Behavior and Dynamic Building Performance: An Agent-Based Model (ABM) and Artificial Intelligence (AI) Approach for Smart Architectural Design. Sustainability 2020, 12, 6672. https://doi.org/10.3390/su12166672
Yi H. Visualized Co-Simulation of Adaptive Human Behavior and Dynamic Building Performance: An Agent-Based Model (ABM) and Artificial Intelligence (AI) Approach for Smart Architectural Design. Sustainability. 2020; 12(16):6672. https://doi.org/10.3390/su12166672
Chicago/Turabian StyleYi, Hwang. 2020. "Visualized Co-Simulation of Adaptive Human Behavior and Dynamic Building Performance: An Agent-Based Model (ABM) and Artificial Intelligence (AI) Approach for Smart Architectural Design" Sustainability 12, no. 16: 6672. https://doi.org/10.3390/su12166672
APA StyleYi, H. (2020). Visualized Co-Simulation of Adaptive Human Behavior and Dynamic Building Performance: An Agent-Based Model (ABM) and Artificial Intelligence (AI) Approach for Smart Architectural Design. Sustainability, 12(16), 6672. https://doi.org/10.3390/su12166672





