A Decision Process for Optimizing Multi-Hazard Shelter Location Using Global Data
Abstract
1. Introduction
1.1. Disaster Risk Management and Resilience
1.2. Disaster Shelter Location
1.3. SMCDA in Disaster Risk Management
1.4. Data Driven Approach for Disaster Risk Management and Shelter Location
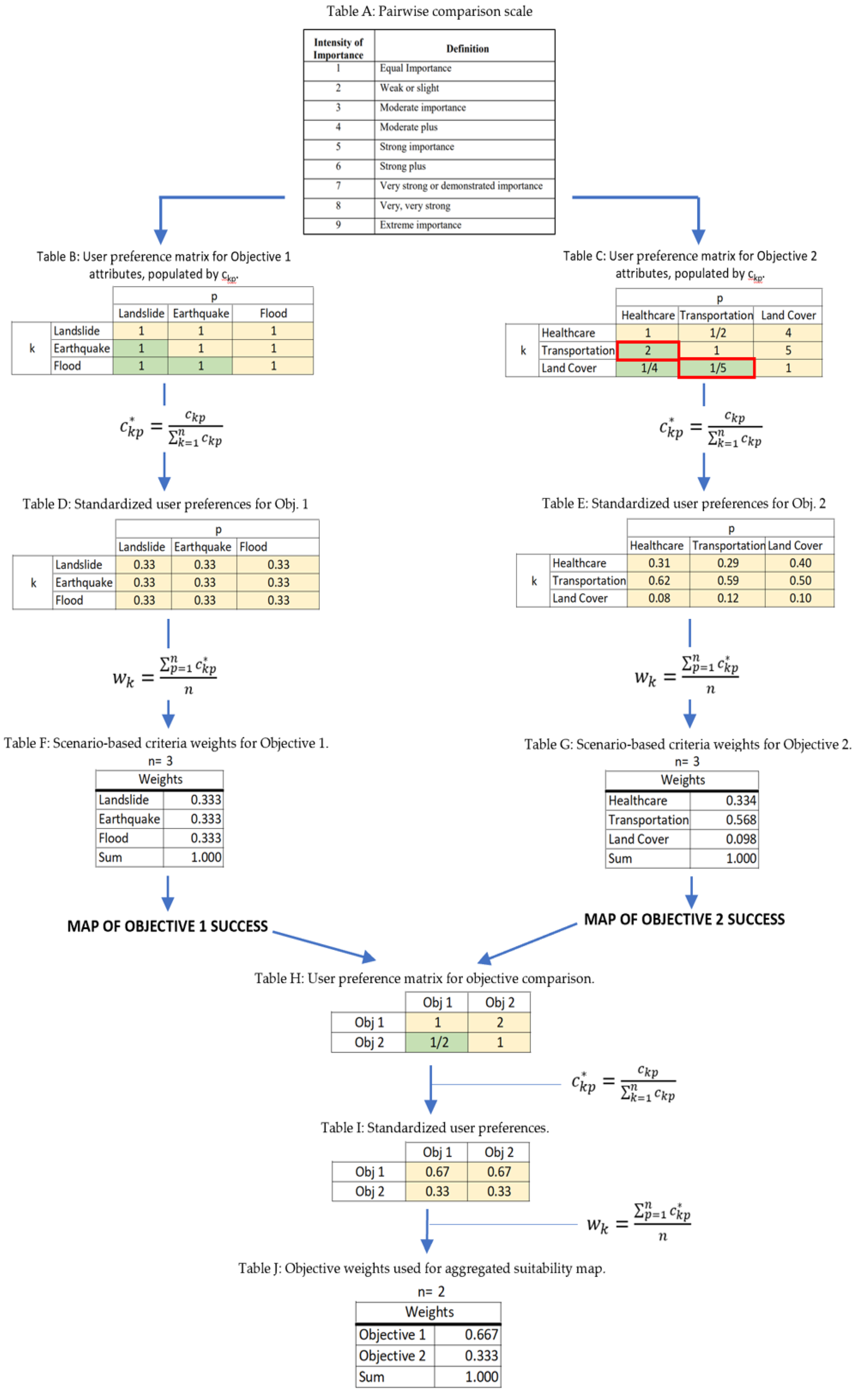
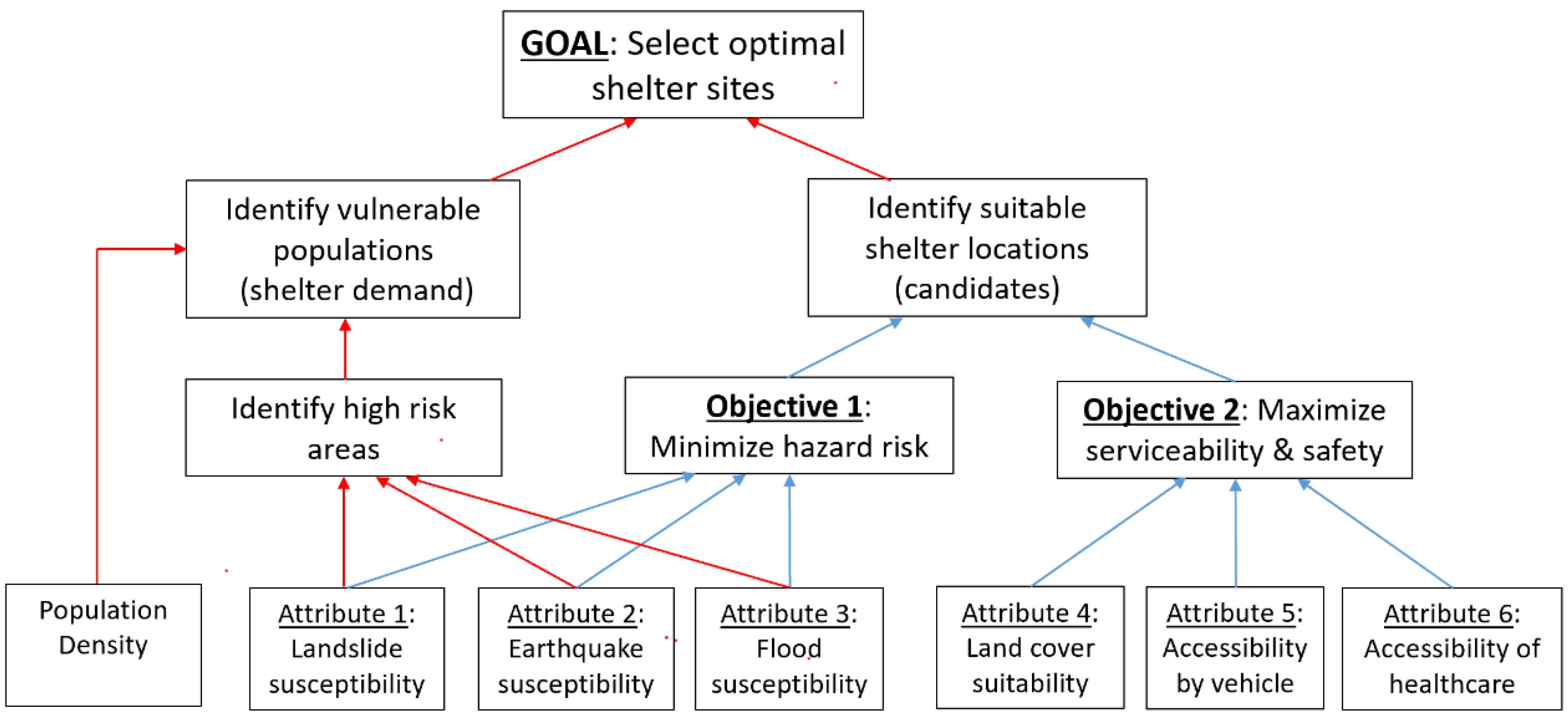
2. Methods
2.1. Identifying Suitable Shelter Locations
2.2. Site Selection Optimization
3. Results
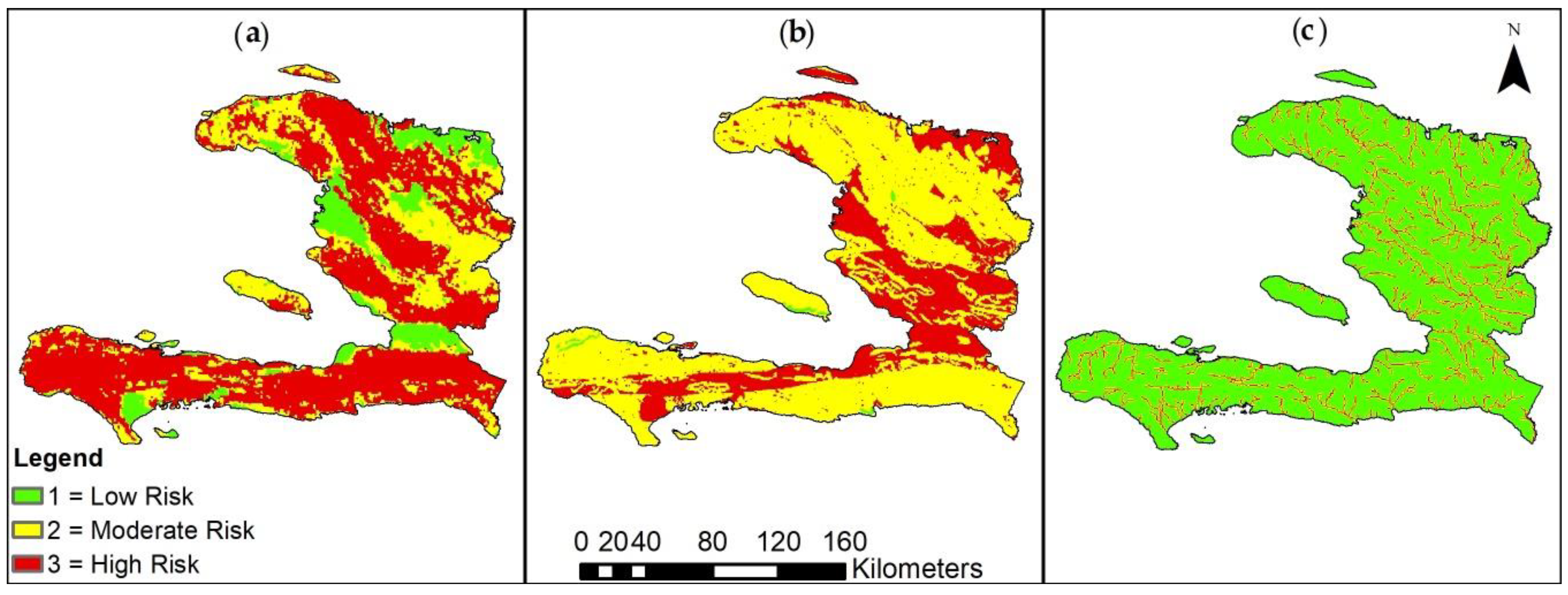
3.1. Tool Outputs
3.2. Sensitivity
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Attribute | Standardized Value | Standardized Attribute Meaning | ||
|---|---|---|---|---|
| 1 = Low Risk | 2 = Moderate Risk | 3 = High Risk | ||
| Landslide susceptibility 1 | 1 | 2, 3 | 4, 5 | Landslide risk |
| Earthquake susceptibility 2 | 2–5 | 6–7 | 7–10 | Earthquake risk |
| Distance to river 3 | >500 | 150–500 | <150 | Fluvial flood risk |
| Attribute | Standardized Value | Standardized Attribute Meaning | |||
|---|---|---|---|---|---|
| 1 = High Serviceability | 2 = Moderate Serviceability | 3 = Low Serviceability | Unsuitable (NoData) | ||
| Road density 1 | >2 | 0.5–2 | <0.5 | N/A | Accessibility by vehicle transportation |
| Healthcare facility density 2 | >0.5 | 0.1–0.5 | <0.1 | N/A | Accessibility to healthcare |
| Land cover 3 | Grassland, Non/sparsely-vegetated | Cropland, Agriculture | Forest | Wetland, In-land water, Ocean | Serviceability of land cover |
References
- Shelter Solutions—UNHCR Emergency Handbook. Available online: https://emergency.unhcr.org/entry/254351/shelter-solutions (accessed on 22 April 2020).
- Giovene di Girasole, E.; Cannatella, D. Social Vulnerability to Natural Hazards in Urban Systems. An Application in Santo Domingo (Dominican Republic). Sustainability 2017, 9, 2043. [Google Scholar] [CrossRef]
- De Silva, M.M.G.T.; Kawasaki, A. Socioeconomic Vulnerability to Disaster Risk: A Case Study of Flood and Drought Impact in a Rural Sri Lankan Community. Ecol. Econ. 2018, 152, 131–140. [Google Scholar] [CrossRef]
- United Nations. The United Nations Office for Disaster Risk Reduction Sendai Framework for Disaster Risk Reduction; UNDRR: Geneva, Switzerland, 2015. [Google Scholar]
- Twigg, J.; Choularton, R. The Asian Tsunami: The Implications for Preparedness and Contingency Planning; Humanitarian Practice Network: London, UK, 2005. [Google Scholar]
- Toya, H.; Skidmore, M. Economic development and the impacts of natural disasters. Econ. Lett. 2007, 94, 20–25. [Google Scholar] [CrossRef]
- Guha-Sapir, D.; Lechat, M.F. Information systems and needs assessment in natural disasters: An approach for better disaster relief management. Disasters 1986, 10, 232–237. [Google Scholar] [CrossRef] [PubMed]
- Abrahams, D. The barriers to environmental sustainability in post-disaster settings: A case study of transitional shelter implementation in Haiti. Disasters 2014, 38, S25–S49. [Google Scholar] [CrossRef]
- Leon, E.; Kelman, I.; Kennedy, J.; Ashmore, J. Capacity building lessons from a decade of transitional settlement and shelter. Int. J. Strat. Prop. Manag. 2009, 13, 247–265. [Google Scholar] [CrossRef]
- Tatem, A.J.; Noor, A.M.; von Hagen, C.; Gregorio, A.D.; Hay, S.I. High Resolution Population Maps for Low Income Nations: Combining Land Cover and Census in East Africa. PLoS ONE 2007, 2, e1298. [Google Scholar] [CrossRef]
- Hosseini, S.M.A.; de la Fuente, A.; Pons, O. Multicriteria Decision-Making Method for Sustainable Site Location of Post-Disaster Temporary Housing in Urban Areas. J. Constr. Eng. Manag. 2016, 142, 04016036. [Google Scholar] [CrossRef]
- Imperiale, A.J.; Vanclay, F. Command-and-control, emergency powers, and the failure to observe United Nations disaster management principles following the 2009 L’Aquila earthquake. Int. J. Disaster Risk Reduct. 2019, 36, 101099. [Google Scholar] [CrossRef]
- Blackman, D.; Nakanishi, H.; Benson, A.M. Disaster resilience as a complex problem: Why linearity is not applicable for long-term recovery. Technol. Forecast. Soc. Chang. 2017, 121, 89–98. [Google Scholar] [CrossRef]
- United Nations. United Nations International Strategy for Disaster Risk Reduction 2009 UNISDR Terminology on Disaster Risk Reduction; UNDRR: Geneva, Switzerland, 2009. [Google Scholar]
- McLoughlin, D. A Framework for Integrated Emergency Management. Public Adm. Rev. 1985, 45, 165–172. [Google Scholar] [CrossRef]
- Strong, K.; Carpenter, O.; Ralph, D. Scenario Best Practices: Developing Scenarios for Disaster Risk Reduction; University of Cambridge: Cambridge, UK, 2020. [Google Scholar]
- Jordan, E.; Javernick-Will, A. Measuring Community Resilience and Recovery: A Content Analysis of Indicators. In Proceedings of the Construction Research Congress 2012, West Lafayette, IN, USA, 21–23 May 2012; American Society of Civil Engineers: West Lafayette, IN, USA, 2012; pp. 2190–2199. [Google Scholar]
- Rizzi, P.; Porębska, A. Towards a Revised Framework for Participatory Planning in the Context of Risk. Sustainability 2020, 12, 5539. [Google Scholar] [CrossRef]
- Ainuddin, S.; Routray, J.K. Community resilience framework for an earthquake prone area in Baluchistan. Int. J. Disaster Risk Reduct. 2012, 2, 25–36. [Google Scholar] [CrossRef]
- Joerin, J.; Shaw, R.; Takeuchi, Y.; Krishnamurthy, R. Assessing community resilience to climate-related disasters in Chennai, India. Int. J. Disaster Risk Reduct. 2012, 1, 44–54. [Google Scholar] [CrossRef]
- Ozbay, E.; Çavuş, Ö.; Kara, B.Y. Shelter site location under multi-hazard scenarios. Comput. Oper. Res. 2019, 106, 102–118. [Google Scholar] [CrossRef]
- The Internal Displacement Monitoring Centre. GRID 2020 Global Report on Internal Discplacement; IDMC: Geneva, Switzerland, 2020. [Google Scholar]
- The World Bank. What Did We Learn? The Shelter Response and Housing Recovery in the First Two Years after the 2010 Haiti Earthquake; The World Bank: Washington, DC, USA, 2016; p. 220. [Google Scholar]
- Turner, J.F.C. Housing as a Verb. In Freedom to Build: Dweller Control of the Housing Process; Turner, J.F.C., Fichter, R., Eds.; Macmillan Company: New York, NY, USA, 1972; pp. 148–175. [Google Scholar]
- Ian, D. Shelter after Disaster; Oxford Polytechnic Press: Oxford, UK, 1978. [Google Scholar]
- Malczewski, J.; Rinner, C. Multicriteria Decision Analysis in Geographic Information Science; Advances in Geographic Information Science; Springer Science+Business Media: New York, NY, USA, 2015. [Google Scholar]
- Hanssen, F.; May, R.; van Dijk, J.; Rød, J.K. Spatial Multi-Criteria Decision Analysis Tool Suite for Consensus-Based Siting of Renewable Energy Structures. J. Environ. Assess. Policy Manag. 2018, 20, 1840003. [Google Scholar] [CrossRef]
- Marzocchi, W.; Garcia-Aristizabal, A.; Gasparini, P.; Mastellone, M.; Ruocco, A. Basic principles of multi-risk assessment: A case study in Italy. Nat. Hazards 2012, 62, 551–573. [Google Scholar] [CrossRef]
- Ismail-Zadeh, A.T.; Cutter, S.L.; Takeuchi, K.; Paton, D. Forging a paradigm shift in disaster science. Nat. Hazards 2017, 86, 969–988. [Google Scholar] [CrossRef]
- Jiang, Z.; Yu, L. Performance evaluation of emergency risk management under group decision making: An approach of incorporating fuzzy AHP and fuzzy TOPSIS. Int. J. Fuzzy Syst. 2013, 8, 845–854. [Google Scholar]
- Sahay, B.S.; Menon, N.V.C.; Gupta, S. Humanitarian Logistics and Disaster Management: The Role of Different Stakeholders. In Managing Humanitarian Logistics; Sahay, B.S., Gupta, S., Menon, V.C., Eds.; Springer India: New Delhi, India, 2016; pp. 3–21. ISBN 978-81-322-2416-7. [Google Scholar]
- Jelokhani-Niaraki, M.; Malczewski, J. The decision task complexity and information acquisition strategies in GIS-MCDA. Int. J. Geogr. Inf. Sci. 2015, 29, 327–344. [Google Scholar] [CrossRef]
- Kar, B.; Hodgson, M.E. A GIS-Based Model to Determine Site Suitability of Emergency Evacuation Shelters. Trans. GIS 2008, 12, 227–248. [Google Scholar] [CrossRef]
- Alçada-Almeida, L.; Tralhão, L.; Santos, L.; Coutinho-Rodrigues, J. A Multiobjective Approach to Locate Emergency Shelters and Identify Evacuation Routes in Urban Areas. Geogr. Anal. 2009, 41, 9–29. [Google Scholar] [CrossRef]
- Xu, J.; Yin, X.; Chen, D.; An, J.; Nie, G. Multi-criteria location model of earthquake evacuation shelters to aid in urban planning. Int. J. Disaster Risk Reduct. 2016, 20, 51–62. [Google Scholar] [CrossRef]
- Redshaw, P.; Boon, D.; Campbell, G.; Willis, M.; Mattai, J.; Free, M.; Jordan, C.; Kemp, S.J.; Morley, A.; Thomas, M. The 2017 Regent Landslide, Freetown Peninsula, Sierra Leone. Q. J. Eng. Geol. Hydrogeol. 2019, 52, 435. [Google Scholar] [CrossRef]
- Jibson, R.W.; Harp, E.L. Field Reconnaissance Report of Landslides Triggered by the January 12, 2010, Haiti Earthquake; U.S. Geological Survey: Hunter Mill, VA, USA, 2011; p. 19. [Google Scholar]
- Karaman, H. Integrated Multi-Hazard Map Creation By using AHP and GIS. Recent Adv. Environ. Life Sci. 2015, 10, 101. [Google Scholar]
- Skilodimou, H.D.; Bathrellos, G.D.; Chousianitis, K.; Youssef, A.M.; Pradhan, B. Multi-hazard assessment modeling via multi-criteria analysis and GIS: A case study. Environ. Earth Sci. 2019, 78, 47. [Google Scholar] [CrossRef]
- Gallina, V.; Torresan, S.; Zabeo, A.; Critto, A.; Glade, T.; Marcomini, A. A Multi-Risk Methodology for the Assessment of Climate Change Impacts in Coastal Zones. Sustainability 2020, 12, 3697. [Google Scholar] [CrossRef]
- Akamatsu, T.; Yamamoto, K. Suitability Analysis for the Emergency Shelters Allocation after an Earthquake in Japan. Geosciences 2019, 9, 336. [Google Scholar] [CrossRef]
- Linders, D. Towards open development: Leveraging open data to improve the planning and coordination of international aid. Gov. Inf. Q. 2013, 30, 426–434. [Google Scholar] [CrossRef]
- Hristidis, V.; Chen, S.-C.; Li, T.; Luis, S.; Deng, Y. Survey of data management and analysis in disaster situations. J. Syst. Softw. 2010, 83, 1701–1714. [Google Scholar] [CrossRef]
- Mann, L. Left to Other Peoples’ Devices? A Political Economy Perspective on the Big Data Revolution in Development. Dev. Chang. 2018, 49, 3–36. [Google Scholar] [CrossRef]
- Opdyke, A.; Javernick-Will, A.; Koschmann, M. A Comparative Analysis of Coordination, Participation, and Training in Post-Disaster Shelter Projects. Sustainability 2018, 10, 4241. [Google Scholar] [CrossRef]
- Fan, L. Shelter strategies, humanitarian praxis and critical urban theory in post-crisis reconstruction. Disasters 2012, 36, S64–S86. [Google Scholar] [CrossRef] [PubMed]
- uFondwa-USA. The History of Natural Disasters in Haiti; uFondwa-USA, Inc.: Houston, TX, USA, 2018. [Google Scholar]
- Esri. Esri World Street Map; Esri: Redlands, CA, USA, 2020. [Google Scholar]
- Stanley, T.; Kirschbaum, D.B. A heuristic approach to global landslide susceptibility mapping. Nat. Hazards 2017, 87, 145–164. [Google Scholar] [CrossRef]
- Allen, T.I.; Wald, D.J. Topographic Slope as a Proxy for Seismic Site-Conditions (VS30) and Amplification around the Globe; U.S. Geological Survey: Hunter Mill, VA, USA, 2007; p. 69. [Google Scholar]
- Frankel, A.; Harmsen, S.; Mueller, C.; Calais, E.; Haase, J. Seismic Hazard Maps for Haiti. Earthq. Spectra 2011, 27, S23–S41. [Google Scholar] [CrossRef]
- Andreadis, K.M.; Schumann, G.J.-P.; Pavelsky, T. A simple global river bankfull width and depth database. Water Resour. Res. 2013, 49, 7164–7168. [Google Scholar] [CrossRef]
- Humanitarian OpenStreetMap Team (HOT)—Humanitarian Data Exchange. Available online: https://data.humdata.org/organization/225b9f7d-e7cb-4156-96a6-44c9c58d31e3 (accessed on 22 April 2020).
- ASCE/SEI (ASCE/Structural Engineering Institute). Minimum Design Loads for Buildings and Other Structures; American Society of Civil Engineers: Reston, VA, USA, 2016. [Google Scholar]
- Martin, A.J.; Diehl, J.G. Practical Experience Using A Simplified Procedure To Measure Average Shear-Wave Velocity To A Depth Of 30 Meters (VS30). In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]
- Foust, B.; Ihinger, P.; Jeffery, T. Modeling Earthquake Risk; CoreLogic: Irvine, CA, USA, 2016. [Google Scholar]
- Giardini, D.; Grünthal, G.; Shedlock, K.M.; Zhang, P. The GSHAP Global Seismic Hazard Map. Ann. Geophys. 1999, 42, 6. [Google Scholar]
- Azizian, A.; Brocca, L. Determining the best remotely sensed DEM for flood inundation mapping in data sparse regions. Int. J. Remote Sens. 2020, 41, 1884–1906. [Google Scholar] [CrossRef]
- Chen, W.; Zhai, G.; Ren, C.; Shi, Y.; Zhang, J. Urban Resources Selection and Allocation for Emergency Shelters: In a Multi-Hazard Environment. Int. J. Environ. Res. Public Health 2018, 15, 1261. [Google Scholar] [CrossRef]
- Drobne, S.; Lisec, A. Multi-attribute Decision Analysis in GIS: Weighted Linear Combination and Ordered Weighted Averaging. Informatica 2009, 33, 459–474. [Google Scholar]
- Velasquez, M.; Hester, P. An analysis of multi-criteria decision making methods. Int. J. Oper. Res. 2013, 10, 56–66. [Google Scholar]
- Documet, P.I.; McDonough, B.L.; Van Nostrand, E. Engaging Stakeholders at Every Opportunity: The Experience of the Emergency Law Inventory. Am. J. Public Health 2018, 108, S394–S395. [Google Scholar] [CrossRef] [PubMed]
- Saaty, T.L. The Analytic Heirarchy Process: Planning, Priority Setting, Resources Allocation; McGraw: New York, NY, USA, 1980. [Google Scholar]
- UNISDR Hyogo Framework for Action 2005–2015: Building the Resilience of Nations and Communities to Disasters; United Nations Office for Disaster Risk Reduction: Geneva, Switzerland, 2007.
- Esri. Esri World Topographic Map; Esri: Redlands, CA, USA, 2020. [Google Scholar]
- Bauer, R. Guidelines for Post-Disaster Housing; Oxfam: Oxford, UK, 2003. [Google Scholar]
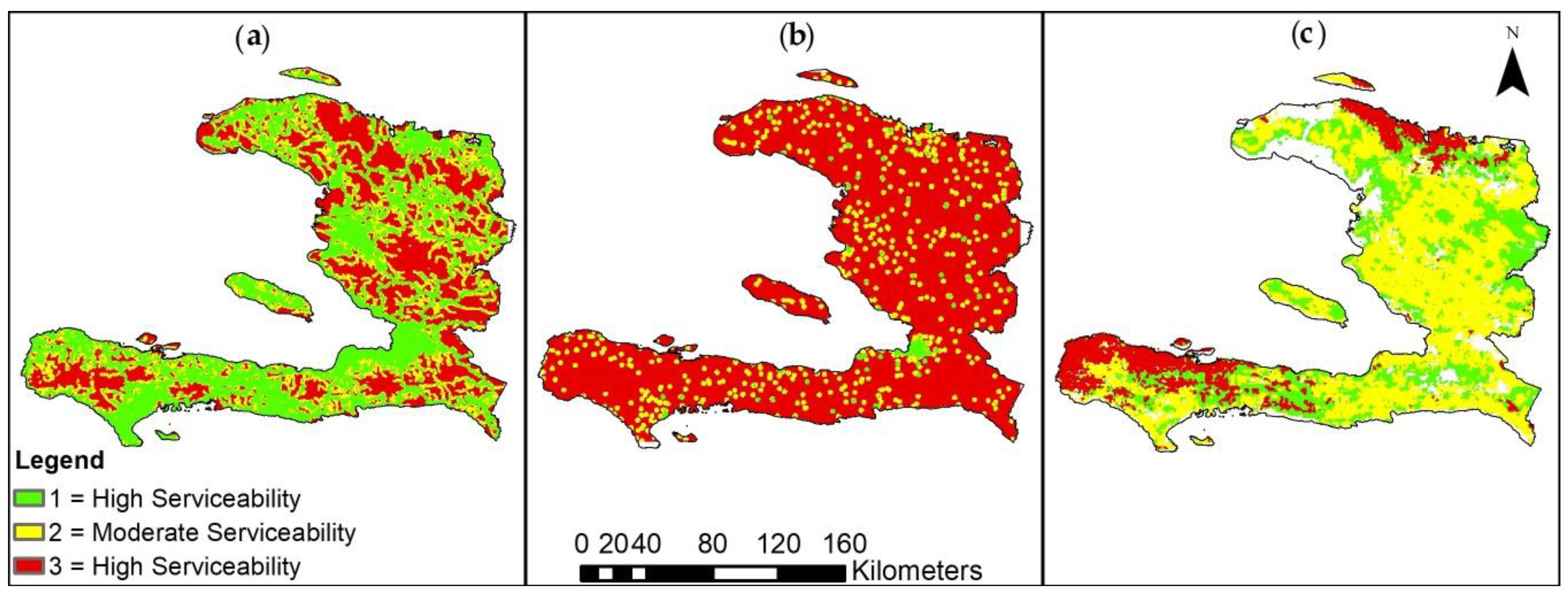
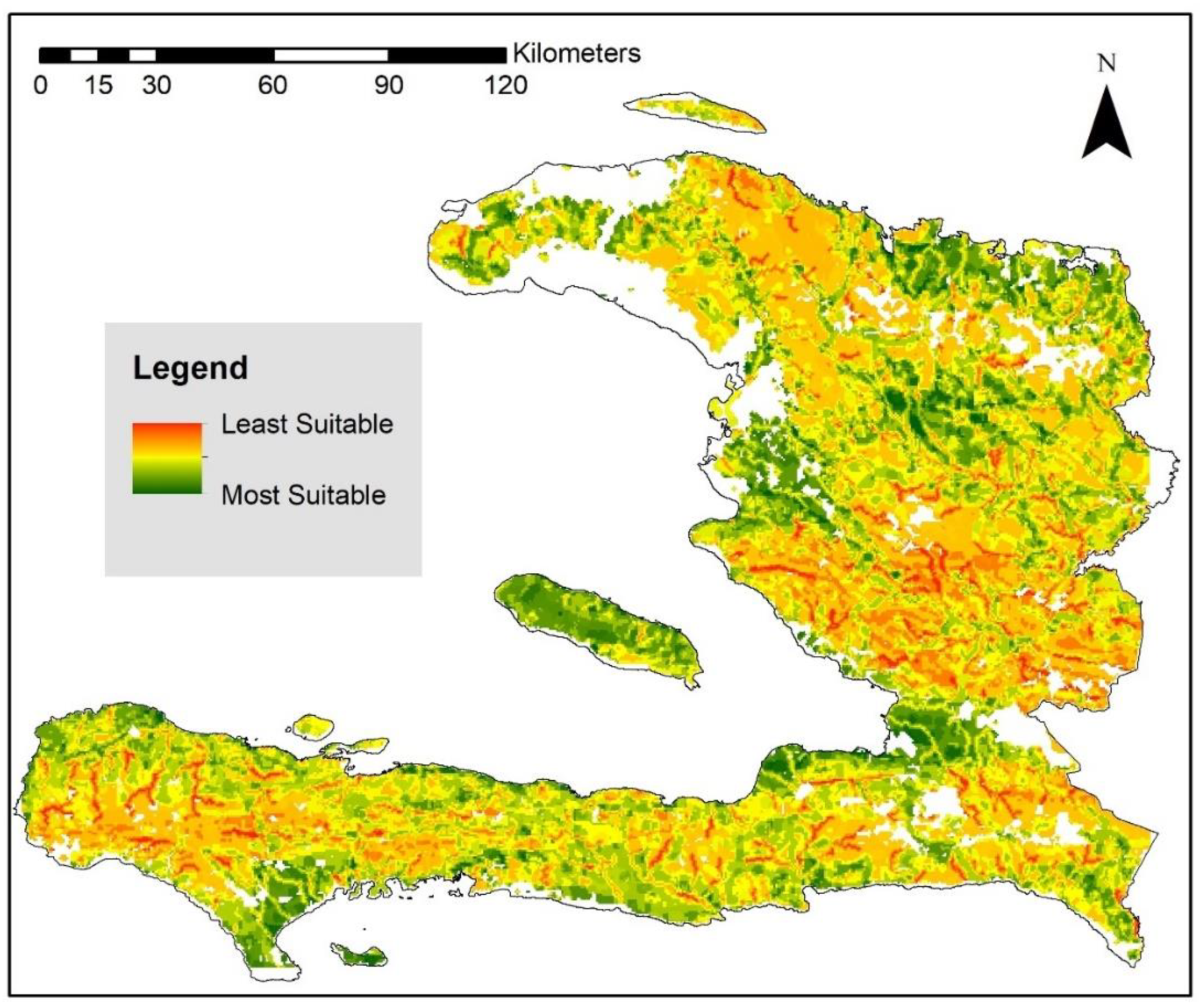
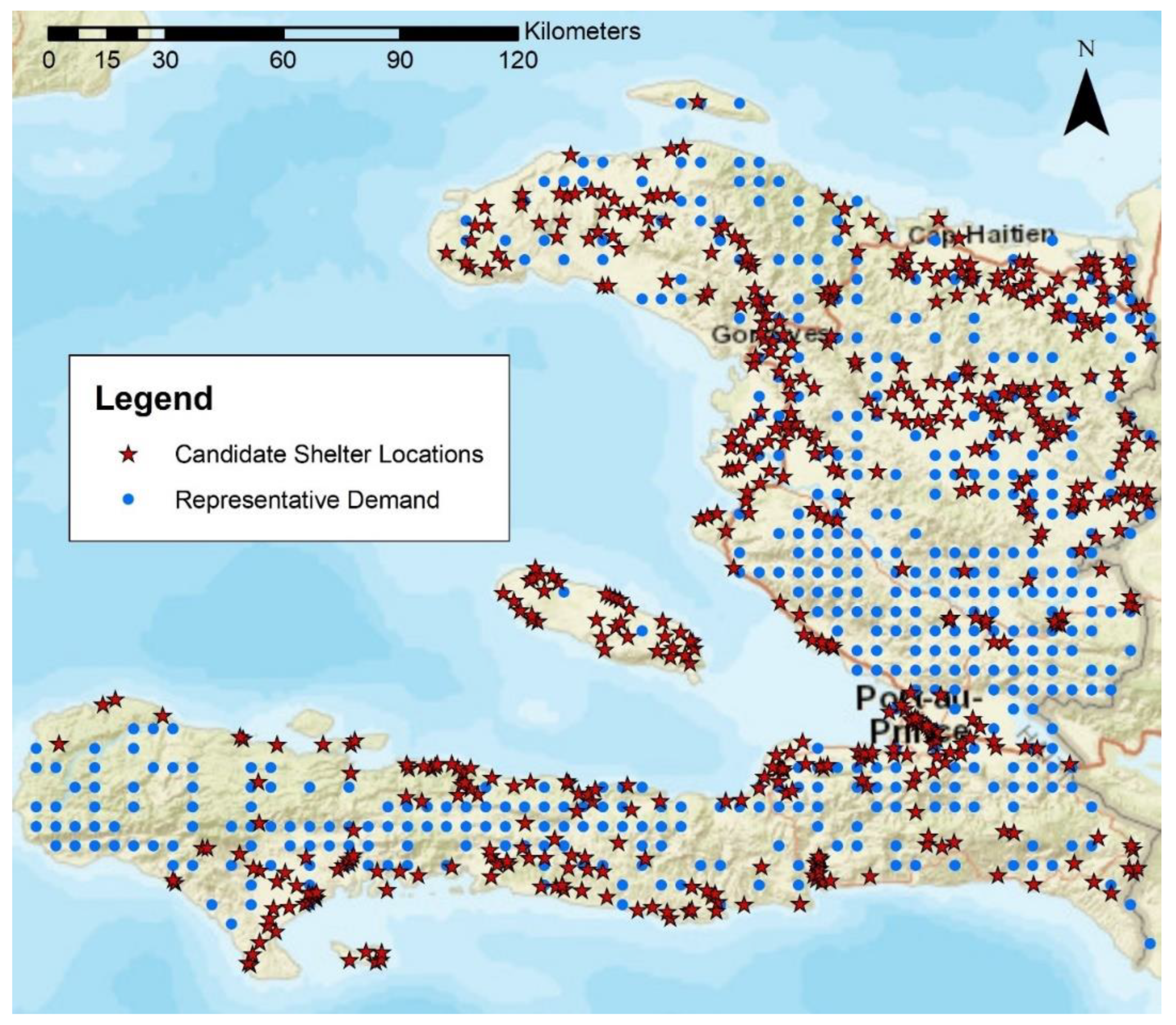
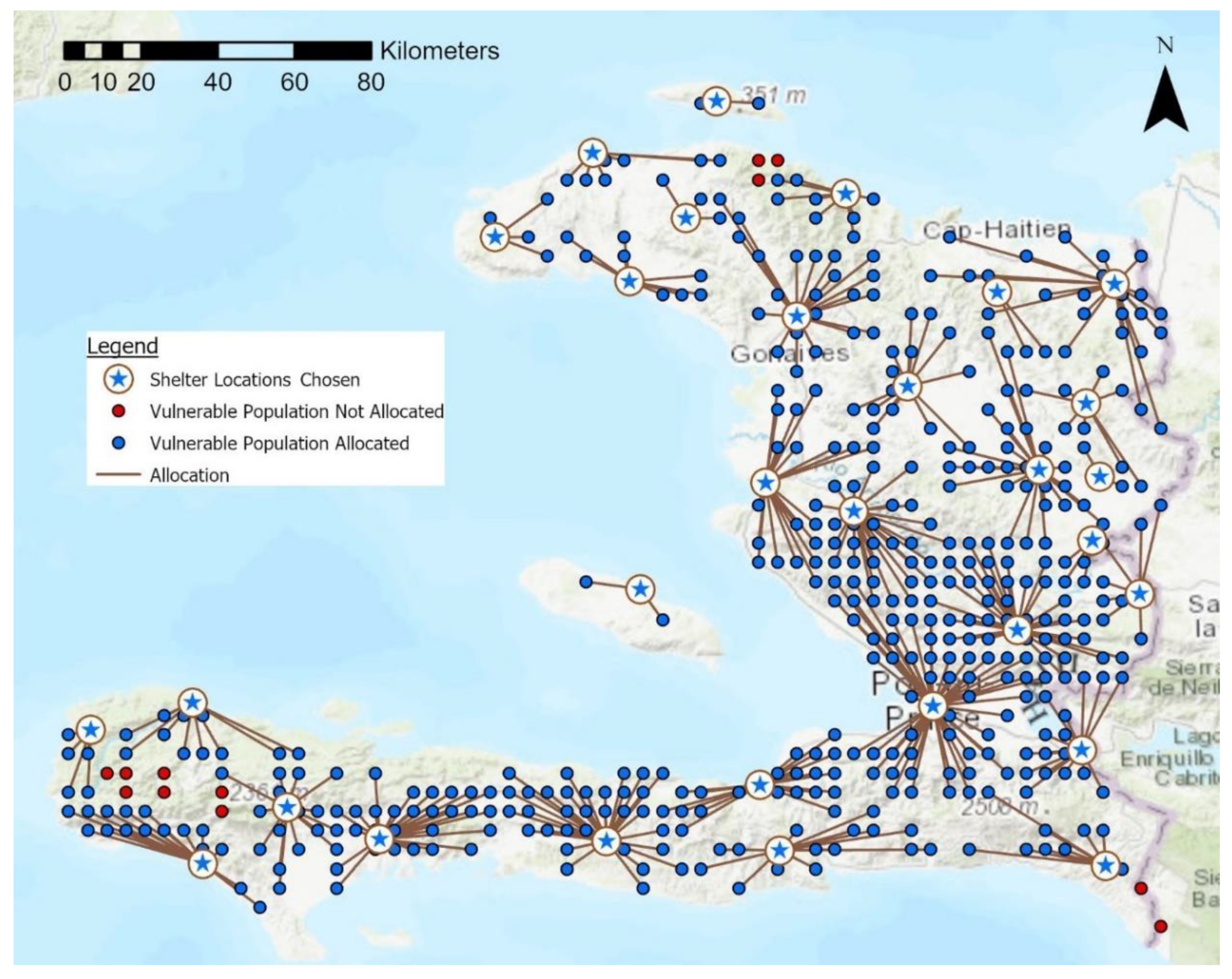
| Criteria | Source Global Dataset | Processing Performed | Attribute Raster (Metric of Criteria Success) | Standardized Attribute Raster (Metric of Objective Success) |
|---|---|---|---|---|
| Minimize hazard risk by minimizing landslide susceptibility | Landslide Susceptibility, 30″ discrete raster [49] | Project coordinate system and resample resolution | Landslide susceptibility | Landslide risk |
| Minimize hazard risk by minimizing susceptibility to earthquake damage | 30 m Shear Wave Velocity (VS,30) [50], 30″ continuous raster, Peak Ground Acceleration (PGA) [51] 3′ continuous raster | Project coordinate system, resample resolution, reclassify and perform weighted overlay | Seismic site conditions overlaid with expected ground acceleration | Earthquake damage risk |
| Minimize hazard risk by minimizing susceptibility to fluvial flooding | Rivers, Vector polyline [52] | Euclidean distance tool to estimate floodplains | Distance to rivers | Fluvial flood risk |
| Maximize serviceability by maximizing accessibility by vehicle | Roads, Vector polyline [53] | Weighted road density by road type classification, discounting insignificant types such as footpaths | Density of roads | Accessibility by transportation |
| Maximize serviceability by maximizing proximity to healthcare | Healthcare Facilities, Vector point [53] | Weighted point density of permanent healthcare facilities and field hospitals | Density of healthcare facilities | Accessibility to healthcare |
| Maximize serviceability by maximizing suitability of land cover | Land Cover, 500 m discrete raster [53] | Project coordinate system and resample resolution | Land cover | Suitability of land cover for shelter site |
| Scenario | % Suitable Area 1 | % Change in Suitable Area |
|---|---|---|
| Original: All hazards equal importance | 38.0 | N/A |
| Earthquake strong importance over flood and landslide 2 | 24.7 | −35 |
| Flood and landslide strong importance over earthquake | 46.8 | 23 |
| Landslide strong importance over flood and earthquake | 25.1 | −34 |
| Flood and earthquake strong importance over landslide | 53.2 | 40 |
| Flood strong importance over earthquake and landslide | 82.8 | 118 |
| Earthquake and landslide strong importance over flood | 18.4 | −52 |
| Max. Impedance (Driving Minutes) | Number of Candidate Shelters | Number of Shelters Chosen | % of Demand Allocated |
|---|---|---|---|
| 30 | 552 | 73 | 85.4 |
| 60 | 552 | 30 | 97.5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Godschall, S.; Smith, V.; Hubler, J.; Kremer, P. A Decision Process for Optimizing Multi-Hazard Shelter Location Using Global Data. Sustainability 2020, 12, 6252. https://doi.org/10.3390/su12156252
Godschall S, Smith V, Hubler J, Kremer P. A Decision Process for Optimizing Multi-Hazard Shelter Location Using Global Data. Sustainability. 2020; 12(15):6252. https://doi.org/10.3390/su12156252
Chicago/Turabian StyleGodschall, Sarah, Virginia Smith, Jonathan Hubler, and Peleg Kremer. 2020. "A Decision Process for Optimizing Multi-Hazard Shelter Location Using Global Data" Sustainability 12, no. 15: 6252. https://doi.org/10.3390/su12156252
APA StyleGodschall, S., Smith, V., Hubler, J., & Kremer, P. (2020). A Decision Process for Optimizing Multi-Hazard Shelter Location Using Global Data. Sustainability, 12(15), 6252. https://doi.org/10.3390/su12156252