1. Introduction
At present, 80 percent of the world’s energy is produced from fossil fuels [
1]. The exhaust products of using these resources affect the environment, mainly through global warming and acid rain. Currently, oil provides more than 35% of the global primary energy, coal and natural gas add 23% and 21%, respectively [
2,
3,
4]. The fossil fuel distribution around the world is uneven, whereas, more than half of the global supply is obtained from the Middle East. This leads to an unbalanced economy around the world that affects the whole political geography. The burning of fossil fuel produces atmospheric emission of CO
2 (carbon dioxide), where its concentration will cause an average temperature rise of 3–5 °C [
3].
Considering the above, as well as the fact that oil is running out quickly, alternatives should be adopted. Renewable energy is one of the promising options for the above problems. PV (photovoltaic) panels can provide a good source of producing clean electricity. The efficiency range of solar radiation conversion is about 5%–20%, depending on the type of cell [
5,
6]. Most commercial PV cells are made from silicon and come in two general types, mono-crystalline and multi-crystalline. These types of PV cells are the most efficient, with approximately 15% efficiency [
7,
8]. The amount of solar energy converted to electrical power depends on the intensity of solar radiation falling on PV cells, as well as PV and ambient temperatures [
9]. When the temperature of the PV module is increased, the efficiency drops. Depending on the PV type, the approximate descent of efficiency is around 0.5%/°C from the cell operating temperature.
The PV cells absorb up to 80% of incident solar radiation but, depending on the efficiency of the PV cell technology used, only a small part of the absorbed incident energy is converted into electricity [
10]. The remainder energy that was absorbed by the PV cell is dissipated as heat and the PV cell can reach a temperature 40 °C above the ambient. The overheating reduces the efficiency of the panels dramatically.
Many ways of cooling the PV module will be presented and discussed. A steady state of a PV/T (photovoltaic/thermal) collector utilizing air and/or water cooling are some examples [
11,
12]. The optimum cooling solution is dependent on several factors, such as PV technology, the type of concentrating system, and weather conditions at which the system is installed. The annual performance indicated that the delivered energy from the PV modules increases by 5% during the dry and warm seasons [
13,
14].
To promote the production of electricity from PV units, it is a must to reduce the operating temperature to improve efficiency. Using water in the PV/T system is more efficient than using air because the thermal properties of water are better than air [
12]. Othman et al. [
15] provided a merge of both air and water mediums with the conventional PV/T collector. The main components fabricated in the system are two transparent PV modules connected in parallel to generate electrical power, double pass air flat plat collector, copper water tube, and reservoir for produced hot water. Experimental values of PV temperature, the air temperature on both channels, and water temperature were measured. The thermal and electric efficiency obtained under 800 W/m
2 solar irradiation are 70.09% and 19.95%, respectively.
Ahmad Fudholi et al. [
16] determined the electrical and thermal performance of PV cells cooled by water under solar irradiation ranging from 500 to 800 W/m
2. For each solar irradiance level, a flow rate of 0.01 kg/s to 1.041 kg/s was introduced. The electrical, thermal, and total efficiency of the PV/T collectors were examined. The results showed that the spiral flow absorption was highest at 800 W/m
2 solar intensity and 0.41 kg/s water flow rate, with an electrical efficiency of 13.8%, thermal efficiency of 54.6%, and overall efficiency of 68.4%.
The mixed solar PV system and solar heat collector, PV/T, is an alternative solar solution, which offers a distinct advantage of providing one-unit form thermal output, as well as an electric output with improved efficiency compared to PV stand-alone units if properly designed [
17]. Other cooling mediums can be used to extract the heat from the PV, such as oils and nanofluids, which can be used in different methods. Attention has been focused on the use of practical, durable, and inexpensive reflectors to increase the electricity produced from PV cells to become price competitive in the market.
The theoretical and experimental work of a linear Fresnel reflector mirror (LFRM) with a horizontal receiver was developed by Gomaa et al. [
14,
18]. The thermal, electric, and total efficiency obtained were 62%, 18%, and 80%, respectively. Whereas, Wang et al. [
19] proposed the use of a horizontal concentrating photovoltaic (CPV) receiver and LFRM and carried out sun-tracking error effect analysis. The normalized optical efficiency resulted, and PV efficiency experimentally was 0.62 when the deviation angle is 1° and 13.6%, respectively.
Prasad et al. [
20] studied LFRM optimization with a secondary mirror and tubular receiver. The study presented a high distribution uniformity of a flux density on the tube receiver collector. Whereas, Abbas et al. [
21] investigated the yearly performance of LFRMs on the thermal receiver using different shapes of mirrors.
Beltagy et al. [
22] studied theoretical and experimental LFRMs with a thermal receiver that results in a daily thermal efficiency over 40%. He et al. [
23] proposed an LFRM system and managed the pertinent optical analysis study. Chemisana et al. [
24] developed the simulation and experimental study of a two-axis LFRM solar concentrator. The results of both revealed good agreements. Zhu and Chen’s [
25] study presented several CLFRM (compact linear Fresnel reflector mirror) system designs. The experimental and simulation investigations of the CLFRM performance were carried out. In addition, Wang et al. [
26] studied the optical and thermodynamic performance of a CLFRM with a combined PV/T receiver.
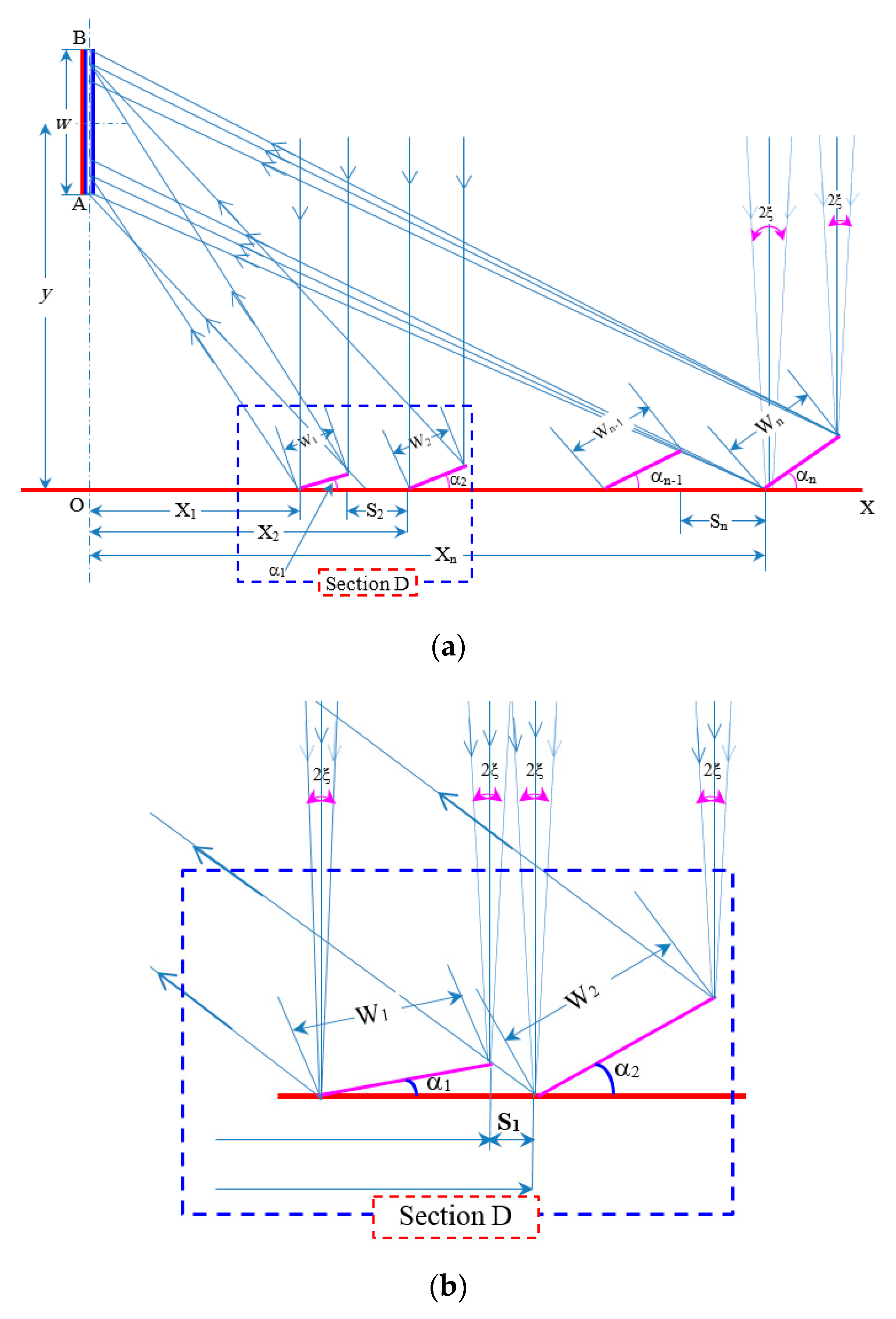
All the above-mentioned research studies have enhanced the contents of LFRM solar concentrators. However, most of these studies have been performed in the field of solar thermal use for LFRM concentrators until now. There were a few studies on solar concentrating PV systems using LFRM. In addition, when the use of LFRM in solar CPV systems is considered, it will also be helpful, by adjusting the geometrical structure of the conventional LFRM concentrator with vertical receiver instead of a horizontal one, to create large solar cell utilization and high solar concentrations uniformity and to overcome the effects of shadows and blocks on solar cells.
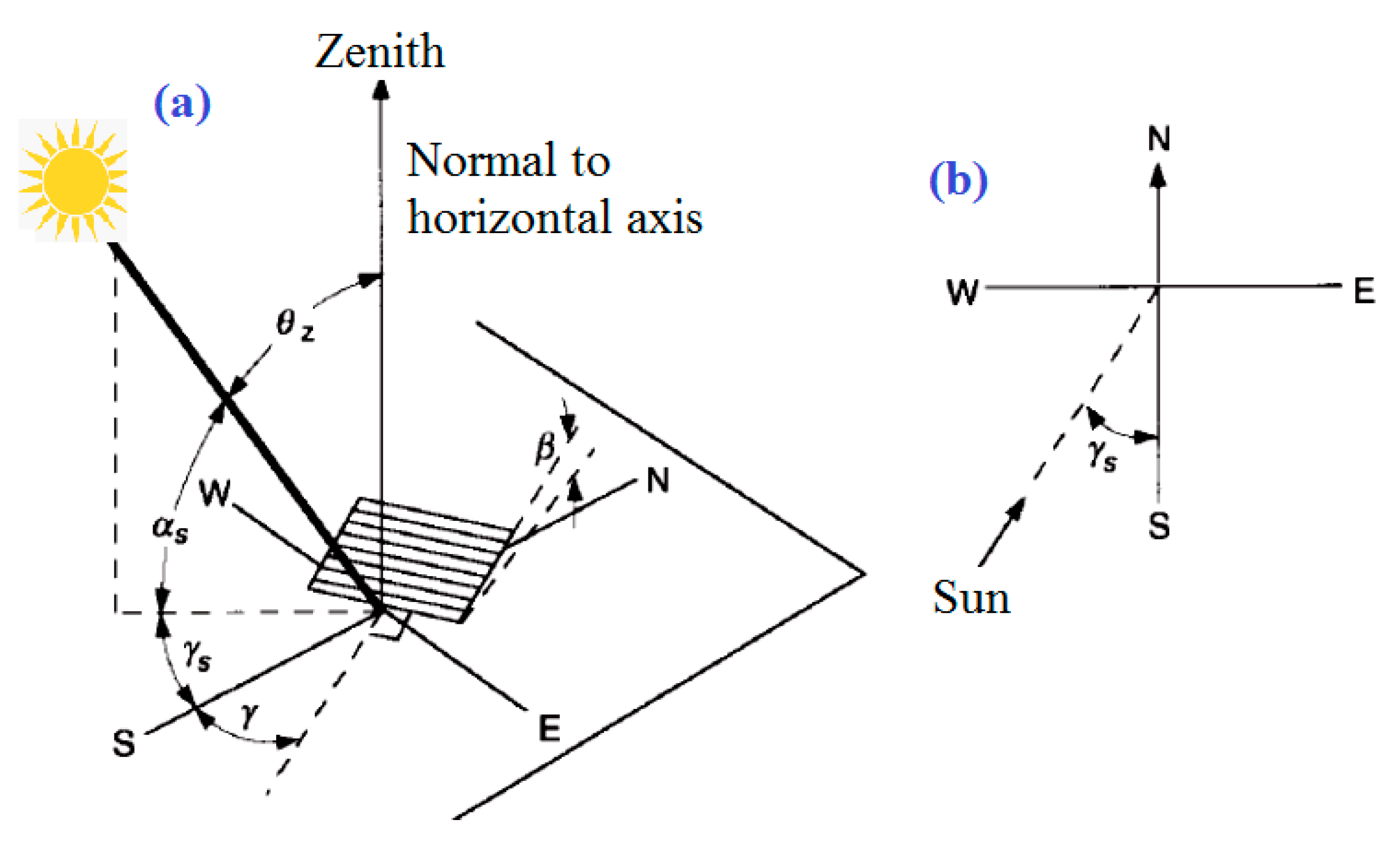
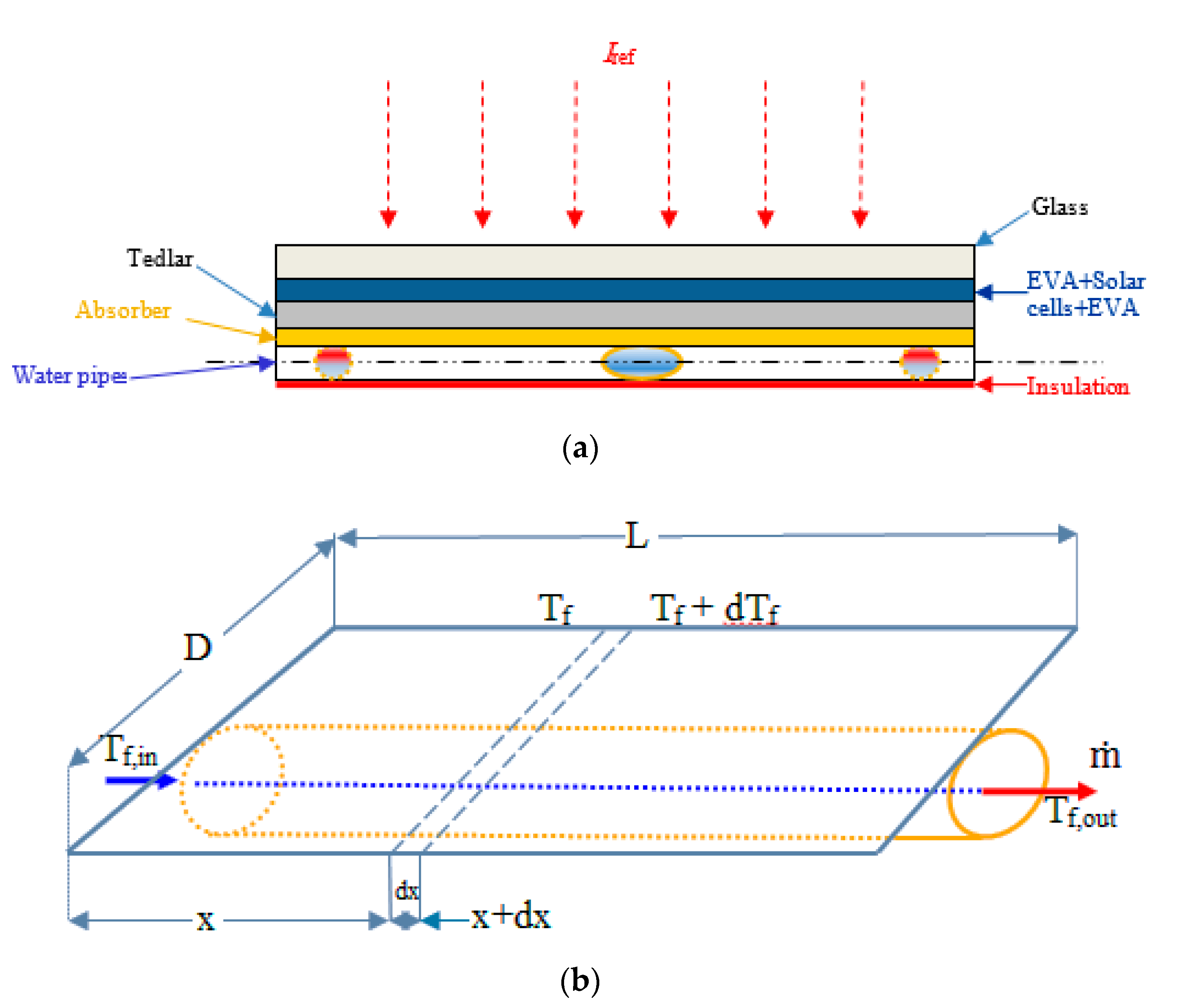
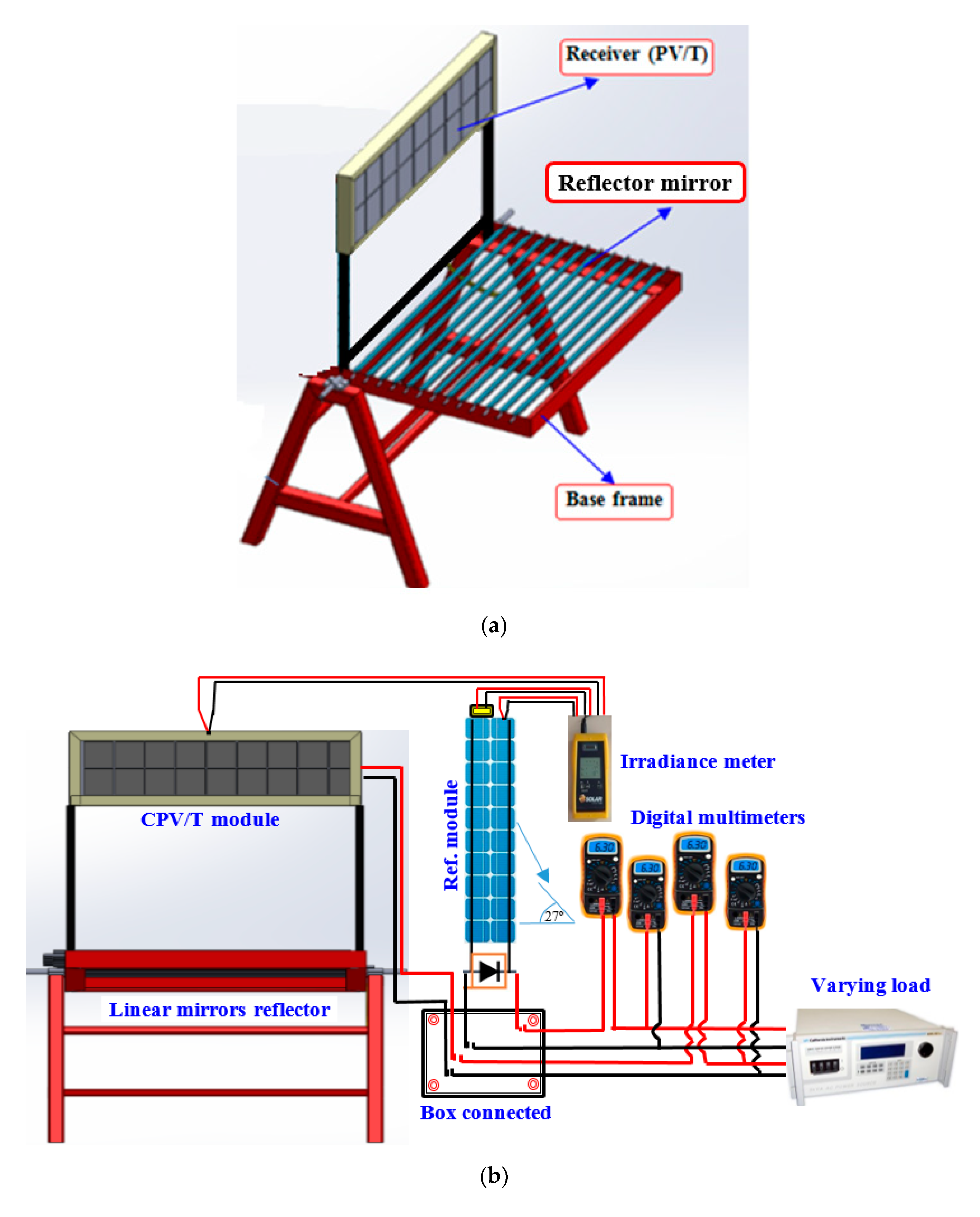
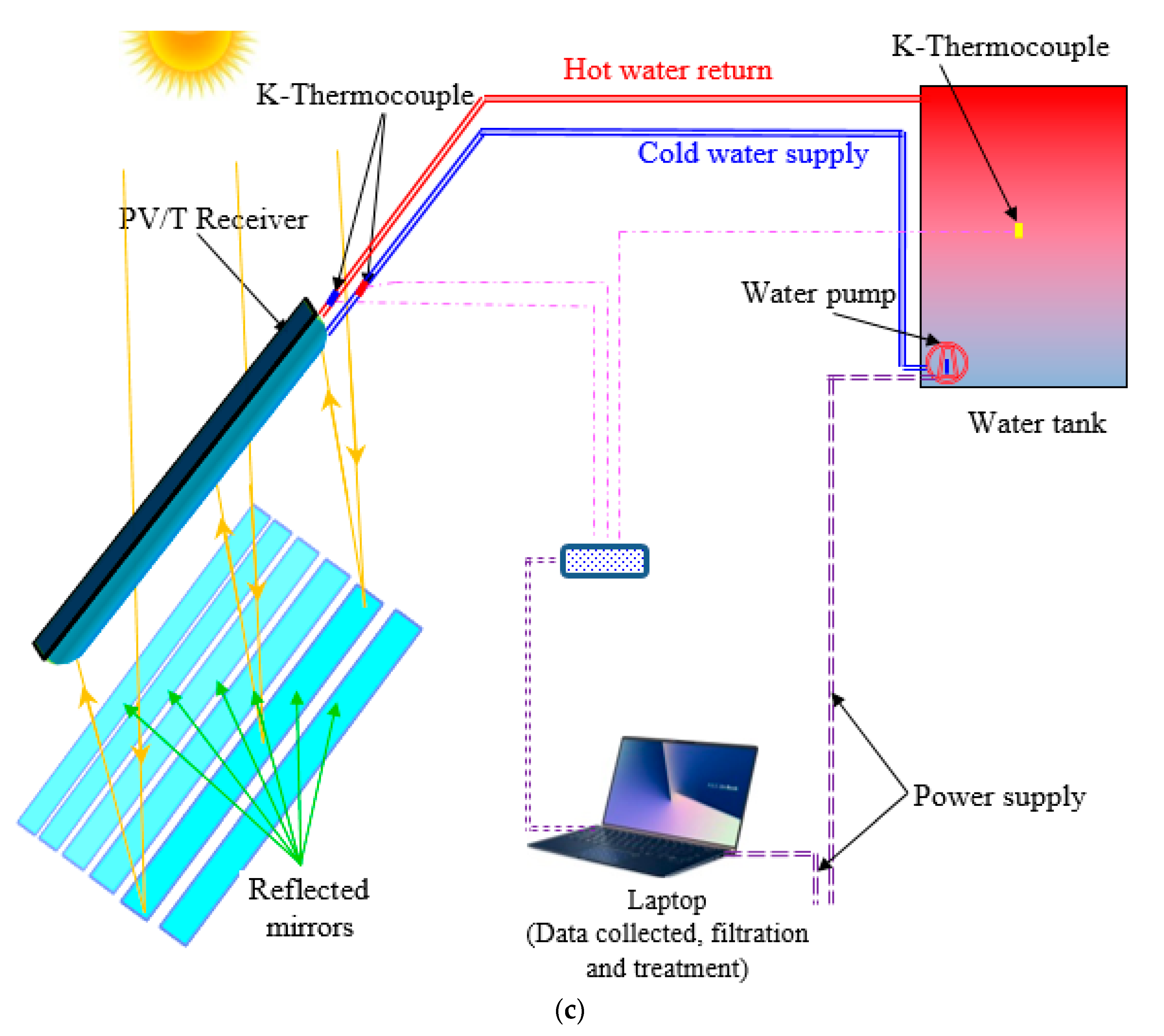
A solar CPV/thermal (CPV/T) with an LFRM concentrator was proposed for the completion of this research gap and the creation of a high solar concentration uniformity CPV/T system. The design theory of the proposed system is provided. It consists of different widths of flat mirrors and can give solar cells a high solar concentration uniformity. To carry out investigations on the actual solar concentrate properties and electric and thermal features of the proposed CPV/T device, a small-scale prototype was produced. The simulation and optical study of the solar CPV/T concentration system with the LFRM concentrator were also performed.
The remainder of the paper is organized as follows.
Section 2 presents the design theory and energy conversion equations for the proposed concentrating system with a vertical PV/T receiver. The contents of the experimental prototype are listed in
Section 3.
Section 4 presents the results and discussions of solar concentrating performance research, performance analytics, electric and thermal power, and testing validation. Finally, the main findings are concluded and highlighted in
Section 5.
4. Results and Discussion
4.1. Theoretical Results
The performance of the PV system was studied when changing the amount of solar irradiation from 200–1000 W/m2 and changing the amount of cooling water flow from 0.1–1 kg/min at different solar concentration ratio. In this study, the average wind speed was 2 m/s, and the temperature of the cooling water inside was 293 K.
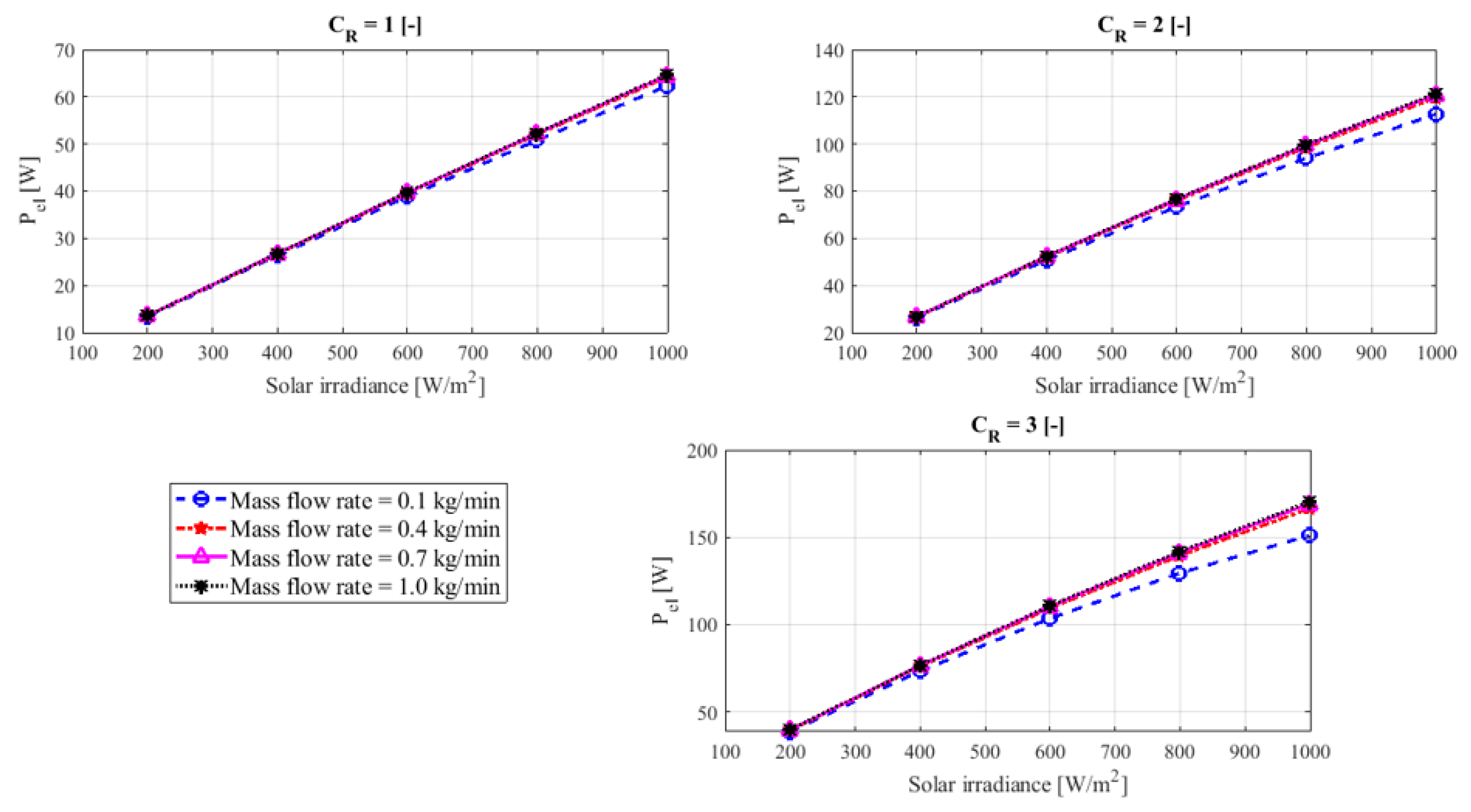
The electrical energy of this system under the influence of solar concentration ratio from 1–3 is shown in
Figure 6. The amount of electrical and thermal energy produced from the system increased with increasing solar concentration and the amount of radiation falling. Where the maximum electric power produced increased from 65 W at a solar concentration ratio 1 to 170 W at the solar concentration ratio 3. Also, the figure showed that the highest amount of energy produced at the highest flow rate of 1 kg/min under different concentration ratio.
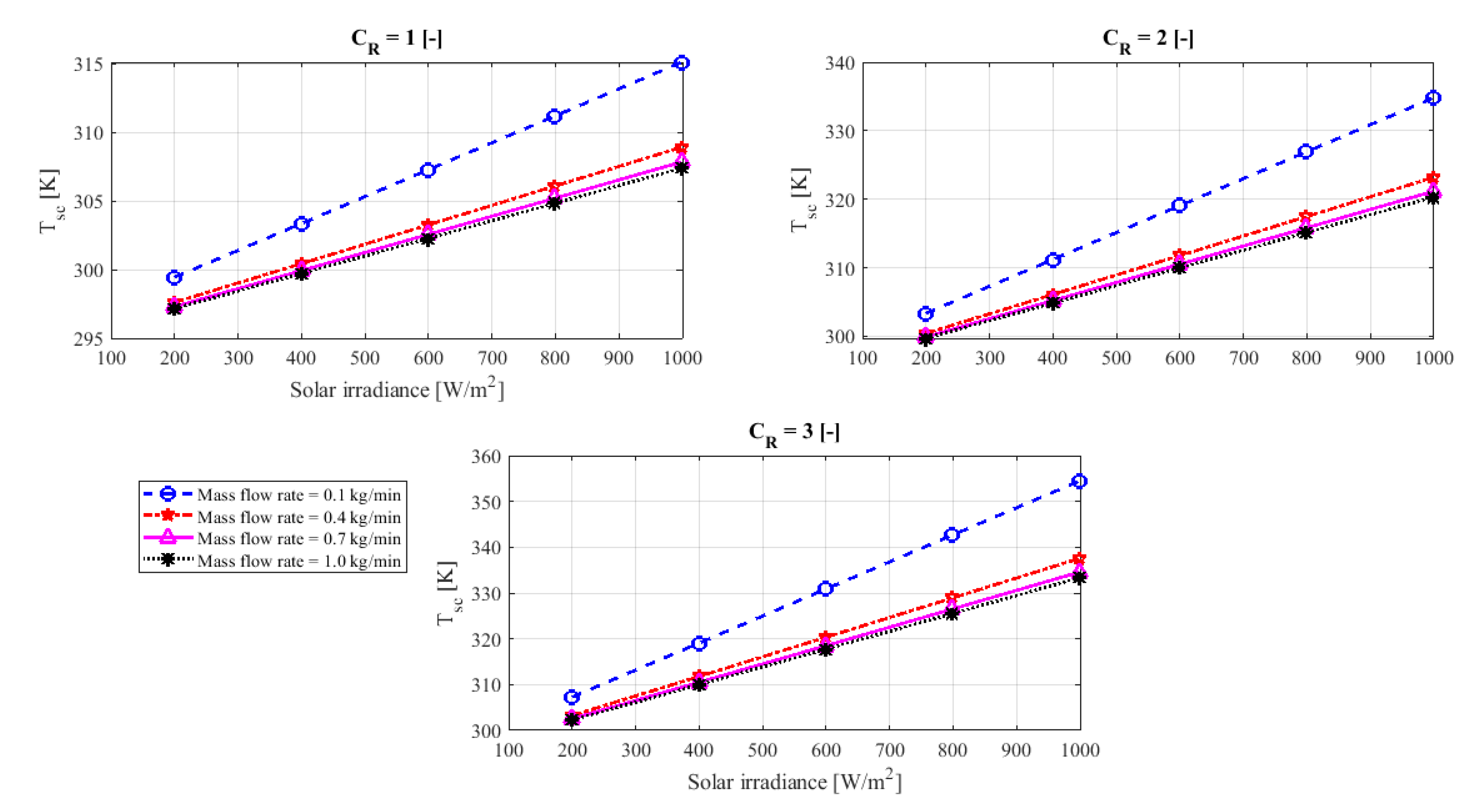
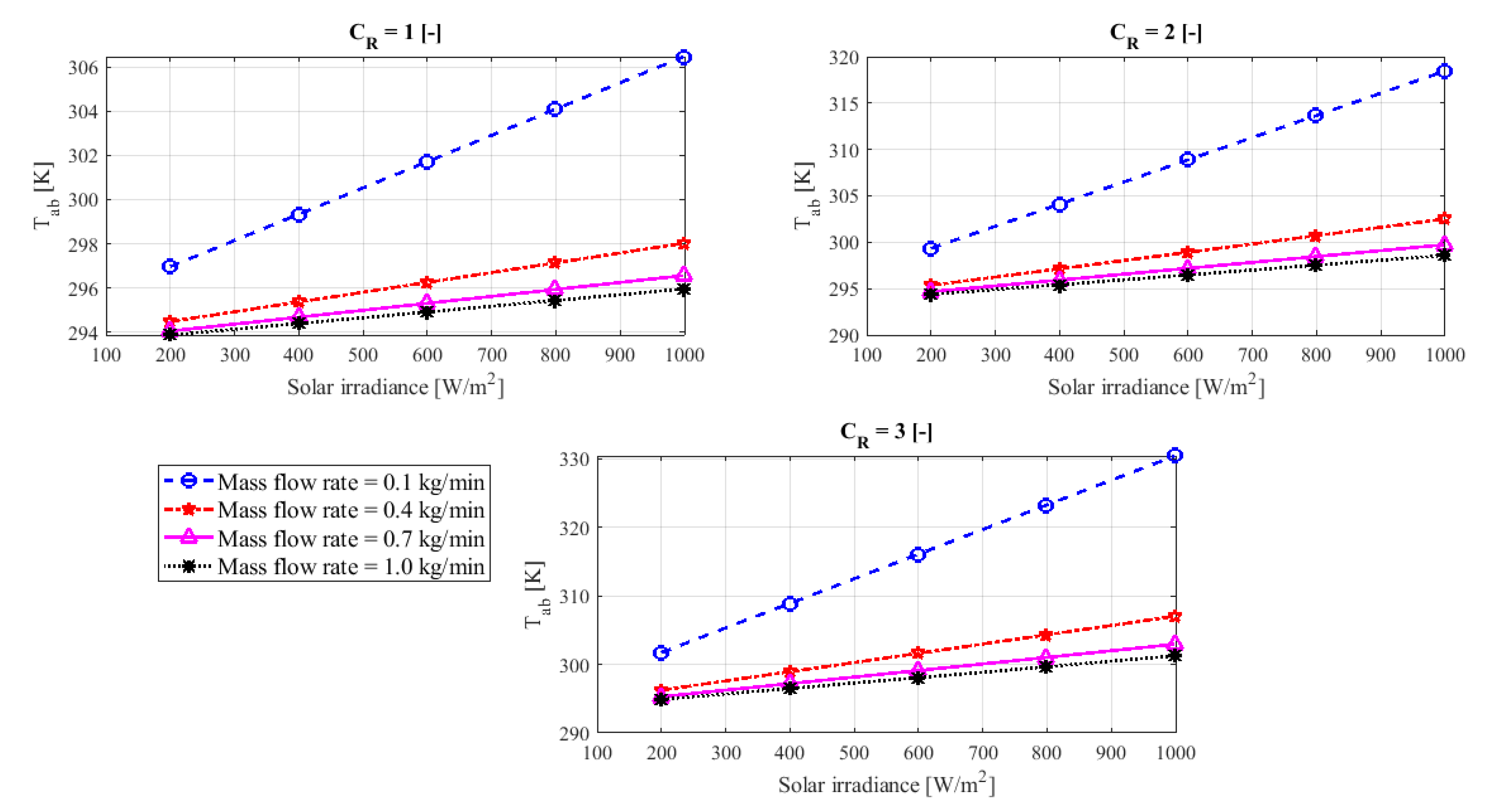
Figure 7 and
Figure 8 show the change in the temperature of the solar cells and the temperature of the heat absorber, respectively, with the change in solar radiation and the solar concentration ratio. The change in the temperature of the solar cells was linked to the change in the temperature of the heat absorber. They increased together with the increase in the amount of solar radiation and solar concentration ratio and decrease together with their decrease.
The cooling of the PV module, as presented, reduced the temperature of the solar cells and the absorber. It was observed that the lower the flow, the higher the temperature of the solar cells, and the absorber plate. The temperature of the solar cells reached to 355 K and the absorber plate temperature was 330 K at the same operational conditions when the solar concentration ratio was 3, the cooling water flow rate was 0.1 kg/min, and at solar irradiance 1000 W/m2. Whereas, the PV cell temperature and absorber temperature were reduced to 333 K and 302 K, respectively, when the cooling flow rate increased to 1 kg/min.
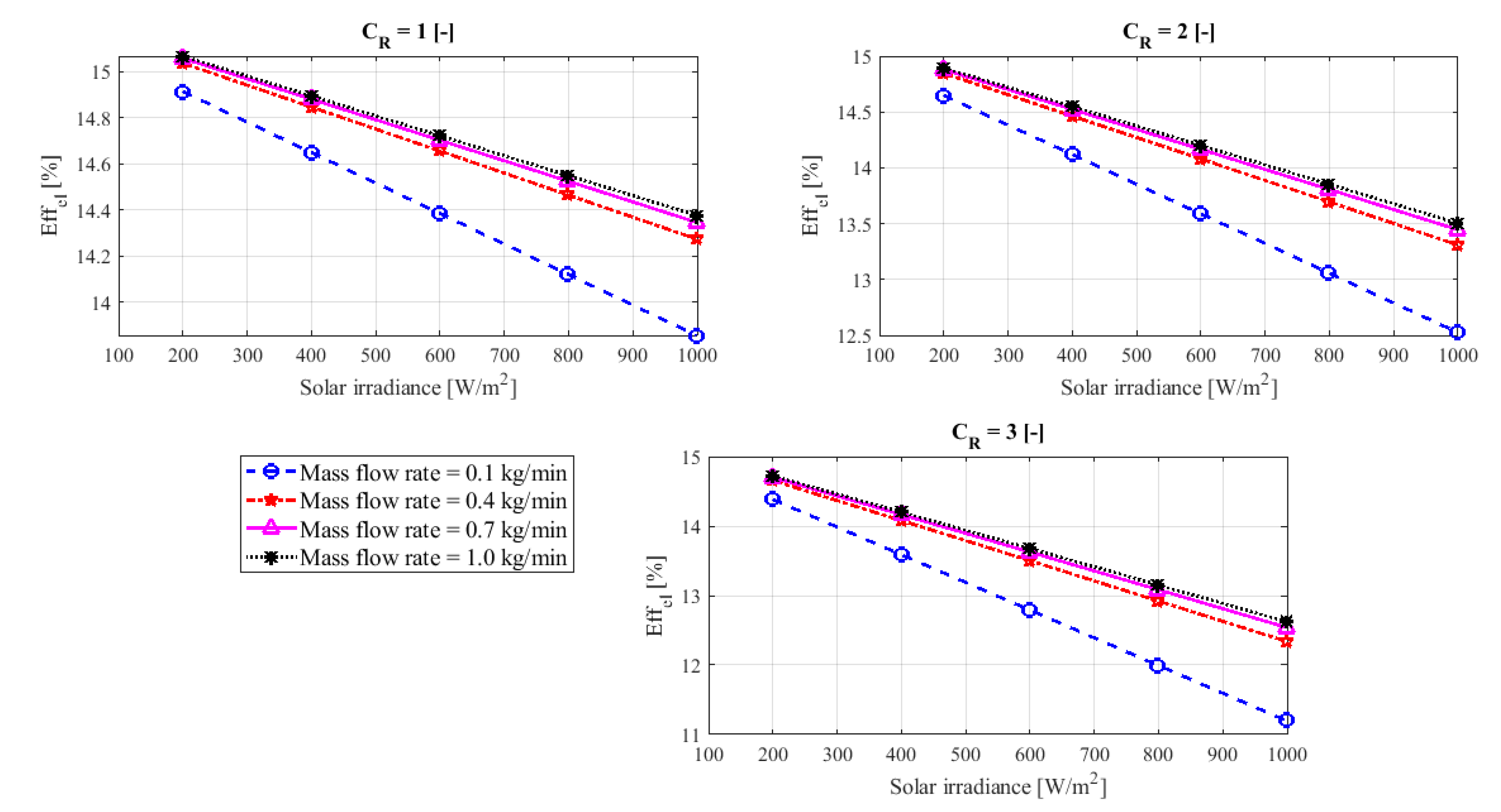
The electrical efficiency of the system under the same operating conditions is presented in
Figure 9. It shows that solar radiation negatively affects electrical efficiency. Since the solar concentration rate reflects the amount of solar radiation falling on the surface, increasing the solar concentration rate also adversely affected the electrical efficiency of the solar system.
It is also evident in
Figure 9 that the electrical efficiency may decrease from 13.9% at the concentration ratio 1 and the amount of flow 0.1 kg/min to 11.2% at the same solar irradiation 1000 W/m
2 and concentration ratio 3. The large decrease in electrical efficiency can be reduced by increasing the flow of cooling water, so that the electrical efficiency increases as an example from 11.2% to 13.1% if the amount of flow rate is increased from 0.1 kg/min to 1 kg/min, respectively, at the concentration ratio 3 and solar irradiation 1000 W/m
2.
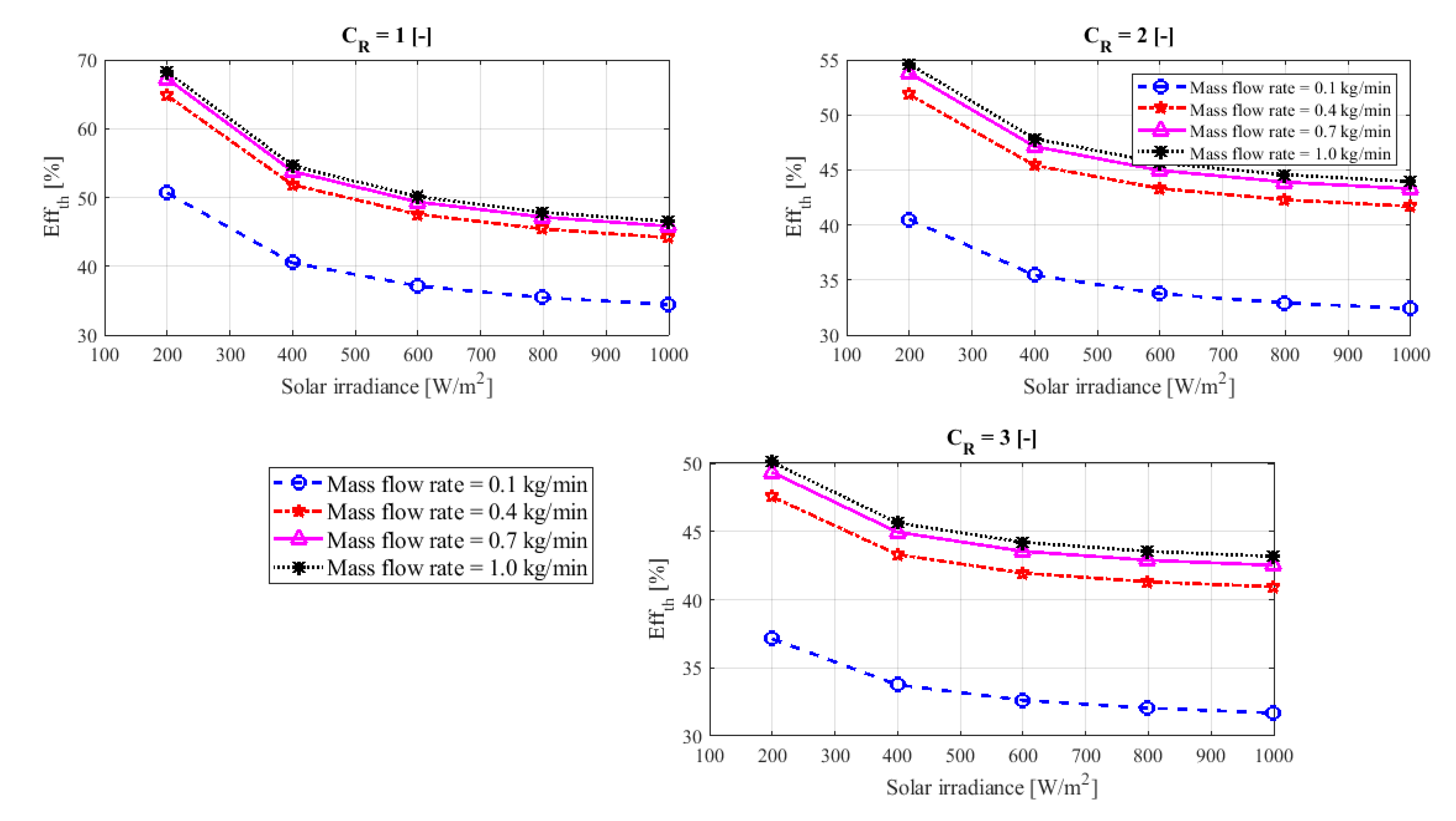
The same impression observed in the electrical efficiency of the system applies to thermal efficiency, as shown in
Figure 10. So, increasing concentration ratio and solar radiation reduced thermal efficiency, while increasing the flow rate of cooling water reduced the efficiency deficit. Based on
Figure 10, the highest thermal efficiency was 68% at unity concentration ratio, and 200 W/m
2 solar irradiation with a flow rate of 1 kg/min and a lower thermal efficiency is 32% at a concentration ratio 3 and 1000 W/m
2 solar irradiation with a flow rate of 0.1 kg/min.
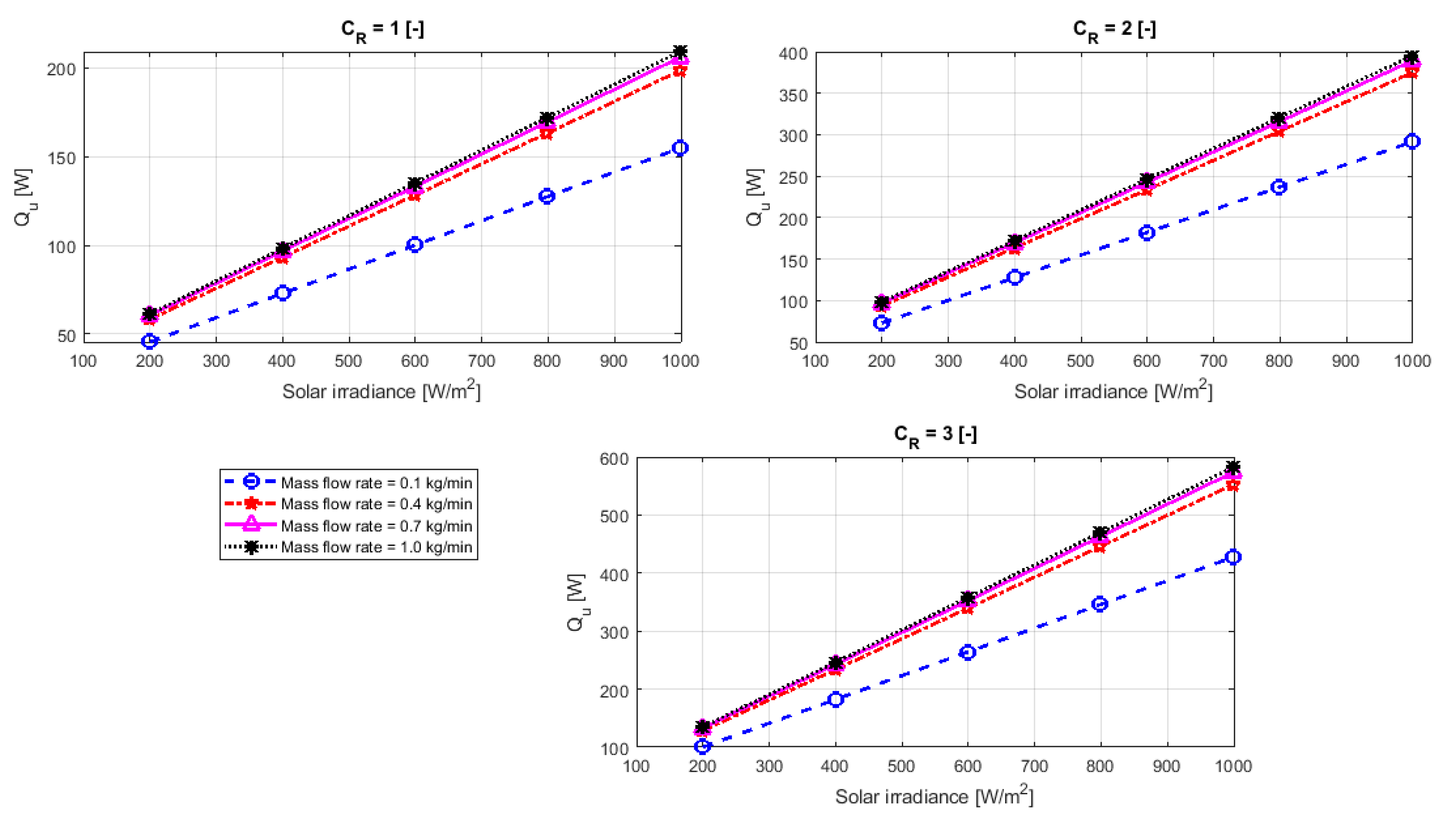
Figure 11 shows the relationship of thermal energy with solar radiation under the influence of a variable solar concentration ratio. The results show a significant increase in thermal energy, when the solar concentration ratio and solar radiation increased, as well as increasing the flow rate of cooling water increased the thermal energy produced.
The highest recorded thermal energy quantity was 580 W at solar concentration 3, solar irradiation 1000 W/m2, and flow quantity 1 kg/min, while thermal energy at solar concentration 1 was 210 W, whereas, at solar concentration 2 was 400 W under the same operating conditions.
After studying a set of variables on the performance of the proposed solar system, it was shown that the electrical and thermal efficiencies decreased with increasing solar concentration ratio, solar radiation, and the amount of flow rate of cooling water. In contrast, the electrical and thermal energy, temperature of solar cells, and temperature of heat absorber increased with increasing solar radiation and the solar cells and absorber temperature decreased by increasing the flow rate of cooling water.
4.2. Experimental Results and Validation
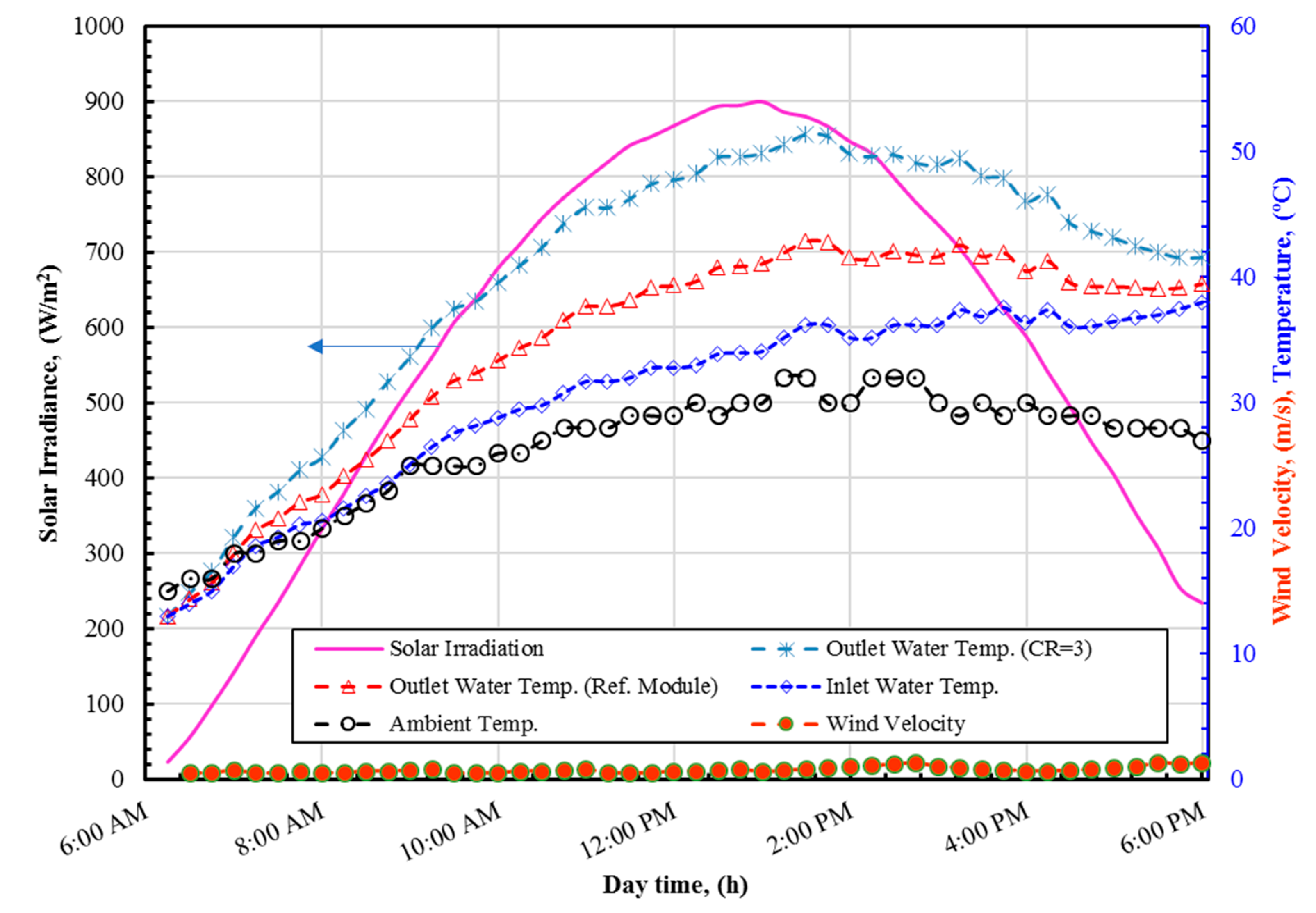
The amount of change in PV power and thermal output, with water cooling under a non-concentrated and concentrated system, due to environmental effects, was calculated from the measured electrical parameters of each module. The measurements of the solar irradiance, wind speed, ambient temperatures, inlet water for PV, and exit water temperature from PV in the case of a non-concentrated and concentrated system are presented in
Figure 12 for the chosen test day.
Figure 12 illustrates that the maximum and average ambient temperature were found to be 32 °C and 28 °C, respectively. In contrast, the average daily wind velocity was found to be 0.75 m/s. Whereas, the solar irradiance pattern on the high-value experiment day was 900 W/m
2. In addition,
Figure 12 illustrates the measured input and output temperatures of the module cooling water during the day of the test for both configurations.
Whereas the daytime progresses, the temperature of outlet cooling water increased with increasing the incident solar irradiance, until it achieved its maximum then reduced as the solar irradiation reduced. It is found that the outlet cooling water temperatures for PV/T and CPV/T systems were higher than the inlet cooling water temperatures during the test day with a maximum temperature difference of about 8 °C and 13.5 °C, respectively, under mass flow rate 0.7 kg/min and solar irradiance 900 W/m2.
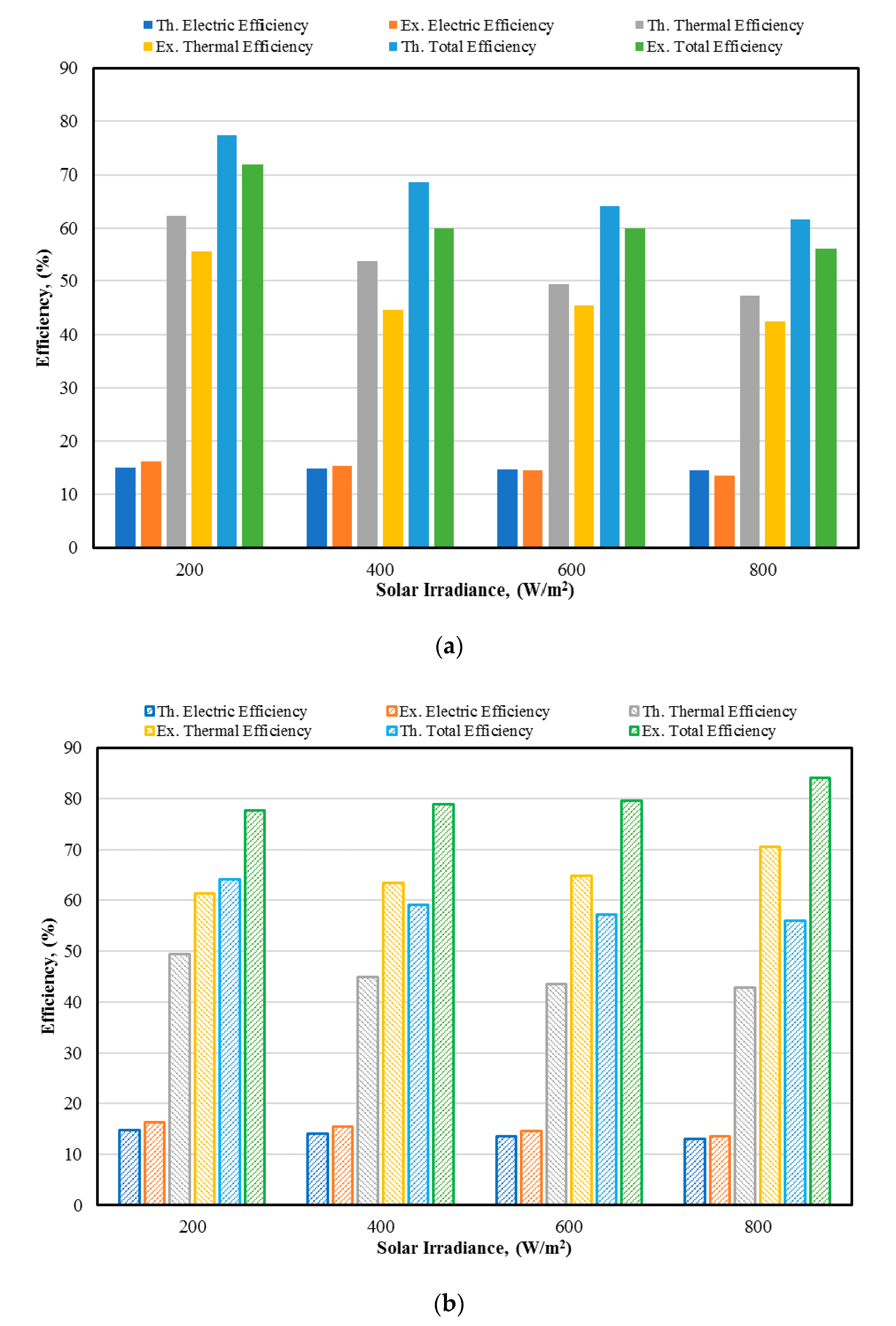
Figure 13 shows the theoretical and experimental validation of electrical and thermal power output for each configuration PV/T and CPV/T under a mass flow rate of cooling water 0.7 kg/min and different solar irradiance.
As illustrated in
Figure 13a, the electrical and thermal power outputs from the PV/T module were 60 W and 185 W, respectively, under solar irradiance 900 W/m
2. Whereas in
Figure 13b, the geometrical concentration ratio was 3, and the produced electrical and thermal power outputs from CPV/T system were 130 W and 525 W, respectively, under 900 W/m
2 solar irradiance. The small deviation in electrical power output may be from the coefficient, which was used in the theoretical model or from self-shading of the mirrors image concentrator, and this referred to reduced output power.
The CPV/T system usefulness is that it produced improvements in both electrical and thermal power output, which are suitable for domestic application as a heat pump.
As shown in
Figure 13, the total power output of the CPV/T module is, therefore, important to highlight in comparison to PV/T and how this differs in comparison to just a CPV or a flat PV only without cooling.
Here in
Figure 14, it can be seen that the CPV/T and PV/T were over 60%, in comparison to the solar photovoltaic modules which typically have almost efficiencies in the range of 15% and the thermal flat plate collectors which have efficiencies in the range of about 40%. Hence, as known, the concentrator offered a significant advantage in terms of utilizing an increase of the incoming solar irradiation and converting it to useful energy.
The presented theoretical model showed the ability to predict parameters of system performance such as solar radiation received, cell and absorber temperatures, outlet cooling water temperature, and module electrical and thermal output power in respect of system input data (wind velocity, environmental temperature, and geometric system). The system output model results were validated by experimental data calculated and estimated for both CPV/T and PV/T on the same input parameters, in order to verify the numerical model.
5. Conclusions
The proposed CPV/T device is generally simple and comfortable. The merit of solar concentrate structural materials is easy to obtain, and the initial costs are not as high in comparison to solar PV cells. In addition, it presents the possibility of using thermal energy produced in domestic applications. It solves the shading issues and blocks of the conventional CPV. In this work, a theoretical and experimental analysis of a CPV/T device was presented.
The theoretical module of the system analysis results found that the maximum electrical and thermal power outputs from PV/T module were 65 W and 170 W, respectively, with cooling water flow of 1 kg/min whereas, the maximum electrical and thermal power obtained from CPV/T system were 170 W and 580 W, respectively, at the solar concentration ratio 3 and cooling water flow rate of 1 kg/min. This amount of electrical and thermal energy was approximately three times the amount produced when using a standard module (PV/T module) without concentration and coolant water flow rate 0.1 kg/min, which was estimated at 61 W and 155 W, respectively. These results showed that increasing the solar concentration, which is a reflection of the increase of solar radiation, increased the electrical and thermal power of the solar cells, as well as the solar cells and the heat absorber temperatures, which negatively affected the electrical and thermal efficiency. Increasing the amount of cooling water through both configurations of CPV/T and PV/T improved the heat recovery from the PV module and thus increases the electrical and thermal efficiency.
The theoretical model was validated by the experimental test, and the results showed a good agreement between them. The experimental results of the electrical and thermal power outputs from PV/T module were 60 W and 185 W, respectively, whereas for CPV/T system under geometrical concentration ratio of 3 are 130 W and 525 W, respectively, at cooling water flow rate of 0.7 kg/min and 900 W/m2 solar irradiance. The total power of the PV/T module was 245 W, and the CPV/T system was 655 W, with power increasing 167%.
The performance and features of the proposed CPV/T system are disclosed by all simulation and analysis results presented in this paper. This can be used as guidance and reference in the further practical applications for the design or production of the proposed CPV/T system. A large-scale testing rig is being developed for further study of the proposed CPV/T device, and research into an LFRM concentrator-driven PV and thermal hybrid system is underway.