Highly Efficient and Robust Grid Connected Photovoltaic System Based Model Predictive Control with Kalman Filtering Capability
Abstract
1. Introduction
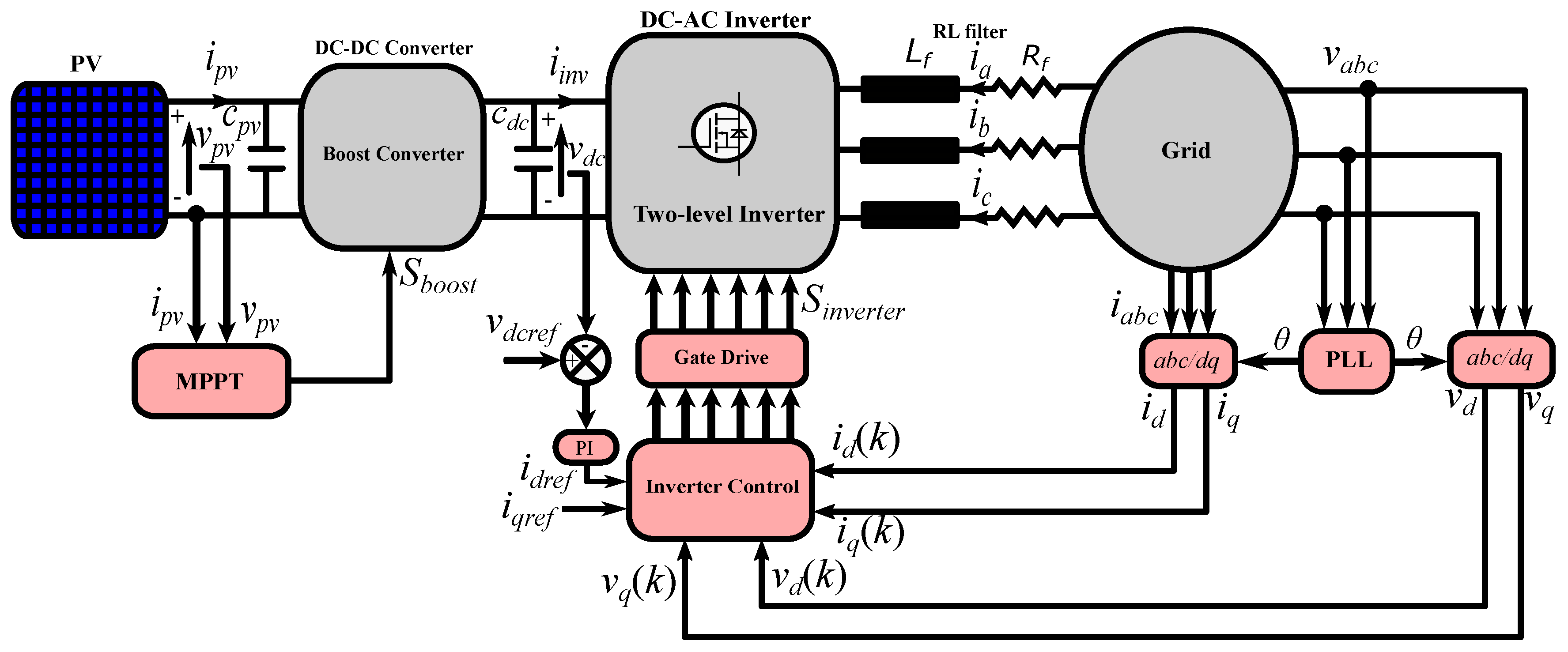
2. PV System Modeling and MPPT
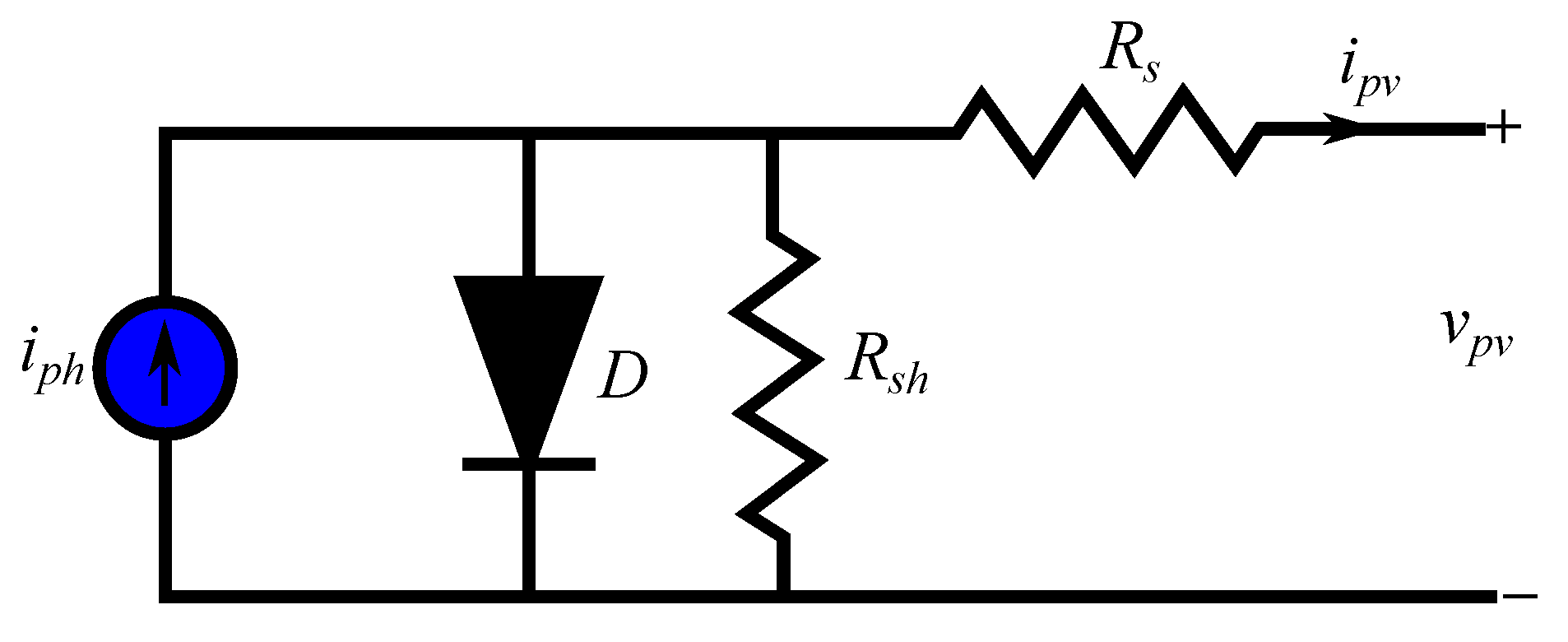
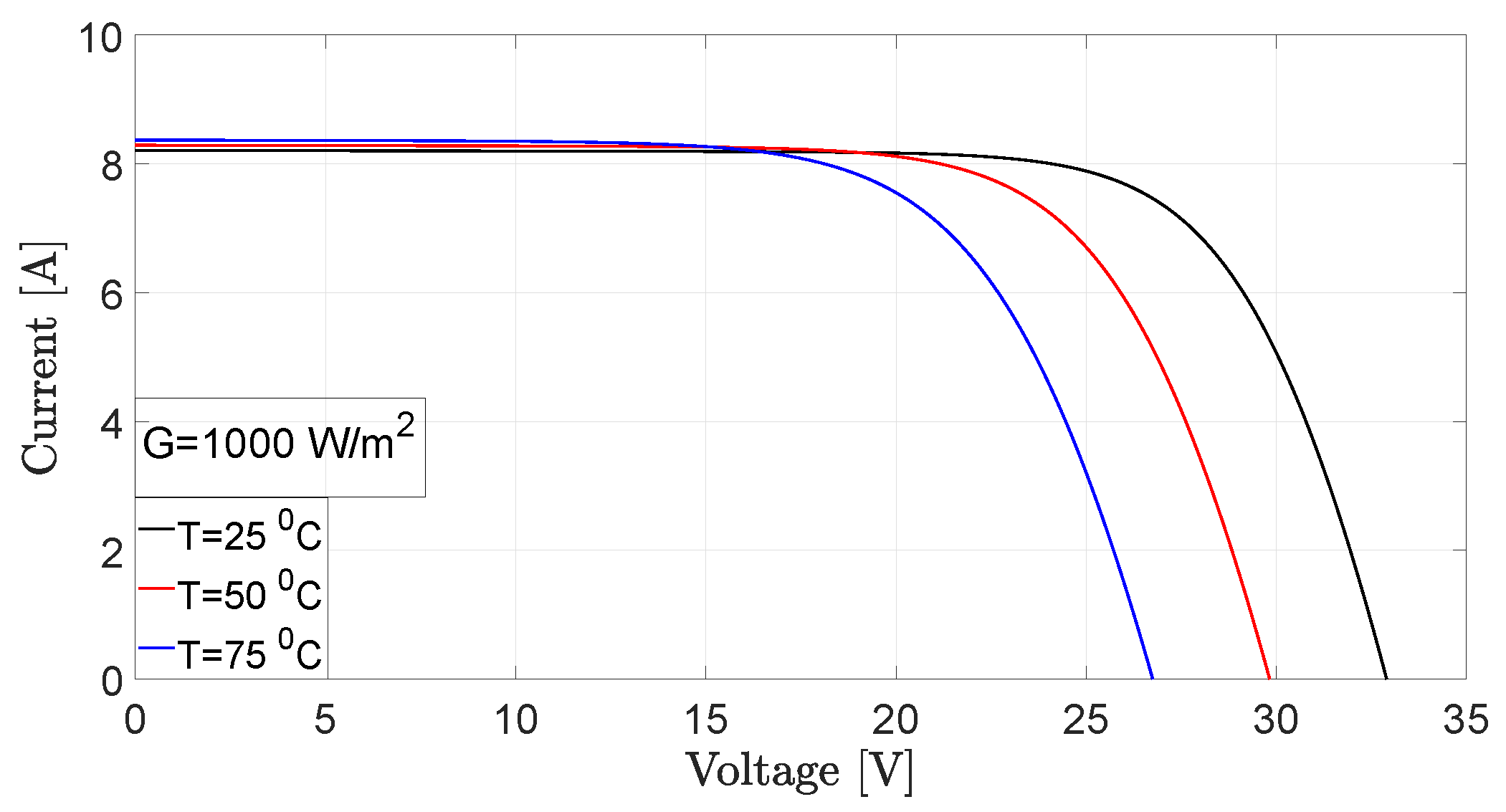
2.1. PV Array Modeling
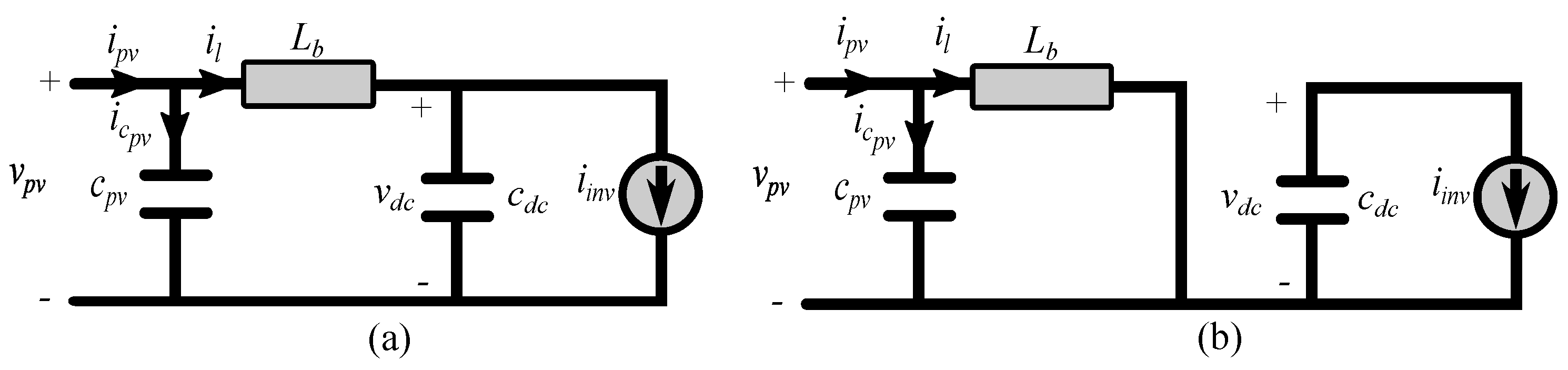
2.2. Boost Converter Model
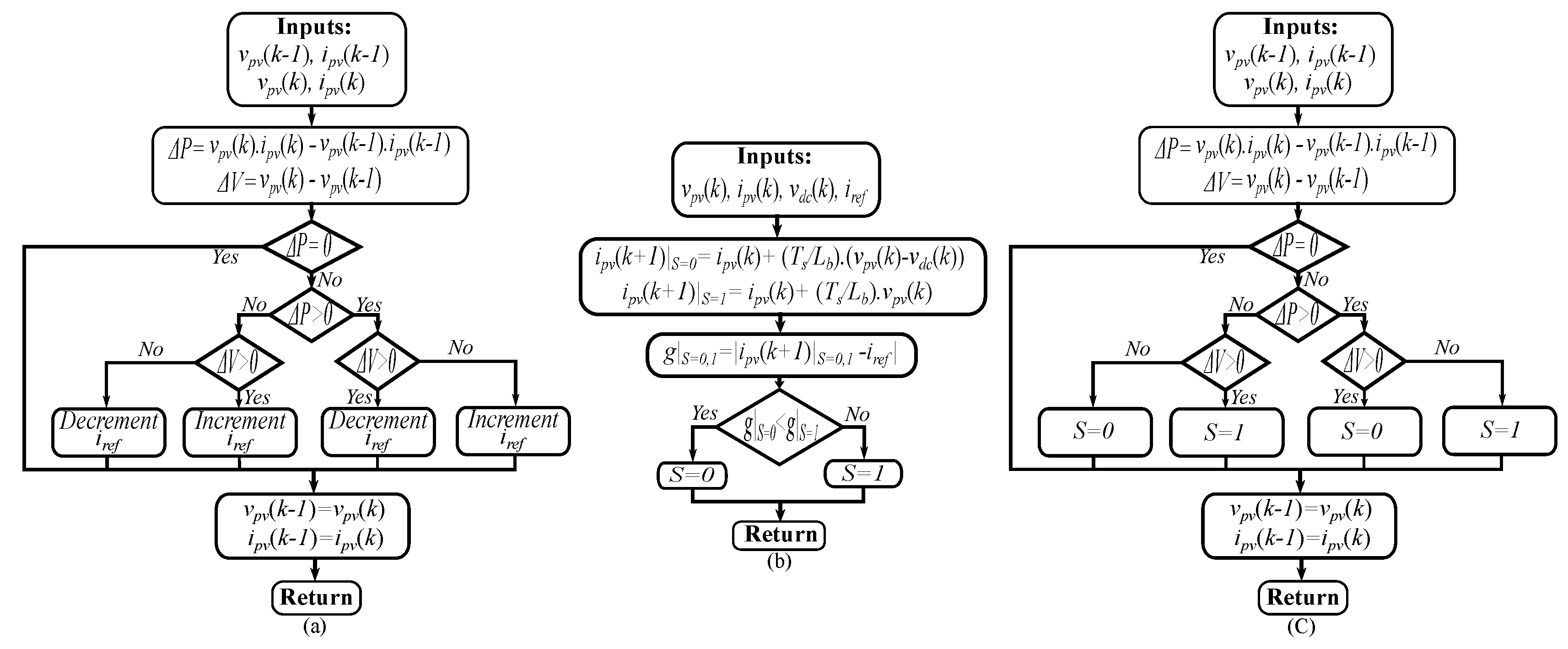
2.3. MPPT Using FCS-MPC
2.4. MPPT Using Direct Switching Technique
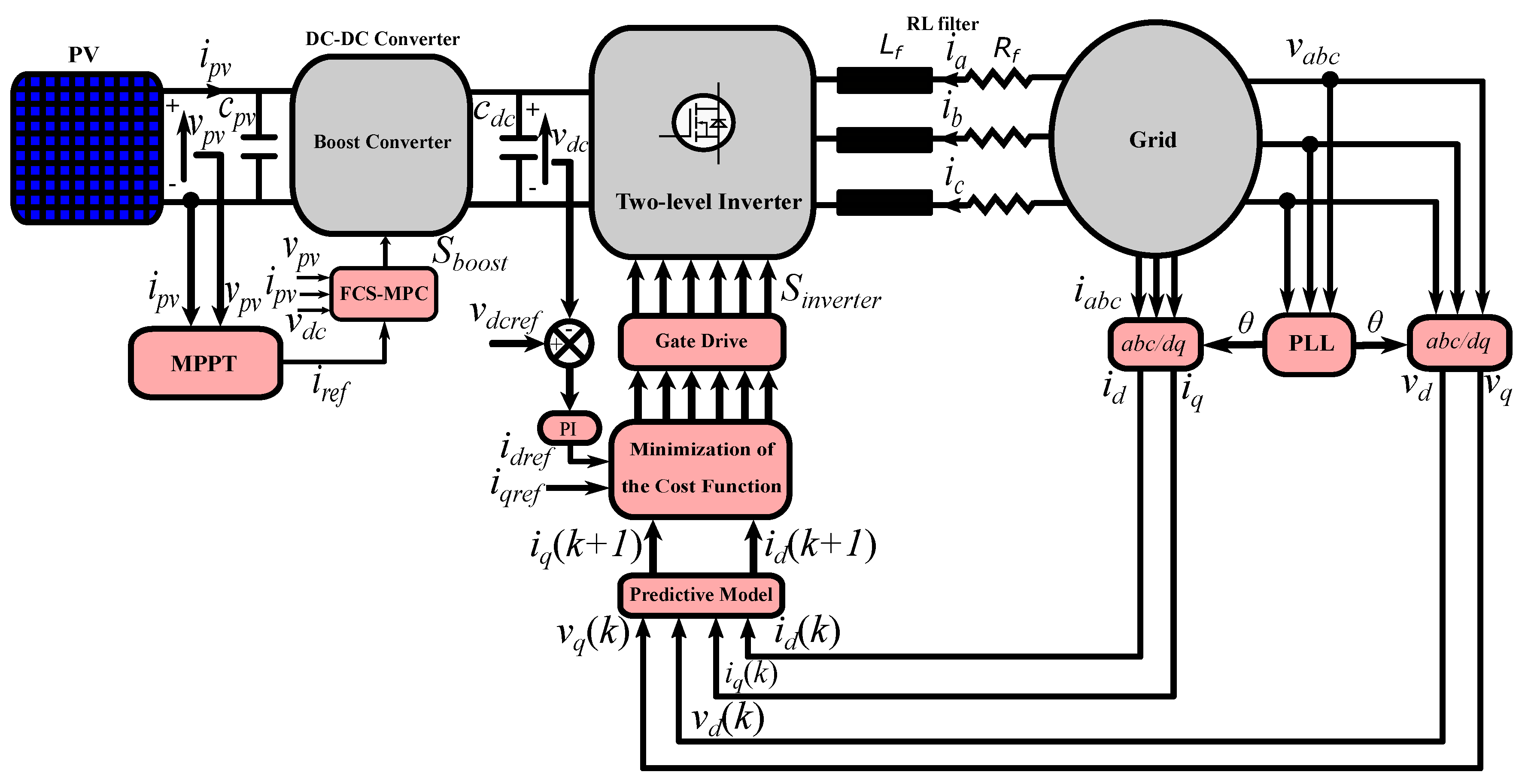
3. Control of the Two-Level Inverter Using FCS-MPC
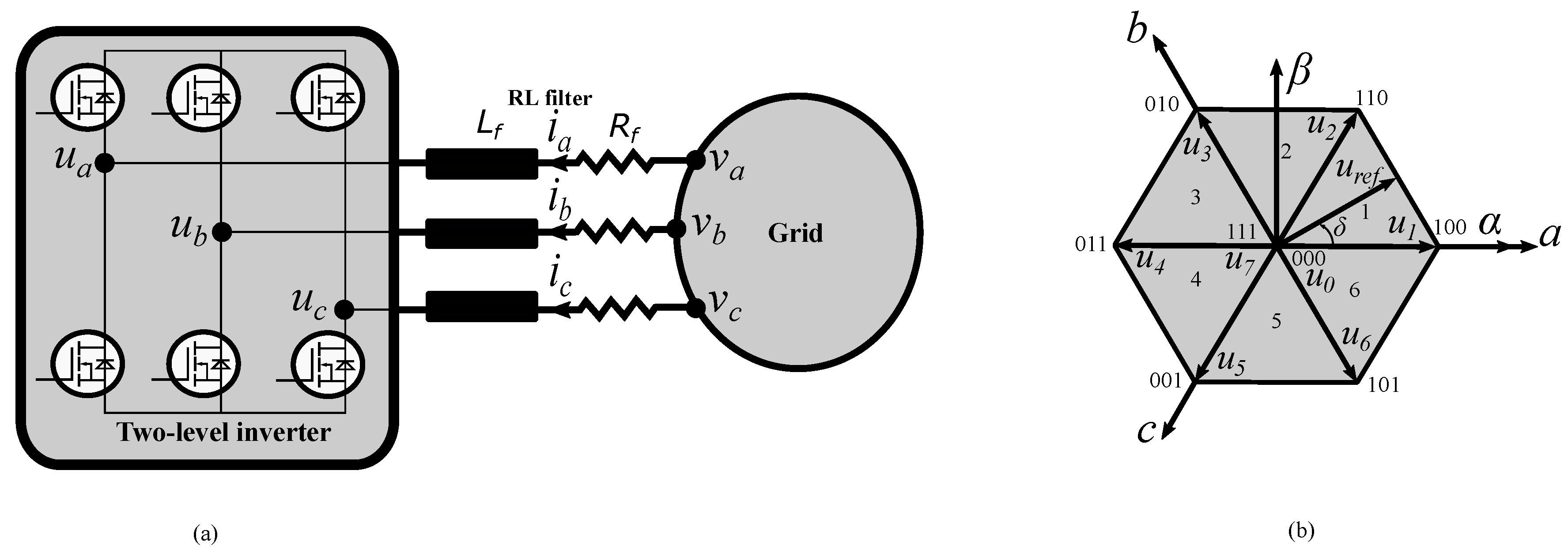
3.1. Two-Level Inverter Model with Grid Connection
3.2. Conventional FCS-MPC
3.3. Proposed FCS-MPC
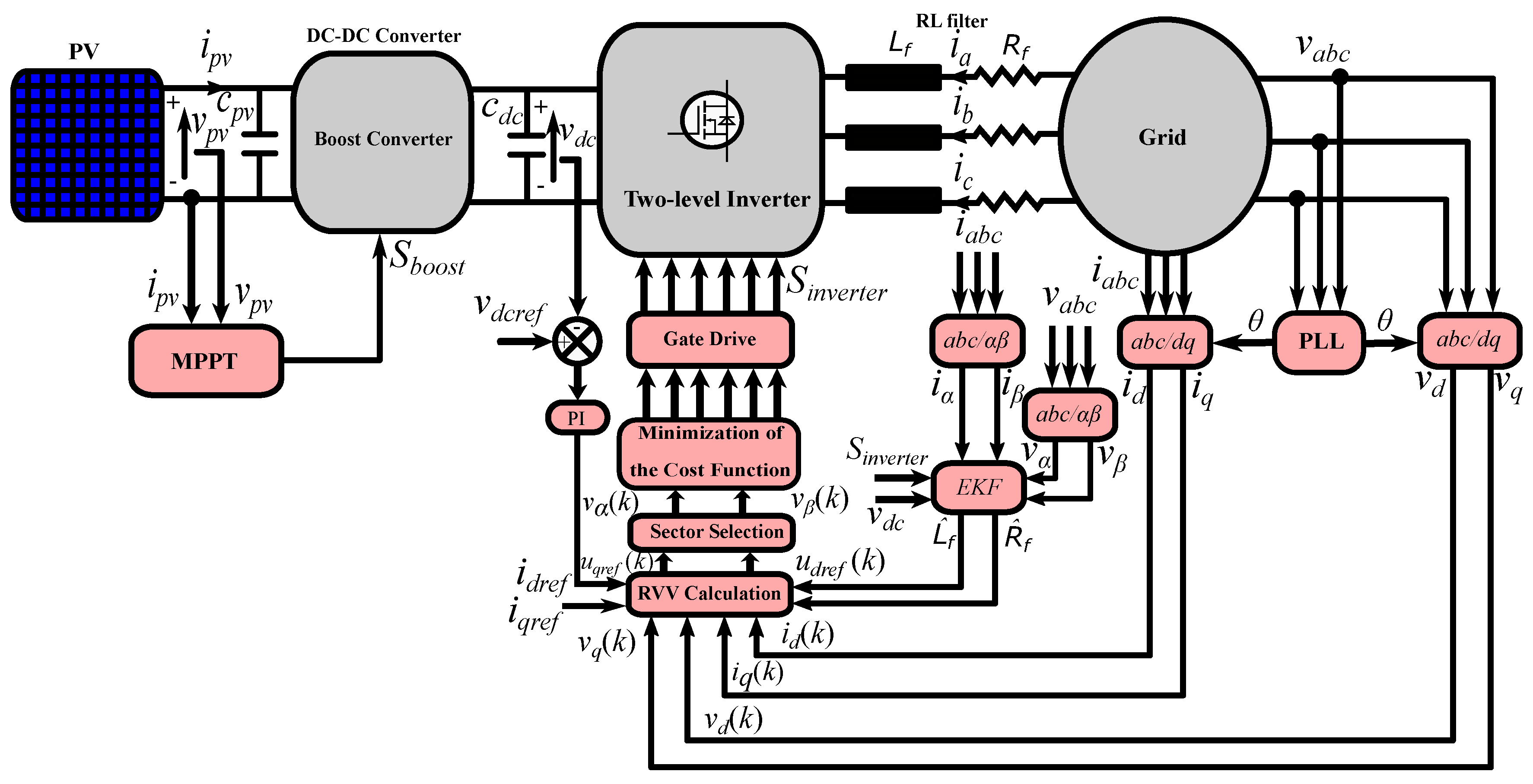
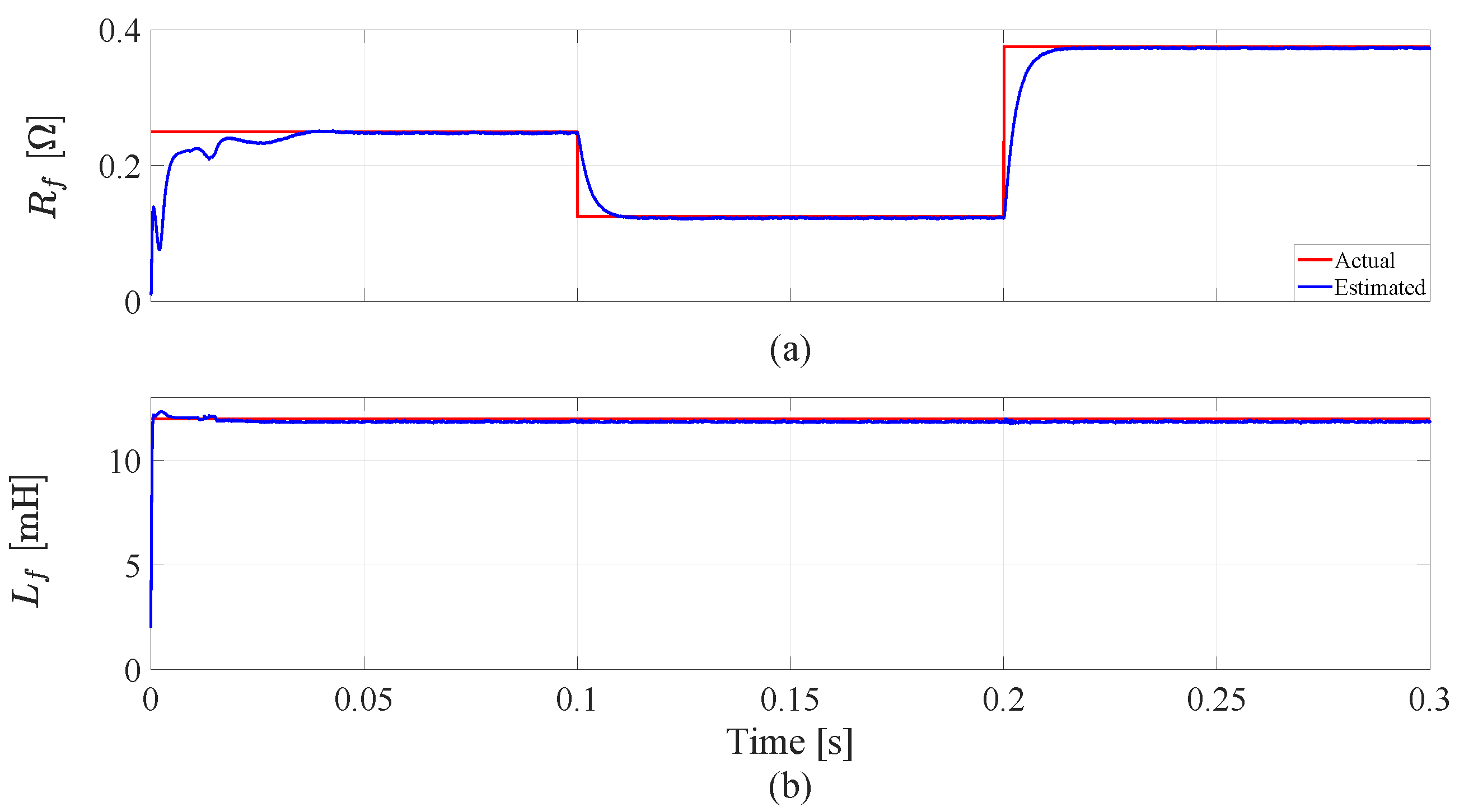
4. Design of the Proposed Extended Kalman Filter
- Initialize the state vector and covariance matrices.
- Prediction of state vector
- Error covariance matrix predictionwhereKalman gain calculation
- Estimation update through measurements
- Error covariance matrix update
- Go back to step 2.
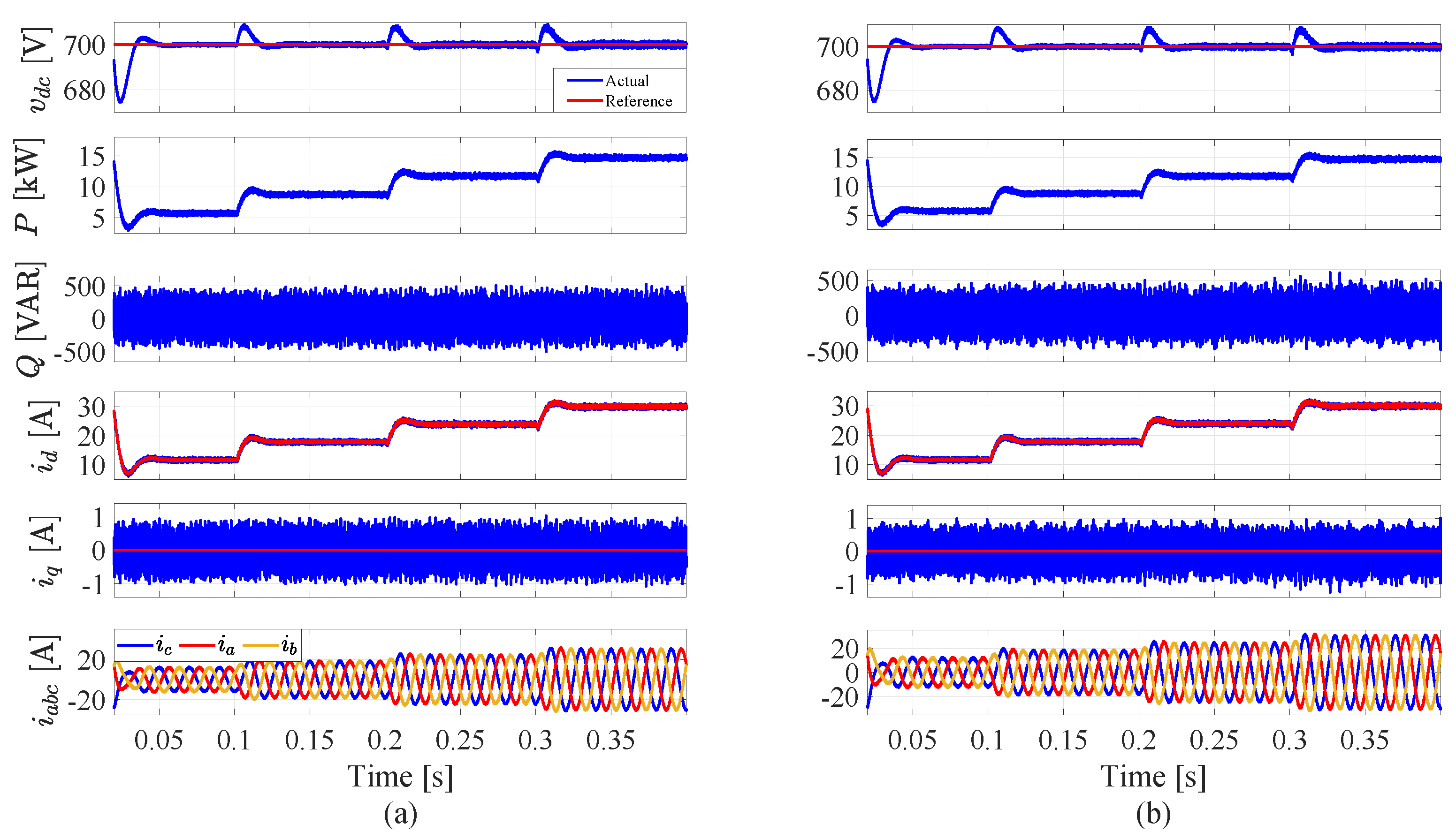
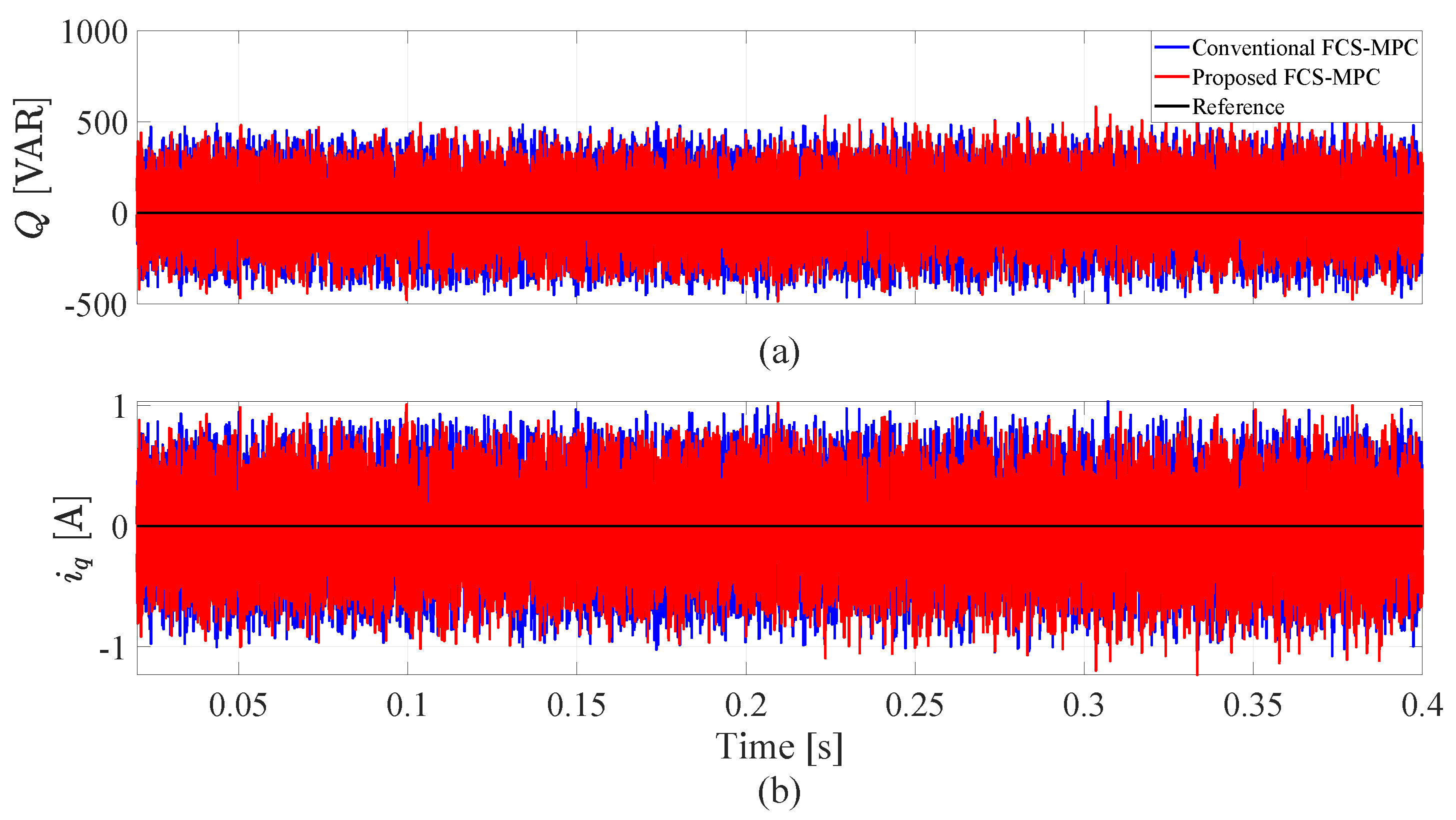
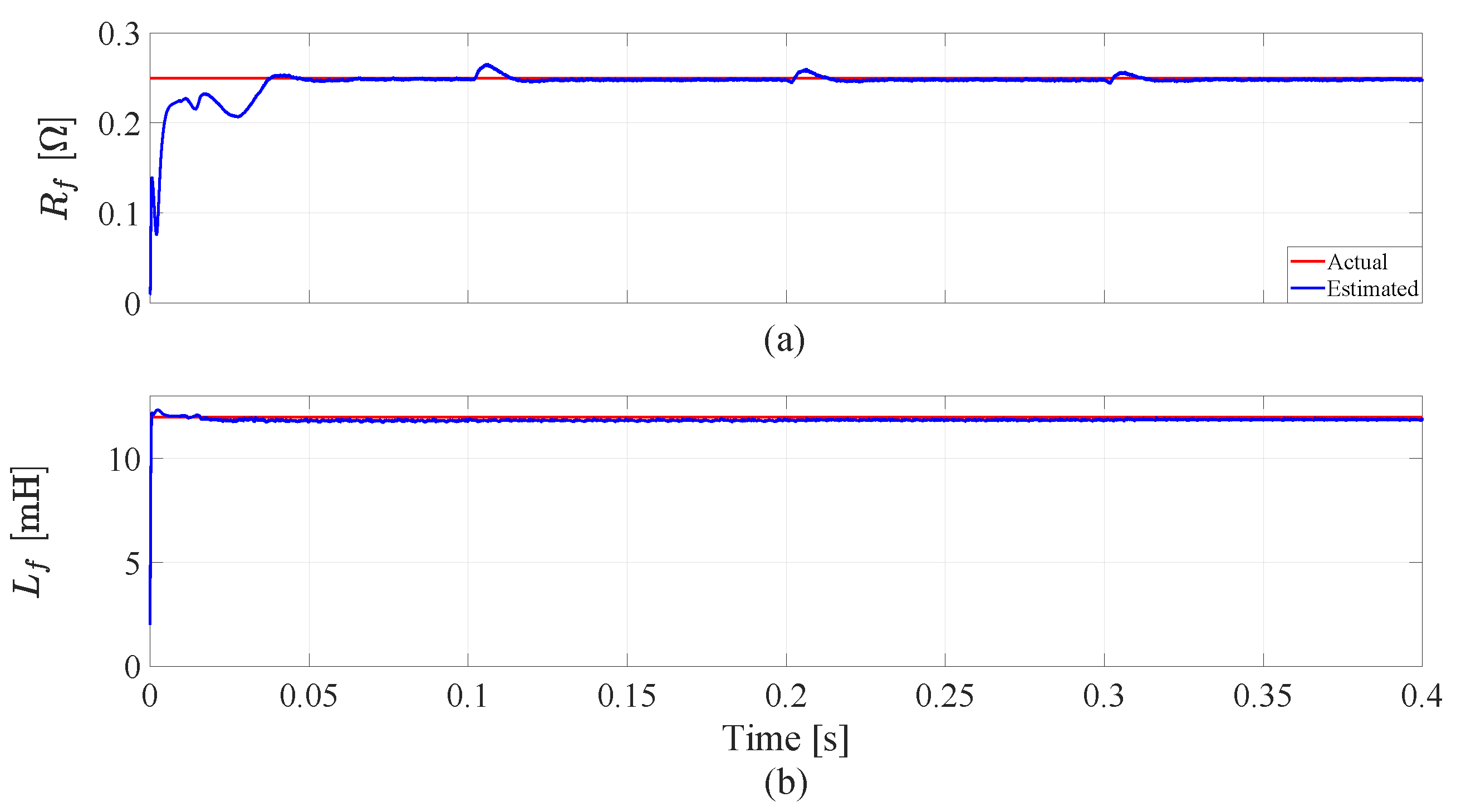
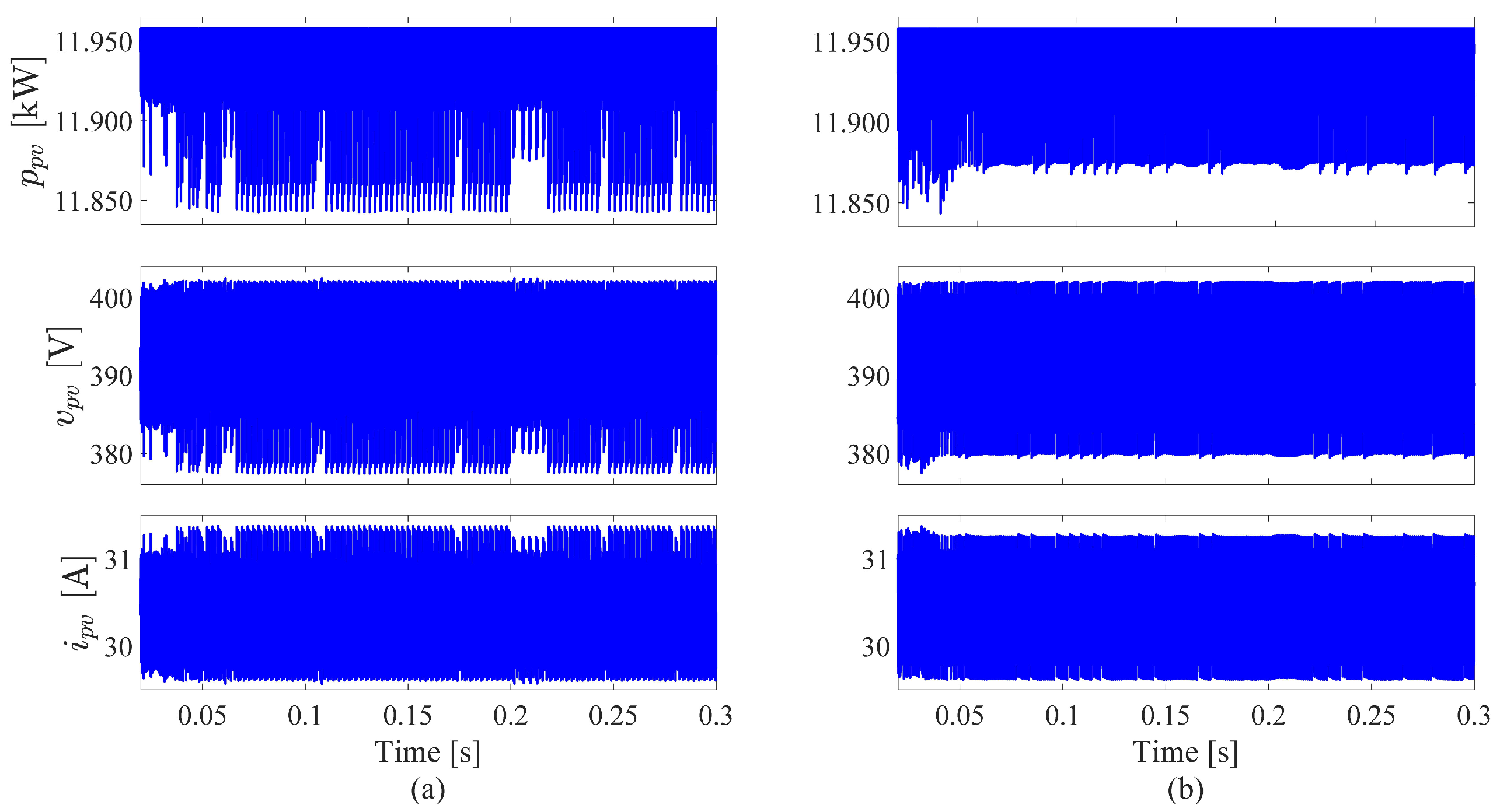
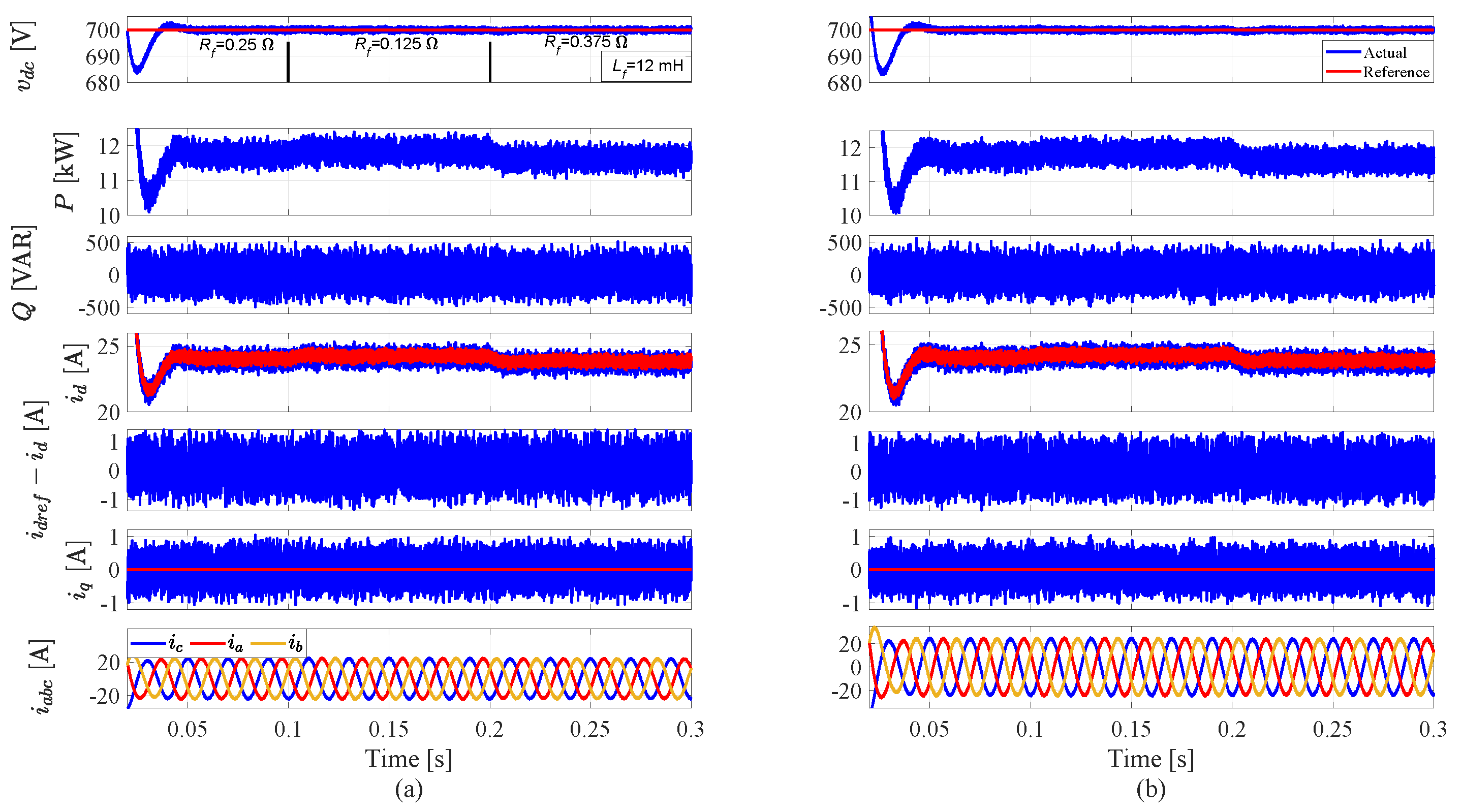
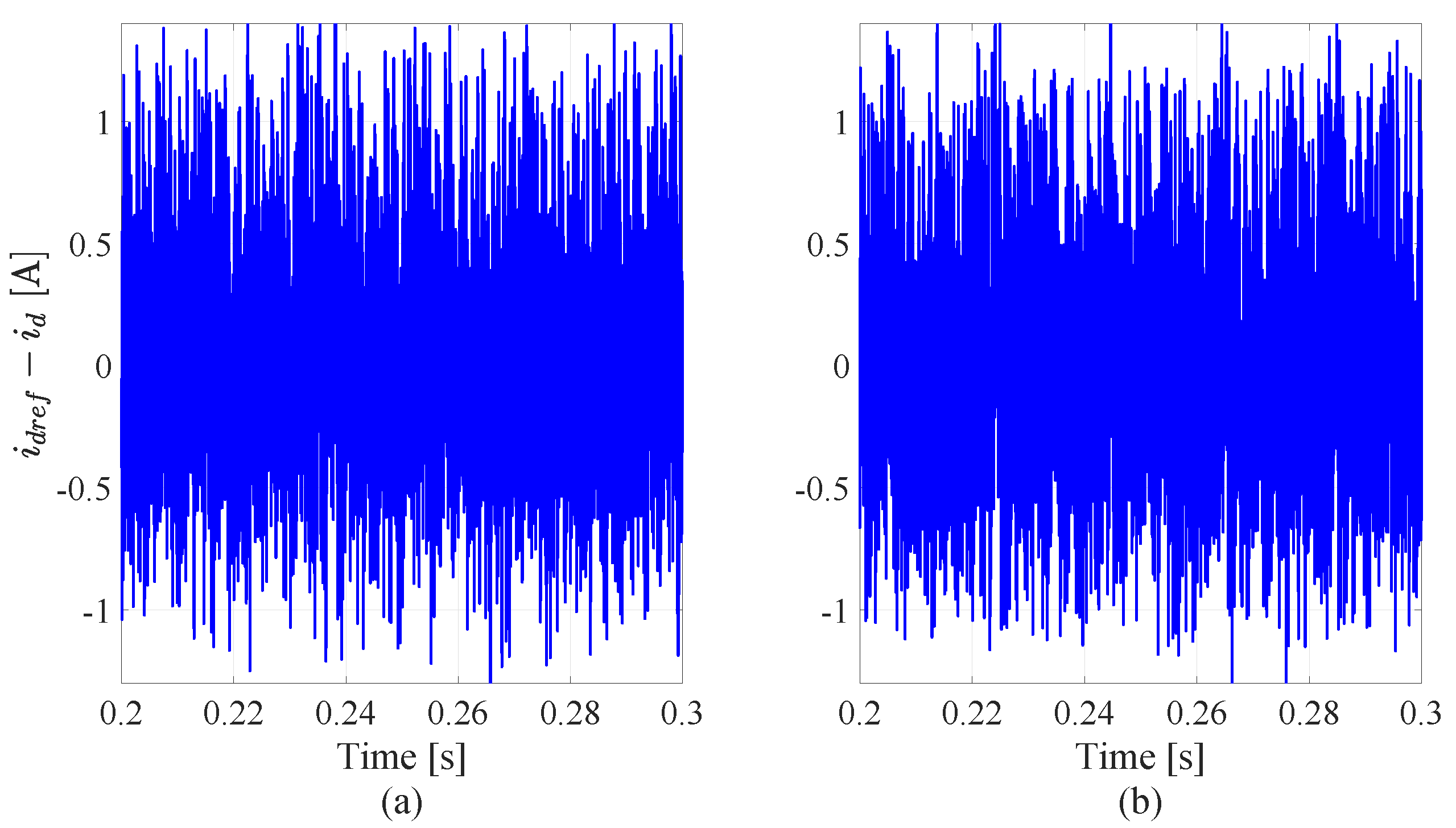
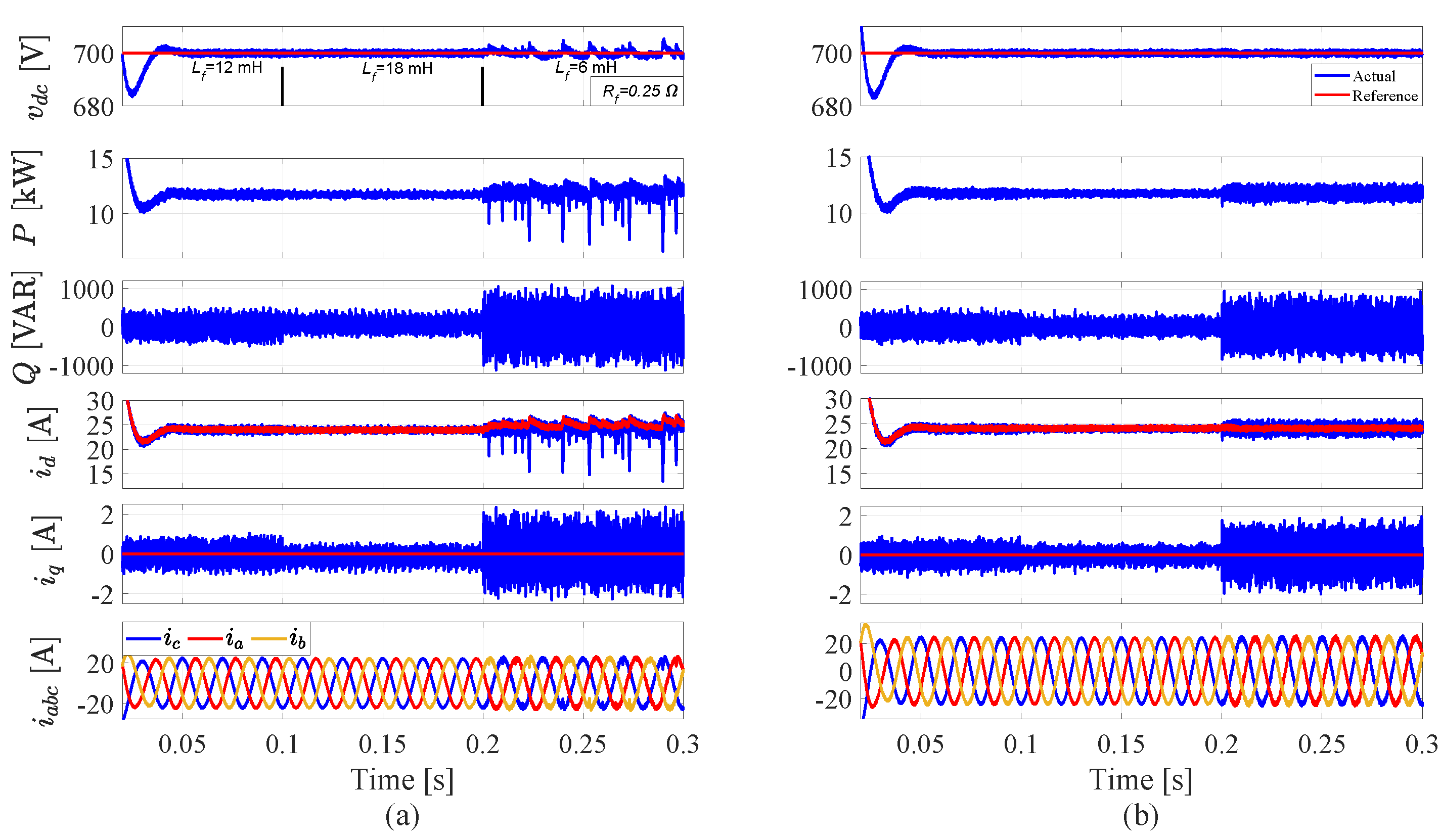
5. Simulation Results and Discussion
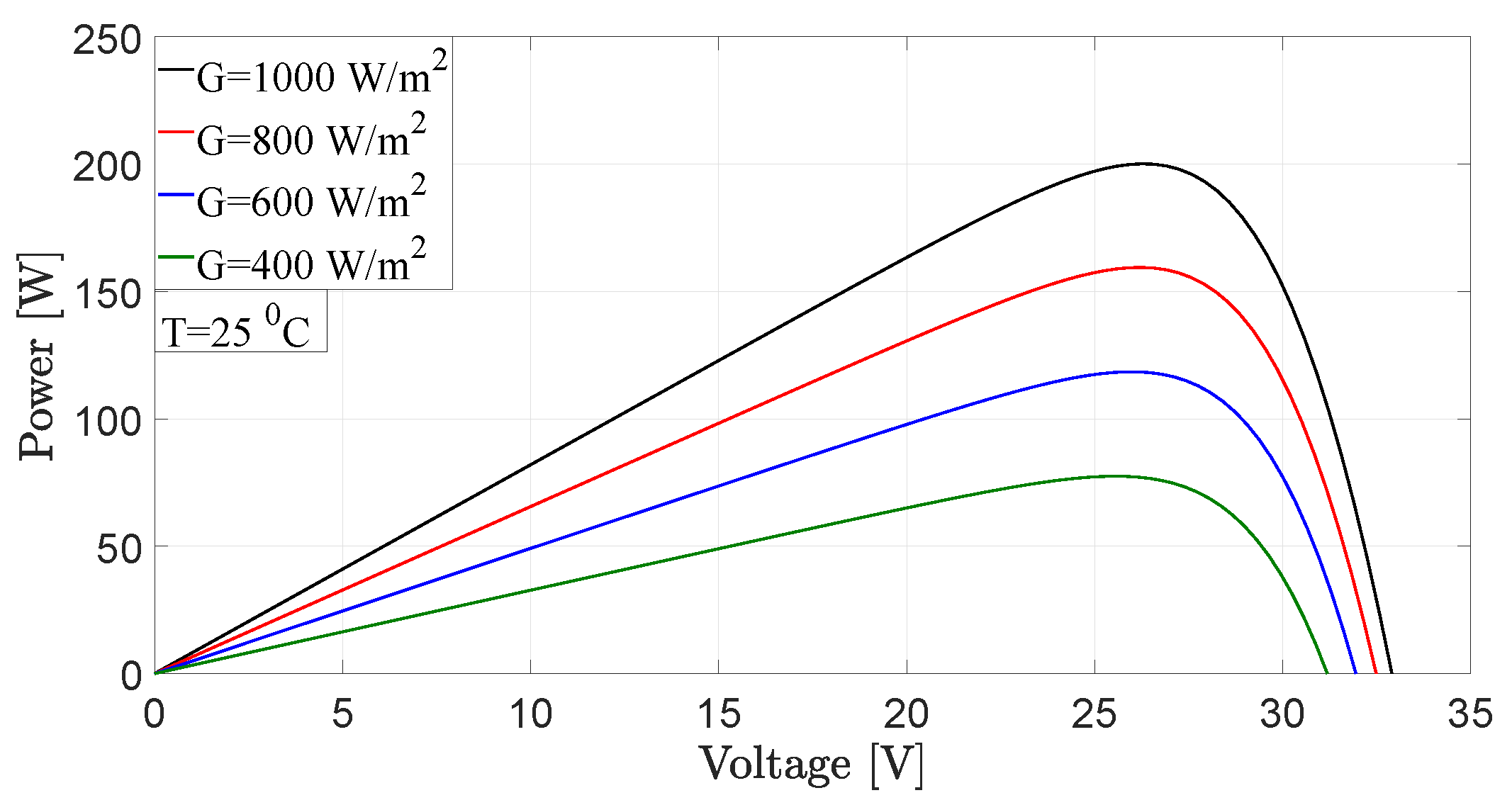
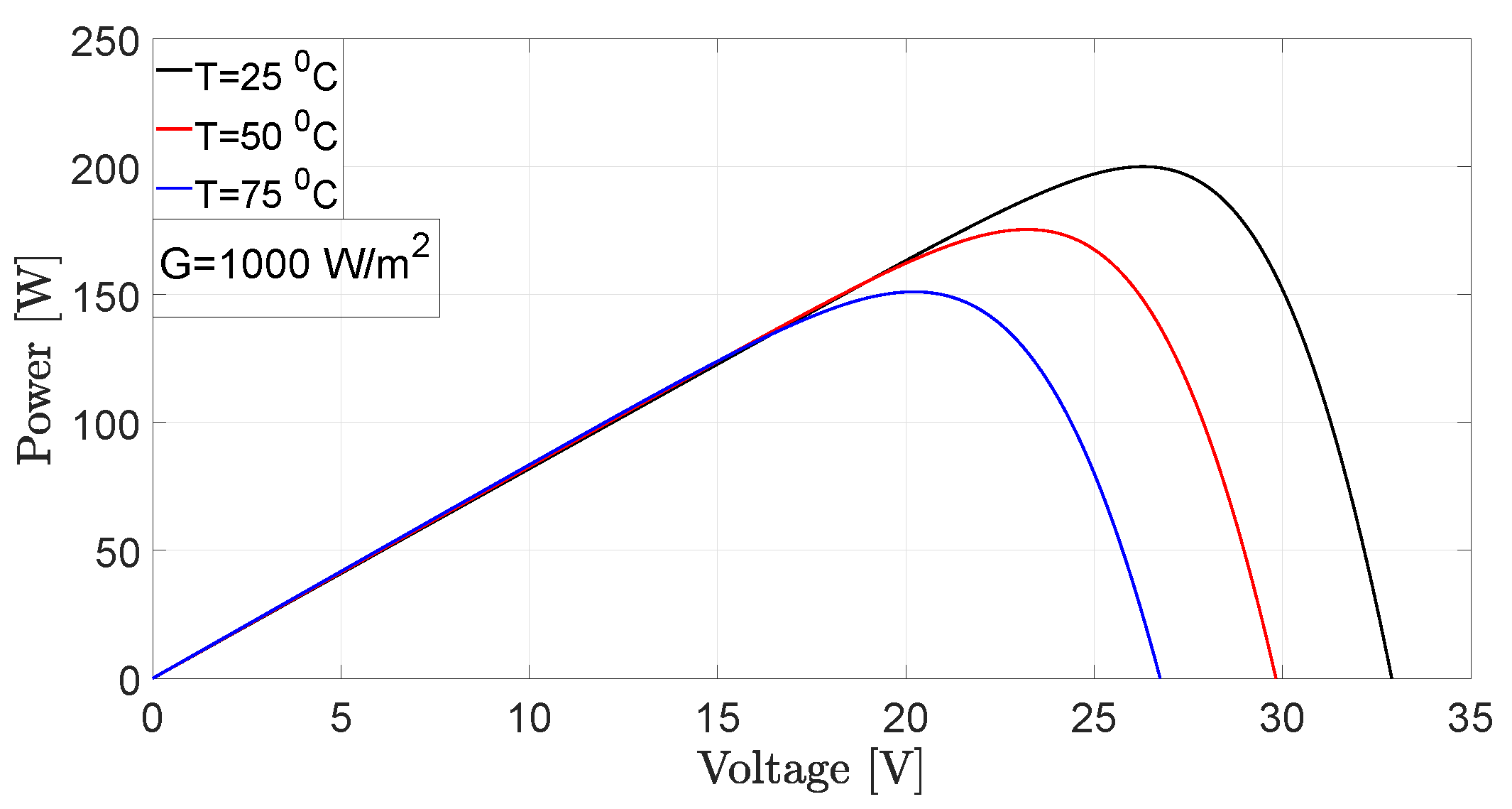
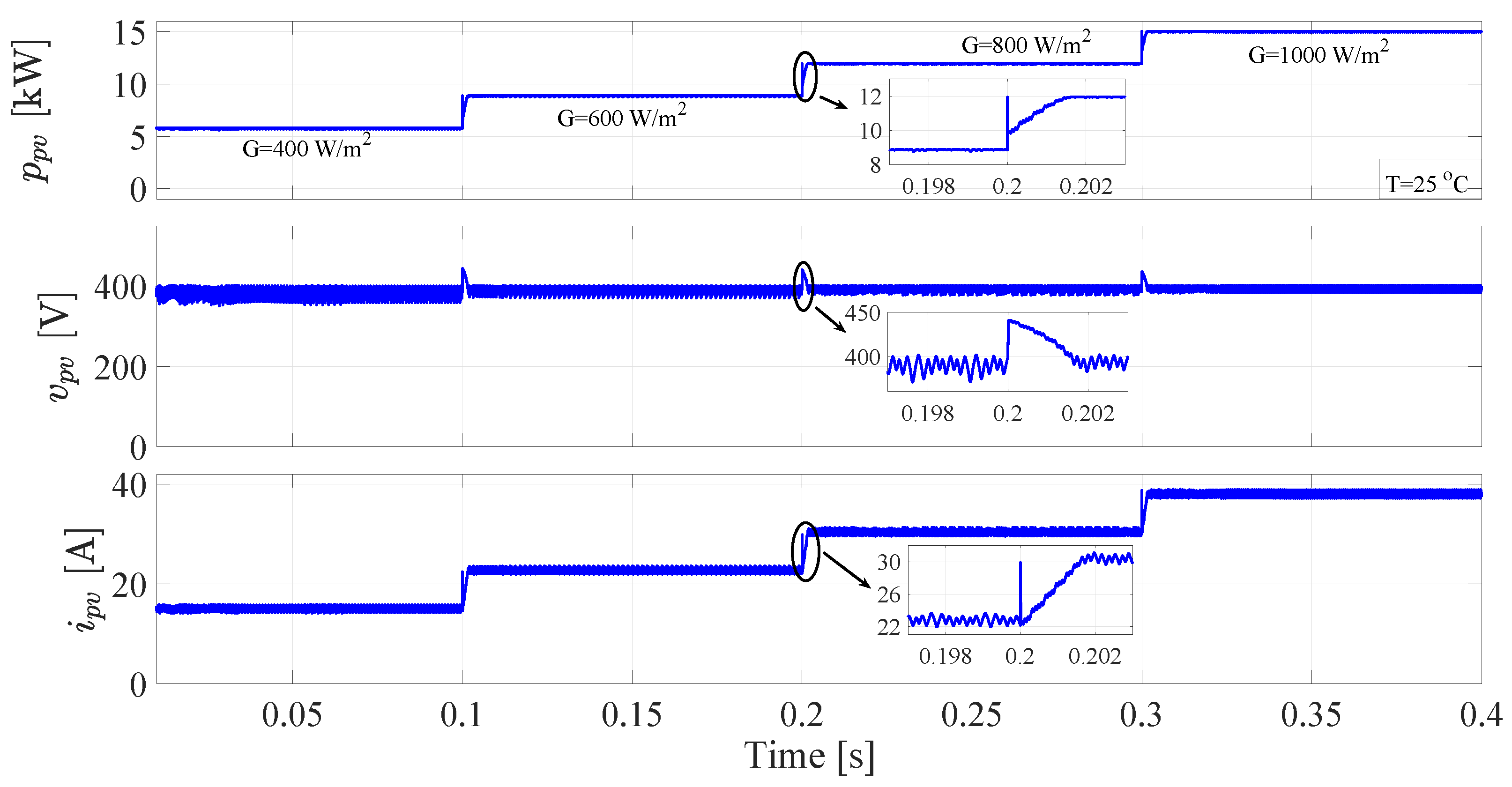
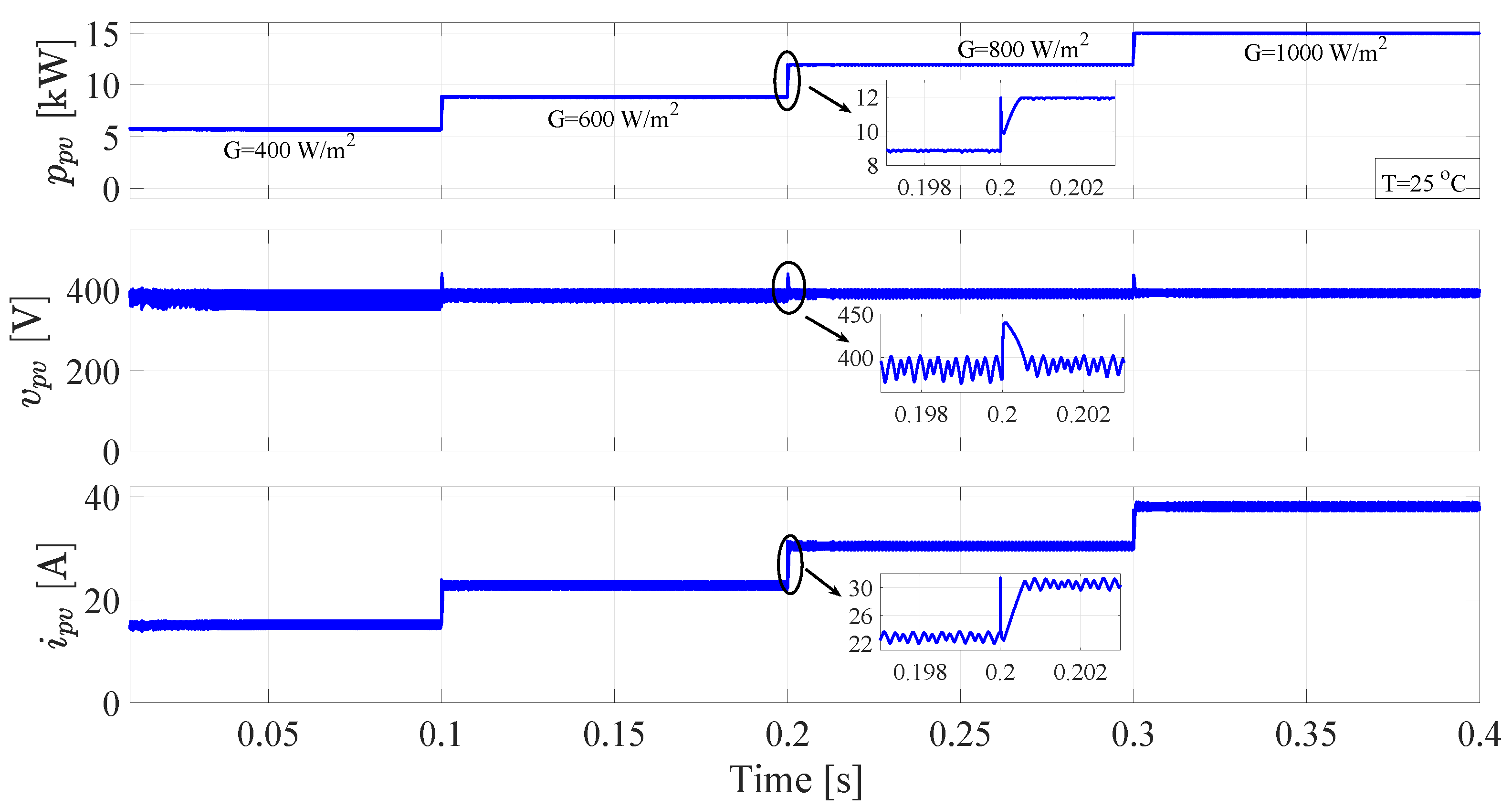
5.1. MPPT and System Behavior under Different Radiation Conditions
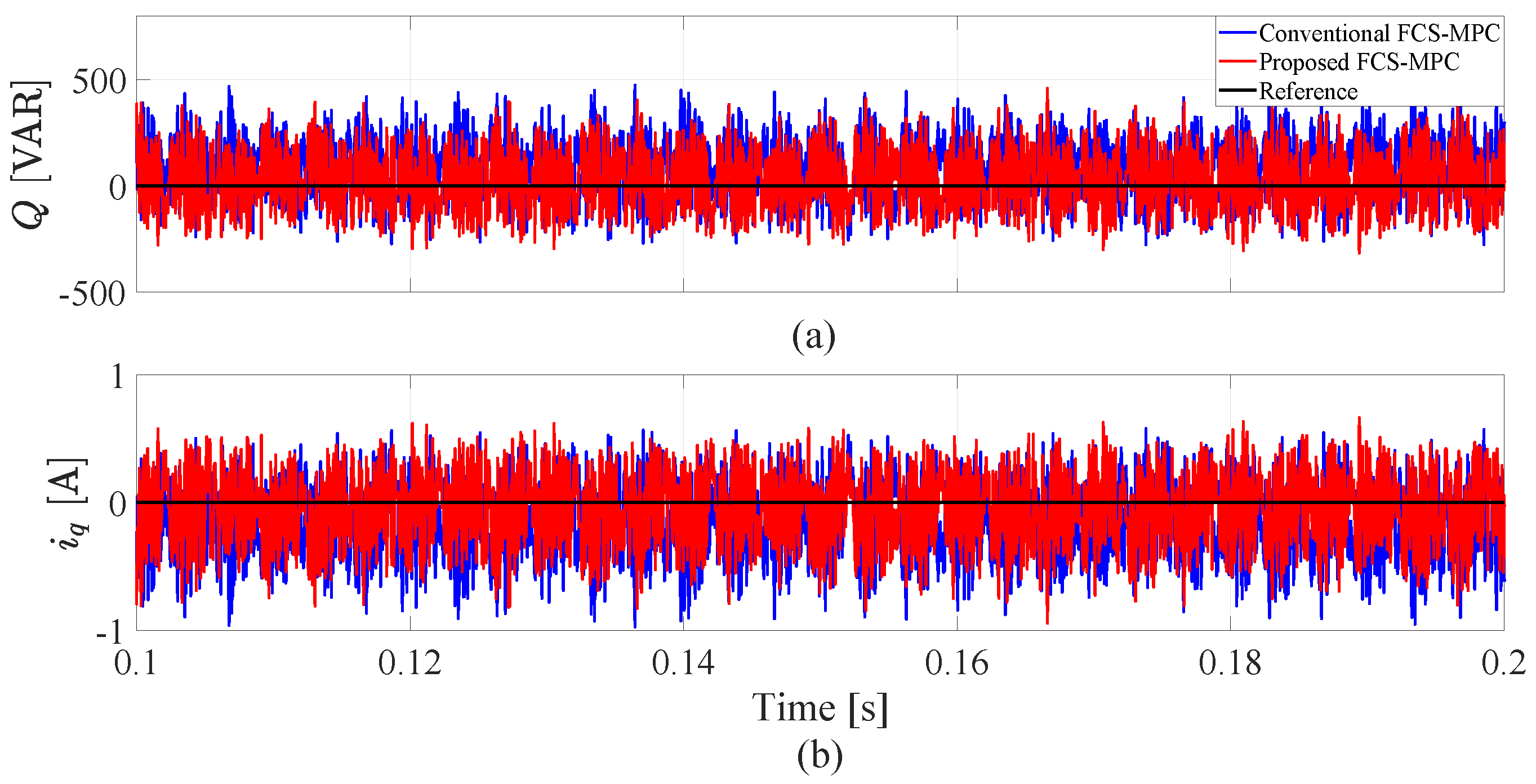
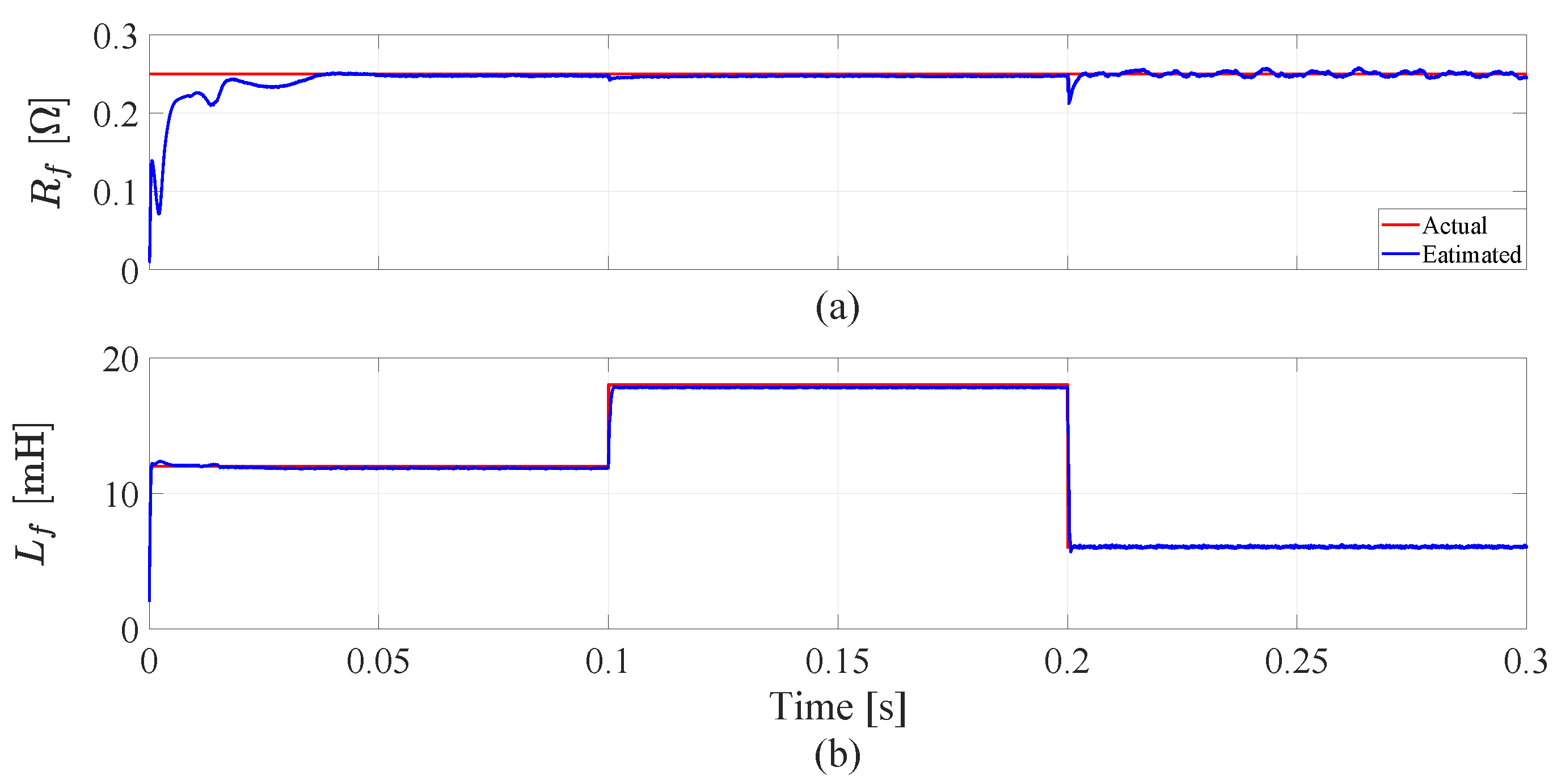
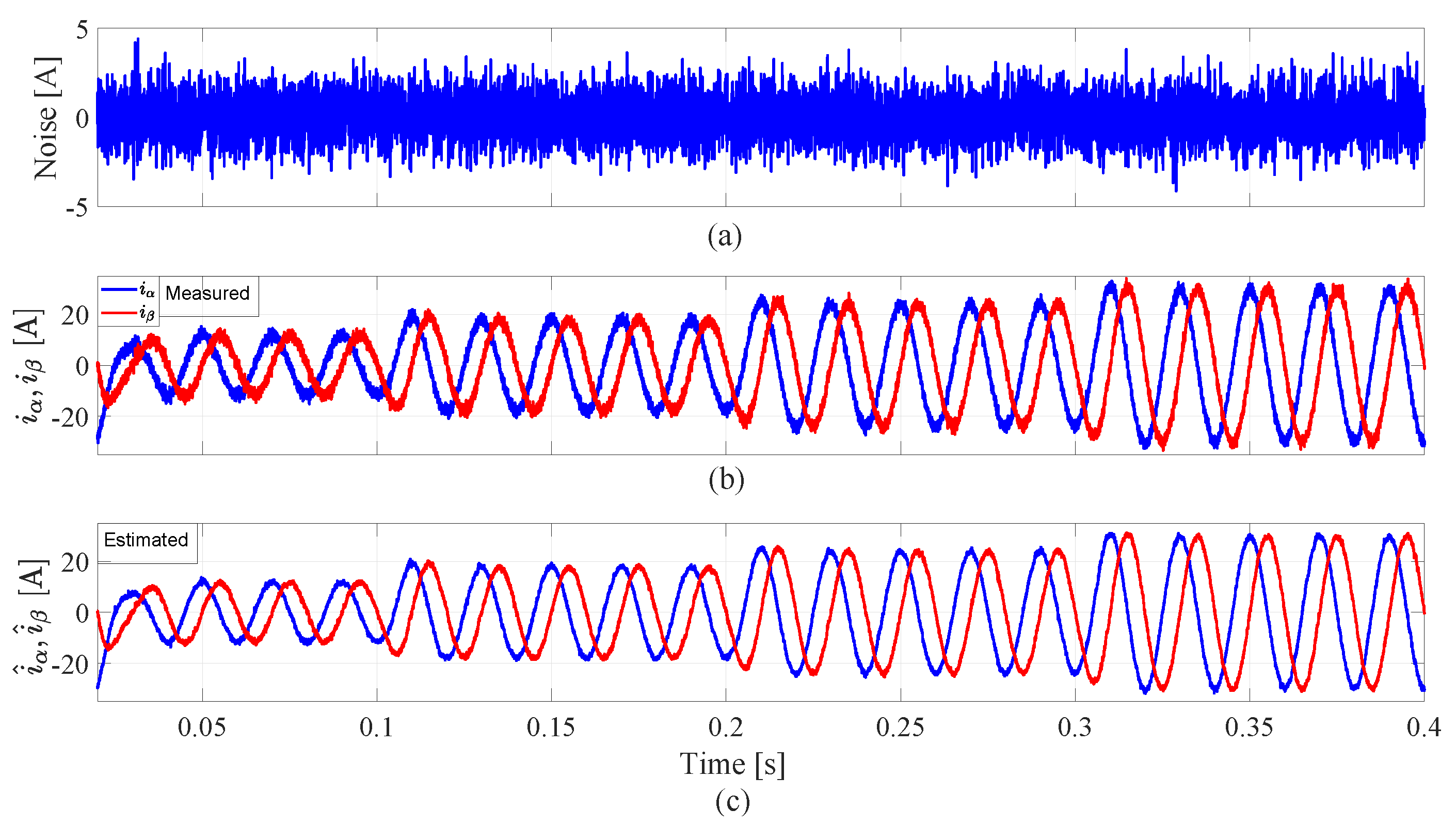
5.2. System Performance with Parameter Variations
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Lee, B.; Liu, J.Z.; Sun, B.; Shen, C.Y.; Dai, G.C. Thermally conductive and electrically insulating EVA composite encapsulants for solar photovoltaic (PV) cell. eXPRESS Polym. Lett. 2008, 2, 357–363. [Google Scholar] [CrossRef]
- Khalil, A.; Rajab, Z.; Asheib, A. Modeling Simulation Analysis and Control of Stand-alone PV System. In Proceedings of the 7th International Renewable Energy Congress IREC 2016, Hammamet, Tunisia, 22–24 March 2016; pp. 1–6. [Google Scholar]
- Mohamed, A.; de Cossio, C.F.; Ma, T.; Farhadi, M.; Mohammed, O. Operation and protection of photovoltaic systems in hybrid AC/DC smart grids. In Proceedings of the IECON 2012—38th Annual Conference on IEEE Industrial Electronics Society, Montreal, QC, Canada, 25–28 October 2012; pp. 1104–1109. [Google Scholar]
- Lekhchine, S.; Bahi, T.; Abadlia, I.; Bouzeria, H. PV-battery energy storage system operating of asynchronous motor driven by using fuzzy sliding mode control. Int. J. Hydrogen Energy 2017, 42, 8756–8764. [Google Scholar] [CrossRef]
- Elgendy, M.A.; Zahawi, B.; Atkinson, D.J. Comparison of directly connected and constant voltage controlled photovoltaic pumping systems. IEEE Trans. Sustain. Energy 2010, 1, 184–192. [Google Scholar] [CrossRef]
- Li, C.-H.; Zhu, X.J.; Cao, G.-Y.; Sui, S.; Hu, M.-R. Dynamic modeling and sizing optimization of stand-alone photovoltaic power systems using hybrid energy storage technology. Renew. Energy 2009, 34, 815–826. [Google Scholar] [CrossRef]
- Vordos, N.; Bandekas, D.; Nolan, J.; Fantidis, J.; Ioannou, A. Design and simulation of hybrid power system with wind turbines, photovoltaics and fuel cells. In Recent Advances in Energy, Environment and Development; WSEAS Press: Rhodes Island, Greece, 16–19 July 2013; pp. 19–24. [Google Scholar]
- Alajmi, B.N.; Ahmed, K.H.; Adam, G.P.; Williams, B.W. Single-phase single-stage transformer less grid-connected PV system. IEEE Trans. Power Electron. 2012, 28, 2664–2676. [Google Scholar] [CrossRef]
- Shayestegan, M. Overview of grid-connected two-stage transformer-less inverter design. J. Mod. Power Syst. Clean Energy 2018, 6, 642–655. [Google Scholar] [CrossRef]
- Das, P.P.; Chattopadhyay, S. A voltage-independent islanding detection method and low-voltage ride through of a two-stage PV inverter. IEEE Trans. Ind. Appl. 2018, 54, 2773–2783. [Google Scholar] [CrossRef]
- Jahanbakhshi, M.-H.; Asaei, B.; Farhangi, B. A novel deadbeat controller for single phase PV grid connected inverters. In Proceedings of the 2015 23rd Iranian Conference on Electrical Engineering, Tehran, Iran, 10–14 May 2015; pp. 1613–1617. [Google Scholar]
- Lakshmi, M.; Hemamalini, S. Coordinated control of MPPT and voltage regulation using single-stage high gain DC DC converter in a grid-connected PV system. Electr. Power Syst. Res. 2019, 69, 65–73. [Google Scholar] [CrossRef]
- Ahmed, M.E.; Orabi, M.; AbdelRahim, O.M. Two-stage micro-grid inverter with high-voltage gain for photovoltaic applications. IET Power Electron. 2013, 6, 1812–1821. [Google Scholar] [CrossRef]
- Sangwongwanich, A.; Yang, Y.; Blaabjerg, F. High-performance constant power generation in grid-connected PV systems. IEEE Trans. Power Electron. 2015, 31, 1822–1825. [Google Scholar] [CrossRef]
- Yau, H.-T.; Wu, C.-H. Comparison of extremum-seeking control techniques for maximum power point tracking in photovoltaic systems. Energies 2011, 4, 2180–2195. [Google Scholar] [CrossRef]
- Yang, B.; Li, W.; Zhao, Y.; He, X. Design and analysis of a grid-connected photovoltaic power system. IEEE Trans. Power Electron. 2010, 25, 992–1000. [Google Scholar] [CrossRef]
- Zhang, G.; Iu, H.H.-C.; Zhang, B.; Li, Z.; Fernando, T.; Chen, S.-Z.; Zhang, Y. An impedance network boost converter with a high-voltage gain. IEEE Trans. Power Electron. 2017, 32, 6661–6665. [Google Scholar] [CrossRef]
- Esram, T.; Chapman, P.L. Comparison of photovoltaic array maximum power point tracking techniques. IEEE Trans. Energy Convers. 2007, 22, 439–449. [Google Scholar] [CrossRef]
- Go, S.; Ahn, D.-J.; Choi, J.-H.; Jung, W.-W.; Yun, S.-Y.; Song, I.-K. Simulation and analysis of existing MPPT control methods in a PV generation system. J. Int. Council Electr. Eng. 2011, 1, 446–451. [Google Scholar] [CrossRef]
- Messalti, S.; Harrag, A.; Loukriz, A. A new variable step size neural networks MPPT controller: Review, simulation and hardware implementation. Renew. Sustain. Energy Rev. 2017, 68, 221–233. [Google Scholar] [CrossRef]
- Zainudin, H.N.; Mekhilef, S. Comparison study of maximum power point tracker techniques for PV systems. In Proceedings of the 14th International Middle East Power Systems Conference (MEPCON 10), Cairo University, Cairo, Egypt, 19–21 December 2010. [Google Scholar]
- Lahfaoui, B.; Zouggar, S.; Elhafyani, M.L.; Seddik, M. Experimental study of P&O MPPT control for wind PMSG turbine. In Proceedings of the 2015 3rd International Renewable and Sustainable Energy Conference (IRSEC), Marrakech, Morocco, 10–13 December 2015; pp. 1–6. [Google Scholar]
- Ezinwanne, O.; Fu, Z.; Li, Z. Energy performance and cost comparison of MPPT techniques for photovoltaics and other applications. Energy Procedia 2017, 107, 297–303. [Google Scholar] [CrossRef]
- Femia, N.; Granozio, D.; Petrone, G.; Spagnuolo, G.; Vitelli, M. Predictive & adaptive MPPT perturb and observe method. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 934–950. [Google Scholar]
- Sera, D.; Mathe, L.; Kerekes, T.; Spataru, S.V.; Teodorescu, R. On the perturb-and-observe and incremental conductance MPPT methods for PV systems. IEEE J. Photovolt. 2013, 3, 1070–1078. [Google Scholar] [CrossRef]
- Kihal, A.; Krim, F.; Talbi, B.; Laib, A.; Sahli, A. A robust control of two-stage grid-tied PV systems employing integral sliding mode theory. Energies 2018, 11, 2791. [Google Scholar] [CrossRef]
- Dehghanzadeh, A.; Farahani, G.; Vahedi, H.; Al-Haddad, K. Model predictive control design for DC-DC converters applied to a photovoltaic system. Int. J. Electr. Power Energy Syst. 2018, 103, 537–544. [Google Scholar] [CrossRef]
- Mohapatra, A.; Nayak, B.; Das, P.; Mohanty, K.B. A review on MPPT techniques of PV system under partial shading condition. Renew. Sustain. Energy Rev. 2017, 80, 854–867. [Google Scholar] [CrossRef]
- Hariharan, R.; Chakkarapani, M.; Saravana Ilango, G.; Nagamani, C. A method to detect photovoltaic array faults and partial shading in PV systems. IEEE J. Photovolt. 2016, 6, 1278–1285. [Google Scholar] [CrossRef]
- Daraban, S.; Petreus, D.; Morel, C. A novel MPPT (maximum power point tracking) algorithm based on a modified genetic algorithm specialized on tracking the global maximum power point in photovoltaic systems affected by partial shading. Energy 2014, 74, 374–388. [Google Scholar] [CrossRef]
- Tey, K.S.; Mekhilef, S. Modified incremental conductance algorithm for photovoltaic system under partial shading conditions and load variation. IEEE Trans. Ind. Electron. 2014, 61, 5384–5392. [Google Scholar]
- Quevedo, D.E.; Aguilera, P.P.; Perez, M.A.; Cortes, P.; Lizana, R. Model predictive control of an AFE rectifier with dynamic references. IEEE Trans. Power Electron. 2011, 27, 3128–3136. [Google Scholar] [CrossRef]
- Kadri, R.; Gaubert, J.-P.; Champenois, G. An improved maximum power point tracking for photovoltaic grid-connected inverter based on voltage-oriented control. IEEE Trans. Ind. Electron. 2010, 58, 66–75. [Google Scholar] [CrossRef]
- Fahem, K.; Chariag, D.; Sbita, L. Control of Three-Phase Voltage Source PWM Rectifier. In Proceedings of the 3rd International Conference on Automation, Control, Engineering and Computer Science (ACECS’16), Hammamet, Tunisia, 20–22 March 2016. [Google Scholar]
- Bouafia, A.; Gaubert, J.-P.; Krim, F. Predictive direct power control of three-phase pulsewidth modulation (PWM) rectifier using space-vector modulation (SVM). IEEE Trans. Power Electron. 2009, 25, 228–236. [Google Scholar] [CrossRef]
- Vazquez, S.; Sanchez, J.A.; Carrasco, J.M.; Leon, J.I.; Galvan, E. A model-based direct power control for three-phase power converters. IEEE Trans. Ind. Electron. 2008, 55, 1647–1657. [Google Scholar] [CrossRef]
- Cortes, P.; Rodrguez, J.; Antoniewicz, P.; Kazmierkowski, M. Direct power control of an AFE using predictive control. IEEE Transa. Power Electron. 2008, 23, 2516–2523. [Google Scholar] [CrossRef]
- Kouro, S.; Corts, P.; Vargas, R.; Ammann, U.; Rodrguez, J. Model predictive control A simple and powerful method to control power converters. IEEE Trans. Ind. Electron. 2008, 56, 1826–1838. [Google Scholar] [CrossRef]
- Stellato, B.; Geyer, T.; Goulart, P.J. High-speed finite control set model predictive control for power electronics. IEEE Trans. Power Electron. 2016, 32, 4007–4020. [Google Scholar] [CrossRef]
- Abdelrahem, M.; Hackl, C.M.; Zhang, Z.; Kennel, R. Robust predictive control for direct-driven surface-mounted permanent-magnet synchronous generators without mechanical sensors. IEEE Trans. Energy Convers. 2017, 33, 179–189. [Google Scholar] [CrossRef]
- Corts, P.; Kazmierkowski, M.P.; Kennel, R.M.; Quevedo, D.E.; Rodrguez, J. Predictive control in power electronics and drives. IEEE Trans. Ind. Electron. 2008, 55, 4312–4324. [Google Scholar] [CrossRef]
- Vazquez, S.; Marquez, A.; Aguilera, R.; Quevedo, D.; Leon, J.I.; Franquelo, L.G. Predictive optimal switching sequence direct power control for grid-connected power converters. IEEE Trans. Ind. Electron. 2014, 62, 2010–2020. [Google Scholar] [CrossRef]
- Vazquez, S.; Leon, J.I.; Franquelo, L.G.; Rodriguez, J.; Young, H.A.; Marquez, A.; Zanchetta, P. Model predictive control: A review of its applications in power electronics. IEEE Ind. Electron. Mag. 2014, 8, 16–31. [Google Scholar] [CrossRef]
- Liu, X.; Wang, D.; Peng, Z. Improved finite-control-set model predictive control for active front-end rectifiers with simplified computational approach and on-line parameter identification. ISA Trans. 2017, 69, 51–64. [Google Scholar] [CrossRef]
- Mehreganfar, M.; Saeedinia, M.H.; Davari, S.A.; Garcia, C.; Rodriguez, J. Sensorless Predictive Control of AFE Rectifier With Robust Adaptive Inductance Estimation. IEEE Trans. Ind. Inform. 2018, 15, 3420–3431. [Google Scholar] [CrossRef]
- Yan, L.; Song, X. Design and Implementation of Luenberger Model-Based Predictive Torque Control of Induction Machine for Robustness Improvement. IEEE Trans. Power Electron. 2019, 35, 2257–2262. [Google Scholar] [CrossRef]
- Yang, H.; Zhang, Y.; Liang, J.; Liu, J.; Zhang, N.; Walker, P.D. Robust deadbeat predictive power control with a discrete-time disturbance observer for PWM rectifiers under unbalanced grid conditions. IEEE Trans. Power Electron. 2018, 34, 287–300. [Google Scholar] [CrossRef]
- Abdelrahem, M.; Hackl, C.; Kennel, R. Sensorless control of doubly-fed induction generators in variable-speed wind turbine systems. In Proceedings of the 2015 International Conference on Clean Electrical Power (ICCEP), Taormina, Italy, 16–18 June 2015; pp. 406–413. [Google Scholar]
- Das, D.; Madichetty, S.; Singh, B.; Mishra, S. Luenberger Observer Based Current Estimated Boost Converter for PV Maximum Power Extraction A Current Sensorless Approach. IEEE J. Photovolt. 2018, 9, 278–286. [Google Scholar] [CrossRef]
- Ahmed, M.; Abdelrahem, M.; Hackl, C.; Kennel, R. An Enhanced Maximum Power Point Tracking Based Finite-Control-Set Model Predictive Control for PV Systems. In Proceedings of the PEDSTC2020-11th Annual Power Electronics, Drive System, and Technologies Conference, Tehran, Iran, 4–6 February 2020. [Google Scholar]
- El-Saady, G.; Ibrahim, E.A.; Ahmed, M. Modeling and maximum power point tracking with ripple control of photovoltaic system. In Proceedings of the MEPCON 14, the International Middle East Power Systems Conference, Cairo, Egypt, 23–25 December 2014. [Google Scholar]
- El-Saady, G.; Ibrahim, E.A.; Ahmed, M. Performance of photovoltaic water pumping system under different MPPT algorithms. In Proceedings of the 17th International Middle-East Power Systems Conference—MEPCON 15, Mansoura, Egypt, 15–17 December 2015. [Google Scholar]
- Abdelrahem, M.; Kennel, R. Fault-ride through strategy for permanent-magnet synchronous generators in variable-speed wind turbines. Energies 2016, 9, 1066. [Google Scholar] [CrossRef]
- Safari, A.; Mekhilef, S. Simulation and hardware implementation of incremental conductance MPPT with direct control method using cuk converter. IEEE Trans. Ind. Electron. 2010, 58, 1154–1161. [Google Scholar] [CrossRef]
- Killi, M.; Samanta, S. Modified perturb and observe MPPT algorithm for drift avoidance in photovoltaic systems. IEEE Trans. Ind. Electron. 2015, 62, 5549–5559. [Google Scholar] [CrossRef]
- El-Saady, G.; Ibrahim, E.A.; Ahmed, M. Optimal photovoltaic water pumping system performance under different operating conditions. J. Eng. Sci. 2015, 43, 16–32. [Google Scholar]
- Radjai, T.; Rahmani, L.; Mekhilef, S.; Gaubert, J.P. Implementation of a modified incremental conductance MPPT algorithm with direct control based on a fuzzy duty cycle change estimator using dSPACE. Sol. Energy 2014, 110, 325–337. [Google Scholar] [CrossRef]
- Elgendy, M.A.; Zahawi, B.; Atkinson, D.J. Assessment of perturb and observe MPPT algorithm implementation techniques for PV pumping applications. IEEE Trans. Sustain. Energy 2011, 3, 21–33. [Google Scholar] [CrossRef]
- Dirscherl, C.; Hackl, C.; Schechner, K. Modellierung und Regelung von modernen Windkraftanlagen: Eine Einf hrung. In Elektrische Antriebe-Regelung von Antriebssystemen; Springer: Berlin/Heidelberg, Germany, 2015; pp. 1540–1614. [Google Scholar]
- Rodriguez, J.; Cortes, P. Predictive Control of Power Converters and Electrical Drives; John Wiley & Sons: New York, NY, USA, 2012; Volume 40. [Google Scholar]
- Shi, K.L.; Chan, T.F.; Wong, Y.K.; Ho, S.L. Speed estimation of an induction motor drive using an optimized extended Kalman filter. IEEE Trans. Ind. Electron. 2002, 49, 124–133. [Google Scholar] [CrossRef]
- IEEE Industry Applications Society. IEEE Recommended Practice and Requirements for Harmonic Control in Electric Power Systems; IEEE Standard 519-2014 (Revision of IEEE Standard 519-1992); Institute of Electrical and Electronics Engieers: New York, NY, USA, 2014; pp. 1–29. [Google Scholar]

| Voltage Vectors | Switching States () | Output Voltages (,) | Output Voltages (,,) | |||
|---|---|---|---|---|---|---|
| 000 | 0 | 0 | 0 | 0 | 0 | |
| 100 | 0 | |||||
| 110 | ||||||
| 010 | ||||||
| 011 | 0 | |||||
| 001 | ||||||
| 101 | ||||||
| 111 | 0 | 0 | 0 | 0 | 0 | |
| Parameter | Value |
|---|---|
| PV array power [kW] | 15 |
| Boost inductance [] | 25 |
| DC-link capacitance [] | 1000 |
| Filter inductance [] | 12 |
| Filter resistance [] | |
| DC-link reference voltage [] | 700 |
| Grid frequency [] | |
| Grid line-line voltage v [] | 400 |
| Sampling time [] | 40 |
| Condition | THD | Average Switching Frequency | ||
|---|---|---|---|---|
| Conventional | Proposed | Conventional | Proposed | |
| 4.24% | 3.87% | |||
| 2.80% | 2.58% | 3.99 kHz | 3.81 kHz | |
| 2.14% | 2.04% | for all conditions | ||
| 1.74% | 1.68% | |||
| Condition | Energy [kWh] | Saving [kWh] | |
|---|---|---|---|
| Conventional | Proposed | ||
| 800 [W/m] | 11.9395 × 60 × 60 × 10/0.3 | 11.9414 × 60 × 60 × 10/0.3 | 228 |
| Condition | THD | |
|---|---|---|
| Conventional | Proposed | |
| 12 [] | 2.17% | 2.07% |
| 18 [] | 1.55% | 1.47% |
| 6 [] | 8.75% | 3.69% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, M.; Abdelrahem, M.; Kennel, R. Highly Efficient and Robust Grid Connected Photovoltaic System Based Model Predictive Control with Kalman Filtering Capability. Sustainability 2020, 12, 4542. https://doi.org/10.3390/su12114542
Ahmed M, Abdelrahem M, Kennel R. Highly Efficient and Robust Grid Connected Photovoltaic System Based Model Predictive Control with Kalman Filtering Capability. Sustainability. 2020; 12(11):4542. https://doi.org/10.3390/su12114542
Chicago/Turabian StyleAhmed, Mostafa, Mohamed Abdelrahem, and Ralph Kennel. 2020. "Highly Efficient and Robust Grid Connected Photovoltaic System Based Model Predictive Control with Kalman Filtering Capability" Sustainability 12, no. 11: 4542. https://doi.org/10.3390/su12114542
APA StyleAhmed, M., Abdelrahem, M., & Kennel, R. (2020). Highly Efficient and Robust Grid Connected Photovoltaic System Based Model Predictive Control with Kalman Filtering Capability. Sustainability, 12(11), 4542. https://doi.org/10.3390/su12114542







