1. Introduction
Logistics service providers (LPs), as providers of logistics outsourcing, play a highly significant role within the supply chain of companies. They enable concentration of the company human resource on core business, improve service quality, eliminate assets investments, reduce costs [
1,
2] and consequently enhance the company’s competitiveness in the scenario of globalization [
3].
The LP is not only a significant contributor to the supply chain success but also one of the greatest consumers of energy and generators of emissions. Freight transport is a major and the fastest growing generator of carbon emissions [
4,
5] and energy consumers, followed by warehousing activities.
Being a significant player within supply chains, which nowadays demands not only operational but also sustainable effectiveness [
6], LPs started to respond to environmental concerns [
7]. A large portion of energy savings is a result of using today’s light- and heavy-duty trucks by LPs with improved fuel efficiency or powered by natural gas, propane or electricity [
8]. LPs are increasing sustainable efficiency in the last miles of deliveries by optimizing routes and thereby removing unnecessary miles or idling due to congestion and by collecting more freight on a single truck and thereby cutting down the number of miles driven [
8].
These environmentally friendly activities are the result of considerable financial contributions, and it would, therefore, be very fair that those LPs that are working in these directions are also rewarded in the sense that they have better opportunities in the selection process. However, the most frequently employed model for evaluating the efficiency of LPs—data envelopment analysis (DEA) models (Charnes, Cooper and Rhodes (CCR) data envelopment analysis (DEA) and the Banker, Charnes and Cooper (BCC)-DEA analysis) only address the desirable (good) outputs offered by the LP but fails to address the undesirable outputs (environmental). Those LPs that invest money and other efforts into emissions reduction [
6] consequently have a lower economic index and a lower probability of success in the process of LP selection. An LP with a very poor environmental index can be evaluated as efficient.
The authors [
9] have begun to fill this gap by using the Slacked Based Measure (SBM)-DEA model for benchmarking 3PLs. However, only economical and not environmental undesired variables were considered in their model. They [
5] continued working on this issue and benchmarked the environmental efficiency of road transport companies by using the SBM-DEA and considering undesired environmental variables. However, evaluation of the efficiency that considers all three pillars of sustainability and their undesired variables remains unexplored.
Moreover, even using the most appropriate DEA model, DEA results are still highly influenced by the identification of appropriate inputs and outputs—yet the method itself does not provide guidance for their identification. The rule of thumb which proposes to have at least two times greater number of decision making units (DMUs) than the sum of the number of inputs and outputs (
[
10] only suggests the number of DMUs, which further influences the number of inputs/outputs, but does not indicate the ratio between the number of inputs or outputs nor any guidance regarding how to select the relevant inputs and outputs. Studies have revealed that the availability of data and suggestions by the authors are factors that most often assist in identifying inputs and outputs [
11,
12,
13,
14,
15,
16,
17]. This, however, raises doubt about the value of the selected inputs/outputs and consequently the robustness and reliability of the results. Moreover, valuable information may be lost.
To close these gaps two research questions (RQ) were developed:
RQ1. Is the SBM DEA model, which is able to divide outputs into two sets, desirable and undesirable units, a more authentic model for evaluating the efficiency of LPs by the buyer of outsourcing?
RQ2. Would the extension of DEA with AHP increase the robustness and reliability of the results?
The objectives of this study are twofold. One is the proposal of a DEA model, which simultaneously evaluates both the undesirable and desirable outputs variables. The second is the proposal of a DEA extension which enables that at least those variables that are influential and contribute most to efficiency will be involved in the analysis.
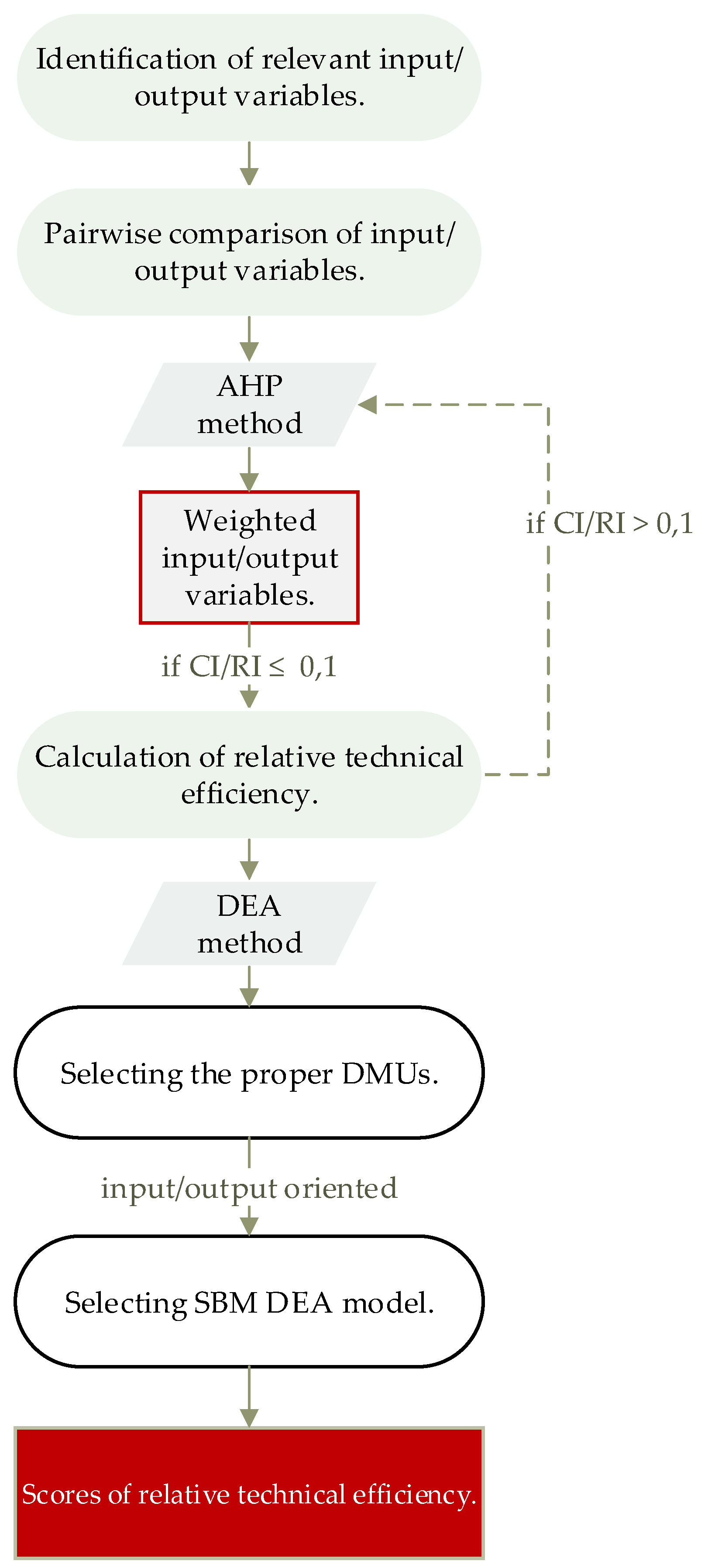
An integrated analytic hierarchy process (AHP) and SBM DEA model is proposed in this study. Firstly, an AHP pairwise comparison is used to rank a set of criteria (inputs, outputs) according to their importance. Then, an SBM DEA model that evaluates both the undesirable and desirable outputs is used.
The present analysis is important for a number of reasons and for stakeholders. First, from a managerial perspective, this paper provides a kind of tool for helping decision makers evaluate the efficiency of LPs in a very comprehensive way with an appropriate methodology. Usually, decision makers are not familiar with multi-criteria decision-making methods, where DEA and AHP belong. They select the method arbitrarily, because the method is popular [
18] or because they have an affinity for the chosen MCDM method [
19]. The proposed model, moreover, considers all three pillars of sustainability, undesirable outputs and also enables simultaneously evaluation of both the undesirable and desirable outputs variables. Real world considerations (environmental concerns) are not ignored any more with the proposed methodology which leads to a more sustainable supply chain and opens entirely new opportunities for companies.
Second, from the LP perspective, this paper enables a more fair evaluation process for those LPs that invest much effort and financial resources into green solutions. The proposed methodology might also open new opportunities for them and can also encourage all the other LPs which are not yet aware of the importance of sustainability to take a step forward [
20]. In this case, all stakeholders will benefit. The set of efficient LPs will increase, which allows decision makers to choose between a larger number of LPs. LPs have better potential to become an LP of choice. Both of which lead to greater efficiency of the applicable countries.
Additionally, in comparison to past models, the proposed integrated AHP-SBM-DEA methodology enables the selection of the most appropriate inputs and outputs. The risk of the most critical step of DEA analysis is consequently reduced and the results even more robust and reliable.
To answer the paper’s research questions the rest of the paper is arranged as follows:
Section 2 presents a comprehensive review of literature on the SBM-DEA model used for LP evaluation and a brief background and explanation of methods/models used.
Section 3 presents DEA models and proposes a novel two-step methodological approach.
Section 4 applies this method to a numerical example of 18 LP. The paper ends with a discussion of the results and the conclusion.
2. Literature Review
In recent years, many performance assessment studies in various levels of logistics sector (firm, regional, national) have been conducted. However, this study only relates to existing literature pertaining to DEA performance evaluations of LPs. So far, authors have mainly developed a benchmarking approach, using traditional CCR and BCC DEA.
Traditional DEA was, for example, used to examine the relationship between the functional heterogeneity of senior less than truck load motor carrier managers’ departmental positions and the relative efficiency of their companies in the production of quality customer service [
21]. The input data in this study were functional categories of senior managers and the output data variables were customer service measures.
Traditional DEA was used to benchmark the operational efficiency of third-party logistics providers in the USA [
22]. Four inputs (account receivables, salaries and wages of employees, operating expenses other than salaries and wages, and property and equipment) and one input (operative income) formed the analysis [
22].
CCR and BCC-DEA models were applied to benchmark Chinese logistics service providers [
23]. Four metrics were selected as inputs (net fixed assets including properties and equipment, salaries and wages of employees, operating expenses other than salaries and wages, and current liabilities such as accounts payable) and one metric as output (operating income).
A comparative analysis of leading third-party logistics providers (3PLs) in the USA was done by using CCR and BCC-DEA models [
9]. The performance was measured by using one output (revenue) and three inputs (cost of sales, selling and administrative expenses including salaries, wages, and fringe benefits of 3PL employees, depreciation and amortization expenses associated with property and equipment (e.g., warehouses, terminals, trucks, airplanes, trailers, and containers) [
9].
CCR model and BCC-DEA models were used to measure the efficiency of 24 leading third-party logistics providers (3PLs) in North America [
24]. The authors selected three different metrics as inputs (size and number of physical facilities and the total number of employees) and one output (revenue).
DEA analysis was employed as well to examine the efficiency and productivity of fourteen Korean logistics providers [
25]. The input elements used in this study were capital, assets and the number of employees. Total revenue was used for the output element.
The traditional DEA model was also applied to measure the performance of logistics service provider, which is characterized by a multistage process (supply chains take this form) [
26].
The reverse logistics provider was also measured using traditional DEA by an Indian apparel manufacturer [
27] and once by [
28] using the SBM-DEA model. In this study, only desired inputs and outputs were selected.
Traditional DEA was also used as a tool to evaluate the efficiency of a group of 3PL that offer warehouse logistics operations [
29]. Labor hours, warehouse space, technology investment and materials handling equipment were used as inputs. Shipping volume, number of orders filled and space utilization were used as outputs. The depot’s efficiency measurements were also made [
30,
31,
32,
33].
The study of Reference [
34] uses a data envelopment analysis (DEA) and a robust regression approach to measure the impact of contextual variables on the efficiency of Brazilian 3PL providers of refrigeration services. Many desirable, also environmental, input/output variables were considered, but no undesired.
The longitudinal efficiency of branch operations of a third party logistics (3PL) company was evaluated by [
35] using SBM-DEA. Undesired economical variables were considered but not environmental variables. In a similar way, 16 LPs in the USA from 2012 to 2015 were evaluated [
36]. A super SBM-DEA model was used, but only desirable economic input/output were analyzed.
Based on the results of this literature review, the negative impacts generated by LP were seldom considered in DEA analyses. The SBM-DEA was used once to benchmark road freight companies [
5]. The authors aimed to minimize CO
2 emissions. Fleet-wise weight, volume utilization and distance travelled by fleet were used as inputs. Greenhouse gases (GHG) were used as an output. SBM was also applied to assess the efficiencies, considering the negative environmental impact, of shipping enterprises [
37].
In summary, the literature review shows (
Table 1) that little effort has been made to develop the sustainable performance measurement of LPs using the SBM-DEA model. LPs are, in comparison to other supply chain partners, very high energy consumers and CO
2 causers. For this reason, undesirable variables have to be considered as output variables. This paper, therefore, proposes to employ an SBM DEA model, further integrated with the AHP method, which reduces the most problematic DEA pitfall—choice of the right input and output.
Data envelopment analysis (DEA) was introduced by Charnes, Cooper and Rhodes in 1978 and is a linear optimization method widely used in efficiency analysis [
38]. There are many variations of the DEA method, formulated for desirable inputs and outputs. The most frequently used are the CCR model [
39], the BCC model [
40], the additive model (ADD) [
41] and the cone ratio model [
42].
Since inputs/outputs are also undesirable, there are many methods (transformations) used to transform undesirable elements into desirable. The most frequently used transformation is the ADD approach that associate with each undesirable element the opposite element [
43].
It is also possible to use the multiplicative inverse approach, but this transformation is not linear and so the DEA optimization method becomes more complicated [
44].
Liu and Sharp [
45] were the first to approach the problem by changing the relationship between inputs and outputs, so they transferred the problem of distinguishing between desirable and undesirable inputs (or outputs) to a minimum or a maximum value search.
Recently many authors have combined the ADD approach and directional distance functions to solve the undesirable elements problem using the slack-based approach and the radial -Russell approach [
38].
The DEA models evaluate the efficiency of DMUs to produce outputs from inputs. The aim of the DEA method is to estimate and maximize the efficiency of each DMU.
The AHP, introduced by Thomas Saaty (1980), is an effective tool which considers a set of evaluation criteria and a set of alternatives among which the best is selected. The AHP generates a weight for each criterion according to the decision maker’s pairwise comparisons of the criteria. In addition, the AHP enables the checking of the consistency of the decision maker’s evaluations in order to reduce the bias in the decision-making process [
46].
The AHP method involves four main stages: decomposition of the decision problem into a hierarchy of interrelated elements, pairwise comparisons of the criteria with 9-degree scale application, calculation of criteria weights and final selection of the best decision [
47].
A 9-degree Saaty scale is used to compare each input/output variable in a pairwise comparison matrix, . The matrix’s element represents the intensity of the preference of the row element over the column element .
The relative weights are given by the eigenvector
corresponding to the highest eigenvalue
:
Generally, the matrix
is not completely consistent. In this case, it is necessary to compute the consistency index
given by [
48]:
In order to conclude whether the evaluations are consistent, the consistency ratio
is calculated as the ratio of the consistency index
and the random consistency index
[
46]:
The inconsistency should not be higher than 10 per cent [
48].
4. Numerical Example
LPs provide many logistics services (domestic and international transportation, warehousing, freight forwarding, customs brokerage, cross-docking, added-value services, reverse logistics, inventory management, consulting services, information technology services, fleet management, customer services, etc.). However, domestic transportation (81%) for many years, including so far 2019, has been the most frequently requested logistics service, followed by international transportation (71%) and warehousing (69%) [
8]. The authors, therefore, decided to apply the proposed model in a numerical example of LPs that provide transport services.
4.1. Identification of Inputs/Outputs
The inputs and outputs variables in this study were selected in two phases. Two databases of efficiency variables, for LPs that provide all, not only transport, services, as a result of very extensive literature reviews [
51,
52] and interviews with academics and practitioners [
52], were compared firstly to select the most commonly used efficiency variables. Cost/price variable, information technology application variable, accurate delivery time variable, circumstance of delivery, transport capacity, staff quality/educated employee variable and the employee/customer satisfaction variable were found to be the most frequently used.
The set of criteria was in the second phase adjusted and harmonized to the measurement of the logistics provider that performs only transport activities. By using very comprehensive and one of the latest performance frameworks for measuring the performance of transport activity of a 3PL firm [
53] some variables were subdivided into more sub-variables (for example the cost variable was divided into turnover per km and profit per delivery; circumstances per delivery was subdivided into correctness and completeness sub-variables), some new variables were added due to their relevance and to cover the overall sustainability performance of the LP (the average lead time per delivery, productivity per driver, the utilization of the cargo space, distance travelled, productivity per driver, transportation accidents per year, total number of orders and total number of employees). Since the group of environmental variables was not sufficiently comprehensive, two more variables were added (Carbon dioxide (CO
2) Greenhouse gas emissions (GSG) and average speed per km) [
5] (
Table 2 and
Table 3).
The final set of variables was, accordingly, the fact that the inputs are the resources consumed by the LP for transport activity and the outputs are results from providing transport activity, divided into input (
Table 3) and output groups of variables (
Table 2).
The variables reflect the economic, environmental and social aspects of an LPs’ performance. Together they cover the overall sustainability performance of LP (
Table 2 and
Table 3).
Ten output variables are desirable, three are undesirable and distance travelled during a certain period of time can be both (Fuel consumption is calculated from distance travelled. Higher distance travelled consequently leads to higher CO
2 emissions. Viewing from this perspective, distance travelled variable is undesirable output. However, distance travelled by a truck during a certain period of time also shows better truck utilization, which increases efficiency and is therefore treated as desirable output) (
Table 2).
Three relevant inputs and 14 relevant outputs were selected by the authors from the database. Due to the low number of inputs, only outputs variables were included in the AHP pairwise comparison.
Table 4 presents the resulting weights
for the output variables. To check the consistency of the comparison matrix, a consistency ratio was computed,
.
4.2. Selecting DMU and Input/Output Variables
Eighteen Slovene LPs with a vehicle fleet of size in the range
were selected as DMUs. Given the rule of thumb (
, all three input variables and the six most influential outputs were applied in the DEA analysis (
Table 5). All three inputs are desirable. They cover the economic and social aspects of sustainability. Output 3, 4, 5 and 6 are desirable. Output 1 and 2 are undesirable and therefore need to be reduced and not increased. All of them cover all three aspects of sustainability.
Since all LPs do not select all the data required by the model, the missing data were calculated from the real LP’s values, according to the equations (
Table 2 and
Table 3), or were simulated according to the data of those LPs that provided data for these input/outputs at all.
4.3. Results and Discussion
In this study, the efficiency scores of LPs were estimated with the use of an input- and output-oriented CCR model and with the use of the output-oriented SBM model (
Table 6).
Both CCR input and output-oriented DEA models indicated the same LPs as inefficient (LP1, LP12 and LP17) (16%). Other DMUs (84%) were found to have an objective function value equal to one. They are efficient.
The output-oriented CCR model shows that in order to attain efficiency, LP1, LP12 and LP17 must increase their outputs. LP1 needs to increase the utilization of the cargo space of a vehicle fleet for additional slack variable , LP12 for and LP17 for Moreover, LP1 needs to increase profit per delivery for and LP12 for The total number of orders in a certain period of time of LP17 needs to be increased by a value of 272.9.
The input-oriented CCR model suggests the reduction of inputs in order that the DMU becomes efficient. In this case, LP1 needs to decrease average years of education per employee for the slack variable , LP12 for the variable and LP17 for the variable . The total number of employees also needs to be decreased in the case of LP1, , and LP17, .
The obtained percentages depict possible savings of LPs. However, none of the abovementioned models distinguishes between desirable and undesirable outputs (the average lead time per delivery and Carbon dioxide (CO2) Greenhouse gas emissions (GHG). The latter are treated in the output CCR model as desirable, which in accordance with DEA rules need to be increased (in the case of LP17, ). However, in reality, they need to be decreased. This is only one drawback of the presented models. The second possible drawback is that an LP with a very poor environmental index can be evaluated as efficient. And vice versa: LPs that invest in emissions reductions have lower efficiency scores, which is rather unfair.
For this purpose, an output-oriented SBM model, which divides outputs into two sets, desirable and undesirable units, is more appropriate. Slack are added only to desirable outputs and to obtain the virtual optimum, undesirable variables are decreased and the desirable are increased.
The number of orders, profit, turnover and average load capacity in our model are desirable outputs. Lead time and GHG emissions are undesirable outputs. The SBM model results indicate that besides LP1 and LP12 (as in the CCR two models) LP2, LP7 and LP18 are technically inefficient. LP17 was found to be efficient. The SBM model estimates a lower efficiency score for LP1 and LP12.
The SBM model extends the set of inefficient DMUs, but at the same time, LP17 becomes efficient, which confirms that the environmental pillar has to be considered in DEA analysis since the environmental or any other undesired output changes the final efficiency score of the DMU. Moreover, in other DEA models, environmental outputs are not treated as undesired.
If only the undesirable output (CO2 emission) is increased by 4% or more in the case of LP17, it becomes inefficient. Therefore, LP17 is critical. It is evaluated as inefficient in CCR models, but efficient in the SBM model. The appropriate evaluation of CO2 emissions is awarded in the case of LP17, which is a good feature of the presented model.
Comparison of efficient DMUs, using the super-efficiency DEA method [
54], which provides the ranking of efficient units, in addition, revealed that LP17 is the best LP (
Table 7). This info is even more useful for decision makers and supply chain managers.
The proposed model is fair to those LPs that are environmentally friendly, which is in line with governmental requirements. Moreover, the model indirectly encourages the decision makers to include environmental aspects into the selection process of LPs.
5. Conclusions and Discussion
This study highlights the shortcomings of traditional CCR and BCC-DEA models in evaluation processes, evaluations of LPs, where undesirable variables need to be considered and confirms the suitability of the SBM-DEA model for such processes. In addition, an integrated AHP-SBM-DEA is proposed in this study to ensure that the key input/output variables are included in the analysis and the results of the analysis are therefore more robust and reliable.
CCR and BCC-DEA models provide input and output orientation, allow an analysis of desirable inputs and outputs but do not distinguish between desirable and undesirable outputs/inputs. Undesirable output variables that should be reduced in order to achieve greater efficiency are treated in the CCR and BCC models as desirable and in accordance with output-oriented models must be increased rather than reduced. The results of DEA methods are consequently not accurate. The set of effective decision-making units does not include all effective units or includes those that are not effective. This is misleading for the performance measurement provider and can lead to the wrong final choice of an effective DMU.
Unlike CCR and BCC-DEA models, the SBM-DEA model has greater discriminatory power and also detects more sources of inefficiencies. The non-separable SBM-DEA model is based on the inseparability of desirable and undesirable outputs in an equation. A reduction in undesirable outputs, therefore, requires a cut in desirable outputs. The separable SBM-DEA model separates outputs into desirable and undesirable without assuming a correlation between them. Both SBM-DEA models add slacks to desirable outputs and to obtain the virtual optimum, undesirable variables are decreased and the desirable are increased. The results are much more credible.
However, even by using SBM-DEA the results are highly influenced by the choice of appropriate inputs and outputs variables. The method itself does not provide guidance for their identification but only suggest several sensitivity analyses to validate the feasibility and robustness of its model. Nevertheless, there is still doubt whether the appropriate variables are applied in the analysis.
Accordingly, an integrated AHP-SBM DEA model is proposed and tested using a numerical example of Slovene small-sized LPs. Compared to past studies on this topic, which do not pay attention to the choice of appropriate inputs and outputs variables, in the present study the relative priorities (weights) for variables are derived using a pairwise comparison of variables. The priorities are not assigned arbitrarily, rather are derived based on the judgments and preferences of the authors. “These priorities, therefore, have mathematical validity, as measurement values derived from a ratio scale” [
55]. Since the priorities are derived from the subjective preferences of the authors a consistency ratio comparing the consistency index (CI) of the matrix versus the random consistency index was calculated. Thus, the bias in the decision-making process is reduced. Moreover, traditionally the DEA methods may conduct several sensitivity analyses to validate the feasibility and robustness of its model. When the method is capable of assessing two to three parameters, as is the DEA (Pearson correlation, Jack-knifing analysis [
56], removable of variables), it is rated medium feasible and robust [
57]. When the DEA would enable assessment of more than three parameters, it would be rated high. These facts answer the RQ2.
In the conventional AHP, which was used in the present study, the pairwise comparison is made using a discrete scale of 1–9, which is simple and easy to use; but it does not take into account the uncertainty related to the mapping of participants’ judgement to a number. The triangular fuzzy numbers, to could be utilized in future research to improve the conventional nine-point scale.
In decision-making problems when criteria independence is assumed, an AHP method might not be appropriate. The analytic network process (ANP) is a more suitable but more time-consuming solution since a decision maker must answer a much larger number of questions [
58].
Regarding the RQ1 (i.e., the credibility of the SBM-DEA model for evaluating the performance of LPs) the CCR and BCC-DEA analyses resulted in three inefficient LPs and 15 efficient LPs. Despite the fact that the obtained results depict possible savings of LPs, none of the applied models distinguishes between desirable and undesirable outputs. The carbon dioxide (CO2) greenhouse gas emissions (GHG) variable was considered in the output CCR model as desirable, which in accordance with DEA rules needs to be increased (in the case of LP17,) and not decreased as expected by the external environment (government, buyers of logistics outsourcing). These facts, therefore, confirm the credibility of the CCR and BCC-DEA models in cases when undesirable variables do not need to be considered. However, the model fails to accurately reflect the efficiency of the LP.
Compared to traditional DEA models, the SBM-DEA model, proposed and tested by the authors, treated the average lead time per delivery and carbon dioxide (CO2) greenhouse gas emissions (GHG) variable as undesirable. Slacks were added in this analysis only to desirable outputs and to obtain the virtual optimum; undesirable variables were decreased and the desirable were increased. The SBM model moreover extended the set of inefficient DMUs and LP17 became efficient. This fact confirms the authors’ doubts in past studies, which applied SBM-DEA models but did not consider all three pillars of sustainability. Results show that the environmental pillar must be considered in DEA analysis since the environmental or any other undesired output changes the final efficiency score of the LP. Moreover, applying the Super-efficiency DEA method it is possible to note that LP17 is the best LP.
The presented model upgrades theoretical knowledge. The topic presented in this paper is actual, significant and only at an early stage, which will, therefore, stimulate further studies. The authors hope that the proposed methodology will be a subject of further refinement using qualitative and quantitative research methods [
59] and will also stimulate new theory building. The initial step would be to test the methodology in more case studies and examples.
Whilst we cannot overemphasize the practical importance of the methodology presented, we believe that this study is a great contribution to the evaluation of LPs efficiency, taking into account all three pillars of sustainability. The model corresponds to a real situation and thus represents the potential for great support for decision-makers. The authors believe that the study offers decision makers and managers in supply chains a starting point for what is needed to become efficient from all sustainable aspects, which would further stimulate such data collection (few companies actually collect all data required) and would also lead to greater acceptance and adoption of the methodology.
The presented methodology, on one hand, enables tailor-made solutions, but on the other hand, is very general, and, with minor adjustments, can in the future be applied in a variety of situations by supply chain partners.
Considering that DEA is a data-driven approach the lack of real data in the case of some inputs/outputs is a limitation in this work. The real data of all inputs and outputs might more effectively demonstrate the potential of this method or might speak to the use of an updated model formulation [
5]. Thus, additional evaluations of the model would need to be undertaken in the future.
Moreover, AHP pairwise comparison reflects the authors’ opinions, which are rather subjective. For a more objective ranking of input/output variables the integrated AHP-DELPHI method may be the most appropriate; or, the number of evaluators in AHP pairwise comparison should be increased.