Multiobjective Mathematical Programming Model for the Optimization of End-of-Life Buildings’ Deconstruction and Demolition Processes
Abstract
1. Introduction
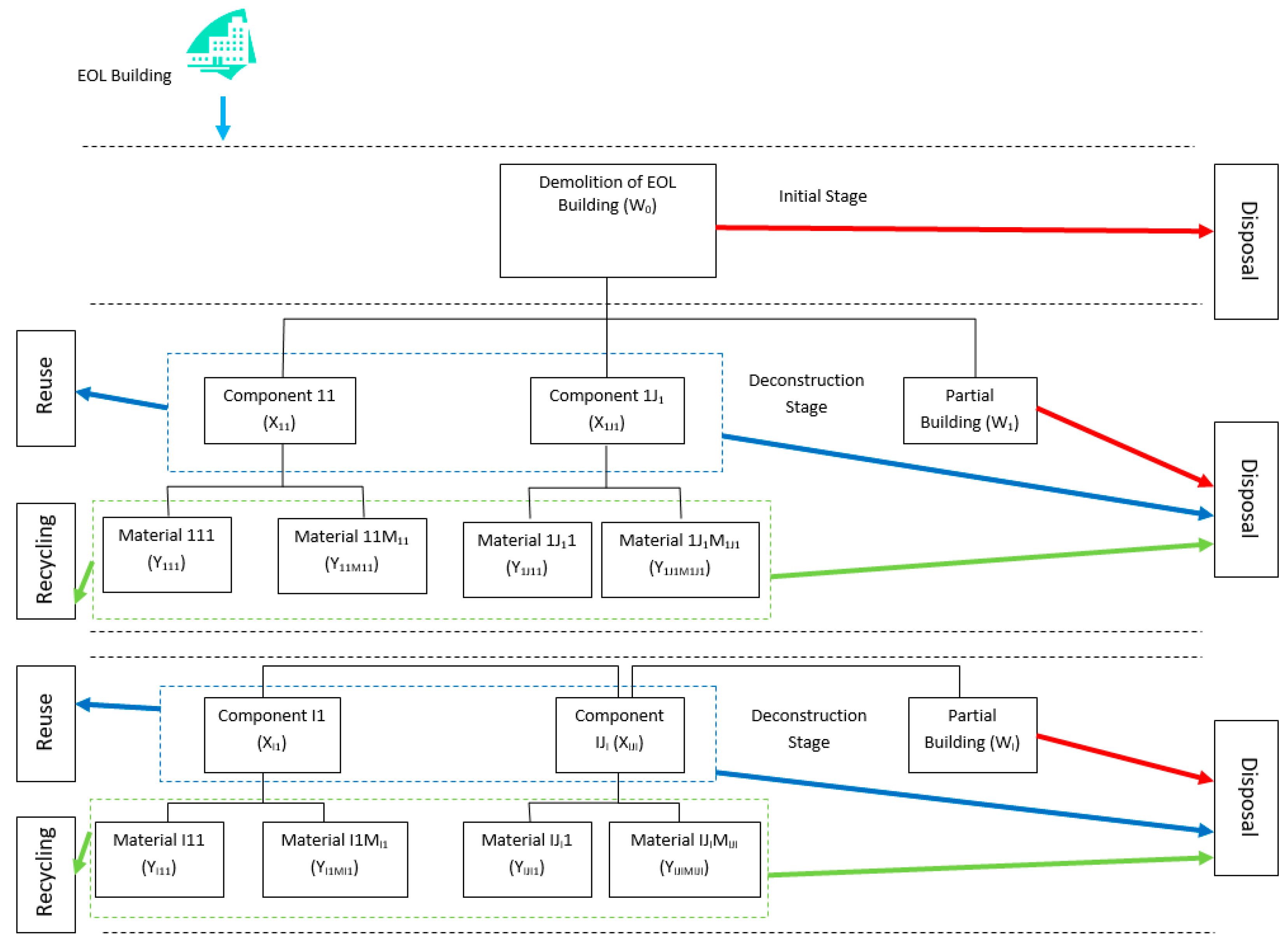
2. System Description
2.1. Problem Definition
2.2. System Assumptions
- The contractor is responsible both for the execution of the deconstruction or demolition processes and the recovery management of the C&D materials;
- In every deconstruction stage, the contractor may not recover all of the building materials before proceeding to demolition work on the rest of the building;
- The total costs of the deconstruction and demolition processes involve variable and fixed costs of producing and recovering EOL building components and materials;
- In some cases, mainly in deconstruction processes, the contractor may have revenues from the sale of specific EOL components and materials;
- During the deconstruction or demolition phase, the operational costs for a specific task are independent of its volume or size. This means that in the proposed mathematical model, economies of scale are not taken into consideration;
- The demolition process and waste handling costs are constant per ton of produced materials and irrespective of the stage of the demolition of the EOL building;
- The sequence of deconstruction processes is subject to specific technological constraints. For example, the recovery of roof skeleton materials first requires the removal of roofing material;
- As for the total execution time of dismantling the EOL building, there is an assumption that all the deconstruction works of the building are executed sequentially, without the possibility of performing parallel tasks.
2.3. Model Formulation
- i = 0, …, I: Deconstruction and demolition stages. The value i = 0 refers to the case of demolition work of the entire building;
- j = 1, …, Ji: Structural components in the ith deconstruction stage, with I {1, …, I};
- m = 0, …, Mij: Materials resulting from disassembling the jth structural component at the ith deconstruction stage, with i {1, …, I};
- k = 0, …, 1: Alternative ways of managing the produced materials. The value k = 0 refers to the final deposition, and the value k = 1 refers to the recycling of building materials.
2.4. Solving Methodology
3. Case Study
4. Conclusions
Funding
Conflicts of Interest
References
- Itoh, Y.; Liu, C. Lifecycle Management Approach for Network-Level Transportation Infrastructure Systems Based on Information Technologies. In INCITE 2000: Implementing IT to Obtain a Competitive Advantage in the 21st Century; The Hong Kong Polytechnic University Press: Hong Kong, China, 2000; pp. 300–314. [Google Scholar]
- European Commission. EU Construction & Demolition Waste Management Protocol; European Commission: Brussels, Belgium, 2016; pp. 1–46. [Google Scholar]
- The European Parliament and the Council of the European Union, Directive 2008/98/EC on waste and repealing certain Directives. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX:32008L0098 (accessed on 21 January 2019).
- Faleschini, F.; Zanini, M.A.; Pellegrino, C.; Pasinato, S. Sustainable management and supply of natural and recycled aggregates in a medium-size integrated plant. Waste Manag. 2016, 49, 146–155. [Google Scholar] [CrossRef] [PubMed]
- Hossain, U.; Ng, S.T. Influence of waste materials on buildings’ life cycle environmental impacts: Adopting resource recovery principle. Resour. Conserv. Recycl. 2019, 142, 10–23. [Google Scholar] [CrossRef]
- Vitale, P.; Arena, N.; Di Gregorio, F.; Arena, U. Life cycle assessment of the end-of-life phase of a residential building. Waste Manag. 2017, 60, 311–321. [Google Scholar] [CrossRef] [PubMed]
- Xanthopoulos, A.; Aidonis, D.; Vlachos, D.; Iakovou, E. A planning optimisation framework for construction and demolition waste management. Int. J. Industrial Syst. Eng. 2012, 10, 257–276. [Google Scholar] [CrossRef]
- Roodman, D.; Lenssen, N. A Building Revolution: How Ecology and Health Concerns are Transforming Construction; Worldwatch Institute: Washington, DC, USA, 1999. [Google Scholar]
- Gordon Engineering. Demolition Energy Analysis of Office Building Structural Systems; Athena Sustainable Materials Institute: Ottawa, ON, Canada, 1997. [Google Scholar]
- Abdullah, A.; Anumba, C.J. Decision Model for the Selection of Demolition Techniques. Adv. Build. Technol. 2002, 1, 1671–1679. [Google Scholar]
- Poon, C.S.; Yu, A.T.W.; Ng, L.H. On-site sorting of construction and demolition waste in Hong Kong. Resources. Conserv. Recycl. 2001, 32, 157–172. [Google Scholar] [CrossRef]
- Kourmpanis, B.; Papadopoulos, A.; Moustakas, K.; Stylianou, M.; Haralambous, K.J.; Loizidou, M. Preliminary Study for the Management of Construction and Demolition Waste. Waste Manag. Res. 2008, 26, 267–275. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, G. Waste Not, Want Not. Architecture 2003, 88, 131–141. [Google Scholar]
- Bruening, S.; Chini, A. Deconstruction and Materials Reuse, An. International Overview, Final Report of Task Group 39 on Deconstruction; CIB Publication: Delft, The Netherlands, 2004. [Google Scholar]
- Greer, D. Building the Deconstruction Industry. Biocycle 2004, 45, 36–42. [Google Scholar]
- Queheille, E.; Taillandier, F.; Saiyouri, N. Optimization of strategy planning for building deconstruction. Autom. Constr. 2019, 98, 236–247. [Google Scholar] [CrossRef]
- Akbarnezhad, A.; Ong, K.C.G.; Chandra, L.R. Economic and environmental assessment of deconstruction strategies using building information modelling. Autom. Constr. 2014, 37, 131–144. [Google Scholar] [CrossRef]
- von Stein, E.L.; Savage, G.M. Current Practices and Applications in Construction and Demolition Debris Recycling. Res. Recycl. 1994, 13, 85–94. [Google Scholar]
- Anumba, C.; Abdullah, A.; Fesseha, T. Selection of Demolition Techniques: A Case Study of the Warren Farm Bridge. Struct. Surv. 2003, 21, 36–48. [Google Scholar] [CrossRef]
- Liu, C.; Pun, S.K.; Langston, C. A Preliminary Study on Building Demolition Engineering and Management. World Trans. Eng. Technol. Education 2005, 4, 201–207. [Google Scholar]
- Chau, C.K.; Xu, J.M.; Leung, T.M.; Ng, W.Y. Evaluation of the impacts of end-of-life management strategies for deconstruction of a high-rise concrete framed office building. Appl. Energy 2017, 185, 1595–1603. [Google Scholar] [CrossRef]
- Ghisellini, P.; Ripa, M.; Ulgiati, S. Exploring environmental and economic costs and benefits of a circular economy approach to the construction and demolition sector: A literature review. J. Clean. Prod. 2018, 178, 618–643. [Google Scholar] [CrossRef]
- Akinade, O.O.; Oydele, L.O.; Ajayi, S.O.; Bilal, M.; Alaka, H.A.; Owolabi, H.A.; Bello, S.A.; Jaiyeoba, B.E.; Kadiri, K.O. Design for Deconstruction (DfD): Critical success factors for diverting end-of-life waste from landfills. Waste Manag. 2017, 60, 3–13. [Google Scholar] [CrossRef] [PubMed]
- Silva, R.V.; De Brito, J.; Dhir, R.K. Properties and composition of recycled aggregates from construction and demolition waste suitable for concrete production. Constr. Build. Mater. 2014, 65, 201–217. [Google Scholar] [CrossRef]
- Coelho, A.; De Brito, J. Influence on construction and demolition waste management on the environmental impact of buildings. Waste Manag. 2012, 32, 532–541. [Google Scholar] [CrossRef] [PubMed]
- Kourmpanis, B.; Papadopoulos, A.; Moustakas, K.; Kourmoussis, F.; Stylianou, M.; Loizidou, M. An Integrated Approach for the Management of Demolition Waste in Cyprus. Waste Manag. Res. 2008, 26, 573–581. [Google Scholar] [CrossRef] [PubMed]
- Ragsdale, C. Spreadsheet Modeling and Decision Analysis: A Practical Introduction to Management Science, 3rd ed.; South-Western College Publishing: Nashville, TN, USA, 2001. [Google Scholar]
- Spengler, T.; Püchert, H.; Penkuhn, T.; Rentz, O. Environmental Integrated Production and Recycling Management. Eur. J. Oper. Res. 1997, 97, 308–326. [Google Scholar] [CrossRef]
- Aidonis, D.; Xanthopoulos, A.; Vlachos, D.; Iakovou, E. An analytical methodological framework for managing reverse supply chains in the construction industry. WSEAS Trans. Environ. Dev. 2008, 11, 1036–1046. [Google Scholar]
| Parameter | Description | |
|---|---|---|
| General | Weight of the jth structural component available at the ith deconstruction stage (tons) | |
| Weight of the mth end material available from the jth structural component at the ith deconstruction stage (tons) | ||
| Total weight of structural elements and end materials (tons) | ||
| Minimum desired deconstruction ratio of the total weight of each EOL building, for recovery purposes (%) | ||
| Value of objective function 1 | ||
| Value of objective function 2 | ||
| Value of objective function 3 | ||
| Coefficient of objective function P1 | ||
| Coefficient of objective function P2 | ||
| Cost | Potential revenues from selling demolition waste (€/ton) | |
| Potential revenues from selling the jth structural component, collected at the ith deconstruction stage (€/ton) | ||
| Potential revenues from final disposal (k = 0 for deposition and k = 1 for recycling) of the mth end material, collected from the jth structural component at the ith deconstruction stage (€/ton) | ||
| Demolition process and waste handling costs (€/ton) | ||
| Deconstruction and handling costs, in order to gain the jth structural component from the ith deconstruction stage (€/ton) | ||
| Deconstruction and handling costs, in order to gain the mth end material from the jth structural component at the ith deconstruction stage (€/ton) | ||
| Disposal (k = 0 for deposition and k = 1 for recycling) costs of the mth end material from the jth structural component at the ith deconstruction stage | ||
| Time | Total time required for demolition process and waste management (hours/ton) | |
| Total time required in order to gain the jth structural component from the ith deconstruction stage (hours/ton) | ||
| Total time required in order to gain the mth end material from the jth structural component at the ith deconstruction stage (hours/ton) | ||
| Variable | Description |
|---|---|
| Boolean variable denoting the ith stage until which the deconstruction process takes place, while the remaining building is demolished (e.g., W0 = 1 entails demolition of the entire building structure, and alternatively W3 = 1 entails that deconstruction continues until the third stage, when the rest of the building is demolished) | |
| Boolean variable denoting whether the jth structural component at the ith deconstruction stage will be recovered (Xij = 1) or not (Xij = 0) | |
| Boolean variable denoting whether the mth end material of the jth structural component at the ith deconstruction stage will be recovered (Yijm = 1) or not (Yijm = 0) | |
| Boolean variable denoting whether the mth end material of the jth structural component at the ith deconstruction stage will be recycled (Zijm1 = 1) or deposited (Zijm0 = 0) | |
| Q | Minimax decision variable |
| Characteristics | Residential Building (Case Study 1) | Industrial Building (Case Study 2) |
|---|---|---|
| Year of construction | 1970 | 1985 |
| Type of construction | Reinforced concrete | Metallic |
| Number of floors | 4 | 1 |
| Floor area (m2) | 130 | 450 |
| Total height (m) | 12.50 | 6.20 |
| Roof type | Tile roof | Metal roof panels |
| Heating type | Boiler | Cooling and heating units |
| Floor coverings | Ceramic tiles | Plastic tiles |
| Windows | Wood | Aluminum |
| Deconstruction Stage | Components | |
|---|---|---|
| Residential Building (Case Study 1) | Industrial Building (Case Study 2) | |
| 1 | Heating devices | Heating devices |
| Heating components | Heating components | |
| Doors | Doors | |
| Windows | Windows | |
| Sanitary devices | Sanitary devices | |
| Shutters | Shutters | |
| Electrical devices | Electrical devices | |
| 2 | Floor covering | Floor covering |
| Roof covering | Roof covering | |
| Wall covering | Wall covering | |
| 3 | Electrical installations | Electrical installations |
| Sanitary | Sanitary | |
| Plumbing | Plumbing | |
| Heating | Heating | |
| 4 | Roof frame | Roof frame |
| 5 | Walls | Walls |
| Insulation materials | Insulation materials | |
| 6 | Floors | Metal stairs |
| Stairs | ||
| Reinforced concrete walls | ||
| Foundation | ||
| 7 | - | Floors |
| Metal skeleton | ||
| 8 | - | Foundation |
| A/A | Coefficient | Value P1 (€) | Value P2 (hr) | Value P3 | Stage | Structural Components | Materials |
|---|---|---|---|---|---|---|---|
| 1 | b1 = 100% b2 = 0% | −20,629.4 | 355 | 0.208 | 1 | Electrical devices Heaters, boilers | - |
| 2 | b1 = 75% b2 = 25% | −20,629.4 | 355 | 0.156 | 1 | Electrical devices Heaters, boilers | - |
| 3 | b1 = 50% b2 = 50% | −20,629.4 | 355 | 0.104 | 1 | Electrical devices Heaters, boilers | - |
| 4 | b1 = 25% b2 = 75% | −20,717.3 | 342.5 | 0.052 | 0 | - | - |
| 5 | b1 = 0% b2 = 100% | −20,717.3 | 342.5 | 0 | 0 | - | - |
| A/A | Coefficient | Value P1 (€) | Value P2 (hr) | Value P3 | Stage | Structural Components | Materials |
|---|---|---|---|---|---|---|---|
| 1 | b1 = 100% b2 = 0% | −13,661.5 | 310.5 | 0.229 | 2 | Electrical devices Cooling and heating units, roof panels | Aluminum, glass, plastic |
| 2 | b1 = 75% b2 = 25% | −13,709.4 | 225 | 0.036 | 1 | Electrical devices Cooling and heating units | Aluminum, glass |
| 3 | b1 = 50% b2 = 50% | −13,742.1 | 217 | 0.005 | 1 | Electrical devices Cooling and heating units | - |
| 4 | b1 = 25% b2 = 75% | −13,796 | 212 | 0.074 | 0 | - | - |
| 5 | b1 = 0% b2 = 100% | −13,796 | 212 | 0 | 0 | - | - |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aidonis, D. Multiobjective Mathematical Programming Model for the Optimization of End-of-Life Buildings’ Deconstruction and Demolition Processes. Sustainability 2019, 11, 1426. https://doi.org/10.3390/su11051426
Aidonis D. Multiobjective Mathematical Programming Model for the Optimization of End-of-Life Buildings’ Deconstruction and Demolition Processes. Sustainability. 2019; 11(5):1426. https://doi.org/10.3390/su11051426
Chicago/Turabian StyleAidonis, Dimitrios. 2019. "Multiobjective Mathematical Programming Model for the Optimization of End-of-Life Buildings’ Deconstruction and Demolition Processes" Sustainability 11, no. 5: 1426. https://doi.org/10.3390/su11051426
APA StyleAidonis, D. (2019). Multiobjective Mathematical Programming Model for the Optimization of End-of-Life Buildings’ Deconstruction and Demolition Processes. Sustainability, 11(5), 1426. https://doi.org/10.3390/su11051426




