Heterogeneous Causal Relationships between Spot and Futures Oil Prices: Evidence from Quantile Causality Analysis
Abstract
1. Introduction
2. Methodology
2.1. Filtering the Long-Run Co-Movement
2.2. Testing Non-Causality in Quantiles
3. Data and Descriptive Statistics
4. Empirical Results
4.1. The Quantile Causality Relationships between Crude Oil Spot and Futures Prices
4.2. Robustness Checks
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bopp, A.E.; Sitzer, S. Are petroleum futures prices good predictors of cash value? J. Futures Mark. 1987, 7, 705–719. [Google Scholar] [CrossRef]
- Serletis, A.; Banack, D. Market efficiency and co-integration: An application to petroleum markets. Rev. Futures Mark. 1990, 9, 372–385. [Google Scholar]
- Schwarz, T.V.; Szakmary, A.C. Price discovery in petroleum markets: Arbitrage, cointegration, and the time interval of analysis. J. Futures Mark. 1994, 14, 147–167. [Google Scholar] [CrossRef]
- Moosa, I.A.; Al-Loughani, N.E. The effectiveness of arbitrage and speculation in the crude oil futures market. J. Futures Mark. 1995, 15, 167–186. [Google Scholar] [CrossRef]
- Quan, J. Two-step testing procedure for price discovery role of futures prices. J. Futures Mark. 1992, 12, 139–149. [Google Scholar] [CrossRef]
- Moosa, I.A. An econometric model of price determination in the crude oil futures markets. In Proceedings of the Econometric Society Australasian Meeting, Perth, Australia, 1 July 1996; Volume 3, pp. 373–402. [Google Scholar]
- Baek, E.; Brock, W. A General Test for Nonlinear Granger Causality: Bivariate Model; Iowa State University and University of Wisconsin at Madison Working Paper: Madison, WI, USA, 1992. [Google Scholar]
- Abhyankar, A. Does the Stock Index Futures Market Tend to Lead the Cash? New Evidence from the FT-SE 100 stock Index Futures Market; Working Paper No 96-01; Department of Accounting and Finance, University of Stirling: Stirling, Scotland, 1996. [Google Scholar]
- Silvapulle, P.; Moosa, I.A. The relationship between spot and futures prices: Evidence from the crude oil market. J. Futures Mark. 1999, 19, 175–193. [Google Scholar] [CrossRef]
- Bekiros, S.D.; Diks, C.G.H. The relationship between crude oil spot and futures prices: Cointegration, linear and nonlinear causality. Energy Econ. 2008, 30, 2673–2685. [Google Scholar] [CrossRef]
- Westgaard, S.; Estenstad, M.; Seim, M.; Frydenberg, S. Co-integration of ICE Gas oil and Crude oil futures. Energy Econ. 2011, 33, 311–320. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, C. Are crude oil spot and futures prices cointegrated? Not always! Econ. Model. 2013, 33, 641–650. [Google Scholar] [CrossRef]
- Beckmann, J.; Belke, A.; Czudaj, R. Regime-dependent adjustment in energy spot and futures markets. Econ. Model. 2014, 40, 400–409. [Google Scholar] [CrossRef]
- Brock, W.A.; LeBaron, B. A dynamic structural mode for stock return volatility and trading volume. Rev. Econ. Stat. 1996, 78, 94–110. [Google Scholar] [CrossRef]
- Lux, T. Herd behaviour, bubbles and crashes. Econ. J. 1995, 105, 881–896. [Google Scholar] [CrossRef]
- Galeotti, M.; Lanza, A.; Manera, M. Rockets and feathers revisited: An international comparison on European gasoline markets. Energy Econ. 2003, 25, 175–190. [Google Scholar] [CrossRef]
- Peters, E.E. Fractal Market Analysis: Applying Chaos Theory to Investment and Economics; John Wiley & Sons: Hoboken, NJ, USA, 1994. [Google Scholar]
- Kahneman, D.; Tversky, A. Prospect theory: An analysis of decision under risk. Econometrica 1979, 47, 263–292. [Google Scholar] [CrossRef]
- Hammoudeh, S.; Dibooglu, S.; Aleisa, E. Relationships among US oil prices and oil industry equity indices. Int. Rev. Econ. Finance 2004, 13, 427–453. [Google Scholar] [CrossRef]
- Kawamoto, K.; Hamori, S. Market efficiency among futures with different maturities: Evidence from the crude oil futures market. J. Futures Mark. 2011, 31, 487–501. [Google Scholar] [CrossRef]
- Serra, T.; Zilberman, D.; Gil, J. Price volatility in ethanol markets. Eur. Rev. Agric. Econ. 2010, 38, 259–280. [Google Scholar] [CrossRef]
- Hassouneh, I.; Serra, T.; Goodwin, B.K. Non-parametric and parametric modeling of biodiesel, sunflower oil, and crude oil price relationships. Energy Econ. 2012, 34, 1507–1513. [Google Scholar] [CrossRef]
- Bekiros, S.D. Exchange rates and fundamentals: Co-movement, long-run relationships and short-run dynamics. J. Bank. Finance 2014, 39, 117–134. [Google Scholar] [CrossRef]
- Cabrera, B.L.; Schulz, F. Volatility linkages between energy and agricultural commodity prices. Energy Econ. 2016, 54, 190–203. [Google Scholar] [CrossRef]
- Chuang, C.C.; Kuan, C.M.; Lin, H.Y. Causality in quantiles and dynamic stock return–volume relations. J. Bank. Finance 2009, 33, 1351–1360. [Google Scholar] [CrossRef]
- Maslyuk, S.; Smyth, R. Cointegration between oil spot and future prices of the same and different grades in the presence of structural change. Energy Policy 2009, 37, 1687–1693. [Google Scholar] [CrossRef]
- Arouri, M.E.H.; Lahiani, A.; Lévy, A.; Nguyen, D.K. Forecasting the conditional volatility of oil spot and futures prices with structural breaks and long memory models. Energy Econ. 2012, 34, 283–293. [Google Scholar] [CrossRef]
- Chen, P.F.; Lee, C.C.; Zeng, J.H. The relationship between spot and futures oil prices: Do structural breaks matter? Energy Econ. 2014, 43, 206–217. [Google Scholar] [CrossRef]
- Huang, B.N.; Yang, C.W.; Hwang, M.J. The dynamics of a nonlinear relationship between crude oil spot and futures prices: A multivariate threshold regression approach. Energy Econ. 2009, 31, 91–98. [Google Scholar] [CrossRef]
- Lee, C.C.; Zeng, J.H. Revisiting the relationship between spot and futures oil prices: Evidence from quantile cointegrating regression. Energy Econ. 2011, 33, 924–935. [Google Scholar] [CrossRef]
- Chang, C.P.; Lee, C.C. Do oil spot and futures prices move together? Energy Econ. 2015, 50, 379–390. [Google Scholar] [CrossRef]
- Fan, Y.; Xu, J.H. What has driven oil prices since 2000? A structural change perspective. Energy Econ. 2011, 33, 1082–1094. [Google Scholar] [CrossRef]
- Bauwens, L.; Hafner, C.M.; Pierret, D. Multivariate volatility modeling of electricity futures. J. Appl. Econom. 2013, 28, 743–761. [Google Scholar] [CrossRef]
- Koenker, R.; Bassett, J.G. Regression quantiles. Econ. J. Econ. Society 1978, 13, 33–50. [Google Scholar] [CrossRef]
- Granger, C. Investigating causal relations by econometric models and cross-spectral methods. Econometrica 1969, 37, 424–438. [Google Scholar] [CrossRef]
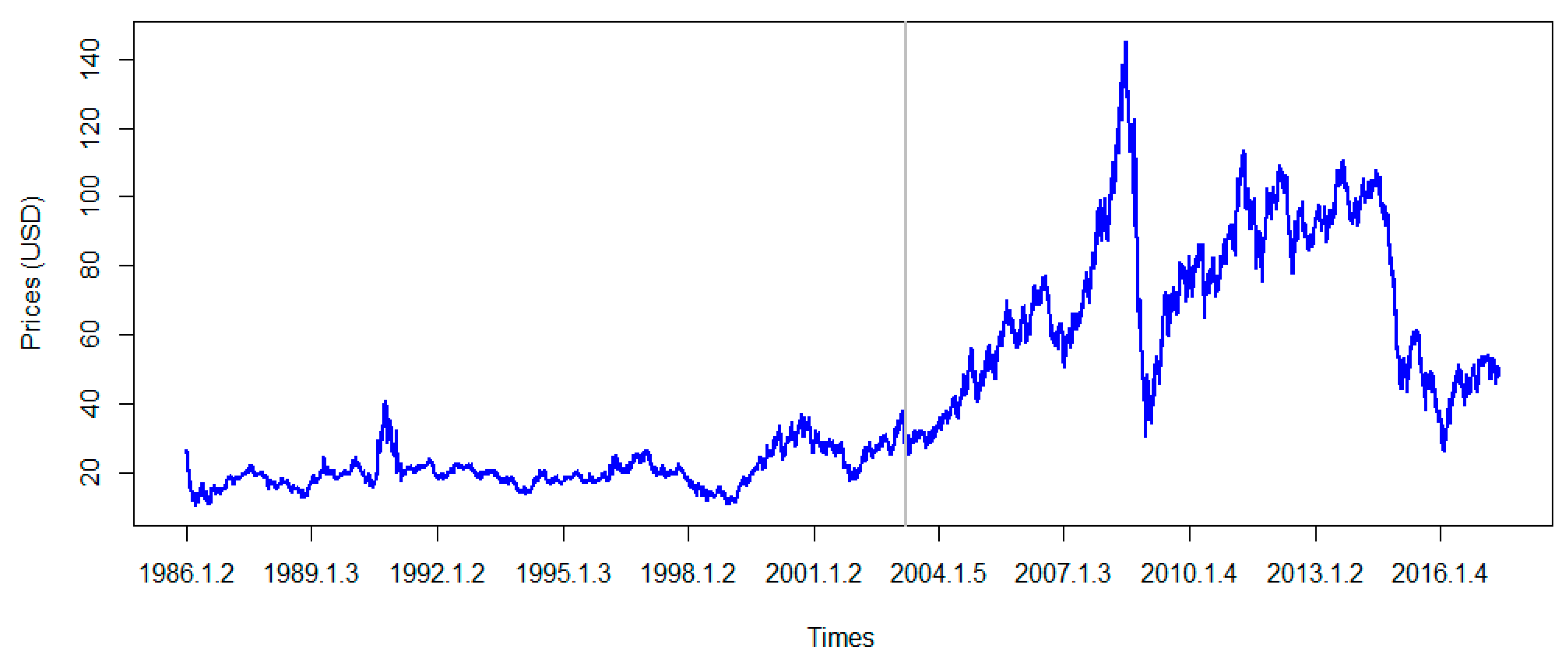
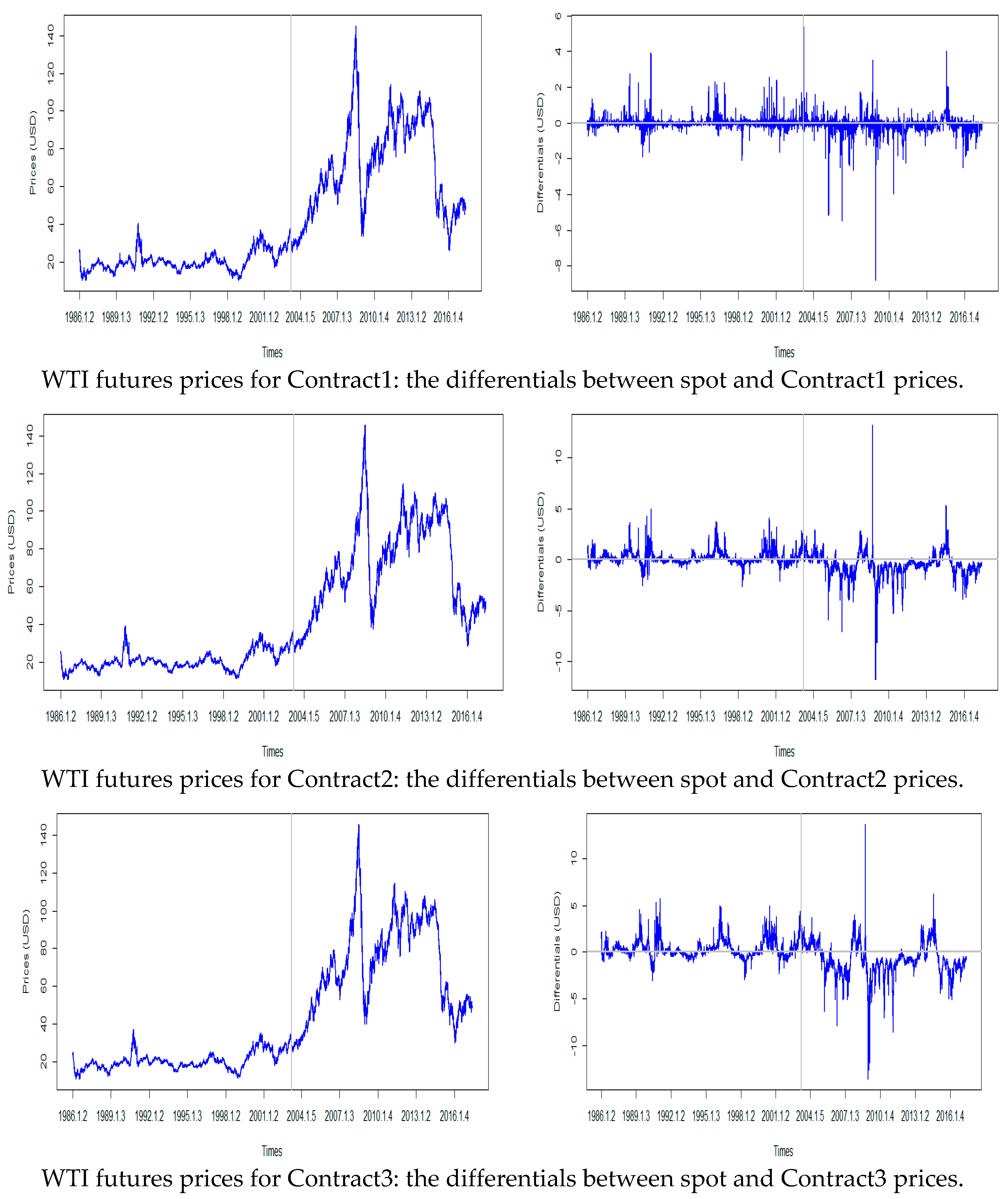
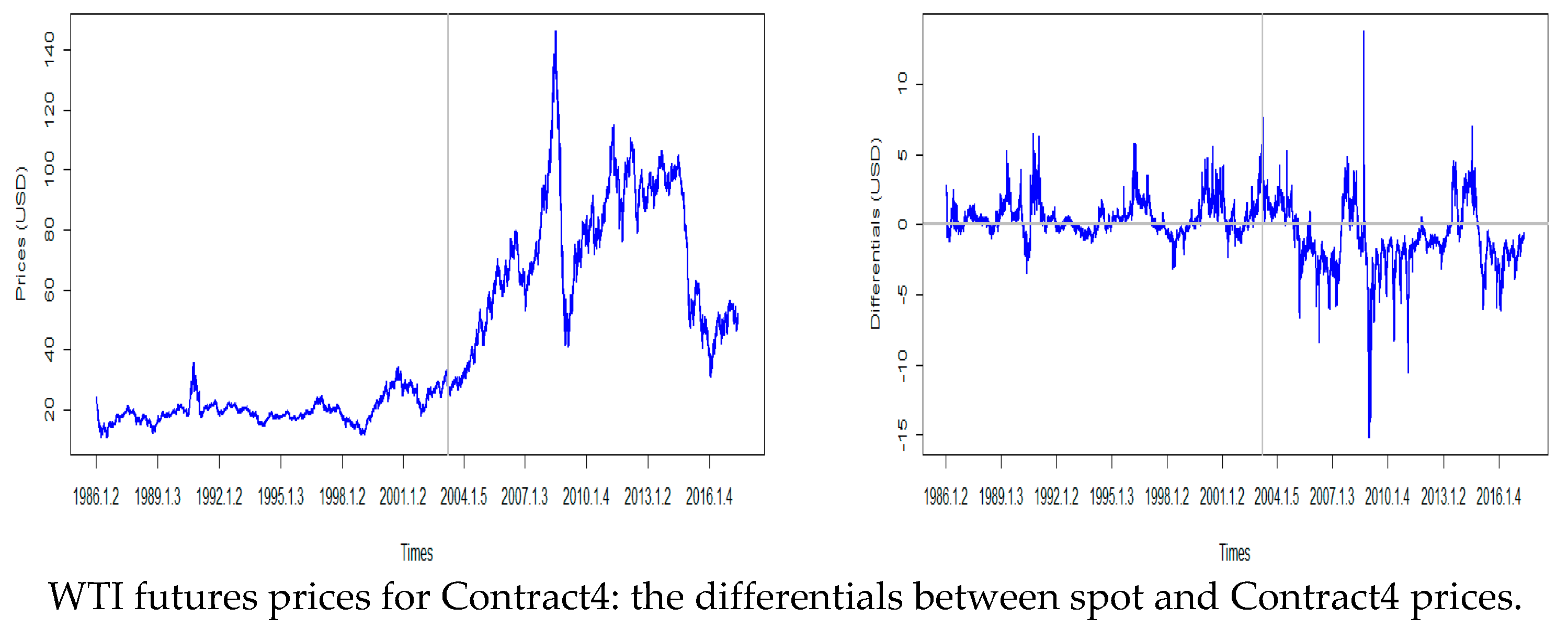
| Mean | Std. Dev. | Skewness | Kurtosis | Shapiro–Wilk Test | Augmented Dickey–Fuller (ADF) Test | KPSS Test | |
|---|---|---|---|---|---|---|---|
| Pre-Iraq War (2 January 1986–20 March 2003) | |||||||
| Spot | 3.0021 | 0.2398 | 0.2411 | 2.9561 | 0.9848 *** | −3.1090 | 1.0077 *** |
| Contract1 | 3.0009 | 0.2390 | 0.2328 | 2.9532 | 0.9847 *** | −3.0849 | 1.0086 *** |
| Contract2 | 2.9941 | 0.2303 | 0.2359 | 2.9560 | 0.9837 *** | −3.0443 | 1.0926 *** |
| Contract3 | 2.9881 | 0.2217 | 0.2300 | 2.9341 | 0.9853 *** | −3.0606 | 1.1541 *** |
| Contract4 | 2.9825 | 0.2133 | 0.2253 | 2.9153 | 0.9835 *** | −3.0638 | 1.1971 *** |
| Post-Iraq War (21 March 2003–26 May 2017) | |||||||
| Spot | 4.1785 | 0.3848 | −0.3781 | 2.1859 | 0.9604 *** | −2.6617 | 0.8450 *** |
| Contract1 | 4.1798 | 0.3841 | −0.3843 | 2.3160 | 0.9603 *** | −2.6745 | 0.8508 *** |
| Contract2 | 4.1880 | 0.3814 | −0.4416 | 2.3160 | 0.9595 *** | −2.5781 | 0.8854 *** |
| Contract3 | 4.1935 | 0.3804 | −0.4978 | 2.4259 | 0.9573 *** | −2.5200 | 0.9173 *** |
| Contract4 | 4.1972 | 0.3804 | −0.5490 | 2.5260 | 0.9545 *** | −2.4751 | 0.9463 *** |
| Full sample period (2 January 1986–26 May 2017) | |||||||
| Spot | 3.5339 | 0.6644 | 0.3742 | 1.7449 | 0.9168 *** | −2.6634 | 5.3136 *** |
| Contract1 | 3.5339 | 0.6651 | 0.3733 | 1.7408 | 0.9162 *** | −2.6634 | 5.3196 *** |
| Contract2 | 3.5339 | 0.6693 | 0.3759 | 1.7084 | 0.9100 *** | −2.5169 | 5.3748 *** |
| Contract3 | 3.5331 | 0.6726 | 0.3812 | 1.6825 | 0.9041 *** | −2.4155 | 5.4146 *** |
| Contract4 | 3.5317 | 0.6752 | 0.3879 | 1.6613 | 0.8984 *** | −2.3317 | 5.4432 *** |
| Variables | Null Hypothesis | Trace Statistics | Max. Eigenvalue Statistics |
|---|---|---|---|
| Pre-Iraq War (2 January 1986–20 March 2003) | |||
| Spot, Contract1 | None | 98.2863 (0.0001) *** | 98.2564 (0.0001) *** |
| At most 1 | 0.0298 (0.8878) | 0.0298 (0.8878) | |
| Spot, Contract2 | None | 24.9617 (0.0003) *** | 24.9203 (0.0001) *** |
| At most 1 | 0.0413 (0.8677) | 0.0413 (0.8677) | |
| Spot, Contract3 | None | 22.5687 (0.0007) *** | 22.5326 (0.0004) *** |
| At most 1 | 0.0361 (0.8764) | 0.0361 (0.8764) | |
| Spot, Contract4 | None | 21.6154 (0.0011) *** | 21.5768 (0.0006) *** |
| At most 1 | 0.0385 (0.8722) | 0.0385 (0.8722) | |
| Post-Iraq War (21 March 2003–26 May 2017) | |||
| Spot, Contract1 | None | 71.3869 (0.0000) *** | 71.3421 (0.0001) *** |
| At most 1 | 0.0448 (0.8623) | 0.0448 (0.8623) | |
| Spot, Contract2 | None | 32.8601 (0.0000) *** | 32.7395 (0.0000) *** |
| At most 1 | 0.1206 (0.7748) | 0.1206 (0.7748) | |
| Spot, Contract3 | None | 26.4837 (0.0001) *** | 26.3483 (0.0001) *** |
| At most 1 | 0.1353 (0.7615) | 0.1353 (0.7615) | |
| Spot, Contract4 | None | 22.5999 (0.0007) *** | 22.4537 (0.0004) *** |
| At most 1 | 0.1461 (0.7522) | 0.1461 (0.7522) | |
| Full sample period (2 January 1986–26 May 2017) | |||
| Spot, Contract1 | None | 153.2081 (0.0001) *** | 153.1900 (0.0001) *** |
| At most 1 | 0.0181 (0.9122) | 0.0181 (0.9122) | |
| Spot, Contract2 | None | 44.3798 (0.0000) *** | 44.3122 (0.0000) *** |
| At most 1 | 0.0675 (0.8311) | 0.0675 (0.8311) | |
| Spot, Contract3 | None | 38.6682 (0.0000) *** | 38.5652 (0.0000) *** |
| At most 1 | 0.1030 (0.7917) | 0.1030 (0.7917) | |
| Spot, Contract4 | None | 35.4214 (0.0000) *** | 35.2815 (0.0000) *** |
| At most 1 | 0.1398 (0.7575) | 0.1398 (0.7575) | |
| Pre-Iraq War (2 January 1986–20 March 2003) | |||||
| 1 | −0.0056 (0.0021) ** | −0.9555 (0.2444) *** | 0.0645 (0.1719) | 0.0397 (0.1749) | |
| 0.0009 (0.0021) | 0.0807 (0.2415) | 0.0345 (0.1699) | 0.0465 (0.1729) | ||
| 2 | −0.0136 (0.0051) ** | −0.1822 (0.0634) ** | −0.1834 (0.0959) | 0.3428 (0.1089) ** | |
| −0.0001 (0.0044) | −0.0061 (0.0553) | 0.0303 (0.0838) | 0.0950 (0.0951) | ||
| 3 | −0.0154 (0.0061) * | −0.1079 (0.0404) ** | −0.1256 (0.0817) | 0.2959 (0.1006) ** | |
| 0.0006 (0.0049) | 0.0017 (0.0325) | 0.0097 (0.0658) | 0.1171 (0.0811) | ||
| 4 | −0.0171 (0.0070) * | −0.0808 (0.0316) * | −0.0717 (0.0738) | 0.2414 (0.0974) * | |
| 0.0017 (0.0053) | 0.0063 (0.0238) | 0.0156 (0.0555) | 0.1027 (0.0732) | ||
| Post-Iraq War (21 March 2003–26 March 2017) | |||||
| 1 | −0.0118 (0.0026) *** | −1.5300 (0.2616) *** | 0.1048 (0.1936) | 0.1005 (0.2012) | |
| −0.0047 (0.0026) | −0.6637 (0.2616) | 0.1404 (0.1936) | 0.0380 (0.2012) | ||
| 2 | −0.0137 (0.0045) ** | −0.2374 (0.0704) *** | 0.0630 (0.1262) | 0.1490 (0.1381) | |
| −0.0054 (0.0041) | −0.1027 (0.0639) | 0.3233 (0.1145) ** | −0.1392 (0.1253) | ||
| 3 | −0.0107 (0.0047) * | −0.1113 (0.0442) * | 0.1709 (0.1074) | 0.0221 (0.1221) | |
| −0.0020 (0.0041) | −0.0277 (0.0382) | 0.3613 (0.0929) *** | −0.1875 (0.1056) | ||
| 4 | −0.0086 (0.0047) | −0.0686 (0.0338) * | 0.2118 (0.0985) * | −0.0314 (0.1156) | |
| −0.0001 (0.0040) | −0.0064 (0.0282) | 0.3529 (0.0822) *** | −0.1847 (0.0965) | ||
| Full sample period (2 January 1986–26 March 2017) | |||||
| 1 | 0.0063 (0.0013) *** | −1.2848 (0.1760) *** | 0.1456 (0.1275) | 0.0024 (0.1308) | |
| 0.0020 (0.0013) | −0.3564 (0.1752) * | 0.1613 (0.1269) | −0.0362 (0.1302) | ||
| 2 | 0.0084 (0.0018) *** | −0.2335 (0.0437) *** | −0.0811 (0.0755) | 0.2646 (0.0842) ** | |
| 0.0038 (0.0016) * | −0.0988 (0.0389) * | 0.1584 (0.0673) * | −0.0020 (0.0751) | ||
| 3 | 0.0086 (0.0020) *** | −0.1316 (0.0274) *** | −0.0146 (0.0644) | 0.1959 (0.0765) * | |
| 0.0034 (0.0017) * | −0.0476 (0.0229) * | 0.1445 (0.0538) ** | 0.0082 (0.0639) | ||
| 4 | 0.0085 (0.0021) *** | −0.0947 (0.0212) *** | 0.0296 (0.0585) | 0.1465 (0.0731) * | |
| 0.0029 (0.0017) | −0.0285 (0.0167) | 0.1375 (0.0463) ** | 0.0094 (0.0579) | ||
| Box–Ljung Test | Shapiro–Wilk Test | ADF Test | KPSS Test | |
|---|---|---|---|---|
| Pre-Iraq War (2 January 1986–20 March 2003) | ||||
| Spot | 0.0004 | 0.9551 *** | −9.5090 *** | 0.1010 |
| Contract1 | 0.0018 | 0.9528 *** | −9.3631 *** | 0.1077 |
| Contract2 | 0.0001 | 0.9543 *** | −9.3493 *** | 0.1013 |
| Contract3 | 0.0038 | 0.9508 *** | −9.2140 *** | 0.1015 |
| Contract4 | 0.0069 | 0.9455 *** | −9.0654 *** | 0.1050 |
| Post-Iraq War (21 March 2003–26 March 2017) | ||||
| Spot | 0.0133 | 0.9767 *** | −7.1097 *** | 0.3090 |
| Contract1 | 0.0429 | 0.9796 *** | −7.1769 *** | 0.2459 |
| Contract2 | 0.2301 | 0.9887 *** | −7.1594 *** | 0.3296 |
| Contract3 | 0.2021 | 0.9893 *** | −7.2937 *** | 0.3358 |
| Contract4 | 0.1770 | 0.9883 *** | −7.3710 *** | 0.3340 |
| Full sample period (2 January 1986–26 March 2017) | ||||
| Spot | 0.0107 | 0.9619 *** | −11.7842 *** | 0.0978 |
| Contract1 | 0.0314 | 0.9624 *** | −12.1272 *** | 0.0685 |
| Contract2 | 0.0387 | 0.9704 *** | −11.8287 *** | 0.0775 |
| Contract3 | 0.0127 | 0.9709 *** | −11.6817 *** | 0.0835 |
| Contract4 | 0.0039 | 0.9693 *** | −11.5503 *** | 0.0895 |
| Spot → Futures | Futures → Spot | |||
|---|---|---|---|---|
| p-Value | Causality | p-Value | Causality | |
| Pre-Iraq War (2 January 1986–20 March 2003) | ||||
| Contract1 | 0.9248 (3) | No | 0.9668 (3) | No |
| Contract2 | 0.7539 (5) | No | 0.5607 (5) | No |
| Contract3 | 0.9589 (2) | No | 0.7166 (2) | No |
| Contract4 | 0.9782 (3) | No | 0.8439 (3) | No |
| Post-Iraq War (21 March 2003–26 March 2017) | ||||
| Contract1 | 0.8932 (7) | No | 0.8485 (7) | No |
| Contract2 | 0.4026 (7) | No | 0.1698 (7) | No |
| Contract3 | 0.6034 (3) | No | 0.3245 (3) | No |
| Contract4 | 0.6993 (2) | No | 0.4058 (2) | No |
| Spot → Futures | Futures → Spot | |||||||
|---|---|---|---|---|---|---|---|---|
| Contract1 | Contract2 | Contract3 | Contract4 | Contract1 | Contract2 | Contract3 | Contract4 | |
| [0.05 0.2] | 9.2374 ** [2] | 8.3121 * [2] | 2.0839 [1] | 2.2403 [2] | 9.4682 ** [2] | 18.2862 *** [2] | 17.1607 *** [2] | 19.9029 *** [2] |
| [0.05 0.5] | 9.2374 ** [2] | 8.3121 * [2] | 2.0839 [1] | 2.0627 [2] | 9.1795 ** [2] | 17.4017 *** [2] | 16.9700 *** [2] | 19.6770 *** [2] |
| [0.05 0.95] | 6.2136 [2] | 6.3121 [2] | 1.8371 [2] | 1.9383 [2] | 23.4537 *** [2] | 29.7522 *** [2] | 16.9700 *** [2] | 19.2939 *** [2] |
| [0.2 0.5] | 4.4442 [2] | 2.6224 [2] | 1.8447 [2] | 2.0627 [2] | 4.0405 [2] | 4.7525 [1] | 5.6666 [2] | 8.7082 * [2] |
| [0.2 0.95] | 4.6850 [2] | 3.4934 [1] | 1.8242 [2] | 1.9994 [2] | 23.4537 *** [2] | 29.4822 *** [2] | 14.8924 *** [2] | 18.7581 *** [2] |
| [0.5 0.8] | 4.8203 [2] | 2.4140 [1] | 1.3420 [1] | 1.0846 [2] | 7.3793 * [2] | 9.4254 ** [2] | 4.0643 [2] | 3.8276 [2] |
| [0.5 0.95] | 4.8203 [2] | 3.4690 [1] | 1.3378 [1] | 1.3442 [2] | 23.4537 *** [2] | 29.7522 *** [2] | 14.6251 *** [2] | 19.5730 *** [2] |
| [0.8 0.95] | 4.2922 [2] | 3.4934 [1] | 0.9152 [1] | 1.5146 [2] | 23.4537 *** [2] | 30.4697 *** [2] | 14.9743 *** [2] | 28.3354 *** [2] |
| Spot → Futures | Futures → Spot | |||||||
|---|---|---|---|---|---|---|---|---|
| Contract1 | Contract2 | Contract3 | Contract4 | Contract1 | Contract2 | Contract3 | Contract4 | |
| [0.05 0.2] | 4.5930 [2] | 5.3037 [1] | 6.5114 [1] | 7.6346 * [1] | 8.4553 * [2] | 3.9274 [1] | 4.0869 [2] | 3.7192 [1] |
| [0.05 0.5] | 4.3737 [2] | 5.3037 [1] | 6.5114 [1] | 7.6346 * [1] | 8.4499 * [2] | 3.9279 [1] | 4.0869 [2] | 6.2898 [2] |
| [0.05 0.95] | 4.3737 [2] | 34.1576 *** [2] | 23.2410 *** [2] | 13.0549 ** [2] | 8.4499 * [2] | 4.05337 [2] | 20.4756 *** [1] | 11.6323 ** [1] |
| [0.2 0.5] | 3.0623 [2] | 5.0740 [2] | 1.9048 [1] | 0.9275 [1] | 3.4061 [2] | 0.7471 [2] | 2.6708 [2] | 3.6211 [2] |
| [0.2 0.95] | 3.0885 [2] | 32.8537 *** [2] | 22.6714 *** [2] | 6.3535 [2] | 2.6947 [1] | 39.5296 *** [2] | 21.4325 *** [1] | 11.6323 ** [1] |
| [0.5 0.8] | 1.9475 [1] | 4.6018 [1] | 3.4892 [1] | 1.8463 [1] | 2.7098 [1] | 1.1411 [1] | 1.3939 [2] | 1.3927 [2] |
| [0.5 0.95] | 3.0885 [2] | 34.1576 *** [2] | 23.2411 *** [2] | 13.0549 *** [2] | 2.7058 [1] | 40.5337 *** [2] | 22.8051 *** [1] | 17.1111 *** [1] |
| [0.8 0.95] | 3.0885 [2] | 34.2209 *** [2] | 23.6555 *** [2] | 13.0649 *** [2] | 2.2274 [2] | 41.0123 *** [2] | 23.1001 *** [1] | 17.3480 *** [2] |
| Spot → Futures | Futures → Spot | |||||||
|---|---|---|---|---|---|---|---|---|
| Contract1 | Contract2 | Contract3 | Contract4 | Contract1 | Contract2 | Contract3 | Contract4 | |
| [0.05 0.2] | 15.4848 *** [2] | 10.8379 ** [2] | 5.4126 [2] | 6.3391 [2] | 25.8221 *** [1] | 22.7705 *** [1] | 16.1468 *** [1] | 34.8730 *** [2] |
| [0.05 0.5] | 14.6070 *** [1] | 7.4860 * [2] | 4.9811 [2] | 5.4934 [2] | 24.7296 *** [1] | 27.1477 *** [1] | 14.5048 *** [1] | 29.1598 *** [2] |
| [0.05 0.95] | 4.6070 [1] | 10.6821 ** [2] | 18.7855 *** [1] | 23.6111 *** [1] | 24.5047 *** [1] | 25.1895 *** [1] | 14.2752 *** [1] | 29.1598 *** [2] |
| [0.2 0.5] | 4.6885 [1] | 2.7414 [1] | 2.3496 [1] | 2.6201 [1] | 4.5315 [2] | 3.4653 [2] | 4.5449 [2] | 2.5674 [1] |
| [0.2 0.95] | 4.6070 [1] | 10.6821 ** [2] | 17.3635 *** [1] | 26.2982 *** [1] | 14.2069 *** [2] | 15.5510 *** [1] | 16.1358 *** [2] | 14.2302 *** [1] |
| [0.5 0.8] | 0.9869 [1] | 4.3991 [2] | 2.3702 [2] | 2.4702 [1] | 8.2765 * [2] | 5.4818 [1] | 6.0435 [2] | 4.2267 [1] |
| [0.5 0.95] | 2.5891 [2] | 10.6821 ** [2] | 4.1296 [2] | 7.8052 * [1] | 14.0264 *** [2] | 15.2937 *** [1] | 15.8470 *** [1] | 14.2169 *** [2] |
| [0.8 0.95] | 1.4630 [2] | 10.6821 ** [2] | 3.4805 [2] | 8.1365 * [1] | 14.9434 *** [2] | 14.6544 *** [1] | 11.6118 ** [1] | 12.0608 ** [1] |
| Spot → Futures | Futures → Spot | |||||||
|---|---|---|---|---|---|---|---|---|
| Contract1 | Contract2 | Contract3 | Contract4 | Contract1 | Contract2 | Contract3 | Contract4 | |
| [0.05 0.2] | 5.9879 [2] | 4.2671 [2] | 4.2104 [2] | 9.8374 * [2] | 60.2010 *** [2] | 29.6089 *** [2] | 26.0349 *** [2] | 5.7807 [1] |
| [0.05 0.5] | 5.7533 [2] | 4.2671 [2] | 3.2104 [2] | 8.1743 * [2] | 60.2010 *** [2] | 29.6089 *** [2] | 25.9487 *** [2] | 5.6538 [1] |
| [0.05 0.95] | 5.4563 [2] | 8.5152 * [2] | 9.2749 * [2] | 5.5018 [2] | 57.8418 *** [2] | 29.0009 *** [2] | 24.7870 *** [2] | 24.7957 *** [2] |
| [0.2 0.5] | 2.4960 [2] | 5.3953 [2] | 6.7061 [2] | 9.4760 ** [2] | 7.0655 [2] | 8.6087 [2] | 5.0962 [2] | 4.0469 [2] |
| [0.2 0.95] | 7.1707 [1] | 4.3990 [2] | 15.0111 *** [2] | 9.3666 ** [2] | 6.1943 [2] | 17.8461 [2] | 18.2479 [2] | 6.7962 [2] |
| [0.5 0.8] | 11.0982 ** [2] | 12.7659 ** [1] | 4.1307 [2] | 14.4846 *** [2] | 8.4318 * [2] | 11.0112 ** [2] | 6.2218 [2] | 5.0121 [2] |
| [0.5 0.95] | 8.3867 [1] | 4.4475 [1] | 15.0111 *** [2] | 14.4846 *** [2] | 5.4098 [2] | 19.8665 *** [2] | 18.2479 *** [2] | 6.7962 [2] |
| [0.8 0.95] | 8.7437 [1] | 4.4668 [1] | 15.0111 *** [2] | 13.0619 *** [2] | 3.0464 [1] | 19.9091 *** [2] | 19.3863 *** [2] | 7.3149 [2] |
| Spot → Futures | Futures → Spot | |||||||
|---|---|---|---|---|---|---|---|---|
| Contract1 | Contract2 | Contract3 | Contract4 | Contract1 | Contract2 | Contract3 | Contract4 | |
| [0.05 0.2] | 8.3865 * [1] | 8.0887 * [1] | 5.1641 [1] | 4.9399 [1] | 9.3865 ** [1] | 8.0932 * [1] | 7.9731 * [1] | 4.6704 [1] |
| [0.05 0.5] | 9.3616 ** [1] | 5.0887 [1] | 7.7232 * [1] | 8.8796 * [1] | 16.3616 *** [1] | 9.9604 ** [1] | 7.6927 * [1] | 4.1412 [1] |
| [0.05 0.95] | 8.1970 * [1] | 9.0991 * [1] | 8.0268 * [1] | 4.7779 [1] | 7.1970 * [1] | 8.3519 * [1] | 10.6387 ** [1] | 7.4150 * [1] |
| [0.2 0.5] | 1.6374 [2] | 4.1192 [2] | 1.8168 [2] | 0.9915 [1] | 1.5952 [2] | 5.6270 [2] | 3.5611 [2] | 0.7510 [1] |
| [0.2 0.95] | 7.7873 * [2] | 7.7286 * [2] | 4.6896 [2] | 1.8588 [1] | 7.8873 * [1] | 8.3848 * [2] | 4.3878 [2] | 4.7086 [2] |
| [0.5 0.8] | 4.1830 [1] | 1.2782 [1] | 2.5044 [2] | 1.3040 [1] | 9.1830 ** [1] | 8.0836 * [1] | 0.8384 [1] | 1.6212 [2] |
| [0.5 0.95] | 5.1970 [1] | 2.4625 [1] | 4.6200 [2] | 1.8588 [1] | 9.1970 ** [1] | 8.3372 * [1] | 4.42106 [2] | 7.4150 * [2] |
| [0.8 0.95] | 5.2425 [1] | 4.7286 [1] | 4.6896 [2] | 1.9002 [1] | 17.2425 *** [1] | 12.3644 *** [1] | 9.8822 ** [2] | 7.4532 * [2] |
| Spot → Futures | Futures → Spot | |||||||
|---|---|---|---|---|---|---|---|---|
| Contract1 | Contract2 | Contract3 | Contract4 | Contract1 | Contract2 | Contract3 | Contract4 | |
| [0.05 0.2] | 4.7512 [2] | 5.1152 [1] | 5.2672 [1] | 6.4581 [1] | 9.1397 ** [2] | 7.4197 * [2] | 8.3580 * [1] | 8.4836 * [2] |
| [0.05 0.5] | 5.7512 [2] | 5.0831 [1] | 3.2672 [1] | 5.3802 [1] | 8.9742 * [2] | 7.4197 * [2] | 8.3580 * [1] | 8.4836 * [2] |
| [0.05 0.95] | 5.5408 [2] | 4.9886 [1] | 4.5152 [1] | 6.2128 [1] | 8.9742 * [2] | 6.7313 [2] | 7.8840 * [1] | 8.2559 * [2] |
| [0.2 0.5] | 1.2418 [1] | 1.8842 [1] | 3.9127 [2] | 3.5803 [2] | 1.2244 [1] | 2.2678 [2] | 2.4113 [2] | 1.9993 [2] |
| [0.2 0.95] | 6.5433 [2] | 1.8842 [1] | 3.9127 [2] | 4.4660 [2] | 7.2887 * [2] | 2.2624 [2] | 2.4113 [1] | 2.9429 [2] |
| [0.5 0.8] | 5.5519 [1] | 8.5700 * [1] | 7.7447 * [1] | 1.7811 [2] | 1.4503 [1] | 1.6580 [1] | 1.4408 [1] | 1.5228 [1] |
| [0.5 0.95] | 6.7397 [2] | 8.7412 * [1] | 9.5149 ** [1] | 8.4168 * [2] | 7.2887 * [2] | 8.7569 * [1] | 8.8760 * [2] | 1.5228 [1] |
| [0.8 0.95] | 6.7397 [2] | 8.7547 * [1] | 11.5755 ** [1] | 10.4434 ** [2] | 7.2887 * [2] | 9.7569 * [1] | 1.4160 [2] | 7.9429 * [2] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, X.; Zhu, H.; Yang, X. Heterogeneous Causal Relationships between Spot and Futures Oil Prices: Evidence from Quantile Causality Analysis. Sustainability 2019, 11, 1359. https://doi.org/10.3390/su11051359
Su X, Zhu H, Yang X. Heterogeneous Causal Relationships between Spot and Futures Oil Prices: Evidence from Quantile Causality Analysis. Sustainability. 2019; 11(5):1359. https://doi.org/10.3390/su11051359
Chicago/Turabian StyleSu, Xianfang, Huiming Zhu, and Xinxia Yang. 2019. "Heterogeneous Causal Relationships between Spot and Futures Oil Prices: Evidence from Quantile Causality Analysis" Sustainability 11, no. 5: 1359. https://doi.org/10.3390/su11051359
APA StyleSu, X., Zhu, H., & Yang, X. (2019). Heterogeneous Causal Relationships between Spot and Futures Oil Prices: Evidence from Quantile Causality Analysis. Sustainability, 11(5), 1359. https://doi.org/10.3390/su11051359





