Abstract
This paper explores the sensitivity of Romanian collective investment undertakings’ returns to changes in equity, fixed income and foreign exchange market returns. We use a sample of 80 open-end investment funds and pension funds with daily returns between 2016 and 2018. Our methodology consists of measuring changes in the daily conditional volatility for the fund returns (EGARCH) and changes in their conditional correlation with selected market risk factors (DCC MV-GARCH) throughout different volatility regimes identified using a Markov Regime Switching model. We argue that, on average, the level of conditional correlations between funds and market risk factors remained stable and unconcerned by the volatility regimes. In addition, for only less than half of the funds in the sample, their volatility regimes were synchronized with those of the selected market risk factors. We found that, on average, fund returns are more correlated with equity returns and less correlated with changes in local bond yields, while not being significantly influenced by changes in foreign bond yields or changes in foreign exchange. During the period investigated equity returns were the most volatile while the funds returns volatility were, on average, much more reduced. Overall, our results show the resilience of the Romanian collective investment sector to the selected market risk factors, during the investigated period.
1. Introduction
Institutional investors represent one of the most important components of the capital market and play an important role in the financial system. In Romania, the most visible local institutional investors are pension funds, mutual funds (comprised of both open-end funds—UCITS and closed end funds—AIFs) and insurance companies.
According to the monthly reports of the Romanian Financial Supervisory Authority [1], pension funds are the largest non-bank sub-sector of the local financial system, with assets of 10.6 billion EUR (5.2% of GDP) at the end of 2018. There are 17 pension funds (split between two pillars: mandatory and optional) which invest mainly in fixed income (83%) and listed equity (17%). These funds hold approximately 20% of the outstanding sovereign bonds issued by the Romanian Government and around 20% of the capitalization of the free float on the national stock exchange, while also accounting for 15% of the exchange turnover.
The mutual funds sub-sector is comprised of 78 UCITS and 31 AIFs, and is comparable in size with the pension funds, with total assets of 8.8 billion EUR (4.3% of GDP). There are several types of open-end funds (e.g., 19 equity funds, 25 bond funds, 33 hybrid funds and 1 money market fund) with the largest category in terms of assets being the bond funds (3.4 billion EUR).
For comparison, at the end of 2018 the main segment of the Romanian stock exchange had a total capitalization of 30.7 billion EUR (15% of GDP) and 87 listed companies (domestic and foreign).
Especially in recent years, this sector was under intense scrutiny by market professionals, supervisory agencies and researchers due to its significant expansion and to its increasing relevance for financial stability. Thus, recent research no longer aims only at understanding performance and risk for individual undertakings (micro level), but also tries to assess determinants of return, volatility and resilience at an aggregated level, for the entire sector.
Regarding the micro level analysis, one important research question that is approached in the literature targets the persistence of performance during different market circumstances and periods of the financial and business cycle. Authors used different methods to distinguish between types of regime, referring to macroeconomic indicators, events selected from crisis databases or indices that reflect the performance of the equity market.
The macro level, with respect to the determinants of the evolution of the asset management sector, its resilience and its implications for financial stability is less documented. For a long period, the focus was on the banking sector, which was seen as the most relevant part of the financial sector and having the most significant implications for the real economy. For instance, investment banks are the fundamental actors in the securities industry, being involved in the creation and flow of financial securities and derivatives [2]. Systemic risk is a property of interrelated structures, by which the failure of a primarily minor set of bodies can lead to the failure of a substantial share of the system [3]. Such interconnectedness is a facet of the contemporary financial system due to financial innovation and liberalization [4]. Only after the global financial crisis triggered in 2007/2008 the non-banking parts of the financial sector started to attract more attention, and the first among them to be included in researchers’ work was the insurance sector. As result of this chain of priorities, for example, we now have criteria to systematically identify global banks and insurers and to monitor their resilience to risk, but we still lack similar tools for the asset management industry. In addition, a consistent framework of macroprudential instruments was developed for banks, but we only have incipient designs of similar constructions for insurance and asset management. In this vein, Spokeviciute et al. [5] emphasized the prominence of supervisory requests that fortify banks in good times, looking forward to upcoming systemic distress.
This study expands the existing literature in two ways. First, it has a mixed micro and macro level approach, computing indicators and measures of risk for individual undertakings, later aggregating them in order to offer a view on the resilience of the entire fund sector. Secondly, it approaches persistence from a different perspective, related to different factors and using different tools than previously investigated in the literature.
We test the sensitivity of fund returns to five market risk factors (domestic equity market returns, international equity market returns, changes in domestic bond yield, changes in international bond yields and changes in the FX rate) expressed by changes in conditional volatility and conditional correlation with each specific factor. We then study the behavior of these measures during periods of two different volatility regimes for each factor (high and low volatility), identified using a Markov switching model.
The past demonstrates that many financial crises and succeeding economic recessions took place in the emerging market sphere. According to Kenc et al. [6] emerging market economies tend to grow at quicker rates than advanced economies and are expected to suffer external imbalances such as trade and/or capital account shortages. Our results serve to identify the most relevant market risk factors for the Romanian asset management sector (domestic and foreign equity market returns), but also show the resilience of the overall sector. In addition, we confirm the persistence of the correlation with the market risk factors unconcerned by the volatility regime (that could be explained by the managers’ reduced ability to adapt the portfolio structure to the volatility cycle). Our sample is made of a significant number of investment vehicles, mostly open-end investment funds but also pension funds.
The rest of the paper is organized as follows. The second section discusses the most relevant related studies. The third section describes the data and the methodology. The fourth section shows the empirical outcomes. The final section summarizes the study, provides policy implications, alongside study limitations and proposes future research avenues in the field.
2. Literature Review
Mutual fund performance is extensively documented in the finance literature, with many authors also focusing on the determinants of persistence over different market regimes (mostly defined by the up or down trend of the main indices). Most of the initial approaches used beta, as a measure of systematic risk, trying to document its behavior over time. Later research also included several measures of performance that relate the fund return (absolute or relative) to risk (in different interpretations). In many articles with this focus, the research questions are formulated in the context of the efficient market hypothesis. If a market is fully efficient and several novel info are directly and properly assimilated by financial markets, it would be impossible for any fund manager to persistently outclass the market [7]. Ferreira et al. [8] highlighted the occurrence of a local advantage in countries with less efficient stock markets, weaker investor protection and more corruption, as well as in the course of market slumps and in more illiquid stocks.
Fabozzi and Francis [9] tested whether the betas for open-end mutual funds in Taiwan were different in bull and bear market periods and found evidence to suggest that, on average, the level of selectivity was insignificant and the market timing was negative, concluding that the managers were not able to adapt their stock selectivity and to “time the market”. Hence, Chen and Lai [10] suggested that fund managers should pick more concentrated funds in less volatile markets, but move their investments to varied funds in turmoil market stages. Yi and He [11] showed that most Chinese mutual funds are able to time the market. Further, Yi, et al. [12] established that Chinese funds have the ability to time the market volatility and liquidity. Asal [7] noticed that the managers which outperform the market due to good skills are occasional. In the same vein, Choi et al. [13] revealed that investors that are more skilled set concentrated portfolios, mainly in overseas markets and industries. Hiraki et al. [14] noticed that the higher performance of concentrated funds is mainly determined by industry rather than country concentration. However, Hornstein and Hounsell [15] noted the superiority of fund performance when unaccompanied managers invest in their own funds rather than team managers co-investing in the funds.
Alexander and Stover [16] investigated a sample of mutual funds for the consistency of their performance and the stability of the systematic risk (measured by beta) during bull and bear market conditions and found that, on average, the managers failed to increase the fund’s systematic risk during positive market periods. In addition, according to their results, the performance of the various classes of mutual funds seemed to be invariant relative to market conditions. Stafylas et al. [17] pointed out several factors that influence hedge fund performance, namely size, age and fees. Hwang et al. [18] concluded that systemic risk is a prevailing cause of cross-sectional deviations in hedge fund returns. Di Tommaso and Piluso [19] showed that fund size, minimum investment, transparency and liquidity are the paramount drivers towards a likelihood of hedge fund failure, although the management variables registered a lower explanatory power. Racicot and Theoret [20] concluded that the beta is the most asymmetric to the business cycle, hedge funds raising their beta throughout periods of expansion and alleviating it in recession.
Carhart [21] argued that persistence in mutual fund performance is not related to the managers’ ability to pick outperforming stocks, but is rather explained by common factors in stock returns and by the fund’s expenses. The author also argues that the exception from this conclusion is observed in the case of the worst underperforming funds for which the returns feature an abnormal behavior. In contrast, Andreu et al. [22] claimed that security selection is the key driver of fund performance unconcerned by the employed sample period or asset-pricing model. Likewise, Abdelmonem Oueslati et al. [23] acknowledged that the global performance of mutual fund managers is due to selectivity and market timing. For instance, Liao et al. [24] established that Chinese mutual fund managers have timing abilities. Nevertheless, Ayadi et al. [25] proved that Canadian fund managers do not show selection and timing skills.
Liang [26] documented differences between hedge funds (for whom empirical evidence suggests they employ dynamic trading strategies and, as a result, usually have low systematic risk) and traditional investment vehicles, such as mutual funds. The author argues that the fee structures used by hedge funds seem to align managers’ compensation with fund performance. There is also documented that funds with a “high watermark” clause in the fee structure significantly outperform the others. The employed data showed that, on average, hedge funds provided higher Sharpe ratios compared with mutual funds between 1992 and 1996, although their returns had higher volatility. According to Schaub and Schmid [27], greater incentive fees help to defeat the illiquidity discount noticed in crisis phases.
In their influential paper, Engle et al. [28] showed that the role of news from nearby regions (the meteor shower) is favored to indigenous effects from the prior day (the heat wave) as a reason for the transmission of volatility in the foreign exchange market. Therefore, the volatility transmission among stock markets in Czech Republic, Hungary, Poland and Slovakia was investigated by Kasch-Haroutounian and Price [29] using a BEKK model. The empirical findings suggested that the volatility in the Polish stock market is affected by the volatility originating in the Hungarian stock market. Bubak et al. [30] revealed the presence of volatility spillovers amongst the Central European foreign exchange markets on an intraday basis. As well, Clements et al. [31] confirmed the certainty that there are significant volatility connections between financial markets. However, BenSaida et al. [32] found that during stages of quietness, the U.S. and Germany are viewed as net spreaders of risk, whereas Hong Kong and Japan are net receivers. By means of the Markov-switching model, Adam et al. [33] acknowledged three regimes of the response of exchange rates to fluctuations in financial stress. By employing time-varying transition probability Markov switching models, Ning and Zhang [34] documented that short-term international capital flows of China are more sensitive to exchange rates, but not sensitive to interest rates and assets prices. Kocenda and Moravcova [35] revealed the uppermost levels of cross-currency volatility were established during the global financial crisis.
Lee and Ward [36] aimed to investigate the relationship between past and present performance of UK real estate between 1981 and 1996, through a Markov Chain approach. The most important remark from the analysis was that persistence did not appear to be driven by volatility. Chang [37] showed via Markov-switching GRG copula that two distinct dependence structures exist between the inflation rate and the real estate investment trust.
Füss et al. [38] used alternative volatility models such as GARCH (p,q) and EGARCH (p,q), for particular hedge fund classes (differentiated by their investment strategies) and then compared with each other. The authors showed that GARCH-type VaR is a better measure of downside risk, especially for trading strategies that present a negative skewness and excess kurtosis. Mishra et al. [39] applied GARCH models such as GRACH, EGRACH and TGRACH to investigate the volatility of the Indian stock market between 1991 and 2008. From all the models, the TGARCH model performed the best in estimating and predicting the volatility of the Indian capital market. Dark [40] noticed robustness when hedging via MS-VECM-FIEGARCH, MS-VECM-FIAPARCH and MS-VECM-FIGARCH as long as such models constantly outperform short memory volatility models, as well as the OLS hedge. Luo et al. [41] found that the optimal portfolio selected by an orthogonal GARCH model outperforms the exponentially weighted moving average (EWMA), Markov switching model (MSM) and the Gaussian mixture model (GMM) with regards to the risk and returns through the entire investment period. Yan and Li [42] assessed the performance of hedge ratios out of Chinese stock index future markets by means of ordinary least squares model, diagonal Bekk-Garch, and regime-switching diagonal Bekk-Garch models. The empirical framework supported that Garch models achieve a better hedge effectiveness than the OLS models.
Amvella et al. [43] investigated the issue of hedge fund performance persistence using a Markov chain model. An approach based on the method of moments and on the model of Getmansky et al. [44] was used so as to unsmooth returns. The advantage of the model is that it allows not imposing the same order of serial correlation for all return series, as it applies the appropriate unsmoothing profile for each fund. Vidal-García [45] proved that European mutual funds register solid indication of noteworthy performance persistence, which is constant across investment styles, on an annual basis and in the longer-term periods. Onwards, Vidal-Garcia et al. [46] ascertain that short-term persistence is strongly significant worldwide.
Roca et al. [47] investigated the systematic risk of Australian SRI funds to the Australian and US equity markets and SRI sectors using the Markov regime switching analysis and an impulse response analysis. The empirical findings showed that the Australian SRI funds were mostly affected by the movements in the US equity market and SRI sector, and that during periods of higher returns the Australian SRI funds show exposure to the Australian equity market. Besides, Leite and Cortez [48] revealed that French SRI funds perform meaningfully better during crisis than during non-crisis periods, whereas Lean et al. [49] conclude that SRI funds outclass the market benchmark in Europe and North America. Likewise, Nakai et al. [50] advocate that SRI funds hold up stronger the ruin of the Lehman Brothers than conventional funds. On the contrary, Matallín-Sáez et al. [51] noticed overall poorer performances of funds with high socially responsible attributes.
Roll [52] argued that when trying to diversify a portfolio, managers need to be concerned about measuring the factors underlying its performance. There was established that one of the most simple and at the same time efficient methods is to relate fund performance to benchmarks in the form of existing market indices (heterogeneous) or different liquid tradable portfolios (e.g., ETFs). Huang et al. [53] pointed out that the performance of Chinese hedge funds is influenced by the stock market to a great extent, whereas Huang et al. [54] noticed that hedge funds are exposed to systematic risk factors.
Hammami et al. [55] analyzed the performance of mutual funds in the Tunisian capital market performing a multivariate generalized autoregressive conditional heteroskedasticity model. There was found that the Jensen alphas are better estimated using the multivariate GARCH model than in the other approaches. The authors demonstrate their primary objective of showing that the capital market in Tunisia was inefficient and present investment opportunities to invest in mutual funds. Likewise, Charfeddine and Ajmi [56] established that the student FIGARCH (1,d,1) model is better than the Markov switching ARCH specification. According to Fulkerson and Riley [57], mutual fund performance increases subsequent to the rise in portfolio concentration. There was documented an annualized 24 basis point growth in risk-adjusted return by a fund which enlarges its concentration via one standard deviation. Based on EurekaHedge and BarclayHedge databases, Stafylas et al. [58] highlighted that hurtful market circumstances adversely influence hedge fund performance as regards alphas since most of the strategies do not offer substantial excess returns. Aboura and Roye [59] used a Markov-Switching Bayesian vector autoregressive model and point out that financial stress conducts intensely to economic activity when the economy is in a high-stress regime, while economic activity remains unchanged in a low-stress regime. Saranya and Prasanna [60] explored the influence of stock market cycles on the volatility of Asian markets and provided evidence that the stochastic volatility model with jumps ensure better estimates during the normal market periods, whereas the stochastic volatility with jumps and asymmetry model has enhanced prediction truthfulness in the crisis period.
Munechika [61] applied an ARMA-GARCH model with a three-year rolling window on daily data between 2003 and 2014 to investigate the profitability and volatility of hedge fund index returns. The rolling regressions revealed that the parameter was strongly affected by the financial crisis of 2007–2009.
3. Data and Methods
3.1. Sample
Our study uses daily data for the period between January 1st 2016 and September 28th 2018. We have collected prices (net assets value per unit—NAV) for 80 Romanian investment vehicles, respectively 63 open-end funds and 17 pension funds. In addition, considering the portfolio structure (asset classes, maturity, and duration) of the respective investment vehicles, we used the following proxies for the market risk factors:
- BET Index of the Bucharest Stock Exchange price index
- Stoxx 600 Index price index
- the yield for the Romanian sovereign bond market with 5 years maturity (ROMGGR05 Index)
- the yield for the German/EUR sovereign bond market with 5 years maturity (GTEUR5YR Corp)
- the EUR/RON exchange rate
Thus, we have achieved 85 time series with daily quotations (prices and yields respectively), each with 714 observations.
According to the Romanian applicable regulation, it is mandatory for all the pension funds to mark-to-market all the financial instruments in their portfolios daily. Furthermore, Romanian law related to open-end investment funds allows the managers to choose between using a full/partial mark-to-market of bond portfolio or accrual interest method, while the mark-to-market of the listed equity portfolio is mandatory (listed equity represents the major part of the equity portfolios of open-end funds in Romania, due to incident legal provisions). Open-end funds computed and published the NAV day-to-day, as did pension funds. By corroborating information from fund managers, we encompassed in our sample the open-end funds that use a mark-to-market method for assessing their bond portfolios.
3.2. Research Methodology
Our aim is to investigate the behavior of fund returns in relation to the volatility of their main market determinants (market risk factors). By considering the information presented above regarding the particularities of the investment vehicles included in our sample, we argue that the variability of their daily returns should be explained by the variability of the market risk factors that are relevant according to the portfolio structure of each vehicle. Thus, we aim to highlight the sensitivity of fund returns to a selection of market risk factors (made according to the most common exposures in the funds’ portfolios). We also identify the potential dissimilar behavior of fund returns during the periods of high and low volatility for each of the selected five market risk factors. In order to identify periods of high and low volatility we used a Markov Regime Switching model, while for highlighting other features of fund returns we used EGARCH and DCC MV GARCH models, all of them being detailed bellow.
- Stage 1: Initial data preparation
The time series for the stock indices and for the fund unit prices were stationarized by transforming prices into logarithmic returns.
Regarding the two series of bond yields, the initial data represents yield to maturity, in annual terms, expressed in percentage points. In order to have comparable data with the series of daily returns (for the stock indices, the FX rates and respectively the NAV for the investment vehicles) we transformed the annual yield into a daily-compounded yield using a 250-day trading year convention, similar with the approach of Kristoufek and Ferreira [62]:
For the reason that the acquired series of daily yields were not stationary, we subsequently applied the first difference.
In our approach, we do not use the yields as a proxy for risk-free rates (e.g., for computing risk premium), but instead as a proxy for the variability of the fixed income market, in connection with the fact that an important part of the portfolios of the investment vehicles are composed of fixed income instruments (with a liquid OTC market), which are marked to market on a daily basis, thus influencing the NAVs of the funds and their daily returns to investors.
After these transformations, we checked each series and confirmed stationarity using Augmented Dickey-Fuller and Philips-Perron unit root tests (see Appendix A, Table A1).
- Stage 2: Computing daily conditional volatilities
Using this database of five time series representing proxies for individual market risk factors and 80 time series representing returns for different investment vehicles we computed conditional volatilities, for each time series, using an EGARCH (P,Q) model according with Tsay [63], where:
After calibrating each model, the results coefficients were tested for significance and only the series for which the coefficients were found to be statistically significant were set aside for further analysis.
- Stage 3: Computing daily conditional correlations
We also computed conditional correlations between each series of fund returns and each of the five market risk factors using an DCC MV-GARCH model according with Engle and Sheppard [64] and Sheppard [65].
where Dt is the k × k diagonal matrix of the time varying standard deviations from univariate GARCH models with on the ith diagonal and Rt is the time varying correlation matrix. Writing the log likelihood of this estimator, we acquire:
where εt ~ N(0, Rt) represent the standardized residuals. If we express the elements of Dt in the form of univariate GARCH(P,Q) processes we obtain that:
As a result, the dynamic correlation structure is:
where signifies the unconditional covariance of the standardized residuals from the initial estimation and is a diagonal matrix composed of the square root of the diagonal elements of Qt.
Besides, the elements of Rt will be representing the time varying correlations among the returns series.
In a similar approach as for the conditional volatilities series, after calibrating each DCC MV-GARCH model, the results coefficients were tested for significance and only the series for which the coefficients were found to be statistically significant were retained for further analysis.
- Stage 4: Identifying volatility regimes
Since our aim is to depict the behavior of fund returns (in terms of volatility and correlations with the market risk factors) under different volatility regimes for the market risk factors, we also computed the probabilities of being either in a high volatility or in a low volatility regime for each of the 85 time series included using a Markov Regime Switching model as represented by Tsay [63], Hamilton [66,67] and Perlin [68]:
where NS and NnS counts the number of switching and non-switching coefficients, is a subset of and represents the explanatory variables which do not switch while is the subset composed of the variables that switch. The term P(Φ) represents the probability density function of the error term (Φ being the vector representing the set of parameters of P).
We have transformed the series of probabilities given by the model into a series of markers for the volatility regimes, respectively. Series with binary (daily) values of 1 and 0, where 1 signifies that the variable is in a regime of high volatility and 0 signifies that the variable is in a low volatility regime. The respective values of 1 and 0 were determined using the following rules:
- (a)
- If the probability of being in a high volatility regime > probability of being in a low volatility regime, the corresponding regime marker is 1;
- (b)
- If the probability of being in a high volatility regime < probability of being in a low volatility regime, the corresponding regime marker is 0.
- Stage 5: Filtering the computed fund returns’ characteristics (volatilities, correlations and volatility regimes) according with market risk factor’s volatility regimes and calculating appropriate statistics
The computations performed in the stages above resulted in series of conditional daily volatilities, conditional daily correlations and markers of daily volatility regimes for the investment vehicles included in the sample. They also provided similar series (except for correlations) for the five market risk factors.
For this final stage of our methodology, we used each of the series with markers for volatility regimes for the five risk factors to split the computed values for each series of the characteristics of fund returns into a subset of values. These values resulted during a high volatility regime of the respective market risk factor and a subset of values resulted during a low volatility regime of the corresponding market risk factor.
For each such sub-set of values, we have computed selected statistics (e.g., mean, standard deviation, as presented in Appendix A—Table A2 and Table A3). This allowed us to compare the aggregated values for the entire sample (at market level), thus observing the eventual differences in the behavior of fund returns between the two regimes. In addition, we compared the aggregated values for each sub-set with the unconditional values of the respective characteristics (e.g., with the average unconditional level of correlation or the unconditional volatility for the entire time period).
We have performed comparative analyses between the investment vehicles in the sample and attempted to identify common characteristics for groups of investment vehicles (e.g., for the pension fund group).
We were also able to use the series with markers for volatility regimes to identify, in the case of each of the volatility regimes of the five market risk factors, how many investment vehicles also entered in a similar regime, highlighting the level of synchronicity of the investment vehicles with the volatility regimes of the market risk factors.
The actual results of the computations described above are presented and interpreted in the next section of our paper.
4. Empirical Results and Discussion
After performing all the computations mentioned in the previous section, the first step to analyze and interpret the results was to understand the characteristics of the volatility regimes for the risk factors. From Table 1, we can observe that each risk factor had its particularities regarding the volatility regimes and behavior during the period investigated. While the two equity indices witnessed a relatively low number of high volatility regimes, the average length of these episodes was larger in comparison with those registered by the other risk factors. On the opposite side, the Romanian sovereign bond index and the FX rate had a much higher number of volatility stages during the period investigated, but their average length was significantly shorter. In general, with the two exceptions above, during the period examined, each risk factor spent about 15% of the time in a high volatility regime.

Table 1.
Synchronization of volatility regimes of funds in relation to the risk factors.
The second step we took was to check for each such volatility event, across each risk factor, how many investment vehicles entered simultaneously in a high volatility regime for their daily returns. The results show that in all cases less than half of the funds synchronized their high volatility regimes with those of the risk factors. Going further into detail, we observe that the equity risk factors are the ones that most often trigger similar volatility regimes for the funds’ returns, while in the case of the other three risk factors the reaction is much weaker in the sample of funds that we used in this research. This prompts us to formulate a preliminary conclusion that the Romanian investment and pension fund sectors are more sensitive to the high volatility regimes of the equity markets in comparison with the bond markets and the FX market. Also, at an overall market level, even in the case of the equity risk factor, the market seems to demonstrate a significant level of resilience.
In Figure 1, we can observe the most significant episodes of synchronization of the high volatility regimes among the equity market risk factors and the mutual funds sample.
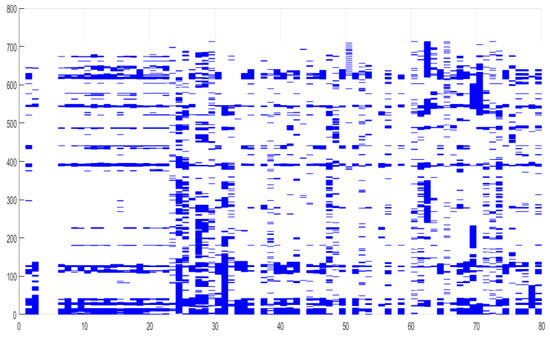
Figure 1.
Heat-map of the high volatility regimes for the first two risk factors and selected mutual funds. Source: Authors’ work.
Each dark spot on the heat map represents one day of a volatility regime for the respective variable. The vertical axis depicts time (the 713 daily observations), while the horizontal axis contains the selected time-series, starting with BET and STOXX600 in the first two columns, followed by the 17 pension funds (from column 5 to column 22) and the mutual funds sample (column 22–80).
We can observe that most of the consistent high volatility regimes of the two risk factors are mirrored by the entire pension funds sample and by a significant portion of the investment funds sample (rows 0–20, 100–130, 380–400, 430–440, 490–500, 540–550, and 610–630 in the heat-map).
Going further, we studied the behavior of daily conditional volatility for each series of risk factors and investment vehicles in correlation with their own volatility regimes. The results presented in Table 2. show that there is significant change in the level of volatility between the regimes. It is also essential to notice that the average level of volatility is much reduced for the investment vehicles in contrast with the two market risk factors previously identified to be the most relevant for their behavior (respectively the domestic and the international equity markets).

Table 2.
Volatility of risk factors and fund returns during high and low volatility regimes.
Figure 2 presents the time-varying values of normalized volatility for each of the five risk factors and the 73 investment vehicles included in the sample (7 funds were excluded because of not having significantly different from zero coefficients in the EGARCH model calibration). The horizontal axis depicts the period (e.g., from 1st to the 713th daily observation), while the on the vertical axis we have the risk factors (from 1 to 5) followed by the 17 pension funds (from 6 to 22) and the 56 open-end investment funds (from 24 to 78). The depth of the chart represents the values of the daily-normalized conditional volatility (on a scale from 0 to 1).
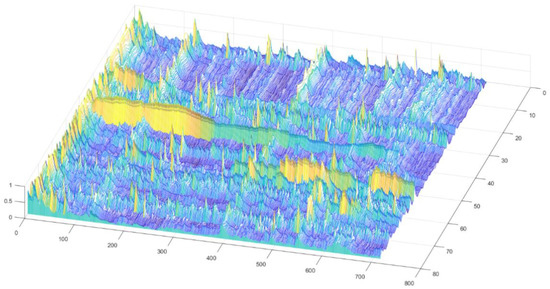
Figure 2.
Normalized volatility of risk factors and fund returns across the entire period. Source: Authors’ work.
Two observations from the chart are particularly important for our analysis:
- All the 17 pension funds spend much more time in a low volatility regime in comparison with the open-end investment funds;
- We can obviously notice at least four distinct periods (around the 120 days mark, respectively the 380, 550 and 600 days marks) when the volatility is rising in synchronization across the entire sample of risk factors and investment vehicles, validating the findings from our Markov Regime Switching model presented earlier.
We also realized a comparative analysis of the distribution of values for daily conditional volatility between the investment vehicles included into the sample. Table A2 (see Appendix A) presents the mean and standard deviation of the values of conditional daily volatility for each fund filtered considering the high/low volatility regimes of each of the five risk factors. Figure 3 presents the features of the distribution of daily conditional volatility for each fund filtered using the volatility regimes of BET Index. We can notice the particularities of each fund and especially the consistent low levels of volatility, regardless of the volatility regime for the BET Index, in the case of the first 17 investment vehicles that are represented by the pension funds.
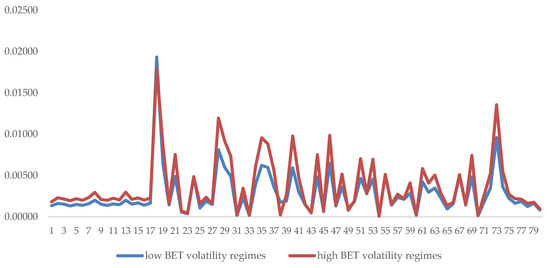
Figure 3.
Mean daily conditional volatility for each investment vehicle in the sample filtered according with the BET volatility regimes. Source: Authors’ work.
The last step in our analysis was to study the behavior of daily conditional correlations between each risk factor and the full sample of the investment vehicles.
As a preliminary analysis, we have computed the unconditional historical correlations for the entire period and found that in the case of the foreign bond and FX risk factors most of them were not significantly different from zero. These results are presented in the right side of Table 3 and can be explained by the fact that most of the investment vehicles in our sample did not have significant exposure to these two sub-categories of market risk during the investigated period. At the same time, we can observe an overall low and negative level of correlation with the evolution of the local bond yields (consistent with its economic significance), but statistically significant for most of the funds in our sample (60 out of 80). The level of correlation with the equity markets is higher, particularly in the case of the local market, but the intensity is still at or below medium.

Table 3.
Conditional and unconditional correlations between returns and risk factors.
When examining the daily conditional correlations computed using the DCC MV-GARCH model (presented in the left side of Table 3), the most important conclusion is that the values do not change significantly between the low and high volatility regimes and remain in both situations very close to the value of the long-term unconditional correlation. Even more, this conclusion remains valid across all the five risk factors in relation to which of the correlations were computed. In our view this is explained by the managers’ inability to significantly change the structure of the portfolios from one volatility regime to another and confirms the conclusions of previous studies that employed different methods (e.g., measures of systematic risk, performance metrics etc.) and the efficient market hypothesis. At the same time, the relatively low levels of average correlations in relation to each of the five risk factors show the resilience of the overall sector to the market fluctuations.
A comparative analysis of the distribution of daily conditional correlations with each market risk factor for every investment vehicle included in the sample is depicted in Table A3 (see Appendix A). The values were previously filtered considering the volatility regimes of the respective market risk factor. Figure 4 shows the features of the distribution of daily conditional correlations for each fund with the BET Index, filtered using this factor’s volatility regimes.
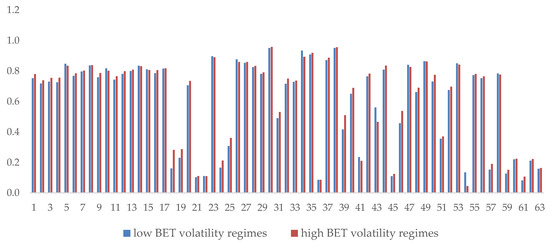
Figure 4.
Mean daily conditional correlations with BET Index for each investment vehicle in the sample filtered according with this risk factor’s volatility regimes. Source: Authors’ work.
Similar to the comparative analysis applied on the values of daily conditional volatility (see Figure 3) we can observe the particularities of each fund and especially the consistent high levels of correlation with the BET-Index, regardless of its volatility regimes, in the case of the first 17 investment vehicles which are represented by the pension funds. Some investment funds were excluded from the sample because of not having significantly different from zero coefficients in the DCC MV-GARCH model calibration.
5. Concluding Remarks
In this paper, we studied the sensitivity of open-end investment funds and pension funds to five relevant market risk factors (local and international equity markets and bond markets, as well as the FX rate) during the period 2016–2018, using daily data. Our methods included computations of conditional volatility and dynamic conditional correlations using EGARCH and DCC MV-GARCH models. In addition, we differentiated the results among high and low volatility regimes that were identified using a Markov Regime Switching model.
First, at micro level, our most important results show that the level of correlations do not change significantly between high and low volatility regimes for the risk factors, confirming conclusions of previous studies (realized with different methods) that in general asset managers have difficulties adapting their portfolios to market conditions.
In our interpretation, the fact that the average levels of correlation, with each of the five risk factors, during the high volatility regimes were not significantly different from the average values registered during the low volatility regimes (and also close to the average level of the unconditional correlations) argue that the structure of the funds’ portfolios did not change significantly during the investigated period. This could imply that in our sample of funds, for the considered period, on average, it was not possible for the managers to alter the investment strategy and the portfolio structure in response to the change in volatility over short periods (given the daily frequency of data considered in our analysis).
Second, at a macro level, we show that the Romanian investment and pension funds are in general resilient to the risks investigated, with less than half of the funds showing a synchronization of their own volatility regimes with those of the risk factors. In addition, the intensity of correlations is in general at or below medium (less than 0.5), unconcerned by the volatility regime. While the level of daily volatility is indeed increasing across the sample of funds during the high volatility regimes of the risk factors, they still remain significantly below the levels measured for the most relevant two risk factors (respectively the local and international equity market returns).
Third, when comparing between investment funds and pension funds, our results show that the latter demonstrate lower levels of volatility and higher resilience to market risk factors. This can be explained by the fact that all the 17 pension funds have almost the same defensive mix of assets: approximately 17% investment in listed equity (on average), the rest being invested in high quality fixed income instruments (approximately 63% investments in government bonds, on average). The sample of the investment funds is more heterogeneous in terms of investment strategy, ranging from monetary and bond funds to equity (and also index) funds. As a result, when aggregating results, the pension funds part of our sample behaved more uniform and showed less responsiveness to risk factors, while the investment funds part of the sample showed larger variability of the results including also in some cases more sensitivity to the risk factors due to a less diversified portfolio structure.
Results from all three kinds are relevant for market supervisors, especially in a risk based supervision approach, showing how the levels of sensitivity to each type of market risk factor are distributed in the investment vehicle sample and what is the overall level of the resilience of this sector to market risk.
Since we use data that is publicly available, market supervisors and fund managers could replicate our approach and the methods that we used, in order to monitor (even in real time) the evolution of the sensitivity to market risk factors for selected investment vehicles (or for the entire population of funds). Based on this approach, comparisons among funds can be made by supervisors or by fund managers and the funds could be ranked in relative terms in relation to their responsiveness to the market risk factors. These tools could prove useful in applying stress tests based on market risk factors, at fund level and at sector level. Such stress tests are mandatory, at an internal level, for the investment funds (both UCITS and AIFs) according to Romanian applicable regulation.
If time series long enough are available, the methods could be adapted to use monthly instead of daily data, so to also include the AIFs in the investment vehicle sample (AIFs only compute monthly NAV, in contrast to UCITS and pension funds, which must publish daily NAV).
For investors, our results show that a diversified portfolio of funds could prove to be resilient to transitory adverse market conditions. It is relevant for investors the fact our results argue that such a diversified portfolio might have relatively constant exposure to the market risk factors, irrespective of the high or low volatility regimes of these factors, so that its level of correlation with these factors might remain relatively unchanged over long periods of time.
One limitation of our research is that it does not differentiate within the sample of investment vehicles according to their investment strategy.
In addition, if we could have used data for a longer interval of time, it would have enabled us to perform the same analysis also using monthly returns, which might have better evidenced if the fund managers were able or not to alter their investment strategy according to the market volatility regime (given the larger period). Moreover, this would have also allowed us to include in the analysis the Romanian AIFs, which according with the applicable regulations only publish the NAV on a monthly basis.
Further studies in this field could employ principal component analysis for identifying the common features of the sample in terms of correlation and volatility with the purpose to analyze it in comparison with the evolution of the marker risk factors.
Author Contributions
Conceptualization, L.B., D.Ş.A., I.P. and Ş.C.G.; Data curation, L.B., D.Ş.A., I.P. and Ş.C.G.; Formal analysis, L.B., D.Ş.A., I.P. and Ş.C.G.; Funding acquisition, L.B., D.Ş.A., I.P. and Ş.C.G.; Investigation, L.B., D.Ş.A., I.P. and Ş.C.G.; Methodology, L.B., D.Ş.A., I.P. and Ş.C.G.; Project administration, L.B., D.Ş.A., I.P. and Ş.C.G.; Resources, L.B., D.Ş.A., I.P. and Ş.C.G.; Software, L.B., D.Ş.A., I.P. and Ş.C.G.; Supervision, L.B., D.Ş.A., I.P. and Ş.C.G.; Validation, L.B., D.Ş.A., I.P. and Ş.C.G.; Visualization, L.B., D.Ş.A., I.P. and Ş.C.G.; Writing—original draft, L.B., D.Ş.A., I.P. and Ş.C.G.; Writing—review & editing, L.B., D.Ş.A., I.P. and Ş.C.G.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Results of the stationarity test for daily returns time series, respectively daily yield differential time series.
Table A1.
Results of the stationarity test for daily returns time series, respectively daily yield differential time series.
| ADF Decision (1 = Reject H0) | ADF Stat. | ADF p-val | PP Decision (1 = Reject H0) | PP Stat. | PP p-val |
|---|---|---|---|---|---|
| 1 | −14.46251141 | 0.001 | 1 | −25.67207249 | 0.001 |
| 1 | −14.71749747 | 0.001 | 1 | −25.51670332 | 0.001 |
| 1 | −13.74619771 | 0.001 | 1 | −19.85175769 77 | 0.001 |
| 1 | −14.4168156868 | 0.001 | 1 | −26.8227921222212 | 0.001 |
| 1 | −15.67140624 | 0.001 | 1 | −29.93817398 | 0.001 |
| 1 | −13.75150867 | 0.001 | 1 | −23.04230664 | 0.001 |
| 1 | −14.41510806 | 0.001 | 1 | −24.44678857 | 0.001 |
| 1 | −14.4866469 | 0.001 | 1 | −23.38573455 | 0.001 |
| 1 | −14.47350004 | 0.001 | 1 | −23.99653015 | 0.001 |
| 1 | −14.04165656 | 0.001 | 1 | −22.87545243 | 0.001 |
| 1 | −14.4701186 | 0.001 | 1 | −23.01454428 | 0.001 |
| 1 | −14.1895212 | 0.001 | 1 | −22.86211801 | 0.001 |
| 1 | −14.27777585 | 0.001 | 1 | −24.14545206 | 0.001 |
| 1 | −13.80303273 | 0.001 | 1 | −23.35305106 | 0.001 |
| 1 | −13.39487642 | 0.001 | 1 | −21.92481766 | 0.001 |
| 1 | −14.21605846 | 0.001 | 1 | −23.69233346 | 0.001 |
| 1 | −14.37602787 | 0.001 | 1 | −23.5253996 | 0.001 |
| 1 | −13.66510147 | 0.001 | 1 | −23.76110164 | 0.001 |
| 1 | −13.87090243 | 0.001 | 1 | −23.72548999 | 0.001 |
| 1 | −13.74141757 | 0.001 | 1 | −23.90521158 | 0.001 |
| 1 | −14.24952924 | 0.001 | 1 | −23.8385252 | 0.001 |
| 1 | −14.24785231 | 0.001 | 1 | −23.74825187 | 0.001 |
| 1 | −18.1211981 | 0.001 | 1 | −29.3784282 | 0.001 |
| 1 | −14.97054851 | 0.001 | 1 | −24.91489984 | 0.001 |
| 1 | −16.89458682 | 0.001 | 1 | −27.61849966 | 0.001 |
| 1 | −14.52044268 | 0.001 | 1 | −24.93244131 | 0.001 |
| 1 | −12.46749362 | 0.001 | 1 | −20.26554129 | 0.001 |
| 1 | −13.10381388 | 0.001 | 1 | −20.15919968 | 0.001 |
| 1 | −16.3976785 | 0.001 | 1 | −26.97416838 | 0.001 |
| 1 | −14.50648437 | 0.001 | 1 | −24.93350715 | 0.001 |
| 1 | −15.9390632 | 0.001 | 1 | −25.98586152 | 0.001 |
| 1 | −15.69851605 | 0.001 | 1 | −27.27256422 | 0.001 |
| 1 | −16.10313129 | 0.001 | 1 | −26.30189119 | 0.001 |
| 1 | −14.9679989 | 0.001 | 1 | −25.3594308 | 0.001 |
| 1 | −14.03266587 | 0.001 | 1 | −24.25485892 | 0.001 |
| 1 | −16.91314654 | 0.001 | 1 | −26.45163322 | 0.001 |
| 1 | −14.21550375 | 0.001 | 1 | −25.76631002 | 0.001 |
| 1 | −14.92956849 | 0.001 | 1 | −26.99957675 | 0.001 |
| 1 | −13.05578484 | 0.001 | 1 | −23.43650104 | 0.001 |
| 1 | −14.49539819 | 0.001 | 1 | −25.15423069 | 0.001 |
| 1 | −12.8688277 | 0.001 | 1 | −25.70748782 | 0.001 |
| 1 | −14.04295952 | 0.001 | 1 | −25.65288941 | 0.001 |
| 1 | −18.55848773 | 0.001 | 1 | −34.48171394 | 0.001 |
| 1 | −13.60773064 | 0.001 | 1 | −24.8948011 | 0.001 |
| 1 | −14.32807956 | 0.001 | 1 | −25.62962947 | 0.001 |
| 1 | −13.95732154 | 0.001 | 1 | −23.91387015 | 0.001 |
| 1 | −16.51992869 | 0.001 | 1 | −26.70605947 | 0.001 |
| 1 | −12.78280984 | 0.001 | 1 | −20.72170805 | 0.001 |
| 1 | −13.87657218 | 0.001 | 1 | −24.61641683 | 0.001 |
| 1 | −24.22159923 | 0.001 | 1 | −36.97449018 | 0.001 |
| 1 | −14.36223355 | 0.001 | 1 | −25.12178851 | 0.001 |
| 1 | −16.26959953 | 0.001 | 1 | −26.82410925 | 0.001 |
| 1 | −14.20075727 | 0.001 | 1 | −24.91899659 | 0.001 |
| 1 | −15.35569887 | 0.001 | 1 | −26.60584895 | 0.001 |
| 1 | −16.82736412 | 0.001 | 1 | −25.89463779 | 0.001 |
| 1 | −13.48370875 | 0.001 | 1 | −23.38590829 | 0.001 |
| 1 | −14.20732995 | 0.001 | 1 | −22.68135885 | 0.001 |
| 1 | −13.65983931 | 0.001 | 1 | −24.76354594 | 0.001 |
| 1 | −14.56761485 | 0.001 | 1 | −26.15871607 | 0.001 |
| 1 | −16.62121155 | 0.001 | 1 | −27.19126885 | 0.001 |
| 1 | −16.6115905 | 0.001 | 1 | −27.96499086 | 0.001 |
| 1 | −13.11616317 | 0.001 | 1 | −26.09995507 | 0.001 |
| 1 | −14.34763599 | 0.001 | 1 | −23.32187934 | 0.001 |
| 1 | −14.03373819 | 0.001 | 1 | −25.18013417 | 0.001 |
| 1 | −13.04567299 | 0.001 | 1 | −24.13211352 | 0.001 |
| 1 | −14.05197831 | 0.001 | 1 | −24.1261206 | 0.001 |
| 1 | −14.29504014 | 0.001 | 1 | −23.90422506 | 0.001 |
| 1 | −14.09690135 | 0.001 | 1 | −22.79890201 | 0.001 |
| 1 | −14.96805238 | 0.001 | 1 | −27.16497495 | 0.001 |
| 1 | −12.79617163 | 0.001 | 1 | −22.67497103 | 0.001 |
| 1 | −15.56014394 | 0.001 | 1 | −28.49937953 | 0.001 |
| 1 | −16.66734214 | 0.001 | 1 | −27.21580369 | 0.001 |
| 1 | −16.45011689 | 0.001 | 1 | −27.96922127 | 0.001 |
| 1 | −13.9101931 | 0.001 | 1 | −25.00185685 | 0.001 |
| 1 | −11.39738538 | 0.001 | 1 | −16.91914925 | 0.001 |
| 1 | −13.75150917 | 0.001 | 1 | −24.35755956 | 0.001 |
| 1 | −13.73742592 | 0.001 | 1 | −24.30617894 | 0.001 |
| 1 | −15.35690246 | 0.001 | 1 | −23.02156195 | 0.001 |
| 1 | −13.48500411 | 0.001 | 1 | −22.9360866 | 0.001 |
| 1 | −14.61724683 | 0.001 | 1 | −22.941735 | 0.001 |
| 1 | −13.4318641 | 0.001 | 1 | −19.76030578 | 0.001 |
| 1 | −14.66877486 | 0.001 | 1 | −24.54519058 | 0.001 |
| 1 | −13.54439039 | 0.001 | 1 | −19.98432505 | 0.001 |
| 1 | −15.39654954 | 0.001 | 1 | −26.97519709 | 0.001 |
| 1 | −12.94530177 | 0.001 | 1 | −20.15765856 | 0.001 |
Source: Authors’ calculations.

Table A2.
Mean and standard deviation of the values of conditional volatility under different volatility regimes of the market risk factors.
Table A2.
Mean and standard deviation of the values of conditional volatility under different volatility regimes of the market risk factors.
| BET Volatility Regimes | STOXX Volatility Regimes | BONDS/RON Volatility Regimes | BONDS/EUR Volatility Regimes | EUR/RON Volatility Regimes | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| LOW | HIGH | LOW | HIGH | LOW | HIGH | LOW | HIGH | LOW | HIGH | |||||||||||
| mean | std | mean | std | mean | std | mean | std | mean | std | mean | std | mean | std | mean | std | mean | std | mean | std | |
| v01 | 0.0014 | 0.0002 | 0.0018 | 0.0004 | 0.0014 | 0.0002 | 0.0018 | 0.0004 | 0.0014 | 0.0003 | 0.0015 | 0.0004 | 0.0014 | 0.0003 | 0.0014 | 0.0003 | 0.0014 | 0.0003 | 0.0014 | 0.0003 |
| v02 | 0.0016 | 0.0003 | 0.0023 | 0.0007 | 0.0016 | 0.0003 | 0.0024 | 0.0006 | 0.0017 | 0.0004 | 0.0018 | 0.0006 | 0.0017 | 0.0005 | 0.0017 | 0.0004 | 0.0017 | 0.0005 | 0.0017 | 0.0004 |
| v03 | 0.0015 | 0.0003 | 0.0022 | 0.0008 | 0.0016 | 0.0004 | 0.0020 | 0.0007 | 0.0016 | 0.0004 | 0.0018 | 0.0007 | 0.0016 | 0.0004 | 0.0016 | 0.0005 | 0.0016 | 0.0004 | 0.0016 | 0.0006 |
| v04 | 0.0013 | 0.0003 | 0.0020 | 0.0006 | 0.0013 | 0.0003 | 0.0020 | 0.0006 | 0.0014 | 0.0004 | 0.0016 | 0.0006 | 0.0014 | 0.0004 | 0.0014 | 0.0004 | 0.0014 | 0.0004 | 0.0014 | 0.0005 |
| v05 | 0.0015 | 0.0003 | 0.0022 | 0.0006 | 0.0015 | 0.0003 | 0.0021 | 0.0006 | 0.0016 | 0.0004 | 0.0017 | 0.0005 | 0.0016 | 0.0004 | 0.0016 | 0.0004 | 0.0016 | 0.0004 | 0.0016 | 0.0004 |
| v06 | 0.0014 | 0.0003 | 0.0020 | 0.0006 | 0.0014 | 0.0003 | 0.0020 | 0.0006 | 0.0014 | 0.0003 | 0.0017 | 0.0005 | 0.0015 | 0.0004 | 0.0015 | 0.0004 | 0.0015 | 0.0004 | 0.0015 | 0.0004 |
| v07 | 0.0016 | 0.0003 | 0.0023 | 0.0007 | 0.0016 | 0.0004 | 0.0022 | 0.0007 | 0.0016 | 0.0004 | 0.0019 | 0.0006 | 0.0017 | 0.0005 | 0.0016 | 0.0005 | 0.0017 | 0.0005 | 0.0017 | 0.0005 |
| v08 | 0.0020 | 0.0004 | 0.0030 | 0.0009 | 0.0020 | 0.0004 | 0.0030 | 0.0009 | 0.0021 | 0.0005 | 0.0023 | 0.0008 | 0.0022 | 0.0006 | 0.0021 | 0.0006 | 0.0022 | 0.0006 | 0.0021 | 0.0006 |
| v09 | 0.0015 | 0.0002 | 0.0021 | 0.0005 | 0.0015 | 0.0003 | 0.0020 | 0.0005 | 0.0016 | 0.0003 | 0.0017 | 0.0004 | 0.0016 | 0.0004 | 0.0016 | 0.0003 | 0.0016 | 0.0004 | 0.0016 | 0.0004 |
| v10 | 0.0014 | 0.0003 | 0.0020 | 0.0006 | 0.0014 | 0.0003 | 0.0019 | 0.0006 | 0.0014 | 0.0004 | 0.0016 | 0.0005 | 0.0015 | 0.0004 | 0.0014 | 0.0004 | 0.0015 | 0.0004 | 0.0014 | 0.0004 |
| v11 | 0.0016 | 0.0003 | 0.0023 | 0.0008 | 0.0016 | 0.0004 | 0.0021 | 0.0007 | 0.0016 | 0.0004 | 0.0018 | 0.0007 | 0.0017 | 0.0005 | 0.0017 | 0.0005 | 0.0017 | 0.0004 | 0.0017 | 0.0006 |
| v12 | 0.0015 | 0.0003 | 0.0020 | 0.0006 | 0.0015 | 0.0003 | 0.0020 | 0.0006 | 0.0015 | 0.0003 | 0.0017 | 0.0005 | 0.0016 | 0.0004 | 0.0015 | 0.0004 | 0.0015 | 0.0004 | 0.0015 | 0.0004 |
| v13 | 0.0020 | 0.0004 | 0.0030 | 0.0008 | 0.0020 | 0.0004 | 0.0030 | 0.0008 | 0.0021 | 0.0005 | 0.0023 | 0.0007 | 0.0021 | 0.0006 | 0.0022 | 0.0006 | 0.0021 | 0.0006 | 0.0022 | 0.0006 |
| v14 | 0.0015 | 0.0003 | 0.0021 | 0.0005 | 0.0015 | 0.0002 | 0.0021 | 0.0006 | 0.0016 | 0.0003 | 0.0018 | 0.0005 | 0.0016 | 0.0004 | 0.0016 | 0.0004 | 0.0016 | 0.0004 | 0.0016 | 0.0004 |
| v15 | 0.0017 | 0.0003 | 0.0023 | 0.0005 | 0.0017 | 0.0003 | 0.0022 | 0.0006 | 0.0018 | 0.0004 | 0.0019 | 0.0004 | 0.0018 | 0.0004 | 0.0018 | 0.0004 | 0.0018 | 0.0004 | 0.0018 | 0.0004 |
| v16 | 0.0014 | 0.0003 | 0.0020 | 0.0006 | 0.0014 | 0.0003 | 0.0020 | 0.0006 | 0.0015 | 0.0004 | 0.0016 | 0.0005 | 0.0015 | 0.0004 | 0.0015 | 0.0004 | 0.0015 | 0.0004 | 0.0015 | 0.0004 |
| v17 | 0.0017 | 0.0003 | 0.0023 | 0.0006 | 0.0017 | 0.0003 | 0.0022 | 0.0006 | 0.0017 | 0.0004 | 0.0019 | 0.0005 | 0.0018 | 0.0004 | 0.0017 | 0.0004 | 0.0018 | 0.0004 | 0.0017 | 0.0004 |
| v18 | 0.0193 | 0.0034 | 0.0179 | 0.0037 | 0.0193 | 0.0034 | 0.0185 | 0.0037 | 0.0191 | 0.0033 | 0.0195 | 0.0041 | 0.0191 | 0.0032 | 0.0192 | 0.0038 | 0.0191 | 0.0035 | 0.0192 | 0.0034 |
| v19 | 0.0065 | 0.0024 | 0.0087 | 0.0032 | 0.0061 | 0.0020 | 0.0107 | 0.0027 | 0.0068 | 0.0026 | 0.0069 | 0.0027 | 0.0067 | 0.0028 | 0.0069 | 0.0025 | 0.0068 | 0.0027 | 0.0066 | 0.0026 |
| v20 | 0.0015 | 0.0003 | 0.0015 | 0.0003 | 0.0015 | 0.0003 | 0.0015 | 0.0003 | 0.0015 | 0.0003 | 0.0015 | 0.0003 | 0.0014 | 0.0003 | 0.0015 | 0.0002 | 0.0014 | 0.0002 | 0.0016 | 0.0003 |
| v21 | 0.0049 | 0.0012 | 0.0075 | 0.0028 | 0.0047 | 0.0009 | 0.0082 | 0.0026 | 0.0051 | 0.0015 | 0.0058 | 0.0024 | 0.0052 | 0.0018 | 0.0053 | 0.0017 | 0.0053 | 0.0018 | 0.0052 | 0.0017 |
| v22 | 0.0006 | 0.0003 | 0.0007 | 0.0004 | 0.0006 | 0.0003 | 0.0008 | 0.0004 | 0.0006 | 0.0003 | 0.0008 | 0.0004 | 0.0005 | 0.0003 | 0.0007 | 0.0003 | 0.0006 | 0.0003 | 0.0007 | 0.0003 |
| v23 | 0.0004 | 0.0001 | 0.0005 | 0.0002 | 0.0004 | 0.0001 | 0.0005 | 0.0002 | 0.0004 | 0.0001 | 0.0005 | 0.0002 | 0.0004 | 0.0002 | 0.0004 | 0.0001 | 0.0004 | 0.0002 | 0.0004 | 0.0001 |
| v24 | 0.0048 | 0.0005 | 0.0049 | 0.0007 | 0.0048 | 0.0005 | 0.0048 | 0.0006 | 0.0048 | 0.0005 | 0.0048 | 0.0005 | 0.0048 | 0.0005 | 0.0049 | 0.0005 | 0.0048 | 0.0005 | 0.0049 | 0.0006 |
| v25 | 0.0011 | 0.0002 | 0.0016 | 0.0005 | 0.0011 | 0.0002 | 0.0017 | 0.0005 | 0.0011 | 0.0003 | 0.0012 | 0.0005 | 0.0011 | 0.0004 | 0.0012 | 0.0003 | 0.0011 | 0.0004 | 0.0012 | 0.0003 |
| v26 | 0.0019 | 0.0006 | 0.0024 | 0.0010 | 0.0018 | 0.0006 | 0.0029 | 0.0008 | 0.0019 | 0.0007 | 0.0021 | 0.0008 | 0.0018 | 0.0006 | 0.0021 | 0.0007 | 0.0019 | 0.0007 | 0.0022 | 0.0007 |
| v27 | 0.0015 | 0.0003 | 0.0016 | 0.0003 | 0.0015 | 0.0003 | 0.0016 | 0.0003 | 0.0015 | 0.0003 | 0.0016 | 0.0003 | 0.0015 | 0.0003 | 0.0016 | 0.0003 | 0.0015 | 0.0003 | 0.0017 | 0.0004 |
| v28 | 0.0081 | 0.0021 | 0.0119 | 0.0047 | 0.0078 | 0.0014 | 0.0135 | 0.0042 | 0.0084 | 0.0025 | 0.0096 | 0.0042 | 0.0086 | 0.0027 | 0.0087 | 0.0031 | 0.0086 | 0.0029 | 0.0087 | 0.0029 |
| v29 | 0.0060 | 0.0014 | 0.0092 | 0.0034 | 0.0058 | 0.0010 | 0.0099 | 0.0032 | 0.0063 | 0.0019 | 0.0070 | 0.0028 | 0.0064 | 0.0022 | 0.0065 | 0.0021 | 0.0065 | 0.0022 | 0.0064 | 0.0020 |
| v30 | 0.0049 | 0.0010 | 0.0073 | 0.0025 | 0.0049 | 0.0009 | 0.0074 | 0.0026 | 0.0052 | 0.0014 | 0.0057 | 0.0019 | 0.0054 | 0.0017 | 0.0051 | 0.0014 | 0.0053 | 0.0016 | 0.0052 | 0.0013 |
| v31 | 0.0002 | 0.0001 | 0.0002 | 0.0001 | 0.0002 | 0.0001 | 0.0002 | 0.0000 | 0.0002 | 0.0001 | 0.0002 | 0.0001 | 0.0002 | 0.0001 | 0.0002 | 0.0001 | 0.0002 | 0.0001 | 0.0002 | 0.0001 |
| v32 | 0.0023 | 0.0005 | 0.0035 | 0.0012 | 0.0023 | 0.0004 | 0.0037 | 0.0011 | 0.0025 | 0.0007 | 0.0027 | 0.0009 | 0.0025 | 0.0008 | 0.0025 | 0.0007 | 0.0025 | 0.0007 | 0.0026 | 0.0007 |
| v33 | 0.0002 | 0.0001 | 0.0002 | 0.0001 | 0.0002 | 0.0001 | 0.0002 | 0.0001 | 0.0002 | 0.0001 | 0.0002 | 0.0001 | 0.0002 | 0.0001 | 0.0002 | 0.0001 | 0.0002 | 0.0001 | 0.0002 | 0.0001 |
| v34 | 0.0039 | 0.0009 | 0.0060 | 0.0021 | 0.0038 | 0.0007 | 0.0063 | 0.0021 | 0.0041 | 0.0013 | 0.0045 | 0.0018 | 0.0042 | 0.0015 | 0.0042 | 0.0012 | 0.0042 | 0.0014 | 0.0042 | 0.0013 |
| v35 | 0.0062 | 0.0013 | 0.0096 | 0.0030 | 0.0062 | 0.0012 | 0.0095 | 0.0031 | 0.0066 | 0.0018 | 0.0072 | 0.0026 | 0.0067 | 0.0021 | 0.0067 | 0.0019 | 0.0067 | 0.0021 | 0.0067 | 0.0018 |
| v36 | 0.0060 | 0.0015 | 0.0088 | 0.0034 | 0.0058 | 0.0010 | 0.0097 | 0.0032 | 0.0063 | 0.0019 | 0.0068 | 0.0026 | 0.0065 | 0.0023 | 0.0062 | 0.0018 | 0.0064 | 0.0021 | 0.0063 | 0.0019 |
| v37 | 0.0036 | 0.0010 | 0.0056 | 0.0025 | 0.0035 | 0.0010 | 0.0056 | 0.0024 | 0.0038 | 0.0013 | 0.0041 | 0.0020 | 0.0039 | 0.0017 | 0.0038 | 0.0013 | 0.0039 | 0.0015 | 0.0038 | 0.0013 |
| v38 | 0.0018 | 0.0217 | 0.0002 | 0.0001 | 0.0018 | 0.0218 | 0.0002 | 0.0001 | 0.0013 | 0.0173 | 0.0026 | 0.0287 | 0.0012 | 0.0175 | 0.0020 | 0.0228 | 0.0018 | 0.0222 | 0.0002 | 0.0001 |
| v39 | 0.0019 | 0.0004 | 0.0027 | 0.0008 | 0.0019 | 0.0003 | 0.0029 | 0.0008 | 0.0020 | 0.0005 | 0.0021 | 0.0007 | 0.0021 | 0.0006 | 0.0020 | 0.0005 | 0.0020 | 0.0006 | 0.0020 | 0.0005 |
| v40 | 0.0059 | 0.0015 | 0.0098 | 0.0045 | 0.0058 | 0.0011 | 0.0101 | 0.0045 | 0.0063 | 0.0023 | 0.0071 | 0.0033 | 0.0066 | 0.0029 | 0.0063 | 0.0020 | 0.0065 | 0.0026 | 0.0064 | 0.0021 |
| v41 | 0.0030 | 0.0007 | 0.0047 | 0.0016 | 0.0029 | 0.0006 | 0.0048 | 0.0016 | 0.0032 | 0.0010 | 0.0035 | 0.0013 | 0.0033 | 0.0011 | 0.0032 | 0.0010 | 0.0032 | 0.0011 | 0.0032 | 0.0009 |
| v42 | 0.0015 | 0.0003 | 0.0016 | 0.0003 | 0.0015 | 0.0003 | 0.0015 | 0.0002 | 0.0015 | 0.0003 | 0.0015 | 0.0003 | 0.0015 | 0.0003 | 0.0016 | 0.0002 | 0.0015 | 0.0003 | 0.0016 | 0.0003 |
| v43 | 0.0005 | 0.0001 | 0.0005 | 0.0002 | 0.0005 | 0.0001 | 0.0005 | 0.0001 | 0.0005 | 0.0001 | 0.0006 | 0.0002 | 0.0005 | 0.0001 | 0.0005 | 0.0001 | 0.0005 | 0.0001 | 0.0005 | 0.0002 |
| v44 | 0.0049 | 0.0010 | 0.0075 | 0.0026 | 0.0048 | 0.0010 | 0.0075 | 0.0025 | 0.0051 | 0.0015 | 0.0056 | 0.0020 | 0.0054 | 0.0018 | 0.0051 | 0.0015 | 0.0053 | 0.0017 | 0.0051 | 0.0015 |
| v45 | 0.0008 | 0.0016 | 0.0007 | 0.0011 | 0.0009 | 0.0016 | 0.0003 | 0.0003 | 0.0008 | 0.0016 | 0.0007 | 0.0010 | 0.0008 | 0.0008 | 0.0007 | 0.0020 | 0.0008 | 0.0016 | 0.0007 | 0.0011 |
| v46 | 0.0065 | 0.0013 | 0.0099 | 0.0031 | 0.0064 | 0.0013 | 0.0098 | 0.0031 | 0.0068 | 0.0019 | 0.0075 | 0.0026 | 0.0070 | 0.0022 | 0.0069 | 0.0019 | 0.0070 | 0.0021 | 0.0069 | 0.0019 |
| v47 | 0.0013 | 0.0003 | 0.0014 | 0.0003 | 0.0013 | 0.0003 | 0.0014 | 0.0003 | 0.0013 | 0.0003 | 0.0013 | 0.0003 | 0.0013 | 0.0004 | 0.0013 | 0.0003 | 0.0013 | 0.0004 | 0.0013 | 0.0002 |
| v48 | 0.0036 | 0.0008 | 0.0052 | 0.0017 | 0.0036 | 0.0008 | 0.0052 | 0.0016 | 0.0038 | 0.0010 | 0.0041 | 0.0015 | 0.0039 | 0.0011 | 0.0038 | 0.0011 | 0.0039 | 0.0012 | 0.0038 | 0.0009 |
| v49 | 0.0011 | 0.0005 | 0.0008 | 0.0005 | 0.0011 | 0.0005 | 0.0005 | 0.0004 | 0.0010 | 0.0005 | 0.0010 | 0.0006 | 0.0012 | 0.0005 | 0.0009 | 0.0005 | 0.0010 | 0.0005 | 0.0010 | 0.0005 |
| v50 | 0.0018 | 0.0003 | 0.0019 | 0.0004 | 0.0019 | 0.0003 | 0.0019 | 0.0003 | 0.0018 | 0.0003 | 0.0020 | 0.0004 | 0.0018 | 0.0003 | 0.0019 | 0.0003 | 0.0018 | 0.0003 | 0.0020 | 0.0004 |
| v51 | 0.0047 | 0.0010 | 0.0070 | 0.0026 | 0.0046 | 0.0009 | 0.0070 | 0.0025 | 0.0049 | 0.0014 | 0.0053 | 0.0019 | 0.0051 | 0.0017 | 0.0049 | 0.0013 | 0.0050 | 0.0016 | 0.0049 | 0.0014 |
| v52 | 0.0029 | 0.0010 | 0.0028 | 0.0017 | 0.0030 | 0.0010 | 0.0020 | 0.0014 | 0.0028 | 0.0010 | 0.0030 | 0.0012 | 0.0029 | 0.0011 | 0.0027 | 0.0010 | 0.0028 | 0.0010 | 0.0030 | 0.0013 |
| v53 | 0.0046 | 0.0009 | 0.0070 | 0.0024 | 0.0046 | 0.0009 | 0.0069 | 0.0023 | 0.0048 | 0.0014 | 0.0053 | 0.0019 | 0.0050 | 0.0016 | 0.0048 | 0.0013 | 0.0049 | 0.0015 | 0.0048 | 0.0013 |
| v54 | 0.0001 | 0.0002 | 0.0001 | 0.0001 | 0.0001 | 0.0002 | 0.0001 | 0.0001 | 0.0001 | 0.0002 | 0.0001 | 0.0001 | 0.0001 | 0.0003 | 0.0001 | 0.0000 | 0.0001 | 0.0002 | 0.0001 | 0.0000 |
| v55 | 0.0050 | 0.0005 | 0.0051 | 0.0007 | 0.0050 | 0.0005 | 0.0051 | 0.0007 | 0.0051 | 0.0005 | 0.0051 | 0.0006 | 0.0050 | 0.0006 | 0.0051 | 0.0006 | 0.0050 | 0.0005 | 0.0051 | 0.0007 |
| v56 | 0.0014 | 0.0003 | 0.0015 | 0.0003 | 0.0014 | 0.0003 | 0.0015 | 0.0003 | 0.0014 | 0.0003 | 0.0015 | 0.0003 | 0.0014 | 0.0003 | 0.0015 | 0.0002 | 0.0014 | 0.0002 | 0.0016 | 0.0003 |
| v57 | 0.0023 | 0.0008 | 0.0027 | 0.0013 | 0.0024 | 0.0008 | 0.0026 | 0.0013 | 0.0024 | 0.0009 | 0.0025 | 0.0009 | 0.0024 | 0.0010 | 0.0024 | 0.0007 | 0.0024 | 0.0009 | 0.0024 | 0.0009 |
| v58 | 0.0021 | 0.0003 | 0.0022 | 0.0006 | 0.0021 | 0.0004 | 0.0021 | 0.0005 | 0.0021 | 0.0004 | 0.0021 | 0.0004 | 0.0022 | 0.0004 | 0.0021 | 0.0003 | 0.0021 | 0.0004 | 0.0021 | 0.0004 |
| v59 | 0.0029 | 0.0005 | 0.0041 | 0.0012 | 0.0028 | 0.0004 | 0.0042 | 0.0012 | 0.0030 | 0.0007 | 0.0032 | 0.0010 | 0.0031 | 0.0009 | 0.0030 | 0.0007 | 0.0030 | 0.0008 | 0.0030 | 0.0007 |
| v60 | 0.0002 | 0.0001 | 0.0002 | 0.0002 | 0.0002 | 0.0001 | 0.0002 | 0.0001 | 0.0002 | 0.0001 | 0.0002 | 0.0001 | 0.0002 | 0.0001 | 0.0002 | 0.0001 | 0.0002 | 0.0001 | 0.0002 | 0.0001 |
| v61 | 0.0042 | 0.0009 | 0.0058 | 0.0018 | 0.0042 | 0.0007 | 0.0061 | 0.0017 | 0.0044 | 0.0011 | 0.0047 | 0.0014 | 0.0045 | 0.0012 | 0.0044 | 0.0011 | 0.0045 | 0.0012 | 0.0044 | 0.0011 |
| v62 | 0.0030 | 0.0005 | 0.0041 | 0.0009 | 0.0030 | 0.0005 | 0.0040 | 0.0009 | 0.0031 | 0.0007 | 0.0033 | 0.0008 | 0.0032 | 0.0006 | 0.0031 | 0.0008 | 0.0031 | 0.0007 | 0.0031 | 0.0007 |
| v63 | 0.0035 | 0.0007 | 0.0051 | 0.0017 | 0.0034 | 0.0006 | 0.0054 | 0.0015 | 0.0037 | 0.0010 | 0.0039 | 0.0013 | 0.0038 | 0.0012 | 0.0036 | 0.0009 | 0.0037 | 0.0011 | 0.0036 | 0.0009 |
| v64 | 0.0023 | 0.0010 | 0.0028 | 0.0013 | 0.0022 | 0.0009 | 0.0033 | 0.0015 | 0.0023 | 0.0011 | 0.0024 | 0.0010 | 0.0023 | 0.0012 | 0.0024 | 0.0010 | 0.0024 | 0.0011 | 0.0023 | 0.0010 |
| v65 | 0.0010 | 0.0005 | 0.0014 | 0.0006 | 0.0009 | 0.0004 | 0.0014 | 0.0007 | 0.0010 | 0.0005 | 0.0011 | 0.0004 | 0.0012 | 0.0006 | 0.0009 | 0.0003 | 0.0010 | 0.0005 | 0.0009 | 0.0004 |
| v66 | 0.0016 | 0.0003 | 0.0018 | 0.0004 | 0.0016 | 0.0003 | 0.0018 | 0.0004 | 0.0016 | 0.0003 | 0.0017 | 0.0003 | 0.0016 | 0.0003 | 0.0016 | 0.0003 | 0.0016 | 0.0003 | 0.0017 | 0.0004 |
| v67 | 0.0050 | 0.0005 | 0.0051 | 0.0008 | 0.0050 | 0.0006 | 0.0051 | 0.0007 | 0.0050 | 0.0006 | 0.0051 | 0.0006 | 0.0050 | 0.0006 | 0.0051 | 0.0006 | 0.0050 | 0.0005 | 0.0051 | 0.0007 |
| v68 | 0.0014 | 0.0003 | 0.0015 | 0.0003 | 0.0014 | 0.0003 | 0.0015 | 0.0002 | 0.0014 | 0.0003 | 0.0015 | 0.0003 | 0.0014 | 0.0003 | 0.0015 | 0.0002 | 0.0014 | 0.0002 | 0.0016 | 0.0003 |
| v69 | 0.0048 | 0.0010 | 0.0074 | 0.0026 | 0.0048 | 0.0009 | 0.0077 | 0.0024 | 0.0051 | 0.0015 | 0.0056 | 0.0021 | 0.0053 | 0.0018 | 0.0051 | 0.0015 | 0.0052 | 0.0017 | 0.0052 | 0.0015 |
| v70 | 0.0001 | 0.0001 | 0.0001 | 0.0000 | 0.0001 | 0.0001 | 0.0001 | 0.0000 | 0.0001 | 0.0000 | 0.0002 | 0.0001 | 0.0001 | 0.0001 | 0.0001 | 0.0000 | 0.0001 | 0.0001 | 0.0002 | 0.0001 |
| v71 | 0.0018 | 0.0004 | 0.0027 | 0.0008 | 0.0018 | 0.0003 | 0.0027 | 0.0008 | 0.0019 | 0.0005 | 0.0020 | 0.0007 | 0.0020 | 0.0006 | 0.0019 | 0.0005 | 0.0019 | 0.0006 | 0.0019 | 0.0005 |
| v72 | 0.0035 | 0.0007 | 0.0052 | 0.0017 | 0.0034 | 0.0006 | 0.0054 | 0.0017 | 0.0037 | 0.0010 | 0.0039 | 0.0014 | 0.0038 | 0.0012 | 0.0036 | 0.0010 | 0.0037 | 0.0011 | 0.0037 | 0.0010 |
| v73 | 0.0096 | 0.0058 | 0.0136 | 0.0076 | 0.0092 | 0.0045 | 0.0155 | 0.0102 | 0.0102 | 0.0063 | 0.0100 | 0.0059 | 0.0107 | 0.0053 | 0.0095 | 0.0071 | 0.0103 | 0.0063 | 0.0095 | 0.0057 |
| v74 | 0.0036 | 0.0007 | 0.0055 | 0.0018 | 0.0036 | 0.0007 | 0.0056 | 0.0018 | 0.0038 | 0.0011 | 0.0041 | 0.0015 | 0.0039 | 0.0013 | 0.0038 | 0.0010 | 0.0039 | 0.0012 | 0.0038 | 0.0011 |
| v75 | 0.0023 | 0.0004 | 0.0027 | 0.0010 | 0.0022 | 0.0004 | 0.0028 | 0.0009 | 0.0023 | 0.0005 | 0.0025 | 0.0007 | 0.0023 | 0.0006 | 0.0023 | 0.0006 | 0.0023 | 0.0006 | 0.0024 | 0.0007 |
| v76 | 0.0016 | 0.0005 | 0.0022 | 0.0009 | 0.0016 | 0.0004 | 0.0023 | 0.0008 | 0.0017 | 0.0005 | 0.0019 | 0.0006 | 0.0018 | 0.0006 | 0.0017 | 0.0005 | 0.0017 | 0.0006 | 0.0017 | 0.0005 |
| v77 | 0.0019 | 0.0004 | 0.0021 | 0.0007 | 0.0019 | 0.0004 | 0.0022 | 0.0006 | 0.0019 | 0.0004 | 0.0021 | 0.0005 | 0.0019 | 0.0004 | 0.0019 | 0.0004 | 0.0019 | 0.0004 | 0.0020 | 0.0005 |
| v78 | 0.0012 | 0.0004 | 0.0016 | 0.0006 | 0.0012 | 0.0003 | 0.0017 | 0.0006 | 0.0013 | 0.0004 | 0.0014 | 0.0005 | 0.0013 | 0.0005 | 0.0013 | 0.0004 | 0.0013 | 0.0004 | 0.0013 | 0.0004 |
| v79 | 0.0017 | 0.0003 | 0.0018 | 0.0004 | 0.0016 | 0.0003 | 0.0018 | 0.0004 | 0.0016 | 0.0003 | 0.0018 | 0.0004 | 0.0016 | 0.0003 | 0.0017 | 0.0003 | 0.0016 | 0.0003 | 0.0018 | 0.0004 |
| v80 | 0.0008 | 0.0003 | 0.0010 | 0.0003 | 0.0008 | 0.0003 | 0.0010 | 0.0004 | 0.0008 | 0.0003 | 0.0010 | 0.0004 | 0.0009 | 0.0003 | 0.0008 | 0.0003 | 0.0009 | 0.0003 | 0.0009 | 0.0003 |
Source: Authors’ calculations.

Table A3.
Mean and standard deviation of the values of conditional correlations with market risk factors under different volatility regimes.
Table A3.
Mean and standard deviation of the values of conditional correlations with market risk factors under different volatility regimes.
| Bet Volatility Regimes | STOXX Volatility Regimes | BONDS/RON Volatility Regimes | BONDS/EUR Volatility Regimes | EUR/RON Volatility Regimes | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| LOW | HIGH | LOW | HIGH | LOW | HIGH | LOW | HIGH | LOW | HIGH | |||||||||||
| mean | std | mean | std | mean | std | mean | std | mean | std | mean | std | mean | std | mean | std | mean | std | mean | std | |
| v01 | 0.7537 | 0.0715 | 0.7808 | 0.1694 | 0.2943 | 0.0267 | 0.3651 | 0.0748 | −0.3506 | 0.0249 | −0.3628 | 0.0432 | 0.0451 | 0.0195 | 0.0420 | 0.0054 | −0.0728 | 0.0105 | −0.0741 | 0.0102 |
| v02 | 0.7184 | 0.0496 | 0.7390 | 0.1089 | 0.6292 | 0.1058 | 0.7970 | 0.0695 | −0.2854 | 0.0372 | −0.3033 | 0.0656 | 0.1167 | 0.0253 | 0.1266 | 0.0607 | −0.0793 | 0.0205 | −0.0816 | 0.0199 |
| v03 | 0.7308 | 0.0649 | 0.7551 | 0.1359 | 0.4690 | 0.0378 | 0.5291 | 0.0917 | −0.3531 | 0.0455 | −0.3687 | 0.0716 | 0.0536 | 0.0159 | 0.0543 | 0.0291 | −0.0256 | 0.0054 | −0.0250 | 0.0004 |
| v04 | 0.7265 | 0.0803 | 0.7564 | 0.1508 | 0.5489 | 0.0713 | 0.6910 | 0.0717 | −0.3555 | 0.0744 | −0.3869 | 0.1048 | 0.0809 | 0.0332 | 0.0889 | 0.0782 | −0.0686 | 0.0108 | −0.0699 | 0.0105 |
| v05 | 0.8478 | 0.0503 | 0.8349 | 0.1642 | 0.2920 | 0.0226 | 0.3863 | 0.0863 | −0.2774 | 0.0563 | −0.2943 | 0.0946 | 0.0455 | 0.0364 | 0.0442 | 0.0281 | −0.0401 | 0.0032 | −0.0397 | 0.0001 |
| v06 | 0.7679 | 0.0702 | 0.7851 | 0.1528 | 0.4672 | 0.0132 | 0.5281 | 0.0629 | −0.3753 | 0.0580 | −0.3994 | 0.0933 | 0.0571 | 0.0233 | 0.0575 | 0.0503 | −0.0302 | 0.0079 | −0.0294 | 0.0022 |
| v07 | 0.7970 | 0.0812 | 0.8031 | 0.1883 | 0.4177 | 0.0296 | 0.5334 | 0.0853 | −0.3504 | 0.0429 | −0.3670 | 0.0684 | 0.0280 | 0.0159 | 0.0259 | 0.0234 | −0.0595 | 0.0145 | −0.0612 | 0.0141 |
| v08 | 0.8369 | 0.0523 | 0.8393 | 0.1547 | 0.4530 | 0.0302 | 0.5243 | 0.0638 | −0.2519 | 0.0591 | −0.2726 | 0.1044 | 0.0678 | 0.0186 | 0.0679 | 0.0407 | −0.0302 | 0.0042 | −0.0297 | 0.0003 |
| v09 | 0.7597 | 0.0632 | 0.7874 | 0.1530 | 0.2871 | 0.0369 | 0.3685 | 0.0801 | −0.3195 | 0.0384 | −0.3346 | 0.0603 | 0.0418 | 0.0117 | 0.0407 | 0.0229 | −0.0531 | 0.0016 | −0.0530 | 0.0000 |
| v10 | 0.8177 | 0.0798 | 0.8020 | 0.2033 | 0.2887 | 0.0359 | 0.4009 | 0.1076 | −0.2425 | 0.0626 | −0.2598 | 0.1009 | 0.0306 | 0.0025 | 0.0304 | 0.0000 | −0.0053 | 0.0083 | −0.0044 | 0.0014 |
| v11 | 0.7436 | 0.0621 | 0.7668 | 0.1422 | 0.4294 | 0.0341 | 0.4971 | 0.0935 | −0.3288 | 0.0471 | −0.3441 | 0.0769 | 0.0681 | 0.0417 | 0.0679 | 0.0328 | −0.0114 | 0.0070 | −0.0106 | 0.0010 |
| v12 | 0.7817 | 0.0687 | 0.7996 | 0.1580 | 0.4573 | 0.0187 | 0.5081 | 0.0530 | −0.3511 | 0.0548 | −0.3759 | 0.0925 | 0.0534 | 0.0184 | 0.0540 | 0.0355 | −0.0248 | 0.0053 | −0.0241 | 0.0006 |
| v13 | 0.7999 | 0.0548 | 0.8096 | 0.1511 | 0.2881 | 0.0435 | 0.3822 | 0.0859 | −0.2292 | 0.0528 | −0.2423 | 0.0870 | 0.0495 | 0.0164 | 0.0483 | 0.0356 | −0.0462 | 0.0015 | −0.0460 | 0.0000 |
| v14 | 0.8353 | 0.0683 | 0.8320 | 0.1863 | 0.3297 | 0.0096 | 0.4040 | 0.0765 | −0.2972 | 0.0545 | −0.3190 | 0.0966 | 0.0449 | 0.0337 | 0.0436 | 0.0260 | −0.0444 | 0.0006 | −0.0443 | 0.0000 |
| v15 | 0.8113 | 0.0703 | 0.8073 | 0.1878 | 0.2838 | 0.0392 | 0.3853 | 0.0833 | −0.3028 | 0.0429 | −0.3215 | 0.0801 | 0.0579 | 0.0215 | 0.0593 | 0.0170 | −0.0468 | 0.0001 | −0.0468 | 0.0000 |
| v16 | 0.7865 | 0.0871 | 0.8060 | 0.1753 | 0.4329 | 0.0474 | 0.5464 | 0.0742 | −0.3519 | 0.0604 | −0.3751 | 0.0895 | 0.0622 | 0.0155 | 0.0627 | 0.0390 | −0.0542 | 0.0008 | −0.0542 | 0.0006 |
| v17 | 0.8162 | 0.1006 | 0.8182 | 0.2149 | 0.3714 | 0.0107 | 0.4375 | 0.0658 | −0.3401 | 0.0396 | −0.3567 | 0.0681 | 0.0622 | 0.0419 | 0.0625 | 0.0329 | −0.0583 | 0.0077 | −0.0592 | 0.0074 |
| v18 | 0.1613 | 0.0498 | 0.2827 | 0.1918 | 0.0873 | 0.0453 | 0.3120 | 0.1991 | −0.0525 | 0.0087 | −0.0542 | 0.0106 | 0.0812 | 0.0383 | 0.0820 | 0.0291 | −0.0569 | 0.0402 | −0.0481 | 0.0635 |
| v19 | 0.2307 | 0.0743 | 0.2870 | 0.1358 | 0.0918 | 0.0910 | 0.3000 | 0.1356 | 0.0156 | 0.1110 | −0.0055 | 0.1529 | 0.0202 | 0.0420 | 0.0263 | 0.0185 | 0.0387 | 0.0416 | 0.0455 | 0.0521 |
| v20 | −0.0431 | 0.0001 | −0.0437 | 0.0016 | −0.0126 | 0.0049 | 0.0520 | 0.0815 | 0.0748 | 0.0662 | 0.0713 | 0.0877 | −0.0766 | 0.0247 | −0.0793 | 0.0171 | 0.3373 | 0.0539 | 0.3396 | 0.0322 |
| v21 | 0.7065 | 0.0473 | 0.7350 | 0.1124 | 0.5396 | 0.0632 | 0.6362 | 0.0566 | −0.1168 | 0.0348 | −0.1263 | 0.0803 | 0.1785 | 0.0324 | 0.1796 | 0.0738 | −0.0268 | 0.0074 | −0.0259 | 0.0011 |
| v22 | 0.1027 | 0.0625 | 0.1111 | 0.1134 | 0.0527 | 0.0091 | 0.0029 | 0.0426 | −0.6560 | 0.0862 | −0.6888 | 0.0933 | −0.0611 | 0.0359 | −0.0602 | 0.0957 | −0.0392 | 0.0885 | −0.0522 | 0.0895 |
| v23 | 0.1109 | 0.0731 | 0.1104 | 0.1359 | 0.0727 | 0.0085 | 0.0677 | 0.0336 | −0.6686 | 0.0316 | −0.6824 | 0.0364 | −0.0709 | 0.0373 | −0.0704 | 0.0941 | −0.0049 | 0.1000 | −0.0157 | 0.1076 |
| v24 | −0.0217 | 0.0764 | −0.0303 | 0.1447 | 0.0406 | 0.1227 | 0.0295 | 0.2275 | 0.0991 | 0.0015 | 0.0992 | 0.0010 | −0.1351 | 0.0582 | −0.1519 | 0.0720 | 0.0946 | 0.0571 | 0.1008 | 0.0463 |
| v25 | 0.8974 | 0.0238 | 0.8913 | 0.0931 | 0.3060 | 0.0282 | 0.4171 | 0.0823 | −0.1018 | 0.0824 | −0.0976 | 0.1629 | 0.0840 | 0.0298 | 0.0814 | 0.0625 | −0.0534 | 0.0014 | −0.0532 | 0.0000 |
| v26 | 0.1657 | 0.0716 | 0.2125 | 0.1024 | 0.3119 | 0.1409 | 0.5692 | 0.1163 | 0.0954 | 0.0550 | 0.0855 | 0.0690 | 0.1058 | 0.0304 | 0.1061 | 0.0421 | 0.2396 | 0.1054 | 0.2374 | 0.1043 |
| v27 | −0.0733 | 0.0046 | −0.0723 | 0.0095 | −0.1172 | 0.0070 | −0.0431 | 0.0870 | 0.1637 | 0.0387 | 0.1682 | 0.0620 | −0.0378 | 0.0349 | −0.0476 | 0.0555 | 0.3823 | 0.0489 | 0.3846 | 0.0282 |
| v28 | 0.3085 | 0.0438 | 0.3610 | 0.1202 | 0.6829 | 0.0355 | 0.7600 | 0.0504 | −0.0478 | 0.0028 | −0.0470 | 0.0044 | 0.2550 | 0.0575 | 0.2823 | 0.1072 | −0.0145 | 0.0330 | −0.0084 | 0.0495 |
| v29 | 0.8774 | 0.0815 | 0.8598 | 0.1879 | 0.4351 | 0.0782 | 0.5820 | 0.0869 | −0.0711 | 0.0815 | −0.0682 | 0.1638 | 0.1759 | 0.0148 | 0.1782 | 0.0365 | −0.0602 | 0.0170 | −0.0572 | 0.0458 |
| v30 | 0.8542 | 0.0276 | 0.8599 | 0.0976 | 0.3643 | 0.0560 | 0.4755 | 0.0740 | −0.0861 | 0.0718 | −0.0793 | 0.1420 | 0.1406 | 0.0000 | 0.1406 | 0.0000 | −0.0647 | 0.0000 | −0.0647 | 0.0000 |
| v31 | 0.0252 | 0.0234 | −0.0394 | 0.1149 | −0.0300 | 0.0000 | −0.0408 | 0.0249 | −0.1812 | 0.2721 | −0.2050 | 0.3562 | −0.0927 | 0.0255 | −0.1032 | 0.0536 | 0.0183 | 0.0760 | 0.0182 | 0.0723 |
| v32 | 0.8258 | 0.0411 | 0.8344 | 0.1168 | 0.2989 | 0.0185 | 0.3760 | 0.0618 | −0.0876 | 0.0483 | −0.0883 | 0.1002 | 0.0949 | 0.0000 | 0.0949 | 0.0000 | −0.0620 | 0.0028 | −0.0618 | 0.0082 |
| v33 | 0.0279 | 0.0717 | −0.1217 | 0.1255 | −0.0355 | 0.0051 | −0.1220 | 0.1175 | 0.0167 | 0.1449 | 0.0118 | 0.1929 | 0.0277 | 0.0338 | 0.0346 | 0.0442 | −0.0254 | 0.0192 | −0.0166 | 0.0341 |
| v34 | 0.7809 | 0.0601 | 0.7917 | 0.1538 | 0.3364 | 0.0878 | 0.4538 | 0.1186 | −0.0972 | 0.0742 | −0.0961 | 0.1455 | 0.1335 | 0.0157 | 0.1315 | 0.0340 | −0.0504 | 0.0019 | −0.0502 | 0.0001 |
| v35 | 0.9515 | 0.0042 | 0.9586 | 0.0174 | 0.3278 | 0.0246 | 0.4279 | 0.0701 | −0.0958 | 0.0886 | −0.0905 | 0.1659 | 0.0746 | 0.0264 | 0.0715 | 0.0552 | −0.0618 | 0.0036 | −0.0618 | 0.0033 |
| v36 | 0.4907 | 0.1309 | 0.5309 | 0.2613 | 0.2294 | 0.0790 | 0.3957 | 0.1329 | −0.0476 | 0.1265 | −0.0441 | 0.1796 | 0.0804 | 0.0170 | 0.0835 | 0.0135 | −0.0051 | 0.0088 | −0.0041 | 0.0016 |
| v37 | 0.7167 | 0.1105 | 0.7503 | 0.1724 | 0.3030 | 0.0873 | 0.4816 | 0.1047 | −0.0713 | 0.0375 | −0.0774 | 0.0794 | 0.0835 | 0.0207 | 0.0829 | 0.0420 | −0.0320 | 0.0053 | −0.0313 | 0.0004 |
| v38 | 0.0212 | 0.0220 | −0.0533 | 0.1340 | 0.0006 | 0.0021 | −0.0370 | 0.0663 | −0.0078 | 0.0509 | −0.0187 | 0.0644 | −0.1078 | 0.0894 | −0.0994 | 0.0632 | 0.0373 | 0.0016 | 0.0373 | 0.0001 |
| v39 | 0.7295 | 0.0654 | 0.7377 | 0.1447 | 0.2934 | 0.0124 | 0.3973 | 0.1109 | −0.1048 | 0.0571 | −0.1047 | 0.1050 | 0.0807 | 0.0015 | 0.0810 | 0.0002 | −0.0343 | 0.0000 | −0.0343 | 0.0000 |
| v40 | 0.9345 | 0.0334 | 0.8942 | 0.1345 | 0.3079 | 0.0308 | 0.3621 | 0.0344 | −0.0897 | 0.0737 | −0.0885 | 0.1390 | 0.0786 | 0.0121 | 0.0772 | 0.0281 | −0.0530 | 0.0121 | −0.0531 | 0.0097 |
| v41 | 0.9088 | 0.0076 | 0.9201 | 0.0322 | 0.3151 | 0.0469 | 0.4258 | 0.0788 | −0.1055 | 0.0861 | −0.0984 | 0.1615 | 0.0776 | 0.0124 | 0.0757 | 0.0279 | −0.0618 | 0.0006 | −0.0617 | 0.0000 |
| v42 | −0.0355 | 0.0001 | −0.0361 | 0.0014 | −0.0215 | 0.0078 | 0.0529 | 0.0842 | 0.0557 | 0.0624 | 0.0533 | 0.0795 | −0.0697 | 0.0156 | −0.0697 | 0.0293 | 0.3326 | 0.0520 | 0.3341 | 0.0361 |
| v43 | 0.0862 | 0.0805 | 0.0865 | 0.0718 | 0.1315 | 0.0205 | 0.1376 | 0.0506 | −0.5862 | 0.0681 | −0.6068 | 0.0770 | −0.0082 | 0.0476 | 0.0127 | 0.0756 | −0.0525 | 0.0916 | −0.0663 | 0.0959 |
| v44 | 0.8721 | 0.0115 | 0.8880 | 0.0456 | 0.3614 | 0.0656 | 0.4864 | 0.0855 | −0.0978 | 0.0801 | −0.0922 | 0.1526 | 0.1148 | 0.0165 | 0.1129 | 0.0376 | −0.0649 | 0.0018 | −0.0651 | 0.0018 |
| v45 | −0.0361 | 0.0018 | −0.0452 | 0.0222 | 0.0031 | 0.1741 | −0.0191 | 0.1329 | 0.0255 | 0.0168 | 0.0230 | 0.0205 | 0.1220 | 0.0027 | 0.1223 | 0.0000 | 0.0086 | 0.0017 | 0.0084 | 0.0017 |
| v46 | 0.9513 | 0.0050 | 0.9565 | 0.0203 | 0.3287 | 0.0242 | 0.4295 | 0.0716 | −0.0948 | 0.0868 | −0.0886 | 0.1635 | 0.0741 | 0.0296 | 0.0707 | 0.0600 | −0.0627 | 0.0000 | −0.0627 | 0.0000 |
| v47 | 0.4165 | 0.1867 | 0.5106 | 0.2619 | 0.2129 | 0.0331 | 0.3512 | 0.0991 | −0.1247 | 0.0587 | −0.1250 | 0.1109 | 0.1069 | 0.0024 | 0.1066 | 0.0001 | −0.0306 | 0.0000 | −0.0306 | 0.0000 |
| v48 | 0.6509 | 0.0761 | 0.6897 | 0.1706 | 0.2839 | 0.0138 | 0.3649 | 0.0942 | −0.0782 | 0.0318 | −0.0812 | 0.0656 | 0.1304 | 0.0058 | 0.1295 | 0.0149 | −0.0178 | 0.0008 | −0.0178 | 0.0002 |
| v49 | 0.2353 | 0.2321 | 0.2108 | 0.2158 | 0.0850 | 0.0445 | 0.0664 | 0.0448 | −0.0417 | 0.0186 | −0.0384 | 0.0252 | 0.0633 | 0.0030 | 0.0635 | 0.0059 | 0.0464 | 0.0305 | 0.0393 | 0.0405 |
| v50 | −0.0333 | 0.0000 | −0.0331 | 0.0011 | 0.0024 | 0.0691 | 0.0434 | 0.1435 | 0.0060 | 0.0381 | 0.0012 | 0.0597 | −0.1160 | 0.0486 | −0.1198 | 0.0776 | 0.2284 | 0.0656 | 0.2335 | 0.0477 |
| v51 | 0.7650 | 0.0292 | 0.7831 | 0.1008 | 0.3074 | 0.0513 | 0.4225 | 0.0888 | −0.1059 | 0.0738 | −0.0999 | 0.1354 | 0.0936 | 0.0090 | 0.0922 | 0.0197 | −0.0473 | 0.0010 | −0.0472 | 0.0000 |
| v52 | 0.5612 | 0.2361 | 0.4668 | 0.2209 | 0.2530 | 0.0794 | 0.2818 | 0.1247 | −0.0472 | 0.0436 | −0.0499 | 0.0879 | 0.0578 | 0.0211 | 0.0540 | 0.0408 | −0.0471 | 0.0057 | −0.0472 | 0.0045 |
| v53 | 0.8089 | 0.0121 | 0.8357 | 0.0477 | 0.3998 | 0.0690 | 0.5231 | 0.0910 | −0.0949 | 0.0610 | −0.0968 | 0.1323 | 0.1564 | 0.0161 | 0.1553 | 0.0367 | −0.0459 | 0.0018 | −0.0457 | 0.0001 |
| v54 | 0.0437 | 0.0387 | −0.0567 | 0.1365 | −0.0066 | 0.0011 | −0.0594 | 0.0921 | −0.0172 | 0.1354 | −0.0139 | 0.1875 | −0.0585 | 0.0744 | −0.0538 | 0.0549 | 0.0095 | 0.0023 | 0.0093 | 0.0002 |
| v55 | −0.0288 | 0.0638 | −0.0463 | 0.0996 | 0.0166 | 0.1339 | 0.0099 | 0.2472 | 0.1489 | 0.0785 | 0.1435 | 0.0770 | −0.1165 | 0.0825 | −0.1507 | 0.1125 | 0.0860 | 0.0708 | 0.0964 | 0.0645 |
| v56 | −0.0432 | 0.0000 | −0.0432 | 0.0000 | −0.0590 | 0.0054 | 0.0045 | 0.0775 | 0.1162 | 0.0528 | 0.1163 | 0.0682 | −0.0619 | 0.0137 | −0.0637 | 0.0196 | 0.3661 | 0.0524 | 0.3684 | 0.0313 |
| v57 | 0.1099 | 0.0663 | 0.1246 | 0.1324 | 0.3068 | 0.2522 | 0.2562 | 0.3858 | −0.0019 | 0.0121 | −0.0027 | 0.0248 | −0.0538 | 0.0788 | −0.1112 | 0.0834 | 0.1881 | 0.0371 | 0.1949 | 0.0203 |
| v58 | 0.4574 | 0.0607 | 0.5384 | 0.1283 | 0.6080 | 0.0858 | 0.4538 | 0.1032 | −0.1011 | 0.0312 | −0.1111 | 0.0690 | 0.1127 | 0.0000 | 0.1127 | 0.0000 | −0.0412 | 0.0306 | −0.0416 | 0.0297 |
| v59 | 0.8415 | 0.0565 | 0.8268 | 0.1426 | 0.3197 | 0.0495 | 0.4246 | 0.0853 | −0.0705 | 0.0735 | −0.0702 | 0.1299 | 0.0948 | 0.0064 | 0.0938 | 0.0001 | −0.0340 | 0.0025 | −0.0337 | 0.0001 |
| v60 | 0.0304 | 0.0132 | −0.0237 | 0.1128 | 0.0010 | 0.0868 | −0.0164 | 0.1284 | −0.0525 | 0.0967 | −0.0429 | 0.1410 | −0.0841 | 0.0506 | −0.0771 | 0.0262 | −0.0133 | 0.0063 | −0.0140 | 0.0009 |
| v61 | 0.6620 | 0.1481 | 0.6909 | 0.1998 | 0.2981 | 0.0841 | 0.4470 | 0.1296 | −0.0477 | 0.1021 | −0.0538 | 0.1741 | 0.1001 | 0.0169 | 0.0986 | 0.0372 | −0.0341 | 0.0076 | −0.0333 | 0.0018 |
| v62 | 0.8647 | 0.0178 | 0.8626 | 0.0874 | 0.2744 | 0.0561 | 0.4239 | 0.0912 | −0.0821 | 0.0691 | −0.0780 | 0.1445 | 0.0750 | 0.0073 | 0.0738 | 0.0005 | −0.0551 | 0.0001 | −0.0551 | 0.0004 |
| v63 | 0.7311 | 0.0689 | 0.7748 | 0.1351 | 0.3516 | 0.0405 | 0.4339 | 0.0608 | −0.1333 | 0.0860 | −0.1193 | 0.1660 | 0.1160 | 0.0259 | 0.1171 | 0.0503 | −0.0502 | 0.0061 | −0.0502 | 0.0055 |
| v64 | 0.3561 | 0.0922 | 0.3714 | 0.1290 | 0.4243 | 0.0666 | 0.4511 | 0.1258 | −0.1636 | 0.0243 | −0.1716 | 0.0447 | 0.1525 | 0.0451 | 0.1518 | 0.0960 | −0.0889 | 0.0680 | −0.0753 | 0.1261 |
| v65 | 0.6758 | 0.0381 | 0.6978 | 0.0513 | 0.4301 | 0.0125 | 0.5438 | 0.1261 | −0.2641 | 0.0433 | −0.2813 | 0.0702 | 0.1781 | 0.0042 | 0.1774 | 0.0003 | −0.0346 | 0.0070 | −0.0328 | 0.0209 |
| v66 | −0.0075 | 0.0036 | 0.0078 | 0.0330 | 0.0015 | 0.0686 | 0.1300 | 0.2105 | 0.1306 | 0.0798 | 0.1349 | 0.1008 | 0.0155 | 0.0229 | 0.0104 | 0.0293 | 0.3448 | 0.0570 | 0.3489 | 0.0295 |
| v67 | −0.0319 | 0.0642 | −0.0506 | 0.1004 | 0.0118 | 0.1343 | 0.0036 | 0.2457 | 0.1494 | 0.0781 | 0.1433 | 0.0771 | −0.1173 | 0.0821 | −0.1507 | 0.1127 | 0.0858 | 0.0735 | 0.0964 | 0.0685 |
| v68 | −0.0510 | 0.0000 | −0.0510 | 0.0000 | −0.0713 | 0.0054 | −0.0082 | 0.0767 | 0.1250 | 0.0530 | 0.1239 | 0.0714 | −0.0559 | 0.0200 | −0.0587 | 0.0319 | 0.3687 | 0.0534 | 0.3708 | 0.0326 |
| v69 | 0.8508 | 0.0440 | 0.8425 | 0.1402 | 0.3722 | 0.0643 | 0.5043 | 0.0875 | −0.0966 | 0.0825 | −0.0935 | 0.1540 | 0.1189 | 0.0139 | 0.1177 | 0.0316 | −0.0525 | 0.0025 | −0.0528 | 0.0024 |
| v70 | 0.1348 | 0.0510 | 0.0454 | 0.1522 | 0.0795 | 0.0012 | 0.0356 | 0.0719 | −0.4286 | 0.1206 | −0.5066 | 0.1280 | −0.0357 | 0.0386 | −0.0300 | 0.0159 | −0.0222 | 0.0104 | −0.0232 | 0.0029 |
| v71 | 0.7736 | 0.0559 | 0.7810 | 0.1390 | 0.3181 | 0.0928 | 0.4974 | 0.1059 | −0.0510 | 0.0775 | −0.0498 | 0.1319 | 0.1243 | 0.0060 | 0.1233 | 0.0002 | −0.0269 | 0.0041 | −0.0264 | 0.0005 |
| v72 | 0.7532 | 0.0354 | 0.7649 | 0.0967 | 0.3045 | 0.0728 | 0.4758 | 0.0901 | −0.0822 | 0.0774 | −0.0837 | 0.1392 | 0.1130 | 0.0182 | 0.1121 | 0.0365 | −0.0291 | 0.0112 | −0.0280 | 0.0030 |
| v73 | 0.1529 | 0.0397 | 0.1905 | 0.0984 | 0.3212 | 0.0522 | 0.3686 | 0.0704 | −0.0043 | 0.0106 | −0.0023 | 0.0128 | 0.1228 | 0.0263 | 0.1257 | 0.0459 | 0.0469 | 0.0842 | 0.0658 | 0.1184 |
| v74 | 0.7839 | 0.0575 | 0.7775 | 0.1635 | 0.3156 | 0.0533 | 0.4277 | 0.0847 | −0.0889 | 0.0784 | −0.0864 | 0.1346 | 0.0692 | 0.0134 | 0.0672 | 0.0269 | −0.0365 | 0.0018 | −0.0362 | 0.0001 |
| v75 | 0.1274 | 0.0326 | 0.1520 | 0.0689 | 0.2197 | 0.0755 | 0.2428 | 0.1307 | −0.0120 | 0.0593 | −0.0133 | 0.0699 | 0.0378 | 0.0643 | 0.0292 | 0.0362 | 0.2224 | 0.0541 | 0.2226 | 0.0504 |
| v76 | 0.2201 | 0.0378 | 0.2242 | 0.0562 | 0.3249 | 0.0899 | 0.3143 | 0.1129 | −0.1677 | 0.0161 | −0.1646 | 0.0244 | 0.0507 | 0.0602 | 0.0417 | 0.0390 | 0.0127 | 0.0706 | −0.0020 | 0.0674 |
| v77 | 0.0822 | 0.0126 | 0.1071 | 0.0556 | 0.1381 | 0.0546 | 0.1754 | 0.1261 | 0.0006 | 0.0559 | 0.0005 | 0.0706 | 0.0274 | 0.0711 | 0.0180 | 0.0409 | 0.2787 | 0.0574 | 0.2792 | 0.0499 |
| v78 | 0.2116 | 0.0358 | 0.2228 | 0.0643 | 0.3319 | 0.0942 | 0.3269 | 0.1180 | −0.2300 | 0.0209 | −0.2256 | 0.0316 | 0.0499 | 0.0694 | 0.0375 | 0.0533 | 0.0032 | 0.0546 | −0.0087 | 0.0515 |
| v79 | 0.0061 | 0.0071 | 0.0227 | 0.0266 | 0.0147 | 0.0348 | 0.0534 | 0.0979 | 0.0267 | 0.0592 | 0.0248 | 0.0787 | 0.0113 | 0.0690 | 0.0024 | 0.0406 | 0.3267 | 0.0522 | 0.3279 | 0.0392 |
| v80 | 0.1584 | 0.0004 | 0.1637 | 0.0149 | 0.2199 | 0.0512 | 0.2167 | 0.0702 | −0.2840 | 0.0114 | −0.2856 | 0.0114 | 0.0279 | 0.0820 | 0.0127 | 0.0662 | 0.0330 | 0.0753 | 0.0176 | 0.0771 |
Source: Authors’ calculations.
References
- Financial Supervisory Authority. Financial Supervisory Authority Monthly Market Report. Available online: https://asfromania.ro/files/ENGLEZA/ASF%20Monthly%20Market%20Report%20-%20December%202018.pdf (accessed on 11 February 2019).
- Wojcik, D.; Cojoianu, T.F. Resilience of the us securities industry to the global financial crisis. Geoforum 2018, 91, 182–194. [Google Scholar] [CrossRef]
- Leduc, M.V.; Thurner, S. Incentivizing resilience in financial networks. J. Econ. Dyn. Control 2017, 82, 44–66. [Google Scholar] [CrossRef]
- Cheng, X.; Zhao, H.C. Modeling, analysis and mitigation of contagion in financial systems. Econ. Model. 2019, 76, 281–292. [Google Scholar] [CrossRef]
- Spokeviciute, L.; Keasey, K.; Vallascas, F. Do financial crises cleanse the banking industry? Evidence from us commercial bank exits. J. Bank. Financ. 2019, 99, 222–236. [Google Scholar] [CrossRef]
- Kenc, T.; Erdem, F.P.; Unalmis, I. Resilience of emerging market economies to global financial conditions. Cent. Bank. Rev. 2016, 16, 1–6. [Google Scholar] [CrossRef]
- Asal, M. Testing for the presence of skill in swedish mutual fund performance: Evidence from a bootstrap analysis. J. Econ. Bus. 2016, 88, 22–35. [Google Scholar] [CrossRef]
- Ferreira, M.A.; Matos, P.; Pereira, J.P.; Pires, P. Do locals know better? A comparison of the performance of local and foreign institutional investors. J. Bank. Financ. 2017, 82, 151–164. [Google Scholar] [CrossRef]
- Fabozzi, F.J.; Francis, J.C. Mutual fund systematic risk for bull and bear markets-empirical-examination. J. Financ. 1979, 34, 1243–1250. [Google Scholar] [CrossRef]
- Chen, X.H.; Lai, Y.J. On the concentration of mutual fund portfolio holdings: Evidence from taiwan. Res. Int. Bus. Financ. 2015, 33, 268–286. [Google Scholar] [CrossRef]
- Yi, L.; He, L. False discoveries in style timing of chinese mutual funds. Pac. Basin Financ. J. 2016, 38, 194–208. [Google Scholar] [CrossRef]
- Yi, L.; Liu, Z.L.; He, L.; Qin, Z.L.; Gan, S.L. Do chinese mutual funds time the market? Pac. Basin Financ. J. 2018, 47, 1–19. [Google Scholar] [CrossRef]
- Choi, N.; Fedenia, M.; Skiba, H.; Sokolyk, T. Portfolio concentration and performance of institutional investors worldwide. J. Financ. Econ. 2017, 123, 189–208. [Google Scholar] [CrossRef]
- Hiraki, T.; Liu, M.; Wang, X. Country and industry concentration and the performance of international mutual funds. J. Bank. Financ. 2015, 59, 297–310. [Google Scholar] [CrossRef]
- Hornstein, A.S.; Hounsell, J. Managerial investment in mutual funds: Determinants and performance implications. J. Econ. Bus. 2016, 87, 18–34. [Google Scholar] [CrossRef]
- Alexander, G.J.; Stover, R.D. Consistency of mutual fund performance during varying market conditions. J. Econ. Bus. 1980, 32, 219–226. [Google Scholar]
- Stafylas, D.; Anderson, K.; Uddin, M. Recent advances in hedge funds’ performance attribution: Performance persistence and fundamental factors. Int. Rev. Financ. Anal. 2016, 43, 48–61. [Google Scholar] [CrossRef]
- Hwang, I.; Xu, S.; In, F.; Kim, T.S. Systemic risk and cross-sectional hedge fund returns. J. Empir. Financ. 2017, 42, 109–130. [Google Scholar] [CrossRef]
- Di Tommaso, C.; Piluso, F. The failure of hedge funds: An analysis of the impact of different risk classes. Res. Int. Bus. Financ. 2018, 45, 121–133. [Google Scholar] [CrossRef]
- Racicot, F.E.; Theoret, R. Multi-moment risk, hedging strategies, & the business cycle. Int. Rev. Econ. Financ. 2018, 58, 637–675. [Google Scholar]
- Carhart, M.M. On persistence in mutual fund performance. J. Financ. 1997, 52, 57–82. [Google Scholar] [CrossRef]
- Andreu, L.; Matallin-Saez, J.C.; Sarto, J.L. Mutual fund performance attribution and market timing using portfolio holdings. Int. Rev. Econ. Financ. 2018, 57, 353–370. [Google Scholar] [CrossRef]
- Oueslati, A.; Hammami, Y.; Jilani, F. The timing ability and global performance of tunisian mutual fund managers: A multivariate garch approach. Res. Int. Bus. Financ. 2014, 31, 57–73. [Google Scholar] [CrossRef]
- Liao, L.; Zhang, X.Y.; Zhang, Y.Q. Mutual fund managers’ timing abilities. Pac. Basin Financ. J. 2017, 44, 80–96. [Google Scholar] [CrossRef]
- Ayadi, M.A.; Lazrak, S.; Liao, Y.S.; Welch, R. Performance of fixed-income mutual funds with regime-switching models. Q. Rev. Econ. Financ. 2018, 69, 217–231. [Google Scholar] [CrossRef]
- Liang, B. On the performance of hedge funds. Financ. Anal. J. 1999, 55, 72–85. [Google Scholar] [CrossRef]
- Schaub, N.; Schmid, M. Hedge fund liquidity and performance: Evidence from the financial crisis. J. Bank. Financ. 2013, 37, 671–692. [Google Scholar] [CrossRef]
- Engle, R.F.; Ito, T.; Lin, W.L. Meteor-showers or heat waves-heteroskedastic intradaily volatility in the foreign-exchange market. Econometrica 1990, 58, 525–542. [Google Scholar] [CrossRef]
- Kasch-Haroutounian, M.; Price, S. Volatility in the transition markets of central europe. Appl. Financ. Econ. 2001, 11, 93–105. [Google Scholar] [CrossRef]
- Bubak, V.; Kocenda, E.; Zikes, F. Volatility transmission in emerging european foreign exchange markets. J. Bank. Financ. 2011, 35, 2829–2841. [Google Scholar] [CrossRef]
- Clements, A.E.; Hurn, A.S.; Volkov, V.V. Volatility transmission in global financial markets. J. Empir. Financ. 2015, 32, 3–18. [Google Scholar] [CrossRef]
- BenSaida, A.; Litimi, H.; Abdallah, O. Volatility spillover shifts in global financial markets. Econ. Model. 2018, 73, 343–353. [Google Scholar] [CrossRef]
- Adam, T.; Benecka, S.; Mateju, J. Financial stress and its non-linear impact on cee exchange rates. J. Financ. Stabil. 2018, 36, 346–360. [Google Scholar] [CrossRef]
- Ning, Y.; Zhang, L.X. Modeling dynamics of short-term international capital flows in china: A markov regime switching approach. N. Am. J. Econ. Financ. 2018, 44, 193–203. [Google Scholar] [CrossRef]
- Kocenda, E.; Moravcova, M. Exchange rate comovements, hedging and volatility spillovers on new eu forex markets. J. Int. Financ. Mark. I 2019, 58, 42–64. [Google Scholar] [CrossRef]
- Lee, S.L.; Ward, C.W.R. Persistence of UK Real Estate Returns: A Markov Chain Analysis. Available online: http://www.reading.ac.uk/LM/LM/fulltxt/1200.pdf (accessed on 3 February 2019).
- Chang, K.L. Does reit index hedge inflation risk? New evidence from the tail quantile dependences of the markov-switching grg copula. N. Am. J. Econ. Financ. 2017, 39, 56–67. [Google Scholar] [CrossRef]
- Füss, R.; Kaiser, D.G.; Adams, Z. Value at risk, garch modelling and the forecasting of hedge fund return volatility. J. Deriv. Hedge Funds 2007, 13, 2–25. [Google Scholar] [CrossRef]
- Mishra, P.K.; Das, K.B.; Pradhan, B.B. Capital market volatility-an econometric analysis. Empir. Econ. Lett. 2009, 8, 469–477. [Google Scholar]
- Dark, J. Futures hedging with markov switching vector error correction fiegarch and fiaparch. J. Bank. Financ. 2015, 61, S269–S285. [Google Scholar] [CrossRef]
- Luo, C.C.; Seco, L.; Wu, L.L.B. Portfolio optimization in hedge funds by ogarch and markov switching model. Omega 2015, 57, 34–39. [Google Scholar] [CrossRef]
- Yan, Z.P.; Li, S.H. Hedge ratio on markov regime-switching diagonal bekk-garch model. Financ. Res. Lett. 2018, 24, 49–55. [Google Scholar]
- Amvella, S.P.; Meier, I.; Papageorgiou, N. Persistence Analysis of Hedge Fund Returns. Available online: http://neumann.hec.ca/pages/iwan.meier/Hedge%20Fund%20Persistence/Persistence_1109.pdf (accessed on 3 February 2019).
- Getmansky, M.; Lo, A.W.; Makarov, I. An econometric model of serial correlation and illiquidity in hedge fund returns. J. Financ. Econ. 2004, 74, 529–609. [Google Scholar] [CrossRef]
- Vidal-García, J. The persistence of european mutual fund performance. Res. Int. Bus. Financ. 2013, 28, 45–67. [Google Scholar] [CrossRef]
- Vidal-Garcia, J.; Vidal, M.; Boubaker, S.; Uddin, G.S. The short-term persistence of international mutual fund performance. Econ. Model. 2016, 52, 926–938. [Google Scholar] [CrossRef]
- Roca, E.D.; Wong, V.S.H.; Tularam, G.A. Markov regime switching modelling and analysis of socially responsible investment funds. J. Math. Stat. 2011, 7, 302–313. [Google Scholar]
- Leite, P.; Cortez, M.C. Performance of european socially responsible funds during market crises: Evidence from france. Int. Rev. Financ. Anal. 2015, 40, 132–141. [Google Scholar] [CrossRef]
- Lean, H.H.; Ang, W.R.; Smyth, R. Performance and performance persistence of socially responsible investment funds in europe and north america. N. Am. J. Econ. Financ. 2015, 34, 254–266. [Google Scholar] [CrossRef]
- Nakai, M.; Yamaguchi, K.; Takeuchi, K. Can sri funds better resist global financial crisis? Evidence from japan. Int. Rev. Financ. Anal. 2016, 48, 12–20. [Google Scholar] [CrossRef]
- Matallín-Sáez, J.C.; Soler-Domínguez, A.; Tortosa-Ausina, E.; de Mingo-López, D.V. Ethical strategy focus and mutual fund management: Performance and persistence. J. Clean. Prod. 2019, 213, 618–633. [Google Scholar] [CrossRef]
- Roll, R. Volatility, correlation, and diversification in a multi-factor world. J. Portfolio Manag. 2013, 39, 11–18. [Google Scholar] [CrossRef]
- Huang, Y.S.; Yao, J.; Zhu, Y. Thriving in a disrupted market: A study of chinese hedge fund performance. Pac. Basin Financ. J. 2018, 48, 210–223. [Google Scholar] [CrossRef]
- Huang, Y.S.; Chen, C.R.; Kato, I. Different strokes by different folks: The dynamics of hedge fund systematic risk exposure and performance. Int. Rev. Econ. Financ. 2017, 48, 367–388. [Google Scholar] [CrossRef]
- Hammami, Y.; Jilani, F.; Oueslati, A. Mutual fund performance in tunisia: A multivariate garch approach. Res. Int. Bus. Financ. 2013, 29, 35–51. [Google Scholar] [CrossRef]
- Charfeddine, L.; Ajmi, A.N. The tunisian stock market index volatility: Long memory vs. Switching regime. Emerg. Mark. Rev. 2013, 16, 170–182. [Google Scholar] [CrossRef]
- Fulkerson, J.A.; Riley, T.B. Portfolio concentration and mutual fund performance. J. Empir. Financ. 2019, 51, 1–16. [Google Scholar] [CrossRef]
- Stafylas, D.; Anderson, K.; Uddin, M. Hedge fund performance attribution under various market conditions. Int. Rev. Financ. Anal. 2018, 56, 221–237. [Google Scholar] [CrossRef]
- Aboura, S.; Roye, B.V. Financial stress and economic dynamics: The case of france. Int. Econ. 2017, 149, 57–73. [Google Scholar] [CrossRef]
- Saranya, K.; Prasanna, P.K. Estimating stochastic volatility with jumps and asymmetry in asian markets. Financ. Res. Lett. 2018, 25, 145–153. [Google Scholar] [CrossRef]
- Munechika, M. Performance dynamics of hedge fund index investing. J. Bus. Econ. 2016, 7, 1729–1742. [Google Scholar]
- Kristoufek, L.; Ferreira, P. Capital asset pricing model in portugal: Evidence from fractal regressions. Port. Econ. J. 2018, 17, 173–183. [Google Scholar] [CrossRef]
- Tsay, R.S. Analysis of Financial Time Series, 3rd ed.; Ruey S. Tsay: Hoboken, NJ, USA, 2010. [Google Scholar]
- Engle, R.F.; Sheppard, K. Theoretical and Empirical Properties of Dynamic Conditional Correlation Multivariate Garch. Available online: https://www.nber.org/papers/w8554.pdf (accessed on 3 February 2019).
- Sheppard, K. Mfe Matlab Function Reference Financial Econometrics. Available online: https://www.kevinsheppard.com/images/9/95/MFE_Toolbox_Documentation.pdf (accessed on 3 February 2019).
- Hamilton, J.D. Time Series Analysis; Princeton University Press: Princeton, NJ, USA, 1994. [Google Scholar]
- Hamilton, J.D. Regime-Switching Models. Prepared for: Palgrave Dictionary of Economics. Available online: https://econweb.ucsd.edu/~jhamilto/palgrav1.pdf (accessed on 3 February 2019).
- Perlin, M. Ms_regress—The Matlab Package for Markov Regime Switching Models. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=1714016 (accessed on 3 February 2019).
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).