Game Modelling and Strategy Research on the System Dynamics–Based Quadruplicate Evolution for High–Speed Railway Operational Safety Supervision System
Abstract
:1. Introduction
2. Analysis of an HSR Operational Safety Supervision Evolutionary Game Model with Multiple Agents in a Static RPCS
2.1. Model Description and Establishment
2.2. Replicator Dynamics of a Multiple Agent Supervision System
2.3. Results of the Stability Analysis of a Multiple–Agent Supervision System
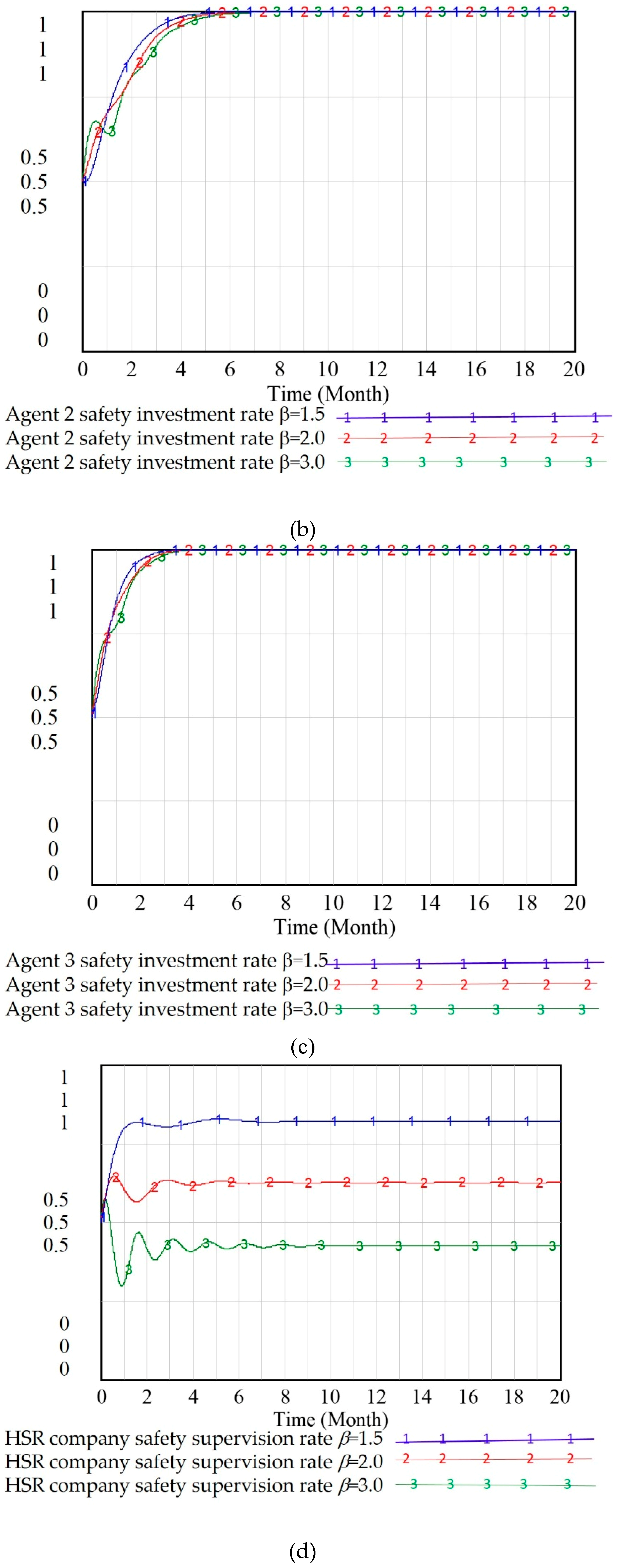
2.4. Stability Analysis of a Multiple–Agent Supervision System Based on SD
3. Analysis of the Optimized HSR Operational Safety Supervision Evolutionary Game Model with Multiple Agents in a Dynamic RPCS
3.1. Results and Stability Analysis of an Optimized Multiple–Agent Supervision System
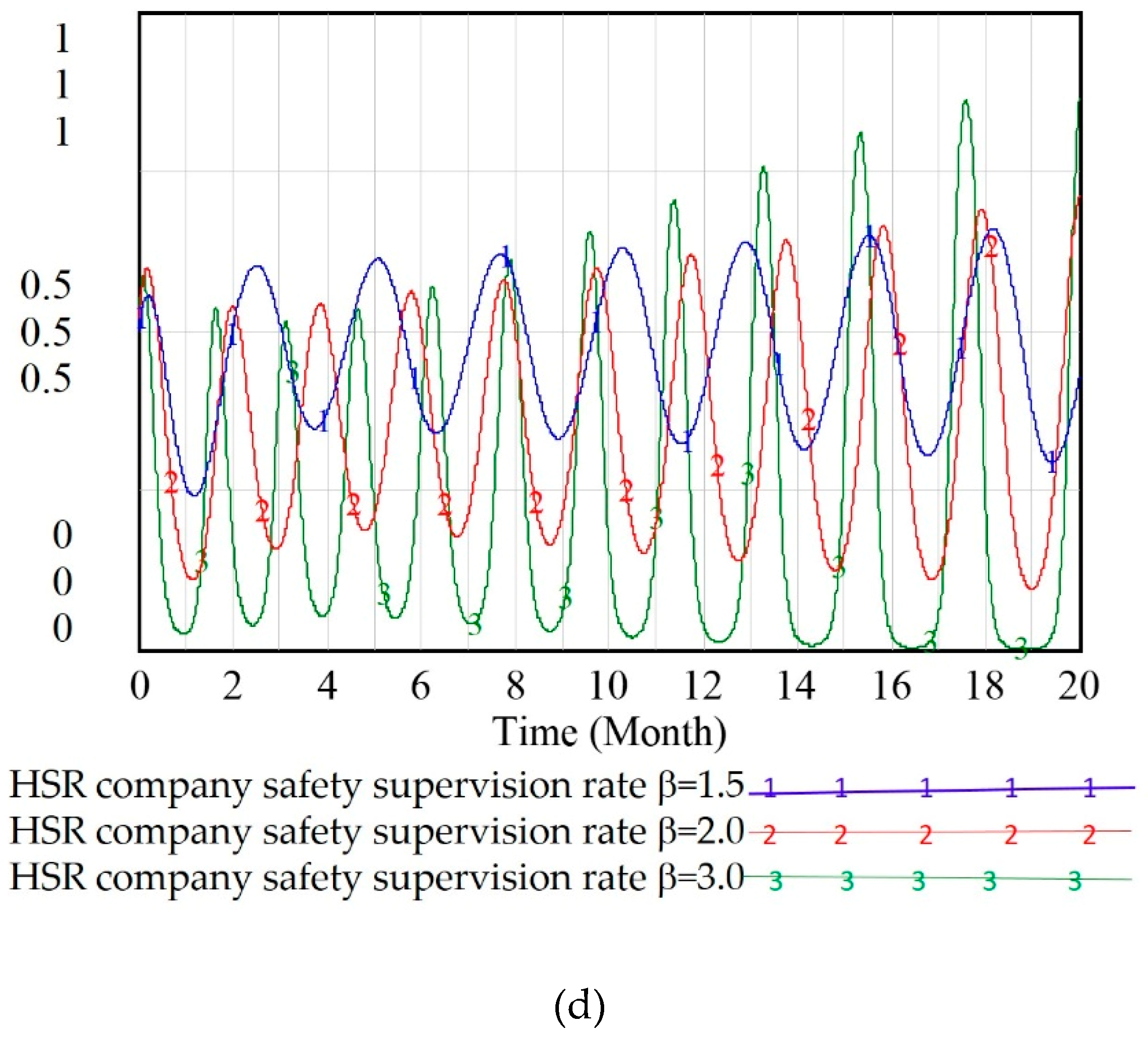
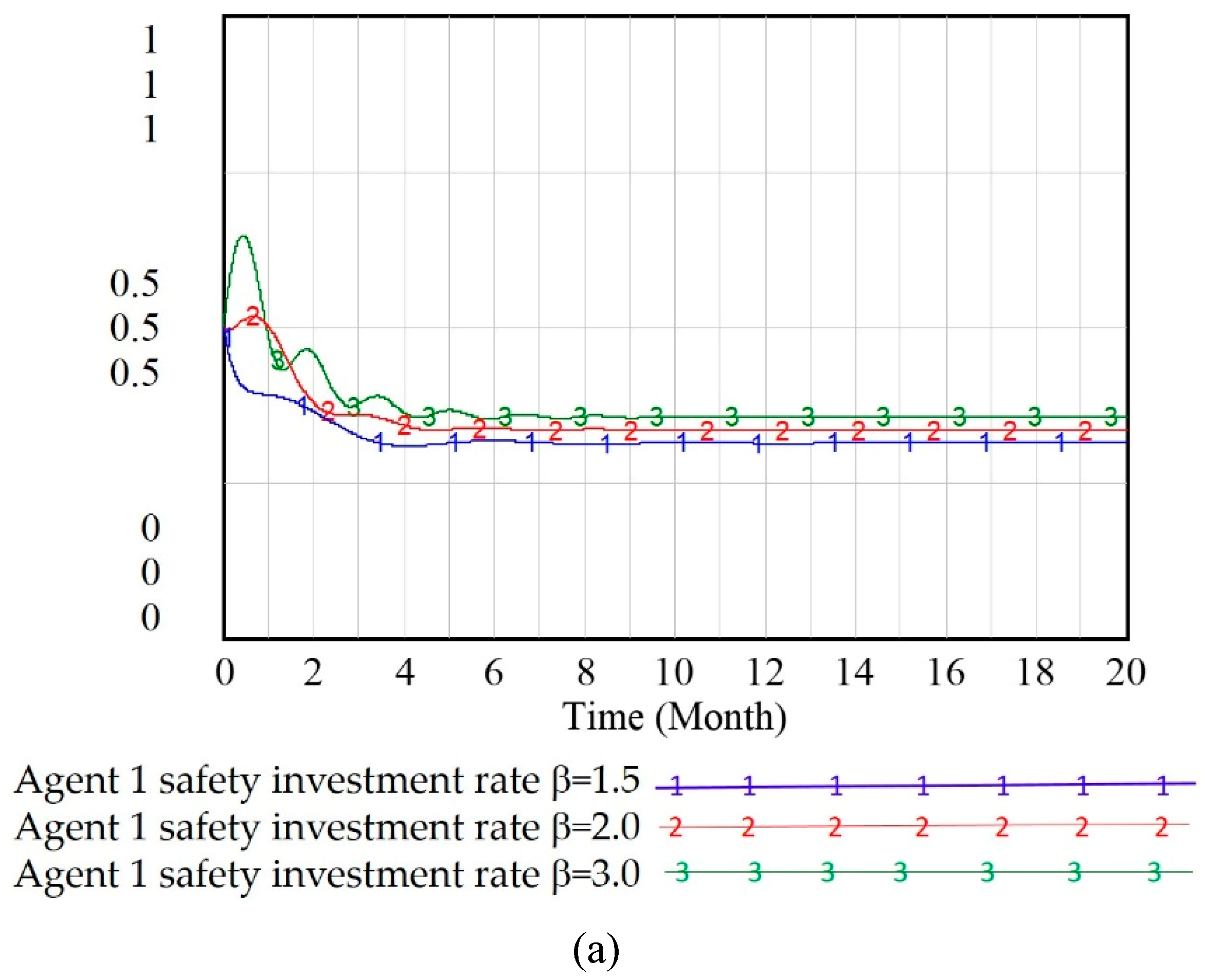
3.2. Stability Analysis of an Optimized Multiple–Agent Supervision System Based on SD
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- He, B.J.; Zhao, D.X.; Zhu, J. Promoting and implementing urban sustainability in China–An integration of sustainable initiatives at different urban scales. Habitat Intern. 2018, 82, 83–93. [Google Scholar] [CrossRef]
- Zhang, P.; Qin, G.; Wang, Y. Optimal Maintenance Decision Method for Urban Gas Pipelines Based on as Low as Reasonably Practicable Principle. Sustainability 2018, 11, 153. [Google Scholar] [CrossRef]
- de Rus, G.; Nombela, G. Is investment in high speed rail socially profitable? JTEP 2007, 41, 3–23. [Google Scholar]
- Bi, M.; He, S. Express delivery with high–speed railway, Definitely feasible or just a publicity stunt. Trans. Res. Part A 2019, 120, 165–187. [Google Scholar] [CrossRef]
- Chai, J. Analysis on shock effect of China’s high–speed railway on aviation transport. Trans. Res. Part A 2018, 108, 35–44. [Google Scholar] [CrossRef]
- Bazin, S. High speed railway, service innovations and urban and business tourisms development. Econ. Manag. Tour. 2011, 1, 115–141. [Google Scholar]
- Martínez–Rodrigo, M.D. Dynamic performance of existing high–speed railway bridges under resonant conditions retrofitted with fluid viscous dampers. Eng. Struct. 2010, 32, 808–828. [Google Scholar]
- Sun, Z. Technology innovation and entrepreneurial state, the development of China’s high–speed rail industry. Technol. Anal. Strateg. Manag. 2015, 27, 646–659. [Google Scholar] [CrossRef]
- Yin, M. The effects of the high–speed railway on urban development, International experience and potential implications for China. Prog. Plan. 2015, 98, 1–52. [Google Scholar] [CrossRef]
- Chester, M. Life–cycle assessment of high–speed rail, the case of California. Environ. Res. Lett. 2010, 5, 014003. [Google Scholar] [CrossRef]
- Marincioni, F.; Appiotti, F. The Lyon–Turin High–Speed Rail, The Public Debate and Perception of Environmental Risk in Susa Valley, Italy. Environ. Manag. 2009, 43, 863–875. [Google Scholar] [CrossRef] [PubMed]
- Albalate, D.; Fageda, X. High speed rail and tourism, Empirical evidence from Spain. Transport. Res. Part A 2016, 85, 174–185. [Google Scholar] [CrossRef]
- Givoni, M.; Banister, D. Speed, the less important element of the High–Speed Train. J. Trans. Geogr. 2012, 22, 306–307. [Google Scholar] [CrossRef]
- State Investigation Team of the China–Yongwen Railway Accident. The Investigation Report on the 7.23 Yongwen Line Major Railway Accident. Available online: https://wenku.baidu.com/view/cf406b601ed9ad51f01df278.html (accessed on 10 February 2019).
- Dong, A. Application of CAST and STPA to Railroad Safety in China. Massachusetts Institute of Technology. 2012. Available online: http://citeseerx.ist.psu.edu/viewdoc/download;jsessionid=F6766C6A6C4263DD67F74BDDA2C1E94C?doi=10.1.1.300.9065&rep=rep1&type=pdf (accessed on 10 February 2019).
- Fan, Y.; Li, Z. Applying systems thinking approach to accident analysis in China, Case study of “7.23” Yong–Tai–Wen High–Speed train accident. Saf. Sci. 2015, 76, 190–201. [Google Scholar] [CrossRef]
- Liu, P.; Yang, L. Fault tree analysis combined with quantitative analysis for high–speed railway accidents. Saf. Sci. 2015, 79, 344–357. [Google Scholar] [CrossRef]
- Wang, D. Study on the Management Mode of Entrusted Operation on High–speed Railways. Railw. Trans. Econ. 2014, 36, 12–14, 41. [Google Scholar]
- China Railway Corporation. Guiding Opinions on Commissioning Transportation Management by New Joint–Venture Railway. Available online: http://ishare.iask.sina.com.cn/f/24751958.html (accessed on 10 February 2019).
- Lazonick, W. Business Organization and the Myth of the Market Economy; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Durlauf, S.N. The New Palgrave, Dictionary of Economics. New Palgravediction. Econ. 2008, 6, 1–40. [Google Scholar]
- Marzband, M. Non–cooperative game theory based energy management systems for energy district in the retail market considering DER uncertainties. IET Gener. Trans. Distrib. 2016, 10, 2999–3009. [Google Scholar] [CrossRef]
- Myerson, R.B. Game Theory; Harvard University Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Weibull, J.W. Evolutionary Game Theory; MIT Press: Cambridge, MA, USA, 1997. [Google Scholar]
- Ji, P. Developing green purchasing relationships for the manufacturing industry–An evolutionary game theory perspective. Int. J. Prod. Econ. 2015, 166, 155–162. [Google Scholar] [CrossRef]
- Xiao, Z. A solution of dynamic VMs placement problem for energy consumption optimization based on evolutionary game theory. J. Syst. Softw. 2015, 101, 260–272. [Google Scholar] [CrossRef]
- Li, Z.L. Evolutionary game of speeding driving behavior. J. Transp. Syst. Eng. Inf. Technol. 2010, 10, 137–142. [Google Scholar]
- Cai, L.R. Multi–person evolutionary game of environment pollution based on system dynamics. Appl. Res. Comput. 2011, 28, 2982–2986. [Google Scholar]
- Cai, L.R. Dynamic Analysis and Control Strategy of the Inspection Game in Environmental Pollution. Ph.D. Thesis, Huazhong University of Science and Technology, Wuhan, China, 2010. [Google Scholar]
- Wang, H.; Cai, L.R.; Zeng, W. Research on the evolutionary game of environmental pollution in system dynamics model. J. Exp. Theor. Artif. Intell. 2011, 23, 39–50. [Google Scholar] [CrossRef]
- Zhu, Q.H. Analysis of an evolutionary game between local governments and manufacturing enterprises under carbon reduction policies based on system dynamics. Oper. Res. Manag. Sci. 2014, 23, 71–82. [Google Scholar]
- Zhang, G.L. Defraud Behavior of Network Toll Highway Based on Evolutionary Game Model. J. Transp. Syst. Eng. Inf. Technol. 2014, 14, 113–119. [Google Scholar]
- Tian, Y.; Govindan, K.; Zhu, Q. A system dynamics model based on evolutionary game theory for green supply chain management diffusion among Chinese manufacturers. J. Clean. Prod. 2014, 80, 96–105. [Google Scholar] [CrossRef]
- Liu, Q.; Li, X.; Hassall, M. Evolutionary game analysis and stability control scenarios of coal mine safety inspection system in China based on system dynamics. Saf. Sci. 2015, 80, 13–22. [Google Scholar] [CrossRef]
- Zhang, C. Small and medium–sized enterprises closed–loop supply chain finance risk based on evolutionary game theory and system dynamics. J. Shanghai Jiaotong Univ. Sci. 2016, 21, 355–364. [Google Scholar] [CrossRef]
- Duan, W. Game modeling and policy research on the system dynamics–based tripartite evolution for government environmental regulation. Clust. Comput. 2016, 19, 2061–2074. [Google Scholar] [CrossRef]
- Guo, S. System dynamics model based on evolutionary game theory for quality supervision among construction stakeholders. J. Civ. Eng. Manag. 2018, 24, 318–330. [Google Scholar] [CrossRef]
- Peng, H.; Zhao, J. Incentive–compatible Mechanism Model of Entrusted Transportation Management for Joint–venture Railway. J. Transp. Syst. Eng. Inf. Technol. 2013, 6, 003. [Google Scholar]
- Han, S.T. Discussion on Strengthening Entrusted Transport Management of Joint Venture Railway. Railw. Transp. Econ. 2015, 37, 57–60. [Google Scholar]
- Ji, Z.Z. The research on regulation of railway based on game theory. J. Railw. Sci. Eng. 2015, 3, 040. [Google Scholar]
- Li, K. System dynamics model for high-speed railway operation safety supervision system based on evolutionary game theory. Concur. Comput. Pract. Exper. 2018, 10, e4743. [Google Scholar] [CrossRef]
- State Council. Regulation on the Administration of Railway Safety. Available online: https://wenku.baidu.com/view/11b5394ef02d2af90242a8956bec0975f465a4dd.html (accessed on 10 February 2019).
- China Railway Corporation. Safety Management Regulations. Available online: https://www.docin.com/p-1861034656.html (accessed on 10 February 2019).
- Gintis, H. Game Theory Evolving, a Problem–Centered Introduction to Modeling Strategic Behavior; Princeton University Press: Princeton, NJ, USA, 2000. [Google Scholar]
- Friedman, D. Evolutionary games in economics. J. Econ. Soc. 1991, 59, 637–666. [Google Scholar] [CrossRef]
- Friedman, D. On economic applications of evolutionary game theory. J. Evol. Econ. 1998, 8, 15–43. [Google Scholar] [CrossRef]
- Ventana Systems, Inc. Vensim User’s Guide Version 5 [EB/OL]. USA, Ventana Systems, Inc. Available online: https://vensim.com/free-download/ (accessed on 10 February 2019).





| Strategy | Agent 1 Makes Safety Investment | Agent 1 Neglects Safety Investment | ||
|---|---|---|---|---|
| Agent 2 Makes Safety Investment | Agent 2 Neglects Safety Investment | Agent 2 Makes Safety Investment | Agent 2 Neglects Safety Investment | |
| Agent 3 makes safety investment | ||||
| Agent 3 neglects safety investment | ||||
| Strategy | HSR Company Profit | |
|---|---|---|
| Performs the Duty of Supervision | Fails to Perform the Duty of Supervision | |
| Agents 1, 2 and 3 make safety investment | 0 | |
| Agent 1 makes safety investment, Agents 2 and 3 neglect safety investment | ||
| Agent 2 makes safety investment, Agents 1 and 3 neglect safety investment | ||
| Agent 3 makes safety investment, Agents 1 and 2 neglect safety investment | ||
| Agents 1 and 2 make safety investment, Agent 3 neglects safety investment | ||
| Agents 1 and 3 make safety investment, Agent 2 neglects safety investment | ||
| Agents 2 and 3 make safety investment, Agent 1 neglects safety investment | ||
| Agents 1, 2 and 3 neglect safety investment | ||
| Variables | Meaning of the Variables | Initial Values |
|---|---|---|
| HSR company safety supervision rate | [0,1] | |
| Agent 1 safety investment rate | [0,1] | |
| Agent 2 safety investment rate | [0,1] | |
| Agent 3 safety investment rate | [0,1] | |
| HSR company safety supervision cost | 1 | |
| HSR company expected losses because Agent 1 neglected safety investment | 6 | |
| HSR company expected losses because Agent 2 neglected safety investment | 3 | |
| HSR company expected losses because Agent 3 neglected safety investment | 1.5 | |
| Agent 1 general rewards | 2 | |
| Agent 2 general rewards | 1 | |
| Agent 3 general rewards | 0.5 | |
| Agent 1 profits | 11 | |
| Agent 2 profits | 6 | |
| Agent 3 profits | 3 | |
| Agent 1 safety investment cost | 5 | |
| Agent 2 safety investment cost | 3 | |
| Agent 3 safety investment cost | 1.5 | |
| Reward–penalty coefficient | 2 |
| Equilibrium Solution | Characteristic Values | State |
|---|---|---|
| saddle point | ||
| saddle point | ||
| saddle point | ||
| saddle point | ||
| saddle point | ||
| saddle point | ||
| . | saddle point | |
| saddle point | ||
| (−3, 0, 1.5, 5) | saddle point | |
| (−8, 1.5, 3, 5) | saddle point | |
| (−5, −3, 1.5, 14) | saddle point | |
| (−5, 1.5, 3, 6) | saddle point | |
| (−18.5, −14, 15, 15) | saddle point | |
| (−15, −8.5, 0, 5) | saddle point | |
| (−15, −12.5, −6, 9) | saddle point | |
| (−9, −5, −2.5, 8) | saddle point | |
| saddle point | ||
| E18 = (163/631, 153/163, 99/163, 0) | (−0.1185 + 2.6873i, −0.1185 − 2.6873i, 0.2371, 0.3003) | saddle point |
| E19 = (5/17, 5/7, 1, 0) | (3.1755i, −3.1755i, −1.0756, 0.5168) | saddle point |
| E20 = (3/11, 1, 1/2, 0) | (2.0889i, −2.0889i, −0.4545, 0.4091) | saddle point |
| E21 = (3/20, 1, 0, 1) | (0, 2, −1.8, 0) | saddle point |
| Equilibrium Solution | Characteristic Values | State |
|---|---|---|
| saddle point | ||
| saddle point | ||
| saddle point | ||
| saddle point | ||
| saddle point | ||
| saddle point | ||
| saddle point | ||
| saddle point | ||
| (−3, 0, 1.5, 5) | saddle point | |
| (−8, 1.5, 3, 5) | saddle point | |
| (−5, −3, 1.5, 14) | saddle point | |
| (−5, 1.5, 3, 6) | saddle point | |
| (−15.5, −14, 11, 13) | saddle point | |
| (−5.5, −5, 0, 3) | saddle point | |
| (−9.5, −9, −6, 5) | saddle point | |
| (0.5, 1, 1, 8) | saddle point | |
| E17′ = (0.2142, 1, 0, 1) | (0, 2.858, −1.7148, 0.0006) | saddle point |
| E18′ = (0.4014, 1, 0.3819, 0) | (−0.1895 + 1.9378i, −0.1895 − 1.9378i, 1.2701, 0.6243) | saddle point |
| E19′ = (0.5362, 0.6125, 1, 0) | (−0.3818 + 2.6109i, −0.3818 −2.6109i, −0.4861, 0.9137) | saddle point |
| E20′ = (1, 0.8792, 0.7877, 0.958) | (−0.9919, −0.073, −0.3227, 5.829) | saddle point |
| E21′ = (0.6250, 0.3333, 1, 1) | (−0.4167 + 2.5482i, −0.4167 −2.5482i, −1.0281, −1.9031) | ESS |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, K.; Wang, W.; Zhang, Y.; Zheng, T.; Guo, J. Game Modelling and Strategy Research on the System Dynamics–Based Quadruplicate Evolution for High–Speed Railway Operational Safety Supervision System. Sustainability 2019, 11, 1300. https://doi.org/10.3390/su11051300
Li K, Wang W, Zhang Y, Zheng T, Guo J. Game Modelling and Strategy Research on the System Dynamics–Based Quadruplicate Evolution for High–Speed Railway Operational Safety Supervision System. Sustainability. 2019; 11(5):1300. https://doi.org/10.3390/su11051300
Chicago/Turabian StyleLi, Kehong, Wenke Wang, Yadong Zhang, Tao Zheng, and Jin Guo. 2019. "Game Modelling and Strategy Research on the System Dynamics–Based Quadruplicate Evolution for High–Speed Railway Operational Safety Supervision System" Sustainability 11, no. 5: 1300. https://doi.org/10.3390/su11051300
APA StyleLi, K., Wang, W., Zhang, Y., Zheng, T., & Guo, J. (2019). Game Modelling and Strategy Research on the System Dynamics–Based Quadruplicate Evolution for High–Speed Railway Operational Safety Supervision System. Sustainability, 11(5), 1300. https://doi.org/10.3390/su11051300





