1. Introduction
Tourism is mentioned as one of the most significant economic fields over the last two decades: its ranking in world trade is second only to oil, which sets it apart from other economic fields. Nowadays, making a reasonable decision, especially under uncertain circumstances, is necessary in the field of tourism. Promotion in the tourism sector would be simpler if it were possible to forecast changes in number of tourists by examining current and past tourism demands. Due to the competitive and complicated environment in the tourism sector, it is required to observe and to enhance the previous standard of performances. In the prediction of tourism demand, the importance of accuracy is undeniable; however selecting a suitable model to fit a problem is as necessary as accuracy of the results. The different tourism forecasting models have been suggested by researchers, and of course each model has superiorities as well as drawbacks.
Time series methods need only one data series, and are based on the level of complexity of the model. By combining linear autoregressive integrated moving average (ARIMA) model and nonlinear artificial neural network model, an effective hybrid methodology for time series forecasting is proposed in [
1], and the experimental results show that the combined approach takes the advantages of both models and significantly improves the forecasting performance.
The time series seasonal ARIMA (SARIMA) and multivariate ARIMA (MARIMA) models are used to forecast a tourism demand in Hong Kong [
2], and application of these models provides better accuracy in comparison with other time series models.
The performances of ARIMA, artificial neural networks, and multivariate adaptive regression splines forecasting models are compared to obtain the appropriate model for tourism demand in Taiwan [
3]. Based on the lowest value of mean absolute percentage error (MAPE), it is confirmed that ARIMA is the more appropriate model for forecasting tourism demand.
Time series data are used to examine a performance of the forecasting accuracy of demand in Taiwanese outbound tourism [
4], and the experimental results show that a combination of linear and nonlinear statistical models enables better forecasting accuracy compare to other individual models.
The forecast accuracy of tourism demand is important issue for the government in terms of planning accommodation and improving transportation infrastructure in the country. The government faces negative economic impact if accurate forecasting fails. Time series forecasting of tourism demand in Malaysia is done by using Box Jenkins model, time series regression and Holt Winters methods [
5]. Holt Winters and time series regression methods show better forecasting accuracy in terms of error magnitude and directional accuracy respectively.
Backpropagation is one of the popular neural network algorithms effectively used in forecasting process. Sometimes this approach does not provide a desirable accuracy of forecasting. The methodology based on combination of backpropagation and genetic algorithms can improve a forecasting accuracy, and the parameters of back propagation algorithm are optimized to minimize the prediction error. The proposed methodology is used on series dataset to predict the foreign tourist arrivals in three cities of Indonesia [
6].
This is an obvious fact that increasing tourist arrivals in country positively affects the rate of employment in both governmental and private sectors of tourism industry. Simple Regression Model (SRM) and Auto Regressive Distributed Lag Model (ARDLM) are compared in [
7] to determine the optimal model for forecasting the tourism generated employment in Sri-Lanka. According to relative and absolute measurements of errors, it is justified that ARDLM is more convenient forecasting model.
Combination of biquadratic polynomial function and autoregressive model can be the useful approach on tourist arrival time series data with seasonal fluctuation [
8]. The proposed approach is used for prediction of monthly tourist arrivals in Nepal.
Although classical time series models have a wide range of applications, they handle with some drawbacks: the model should be specified formally and a probability distribution needs to be assumed for data [
9]; it should be examined carefully whether the time series is stationary or not, since in nonstationary case, data have a stochastic trend or have a random probability distribution which causes an inaccurate forecasting [
10]; the models are mostly based on a piecewise linear function; the classical models are time consuming due to selecting and testing the proper functional form by a user among various possibilities; accurate results depend on a large amount of past data [
11]; and the model construction does not rely on any economic theory, which is not helpful for policy making and planning [
12].
Fuzzy time-series approach is an effective tool to overcome the above mentioned drawbacks of classical time series models. Some other advantages of fuzzy time series models can be interpreted as follows: fuzzy models are effectively applied in complex and optimization problems [
13]; they have more capability in nonlinear relationship [
14]; they are applicable with a small set of data; they use linguistic values instead of crisp ones; they can deal with incomplete and deficient data under unclear circumstances [
15].
By using fuzzy logic theory, Song and Chissom defined the fuzzy time series for the first time and used it to design a forecasting system [
16]. Traditional time series data are based on numerical values which are unreliable whereas fuzzy time series data are based on linguistic values. The use of fuzzy time series was expanded due to its potential to cope with incomplete and ambiguous data [
17]. Later on there have been some modifications on Song and Chissom model, such as reducing the overload computation by enhancing the fuzzy logic relationship rules [
18], and designing the system to improve prediction by integrating problem-specific heuristic knowledge [
19].
The forecast accuracies of fuzzy time series and grey theory are calculated to predict the annual number of visitors to the U.S. [
20]. In order to enhance the forecasting accuracy of tourism demand, a novel forecasting method by combining fuzzy c-means (FCM) algorithm and logarithm least-squares support vector regression technologies is developed [
21].
While designing a system for predicting tourism demand, large fluctuation and presence of limitation in collecting historical data would be critical issues. In order to be able to deal with these issues, a system based on particle swarm optimization (PSO) and adaptive fuzzy time series is proposed to predict the number of tourists from Taiwan to the U.S. [
22].
The following three fuzzy time series models are proposed for predicting the number of tourist arrivals in Taiwan: neural network (NN) based fuzzy time series model is suggested in [
23] to handle and manage nonlinear data. In [
24], the system is designed by combining the fuzzy time series and genetic algorithm (GA) methods. The reason of this combination is mentioned as calibrating the interval’s length and obtaining the best fuzzy interval sizes to have a minimum error. Moreover, the effect of some parameters in fuzzy time series such as population size, number of intervals and order of fuzzy time series are tested and analyzed. An adaptive fuzzy time series model is developed in [
25], and the efficiency of this model is verified by obtaining small values of MAPE and RMSE errors.
There is a common agreement that there is no single forecasting method to exceed all other methods consistently to provide the best forecasting result. However by combining some methods the desirable outcome can be achieved. Therefore, in order to increase accuracy and to decrease the level of complexity and the overload of calculation in forecasting, in this paper we propose a system based on combination of FCM technique and Mamdani fuzzy rule-based system (FRBS). The main advantage of this combination is stipulated by the possibility of managing the number of linguistic rules.
2. Preliminaries
Time series. It is formally represented as follows:
where
is any nonlinear function,
are the values of variable
in periods
of time series.
is a forecast value of the variable
X for the period
t. We need to find such a function
and input number
q to fulfill the condition.
where
is a prediction| forecast value at a time
t based on the obtained model, and
is an experimental value of a variable.
Fuzzy time series. Assume be the universe of discourse such that , where is a subset of real numbers on which is fuzzy set with and . Then, the fuzzy time series on is defined by , i.e., is a collection of .
Fuzzy c-means clustering. Fuzzy clusterization (FC) is a powerful scientific tool to mine knowledge from a time series consisting lots of data. By taking into consideration the fuzziness of data in time series, the fuzzy clusterization problem for m-fuzzificator (fuzzification parameters) can be described in the following form.
Let be a set of n data or objects where , and is the set of p tuples of reals, and fuzzy c partition of the set X with is shown by a partition matrix , and . The entries of the matrix A show the ’s degree of membership that belongs to cluster j and satisfy the following properties:
;
;
.
FCM aims to minimize the following objective function:
where
, and the notation
means the Euclidean distance;
, where
is the center of cluster
j. The partition matrix
would be the collection of all memberships. The power of
is
which is used to control the degree of fuzzy overlap.
The FCM algorithm can be described as follows:
Step 1: Initialize .
Step 2: Compute
as follows:
Step 3: Update
as follows:
Step 4: Compute .
Step 5: Repeat steps 2–4 until the specified number of iterations is reached or the differences between the values of in the last two steps would be less than the minimum threshold.
FCM computes the degree of membership instead of computing the absolute membership of each
to one of the clusters [
26].
Fuzzy rule-based system. The classical method of rule-based system which is based on IF-THEN rules is expanded to FRBS where the conditional statements look like “IF C (condition) THEN R (restriction)“, and characterized by membership functions [
27].
Mamdani type fuzzy rule-based system. This is a system with multi-inputs and single-output (MISO). In Mamdani model, the rules normally include linguistic variables which are formed as follows [
28,
29,
30,
31]:
where
and
y denote respectively the input and output linguistic variables, and
and
B denote the linguistic values of input and output linguistic variables.
Mamdani model of FRBS consists of four main components. The first component is knowledge base which consists of a rule-base including fuzzy IF-THEN rules, and a database which stores fuzzy sets.
Inference engine is another component of Mamdani model, and reasoning process is carried out upon input values and fuzzy IF…THEN rules.
The fuzzification and defuzzification interfaces are other two components of Mamdani model. The fuzzification interface is required to convert crisp input values into fuzzy values. The fuzzy values are important to be used in the process of fuzzy reasoning. The defuzzification interface performs the reverse operation of a fuzzification, and transforms fuzzy output value into crisp value.
Mamdani model is appropriate in fuzzy control applications and linguistic modeling. The drawback of this model is its unsuitability for complex problems.
4. Numerical Example and Results
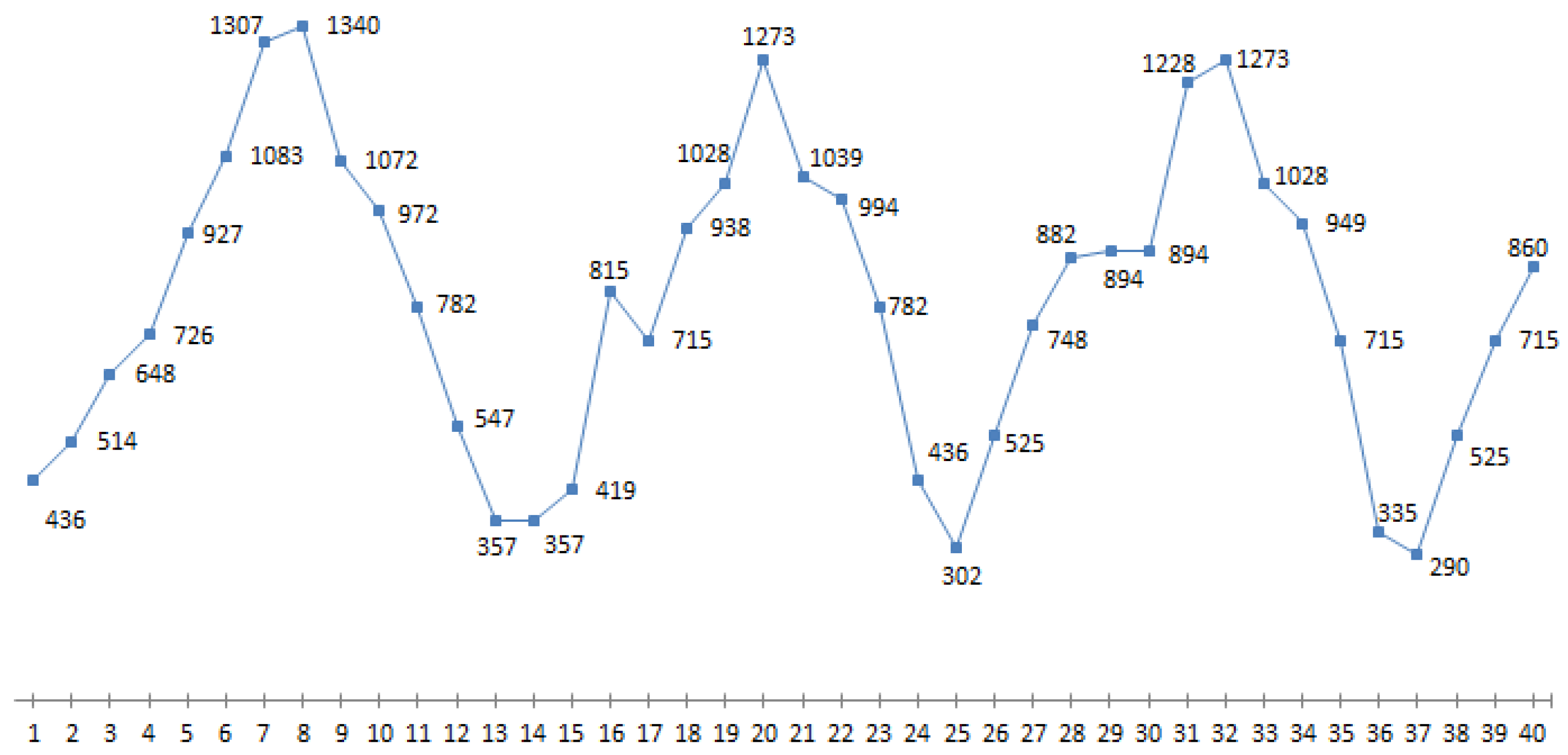
This paper aims to develop fuzzy time series model for forecasting an occupancy of one of the hotels of North Cyprus. The efficiency of this model using data (observations) on guest arrivals over 40 months, is validated and proved.
Figure 1 represents the number of guest arrivals in one of the hotels of North Cyprus over 40 months.
For applying FCM clustering, we use the parameters as shown in
Table 1. By using FCM, the data are clustered into
clusters. The coordinates of the cluster centers with 5, 6, and 7 clusters are described in
Table 2,
Table 3 and
Table 4, repectively.
After obtaining the center of each cluster, IF-THEN rules in Mamdani model should be considered. In order to have the system with high accuracy and low error value, different parameter values are tested. Mamdani-type FRBSs are designed which are based on
clusters and
inputs (the results for
and
are given in the text of the paper, and the results for
and
are given in
Appendix A). All data are splitted into two sets called training set and testing set, and 70% of data are used for training, and other 30% of data are used for testing. To find the accuracy of each system, testing data are used. The accuracy and efficiency of each system is estimated based on the root mean square error (RMSE) and mean absolute percentage error (MAPE).
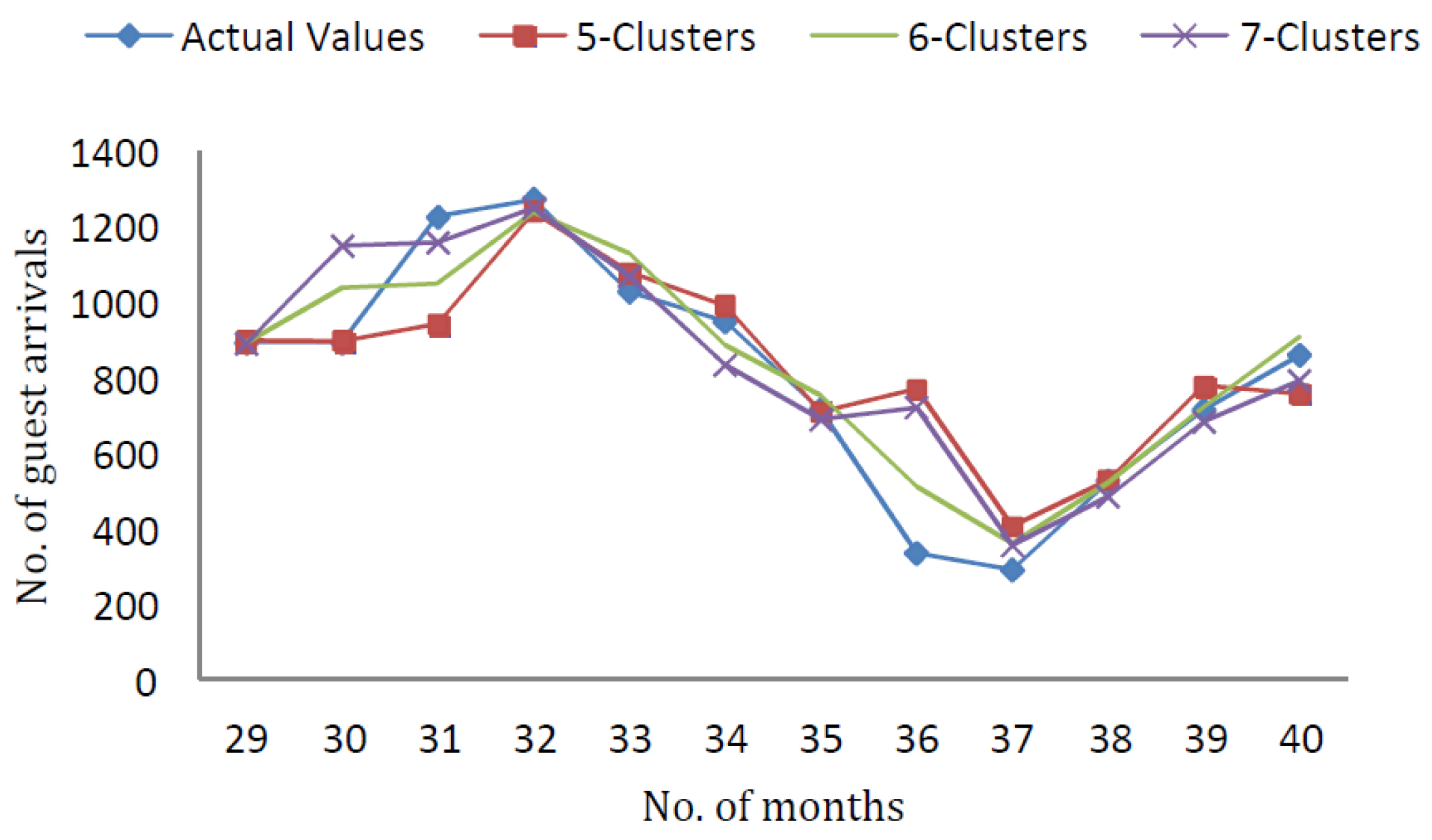
In
Figure A1, the forecasting results of Mamdani-type (FRBSs) using testing data with
clusters and
inputs are demonstrated.
In
Figure A2, the forecasting results of Mamdani-type FRBSs using testing data with
clusters and
inputs are demonstrated.
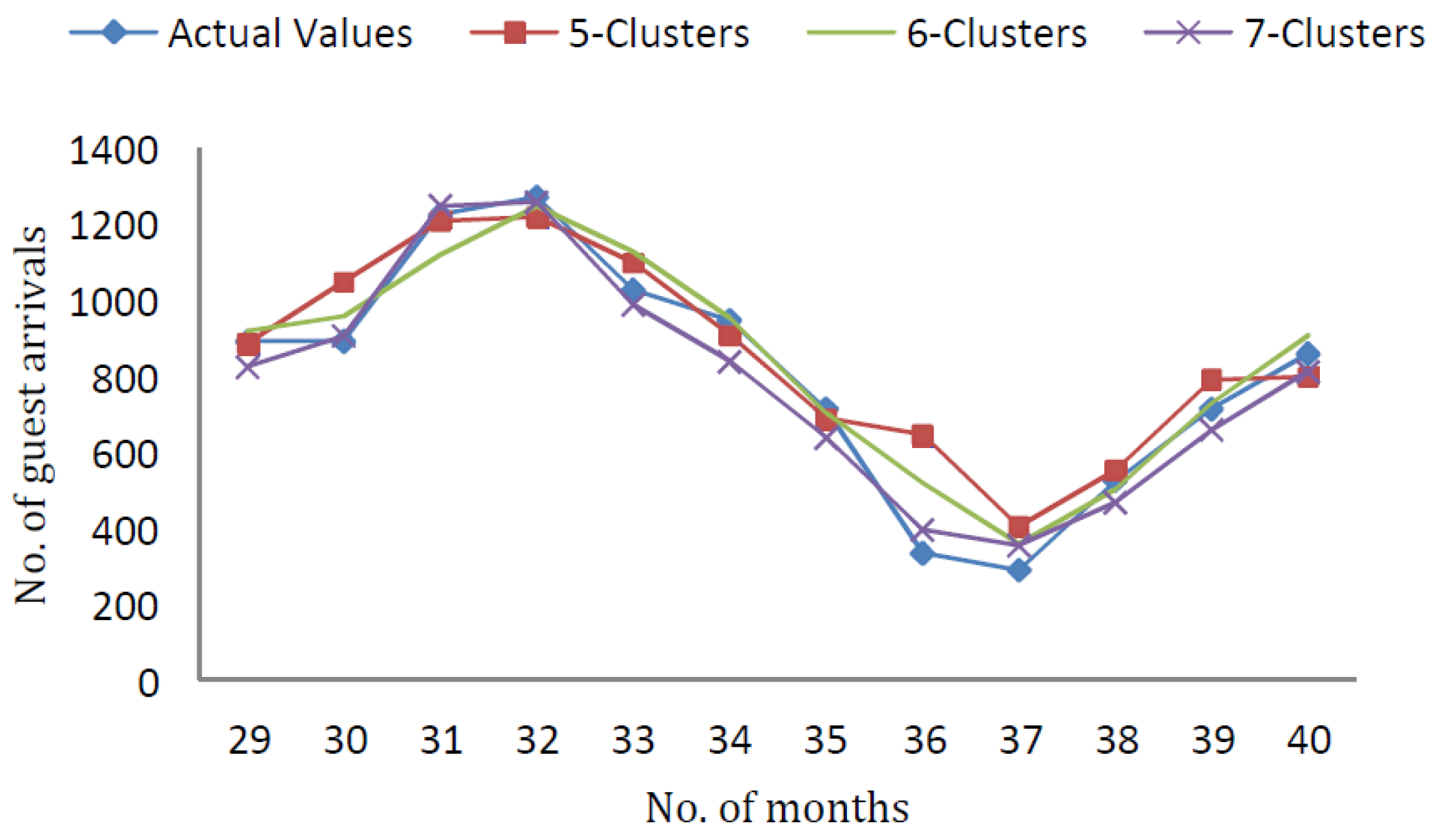
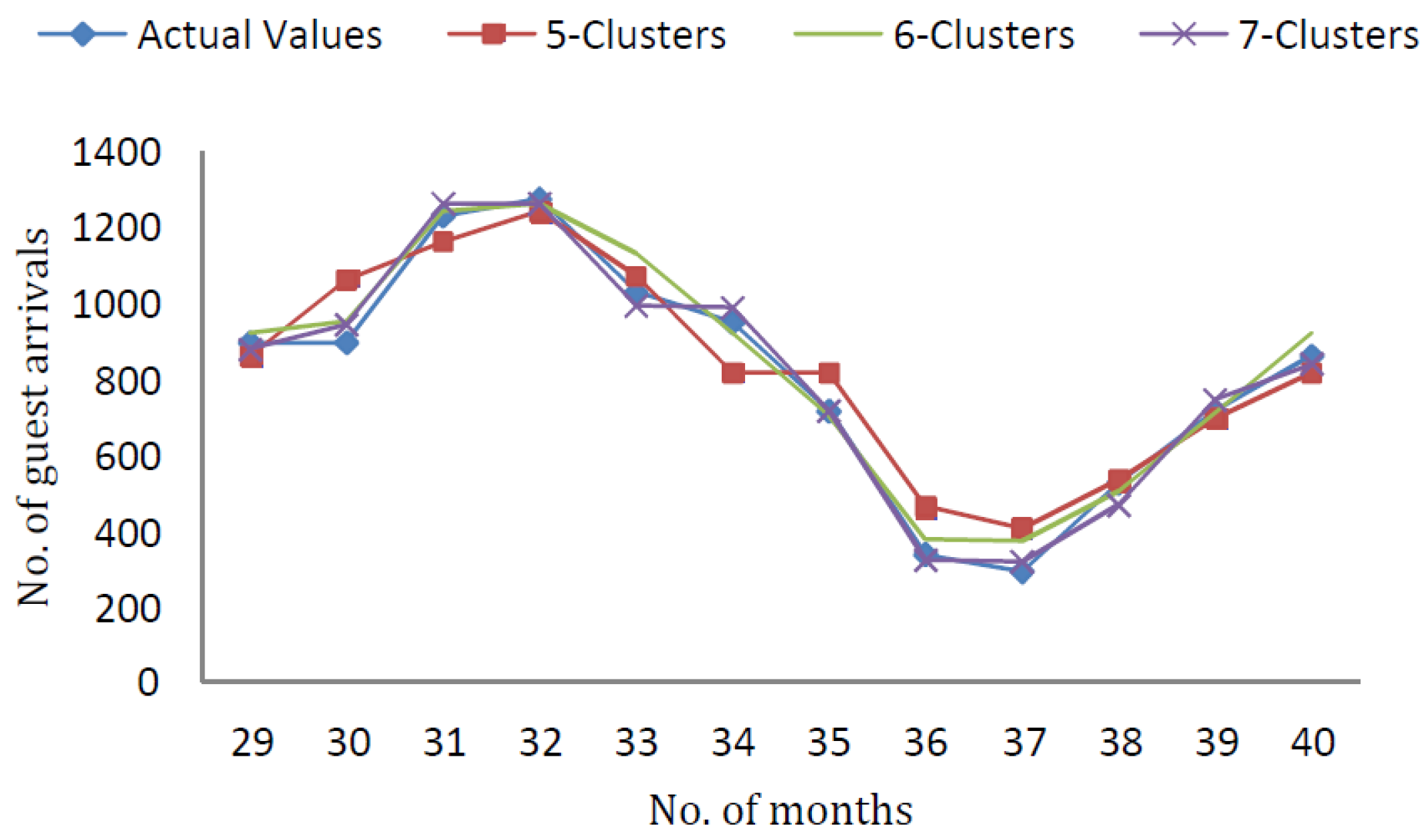
In
Figure 2, the forecasting results of Mamdani-type FRBSs using testing data with
clusters and
inputs are demonstrated.
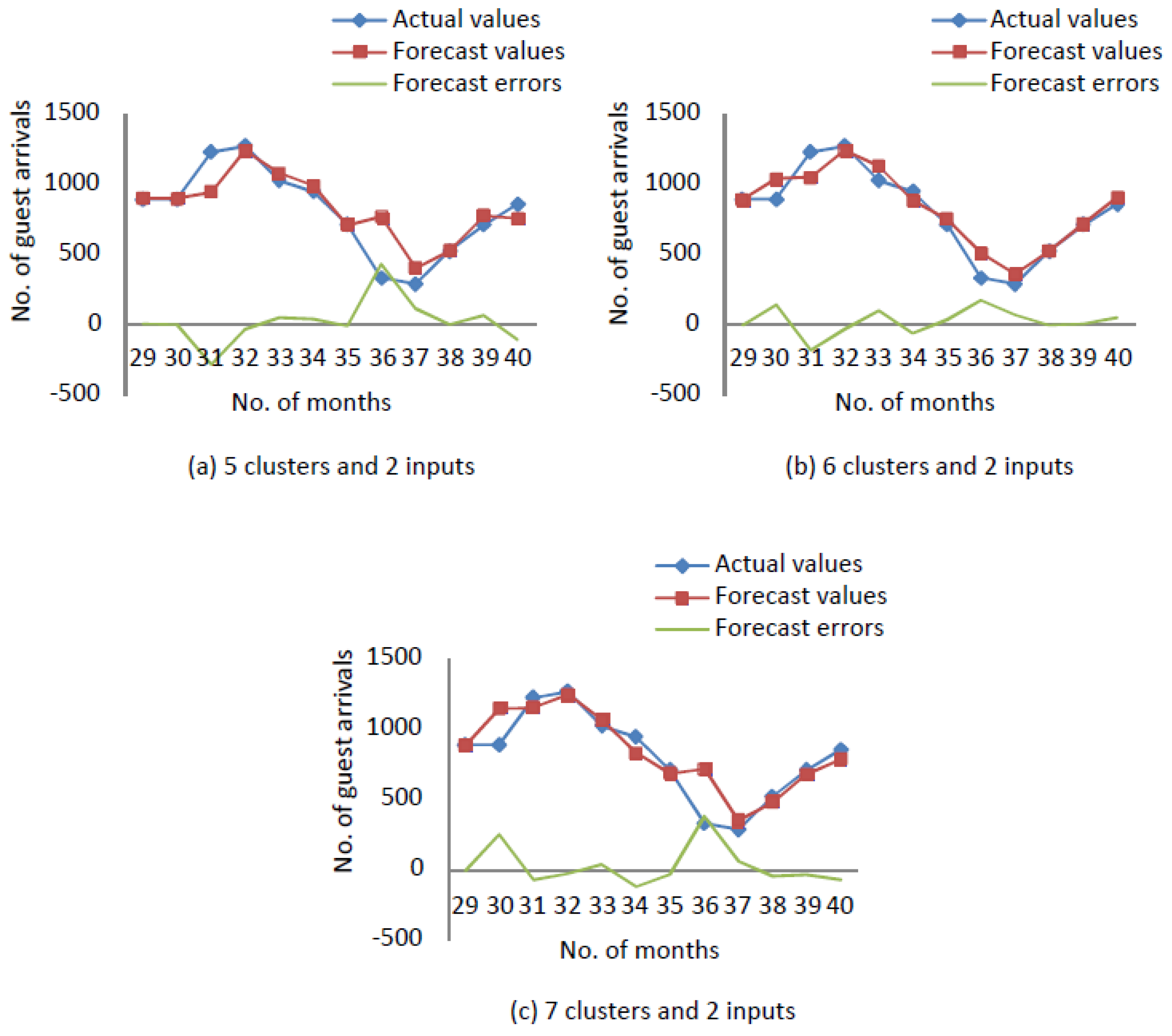
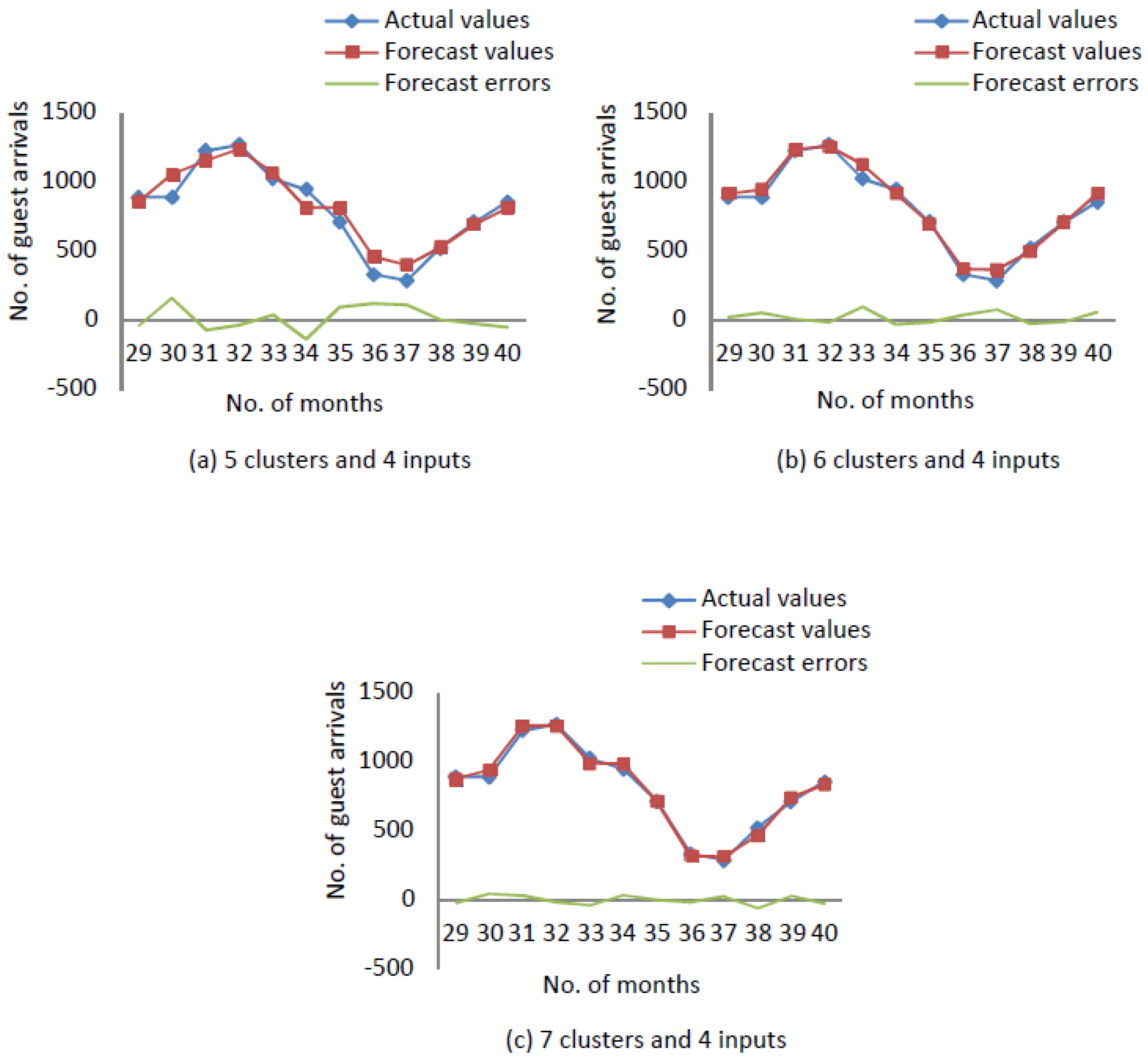
After designing process, it is necessary to find errors for each of these models, and compare them to find the best model.
Figure A3 illustrates the actual values, forecast values and forecast errors of a time series with
clusters and
inputs.
Figure A4 illustrates the actual values, forecast values and forecast errors of a time series with
clusters and
inputs.
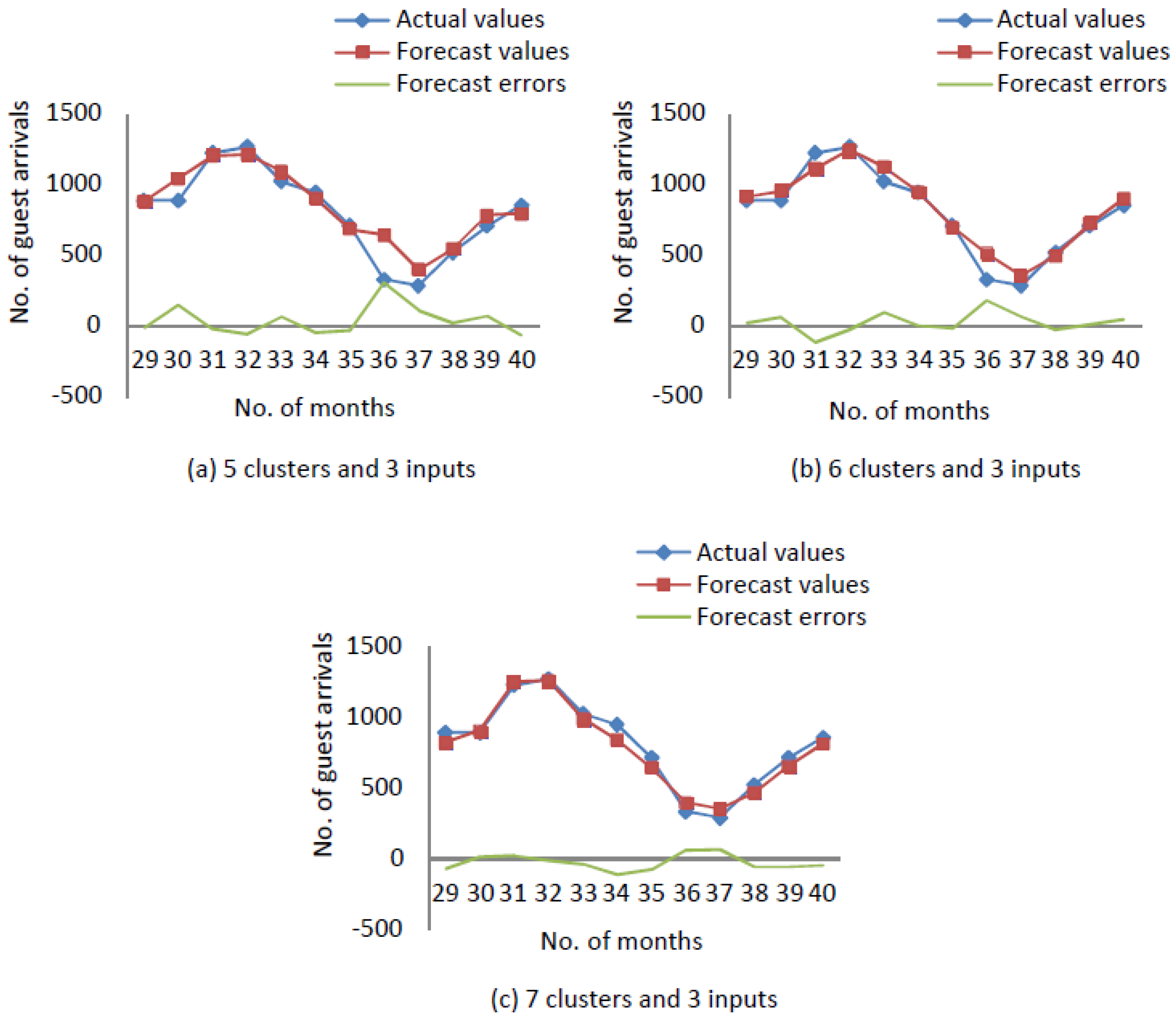
Figure 3 illustrates the actual values, forecast values and forecast errors of a time series with
clusters and
inputs. The forecast errors in
Figure A3,
Figure A4 and
Figure 3 remark the performance of forecasting.
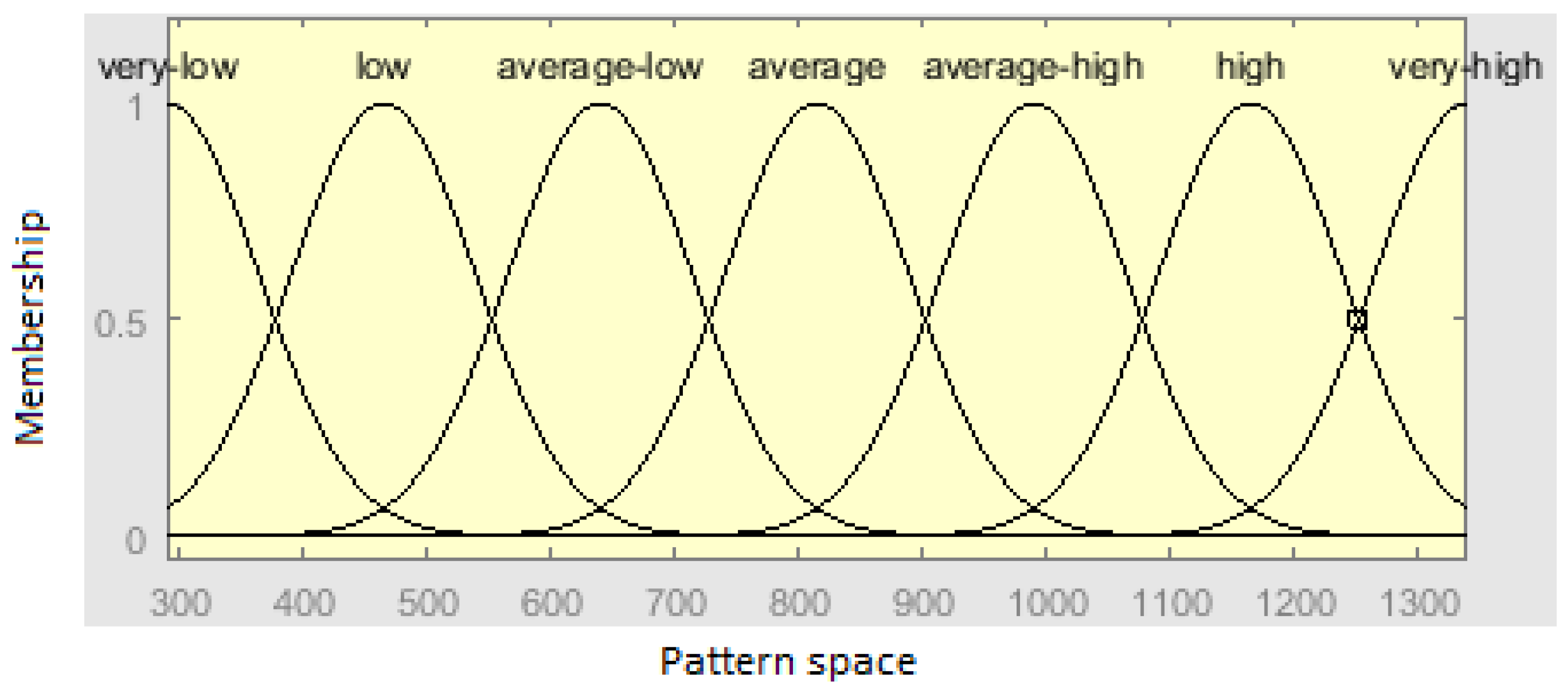
The Gaussian membership function plot and homogeneous fuzzy partitions with 7 clusters and 4 inputs are demonstrated in
Figure 4.
The fuzzy sets and their corresponding membership functions for inputs and output of fuzzy rules are described in
Figure 5.
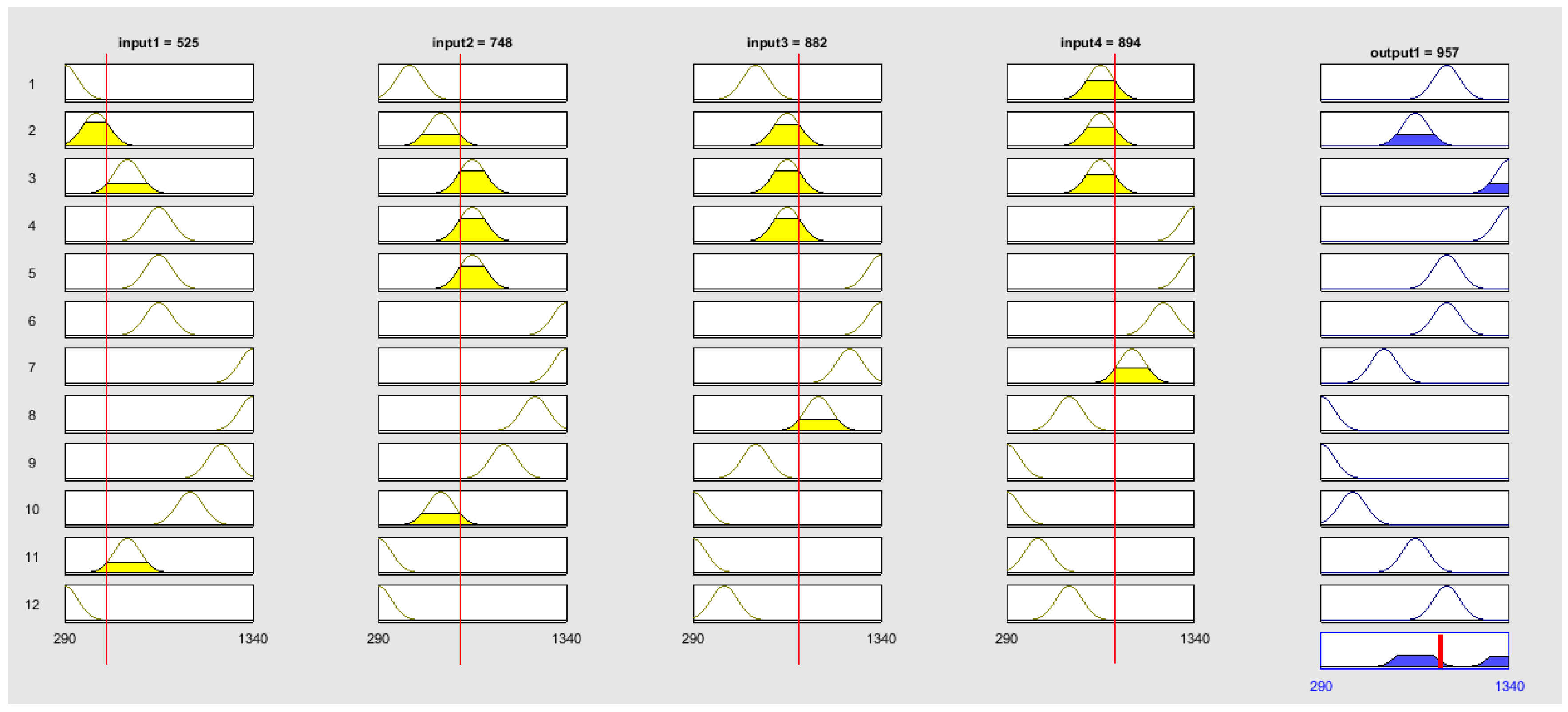
In Mamdani-type FRBS with 7 clusters and 4 inputs, the obtained rules from testing data are represented as follows:
Rule 1: IF input1 is Gaussian(74.32, 290) and input2 is Gaussian(74.32, 465) and input3 is Gaussian(74.32, 640) and input4 is Gaussian(74.32, 815) THEN output is Gaussian(74.32, 815).
Rule 2: IF input1 is Gaussian(74.32, 290) and input2 is Gaussian(74.32, 290) and input3 is Gaussian(74.32, 465) and input4 is Gaussian(74.32, 640) THEN output is Gaussian(74.32, 990).
Rule 3: IF input1 is Gaussian(74.32, 465) and input2 is Gaussian(74.32, 640) and input3 is Gaussian(74.32, 815) and input4 is Gaussian(74.32, 815) THEN output is Gaussian(74.32, 815).
Rule 4: IF input1 is Gaussian(74.32, 640) and input2 is Gaussian(74.32, 815) and input3 is Gaussian(74.32, 815) and input4 is Gaussian(74.32, 815) THEN output is Gaussian(74.32, 1340).
Rule 5: IF input1 is Gaussian(74.32, 640) and input2 is Gaussian(74.32, 290) and input3 is Gaussian(74.32, 290) and input4 is Gaussian(74.32, 465) THEN output is Gaussian(74.32, 815).
Rule 6: IF input1 is Gaussian(74.32, 815) and input2 is Gaussian(74.32, 815) and input3 is Gaussian(74.32, 815) and input4 is Gaussian(74.32, 1340) THEN output is Gaussian(74.32, 1340).
Rule 7: IF input1 is Gaussian(74.32, 815) and input2 is Gaussian(74.32, 1340) and input3 is Gaussian(74.32, 1340) and input4 is Gaussian(74.32, 1165) THEN output is Gaussian(74.32, 990).
Rule 8: IF input1 is Gaussian(74.32, 815) and input2 is Gaussian(74.32, 815) and input3 is Gaussian(74.32, 1340) and input4 is Gaussian(74.32, 1340) THEN output is Gaussian(74.32, 990).
Rule 9: IF input1 is Gaussian(74.32, 990) and input2 is Gaussian(74.32, 640) and input3 is Gaussian(74.32, 290) and input4 is Gaussian(74.32, 290) THEN output is Gaussian(74.32, 465).
Rule 10: IF input1 is Gaussian(74.32, 1165) and input2 is Gaussian(74.32, 990) and input3 is Gaussian(74.32, 640) and input4 is Gaussian(74.32, 290) THEN output is Gaussian(74.32, 290).
Rule 11: IF input1 is Gaussian(74.32, 1340) and input2 is Gaussian(74.32, 1340) and input3 is Gaussian(74.32, 1165) and input4 is Gaussian(74.32, 990) THEN output is Gaussian(74.32, 815).
Rule 12: IF input1 is Gaussian(74.32, 1340) and input2 is Gaussian(74.32, 1165) and input3 is Gaussian(74.32, 990) and input4 is Gaussian(74.32, 640) THEN output is Gaussian(74.32, 290).
As it was mentioned, fuzzy IF-THEN rules with linguistic variables are used in Mamdani-type FRBS. The variables are expressed by such linguistic terms as “very low”, “low“, “average-low“, etc. Dealing with the linguistic terms is consistent with the vague and uncertain information. The experimental values with respect to the number of guest arrivals in the hotel include uncertainty, complexity, and nonlinearity. The traditional methods using a quantitative analysis disenable to address the matter of such imprecision and inaccuracy, and therefore, are unsuitable in these situations.
Before producing rules, the number of linguistic variables should be alleviated to a considerable size to prevent creating extra rules. With
n linguistic variables,
m inputs and one output, there are totally
rules to be produced. However, in this research the number of rules is significantly reduced as it is depicted in
Table 5 by classifying time series data.
The accuracy of forecasting model is measured by applying such metrics as root mean square error (RMSE) and mean absolute percentage error (MAPE). It is obvious that the lowest values of RMSE and MAPE are the desired ones. RMSE and MAPE are calculated as follows:
where
is the prediction|forecast value, and
is the experimental value of
ith testing data to be defined from the model, and
N is the number of data used in testing.
As it can be observed from
Table 5, the optimal forecasting model is the one with 7 clusters and 4 inputs with the value of RMSE equal to 31.8355 and value of MAPE equal to 4.1155%.