Abstract
The urban mobility system is an important factor in social development and must, therefore, be tackled in a way that enables balanced, sustainable development. The purpose of the present work was to introduce a new holistic approach to urban mobility system (UMS) planning, which involves a strategic decision-making process with a broad involvement of various stakeholders. For this purpose, an innovative model was created by synthesizing the focus group (FG) method with the nominal group technique (NGT), SWOT (Strengths, Weaknesses, Opportunities, and Threats) analysis, and the fuzzy analytical hierarchical process (FAHP) method. The fuzzy approach was chosen for its ability to incorporate imprecise and vague information and make a decision-making UMS process more realistic. Accordingly, the objective of the paper was to propose a newly developed model that will (considering the integration of various urban mobility subsystems) enable the detection, identification, and ranking of key priorities required for a more holistic approach to UMS planning. The results revealed that the developed integrated model enables acquired areas to be ranked according to priorities, which further allows the development of scenarios. Moreover, the model allows a better understanding of how to search for compromises when one is faced with multi-criteria decision-making and coordination of frequently contradictory goals. A new integrated urban mobility model, as proposed herein, was also successfully tested in a real-life application, which proves its potential for use in sustainable urban mobility planning in a holistic way.
1. Introduction
Modern society greatly depends on mobility [1], which is an essential factor for both society [2] and human development [1,3]. Mobility is a basic human right [4] and an important indicator of social development, not only of individuals but of society as a whole [5]. Mobility, as we know it today, is a movement between different points or cities [6,7], and has thus become a key factor in the sustainable and economic development of urban areas [8,9], where more than half of the world’s population lives [10]. More than 60% of all travel is made within urban environments, whereas the total sum of urban kilometres is expected to triple by the end of the year 2050 [11]. Masuch, Lützenberger, and Keiser [12] reported that people think mobility is one of the fundamental elements that play a crucial role in the quality of life.
The dependence on a high-quality urban mobility system, which can be understood as a solution that satisfies the derived demand of people who need to perform an activity at some destination [13,14], has negative impacts, such as traffic congestion [15], accidents [16], and environmental pollution [17], which, in turn, affect the level of mobility [1,18]. As a key urban system [19], urban mobility systems (UMS) directly or indirectly affect every substantial social theme [20]. Therefore, any UMS improvement is a critical political decision, as it has a direct impact on urban society, economy, and urban connectivity [21]. According to the United Nations [22], there are urges-for-action that should be undertaken towards a more sustainable mobility system and to ensure that mobility will become a priority for every transport policy [23,24,25,26].
1.1. Urban Mobility Planning
Many studies have emphasized (see [27,28]) that traditional urban mobility planning, in which new infrastructure (especially for automobiles) is continuously built, is no longer adequate, as it creates a vicious cycle of development. Namely, the expansion of infrastructure (especially for automobiles) causes the cities to overgrow, as access to the urban periphery is easier. However, such expansion contributes to an increase in car use, which further promotes the need for new infrastructure, and the vicious cycle of development is established. The outcome of such an approach is the fragmentation of an urban mobility management, poor adaptation to requirements regarding the mobility increase, confusion over goals, priorities, and strategies, and what the urban mobility system should be in the future and, finally, lack of networking between the different stakeholders involved (decision-makers, local community, economy, users, and experts) [11,27,29].
Many studies have pointed out that the design of an urban mobility policy needs to take into consideration a holistic strategic approach [30,31,32,33]. The latter is also evident from the Committee of the Regions of the European Union recommendations [34], where it is stated that the development of urban environments must be based on a sustainable approach and the mobility should not be solved through a partial approach [34]. Therefore, the European Committee proposes the creation of such mobility plans that are based on [35]: (a) a sustainable approach that seeks to balance economic development, social justice, and the environmental quality; (b) a holistic approach that encompasses practices and policies of different sectors, levels of authorities, and administrative areas; (c) a participative and transparent approach that involves public empowerment through all stages of the planning process; (d) a clear vision and compelling goals that are an integral part of the sustainable development strategy proposed.
A holistic approach to UMS decision-making is nowadays recognized as a prerequisite to achieving sustainable mobility [36], as it helps to reduce the aforementioned negative impact of urban mobility growth [7,37]. With a holistic approach, which is also proposed in this article, the urban environment is created with more social responsibility (safety, equality, and fairness of accessibility to transportation), environmentally (use of non-fossil energy for vehicles, lowering the emissions of vehicles and infrastructures) and economically (using resources efficiently) sustainable [15,22].
The advantages of such an approach to decision-making in UMS (and also challenges of the planning process) are, among others: focus on people, not on traffic [38]; balanced development of all relevant transport modes that are not modal-focused [38]; integrated set of actions to achieve cost-effective solutions, not just infrastructure focus [38]; short- and medium-term delivery plans embedded in a long-term vision and strategy [38]; cooperation across institutional boundaries; reduced demand for transport and car-dependence [7]; secure, reliable, integrated, multimodal, efficient, and environmentally friendly UMS [35]; strategic and goal-oriented management; transparent decision-making with the involvement of a wide range of stakeholders [39]; improved urban traffic flows; sustainable freight transport [7]; creating linkages between different policy areas and removing institutional barriers [40]; and interdisciplinarity and integration of different transport modes (public transport, walking, cycling) [41].
Successfully pursuing a holistic approach to UMS planning requires complex decisions that are intertwined with different, often conflicting, interests and goals [30]. Thus, the planning of urban mobility or the urban mobility system (UMS) is even more complicated, as it has to satisfy different stakeholders [21] with different views and interests, which are usually co-dependent [37,39,42,43]. As [44] explains, because of the different motivations of the people involved, the information that they possess, the perception, expertise, and interest that they have, and also their need for development of the system might differ severely among stakeholders in UMS planning. Moreover, the complexity of decision-making is compounded by the need to integrate the different practices and policies of different sectors, levels of government, and neighbouring administrative areas [35].
1.2. Fuzzy Analytical Hierarchical Process and Urban Mobility Planning
Multi-criteria decision-making models (MCDM) have been recently used as a way to solve such complex decision problems encompassing more criteria and more decision-makers. According to Mardani and colleagues [37], MCDM is an appropriate solution, since it decreases uncertainty and improves the quality of the decisions. The area of MCDM is among the fastest-growing areas in different disciplines and represents an essential group of decision-making techniques used by many authors, academics, and researchers in the area of UMS (see [37,39,42,43,45,46]). Pérez, Carrillo, and Montoya-Torres [39] argue that 58 different techniques have been applied in urban passenger transport systems between 1982 and 2014, and that these techniques have become among the most useful ones for decision-making and the assessment of various projects in the field of mobility systems over the last decade.
Among various techniques and models of multi-criteria decision-making in optimizing urban mobility planning, the most commonly used is the analytical hierarchy process (AHP) [37,39,47], developed and proposed by Saaty [48]. However, regardless of its usefulness, its simplicity in dealing with multi-criteria decision-making problems is often criticized for the inadequate consideration of human expression in ranking the individual criteria [49,50].
In order to appropriately alleviate problems of the basic AHP model, the fuzzy analytical hierarchical process (FAHP) was established. The usage of FAHP in the field of urban mobility planning significantly increased over recent years, which proves its usefulness in solving the multi-criteria decision-making problems of the UMS. An extensive review of deploying the FAHP methodology for UMS problems can be found in [1]. In this work, the classification of works by major UMS categories revealed that most papers were related to transport technology (53%), followed by passenger transport (26%), freight transport (10%), and finally, the general area [1,42]. In these works, many different approaches and methodologies were used.
Regarding passenger transportation, some authors used FAHP and SERVQUAL (Service Quality Model) to assess customer satisfaction [51,52] or to evaluate the value of gaps in public transport services [53]. In the freight transport category, one work used an integrated FAHP and FTOPSIS (Fuzzy Technique for Order of Preference by Similarity to Ideal Solution) to select a logistics scenario for a central business zone [54], while John and his colleagues [55] conducted the FAHP to analyse the complex structure of operations in ports and determined the risk factor weights.
Within the field of transportation technology, papers have emerged where FAHP combined with the VIKOR (VIseKriterijumska Optimizacija I Kompromisno Resenje) method has been used for classifying the priorities of pavement maintenance, or combined with GIS (geographic information system) for determining the location of an underground parking lot [56]. Among the “general area” category, only one paper has appeared partially focusing on the whole UMS context, where the classification of different modes of transport was conducted with respect to their effects on the environment [57].
However, according to our knowledge, there are almost no identifiable holistic-based studies in the UMS field, which would involve a fuzzy logic combined with the AHP within the scope of multi-criteria decision models.
1.3. Proposed Hybrid Methodology
This paper describes the development of such a holistic approach to UMS planning, which enables strategic decisions to be taken with the involvement of various stakeholders. The suggested innovative methodology is based on the FAHP model combined with the well-known SWOT (Strengths, Weaknesses, Opportunities, and Threats) analysis, where a modified method of focus groups (FG) processed by the nominal group technique (NGT) is also involved. The FG method, through a carefully defined series of discussions with stakeholders, gains perceptions of a particular area of interest [58]. This way, information about the opinions, perceptions, attitudes, beliefs, and attitudes of a small group of key participants can be obtained. Based on modified FG results, SWOT and FAHP methodologies can be further conducted. Within the framework presented in this paper, the mix of SWOT and FAHP is particularly essential. Namely, the hierarchical structure of the FAHP model is defined with the identified basic elements (and sub-elements) of the SWOT analysis, i.e., with strengths, weaknesses, opportunities, and threats of the UMS planning. By deploying such a methodological combination, it becomes possible to obtain opinions from a wide range of stakeholders and to design priority areas, which are then ranked by their relevance. This way, a more holistic solution for solving UMS problems is achieved, where various urban mobility subsystems are integrated through a wider circle of stakeholders. Furthermore, the presented methodology allows for defining the priority areas, which are the base for the development of scenarios and the adoption of strategic decisions. To the best of our knowledge, the approach introduced in this paper has not been detected in the existing literature yet, particularly within the field of UMS planning. The developed model is tested for a case of a real-life application, where the achieved results confirm the model’s practical value, considering a holistic approach to UMS planning. On these grounds, it is believed that a novel approach might have brought some important contribution to the field of UMS planning.
2. Materials and Methods
2.1. The Conceptual Framework of Research
The research covered three main phases within the conceptual model that is shown in Figure 1. In the first phase, we defined the input elements based on the literature survey as follows: UMS development guidelines, key stakeholders, and experts on FAHP implementation. The stakeholders represent an important aspect of UMS planning, as they frequently affect how the UMS will function in the future due to their contradictory interests. This has to be identified and carefully managed as a part of the decision-making process in the future UMS [30].
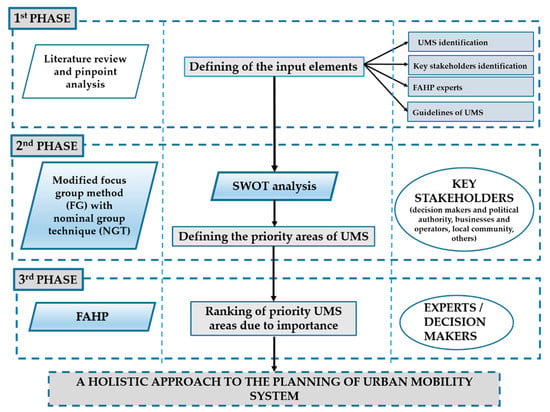
Figure 1.
The conceptual framework of a holistic approach to urban mobility system (UMS) planning.
In the second phase, a modified focus group method was performed with the nominal group technique, before the SWOT analysis was executed. By doing so, key priority areas (KPAs) of UMS were acquired, which were then sorted by their importance by using FAHP in the final, third phase. In this phase, the hierarchical structure of the FAHP model was established with respect to KPAs obtained based on the SWOT results, while the importance of the KPAs was ranked by means of defuzzified weights of joint fuzzy matrices of decision-makers. The individual phases of the holistic approach to the UMS planning model are depicted in Figure 1.
2.2. Modified Method of Focus Groups with the Nominal Group Technique
As aforementioned, we used the focus groups method for the second phase of the suggested model in order to define priority UMS areas that were combined with the NGT technique. The FG method is widely used in various scientific fields [59,60] and is one of the most frequently used qualitative research tools to collect information in many organizations [61].
Engaging focus groups in a complex decision-making process of urban mobility problems turned out to be a very effective method, which required the connection of different experts and knowledge from different disciplines [62]. The most important advantage of the FG method is its ability to achieve a synergistic effect, which is not possible with any other individual interview [63]. However, despite the many advantages of using the FG method, it also has some drawbacks. For example, in reality, usually not all of the participants are comfortable working in groups due to various reasons, such as social dominance, bullying, shyness, overexposure, and difficulties expressing opinions [64]. This fact can lead to the so-called “group effect”, where the opinion of one prevails, and others cannot express their own views. Due to the open-ended questions and a large number of different opinions, it is difficult for the researchers to analyse data and not to be biased in their analysis. In order to avoid this problem, the FG method was combined with the nominal group technique method [64,65] in our research.
The NGT technique combined with the FG method increases the FG-value by generating certain topic data via ranking the challenges and their answers or giving preferential treatment to certain content [66]. The NGT also enables the FG-collected data to be appropriately ranked, and strategies properly formulated [66]. Hence, triangulation—the combination of the FG with NGT method—has been used many times to date ([64] or [67]), where it was shown that this combination eliminates the major drawbacks of the basic FG method.
2.3. SWOT Analysis
SWOT analysis is one of the most frequently used techniques in relation to strategic planning [68] and has already been applied in combination with the FG method ([69] or [70]). On one hand, it is an important decision-making tool that is frequently used for the systematic analysis of the outer and inner systems’ environment [71], and on the other hand, it also enables the shaping of long-term development strategies [72].
However, there are also some major drawbacks with a traditional SWOT approach, such as the following: the identified strategic factors are not qualified or ranked [72], inadequate definition or ambiguity of identified factors (factors which appear to fit into more than one category, and it is not possible to differentiate the factors clearly, i.e., whether they are opportunities or threats, or strengths or weaknesses) [73,74,75], or numerous criteria and interdependencies, which often complicate the decision-making process [76].
Therefore, SWOT analysis has often been combined with other methods in MCDM, among which the AHP or FAHP methods [77,78] are the most appropriate, as they both enable the SWOT factor priorities to be precisely defined. None of the combinations, i.e., AHP or FAHP with SWOT, have been used in holistic-based urban mobility planning yet [1,79].
2.4. The Action Plan and Some Further Details of the Second Phase of Research
The second phase was more detailed, as illustrated in Figure 2. Within the first step, planning of the method implementation, the content, and the open-ended questions was carried out. Selected participants and the moderator were informed about the content, wherein the moderator additionally needed to familiarise themselves with the participants and the modified method of focus groups with NGT. The next step was meeting with the participants. The goal of participants meeting was to present the current state-of-the-art in the UMS field and to identify key priority areas of UMS. Afterwards, the moderator gave the material to the participants, where each one independently identified and formulated what the strengths, weaknesses, opportunities, and threats of the chosen UMS were by using the NGT method.
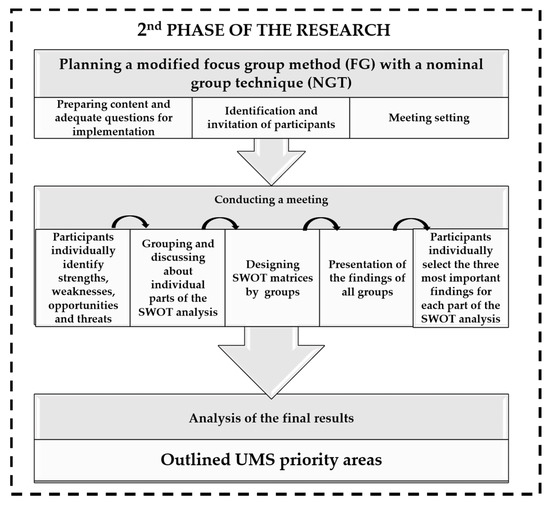
Figure 2.
The more detailed illustration of the second phase of research.
Then, the FG method followed, where groups of four to eight people were formed, where participants presented and explained their opinions to each other and each group formed their own SWOT analysis. The SWOT analysis results of each group were presented and discussed, where the moderator summarized them on the board for everyone to see. In the last step, the NGT method was performed again, but this time, the moderator invited all participants to independently select three of the most important strengths, weaknesses, opportunities, and threats from the presented results. After selection, the four to five most important strengths, weaknesses, opportunities, and threats were chosen for each part of the SWOT analysis.
The result of the second phase was, therefore, SWOT analysis that identified priority areas that represented the input elements for the third phase, where, with the help of the FAHP, the priority areas were ranked by their relevance. This provided us with the key data for constructing the future steps of strategic planning for UMS.
2.5. The FAHP Method
2.5.1. A Combined SWOT–FAHP Hierarchical Structure
After conducting the SWOT analysis and obtaining the key priority areas of UMS, the FAHP method could be engaged. This made it possible to rank the priority areas by their relevance, which is essential since not all goals from all areas can be simultaneously achieved, and one cannot deal with all areas at the same time. When performing the FAHP method, experts who knew the UMS area and its limitations could be present during this process and had the chance to take decisions or represent the decision-makers. Here, a particularly important goal was to follow the previously obtained SWOT group criteria under those priority areas obtained from the previous stages of research. On this basis, a hierarchical structure with local fuzzy weights of criteria with respect to the goal, sub-criteria with respect to the criteria, and global fuzzy weights of sub-criteria with respect to the goal arose, as shown in Figure 3. Such a construction represents the general structure of the SWOT–FAHP hybrid model as a core part of our research. Weights in Figure 3 refer to aggregated weights of all decision-makers, either via their reflection for the criteria, or the sub-criteria. When the obtained fuzzy weights were defuzzified into the crisp numbers, the KPA of UMS could also be appropriately ranked by their relevance.
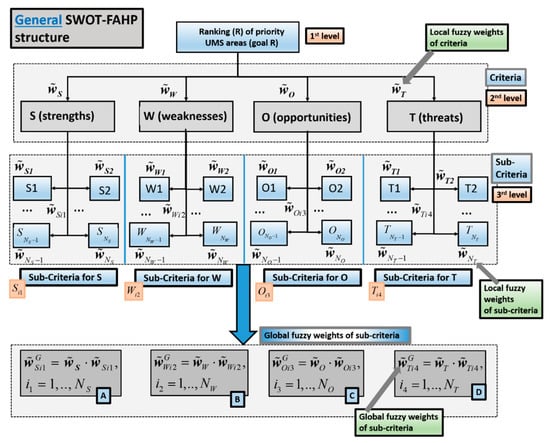
Figure 3.
The core part of our research: Hierarchical structure of the SWOT–FAHP (Strengths, Weaknesses, Opportunities, and Threats–fuzzy analytical hierarchical process) hybrid model with aggregated fuzzy weights of all decision-makers.
2.5.2. Diagram of the 10 Essential Steps of the FAHP Method
A more precise illustration of the consecutive steps of the FAHP method (see also Figure 1, third phase) is shown in Figure 4. In the first five steps, an ordinary (conventional) AHP is conducted, where decomposition of the problem into a hierarchical structure is applied, by taking into consideration previously obtained SWOT results. In this given structure, a pairwise comparison is then made between the AHP structural elements (such as criteria and sub-criteria) of individual experts [80,81]. As can be seen from Figure 4, the AHP implementation process can be broken down into five crucial steps: (1) defining inputs; (2) design of a hierarchical structure; (3) establishment of pair comparisons; (4) design of a matrix of pair comparisons and calculation of weights; (5) verification of consistency of pair comparisons. The first five steps are needed to check the consistency of individual experts in particular, since the FAHP process cannot proceed in the case of inconsistency.
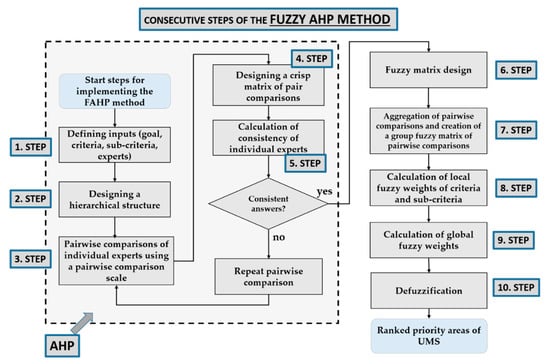
Figure 4.
The consecutive steps of the FAHP method.
In the next section, some details of the consecutive steps of the FAHP method from Figure 4 will be briefly explained.
2.5.3. The AHP Method and a Brief Explanation of the First Five Steps of FAHP
Let us assume that we have a pairwise comparison matrix of a given decision-maker—expert for N = 4 criteria with respect to the goal and N = 4 groups of sub-criteria with respect to their criteria (see Figure 3). Thus, an individual f-th decision-maker deals with groups of criteria/sub-criteria. In addition, they deal with an equal number of the corresponding pairwise comparison matrices (one for criteria and four for sub-criteria), while all f = 1,2,…,m of experts are dealing with of such matrices. Accordingly, we can write the following compact form of the given pairwise comparison matrix,
where m is the number of experts, h refers to the h-th group of criteria/sub-criteria, while is the total number of such matrices.
If estimates are consistent, i.e., , the matrix can be written in the form: A. Thus, individual is equal to the ratio of weights of compared criteria i and j. In this case, the vector of weights can be obtained as a solution of the homogenous system: , where and the corresponding eigenvector is the principal one. Unfortunately, the pairwise comparison matrix is often not completely consistent, and consequently, the maximal eigenvalue is . In order to discover the inconsistency level, the following consistency index of matrix must be calculated [81]:
The latter can be compared with the random index RI (average consistency index), which gives the consistency ratio [81]:
If , the pair comparisons of the given f-th decision-maker are treated as being sufficiently consistent; otherwise, the decision-maker needs to repeat the paired comparison.
The maximal eigenvalue needed in Equation (2) can be calculated in the following way [81],
where the calculation of corresponding weights can be in the simplified form obtained by using the geometric mean method [82,83,84,85]:
2.5.4. A Brief Explanation of the Last Five Steps of FAHP
After calculating the consistency and completing the AHP calculation process carried out by participating (m) experts, fuzzy matrices of pairwise comparisons are formed in the next, sixth step (see Figure 4). For this purpose, the AHP crisp numbers are first transformed into fuzzy numbers on the basis of linguistic statements of m decision-makers. In our case, the triangular fuzzy numbers were used, while the pairs chosen by the individual decision-makers/experts were compared based on the pair-based comparison scales (see Table 1 for the case of fuzzy triangular numbers) [86,87].

Table 1.
A scale of pair comparisons and the corresponding triangular fuzzy numbers.
Fuzzy matrices of pair comparisons (for criteria and sub-criteria) were formed on the basis of the Buckley’s “geometric mean method” approach [88,89,90,91,92,93,94,95] conducted for triangular fuzzy numbers , where the following form of the fuzzy matrix can be created by a given decision-maker (derived from crisp matrix (1)) [90,95]:
where m is the number of experts, h refers to the h-th group of criteria/sub-criteria, while is the total number of such matrices (see Equation (1)).
Here, each element of the matrix represents the lower, middle, and upper values, respectively, of the triangular fuzzy numbers inside the matrix (6). The same logic stands for all other triangular numbers presented in this paper.
The next, seventh, step from Figure 4 encompasses the aggregation of the decision-makers using the geometric mean of their fuzzy pairwise comparisons. After obtaining all pairwise comparisons of all decision-makers and designing fuzzy matrices of pairwise comparisons, their geometric means can be calculated. Moreover, N + 1 = 5 joint (group) fuzzy matrices of pairwise comparisons of all m decision-makers can also be formed (one for criteria: , and four for sub-criteria: , , , —see Figure 3), where the dimensions of these matrices are as follows:
While performing the seventh step, the geometric mean of the fuzzy pair comparisons to aggregate the m decision-makers was expressed in the form of triangular fuzzy numbers, as follows [95]:
where are the fuzzy pair comparisons of the h-th group of criteria/sub-criteria, while m is the number of decision-makers. For the sake of simplicity of explanation, the calculated values symbolize either the elements of the joint fuzzy matrix of pairwise comparisons of all m decision-makers for N = 4 criteria (S, W, O, T) or the elements of the N joint fuzzy matrices for the corresponding M sub-criteria (where —see Figure 3).
Calculations of the local fuzzy weights for N criteria and M sub-criteria are carried out in the eighth step (see Figure 4 and also, Figure 3), where we used Buckley’s approach once again. Firstly, the calculation of the geometric mean should be derived as follows (see Equations (7) and (8)) [90,95]:
The local fuzzy weights for N = 4 criteria and M sub-criteria are computed in the eighth step (see Figure 3 and Figure 4, and Equation (9)), as follows [90,95]:
According to Figure 3, we can split the weights in (10) into the weights for the criteria, and the weights for sub-criteria. For the criteria, the local weights can be denoted more simply: , while for the sub-criteria, they include the following weights: , whose indices are defined in Figure 3 (blocks A, B, C, D below).
Within the ninth step from Figure 4, the calculation of global (collective) fuzzy weights is also carried out for the sub-criteria, by means of multiplying the local fuzzy weights of criteria with the ones of the sub-criteria (see Figure 3, blocks A, B, C, D below). This way, the following global weights are obtained,
In the last, tenth step, the fuzzy weights are defuzzified, wherein the fuzzy numbers (weights) are transformed into the crisp numbers for the needs of ranking and comparison of priority areas. Many authors (for example, [96,97]) claim that the most frequent among all the suggested defuzzification methods is the so-called centre of gravity (COG) method, also known as “centroid”. It is useful due to its simplicity [98,99] and the reliability of the results [91,92,96,98,99,100,101]. By using the COG method, the crisp weights of criteria and sub-criteria are calculated as follows [98]:
The formed crisp numbers (weights) offer an important insight into the individual priority areas and present a basis to construct a comprehensive UMS development strategy.
3. The Numerical Results of the Real Case Study
The developed integrated model was tested for the case of one Slovenian city, called Zagorje ob Savi (ZOS). This is a small city located in the heart of Slovenia, which has approximately 18,000 inhabitants. The most significant problem of the city is emissions of particulate matter, especially PM10 particles, as a result of an average annual growth rate in traffic of 2.2%, in which car mobility represents the most substantial part (44%). Therefore, the proposed model was tested in order to change the mobility system in a chosen urban area in a more holistic way.
3.1. The First Two Stages of the Research Framework
In the first phase (see Figure 1), the relevant input elements were defined. By reviewing existing documents, considering the status and the collection of statistical data, the analysis of the state of the UMS situation was initially carried out in order to identify the future guidelines of UMS development [80]. Stakeholders were also identified from four main groups [30]: (1) the decision-makers and the political authorities; (2) the companies and operators; (3) the community and local environment; (4) the others (e.g., from different professions).
In the second phase from Figure 1, the FG method combined with the NGT method was used, where 59 stakeholders from the previously identified four main groups cooperated and worked on the problem. After the introduction, the stakeholders were informed about the state-of-the-art of the selected UMS area, the guidelines of sustainable development, and the workflow. Afterwards, each participant independently identified the strengths, weaknesses, opportunities, and threats of the chosen UMS, and reported them in the enclosed table (see Appendix A). In order to facilitate the work, the individual parts of the SWOT analysis and the related questions were divided into eight UMS areas: parking, traffic calming, walking (pedestrians), cycling, public transport, use of private cars, soft measures, and freight transportation. As the basis, the following questions were used regarding the existing urban mobility system (UMS):
- What do you think are the strengths of the UMS in the municipality of ZOS?
- What do you think are the weaknesses of the UMS in the municipality of ZOS?
- What do you think are the opportunities for the UMS in the municipality of ZOS?
- What do you think are the threats to the UMS in the municipality of ZOS?
After the individually and independently obtained SWOT analyses, eight focus groups were formed, each composed of seven to eight participants, who, with the help of the moderator, formed common strengths, weaknesses, opportunities, and threats of the whole UMS of the chosen urban area. The presentation of the identified individual parts of the SWOT analysis was carried out afterwards. The moderator invited each group to present findings and write them on the board so that everyone could see the results. A debate followed, where different answers were explained, and, only if necessary, they were added or changed. In the end, the moderator invited all the participants to, independently from each other, choose the three most important strengths, weaknesses, opportunities, and threats from the presented results. They had to award one, two, or three points to the individual answers, where one carried the largest importance. Thus, they created all four parts of the SWOT analysis, where the final result represented the key priority areas that were then transferred to the next phase, where the FAHP method was performed, and the results were adequately ranked (see Table 2).

Table 2.
SWOT analysis with M = 17 key priority areas of the chosen urban environment.
3.2. Analysis of the Fuzzy Analytical Hierarchy Model Construction (3rd Stage of the Research Framework)
In the third and final phase, the FAHP method, with its ten steps, was conducted (see Figure 4), which provided the results for the ranked priority areas. These priority areas further presented the basis of forming the strategies for the future UMS development of the chosen urban environment. In the continuation, an excerpt of implementing consecutive steps of the FAHP procedure is presented. In order to easily follow the main path over all of the consecutive steps, simultaneously referring to Figure 4 is recommended.
3.2.1. The First and Second Steps of the FAHP (Defining Inputs and Designing a Hierarchical Structure)
In the first two steps (see Figure 4), the input elements were defined and the hierarchical structure created based on the results of the modified FG method, SWOT analysis (see Table 2), and hierarchical structure of the SWOT–FAHP hybrid model from Figure 3. This way, the structure appeared, as shown in Figure 5. Here, at the top of the hierarchy structure is the goal (R)—ranking of priority UMS areas, followed by the SWOT group criteria that were placed at the second level (i.e., S—strengths, W—weaknesses, O—opportunities, T—threats), under which the pre-identified priority areas from Table 2 are present as the sub-criteria (third level). It can be seen that Figure 5 is relatively similar to Figure 3, except that we are now dealing with the conditioned structure of a real case study as opposed to a generalized structure.
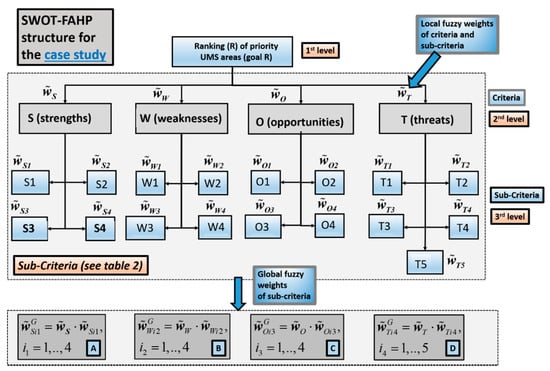
Figure 5.
Hierarchical structure of the SWOT–FAHP decision-making model for the chosen urban area (N = 4 criteria, M = 17 sub-criteria).
3.2.2. The Third Step of the FAHP (Pair Comparisons)
The pair comparisons (PCs) were executed by means of specially designed questionnaires (see Appendix A and Appendix B). The PCs were accomplished for the individual criteria (SWOT groups—second level) with respect to the first level (goal R) (see Figure 5). Moreover, they were also carried out for the priority areas (sub-criteria—third level) with respect to the second level (criteria). Fourteen experts (—see Equations (1) and (6)), who were chosen from the groups of decision-makers and the area of mobility (and/or transport) experts, cooperated in the execution of the pair comparisons.
3.2.3. The Fourth and Fifth Steps of the FAHP (Crisp Matrix of Pair Comparisons, Consistency Verification)
In the fourth and fifth steps of the FAHP method from Figure 4, Equations (1)–(5) from Section 2.5.3 were calculated for each decision-maker DM (for criteria and sub-criteria). This way, in order to check the consistency of the experts’ responses, the matrices of pair comparisons with crisp numbers (see Equation (1)) were formed at the beginning, and later on, 70 consistency indice ratios (see Equation (3)) were calculated for all 14 experts with the help of Equations (1)–(5).
Table 3 presents an example of the calculated results for the consistency index ratio for the first decision-maker (f = 1), when dealing with the first group (h = 1) of N = 4 SWOT criteria and is: (i, j = 1, 2, …, n = 4) (see Appendix C for a structure of in this case). As we can see from Table 3, ; thus, we can conclude that the first expert was consistent in terms of the criteria with respect to the goal. The calculations, as shown here for the first expert, revealed that the consistency verification was successful for the other 13 experts as well. The latter means that the calculations for all 70 consistency index ratios were adequate for all 14 decision-makers for all pair comparisons (for criteria (S, W, O, T) with respect to the goal, and for sub-criteria with respect to criteria). Therefore, the Consistency Ratio (CR) indices were always lower than 0.1. The results, which show the consistency of all decision-makers, are depicted in Appendix D. Moreover, from Table 2 and Figure 5, it can also be seen that the dimensions of criteria and sub-criteria were as follows (see Equation (7)): .

Table 3.
An example of the consistency index ratio calculation and other corresponding calculations for the first expert for the pair comparisons of four (SWOT) criteria () (see Equations (1)–(5)).
3.2.4. The Sixth step of the FAHP (Fuzzy Matrices Design)
In the sixth step of the FAHP method from Figure 4, the formation of the pair comparisons of fuzzy matrices with triangular fuzzy numbers was carried out. At this step, five fuzzy matrices of pair comparisons for each f-th individual of m = 14 decision-makers were formed, where their linguistic statements were transformed into fuzzy numbers depicted in Table 1. In this case, Equation (6) from Section 2.5.4 took the form:
An example of such a fuzzy matrix for the first decision-maker and the group of SWOT criteria, i.e., the matrix , is presented in Table 4 (compare with the corresponding crisp matrix in Appendix C).

Table 4.
An example of the fuzzy matrix of pair comparisons for the first decision-maker and a group of N = 4 criteria (second level) with respect to the first level (goal R).
3.2.5. The Seventh Step of the FAHP (Aggregation of Decision-Makers and Formation of Group Fuzzy Matrices for Criteria and Sub-Criteria)
In this step, the following equations based on equations and the explanation provided in Section 2.5.4 could be formed for all 14 decision-makers and the specific case of the real case study (see also Equation (12), Figure 5 and Table 2):
This way, by applying the aggregation and performing the Equations from (13), the collective (group) fuzzy matrices of all decision-makers’ pair comparisons could be constructed for 4 criteria and 17 sub-criteria. An example of a collective fuzzy matrix of pair comparisons for a group of SWOT criteria is shown in Table 5. At this point, it is perhaps worth mentioning that all operations over the fuzzy numbers (i.e., addition, subtraction, multiplication, division) were conducted by means of predefined rules for triangular fuzzy numbers [89,102].

Table 5.
Collective (group) fuzzy matrix of pair comparisons of all (m = 14) decision-makers for a group of four (S, W, O, T) criteria.
3.2.6. The Eighth step of the FAHP (Calculation of Local Fuzzy Weights of Criteria and Sub-Criteria)
The local fuzzy weights of criteria and sub-criteria could be computed by means of the previously aggregated fuzzy matrices of pair comparisons (see Equation (13)), where the general Equations (9, 10) from Section 2.5.4 evolved into the specific form of the present case (i.e., N = 4 criteria, M = 17 sub-criteria, etc.). The local fuzzy weights for the specific case study were as follows: , with the corresponding geometric means, . When the results for the group of four (S, W, O, T) criteria were taken into account, the obtained four weights were as follows: (see Section 2.5.4). In this case, the corresponding geometric means were , with the elements (see Table 5) of the group fuzzy matrix for the SWOT criteria (see also Equations (9) and (13), and Figure 5). The acquired results are presented in Table 6.

Table 6.
Calculated local fuzzy weights for SWOT criteria (h = 1).
The next stage was the calculation of the local fuzzy weights— (see Equations (9), (10) and (13) and Figure 5)—that belonged to the M = 17 sub-criteria, i.e., the calculation of the following weights (denoted in a simpler way): (see Section 2.5.4). In this case, the geometric means were as follows: . The following results appeared for the local fuzzy weights related to 17 sub-criteria, as shown in Table 7 (see also Figure 5 and Table 2 for the meaning of sub-criteria).

Table 7.
The calculated local fuzzy weights for 17 sub-criteria ( ).
3.2.7. The Ninth and Tenth Steps of the FAHP (Global Fuzzy Weights of Sub-Criteria and Defuzzification of all Fuzzy Weights)
In the ninth step from Figure 4, the global fuzzy weights of 17 sub-criteria were calculated by means of multiplying the local fuzzy weights of criteria (from Table 6) with the ones of the sub-criteria (from Table 7) (see also Figure 5, blocks A, B, C, D below). This way, the 17 global weights: arose for 17 sub-criteria . Due to limitations in the article length, their results are not shown here. However, the relationships of results between the local fuzzy weights for criteria and sub-criteria on one hand, and the global fuzzy weights for sub-criteria on the other hand, can be easily observed in Appendix E.
In the tenth and final step, the fuzzy weights were defuzzified and transformed into the crisp numbers from (11), where . This way, by means of Equation (11), all the crisp weights were obtained for the purpose of the ranking and comparison of priority areas. When the process of defuzzification was finished (over the fuzzy weights in Appendix E, see also Table 6 and Table 7), the crisp local weights for criteria and sub-criteria, as well as the global crisp weights for sub-criteria, were obtained. Their results are shown in Table 8, where the ranking of sub-criteria within the individual criteria, as well as the collective ranking of all sub-criteria in a comprehensive way, is also depicted (see also Table 2 and Figure 5, blocks A, B, C, D).

Table 8.
The crisp weights , where ; ranking of criteria (c.f. for Rank 1), sub-criteria inside the criteria (c.f. for Rank 2), and collective ranking of all sub-criteria (c.f. for Rank 3).
As can be seen from Table 8, the individual criteria and sub-criteria were ranked by priority by means of the obtained crisp weights . Regarding the (S, W, O, T) criteria (see Rank 1 in Table 8), the most important was the opportunity (O; weight 0.3258), followed by weaknesses (W; 0.3235), threats (T; 0.2036), and finally, strengths (S; 0.1985). The criteria O and W were approximately equally weighted and were significantly more important than criteria T and S.
Regarding the monitoring of the ranking of sub-criteria inside the SWOT criteria (see Rank 2 in Table 8), i.e., when observing their relevance among four corresponding groups (S, W, O, T), the following can be concluded. For the criterion strengths (S), the sub-criterion S2 (readiness and the desire of the municipality to change (in the direction of sustainable mobility)) (weight 0.08150) was the most important, followed closely by S4—arranged school transportation (0.05317); S1—already in construction—cycling and walking paths (0.05159); and S3—vicinity of a highway and railway (0.04074) as the least important. For the criterion weaknesses (W), the sub-criterion W2 (neglected remote places and their connection to public transport) (weight 0.13040) was the most important, followed by W4—insufficient cycling infrastructure and awareness about the advantages of cycling (0.11309); W1—freight (transit) transport through the municipality (0.07301); and W3—poor arrangement of a parking system (0.05195) as the least important. For the criterion opportunities (O), the sub-criterion O2 (arrangement of infrastructure for pedestrians and cyclists) (weight 0.13186) was the most important, followed by O1—possibilities for constructing safe cycling paths (0.11056); O4—arrangement of the parking system (0.07287); and O3—possibility to construct parking lots on the outskirts of settlements (0.06583) as the least important. For the criterion threats (T), the sub-criterion T3 (unpreparedness to change travelling habits) (weight 0.06865) was the most important, followed by T1—increase in transportation (0.05209); T5—deterioration of the stationary traffic situation (0.05152); T4—neglect of the surrounding places (0.03182); and T2—strict regulations (0.03035) as the least important.
When the collective ranking and comparison of all 17 sub-criteria was conducted (see Rank 3 in Table 8), the following could be concluded. The four most important sub-criteria were: (1) the sub-criterion O2 (arrangement of infrastructure for pedestrians and cyclists); (2) the sub-criterion W2 (neglected remote places and their connection to public transport); (3) the sub-criterion W4 (insufficient cycling infrastructure and awareness about the advantages of cycling); and (4) the sub-criterion O1 (possibilities for constructing safe cycling paths). The collective importance of the subsequent 17 sub-criteria can observed in Table 8. As we can see, the least important sub-criterion was T5 (deterioration of the stationary traffic situation).
4. Discussion
The suggested innovative model was proven to be effective because it enabled a more holistic approach to the planning of an urban mobility system. It was shown in this paper that by using the developed model, the ranked priority areas can be exactly determined. The identified significance of the individual priority areas might help the decision-makers during the design of further steps of UMS planning in the future. Furthermore, we created a new approach for solving the complex multi-criteria decision issues that arise in the field of UMS planning.
The proposed model was tested for a real case study that referred to a practical environment. According to the defined input elements in the first phase of the proposed model (UMS development guidelines, 59 key stakeholders, and 14 experts on FAHP implementation), the SWOT analysis was performed using the modified FG with NGT method (second phase of the proposed model, as shown in Figure 2). The modified FG with NGT implemented enabled the involvement of a wide range of stakeholders. The combination of both also reduced the bias of the results obtained. The results in Table 2 show that, with regard to different mobility areas, cycling (partly walking) and parking or stationary traffic policy stood out. The travel habits and accessibility throughout the urban area, which appear as both weaknesses and threats, were also prominent.
An interesting fact is that, for example, the field of cycling is emerging as a strength and opportunity, and on the other hand, as a weakness. Similarly, the area of stationary traffic is both a threat and an opportunity. This points to the previously presented weakness of the traditional SWOT analysis, which has also been discussed by other authors [73,74,75] (due to the wide or inadequate description of KPAs, a specific KPA (key priority area) cannot be accurately placed in a single category or fit into more than one category or there is lack of prioritization of KPAs). Thus, it can be assumed that stakeholders perceive certain KPAs (such as cycling) as areas that are already regulated (strength), but too slowly or unsatisfactorily (weakness). To eliminate these ambiguities of SWOT analysis, the FAHP method was implemented in the third, last phase (see Figure 4 for steps and Table 8 for final results). FAHP allowed the quantification and ranking of the obtained KPAs. This established whether a particular KPA area was greater, for example, a strength or a weakness. This can be seen in the case of cycling, where this area was shown to represent a greater weakness (W3 is ranked third) than strength (S1 is ranked 13). This means something has already been done (strength), but at the same time, not enough has been done (weakness). This is further underpinned by the fact that opportunities are emerging for cycling improvements (O2 is ranked first and O1 as fourth).
Regardless of the ambiguities presented, four different strategies can be formed and intertwined [72]: (1) SO (building on strengths for taking advantage of opportunities); (2) ST (building on strengths to avoid threats); (3) WO (an improvement of weaknesses to take advantage of opportunities); and (4) WT (lowering weaknesses and avoiding threats) strategies. The proposed strategies, using the results for criteria and sub-criteria, are shown in Appendix F.
If we now look at the numerical data obtained by the FAHP method (Table 8), we can see that among the individual priority areas (i.e., the SWOT criteria), areas of opportunities and weaknesses prevailed approximately to the same degree, with a slight domination of opportunities. Moreover, the area of strengths was the least important. Based on the aforementioned facts, we can conclude that it is important to build on WO strategies (the elimination of weaknesses and exploitation of the opportunities): WO1: building infrastructure for pedestrians and cyclists while encouraging their increased use, and WO2: improvement of the existing parking system (see Appendix F).
A higher analytical value was obtained if we compared individual sub-areas (Table 8 and Figure 6). Given the final ranked priority areas of the UMS planning, which should be considered when designing strategies for the future development of the UMS of the chosen urban area, there were four sub-areas of essential importance (see Figure 6, focus on the sub-criteria O1, O2, W2, W4 surrounded by circles):
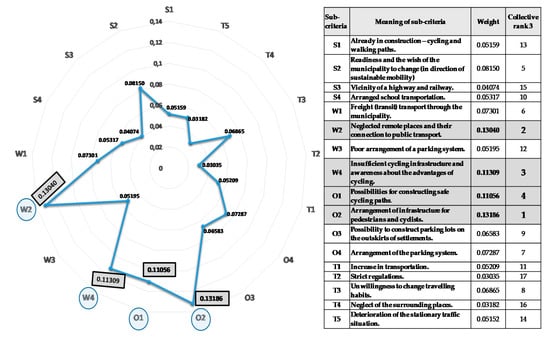
Figure 6.
Graphical illustration of priority areas’ importance for the UMS planning of the chosen urban area (sub-criteria O1, O2, W2, W4 surrounded by circles are the most important due to the most significant weights).
- Two sub-areas in the group opportunities, i.e., O2 (arrangement of infrastructure for pedestrians and cyclists) (weight 0.13186) as the first collectively ranked sub-area, and O1 (possibilities for constructing safe cycling paths) as the fourth collectively ranked sub-area (weight 0.11056).
- Two in the group weaknesses, i.e., W2 (neglected remote places and their connection to public transport) (weight 0.13040) as the second collectively ranked sub-area, and W4 (insufficient cycling infrastructure and awareness of cycling advantages) (weight 0.11309) as the third collectively ranked sub-area.
Of note is the aforementioned weakness, W2—second rank. Based on the results, it is evident that stakeholders perceived this as a threat T4: neglect of the surrounding places, although not very important (rank 16). In spite of the low-level threat, this means that when planning, they must keep in mind the balanced level of the whole UMS and look for synergistic effects of the connections of different mobility subsystems (for example, walking, cycling, public transport, changing traveling habits and parking policy). Given the relatively high rank of the identified strength S2: readiness and the desire of the municipality to change (in the direction of sustainable mobility (rank 5)), improvements in this direction can be expected. We can also point out the connection between W1: freight (transit) transport through the municipality (rank 6), in conjunction with T1: increase in transportation (rank 11), indicating potential problems in the future in terms of congestion and increased environmental impact.
As we have already noted, the essential priority areas were highlighted as areas of opportunities and weaknesses. Following a thorough analysis from specific sub-areas inside the groups’ opportunities and weaknesses, the most important strategy seemed to be the one utilizing opportunities of the arrangement of infrastructure for pedestrians and especially, for the cyclists, that the UMS environment offers (WO1—see Appendix F). This would reduce the shortcomings of the current situation, where the bicycle infrastructure was identified as being deficient. Such a strategy would also successfully exploit the willingness and desire of the municipality to make changes towards sustainable mobility (as the most important strength, S2) and face the most important threat: unwillingness to change travelling habits (T3).
5. Conclusions
The present work proposed a new model, which enables an advanced, holistic approach to UMS planning. The latter is based on a hybrid mechanism that includes a combination of the modified method of FG with NGT, SWOT analysis, and the FAHP method. Within such a framework, the modified FG–NGT method is used to transparently involve key stakeholders and the FAHP method is used for ranking the importance of priority areas that refer to the identified SWOT criteria and sub-criteria.
In order to prove the applicability of the proposed model, it was tested on a real-life example, where the ranked priority areas were shown to represent a viable view of the future of the UMS of the selected urban area. The WO1 strategy proposed, based on the ranking of key priority areas (building infrastructure for pedestrians and cyclists while encouraging their increased use), is in line with the basic goals of the sustainable development of UMS and provides a good basis for further decision-making processes (for example, defining strategic goals and action plans). Based on these findings, the founders of the future development of the UMS of the selected urban area were able to formulate more transparent, holistic solutions; the proposed solutions have already been integrated into the design of a holistic transport strategy plan.
Relating to the successful implementation, this novel approach provides: (1) The decision-makers the ability to search for compromises with an in-depth understanding when they are faced with contradictory goals during the decision and coordination processes. Therefore, the suggested model presents a new holistic way to solve complex multi-criteria issues about decisions that appear in the UMS area; (2) Strategic planning of the whole UMS by defining KPAs and consequently creating scenarios, goals, and an action plan; (3) A basis for balanced development of all relevant urban mobility subsystems through the ranking of KPAs at UMS level; (4) Holistic planning with the involvement of a wide range of stakeholders using a participatory and transparent approach, taking into account the interdependence and the interconnections of different mobility subsystems; (5) Reducing subjectivity and the ability to influence strategic decision-making; (6) Enriched theoretical aspects of more holistic UMS planning (the use of the FAHP method in the UMS field for holistic decision-making has not yet been observed); (7) Practical applicability in real urban areas.
The proposed model also eliminates some of the shortcomings identified in the literature: (1) With the help of the FAHP, the weakness of traditional standalone SWOT analysis is reduced, such as the lack of clarity, the lack of quantification of priority areas and the lack of prioritization. This reduces the subjective bias in the formulation of scenarios and, consequently, strategic goals (the possibility of influencing on the basis of authority, power, etc.); (2) The modified FG method with NGT also reduces the bias (subjectivity) of decision-makers in determining inputs (the combination of methods reduces the ability to influence the results or override individual stakeholders); (3) Compared to basic MCDM models (for example, basic AHP), fuzzy logic increases the ability to incorporate ambiguous, imprecise, and vague information and thus make a decision-making UMS process more realistic; (4) Checking the consistency of decision-makers’ responses (results), when comparing individual KPAs with each other (calculating the consistency index within the FAHP method); (5) Combining different methods thus eliminates the disadvantages of them, which, in turn, means better results in the field of decision-making than their independent implementation.
With proper definition of the input elements (development guidelines and characteristics of UMS, key stakeholders, decision-makers), the developed model can also be transferred to other urban areas or different specific UMS subsystems. Its usefulness is especially evident in areas where we face the problem of introducing a more holistic approach, multi-criteria decisions, and conflicting goals or interests. This applies to both small and large urban areas. The stages or phases of decision-making can be treated as standardized regardless of the characteristic of the UMS (defining input elements and executing the FG–NGT method, producing the SWOT, and implementing the FAHP method). The latter means that once the input elements are defined, the FG–NGT method is executed, and the SWOT is conducted, some sub-criteria emerge. Their number and characteristics can be different in different cases, it is true, but the further procedure by using the FAHP always continues similarly. Namely, the FAHP hierarchical structure is always pre-defined and established by its inputs, i.e., the sub-criteria, so from this point of view, the whole constellation in this paper can be looked at through the eyes of some sort of methodological generalization, regardless of the dimension and/or nature of the addressed problem.
It should be noted, however, that the proposed approach for implementation in practice requires knowledge of individual methods (FG, NGT, and FAHP) and the involvement of those responsible for decision-making. For the time being, only individual phases can be executed through computer programs and applications. The latter means that, so far, only a prototype of a decision-making support system has been developed within the MS Excel environment. Thus, only the results of the real testing of the proposed model (prototype) have been given to the responsible personnel in the observed municipality (the client, i.e., the customer) in terms of advising them, how to make easier decisions, and to formulate a strategic holistic plan.
Of course, we are aware of the limitations of the proposed model, which would need to be tested in several different urban areas to provide some degree of generalization. Namely, different cases may have different specificities and limitations. Only if the model would work well in such diverse cases of urban areas would its validation be confirmed in terms of generalization to any urban area example.
In general, we recognize the following opportunities for further research: (1) Extension of the model with added alternatives (pre-formulated scenarios, defined actions, or proposed goals) to allow a paired comparison of these alternatives according to the KPAs; (2) As indicated above, the usefulness of the proposed model could be explored in different UMSs and in areas other than UMS, especially where we encounter multi-criteria decisions and a participatory approach. It would also be interesting to investigate the usefulness of the developed model at lower levels of UMS planning (or other systems), such as the creation of an action plan or the formulation of priority actions; (3) One possible direction of further research is to also use another MCDM method (for example, fuzzy VIKOR or FTOPSIS) or to combine our approach with other MCDM methods on the same data and compare the results obtained; (4) Develop a special computer software program or application that would help to perform the entire process; (5) It would also be interesting to test the usefulness of the model in defining and ranking obstacles encountered in UMS planning or in the implementation of UMS planning goals.
We can conclude that the suggested advanced model will hopefully not only improve the theoretical view of comprehensive UMS planning but also likely allow relatively easier acceptance of complex multi-criteria decisions in the real-life systems of urban environments.
Author Contributions
This paper represents a result of collaborative teamwork. U.K. developed the concept and drafted the manuscript; D.T. and D.D. provided constructive suggestions and revised the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Table for forming the individual SWOT analysis in the frame of the modified method of focus groups—an example for the area of strengths and weaknesses.
Table A1.
Table for forming the individual SWOT analysis in the frame of the modified method of focus groups—an example for the area of strengths and weaknesses.
| What is the Current State of the Individual Transportation Area? | ||
|---|---|---|
| Area | Strengths (What is Well Arranged in Your Opinion) | Weaknesses (What is Badly Arranged in Your Opinion) |
| What is the state in the area of parking? | ||
| What is the state in the area of traffic-calming (speed bumps, pedestrian zones, green areas, etc.)? | ||
| What is the state in the area of walking? | ||
| What is the state in the area of cycling? | ||
| What is the state in the area of public transport? | ||
| What is the state in the area of use of private cars? (green interval, limitation of access, fluent transport, information, etc.)? | ||
| What is the state in the area of “soft” measures? (changing of travelling habits, information about different modes of transport, education campaigns, actions to promote walking, cycling, public transport, etc.)? | ||
| What is the state in the area of freight transportation? | ||
Appendix B

Table A2.
An example of a question and the tables for the execution of the paired comparison between the criteria, according to the goal.
Table A2.
An example of a question and the tables for the execution of the paired comparison between the criteria, according to the goal.
| We ask you to circle (the left side of the table) and choose which criterion is, in your opinion, the most important (or influences the most) when planning the urban mobility system in the municipality of Zagorje ob Savi (or we have to consider when planning and form from it), and then mark on the right side of the table how important this criterion is when planning the urban mobility system in the municipality. | |||||||||||
| Which Criterion is the Most Important (or the Most Influential) (Circle)? | How important (or influential) is an Individual Criterion when Planning Mobility (Transport) in the Municipality (Circle) 1 = Criteria are both equally important; 3 = Moderately more important; 5 = Strongly more important; 7 = Very strongly more important; 9 = Absolutely more important; 2, 4, 6, 8 = Interim values | ||||||||||
| Strengths of the current state | or | Weaknesses of the current state | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Threats of the current state | or | Opportunities the municipality has to develop traffic | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Strengths of the current state | or | Threats in the future | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Threats of the current state | or | Opportunities that the municipality has to develop | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Threats of the current state | or | Threats in the future | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Threats in the future | or | Threats in the future | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Appendix C

Table A3.
Structure of the matrix of the pair comparisons of the first expert for N = 4 criteria.
Table A3.
Structure of the matrix of the pair comparisons of the first expert for N = 4 criteria.
| Criteria (i) | Strengths (S) | Weaknesses (W) | Opportunities (O) | Threats (T) |
|---|---|---|---|---|
| Strengths (S) | 1 | 1/7 | 1/6 | 1 |
| Weaknesses (W) | 7 | 1 | 2 | 6 |
| Opportunities (O) | 6 | 1/2 | 1 | 5 |
| Threats (T) | 1 | 1/6 | 1/5 | 1 |
Appendix D

Table A4.
Calculated 70 consistencies of all m = 14 decision-makers for a group of criteria with respect to the goal, and for the four groups of sub-criteria with respect to SWOT criteria:
Table A4.
Calculated 70 consistencies of all m = 14 decision-makers for a group of criteria with respect to the goal, and for the four groups of sub-criteria with respect to SWOT criteria:
| Decision-maker (f = 1,…7) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| CR for a group of criteria (SWOT) (h = 1) | 0.05740 | 0.06267 | 0.06675 | 0.09894 | 0.08615 | 0.08881 | 0.07952 |
| CR for according to strengths (S) (h = 2) | 0.08556 | 0.09145 | 0.06969 | 0.04519 | 0.04935 | 0.08739 | 0.04387 |
| CR for according to weaknesses (W) (h = 3) | 0.08637 | 0.09834 | 0.08739 | 0.05915 | 0.09032 | 0.08264 | 0.00000 |
| CR for according to opportunities (O) (h = 4) | 0.08499 | 0.09451 | 0.01657 | 0.08758 | 0.08333 | 0.08238 | 0.08046 |
| CR for according to threats (T) (h = 5) | 0.08529 | 0.08074 | 0.08055 | 0.08520 | 0.08190 | 0.09050 | 0.08764 |
| Decision-maker (f = 8,…14) | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| CR for a group of criteria (SWOT) (h = 1) | 0.08958 | 0.01430 | 0.095282 | 0.080463 | 0.07667 | 0.043873 | 0.056386 |
| CR for according to strengths (S) (h = 2) | 0.09754 | 0.01382 | 0.079065 | 0.083674 | 0.048438 | 0.086375 | 0.050247 |
| CR for according to weaknesses (W) (h = 3) | 0.09032 | 0.06872 | 0.073956 | 0.094429 | 0.083674 | 0.047042 | 0.071269 |
| CR for according to opportunities (O) (h = 4) | 0.08584 | 0.07676 | 0.087092 | 0.043873 | 0.031866 | 0.082385 | 0.062065 |
| CR for according to threats (T) (h = 5) | 0.09279 | 0.09987 | 0.099725 | 0.069757 | 0.081741 | 0.089085 | 0.084292 |
.
Appendix E

| Criteria | Aggregated Fuzzy Local Weights for Criteria | Sub-Criteria | Aggregated Fuzzy Local Weights for Sub-Criteria | Global (Collective) Weights for Sub-Criteria |
|---|---|---|---|---|
| Strength (S) | (0.1285; 0.1881; 0.2790) | S1 | (0.1570; 0.2261; 0.3300) | (0.0202; 0.0425; 0.0921) |
| S2 | (0.2479; 0.3604; 0.5192) | (0.0319; 0.0678; 0.1449) | ||
| S3 | (0.1231; 0.1791; 0.2607) | (0.0158; 0.0337; 0.0727) | ||
| S4 | (0.1623; 0.2344; 0.3389) | (0.0209; 0.0441; 0.0946) | ||
| Weaknesses (W) | (0.2087; 0.3113; 0.4505) | W1 | (0.1337; 0.1967; 0.2883) | (0.0279; 0.0612; 0.1299) |
| W2 | (0.2444; 0.3563; 0.5090) | (0.0510; 0.1109; 0.2293) | ||
| W3 | (0.0996; 0.1409; 0.2024) | (0.0208; 0.0439; 0.0912) | ||
| W4 | (0.2162; 0.3061; 0.4414) | (0.0451; 0.0953; 0.1989) | ||
| Opportunities (O) | (0.2074; 0.3095; 0.4605) | O1 | (0.1881; 0.2860; 0.4434) | (0.0390; 0.0885; 0.2042) |
| O2 | (0.2297; 0.3484; 0.5215) | (0.0476; 0.1078; 0.2401) | ||
| O3 | (0.1139; 0.1737; 0.2608) | (0.0236; 0.0537; 0.1201) | ||
| O4 | (0.1292; 0.1919; 0.2875) | (0.0268; 0.0594; 0.1324) | ||
| Threats (T) | (0.1322; 0.1912; 0.2876) | T1 | (0.1558; 0.2252; 0.3221) | (0.0206; 0.0430; 0.0926) |
| T2 | (0.0881; 0.1292; 0.1902) | (0.0116; 0.0247; 0.0547) | ||
| T3 | (0.1912; 0.2903; 0.4354) | (0.0253; 0.0555; 0.1252) | ||
| T4 | (0.0960; 0.1379; 0.1962) | (0.0127; 0.0264; 0.0564) | ||
| T5 | (0.1503; 0.2175; 0.3238) | (0.0199; 0.0416; 0.0931) |
Appendix F

Table A6.
Proposed UMS strategies of the chosen urban area.
Table A6.
Proposed UMS strategies of the chosen urban area.
| Strengths (S) | Weaknesses (W) | |
|---|---|---|
| Opportunities (O) | SO strategies: | WO strategies: |
| SO1: Accelerated investment in cycling and pedestrian infrastructure. | WO1: Building infrastructure for pedestrians and cyclists while encouraging their increased use. | |
| SO2: Reducing dependence on cars by changing travel habits, along with regulating parking policies in conjunction with parking lots on the outskirts. | WO2: Improvement of the existing parking system. | |
| Threats (T) | ST strategies: | WT strategy: |
| ST1: Increased effort in raising awareness and changing travel habits while taking action to limit car use. ST2: Arrangement of public transport and regulation of the system of commuting. | WT2: Redirecting primarily freight to rail and restricting the use of cars and heavy freight in urban centers. |
References
- Kramar, U.; Topolšek, D. Applications of Fuzzy Analytic Hierarchy Process in Urban Mobility System. Tech. Gaz. 2018, 25, 1553–1560. [Google Scholar]
- Cavalcanti, C.O.; Limont, M.; Dziedzic, M.; Fernandes, V. Sustainability of urban mobility projects in the Curitiba metropolitan region. Land Use Policy 2017, 60, 395–402. [Google Scholar] [CrossRef]
- Moore, T.; Pulidindi, J. Understanding Urban Transportation Systems: An Action Guide for City Leaders; National League of Cities: Washington, DC, USA, 2013. [Google Scholar]
- European Commission. Mobility and Transport. In Urban Mobility; European Commission: Brussels, Belgium, 2017. [Google Scholar]
- Spinney, J.; Scott, D.; Newbold, K. Transport mobility benefits and quality of life: A time-use perspective of elderly Canadians. Transp. Policy 2009, 16, 1–11. [Google Scholar] [CrossRef]
- Hanson, S.; Giuliano, G. The Geography of Urban Transportation; The Guilfor Press: New York, NY, USA, 2004. [Google Scholar]
- Okraszewska, R.; Romanowska, A.; Wołek, M.; Oskarbski, J.; Birr, K.; Jamroz, K. Integration of a Multilevel Transport System Model into Sustainable Urban Mobility Planning. Sustainability 2018, 10, 479. [Google Scholar] [CrossRef]
- Wegener, M. The future of mobility in cities: Challenges for urban modelling. Transp. Policy 2013, 29, 275–282. [Google Scholar] [CrossRef]
- UN-Habitat: Urban transport. Urban Transport Programme; UN-Habitat: Urban transport: Nairobi, Kenya, 2014. [Google Scholar]
- World Bank. Urban Population. 2017. Available online: http://data.worldbank.org/indicator/SP.URB.TOTL.IN.ZS?end=2015&locations=XC&start=1960&view=chart (accessed on 14 March 2017).
- Van Audenhove, F.-J.; Korniichuk, O.; Dauby, L.; Pourbaix, J. The Future of Urban Mobility 2.0; ADL UITP: Paris, France, 2014. [Google Scholar]
- Masuch, N.; Lützenberger, M.; Keiser, J. An Open Extensible Platform for Intermodal Mobility Assistance. Procedia Comput. Sci. 2013, 19, 396–403. [Google Scholar] [CrossRef]
- Maghraoui, O.A.; Vallet, F.; Puchinger, J.; Yannou, B. Modeling traveler experience for designing urban mobility system. Des. Sci. 2010, 5, e7. [Google Scholar] [CrossRef]
- Banister, D. The sustainable mobility paradigm. Transp. Policy 2008, 15, 73–80. [Google Scholar] [CrossRef]
- Maghraoui, O.A.; Vallet, F.; Puchinger, J.; Yannou, B. Framing key concepts to design a human centered urban mobility system. In Proceedings of the 21st International Conference on Engineering Design (ICED 17), Vancouver, BC, Canada, 21–25 August 2017; pp. 91–100. [Google Scholar]
- Santos, S.B.; Goncalves, J. Pedestrian Environment Quality Assessment in Portuguese Medium-Sized Cities. In Proceedings of the IOP Conf. Series: Materials Science and Engineering, Pregue, Czech Republic, 24 February 2019; Volume 471. [Google Scholar]
- Ghorbanzadeh, O.; Moslem, S.; Blaschke, T.; Duleba, S. Sustainable Urban Transport Planning Considering Different Stakeholder Groups by an Interval-AHP Decision Support Model. Sustainability 2019, 11, 9. [Google Scholar] [CrossRef]
- Kiba-Janiak, M.; Witkowski, J. Sustainable Urban Mobility Plans: How Do They Work? Sustainability 2019, 11, 4605. [Google Scholar] [CrossRef]
- Stull, T.; Kuilboer, J.-P. Three Languages for Urban Mobility. In Proceedings of the STPIS@ECIS, Stockholm, Sweden, 10 June 2019. [Google Scholar]
- Sheller, M. The new mobilities paradigm for a live sociology. Curr. Sociol. 2014, 62, 789–811. [Google Scholar] [CrossRef]
- Curiel-Esparza, J.; Mazario-Diez, J.L.; Canto-Perello, J.; Martin-Utrillas, M. Prioritization by consensus of enhancements for sustainable mobility in urban areas. Environ. Sci. Policy 2016, 55, 248–257. [Google Scholar] [CrossRef]
- United Nations Human Settlements Programme (UN-Habitat). Planning and Design for Sustainable Urban Mobility: Global Report on Human Settlements; Routledge: New York, NY, USA, 2014. [Google Scholar]
- Keller, P. Challenge in Future Transportation Research and Planning. Energy Technologies for a Sustainable Future; Paul Scherrer Institute: Villigen, Switzerland, 2000. [Google Scholar]
- Karjalainen, L.E.; Juhola, S. Framework for Assessing Public Transportation Sustainability in Planning and Policy-Making. Sustainability 2019, 11, 1028. [Google Scholar] [CrossRef]
- Banister, D. Sustainable Urban Development and Transport—A Eurovision for 2020. Transp. Rev. 2000, 20, 113–130. [Google Scholar] [CrossRef]
- Marques da Costa, L.; da Costa, E.M. Sustainable Urban Mobility Policies as a Path to Healthy Cities—The Case Study of LMA, Portugal. Sustainability 2019, 11, 2929. [Google Scholar]
- UN-Habitat. Mobility; UN-Habitat: Nairobi, Kenya, 2012. [Google Scholar]
- Tafidis, P.; Sdoukopoulos, A. Pitsiava-Latinopoulou, M. Sustainable urban mobility indicators: Policy versus practice in the case of Greek cities. Transp. Res. Procedia 2017, 24, 304–312. [Google Scholar] [CrossRef]
- Hull, A. Policy integration: What will it take to achieve more sustainable transport solutions in cities? Transp. Policy 2008, 15, 94–103. [Google Scholar] [CrossRef]
- Guidemaps consortium. Successful Transport Decision-Making. A Project Management and Stakeholder Engagement Handbook; Fastcolour Limited: Brussels, Belgium, 2004. [Google Scholar]
- Hautala, R.; Karvonen, V.; Laitinen, J.; Laurikko, J.; Nylund, N.-O.; Pihlatie, M.; Rantasila, K.; Tuominen, A. Smart Sustainable Mobility; VTT Visions 5: Espoo, Finland, 2014. [Google Scholar]
- Macário, R. Upgrading quality in urban mobility systems. Manag. Ser. Qual. Int. J. 2001, 11, 93–99. [Google Scholar] [CrossRef]
- György, K.; Attila, A.; Tamás, F. New framework for monitoring urban mobility in European cities. Transp. Res. Procedia 2017, 24, 155–162. [Google Scholar] [CrossRef][Green Version]
- Uradni list Evropske unije, “Informacije in objave”. 2014. Available online: https://eur-lex.europa.eu/legal-content/SL/TXT/?uri=OJ:C:2014:271:TOC (accessed on 21 September 2017).
- Rupprecht Consult. Trajnostna mobilnost za uspešno prihodnost, Smernice za pripravo CPS.; Ministrstvo za infrastrukturo in prostor: Ljubljana, Slovenia, 2015.
- Bertolini, L.; Le Clerk, F.; Kapoen, L. Sustainable accessibility: A conceptual framework to integrate transport and land use plan-making. Two test-applications in the Netherlands and a reflection on the way forward. Transp. Policy 2005, 12, 207–221. [Google Scholar] [CrossRef]
- Mardani, A.; Zavadskas, E.K.; Khalifah, Z.; Jusoh, A.; Nor, K.M. Multiple criteria decision-making techniques in transportation systems: A systematic review of the state of the art literature. Transport 2015, 31, 359–385. [Google Scholar] [CrossRef]
- Rupprecht Consult (Ed.) Guidelines for Developing and Implementing a Sustainable Urban Mobility Plan, 2nd ed. Available online: https://www.eltis.org/mobility-plans/sump-guidelines (accessed on 10 June 2019).
- Pérez, J.C.; Carrillo, M.H.; Montoya-Torres, J.R. Multi-criteria approaches for urban passenger transport systems: A literature review. Ann. Oper. Res. 2015, 226, 69–87. [Google Scholar] [CrossRef]
- Sarasini, S.; Diener, D.; Sochor, J.; Vanacore, E. Stimulating a Transition to Sustainable Urban Mobility; JPI Urban Europe: Gothenburg, Sweden, 2018. [Google Scholar]
- Buhrmann, S.; Wefering, F.; Rupprecht, S.; Plevnik, A.; Mladenovič, L.; Balant, M.; Ružič, L. Trajnostna mobilnost za uspešno prihodnost: Smernice za pripravo Celostne prometne strategije; Ministrstvo za infrastrukturo in prostor RS: Ljubljana, Slovenia, 2012. [Google Scholar]
- Macharis, C.; Bernardini, A. Reviewing the use of Multi-Criteria Decision Analysis for the evaluation of transport projects: Time for a multi-actor approach. Transp. Policy 2015, 37, 177–186. [Google Scholar] [CrossRef]
- Janic, M. Multicriteria Evaluation of High-speed rail, Transrapid Maglev and Air Passenger Transport in Europe. Transp. Plan. Technol. 2003, 26, 491–512. [Google Scholar] [CrossRef]
- Duleba, S.; Moslem, S. Sustainable Urban Transport Development with Stakeholder Participation, an AHP-Kendall Model: A Case Study for Mersin. Sustainability 2018, 10, 3647. [Google Scholar] [CrossRef]
- Tsamboluas, D. A tool for prioritizing multinational transport infrastructure investments. Transp. Policy 2007, 14, 11–26. [Google Scholar] [CrossRef]
- Tsamboulas, D.; Yiotis, G.; Panou, K. Use of multicriteria methods for assessment of transport. J. Transp. Eng. 1999, 125, 407–414. [Google Scholar] [CrossRef]
- Hassan, M.N.; Hawas, Y.E.; Ahmed, K. A multidimensional framework for evaluating the transit service performance. Transp. Res. Part A Policy Pract. 2013, 50, 47–61. [Google Scholar] [CrossRef]
- Saaty, T. The Analytic Hierarchy Process; McGraw Hill Company: New York, NY, USA, 1980. [Google Scholar]
- Javanbarg, M.; Scawthorn, C.; Kiyono, J.; Shahbodaghkhan, B. Fuzzy AHP-based multicriteria decision making systems using particle swarm optimization. Expert Syst. Appl. 2012, 39, 960–966. [Google Scholar] [CrossRef]
- Kabir, G.; Hasin, A.A. Comparative analysis of AHP and Fuzzy AHP models for multicriteria inventory classification. Int. J. Fuzzy Log. Syst. 2011, 1, 1–16. [Google Scholar]
- Lupo, T. Strategic Analysis of Transit Service Quality Using Fuzzy AHP Methodology. Eur. Transp. 2013, 53, 1–18. [Google Scholar]
- Babashamsi, P.; Golzadfar, A.; Yusoff, N.I.M.; Ceylan, H.; Nor, N.G.M. Integrated fuzzy analytic hierarchy process and VIKOR method in the prioritization of pavement maintenance activities. Int. J. Pavement Res. Technol. 2016, 9, 112–120. [Google Scholar] [CrossRef]
- Lupo, T. Handling stakeholder uncertain judgments in strategic transport service analyses. Transp. Policy 2013, 29, 54–63. [Google Scholar] [CrossRef]
- Tadić, S.R.; Zečević, S.M.; Krstić, M.D. Ranking of logistics system scenarios for central business district. Promet Traffic Traffico. 2014, 26, 159–167. [Google Scholar] [CrossRef]
- John, A.; Paraskevadakis, D.; Bury, A.; Yang, Z.; Riahi, R.; Wang, J. An integrated fuzzy risk assessment for seaport operations. Saf. Sci. 2014, 68, 180–194. [Google Scholar] [CrossRef]
- Pashmakian, N.; Saeed Izadi, M. Optimizatized planning and location of under-subsurface parking on the southern side of the central area of Hamadan using AHP and GIS. Adv. Environ. Biol. 2014, 8, 328–343. [Google Scholar]
- Tuzkaya, U. Evaluating the environmental effects of transportation modes using an integrated methodology and an application. Int. J. Environ. Sci. Technol. 2009, 6, 277–290. [Google Scholar] [CrossRef]
- Krueger, R.; Casey, M. Focus Groups: A Practical Guide for Applied Research, 4th ed.; Sage Publications: Thousand Oaks, CA, USA, 2009. [Google Scholar]
- Powell, R.; Single, H. Focus groups. Int. J. Qual. Health Care 1996, 8, 299–504. [Google Scholar] [CrossRef]
- Dilshad, R.M.; Latif, M.I. Focus Group Interview as a Tool for Qualitative Research: An Analysis. Pak. J. Soc. Sci. 2013, 33, 191–198. [Google Scholar]
- McClelland, S. Training Needs Assessment Data-gathering Methods: Part 3, Focus Groups. J. Eur. Ind. Train. 1994, 18, 29–32. [Google Scholar] [CrossRef]
- Kramar, U.; Cvahte, T.; Sternad, M.; Topolšek, D. Designing a strategic mobility plan for a small and medium sized ities using a multi-stage methodology: Case of Celje. Spatium 2015, 33, 47–54. [Google Scholar] [CrossRef]
- Kress, V.E.; Shoffner, M. Focus Groups: A Practical and Applied Research Approach for Counselors. J. Couns. Dev. 2007, 85, 189–195. [Google Scholar] [CrossRef]
- Barry, M.-L.; Steyn, H.; Brent, A. The Use of the Focus Group Technique in Management Research: The Example of Renewable Energy Technology Selection in Africa. J. Contemp. Manag. 2009, 6, 229–240. [Google Scholar]
- Weng, W.-H.; Lin, W.-T. Development Assessment and Strategy Planning in Cloud Computing Industry. Int. J. Electron. Commer. Stud. 2014, 5, 257–266. [Google Scholar] [CrossRef]
- Harvey, N.; Holmes, C.A. Nominal group technique: An effective method for obtaining group consensus. Int. J. Nurs. Pract. 2012, 18, 188–194. [Google Scholar] [CrossRef]
- Van Teijlingen, R.; Pitchforth, E. Delphi method and nominal group techniques in family planning and reproductive health research. J. Fam. Plan. Reprod. Health Car 2006, 32, 249–252. [Google Scholar] [CrossRef]
- Ghazinoory, S.; Abdi, M.; Azadegan-Mehr, M. SWOT Methodology: A State-Of-The-Art Review For The Past, A Framework For The Future. J. Bus. Econ. Manag. 2011, 12, 24–48. [Google Scholar] [CrossRef]
- Yuan, H. A SWOT analysis of successful construction waste management. J. Clean. Prod. 2013, 39, 1–8. [Google Scholar] [CrossRef]
- Catron, J.; Stainback, A.; Dwivedi, P.; Lhotka, J.M. Bioenergy development in Kentucky: A SWOT-ANP analysis. For. Policy Econ. 2013, 28, 38–43. [Google Scholar] [CrossRef]
- Kotler, P. Marketing Management: Analysis, Planning, Implementation and Control, 6th ed.; Prentice-Hall: Englewood Cliffs, NJ, USA, 1988. [Google Scholar]
- Bull, J.W.; Jobstvogt, N.; Böhnke-Henrichs, A.; Mascarenhas, A.; Sitas, N.; Baulcomb, C.; Labmini, C.K.; Rawlins, M.; Baral, H.; Zähringer, J.; et al. Strengths, Weaknesses, Opportunities and Threats A SWOT analysis of ecosystems services framework. Ecosyst. Serv. 2016, 17, 99–111. [Google Scholar] [CrossRef]
- Phadermrod, B.; Crowder, R.M.; Wills, G.B. Importance-Performance Analysis based SWOT analysis. Int. J. Inf. Manag. 2019, 44, 194–203. [Google Scholar] [CrossRef]
- Hill, T.; Westbrook, R. SWOT Analysis: It’s Time for a Product Recall. Long Range Plan. 1997, 30, 46–52. [Google Scholar] [CrossRef]
- Pickton, D.W.; Wright, S. SWOT Analysis—Its Role in Strategic and Management Development in SMEs. In Small Business and Enterprise Development Conference; Sheffield University: Sheffield, UK, 1997. [Google Scholar]
- Wickramasinghe, V.; Takano, S. Application of Combined SWOT and Analytic Hierarchy Process (AHP) for Tourism Revival Strategic Marketing Planning: A Case of Sri Lanka Tourism. J. East. Asia Soc. Transp. Stud. 2009, 8, 954–969. [Google Scholar]
- Tavana, M.; Zereinejad, M.; Di Caprio, D.; Kaviani, M. An integrated intuitionistic fuzzy AHP and SWOT method for outsourcing reverse logistics. Appl. Soft Comput. J. 2016, 40, 544–557. [Google Scholar] [CrossRef]
- Ekmekçioglu, M.; Can Kutlu, A.; Kahraman, C. A fuzzy multi-criteria swot analysis: An application to nuclear power plant site selection. Int. J. Comput. Intell. Syst. 2011, 4, 583–595. [Google Scholar] [CrossRef]
- Ren, J.; Dong, L.; Sun, L.; Goodsite, M.; Dong, L.; Luo, X.; Savacool, K.B. “Supply push” or “demand pull?”: Strategic recommendations for the responsible development of biofuel in China. Renew. Sustain. Energy Rev. 2015, 52, 382–392. [Google Scholar] [CrossRef]
- Felice, F.; Petrillo, A. Hierarchical model to optimize performance in logistics policies: Multi attribute analysis. Procedia Soc. Behav. Sci. 2012, 58, 1555–1564. [Google Scholar] [CrossRef]
- Saaty, T.; Vargas, L.V. Models, Methods, Concepts & Applications of the Analytic Hierarchy Proces, 2nd ed.; Springer Science+Business Media: New York, NY, USA, 2012. [Google Scholar]
- Gao, S.; Zhang, Z.; Cao, C. Calculating Weights Methods in Complete Matrices and Incomplete Matrices. J. Softw. 2010, 5, 304–311. [Google Scholar] [CrossRef][Green Version]
- Brunelli, M. Introduction to the Analytic Hierarchy Process; SpringerBriefs in Operations Research: Cham, Germany, 2015. [Google Scholar]
- Ishizaka, A.; Nemery, P. Multi-Criteria Decision Analysis. Methods and Software; John Wiley & Sons, Ltd.: Chichester, UK, 2013. [Google Scholar]
- Mangalathu, G.; Shanmugam, S.; Sankaranarayanasamy, K. System Safety in Lpg Fired Furnace—A Multi Criteria Decision Making Technique. Adv. Prod. Eng. Manag. 2012, 7, 123–134. [Google Scholar]
- Ayhan, M.B. A Fuzzy AHP Approach for Supplier Selection Problem: A Case Study in a Gearmotor Company. Int. J. Manag. Value Supply Chain. 2013, 4, 11–23. [Google Scholar] [CrossRef]
- Lee, A.H.I.; Chen, W.-C.; Chang, C.-J. A fuzzy AHP and BSC approach for evaluating performance of IT department in the manufacturing industry in Taiwan. Expert Syst. Appl. 2008, 34, 96–107. [Google Scholar] [CrossRef]
- Sun, C.-C. A performance evaluation model by integrating fuzzy AHP and fuzzy TOPSIS methods. Expert Syst. Appl. 2010, 37, 7745–7754. [Google Scholar] [CrossRef]
- Chen, C.-F.; Lee, C.-L. Determining the attribute weights of professional conference organizer selection an application of the fuzzy AHP approach. Tour. Econ. 2011, 17, 1129–1139. [Google Scholar] [CrossRef]
- Wang, T.; Chen, Y. Applying fuzzy linguistic preference relations to the improvement of consistency of fuzzy AHP. Inf. Sci. 2008, 178, 3755–3765. [Google Scholar] [CrossRef]
- Vinodh, S.; Prasanna, M.; Prakash, N. Integrated Fuzzy AHP–TOPSIS for selecting the best plastic recycling method: A case study. Appl. Math. Model. 2014, 38, 4662–4672. [Google Scholar] [CrossRef]
- Hsieh, T.-Y.; Lu, S.-T.; Tzeng, G.-H. Fuzzy MCDM approach for planning and design tenders selection in public office buildings. Int. J. Proj. Manag. 2004, 22, 573–584. [Google Scholar] [CrossRef]
- Huang, H.-C.; Ho, C.-C. Applying the Fuzzy Analytic Hierarchy Process to Consumer Decision-Making Regarding Home Stays. Int. J. Adv. Comput. Technol. 2013, 5, 981–990. [Google Scholar]
- Buckley, J. Fuzzy Hierarchical Analysis. Fuzzy Sets Syst. 1985, 17, 233–247. [Google Scholar] [CrossRef]
- Emrouznejad, A.; Ho, W. Fuzzy Analytic Hierarchy Process; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Husain, S.; Ahmad, Y.; Sharma, M.; Ali, S. Comparative Analysis of Defuzzification Approaches from an Aspect of Real life problem. IOSR J. Comput. Eng. 2017, 19, 19–25. [Google Scholar]
- Patel, A.; Mohan, B. Some numerical aspects of center of area defuzzi!cation method. Fuzzy Sets Syst. 2002, 132, 401–409. [Google Scholar] [CrossRef]
- Tzeng, G.-H.; Huang, J.-J. Multiple Attribute Decision Making. methods and applications; Taylor & Francis Group: Boca Raton, FL, USA, 2011. [Google Scholar]
- Lu, S.-T.; Yu, S.-H.; Chang, D.-S.; Su, S.-C. Using the Fuzzy Linguistic Preference Relation Approach for Assessing the Importance of Risk Factors in a Software Development Project. Hindawi Publ. Corp. Math. Probl. Eng. 2013, 2013, 376375. [Google Scholar] [CrossRef]
- Ross, T. Fuzzy Logic with Engineering Applications, 3rd ed.; John Wiley & Sons Ltd.: Chichester/West Sussex, UK, 2010. [Google Scholar]
- Sugeno, M. An Introductory survey on fuzzy control. Inf. Sci. 1985, 36, 59–83. [Google Scholar] [CrossRef]
- Chakraborty, D.; Guha, D. Addition of Two Generalized Fuzzy Numbers. Int. J. Ind. Math. 2010, 2, 9–20. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).