A Unified Approach to Efficiency Decomposition for a Two-Stage Network DEA Model with Application of Performance Evaluation in Banks and Sustainable Product Design
Abstract
1. Introduction
2. Two-Stage Process
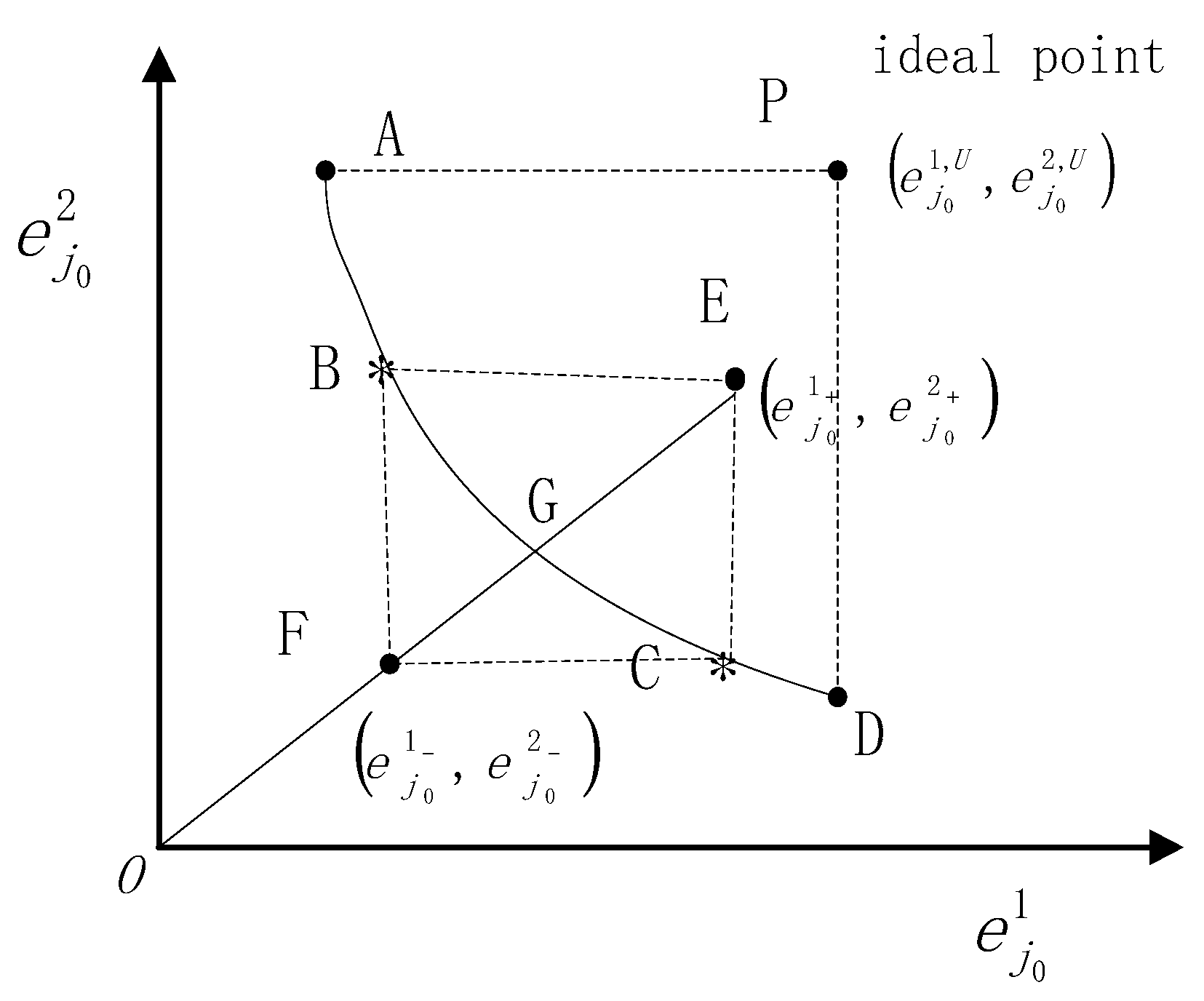
3. Geometric Properties of Pareto Front
4. Rank-Based Efficiency Decomposition Approach
5. Comparison of Different Efficiency Decomposition Methods
5.1. Priority Decomposition Method
5.2. Uniform Efficiency Decomposition Method
6. Empirical Tests
6.1. Performance Evaluation of Banking
6.2. Performance Evaluation of Sustainable Designs
7. Concluding Remarks
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Proofs
Appendix A.1.1. The Proof of the Lemma
Appendix A.1.2. The Proof of the Theorem
Appendix A.2. Datasets
| DMU | Branch | EM (103) | FA (¥108) | EX (¥108) | CR (¥108) | IL (¥108) | LO (¥108) | PR (¥108) |
|---|---|---|---|---|---|---|---|---|
| 1 | Maanshan | 0.4775 | 0.526 | 0.3848 | 49.9174 | 5.4613 | 34.9897 | 0.843 |
| 2 | Anqing | 1.2363 | 0.713 | 0.5547 | 37.4954 | 4.0825 | 20.6013 | 0.4864 |
| 3 | Huangshan | 0.446 | 0.443 | 0.3419 | 20.9846 | 0.6897 | 8.6332 | 0.1288 |
| 4 | Fuyang | 1.2481 | 0.638 | 0.4574 | 45.0508 | 1.7237 | 9.2354 | 0.3019 |
| 5 | Suzhou | 0.705 | 0.575 | 0.4036 | 38.1625 | 2.2492 | 12.0171 | 0.3138 |
| 6 | Chuzhou | 0.6446 | 0.432 | 0.4012 | 30.1676 | 2.3354 | 13.813 | 0.3772 |
| 7 | Luan | 0.7239 | 0.51 | 0.3709 | 26.5391 | 1.3416 | 5.0961 | 0.1453 |
| 8 | Chizhou | 0.3363 | 0.322 | 0.2334 | 16.1235 | 0.4889 | 5.9803 | 0.0928 |
| 9 | Chaozhou | 0.6678 | 0.423 | 0.3471 | 22.1848 | 1.1767 | 9.2348 | 0.2002 |
| 10 | Bozhou | 0.3418 | 0.256 | 0.1594 | 13.4364 | 0.4064 | 2.5326 | 0.0057 |
| Vehicle Manufacturer Name | Test Vehicle ID | Cid | Rhp | n/v Ratio | Axle | Etw | Mpg | Hc | CO | CO2 | Nox |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Land Rover | LBDVP001 | 122.04749 | 240 | 30.6 | 3.75 | 4500 | 21.8 | 0.04564 | 0.6178 | 406.99 | 0.0012 |
| Land Rover | 0AVP0002 | 305.11872 | 375 | 31 | 3.54 | 6000 | 15.3 | 0.01596 | 0.2238 | 576.48 | 0.0181 |
| Land Rover | LKDTT066 | 305.11872 | 375 | 23.9 | 3.21 | 5500 | 16.8 | 0.01342 | 0.1923 | 531.45 | 0.0114 |
| Land Rover | 3CTTP036 | 122.04749 | 240 | 30.5 | 3.75 | 4250 | 24.6 | 0.0169 | 0.1359 | 362.42 | 0.0078 |
| Land Rover | VX10HWS | 305.11872 | 375 | 32.5 | 3.54 | 6000 | 15.6 | 0.014 | 0.17 | 570.95 | 0.012 |
| Land Rover | 0AVP0049 | 305.11872 | 510 | 32.5 | 3.54 | 6000 | 14.4 | 0.01689 | 0.3361 | 612.43 | 0.0066 |
| Land Rover | LKDTT065 | 305.11872 | 510 | 24.1 | 3.21 | 6000 | 15.7 | 0.02768 | 0.2859 | 565.05 | 0.0112 |
| Maserati | 48675 | 286.8116 | 444 | 32.1 | 3.73 | 4750 | 15.75 | 0.0405 | 0.6305 | 566.841 | 0.017 |
| Maserati | 45367 | 286.8116 | 454 | 30.5 | 3.54 | 4500 | 15.8 | 0.018 | 0.469 | 564.07 | 0.008 |
| Maserati | ZAMJK39A690027157 | 286.8116 | 424 | 31.4 | 3.54 | 4750 | 14.25 | 0.017 | 0.346 | 621.803 | 0.008 |
| VPG | 523MF1163BM000007 | 194.78779 | 240 | 33.3 | 4.06 | 5000 | 19.8 | 0.018 | 0.27 | 441 | 0.022 |
| VPG | 523MF1267BT000001 | 280.70922 | 248 | 28.4 | 3.45 | 5250 | 15.55 | 0.12011 | 2.17351 | 565.85 | 0.0341 |
References
- Charnes, A.; Cooper, W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Kou, G.; Peng, Y.; Wang, G. Evaluation of clustering algorithms for financial risk analysis using MCDM methods. Inf. Sci. 2014, 275, 1–12. [Google Scholar] [CrossRef]
- Li, G.; Kou, G.; Peng, Y. A Group Decision Making Model for Integrating Heterogeneous Information. IEEE Trans. Syst. Man, Cybern. Syst. 2018, 48, 982–992. [Google Scholar] [CrossRef]
- Zhang, H.; Kou, G.; Peng, Y. Soft consensus cost models for group decision making and economic interpretations. Eur. J. Oper. Res. 2019, 277, 964–980. [Google Scholar] [CrossRef]
- Cook, W.D.; Liang, L.; Zhu, J. Measuring performance of two-stage network structures by DEA: A review and future perspective. Omega 2010, 38, 423–430. [Google Scholar] [CrossRef]
- Halkos, G.E.; Tzeremes, N.G.; Kourtzidis, S.A. A unified classification of two-stage DEA models. Surv. Oper. Res. Manag. Sci. 2014, 19, 1–16. [Google Scholar] [CrossRef]
- Chen, Y.; Cook, W.D.; Li, N.; Zhu, J. Additive efficiency decomposition in two-stage DEA. Eur. J. Oper. Res. 2009, 196, 1170–1176. [Google Scholar] [CrossRef]
- Färe, R.; Grosskopf, S. Productivity and intermediate products: A frontier approach. Econ. Lett. 1996, 50, 65–70. [Google Scholar] [CrossRef]
- Du, J.; Liang, L.; Chen, Y.; Cook, W.D.; Zhu, J. A bargaining game model for measuring performance of two-stage network structures. Eur. J. Oper. Res. 2011, 210, 390–397. [Google Scholar] [CrossRef]
- Seiford, L.M.; Zhu, J. Profitability and Marketability of the Top 55 U.S. Commercial Banks. Manag. Sci. 1999, 45, 1270–1288. [Google Scholar] [CrossRef]
- Zhu, J. Multi-factor performance measure model with an application to Fortune 500 companies. Eur. J. Oper. Res. 2000, 123, 105–124. [Google Scholar] [CrossRef]
- Mardani, A.; Zavadskas, E.K.; Streimikiene, D.; Jusoh, A.; Khoshnoudi, M. A comprehensive review of data envelopment analysis (DEA) approach in energy efficiency. Renew. Sustain. Energy Rev. 2017, 70, 1298–1322. [Google Scholar] [CrossRef]
- Sueyoshi, T.; Yuan, Y.; Goto, M. A literature study for DEA applied to energy and environment. Energy Econ. 2017, 62, 104–124. [Google Scholar] [CrossRef]
- An, Q.; Wang, Z.; Ali, E.; Zhu, Q.; Zhu, X. Efficiency evaluation of parallel interdependent processes systems: An application to Chinese 985 Project universities. Int. J. Prod. Res. 2018, 1–13. [Google Scholar] [CrossRef]
- Wu, J.; Zhu, Q.; Chu, J.; An, Q.; Liang, L. A DEA based approach for allocation of emission reduction tasks. Int. J. Prod. Res. 2016, 54, 5618–5633. [Google Scholar] [CrossRef]
- Zhou, H.; Yang, H.; Chen, Y.; Zhu, J. Data envelopment analysis application in sustainability: The origins, development and future directions. Eur. J. Oper. Res. 2018, 264, 1–16. [Google Scholar] [CrossRef]
- Hwang, S.-N.; Chen, C.; Chen, Y.; Lee, H.-S.; Shen, P.-D. Sustainable design performance evaluation with applications in the automobile industry: Focusing on inefficiency by undesirable factors. Omega 2013, 41, 553–558. [Google Scholar] [CrossRef]
- Chen, C.; Zhu, J.; Yu, J.-Y.; Noori, H. A new methodology for evaluating sustainable product design performance with two-stage network data envelopment analysis. Eur. J. Oper. Res. 2012, 221, 348–359. [Google Scholar] [CrossRef]
- Liang, L.; Cook, W.D.; Zhu, J. DEA models for two-stage processes: Game approach and efficiency decomposition. Nav. Res. Logist. 2008, 55, 643–653. [Google Scholar] [CrossRef]
- Kao, C.; Hwang, S.-N. Efficiency decomposition in two-stage data envelopment analysis: An application to non-life insurance companies in Taiwan. Eur. J. Oper. Res. 2008, 185, 418–429. [Google Scholar] [CrossRef]
- Kao, C. Efficiency decomposition and aggregation in network data envelopment analysis. Eur. J. Oper. Res. 2016, 255, 778–786. [Google Scholar] [CrossRef]
- Kao, C. Efficiency decomposition for general multi-stage systems in data envelopment analysis. Eur. J. Oper. Res. 2014, 232, 117–124. [Google Scholar] [CrossRef]
- Zhou, Z.; Sun, L.; Yang, W.; Liu, W.; Ma, C. A bargaining game model for efficiency decomposition in the centralized model of two-stage systems. Comput. Ind. Eng. 2013, 64, 103–108. [Google Scholar] [CrossRef]
- Li, H.; Chen, C.; Cook, W.D.; Zhang, J.; Zhu, J. Two-stage network DEA: Who is the leader? Omega 2018, 74, 15–19. [Google Scholar] [CrossRef]
- Amin, G.R.; Toloo, M. A polynomial-time algorithm for finding ε in DEA models. Comput. Oper. Res. 2004, 31, 803–805. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W. Programming with linear fractional functionals. Nav. Res. Logist. Q. 1962, 9, 181–186. [Google Scholar] [CrossRef]
- AlHassany, H.; Faisal, F. Factors influencing the internet banking adoption decision in North Cyprus: an evidence from the partial least square approach of the structural equation modeling. Financ. Innov. 2018, 4, 29. [Google Scholar] [CrossRef]
- Tang, Y.; Moro, A.; Sozzo, S.; Li, Z. Modelling trust evolution within small business lending relationships. Financ. Innov. 2018, 4, 19. [Google Scholar] [CrossRef]
- Asongu, S.A.; Odhiambo, N.M. Size, efficiency, market power, and economies of scale in the African banking sector. Financ. Innov. 2019, 5, 4. [Google Scholar] [CrossRef]
- Kou, G.; Chao, X.; Peng, Y.; Alsaadi, F.E.; Herrera-Viedma, E. MACHINE LEARNING METHODS FOR SYSTEMIC RISK ANALYSIS IN FINANCIAL SECTORS. Technol. Econ. Dev. Econ. 2019, 1–27. [Google Scholar] [CrossRef]
- China Construction Bank (Anhui Branch). Annual Report 2004 of China Construction Bank in Anhui Province. 2004. Available online: http://www.ccb.com/cn/uploads/1-26.1118369283972.pdf (accessed on 14 June 2019). (In Chinese).
- United States Environmental Protection Agency. Certification Emission Test Data. 2013. Available online: https://www.epa.gov/ (accessed on 14 June 2019).

| Stage 1 | Stage 2 | Stage 1 | Stage 2 | ||||
|---|---|---|---|---|---|---|---|
| DMU | Overall | CCR | CCR | ||||
| 1 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| 2 | 0.4344 | 0.5526 | 0.5541 | 0.7838 | 0.7861 | 0.5541 | 0.7861 |
| 3 | 0.2930 | 0.2930 | 0.4991 | 0.5869 | 1.0000 | 0.4991 | 1.0000 |
| 4 | 0.3013 | 0.3209 | 0.7593 | 0.3968 | 0.9389 | 0.7593 | 0.9699 |
| 5 | 0.3549 | 0.4304 | 0.7289 | 0.4869 | 0.8246 | 0.7289 | 0.8334 |
| 6 | 0.5448 | 0.5448 | 0.7359 | 0.7404 | 1.0000 | 0.7359 | 1.0000 |
| 7 | 0.1788 | 0.2881 | 0.5516 | 0.3242 | 0.6206 | 0.5516 | 0.6316 |
| 8 | 0.2818 | 0.3052 | 0.5325 | 0.5291 | 0.9232 | 0.5325 | 1.0000 |
| 9 | 0.3282 | 0.3845 | 0.5526 | 0.5939 | 0.8535 | 0.5526 | 1.0000 |
| 10 | 0.1747 | 0.3722 | 0.6498 | 0.2689 | 0.4695 | 0.6498 | 0.4979 |
| Stage 1 | Stage 2 | Stage 1 | Stage 2 | |
|---|---|---|---|---|
| DMU | CCR | CCR | BG model | BG model |
| 1 | 1(1) | 1(1) | 1.0000(1) | 1(1) |
| 2 | 0.5541(6) | 0.7861(8) | 0.5534(4) | 0.785(3) |
| 3 | 0.4991(10) | 1(1) | 0.3824(10) | 0.7661(4) |
| 4 | 0.7593(2) | 0.9699(6) | 0.4936(5) | 0.6104(8) |
| 5 | 0.7289(4) | 0.8334(7) | 0.5601(3) | 0.6337(7) |
| 6 | 0.7359(3) | 1(1) | 0.6332(2) | 0.8605(2) |
| 7 | 0.5516(8) | 0.6316(9) | 0.3987(9) | 0.4485(9) |
| 8 | 0.5325(9) | 1(1) | 0.4032(8) | 0.6989(6) |
| 9 | 0.5526(7) | 1(1) | 0.461(7) | 0.749(5) |
| 10 | 0.6498(5) | 0.4979(10) | 0.4918(6) | 0.3553(10) |
| RD = 10 | RD = 20 |
| Stage 1 | Stage 2 | Stage 1 | Stage 2 | Stage 1 | Stage 2 | |
|---|---|---|---|---|---|---|
| DMU | M = 1 | M = 1 | M = 2 | M = 2 | M = 3 | M = 3 |
| 1 | 1(1) | 1(1) | 1(1) | 1(1) | 1(1) | 1(1) |
| 2 | 0.5534(5) | 0.7848(4) | 0.5535(5) | 0.7848(5) | 0.5536(6) | 0.7847(6) |
| 3 | 0.3484(10) | 0.841(3) | 0.3326(10) | 0.8808(3) | 0.3237(10) | 0.905(3) |
| 4 | 0.5633(4) | 0.5349(8) | 0.6062(3) | 0.497(8) | 0.6343(2) | 0.475(8) |
| 5 | 0.5905(3) | 0.601(7) | 0.6123(2) | 0.5796(7) | 0.6284(3) | 0.5648(7) |
| 6 | 0.6081(2) | 0.8959(2) | 0.5939(4) | 0.9173(2) | 0.5848(4) | 0.9316(2) |
| 7 | 0.4068(8) | 0.4396(9) | 0.4142(8) | 0.4317(9) | 0.421(7) | 0.4247(9) |
| 8 | 0.3659(9) | 0.7702(5) | 0.3486(9) | 0.8084(4) | 0.3388(9) | 0.8316(4) |
| 9 | 0.4345(7) | 0.7553(6) | 0.4214(7) | 0.7788(6) | 0.4137(8) | 0.7934(5) |
| 10 | 0.5242(6) | 0.3333(10) | 0.5463(6) | 0.3199(10) | 0.562(5) | 0.3109(10) |
| RD | 6 | 18 | 6 | 16 | 4 | 17 |
| Stage 1 | Stage 2 | Stage 1 | Stage 2 | Stage 1 | Stage 2 | |
|---|---|---|---|---|---|---|
| DMU | M = 4 | M = 4 | M = 5 | M = 5 | M = 6 | M = 6 |
| 1 | 1(1) | 1(1) | 1(1) | 1(1) | 1(1) | 1(1) |
| 2 | 0.5536(6) | 0.7846(6) | 0.5536(6) | 0.7846(6) | 0.5537(6) | 0.7845(6) |
| 3 | 0.3181(10) | 0.9211(3) | 0.3141(10) | 0.9326(3) | 0.3113(10) | 0.9412(3) |
| 4 | 0.6539(2) | 0.4608(8) | 0.6682(2) | 0.4509(8) | 0.6792(2) | 0.4436(8) |
| 5 | 0.6407(3) | 0.5539(7) | 0.6504(3) | 0.5456(7) | 0.6583(3) | 0.5392(7) |
| 6 | 0.5785(4) | 0.9417(2) | 0.574(5) | 0.9492(2) | 0.5705(5) | 0.955(2) |
| 7 | 0.4272(7) | 0.4186(9) | 0.433(7) | 0.413(9) | 0.4382(7) | 0.4081(9) |
| 8 | 0.3326(9) | 0.8471(4) | 0.3284(9) | 0.8582(4) | 0.3252(9) | 0.8664(4) |
| 9 | 0.4086(8) | 0.8033(5) | 0.405(8) | 0.8104(5) | 0.4023(8) | 0.8157(5) |
| 10 | 0.5737(5) | 0.3046(10) | 0.5827(4) | 0.2999(10) | 0.5899(4) | 0.2962(10) |
| RD | 4 | 14 | 6 | 14 | 6 | 14 |
| Stage 1 | Stage 2 | Stage 1 | Stage 2 | ||||
|---|---|---|---|---|---|---|---|
| DMU | Overall | CCR | CCR | ||||
| 1 | 0.8891 | 0.9475 | 0.9633 | 0.9229 | 0.9383 | 0.9475 | 1 |
| 2 | 0.8127 | 0.9295 | 0.9295 | 0.8742 | 0.8742 | 0.9735 | 1 |
| 3 | 0.9171 | 0.9171 | 0.9171 | 1 | 1 | 1 | 0.9951 |
| 4 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 5 | 0.8791 | 0.9295 | 0.9295 | 0.9457 | 0.9457 | 1 | 1 |
| 6 | 0.8134 | 1 | 1 | 0.8134 | 0.8134 | 1 | 1 |
| 7 | 0.7593 | 0.9413 | 0.9413 | 0.8067 | 0.8067 | 1 | 0.99 |
| 8 | 0.7119 | 1 | 1 | 0.7119 | 0.7119 | 1 | 0.9787 |
| 9 | 0.7579 | 1 | 1 | 0.7579 | 0.7579 | 1 | 0.986 |
| 10 | 0.7134 | 0.9734 | 0.9734 | 0.7328 | 0.7328 | 0.9741 | 0.996 |
| 11 | 0.9291 | 0.98 | 0.98 | 0.9481 | 0.9481 | 1 | 1 |
| 12 | 0.6552 | 0.8958 | 0.8958 | 0.7314 | 0.7314 | 0.9456 | 0.9924 |
| R-B model | |||
|---|---|---|---|
| DMU1 | Stage 1 | Stage 2 | RD |
| M = 1 | 0.9529 | 0.9330 | 8 |
| M = 2 | 0.9517 | 0.9343 | 8 |
| M = 3 | 0.9509 | 0.9350 | 8 |
| M = 4 | 0.9503 | 0.9356 | 8 |
| BG model | 0.9554 | 0.9306 | 8 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Xiong, J.; Xie, J.; Zhou, Z.; Zhang, J. A Unified Approach to Efficiency Decomposition for a Two-Stage Network DEA Model with Application of Performance Evaluation in Banks and Sustainable Product Design. Sustainability 2019, 11, 4401. https://doi.org/10.3390/su11164401
Li H, Xiong J, Xie J, Zhou Z, Zhang J. A Unified Approach to Efficiency Decomposition for a Two-Stage Network DEA Model with Application of Performance Evaluation in Banks and Sustainable Product Design. Sustainability. 2019; 11(16):4401. https://doi.org/10.3390/su11164401
Chicago/Turabian StyleLi, Haitao, Jie Xiong, Jianhui Xie, Zhongbao Zhou, and Jinlong Zhang. 2019. "A Unified Approach to Efficiency Decomposition for a Two-Stage Network DEA Model with Application of Performance Evaluation in Banks and Sustainable Product Design" Sustainability 11, no. 16: 4401. https://doi.org/10.3390/su11164401
APA StyleLi, H., Xiong, J., Xie, J., Zhou, Z., & Zhang, J. (2019). A Unified Approach to Efficiency Decomposition for a Two-Stage Network DEA Model with Application of Performance Evaluation in Banks and Sustainable Product Design. Sustainability, 11(16), 4401. https://doi.org/10.3390/su11164401




