Abstract
In this paper, the problem of the Optimal Reactive Power Flow (ORPF) in the Algerian Western Network with 102 nodes is solved by the sequential hybridization of metaheuristics methods, which consists of the combination of both the Genetic Algorithm (GA) and the Particle Swarm Optimization (PSO). The aim of this optimization appears in the minimization of the power losses while keeping the voltage, the generated power, and the transformation ratio of the transformers within their real limits. The results obtained from this method are compared to those obtained from the two methods on populations used separately. It seems that the hybridization method gives good minimizations of the power losses in comparison to those obtained from GA and PSO, individually, considered. However, the hybrid method seems to be faster than the PSO but slower than GA.
1. Introduction
The objective of any company producing and distributing electrical energy is to ensure that the required power is available at all points and at all times. This electrical energy is produced at the same time as it is consumed; therefore, at all times, production must be adapted to consumption. It is therefore necessary to adjust the active and reactive powers of the interconnected generators in an electrical grid within their permissible limits in order to satisfy the fluctuating electrical load while maintaining the various parts of the grid at stable voltages. This is called the optimal load distribution of OPF (Optimal Power Flow) and is sometimes known as the economic dispatching problem of power flow. It was addressed in these works [1].
The Problem of Optimal Power Flow (OPF) is a non-linear optimization problem, proposed by Carpenter in the early 1960s and based on the economic distribution of reactive power. It was addressed in these works [1].
The optimal reactive power flow or optimal reactive power distribution (ORPF) is a special case of the optimal power flow in which the active energy control means are fixed while the reactive energy control means are adjustable. It was addressed in these works [1].
ORPF has usually been considered as the minimization of an objective function representing active losses in power grids. The constraints involved are the physical laws governing power generation–transmission systems and the operating limitations of the equipment. The already used optimization methods to solve the ORPF problem are numerous, such as conventional deterministic methods that are good for objective quadratic functions with a single optimum. These methods have the disadvantage of not guaranteeing global convergence since they can converge towards one of these local optimums and stop and sometimes even diverge.
Besides, they are sometimes inconsistent and imprecise. The quality of the results is therefore dependent on the quality of the data available [2].
New metaheuristic methods have emerged that provide a solution to the problems of conventional methods; these methods are based on the natural evolution of biology such as the Genetic Algorithm method (GA) [3] and the Particle Swarm Optimization method (PSO) [4], which have already been used in the ORPF resolution in the work of [5,6,7,8,9,10]. The improvement of these methods can always be achieved through hybridization between them, which combines different concepts and components of different metaheuristics [11] and, to this end, attempts to merge the strengths and eliminate the weaknesses of these methods.
Until now, several hybridizations between the metaheuristic methods with population GA and PSO and other metaheuristic methods with local research such as simulated annealing, taboo research, have been applied to solve the problem of ORPF such as the work of [6,7].
In this article, it is proposed to solve the problem of optimal reactive power flow (ORPF) for the Western Algerian network by using the sequential hybridization method of the two population-based metaheuristic techniques, namely, the Genetic Algorithm and the Optimization Particle Swarm, to improve the results obtained by each method individually.
A hybrid method may seem interesting depending on the choice and role of its components. To define an effective hybrid method, it is necessary to know a good characterization of the advantages and limitations of each method [12].
The purpose of this study is to determine how the combination of two-particle techniques within hybridization could lead to some interesting characteristics in relation to each technique considered alone.
This document is organized as follows:
In the following section, the metaheuristic methods (GA, PSO) and the sequential hybridization of metaheuristic methods were presented. A brief overview of the ORPF problem function is provided in Section 3.
In Section 4, an application of the methods was carried out on the International Explorer Electrical Engineering IEEE 14 nodes network to verify the effectiveness of the program, then an application on the Western Algerian network to solve the ORPF problem and the discussion and analysis of the numerical results obtained. Finally, the conclusion is in Section 5.
2. Metaheuristic Methods and Their Hybridization
The metaheuristics are stochastic algorithms which progress towards an optimum by a sampling of an objective function. They are generic methods being able to treat a broad range of different problems without requiring deep changes in the used algorithm. They appear of great effectiveness to provide approximate solutions of good quality for a large number of classical problems of optimization and real applications of big sizes. For these reasons, their investigations are in full development [13].
2.1. The Genetic Algorithms
The genetic algorithms belong to the class of the evolutionary algorithms (metaheuristics with population). They consist of working simultaneously with a set of solutions that we make evolve gradually. The use of several solutions together makes it possible to naturally improve exploration of the space of the configurations; their goal is to obtain an approached solution with a problem of optimization. They use three genetic operations—selection, crossover, and mutation—to transform an initial population of chromosomes in the objective to improve their quality. To carry out these phases of reproduction, it is necessary to code the individuals of the population [3,5,14].
2.2. Particle Swarm Optimization
Particle Swarm Optimization (PSO) was first introduced by Eberhart and Kennedy [4]. This algorithm belongs to the family of evolutionary algorithms. It is inspired by the behavior of the great regroupings of animals such as the clouds of birds, the fish’s benches and the swarms of locusts. It is based in particular on a model developed by Reynolds at the end of 1980 making it possible to simulate the displacement of a group of birds. It was addressed in these works [7].
2.3. Sequential Hybridization of Metaheuristics
Hybridization is a trend observed in many works completed on metaheuristics these ten last years. It makes it possible to benefit from the advantages cumulated from different metaheuristics. The origins of the hybrid algorithms of metaheuristics return to the work of Glover. It was addressed in these works [13].
A hybrid method is a research method that used at least two distinct search methods [11,12].
It is possible to hybrid all the metaheuristics methods. In practice, the preoccupation with performance or the constraints of computer resource is limiting the possibilities of hybridization. It is thus necessary to be careful in the choice of the methods used in order to obtain good cooperation between the various components of the hybrid method [11,12].
There exist several types of hybridization such as sequential, parallel, and integrative ones.
The sequential hybridization is the most popular. It consists of applying several methods in such a manner that the results of a given method are taken as initial solutions to the next method [11,12].
In this study, we propose the technique of sequential hybridization, which consists of the combination [13] of both the genetic algorithm and the particles swarm optimization.
3. Mathematics Setting
The problem of the optimal reactive power flow is relevant to the optimization process of the reactive power. It consists of minimizing a definite nonlinear objective function with nonlinear constraints. In our situation, the objective function represents the active power losses in the electrical network given by:
where Gij is the conductance between the i-th and j-th nodes, the voltage at the i-th node, θi is the angle at the i-th node, and θij = θi − θj. The sum in relation (1) runs over the total number of nodes n.
The constraints of equality represent a balance between the production and the consumption, i.e.;
and
where Bij is the susceptance of the pair of nodes i and j, and, and the active powers generated and consumed at i-th node, respectively. and are, respectively, the generated and consumed reactive powers at the i-th node. Here, is the reactive power of the compensator at node i.
The constraints of inequality are the limits of the variables given by:
where ng, nT, and ncomp are the number of generators, transformers, and compensators, respectively. The transformation ratio of the i-th transformer is denoted by ai. Subscripts ‘min’ and ‘max’ are relevant to the minimum and maximum of the considered variables.
4. Illustration
In order to determine the efficiency of the hybridization of the two metaheuristic methods with population to control the reactive power, the transformation ratio of the transformers and the voltage of the nodes corresponding to the values of the minimum losses, a program under the MATLAB environment was developed.
The algorithm of this hybridization begins with the execution of the method of the genetic algorithm then the execution of the PSO method. This signifies that the solution given by the Genetic Algorithm is chosen as the initial solution of the Particle Swarm Optimization. The corresponding flowchart is reported in Figure 1
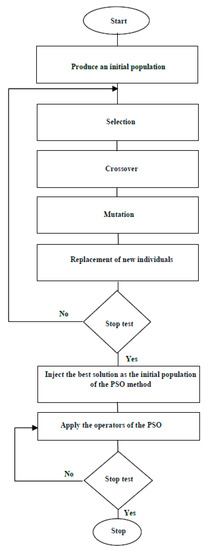
Figure 1.
The flowchart representation of the sequential hybridization algorithm.
The procedure of the proposed hybrid method is summarized as follows:
- Step 1: Carry out a load flow study to determine an operating point (see node voltage profile and active losses by Fast Decoupled Load Flow Method (FDLF) [1])
- Step 2: Initialization of the genetic algorithm and production of an initial population with the following parameters:
- maximum number of iterations;
- population size;
- probability of crossover;
- probability of mutation.
- Step 3: Application of the three operators of the genetic algorithm (selection, crossover, and mutation) to have the new individuals until the stopping criterion is reached.
- Step 4: Injection of the best solution obtained by GA as an initial population of the PSO method.
- Step 5: Initialization of the PSO program with the following parameters:
- initial weight Wmax;
- final weight Wmin;
- maximum number of iterations itmax;
- weighting factor C1 = C2;
- population size nind;
- number of variables nvar.
- Step 6: Applying the operators of the PSO method (speed and position of updates).
For the update of N affected individuals.
Updating speed and particle positions
Until the stopping criterion is reached.
To evaluate the performance of the hybrid method, we have it applied on a small network, the electrical network IEEE 14 nodes (International Explorer Electrical Engineering) [15], then on the West Algerian network with 102 nodes [1,5]. A comparative study of the results will be presented later for each network.
4.1. The Electrical Network IEEE14 Nodes
The electrical network IEEE 14 nodes is a part of the American power grid (specifically in the US Midwest) dating from February 1962. It was introduced in the IEEE Common Data Format by Rich Christie at the University of Washington in August 1993 [15].
It contains 10 load nodes, 4 generation nodes, 3 transformers, and 20 lines [15]. The limit of the voltages in the nodes is between 0.99 p.u and 1.1 p.u.
The results of the control variables are shown in Figure 2 for the node voltage, Table 1 for the generated power and transformation ratios, as well as the minimum loss values and execution time in Table 2.
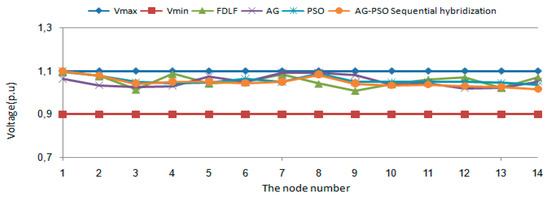
Figure 2.
The node voltage in the IEEE 14 node electrical network.

Table 1.
The generated power and transformation ratios.

Table 2.
The active losses values and execution time.
The curve in Figure 2 shows the voltage profile in the different nodes of the 14-node network for the different cases studied; we noticed after the application of optimization methods that the voltages in the nodes improved compared to the first case, which is the power flow, the voltages are approaching the upper limit.
Table 1 shows the reactive powers generated by the generators as well as the steps of the transformation ratios of the controllers into transformer loads. It can be seen that the values are within the given limits, for the balance generator in the PSO and hybrid methods, the reactive power consumed is low compared to the other two methods.
Table 2 shows the loss values and execution time of the different methods. It can be seen that the losses are reduced by the PSO method but the time is much more significant, while the hybrid method gives a considerable reduction of active losses in the network lines and an acceptable execution time.
The results show that the hybrid method minimized the active losses with a percentage of 6.49%, the AG 6.34%, and the PSO 6.12% (Table 2), while keeping the control variables within the limits (Table 1 and Figure 2). Thus, the hybrid method is more effective than the other two methods, AG and PSO.
At this stage, one applied the methods to the Algerian Western Network with 102 nodes.
4.2. The Algerian Western Wetwork with 102 Nodes
The Algerian network is characterized by long transmission lines, an uneven distribution of reactive power reserves among available generators, as well as an insufficient number of shunt capacitors.
As a consequence, operators are routinely facing severe voltage problems (violation), and the reactive power dispatch has become one of the most relevant concerns in the control center for the western Algerian transmission system.
This network is constituted of three subnetworks that are the 400 kV electrical network, the 220 kV electrical network and the 60 kV electrical network (see Figure 3) [5].
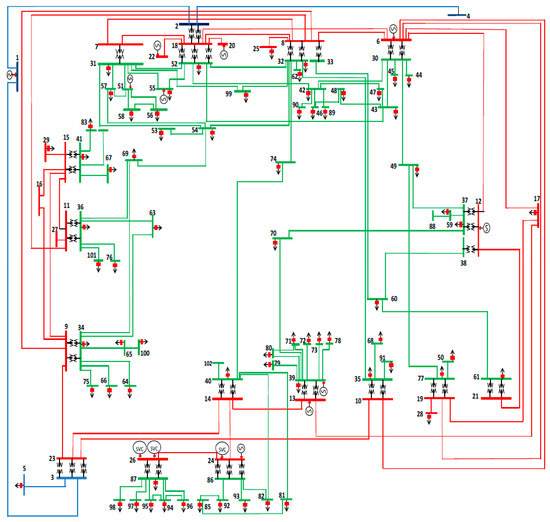
Figure 3.
The one-line diagram of the Algerian Western Network with the three voltage levels 400 kV (blue lines)/220 kV (red lines)/60 kV (green lines).
The essential data for the Algerian Western Network are reported in Table 3.

Table 3.
Essential data for the Algerian Western Network.

Table 4.
The limits voltage of the nodes.

Table 5.
The limits of the variables of control.
4.3. Results Analysis
As a first step, a study was performed by the fast decoupled load flow method (FDLF) to visualize the profile of nodes voltage and active losses.
Then, the optimization of the network by the GA and PSO methods was made, separately. In the end, the sequential hybridization of these two methods was applied. This optimization consists of controlling the voltages of the nodes.
In Figure 4, the variation of the voltage on the nodes in different cases before and after the optimization for GA, PSO, and GA-PSO hybridization are drawn in the case of the 400 kV electrical network. It appears that these variations obey practically the range of acceptance within the imposed limits.
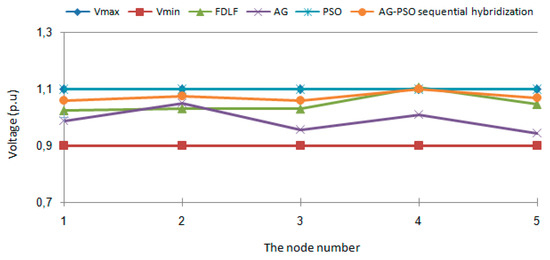
Figure 4.
The variation of the voltage on the nodes in different cases before and after the optimization for GA, PSO, and GA–PSO hybridization in the 400 kV electrical network.
The case of the 220 kV electrical network is presented in Figure 5. Before optimizations, the voltage at the 26th node is exceeding the maximal limit according to the (FDLF) graph. This anomaly disappeared after applying the optimization methods, i.e.; GA, PSO, and GA–PSO hybridization.
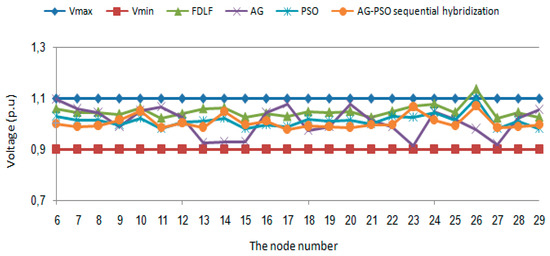
Figure 5.
The voltage of nodes in different cases before and after the optimization for GA, PSO, and GA–PSO hybridization in the 220 kV electrical network.
For the 60 kV electrical network, Figure 6b shows the presence of several violations of the voltage limits that concern the nodes (85, 86, 87) and (92 to 98). The use of the three methods of optimization has corrected these anomalies.
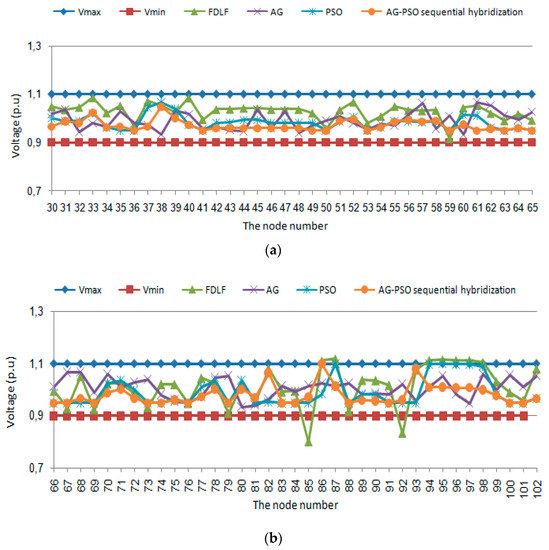
Figure 6.
The voltage of nodes from the FDLF and the different optimization methods (GA, PSO, and GA–PSO hybridization) in the case of the 60 kV electrical network: (a) The voltage of the nodes numbers 30 to 65; (b) The voltage of the nodes numbers 66 to 102.
The generated reactive powers obtained from the methods lay in their authorized ranges (see Table 6).

Table 6.
The generated reactive powers obtained from the methods.
The transformation ratios obtained from these methods are in agreement with their range of variation as shown in Table 7.

Table 7.
Transformation ratios obtained from the different methods.
In Table 8, we reported the results concerning the minimal losses in the network and the duration of the execution of programs.

Table 8.
Active losses and times of execution.
The results presented in Table 6 show that the hybrid GA–PSO method gives the minimum value of active losses (29.19 MW), while the GA method (36.60 MW) and the PSO method (45.07 MW), so the hybrid method, gives a remarkable reduction of 21.87 MW compared to the initial value of the active losses (51.06 MW by the FDLF method).
For the execution time, we noticed that the hybrid method is faster than the PSO method but slower than the GA.
So in terms of loss reduction, the hybrid method is more efficient, but in terms of speed, the AG method is faster.
The results presented in this section show that:
At the level of voltages (at the tension’s level) in the nodes, the FDLF method shows several exceedances of the lower limit in nodes 85 and 92 also for the upper limit in nodes 94, 95, 96, 97, 98. The application of GA, PSO, and hybrid optimization methods eliminates these exceedances, but the hybrid method is the one that gives the most appropriate voltage profile.
For the control variables, it can be seen that the reactive powers of generators have remained within the limits imposed. Also, the transformer transformation ratios are pushed towards the upper limits for both the PSO and hybrid methods.
For losses, we noticed (it was noted) that the application of the hybrid method gives a good reduction of active losses and also a minimum execution time.
5. Conclusions
The problem of the optimal powers flow became extremely difficult, following the fast growth of the electrical networks. To improve the solutions which provide the methods metaheuristic, we applied the approach of sequential hybridization between the two populations metaheuristic, GA and PSO in the West Algerian network with 102 nodes.
It appears that this sequential hybridization method reproduces better solutions than the standard ones. All voltages were corrected with a better minimization on the losses of a percentage of 42.82%.
The comparative study of the solutions obtained by the basic metaheuristics GA and PSO and those obtained by their sequential hybridization shows that the last method gives better solutions in terms of minimization of the losses. However, the sequential hybridization method seems to be less effective for the time of execution.
On the other hand, this study can be extended to:
- development of the sequential hybridization of GA and PSO to improve the execution time, to have minimum losses in minimum time;
- development of other types of hybridization such as integrative hybridization.
Author Contributions
Conceptualization, I.C. and N.K.; methodology, I.C.; software, I.C.; validation, A.C., N.K., F.B.; formal analysis, I.C., K.N. and A.C.; data curation, I.C., Z.D.; writing—original draft preparation, I.C.; writing—review and editing, I.C., N.A.; supervision, A.C.
Acknowledgments
We thank Hachi Mostefa at ORAN 1 University, Algeria, for his assistance with the writing and editing of this manuscript, as well as the comments that have greatly improved the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Cherki, I. Modélisation des FACTS et Contrôle des Puissances dans un Réseau Electrique par les Méthodes Métaheuristiques; ENPO-MA: Oran, Algéria, 2013. [Google Scholar]
- Lahdeb, M. Théorie et Application de Méthodes D’hybridations Métaheuristiques Dans les Réseaux Electriques; Université Amar Telidji-Laghouat: Laghouat, Algeria, 2007. [Google Scholar]
- Goldberg, D. Genetic Algorithms; Addison-Wesley: Boston, MA, USA, 1991. [Google Scholar]
- Eberhart Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science (MHS’95), Nagoya, Japan, 4–6 October 1995. [Google Scholar]
- Kalfallah, N.; Benzergua, F.; Cherki, I.; Chaker, A. USE of Genitic Algorithm and Particle Swarm Optimisation Methods for the Optimal Control of the Reactive Power in Western Algerian Power System. Energy Procedia 2015, 74, 265–272. [Google Scholar]
- Khiat, M.; Marano, A.; Chettih, S.; Martinez, J.L. A hybrid methodology for optimal var dispatch in the western algerian power system. RAMOS Roum. Sci. Technol. Lectrotechn. Énergy 2012, 57, 361–370. [Google Scholar]
- Lahdeb, M.; Hellal, A.; Arif, S. Hybridations métaheuristiques en lots appliquées à l’écoulement optimal de la puissance réactive. EJEE 2012, 15, 587–612. [Google Scholar] [CrossRef]
- Oo, K.Z.; Lin, K.M.; Aung, T.N. Particle Swarm Optimization Based Optimal Reactive Power Dispatch for Power Distribution Network with Distributed Generation. IJEPE 2017, 6, 54–60. [Google Scholar]
- Chettih, S.; Khiat, M.; Chaker, A. Voltage Control and Reactive Power Optimisation using the Meta Heuristics Method: Application in the Western Algerian Transmission System. JAI 2011, 4, 12–20. [Google Scholar] [CrossRef]
- Daoudi, R. Optimisation des Puissances Réactives par la Méthode Essaim Particules (PSO) Dans un Réseau D’énergie Electrique; ENPO-MA: Oran, Algéria, 2012. [Google Scholar]
- Cotta, C.; Talbi, E.G.; Alba, E. Parallel hybrid metaheuristics. In Parallel Metaheuristics, a New Class of Algorithms; Alba, E., Ed.; John Wiley: Hoboken, NJ, USA, 2005; pp. 347–370. [Google Scholar]
- Duvivier, D. Etude de L’hybridation des Métaheuristique, Application à un Problème D’ordonnancement de Type JOBSHOP; Université du littoral Cote D’OPALE: Dunkerque, France, 2000. [Google Scholar]
- Hachimi, H. Hybridations d’algorithmes métaheuristiques en optimisation globale et leurs applications; INSA de Rouen: Rouen, France, 2013. [Google Scholar]
- Yan, X.-S. Engineering Optimization an Introduction with Metaheuristic Applications; Johnwiley & sons Publication: Hoboken, NJ, USA, 2010. [Google Scholar]
- DR POWER. Available online: https://egriddata.org/dataset/ieee-14-bus-power-flow-test-case (accessed on 21 January 2019).
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).