Differential Pricing Strategies of High Speed Railway Based on Prospect Theory: An Empirical Study from China
Abstract
1. Introduction
2. Literature Review
2.1. Development and Application of Price Discrimination
2.2. Development and Research of HSR Pricing
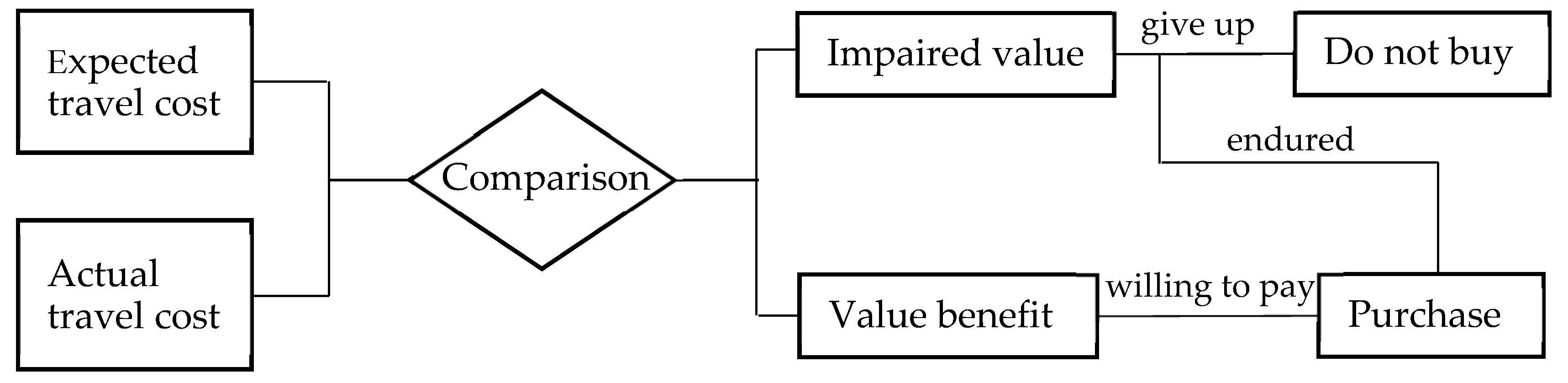
2.3. Applicability of Prospect Theory to HSR Pricing
3. Problem Analysis
3.1. Passenger Classification
3.2. Selection of Reference Point
4. Methodology
5. Solution Algorithm
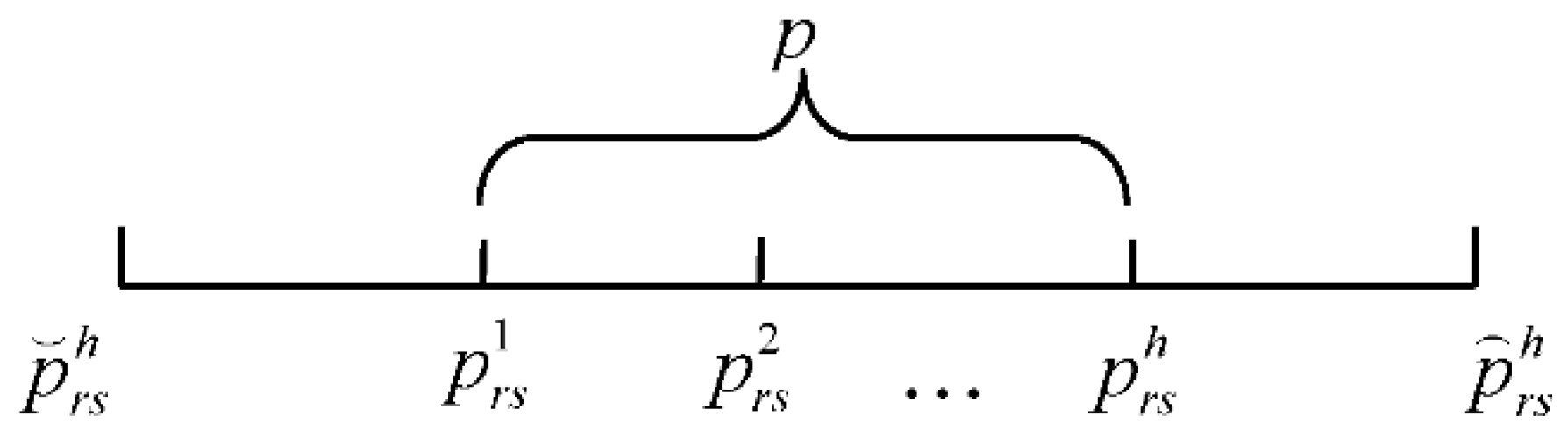
5.1. Generate Initial Solution
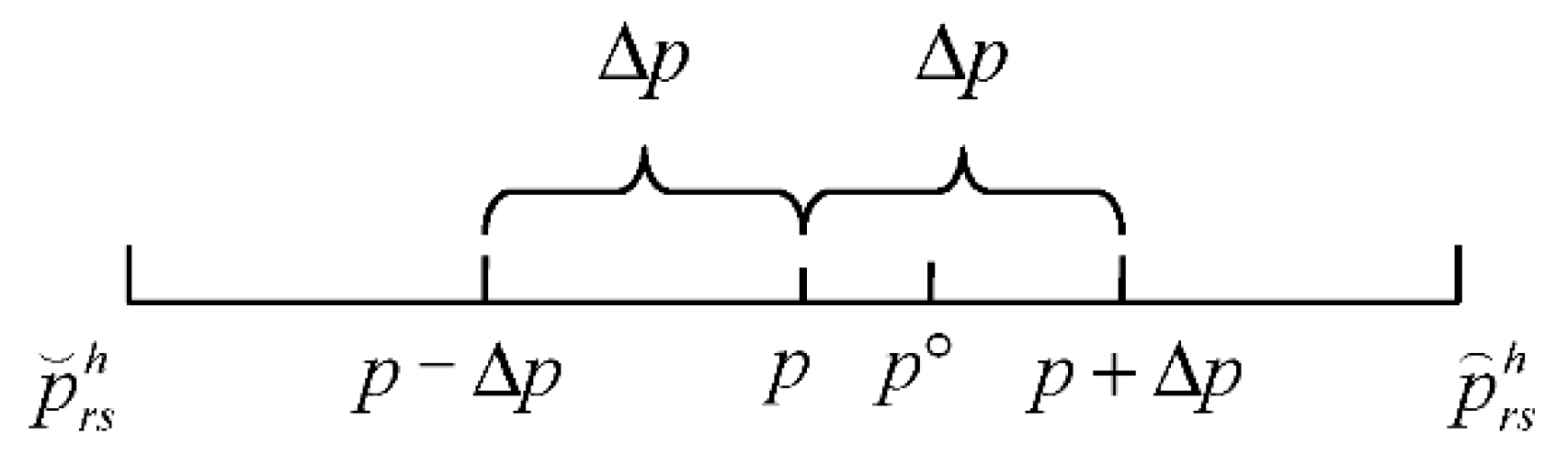
5.2. Neighborhood Structure
5.3. Specific Steps of SA Algorithm
| Algorithm 1. Get the best solution for each train fare through simulated annealing, maximizing HSR revenue. |
| Input: initial temperature T0, temperature drop ratio , final temperature , price range (,) |
| Output: , |
| for to do |
| Set ←0; |
| for to do |
| Generate initial solution ←; |
| Construct a neighborhood solution of the current solution →; |
| Update the global optimal solution: if , ← , ← , ← , ← ; if , acceptance probability , generates a random number from (0,1), satisfy , ← , ← ; |
6. Examples and Results
6.1. Differential Pricing
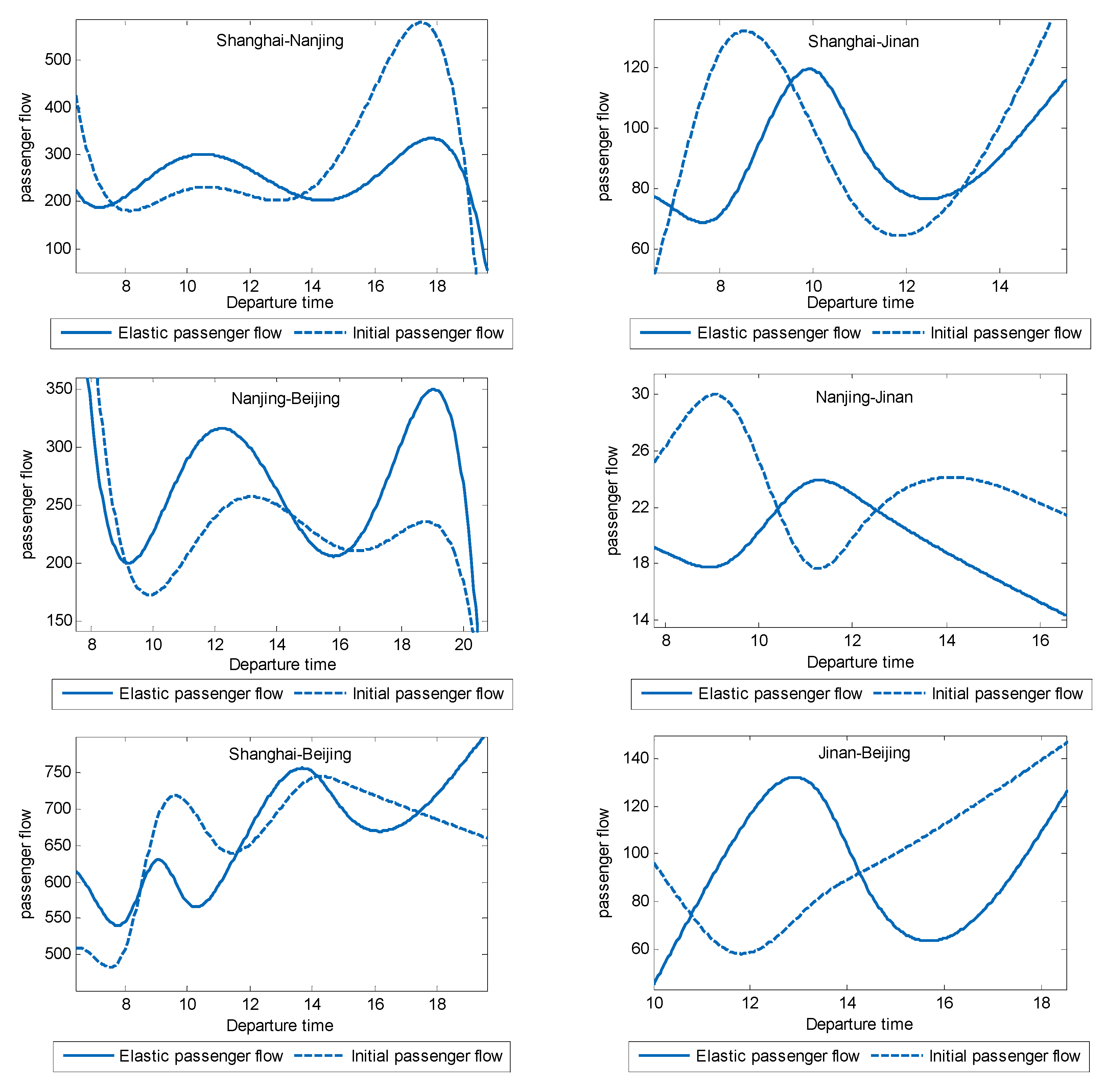
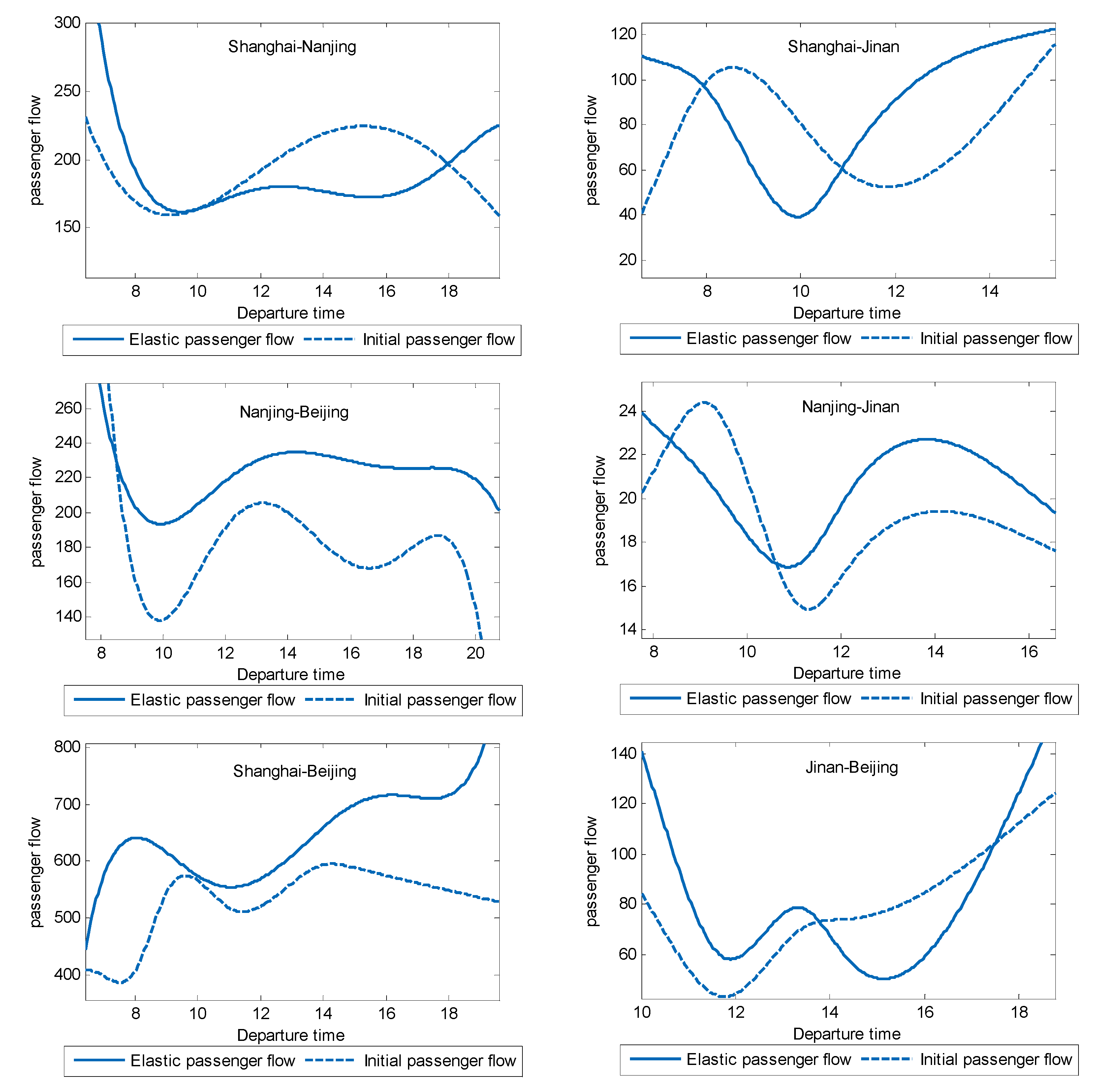
6.2. Elastic Passenger Flow
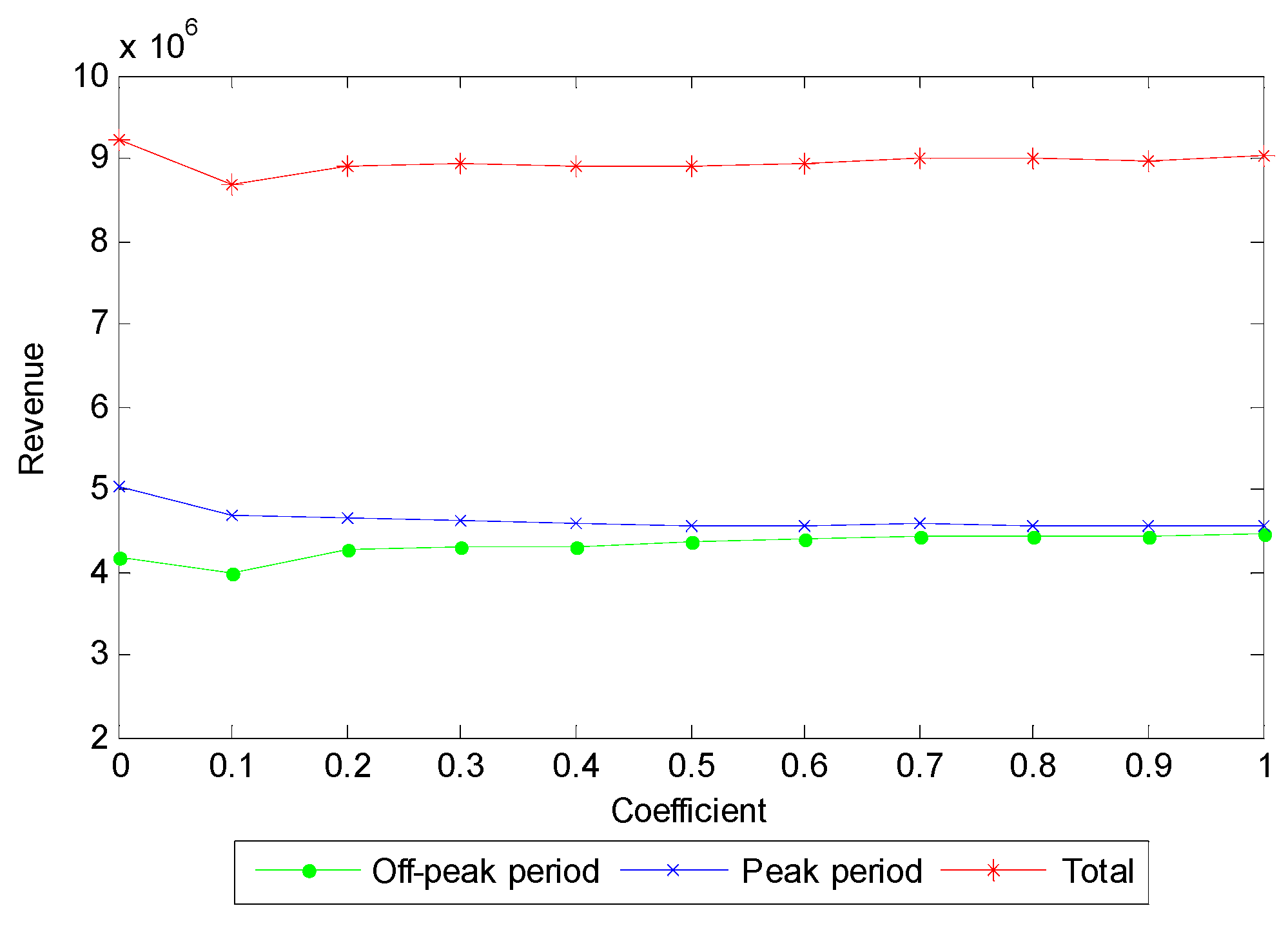
6.3. Impact of Passenger Expectations on HSR Revenue
7. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yu, X.Q.; Lang, M.X.; Gao, Y.; Wang, K.; Su, C.H.; Tsai, S.B.; Huo, M.K.; Yu, X.; Li, S.Q. An Empirical Study on the Design of China High-Speed Rail Express Train Operation Plan-From a Sustainable Transport Perspective. Sustainability 2018, 7, 2478. [Google Scholar] [CrossRef]
- Zheng, J.; Liu, J. The research on ticket fare optimization for China’s high-speed train. Math. Probl. Eng. 2016, 2016, 1–8. [Google Scholar] [CrossRef]
- Su, M.; Luan, W.X.; Yuan, L.Y.; Zhang, R.; Zhang, Z.C. Sustainability Development of High Speed Rail and Airline-Understanding Passengers’ Preferences: A Case Study of the Beijing-Shanghai Corridor. Sustainability 2019, 3, 1352. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, T.L.; Huang, H.J.; Chen, J. A cumulative prospect theory approach to commuters’ day-to-day route-choice modeling with friends’ travel information. Transp. Res. Part C Emerg. Technol. 2018, 86, 527–548. [Google Scholar] [CrossRef]
- Zhang, L.; Zhu, L.H.; Wu, X.Y.; Shen, B.B.; Song, Y.X. Analysis on examples of high-speed railway ticket pricing mechanism based on floating pricing model. Railw. Transp. Econ. 2014, 36, 1–4. [Google Scholar]
- Dupuit, J. On tolls and transport charges. Annales des Ponts et Chaussees 1894, 17, 445–467. [Google Scholar]
- Pigou, A.C. The Economics of Welfare, 4th ed.; Macmillan and Company: London, UK, 1932. [Google Scholar]
- Borenstein, S. Hubs and High fares: Dominance and Market Power in the U.S. Airline Industry. RAND J. Econ. 1989, 20, 344–365. [Google Scholar] [CrossRef]
- Giaume, S.; Guillou, S. Price Discrimination and Concentration in European Airline Markets. J. Air Transp. Manag. 2004, 10, 305–310. [Google Scholar] [CrossRef]
- Wu, C.C.; Liu, Y.F.; Chen, Y.J.; Wang, C.J. Consumer responses to price discrimination: Discriminating bases, inequality status, and information disclosure timing influences. J. Bus. Res. 2012, 65, 106–116. [Google Scholar] [CrossRef]
- Julia, V.; Michael, P. One firm, one product, two prices: Channel-based price differentiation and customer retention. J. Retail. Consum. Serv. 2015, 27, 126–139. [Google Scholar] [CrossRef]
- Asplund, M.; Eriksson, R.; Strand, N. Price Discrimination in Oligopoly: Evidence from regional newspapers. J. Ind. Econ. 2008, 56, 333–346. [Google Scholar] [CrossRef]
- Puller, S.L.; Taylor, L.M. Price Discrimination by Day-of-week of Purchase: Evidence from the U.S. Airline Industry. J. Econ. Behav. Organ. 2012, 84, 801–812. [Google Scholar] [CrossRef]
- Nocke, V.; Peitz, M.; Rosar, F. Advance-purchase discounts as a price discrimination device. J. Econ. Theory 2011, 146, 141–162. [Google Scholar] [CrossRef]
- David, F. Second-degree price discrimination by Japanese newspapers. Jpn. World Econ. 2017, 44, 14–25. [Google Scholar] [CrossRef]
- Holmes, T. The Effects of Third-Degree Price Discrimination in Oligopoly. Am. Econ. Rev. 1989, 79, 244–250. [Google Scholar]
- Janic, M. A model of competition between high speed rail and air transport. Transp. Plan. Technol. 1993, 17, 1–23. [Google Scholar]
- Taniguchi, M. High Speed Rail in Japan: A Review and Evaluation of the Shinkansen Train; UC Berkeley, University of California Transportation Center: Berkeley, CA, USA, 1992. [Google Scholar]
- Voss, A. Collective public-transport tickets and anticipated majority choice: A model of student tickets. Transp. Res. Pol. Pract. 2015, 80, 263–276. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, P.F.; Zhu, X.F.; Zhang, X.Q. Pricing model of railway passenger transportation under competition. J. Transp. Eng. Inf. 2016, 14, 101–106. [Google Scholar]
- Daniel, F.O.; Raha, A.T. A stochastic dynamic pricing model for the multiclass problems in the airline industry. Eur. J. Oper. Res. 2015, 242, 188–200. [Google Scholar] [CrossRef]
- Bitran, G.; Caldentey, R. An overview of pricing models for revenue management. Manuf. Serv. Oper. Manag. 2003, 5, 203–229. [Google Scholar] [CrossRef]
- Sibdari, S.; Lin, K.Y.; Chellappan, S. Multiproduct Revenue Management: An Empirical Study of Auto Train at Amtrak. J. Revenue Pricing Manag. 2008, 7, 172–184. [Google Scholar] [CrossRef]
- Jiang, X.; Chen, X.; Zhang, L.; Zhang, R. Dynamic demand forecasting and ticket assignment for high-speed rail revenue management in China. Transp. Res. Rec. 2015, 2475, 37–45. [Google Scholar] [CrossRef]
- Bharill, R.; Rangaraj, N. Revenue Management in Railway Operations: A Study of the Rajdhani Express, Indian Railways. Transp. Res. Part A Policy Pract. 2008, 42, 1195–1207. [Google Scholar] [CrossRef]
- Gallego, G.; van Ryzin, G. Optimal dynamic pricing of inventories with stochastic demand over finite horizons. Manag. Sci. 1994, 40, 999–1020. [Google Scholar] [CrossRef]
- Armstrong, A.; Meissner, J. Railway Revenue Management: Overview and Models; Lancaster University Management School: Lancaster, UK, 2010. [Google Scholar]
- Yuan, T.; Simin, H.; Jikun, L. Application of revenue management in European and American railways. China Railw. 2008, 6, 63–66. [Google Scholar]
- Kahneman, D.; Tversky, A. Prospect Theory: An Analysis of Decision under Risk. Econometrica 1979, 47, 263–291. [Google Scholar] [CrossRef]
- Ramos, G.M.; Daamen, W.; Hoogendoorn, S. A state-of-the-art review: Developments in utility theory, prospect theory and regret theory to investigate travelers’ behaviour in situations Involving travel time uncertainty. Transp. Rev. 2014, 34, 46–67. [Google Scholar] [CrossRef]
- Gao, S.; Frejinger, E.; Ben-Akiva, M. Adaptive route choices in risky traffic networks: A prospect theory approach. Trans. Res. Part C Emerg. Technol. 2010, 18, 727–740. [Google Scholar] [CrossRef]
- Avineri, E. A cumulative prospect theory approach to passengers’ behavior modeling: Waiting time paradox revisited. J. Intell. Transp. Syst. 2004, 8, 195–204. [Google Scholar] [CrossRef]
- Jou, R.C.; Chen, K.H. An application of cumulative prospect theory to freeway drivers’ route choice behaviors. Transp. Res. Part A Policy Pract. 2013, 49, 123–131. [Google Scholar] [CrossRef]
- Schwanen, T.; Ettema, D. Coping with unreliable transportation when collecting children: Examining parents’ behavior with cumulative prospect theory. Transp. Res. Part A Policy Pract. 2009, 43, 511–525. [Google Scholar] [CrossRef]
- Liu, D.; Lam, W.H.K. Modeling the Effects of Population Density on Prospect Theory-Based Travel Mode-Choice Equilibrium. J. Intell. Transp. Syst. 2014, 18, 379–392. [Google Scholar] [CrossRef]
- Jou, R.C.; Kitamura, R.; Weng, M.C.; Chen, C.C. Dynamic commuter departure time choice under uncertainty. Transp. Res. Part A Policy Pract. 2008, 42, 774–783. [Google Scholar] [CrossRef]
- Barberis, N.; Huang, M.; Santos, T. Prospect theory and asset prices. Q. J. Econ. 2001, 116, 1–53. [Google Scholar] [CrossRef]
- Wang, Y.; Yan, X.; Zhou, Y. Influencing Mechanism of Potential Factors on Passengers’ Long-Distance Travel Mode Choices Based on Structural Equation Modeling. Sustainability 2017, 9, 1943. [Google Scholar] [CrossRef]
- Deng, L.B.; Zhang, Z.; Liu, K.N.; Zhou, W.L.; Ma, J.F. Fare optimality analysis of urban rail transit under various objective functions. Discret. Dyn. Nat. Soc. 2014, 2014, 1–8. [Google Scholar] [CrossRef]
- Shi, F.; Xu, G.M.; Liu, B.; Huang, H.L. Optimization Method of Alternate Traffic Restriction Scheme Based on Elastic Demand and Mode Choice Behavior. Transp. Res. Part C Emerg. Technol. 2014, 39, 36–52. [Google Scholar] [CrossRef]
- Qin, J.; Ni, L.L.; Shi, F. Combined Simulated Annealing Algorithm for the Discrete Facility Location Problem. Sci. World J. 2012, 2012, 1–7. [Google Scholar] [CrossRef]
| Passenger Type | Time Sensitivity | Price Sensitivity | Elasticity | Elastic Coefficient | Choice | |
|---|---|---|---|---|---|---|
| Economy | 1 | Weak | Strong | Large | >1 | Price priority |
| Middle | 2 | Medium | Medium | Single | =1 | Comprehensive |
| Business | 3 | Strong | Weak | Small | <1 | Time priority |
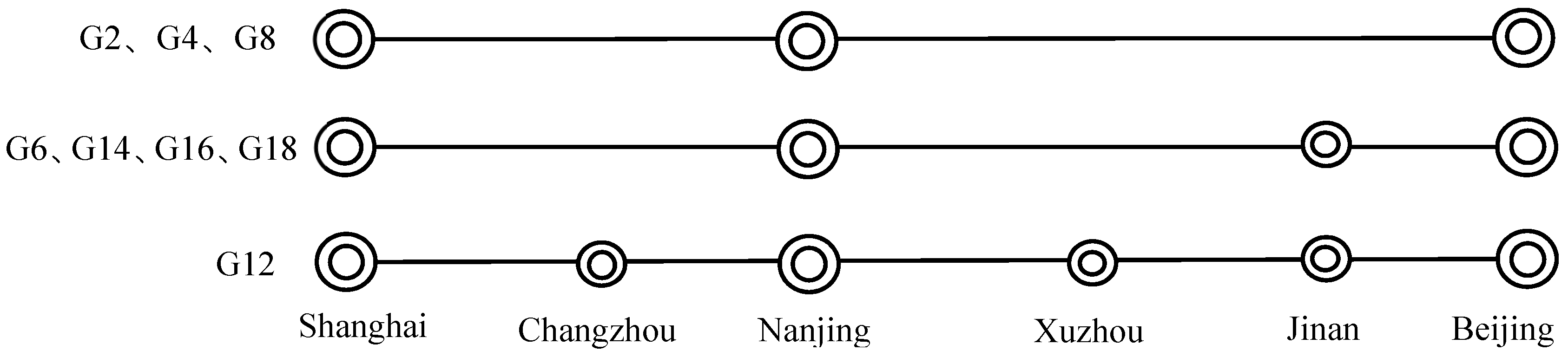
| Starting Station | Shanghai | Changzhou | Nanjing | Xuzhou | Jinan |
|---|---|---|---|---|---|
| G2 | 09:00 | 10:09 | |||
| G4 | 14:00 | 15:09 | |||
| G6 | 07:00 | 08:09 | 10:23 | ||
| G8 | 19:00 | 20:09 | |||
| G12 | 08:00 | 08:42 | 09:16 | 10:33 | 11:44 |
| G14 | 10:00 | 11:09 | 13:23 | ||
| G16 | 11:00 | 12:09 | 14:23 | ||
| G18 | 15:00 | 16:09 | 18:23 |
| Starting Station | Terminal | G2 | G4 | G6 | G8 | G12 | G14 | G16 | G18 | Initial Price |
|---|---|---|---|---|---|---|---|---|---|---|
| Shanghai | Changzhou | – | – | – | – | 89 | – | – | – | 74.5 |
| Shanghai | Nanjing | 144 | 133 | 147 | 137 | 160 | 154 | 142 | 132 | 134.5 |
| Shanghai | Xuzhou | – | – | – | – | 332 | – | – | – | 279 |
| Shanghai | Jinan | – | – | 435 | – | 474 | 458 | 422 | 392 | 398.5 |
| Shanghai | Beijing | 593 | 547 | 604 | 561 | 658 | 635 | 585 | 544 | 553.5 |
| Changzhou | Nanjing | – | – | – | – | 71 | – | – | – | 59.5 |
| Changzhou | Xuzhou | – | – | – | – | 249 | – | – | – | 209 |
| Changzhou | Jinan | – | – | – | – | 397 | – | – | – | 334 |
| Changzhou | Beijing | – | – | – | – | 587 | – | – | – | 493.5 |
| Nanjing | Xuzhou | – | – | – | – | 178 | – | – | – | 150 |
| Nanjing | Jinan | – | – | 305 | – | 332 | 320 | 295 | 274 | 279 |
| Nanjing | Beijing | 475 | 439 | 484 | 450 | 527 | 509 | 469 | 436 | 443.5 |
| Xuzhou | Jinan | – | – | – | – | 154 | – | – | – | 129.5 |
| Xuzhou | Beijing | – | – | – | − | 368 | – | – | – | 309 |
| Jinan | Beijing | – | – | 201 | – | 219 | 211 | 195 | 181 | 184.5 |
| Starting Station | Terminal | G2 | G4 | G6 | G8 | G12 | G14 | G16 | G18 | Initial Price |
|---|---|---|---|---|---|---|---|---|---|---|
| Shanghai | Changzhou | - | - | - | - | 68 | - | - | - | 74.5 |
| Shanghai | Nanjing | 126 | 118 | 136 | 116 | 122 | 113 | 133 | 123 | 134.5 |
| Shanghai | Xuzhou | - | - | - | - | 253 | - | - | - | 279 |
| Shanghai | Jinan | - | - | 402 | - | 361 | 333 | 393 | 363 | 398.5 |
| Shanghai | Beijing | 517 | 485 | 558 | 478 | 502 | 463 | 545 | 504 | 553.5 |
| Changzhou | Nanjing | - | - | - | - | 54 | - | - | - | 59.5 |
| Changzhou | Xuzhou | - | - | - | - | 190 | - | - | - | 209 |
| Changzhou | Jinan | - | - | - | - | 303 | - | - | - | 334 |
| Changzhou | Beijing | - | - | - | - | 448 | - | - | - | 493.5 |
| Nanjing | Xuzhou | - | - | - | - | 136 | - | - | - | 150 |
| Nanjing | Jinan | - | - | 281 | - | 253 | 233 | 275 | 254 | 279 |
| Nanjing | Beijing | 415 | 389 | 447 | 383 | 402 | 371 | 437 | 404 | 443.5 |
| Xuzhou | Jinan | - | - | - | - | 117 | 0 | 129.5 | ||
| Xuzhou | Beijing | - | - | - | - | 280 | 0 | 309 | ||
| Jinan | Beijing | - | - | 186 | - | 167 | 154 | 182 | 168 | 184.5 |
| Starting Station | Terminal | Off-Peak Period | Peak Period | ||||
|---|---|---|---|---|---|---|---|
| Shanghai | Changzhou | 161 | 161 | 0 | 183 | 183 | 0 |
| Shanghai | Nanjing | 1485 | 1536(+51) | 0.0606 | 1858 | 1904(+46) | 0.0392 |
| Shanghai | Xuzhou | 50 | 50 | 0 | 55 | 55 | 0 |
| Shanghai | Jinan | 404 | 509(+105) | 0.3968 | 504 | 468(−36) | −0.0979 |
| Shanghai | Beijing | 4151 | 5109(+958) | 0.3475 | 5187 | 5143(−44) | −0.0114 |
| Changzhou | Nanjing | 37 | 37 | 0 | 41 | 41 | 0 |
| Changzhou | Xuzhou | 17 | 17 | 0 | 19 | 19 | 0 |
| Changzhou | Jinan | 13 | 13 | 0 | 14 | 14 | 0 |
| Changzhou | Beijing | 102 | 102 | 0 | 113 | 113 | 0 |
| Nanjing | Xuzhou | 23 | 23 | 0 | 23 | 23 | 0 |
| Nanjing | Jinan | 95 | 101(+6) | 0.1392 | 117 | 98(−19) | −0.2001 |
| Nanjing | Beijing | 1443 | 1758(+315) | 0.3339 | 1811 | 1993(+182) | 0.1448 |
| Xuzhou | Jinan | 10 | 10 | 0 | 11 | 11 | 0 |
| Xuzhou | Beijing | 51 | 51 | 0 | 57 | 57 | 0 |
| Jinan | Beijing | 377 | 469(+92) | 0.3713 | 463 | 537(+74) | 0.2239 |
| Original income | 3,499,017 | 4,359,156 | |||||
| Current income | 3,863,277 | 4,706,952 | |||||
| Growth ratio | 10.41% | 7.98% | |||||
| Expected Travel Cost | |||||
|---|---|---|---|---|---|
| Increase by 1% | Increase by 2% | Increase by 3% | |||
| Off-peak period | Original income | 3,499,017 | |||
| Current income | 3,863,277 | 4,241,360 | 4,521,127 | 4,807,496 | |
| Growth ratio | 10.41% | 21.22% | 29.21% | 37.40% | |
| Peak period | Original income | 4,359,156 | |||
| Current income | 4,706,952 | 4,850,718 | 5,004,958 | 5,145,175 | |
| Growth ratio | 7.98% | 11.28% | 14.81% | 18.03% | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, J.; Qu, W.; Wu, X.; Zeng, Y. Differential Pricing Strategies of High Speed Railway Based on Prospect Theory: An Empirical Study from China. Sustainability 2019, 11, 3804. https://doi.org/10.3390/su11143804
Qin J, Qu W, Wu X, Zeng Y. Differential Pricing Strategies of High Speed Railway Based on Prospect Theory: An Empirical Study from China. Sustainability. 2019; 11(14):3804. https://doi.org/10.3390/su11143804
Chicago/Turabian StyleQin, Jin, Wenxuan Qu, Xuanke Wu, and Yijia Zeng. 2019. "Differential Pricing Strategies of High Speed Railway Based on Prospect Theory: An Empirical Study from China" Sustainability 11, no. 14: 3804. https://doi.org/10.3390/su11143804
APA StyleQin, J., Qu, W., Wu, X., & Zeng, Y. (2019). Differential Pricing Strategies of High Speed Railway Based on Prospect Theory: An Empirical Study from China. Sustainability, 11(14), 3804. https://doi.org/10.3390/su11143804





