Method for the Improvement of the Elasticity Module of Concrete Specimens by Active Confinement
Abstract
1. Introduction
2. Methods
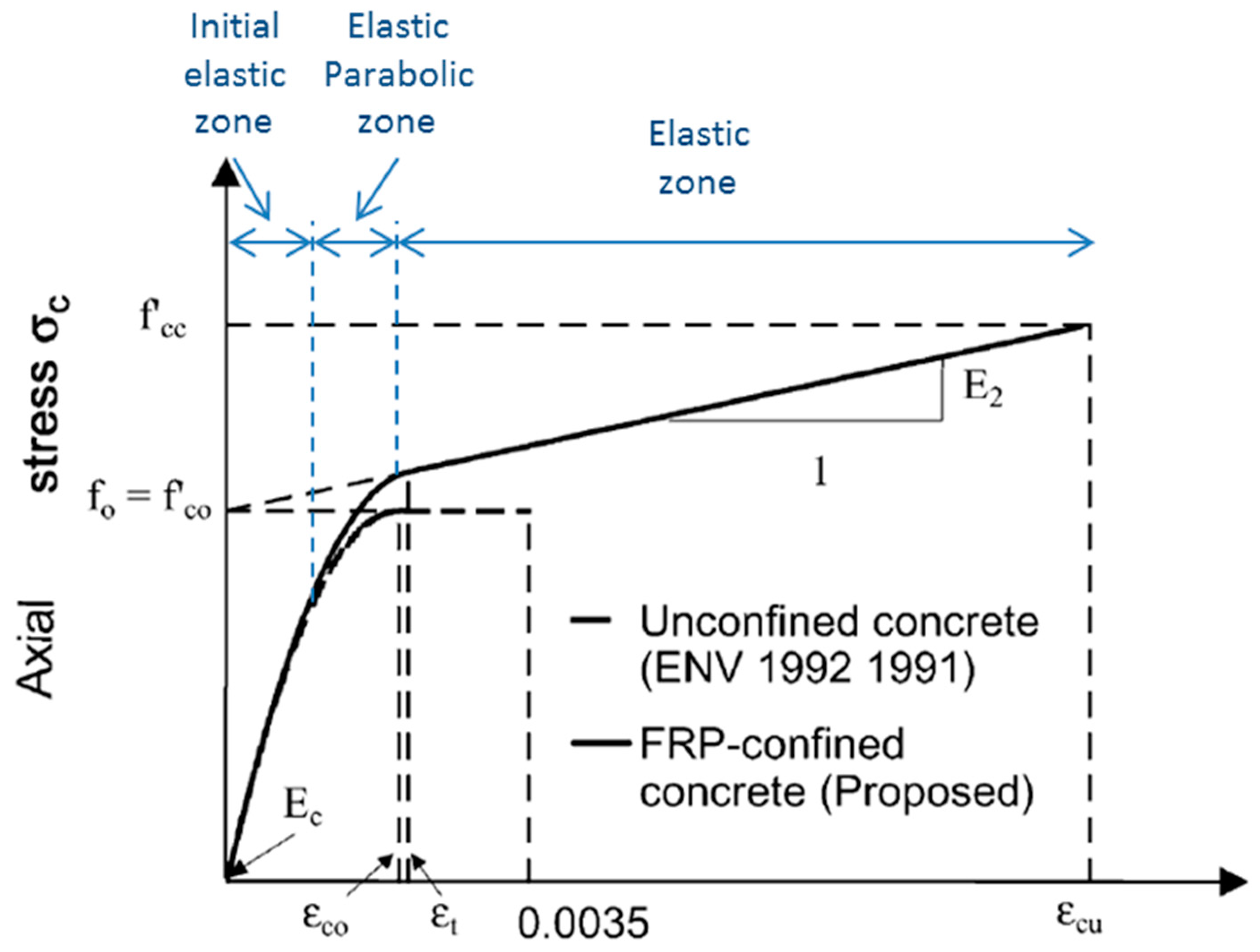
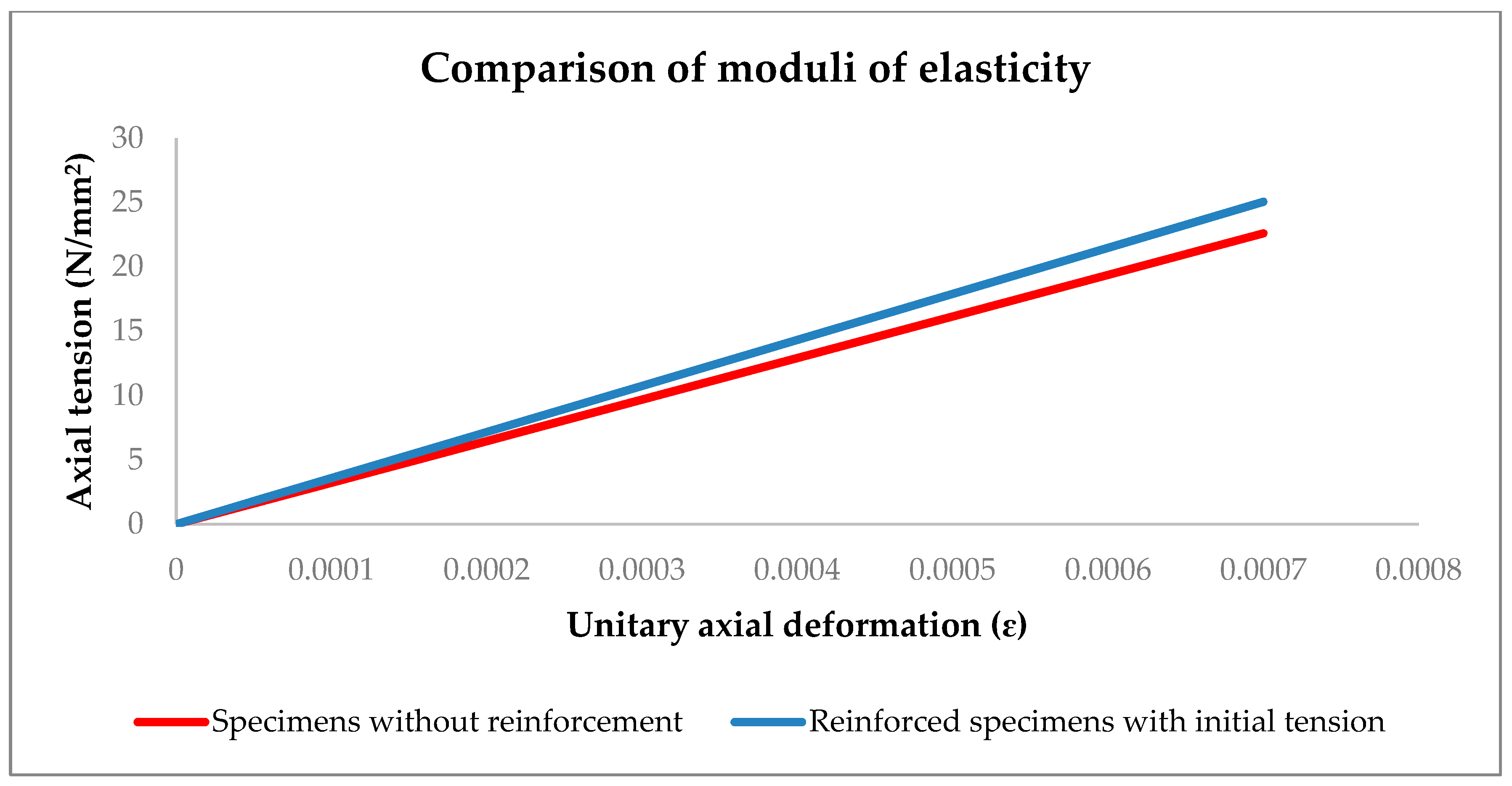
- The initial elastic zone was clearly influenced by the initial modulus of elasticity of the concrete () up to approximately . In this zone, the reinforcement fabric is unimportant, due to the zero or scarce transverse deformation of the element.
- The elastic-parabolic zone is a parabolic transition in which the two materials interact with each other; the concrete is in its plastic phase and the reinforcement fabric has a perfectly elastic behavior up to the point of fragmentation of the concrete at .
- Finally, the elastic zone in the concrete ceases to have any prominence and is simply a filling material. Here, the modulus of elasticity () effectively decreases and integrates entirely with the reinforcement fabric. The collapse of the pillar occurs around an axial deformation of 0.01. The difference between and can be considered as an increase in structural ductility.
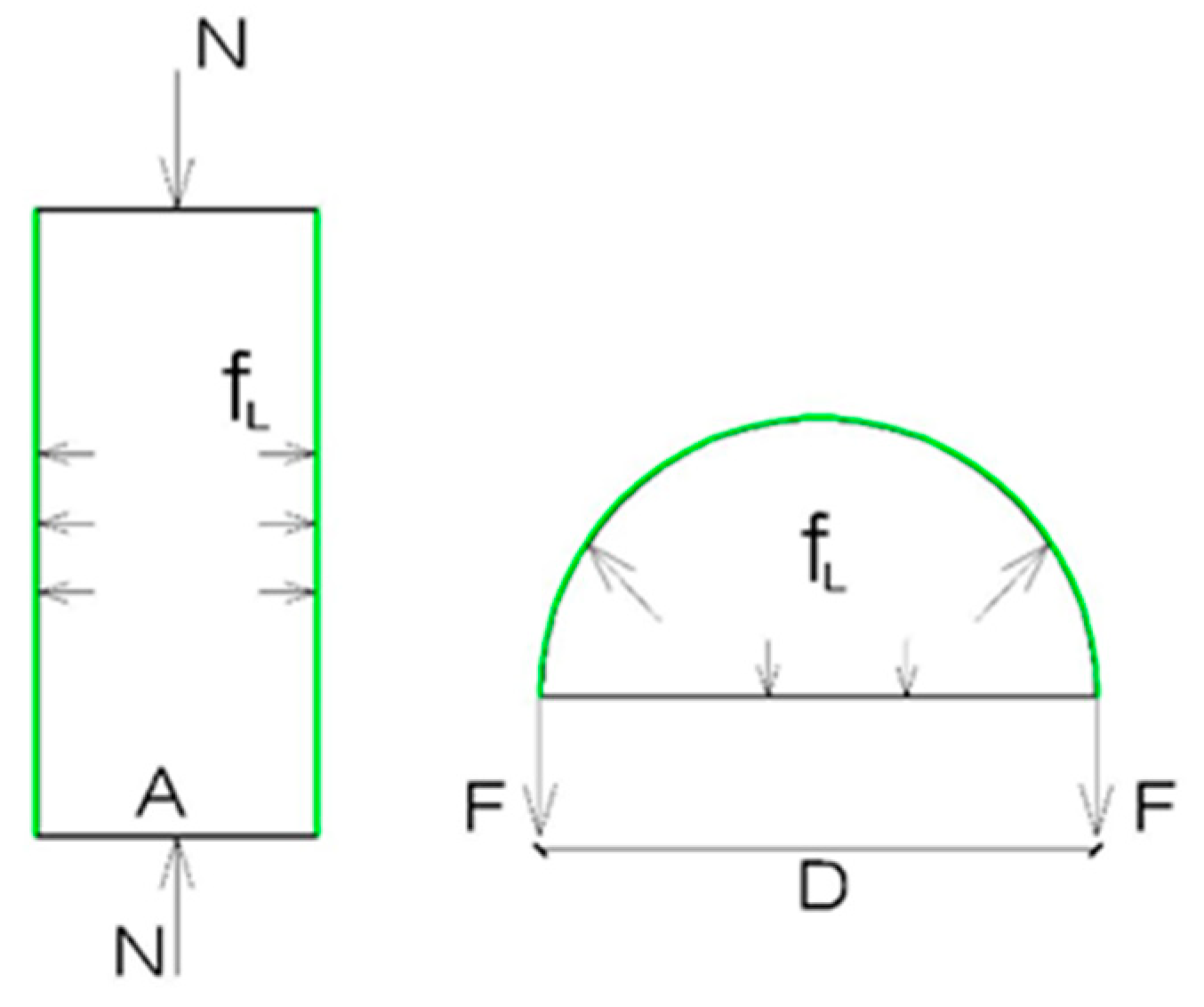
- The reinforcement does not have any vertical loads.
- The deformation in the circumference of the tissue is the same as that of the lateral surface of the specimen.
- The tensile tension of the fabric is uniform along the perimeter.
Experimental Plan
- Batch No. 1: five specimens without reinforcement, used to determine the mechanical characteristics of the concrete.
- Batch No. 2: five specimens reinforced with a layer of carbon fiber fabric.
- Batch No. 3: five specimens reinforced with a layer of carbon fiber fabric to which an initial tension was applied during the bonding of the fabric.
3. Materials
3.1. Concrete
3.2. Carbon Fiber Fabric (CF)
- Thickness: 0.167 mm
- Modulus of elasticity: 230,000 N/mm2
- Tensile strength: 3400 N/mm2
- Unitary rupture deformation: 0.014
3.3. Epoxy Resin
- Concrete characteristic stress:
- Modulus of elasticity:
- Poisson’s ratio:
3.3.1. Passive Reinforcement
3.3.2. Active Reinforcement
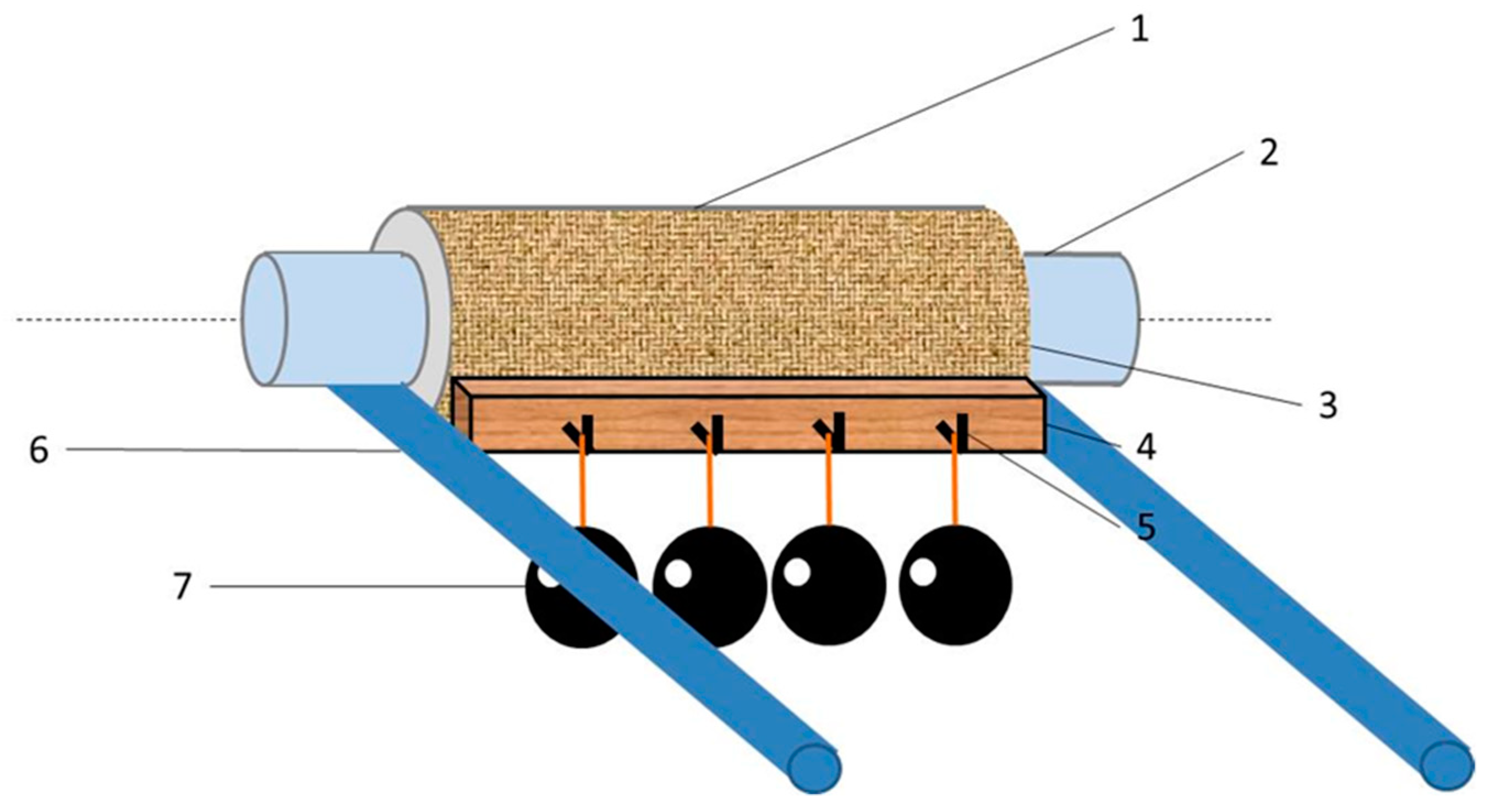
3.3.3. Active Reinforcement Process
- Fabric specimen to be reinforced.
- Auxiliary elements placed on both ends of the specimen to be reinforced.
- CF adhered to the specimen to be reinforced.
- Auxiliary specimen (not visible in the diagram) to distribute the load applied by gravitational force into the fabric without tearing it.
- Plugs to fix the loads.
- Guide rails supports, on which the specimen is placed, which allows the operator to turn the assembly.
- Weights that apply a gravitational force tension in the fabric.
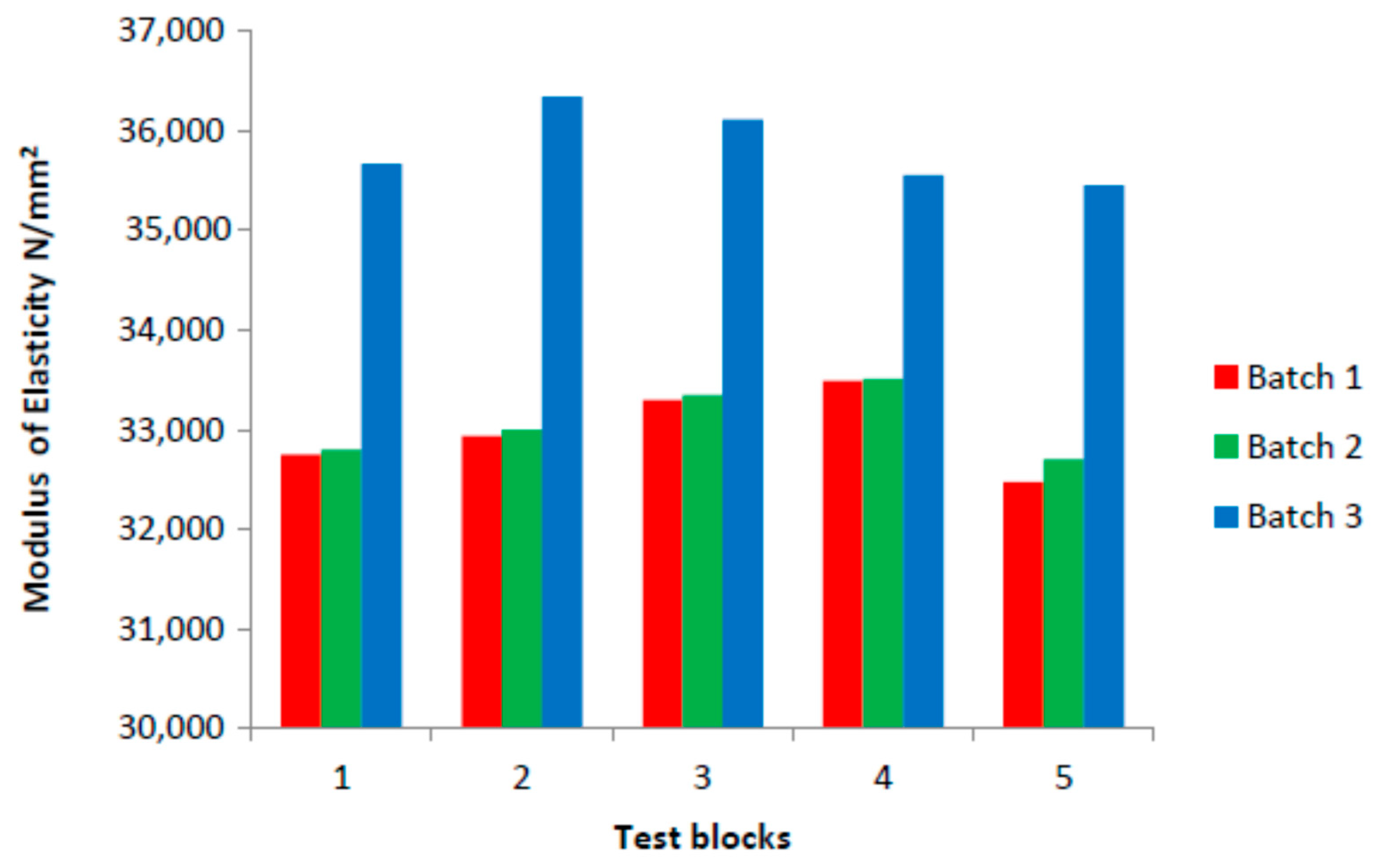
4. Results
5. Discussion
6. Conclusions
- The technique was employed with prefabricated elements which could adopt a horizontal position during the reinforcement procedure.
- The prefabricated elements did not support any compression at the time of reinforcement.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Baji, H.; Reza, H.; Li, C. Probabilistic assessment of FRP-confined reinforced concrete columns. Compos. Struct. 2016, 153, 851–865. [Google Scholar] [CrossRef]
- Song, X.; Gu, X.; Li, Y.; Chen, T.; Zhang, W. Mechanical behavior of FRPstrengthened concrete columns subjected to concentric and eccentric compression loading. Compos. Constr. 2013, 17, 336–346. [Google Scholar] [CrossRef]
- Saljoughian, A.; Mostofinejad, D. Corner Strip-Batten Technique for FRP-Confinement of Square RC Columns under Eccentric Loading. Compos. Constr. 2015, 20, 04015077. [Google Scholar] [CrossRef]
- Rochette, P.; Labossiere, P. Axial Testing of Rectangular Column Models Confined with Composites. Compos. Constr. 2000, 4, 129–136. [Google Scholar] [CrossRef]
- Breveglieri, M.; Barros, J.A.O.; Dalfré, G.M.; Aprile, A. Composites: Part B A parametric study on the effectiveness of the NSM technique for the flexural strengthening of continuous RC slabs. Compos. Part B 2012, 43, 1970–1987. [Google Scholar] [CrossRef]
- Xiao, Y.; Wu, H. Compressive Behavior of Concrete confined by various types of FRP composites jackets. J. Reinf. Plast. Compos. 2003, 22, 1187–1201. [Google Scholar] [CrossRef]
- Bisby, L.; Ranger, M. Axial—Flexural interaction in circular FRP-confined reinforced concrete columns. Constr. Build. Mater. 2010, 24, 1672–1681. [Google Scholar] [CrossRef]
- Puhrsch, C.; Kingsbury, B.; Lecun, Y. Guide for the Design and Construction of Externally Bonded FRP Systems. Structures 2005, 2, 2–6. [Google Scholar]
- Ozbakkaloglu, T.; Lim, J.C.; Vincent, T. FRP-confined concrete in circular sections: Review and assessment of stress-strain models. Eng. Struct. 2013, 49, 1068–1088. [Google Scholar] [CrossRef]
- Lam, L.; Teng, J.G. Ultimate Condition of Fiber Reinforced Polymer-Confined Concrete. J. Compos. Constr. 2004, 8, 539–548. [Google Scholar] [CrossRef]
- Spoelstra, M.R.; Monti, G. FRP-Confined Concrete Model. Compos. Constr. 1999, 3, 143–150. [Google Scholar] [CrossRef]
- Jiang, T.; Teng, J.G. Theoretical model for slender FRP-confined circular RC columns. Constr. Build. Mater. 2012, 32, 66–76. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, L. Unified strenght model for square and circular concrete columns confined by external jacket. J. Struct. Eng. ASCE 2009, 135, 253–261. [Google Scholar] [CrossRef]
- Jiang, T.; Teng, J.G. Analysis-oriented stress-strain models for FRP-confined concrete. Eng. Struct. 2007, 29, 2968–2986. [Google Scholar] [CrossRef]
- Fardis, M.N.; Khalili, H.H. FRP-encased concrete as a structural material. Concr. Res. 1982, 34, 191–202. [Google Scholar] [CrossRef]
- Li, G. Experimental study of FRP confined concrete cylinders. Eng. Struct. 2006, 28, 1001–1008. [Google Scholar] [CrossRef]
- Richart, F.; Brandtzaeg, A.; Brown, R.L. A Study of the Failure of Concrete under Combined Compressive Stresses; Bulletin No. 26; Engineering Experiment Station, University of Illinois at Urbana Champaign, College of Engineering: Champaign County, IL, USA, 1928; pp. 1–104. [Google Scholar]
- Parvin, A.; Wang, W. Concrete columns confined by fiber composite wraps under combined axial and cyclic lateral loads. Compos. Struct. 2002, 58, 539–549. [Google Scholar] [CrossRef]
- Parvin, A.; Wang, W. Behavior of FRP Jacketed Concrete Columns under Eccentric Loading. Compos. Constr. Constr. 2001, 5, 146–152. [Google Scholar] [CrossRef]
- Chai, Y.H.; Priestley, M.N.; Seible, F. Analytical Model for Steel-Jacketed RC Circular Bridge Columns. Struct. Eng. 1994, 120, 2358–2376. [Google Scholar] [CrossRef]
- Xiao, Y.; Wu, H. Compressive behavior of concrete confined by carbon fiber composite jackets. J. Mater. Civ. Eng. 2000, 12, 139–146. [Google Scholar] [CrossRef]
- Lam, L.; Teng, J.G. Design-oriented stress—Strain model for FRP-confined concrete. Constr. Build. Mater. 2003, 17, 471–489. [Google Scholar] [CrossRef]
- Teng, J.G.; Jiang, T.; Lam, L.; Luo, Y.Z. Refinement of a design-oriented stress-strain model for FRP-confined concrete. J. Compos. Constr. 2009, 13, 1–27. [Google Scholar] [CrossRef]
- ACI Committee 440. Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Existing Structures; CNR—Advisory Committee on Technical Recommendations for Construction: Roma, Italy, 1996. [Google Scholar]
- Wu, G.; Lü, Z.T.; Wu, Z.S. Strength and ductility of concrete cylinders confined with FRP composites. Constr. Build. Mater. 2006, 20, 134–148. [Google Scholar] [CrossRef]
- De Lorenzis, L.; Tepfers, R. Comparative Study of Models on Confinement of Concrete Cylinders with Fiber-Reinforced Polymer Composites. J. Compos. Constr. 2003, 7, 219–237. [Google Scholar] [CrossRef]
- Pessiki, S.; Harries, K.; Kestner, J.; Sause, R. The axial Behavior of concrete confined with fiber reinforced Jackets. J. Compos. Constr 2013, 5, 237–245. [Google Scholar] [CrossRef]
- Ozbakkaloglu, T.; Oehlers, D.J. Manufacture and testing of a novel FRP tube confinement system. Eng. Struct. 2008, 30, 2448–2459. [Google Scholar] [CrossRef]
- Lam, L.; Teng, J.G. Stress–strain model for FRP-confined concrete under cyclic axial compression. Eng. Struct. 2009, 31, 308–321. [Google Scholar] [CrossRef]



| Material | Density (kg/dm3) | Dosage (dm3) | Dosage (kg) |
|---|---|---|---|
| Cement | 2.81 | 131 | 370 |
| Sand | 2.61 | 214 | 560 |
| Gravel | 2.81 | 427 | 1200 |
| Water | 1.00 | 235 | 235 |
| Concrete density = 2.35 kg/dm3 | |||
| Ratio water/cement = 0.64 | |||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mañero-Sanz, H.; García del Toro, E.M.; Alcaraz-Carrillo de Albornoz, V.; Luizaga Patiño, A. Method for the Improvement of the Elasticity Module of Concrete Specimens by Active Confinement. Sustainability 2019, 11, 3289. https://doi.org/10.3390/su11123289
Mañero-Sanz H, García del Toro EM, Alcaraz-Carrillo de Albornoz V, Luizaga Patiño A. Method for the Improvement of the Elasticity Module of Concrete Specimens by Active Confinement. Sustainability. 2019; 11(12):3289. https://doi.org/10.3390/su11123289
Chicago/Turabian StyleMañero-Sanz, Hugo, Eva M. García del Toro, Vicente Alcaraz-Carrillo de Albornoz, and Alfredo Luizaga Patiño. 2019. "Method for the Improvement of the Elasticity Module of Concrete Specimens by Active Confinement" Sustainability 11, no. 12: 3289. https://doi.org/10.3390/su11123289
APA StyleMañero-Sanz, H., García del Toro, E. M., Alcaraz-Carrillo de Albornoz, V., & Luizaga Patiño, A. (2019). Method for the Improvement of the Elasticity Module of Concrete Specimens by Active Confinement. Sustainability, 11(12), 3289. https://doi.org/10.3390/su11123289





