1. Introduction
The last decade has seen a notable increase in the emphasis on sustainable development as an integral aspect of energy planning and policy making in many countries [
1]. At the same time, it is widely acknowledged that increasing energy is required to maintain comfortable conditions and services in buildings. The use of conventional generation is considered to be inefficient, as it is only capable of converting, on average, about a third of the input fuel’s potential energy into usable energy [
2]. As a result, governments in many countries have developed policies designed to encourage greater deployment of combined heat and power systems (CHPS).
CHPS generate electricity and useful thermal energy in a single, integrated system. It is a distribution energy system which offers an effective way to make use of the waste heat energy from an on-site electric power generation unit, to contribute to satisfying the thermal load of a building [
3]. By doing so, heat that is normally wasted in conventional power generation is recovered as useful energy, which avoids the losses that would otherwise be incurred from separate generation of heat and power. Thus, the use of CHPS are important, as these systems can significantly reduce electricity grid dependence and save operational costs [
4,
5].
However, evaluating the performance of CHPS is challenging due to the presence of (a) multiple alternatives, (b) conflicting and incommensurable objectives, and (c) qualitative indicators that are used instead of quantitative values. To deal with the performance evaluation process of CHPS in an effective manner, multicriteria decision analysis is applied. Evaluating the performance of CHPS is a multicriteria analysis problem. This is because multicriteria analysis refers to selecting or ranking alternative(s), from available alternatives with respect to multiple, usually conflicting criteria [
6]. With the characteristics of the CHPS evaluation problem, multicriteria analysis methodology is suited for evaluating the performance of individual CHPS.
Much research has been done on the development of approaches for evaluating the performance of CHPS [
1,
2,
3]. Cavallaro et al. [
1] applied a combination of the fuzzy Shannon’s entropy and the fuzzy technique for order of preference by similarity to ideal solution (TOPSIS), for evaluating the performance of CHPS. The Shannon’s entropy concept is introduced for assigning weights to the criteria. Then, the fuzzy TOPSIS approach is used for describing the overall performance of all alternatives. However, the approach is inflexible in weight elicitation and consistency checking in the performance evaluation process. Zangeneh et al. [
2] applied the analytical hierarchy process (AHP) approach for evaluating the performance of CHPS, with respect to their economic, technical, and environmental criteria. With the use of this method, multiple evaluation criteria were simultaneously considered. To reduce the cognitive burden on the decision maker, pairwise comparison is used for assessing the performance of individual alternatives and the relative importance of the criteria. Nonetheless, the approach becomes cumbersome and may lead to inconsistent decisions, when the number of alternatives and criteria increases. Carvalho et al. [
3] presented the mixed-integer linear programming approach for assessing the performance of CHPS. A linearization procedure was applied to formulate the problem as a linear mixed integer programming approach. The approach is very realistic, as it can consider multiple objectives and multiple constraints, with a certain degree of flexibility. However, it requires tedious mathematical computation in the performance evaluation process. To effectively address the limitations of the existing approaches, this paper presents a multicriteria assessment model for evaluating the performance of CHPS. Intuitionistic fuzzy numbers are used for representing the subjective and imprecise assessments of the decision makers in evaluating the relative importance of the criteria and the performance of individual CHPS. An effective algorithm is developed based on the concept of ideal solutions for calculating the performance index, for each alternative across all criteria. An example is given to demonstrate the applicability of the proposed multicriteria assessment model.
2. Performance Evaluation of CHPS
Evaluating the performance of the CHPS with respect to a set of specific criteria is complex and challenging [
2,
4]. This is due to the presence of (a) multiple alternatives; (b) conflicting and incommensurable objectives; and (c) fuzzy data derived from imprecise judgments of qualitative performance ratings, resulting from human subjectivity [
7]. To effectively solve this problem, an overall performance evaluation of individual CHPS is desirable.
Several studies have been carried out on identifying the relevant criteria for evaluating the performance of CHPS [
1,
2,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19,
20,
21,
22,
23,
24,
25,
26,
27,
28,
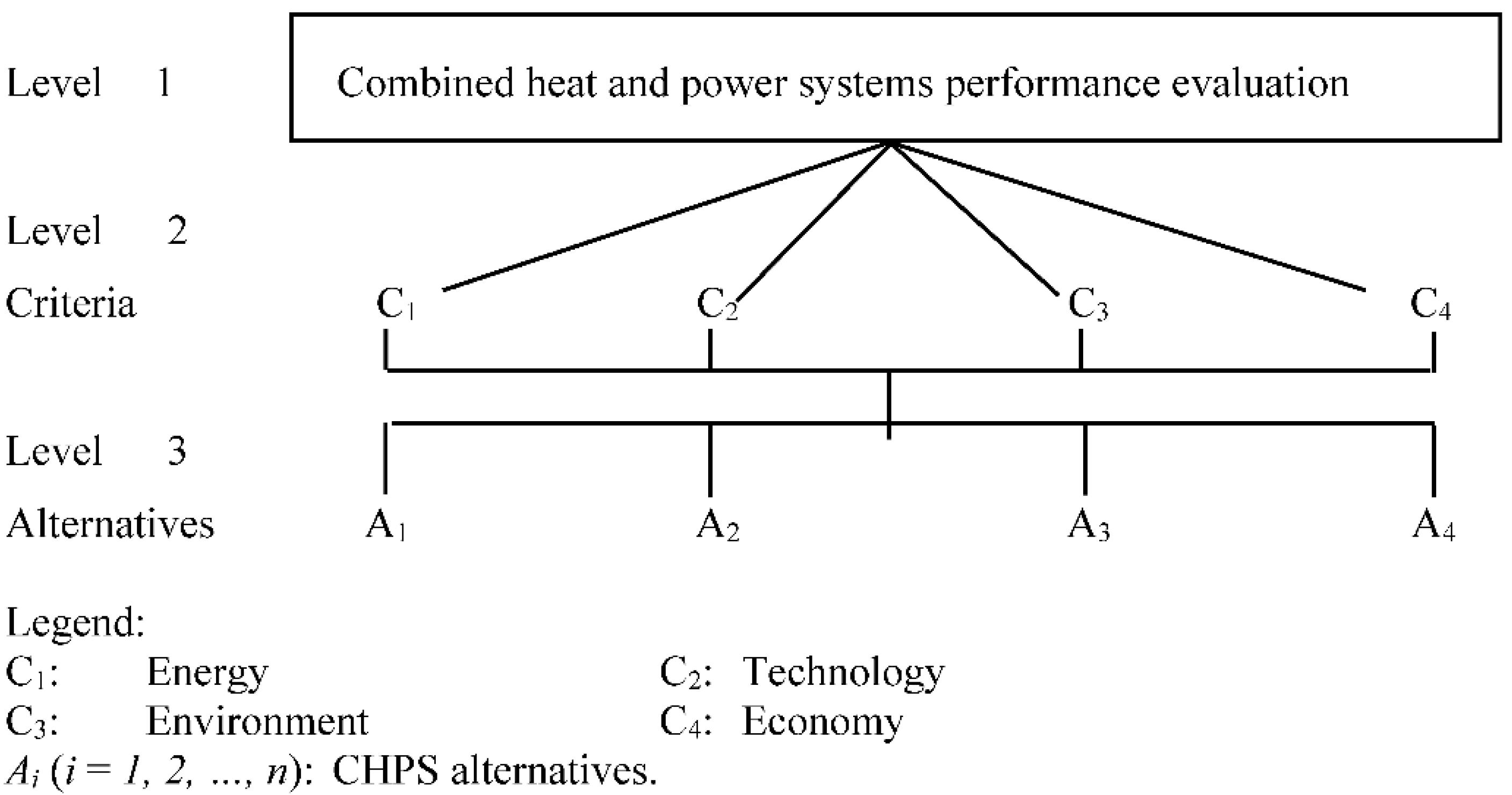
29]. A review of the related literature leads to the classification of these critical criteria into (a) energy, (b) technology, (c) environment, and (d) economy.
Figure 1 shows the hierarchical structure of the CHPS performance evaluation problem.
Energy criteria considers the electric efficiency, utilization policy relating to fuel usage, power to heat ratio, and overall efficiency of the CHPS. Input–output power ratio is both technology and size dependent, which ultimately influences electric efficiency. Fuel usage is determined by the net electrical output, whilst power to heat ratio determines the amount of heat generated to a certain quantity of power. However, the overall CHPS efficiency relates to the fuel consumed to produce the net electrical and thermal power [
1]. Zangeneh et al. [
2] state that energy usage and emissions should be considered when evaluating the performance of CHPS. Zmeureanu and Xin [
9] believe that total energy and energy efficiency analysis are very helpful when conducting the performance evaluation of CHPS. Cho et al. [
10] state that primary energy consumption is the relevant factor in the evaluation of CHPS. Jannelli et al. [
11] state that efficiency of the system and energy utilization factor, are the important criteria for measuring the performance of CHPS. Barbieri et al. [
12] point out that economic performances are relevant factors in evaluating the performance of CHPS. Energy criteria are usually assessed by the efficiency of the CHPS, and the utilization policy. The efficiency of the CHPS, refers to the measure commonly used to establish the superiority of CHP systems, by comparing its fuel usage with conventional systems that supply electricity and thermal energy. Utilization policy refers to the strategies adopted to estimate the amount of fuel consumed to generate energy [
1]. This utilization policy helps to determine the costs and efforts associated with power generation.
CHPS generate both electricity and heat in a single integrated system. It is an approach to implementing the best available technology, to reduce wastage and improve efficiencies. Technology criteria deals with efficiency of the system operation, and the use of a single source for both electricity and heat generation. These criteria look at the improvement of both economic and environmental efficiencies [
13]. Teymouri-Hamzehkolaei and Sattari [
14] and Kialashaki [
15] point out that technical factors must be considered in the performance evaluation of CHPS. Zamfirescu et al. [
16] and Wang et al. [
13] believe that the performance evaluation of the CHPS, should consider energetic and environmental criteria. To deal with the needs of environmental issue, maintenance cost, regulatory convenience, and technological maturity of CHPS are considered in technology evaluation [
17]. The reliability of CHPS refers to consistent performance of the CHPS to generate power and thermal energy, with low failure and maintenance. The regulatory convenience reflects the local government’s policies on financial incentives for adopting CHPS, and funding of research and development projects. The CHPS technology maturity aspect details the use of particular CHPS, and its widespread applications [
13].
CHPS offer several environmental benefits by minimizing greenhouse gas emissions [
15]. Environment criteria considers various factors, including the amount of fuel combusted, the emission factor, and emission of NO
x, SO
2, PM
10, and CO
2, from burning natural gas and the default emission factor. Alanne et al. [
18] believe that financial and environmental performances are critical in evaluating the performance of CHPS. Aussant et al. [
19] state that environmental characteristics should both be considered, whilst evaluating the performance of CHPS. Meanwhile, Ren and Gao [
20] consider environmental factors to assess fuel cell and gas engine CHPS alternatives. Earlier studies suggest that electricity generation leads to carbon emissions. Wang et al. [
21] believe that emission of the energy system is certainly a criterion to be considered in the performance evaluation process. Jannelli et al. [
11] point out that by reducing the primary energy sector consumption and using the appropriate CHPS, this will have a positive impact on the environment. Wang et al. [
22] point out the monetary values of damage to the environment and health, resulting from atmospheric emissions created by the CHPS. Thus, the assessment of environmental factors, in terms of the benefits to end users, will support the goal of minimizing carbon emissions [
23].
CHPS are designed to achieve energy efficiency by minimizing energy consumption [
24]. These systems are considered sustainable in energy production and management, due to their efficient fuel usage by combining heat and power systems and utilizing the heat generated along the electricity generation path [
1,
9]. To achieve efficient energy management goals through CHPS, an overall evaluation of relevant criteria is important. Undoubtedly, CHPS are proven sustainable, but the inclusion of economic and environmental criteria in the performance evaluation process helps the decision maker to identify an appropriate system [
13,
25]. Pilavachi et al. [
26] believe that economic feasibility of CHPS is the most important factor to be considered. Zheng et al. [
27] state that the operating costs of a combined district heating system need to include the economic base load ratio, critical peak heating temperature, and the operation strategy for the system. At the same time, Gonzalez-Pino et al. [
4] point out that the operational and economic viability of CHPS must be considered in the performance evaluation process. Skorek-Osikowska et al. [
8] believe that an effective CHPS must yield economical savings and real energy savings, based on primary energy consumption, and the ability to reduce the emission of pollutants. Meanwhile, Hawkes et al. [
28] believe that operation costs, including wages and the funds spent for energy, products and services, need to be considered while evaluating the performance of CHPS. Possidente et al. [
25] point out that operation and maintenance costs must be considered in the performance evaluation process of CHPS. Economic criteria deal with the costs associated with the set up and operation of CHPS. Most importantly, it deals with the maintenance, net heating, and operating costs. The maintenance costs are associated with regular inspections, scheduled equipment service, and labor costs. The net heating costs, include costs associated with energy conversion for heating. The operating costs involve costs associated with generating electricity and thermal energy [
10].
There are various CHPS technologies available in the market. These include steam turbine systems, gas turbines, micro turbines, fuel cells, and reciprocating engine technologies [
29]. Steam turbine systems are widely used in the United States and European nations. They generate power as a by-product of heat generation systems. In gas turbines, a compressor pulls high temperature air and compresses it to produce high-pressure steam. Micro turbines are compact gas turbines that operate on truck turbocharger technology, which generate energy by capturing engine exhaust heat [
29]. Fuel cells are based on the chemical reaction of oxygen and hydrogen. They generate electricity and heat by oxidizing the fuel. This process can be accelerated with the help of catalysts or acidic solutions. Reciprocating engines are commonly used in mobile portable engines and garden equipment. The technology is over a century old. These are commonly used to produce hot water by compressing the fuel and air [
29]. There are several benefits and limitations of each of these systems, in terms of technological reliability, emissions, cost, and energy production capacity. Fuel micro turbine and reciprocating engine technologies are suitable for producing lesser energy capacity, ranging from 30 kW to 1000 kW. However, steam turbine, gas turbine, and fuel cells, combine heat and power technologies, and are suitable for producing energy ranging from 50 kW to several hundred million kW [
29].
Section 4 presents an example of evaluating the performance of three CHPS technologies, for an Indian sugar company. Sugar companies generally require high capacity CHPS technologies [
30]. The low capacity of micro turbine and reciprocating engine technologies, make them unsuitable for sugar companies. Considering the size of the Indian sugar company’s needs for a high capacity CHPS, steam turbine (
A1), gas turbine (
A2), and micro turbine (
A3) technology alternatives were considered for evaluation.
To effectively evaluate the performance of CHPS in a given situation, it is important for decision makers to simultaneously consider the multiple evaluation criteria discussed above and apply the multicriteria assessment model presented in the following section.
3. The Multicriteria Assessment Model
Evaluating the performance of CHPS usually involves (a) discovering all the available alternatives; (b) identifying the performance evaluation criteria; (c) assessing the performance ratings of CHPS alternatives, and the weights of the criteria by multiple decision makers; (d) aggregating the alternative ratings and criteria weights, for producing an overall performance index value, for each alternative across all criteria, on which the final decision can be made [
24].
To model the subjectiveness inherently present in the group decision making process, interval-valued intuitionistic fuzzy numbers [
31] are used to facilitate the subjective assessment made by the decision makers. The introduction of intervals for describing the value of membership and non-membership, helps to reduce the cognitive demand on decision makers in representing their subjective assessments in the decision-making process [
32].
The performance evaluation process starts with assessing the performance ratings of each decision alternative Ai (i = 1, 2, …, m), with respect to all available criteria from the decision makers Dk (k = 1, 2, …, s). The interval-valued intuitionistic fuzzy decision matrix for each decision maker is represented as , where k = 1, 2, …, s and is an interval-valued intuitionistic fuzzy number, which represents the performance rating of alternatives with respect to all available criteria. indicates the degree to which alternative Ai satisfies criterion Cj, whilst indicates the degree to which alternative Ai dissatisfies criterion Cj. is the weight of each decision maker where
To make an effective decision in multicriteria group decision making, the collective interval-valued intuitionistic fuzzy decision matrix, which represents the overall performance of each alternative on each criterion from all the decision makers, has to be determined. Here, the interval-valued intuitionistic fuzzy weighted geometric (IIFWG) operator, as described in Reference [
33], is introduced for aggregating individual fuzzy decision matrices into a collective interval-valued intuitionistic fuzzy decision matrix
as in (1).
To rank all the alternatives based on the collective interval-valued intuitionistic fuzzy decision matrix in (1), the concept of the positive and negative ideal solutions is used. The interval-valued intuitionistic fuzzy positive ideal solution
and the interval-valued intuitionistic fuzzy negative ideal solution
can be determined, respectively, as in Equations (2) and (3).
where
B and
C are the set of benefit and cost criteria,
and
.
Based on Equations (4) and (5), the weighted separation measures between alternative
Ai and the positive ideal solution and the negative solution can be respectively calculated as
The most preferred alternative should not only have the shortest distance from the positive ideal solution, but also the longest distance from the negative ideal solution [
32]. Following this line, an overall performance index for each alternative
Ai across all the criteria can be determined by
Based on the performance index Pi values obtained as in Equation (6), the ranking order of each alternative Ai can be determined. The larger the performance index Pi, the better the performance of the alternative Ai.
The procedure for evaluating the performance of CHPS using the multicriteria assessment model is summarized as:
- Step 1:
Obtain the performance ratings, with respect to all available criteria from the decision makers.
- Step 2:
Aggregate individual fuzzy decision matrices into a collective interval-valued intuitionistic fuzzy decision matrix by using Equation (1).
- Step 3:
Determine the interval-valued intuitionistic fuzzy positive ideal solution , and the interval-valued intuitionistic fuzzy negative ideal solution , as in Equations (2) and (3), respectively.
- Step 4:
Calculate the weighted separation measures by using Equations (4) and (5).
- Step 5:
Calculate the performance index Pi by using Equation (6).
- Step 6:
Determine the ranking order of each alternative Ai, based on the performance index Pi.
4. Application of the Model to a Case Study
To demonstrate the applicability of the proposed multicriteria assessment model above, an example evaluating the performance of three CHPS for a sugar company in India is presented. The development and implementation of CHPS have become widespread in the Indian sugar industry, not only for meeting onsite power requirements, but also for increasing revenues through exports of excess power. At the same time, the CHPS help cooperatives in the sugar industry in replacing high-cost grid power and reducing fuel requirements. As a result, three cooperatives decided to undergo modernization projects by replacing their existing power systems with CHPS.
The CHPS performance evaluation process starts with the formation of a committee consisting of three decision makers. Four relevant criteria including (a) energy (C1), (b) technology (C2), (c) environment (C3), and (d) economy (C4), were used to evaluate the performance of three CHPS, consisting of the steam turbine (A1), gas turbine (A2), and micro turbine (A3).
The procedure for the performance evaluation process is explained below:
Step 1: The performance ratings of all available CHPS can be determined by the decision makers, as shown in
Table 1.
Step 2: The collective interval-valued intuitionistic fuzzy decision matrix can be calculated by using Equation (1).
Table 2 shows the results.
Step 3: Based on Equations (2) and (3), the interval-valued intuitionistic fuzzy positive ideal solution
, and the interval-valued intuitionistic fuzzy negative ideal solution
, can be determined.
Table 3 shows the calculated results.
Step 4: Using Equations (4) and (5), the weighted separation measures between the alternatives and the positive ideal solution and the negative solution can be calculated. Here,
w is taken as {0.2, 0.3, 0.2, 0.15, 0.15},
p = 1, and
t = 1.
Table 4 shows the results.
Step 5: The overall performance index
Pi values, for each CHPS across all the criteria, can then be calculated using Equation (6).
Table 5 shows the calculated results.
Step 6: Based on
Table 5, the ranking order of each alternative can be determined. Alternative
A2, is the best alternative, as it has the highest performance index value of 0.709.
The result in
Table 5 provides information about the performance index values and rankings of all CHPS alternatives.
Table 5 shows that alternative
A2, which is the gas turbine alternative, was found to be the most suitable CHPS alternative for implementation at the sugar company, compared to the steam turbine (
A1) and micro turbine (
A3).
An analysis of the requirements of the CHPS performance evaluation problem, as described above, reveals that (a) multiple decision makers are involved in the performance evaluation process; (b) all the decision makers’ assessments on criteria weights and performance ratings are subjective; and (c) the conflicting nature of the multiple evaluation criteria in the decision making process must be considered. Existing approaches for dealing with this class of decision situations are often (a) unable to adequately handle the inherent subjectiveness in the decision-making process, and (b) cognitively demanding on the decision makers in the evaluation process. To effectively handle the CHPS performance evaluation problem, a structured approach is desirable. From the discussion above, it is evident that the multicriteria assessment model is capable of effectively handling the presence of multiple alternatives, conflicting criteria, and fuzzy data derived from imprecise judgments of qualitative performance ratings, resulting from human subjectivity. With its simplicity in concept and computation, the multicriteria assessment model is applicable for dealing with the general multicriteria performance evaluation problem.
5. Conclusions
The performance evaluation of CHPS is complex and challenging due to the involvement of multiple decision makers, the multi-dimensional nature of the decision problem, and the subjectiveness and imprecision inherent in the human decision-making process. This paper formulated the performance evaluation of CHPS as a multicriteria group decision making problem and developed a multicriteria assessment model for evaluating the performance of CHPS. Four important criteria for evaluating the performance of CHPS were identified. To model the subjectiveness inherently present in the group decision making process, interval-valued intuitionistic fuzzy numbers were used to facilitate the subjective assessment to be made by the decision makers. An effective algorithm was developed based on the concept of ideal solutions for calculating the overall performance index, for each alternative across all criteria. An example was presented that showed the multicriteria assessment model was useful and effective, for solving the group decision making problem.
The multicriteria assessment is capable of adequately considering the involvement of multiple decision makers, the multi-dimensional nature of the decision problem, and the subjectiveness and imprecision of the performance evaluation process. A sugar company in India was chosen in this study to demonstrate the applicability of the multicriteria assessment model, for evaluating benchmarking the performance of available CHPS. Three CHPS are evaluated against four important criteria. Based on the performance evaluation process, gas turbine technology (alternative A2) was found to be the most suitable alternative for selection. Thus, the proposed multicriteria assessment model was able to help organizations understand the performance of CHPS, and provide opportunities for these organizations to improve the overall performance of available CHPS.
In terms of practical contributions, the proposed multicriteria assessment model has demonstrated its effectiveness in evaluating the performance of CHPS. The evaluation outcome will help organizations to better manage the development and implementation of strategies related to CHPS. Thus, the multicriteria assessment model is a useful tool for evaluating the performance of CHPS in organizations. In addition, the multicriteria assessment model can deal with the multicriteria group decision making problems in real world settings effectively and efficiently.
The limitations of this study include: (a) The outcome of the multicriteria assessment model is highly dependent on the inputs provided by the decision makers; and (b) the need to consider each specific sub-criteria weightage, provided by the decision makers in the performance evaluation process. Future studies on this research area can include: (a) The development of an optimization method for dealing with the performance evaluation problem, and (b) the development of a decision support system to increase the efficiency of the performance evaluation process.