Substructure Hybrid Simulation Boundary Technique Based on Beam/Column Inflection Points
Abstract
1. Introduction
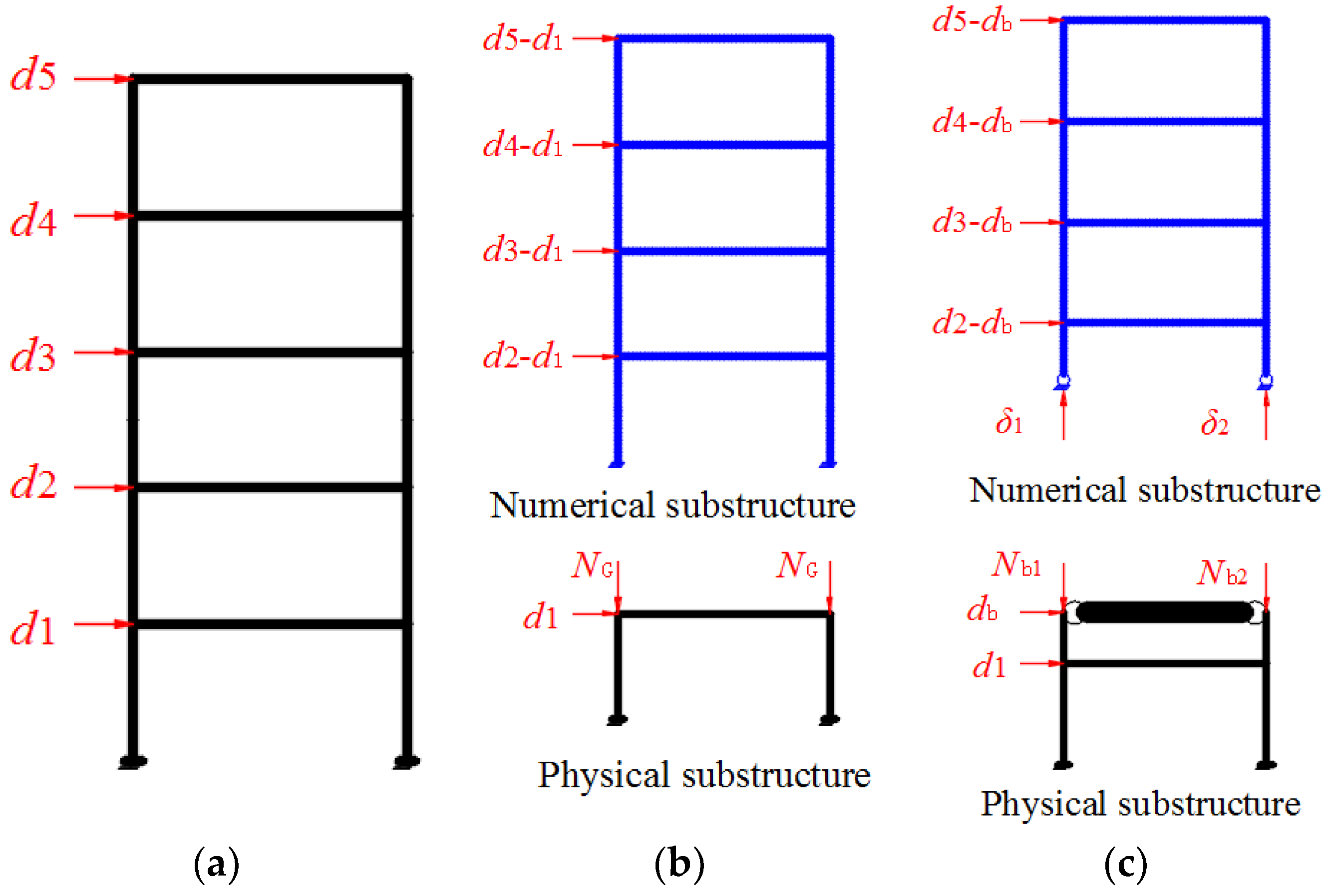
2. Boundary Technique for the HS
3. Implement of Boundary Technique
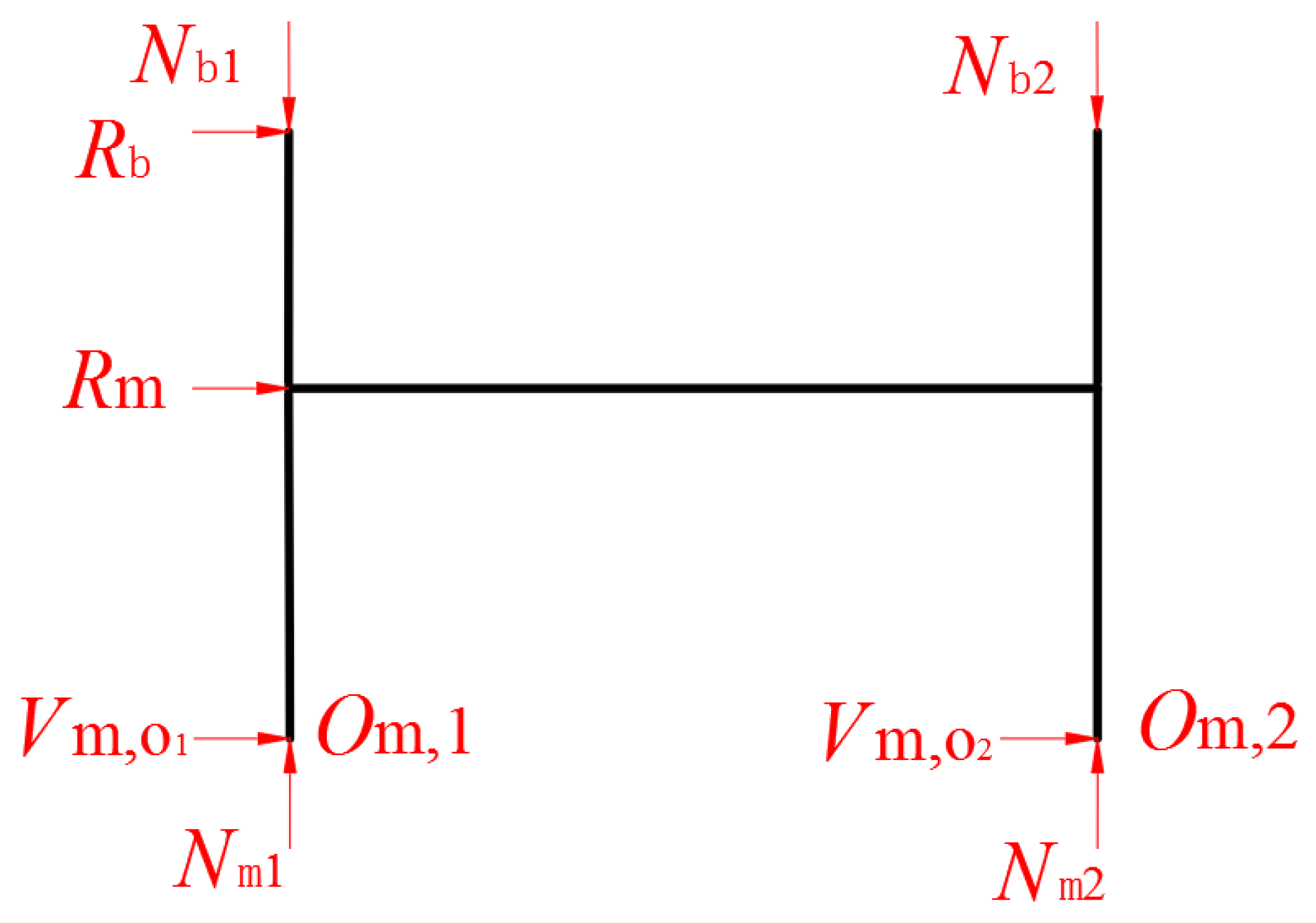
3.1. HS Component Interaction
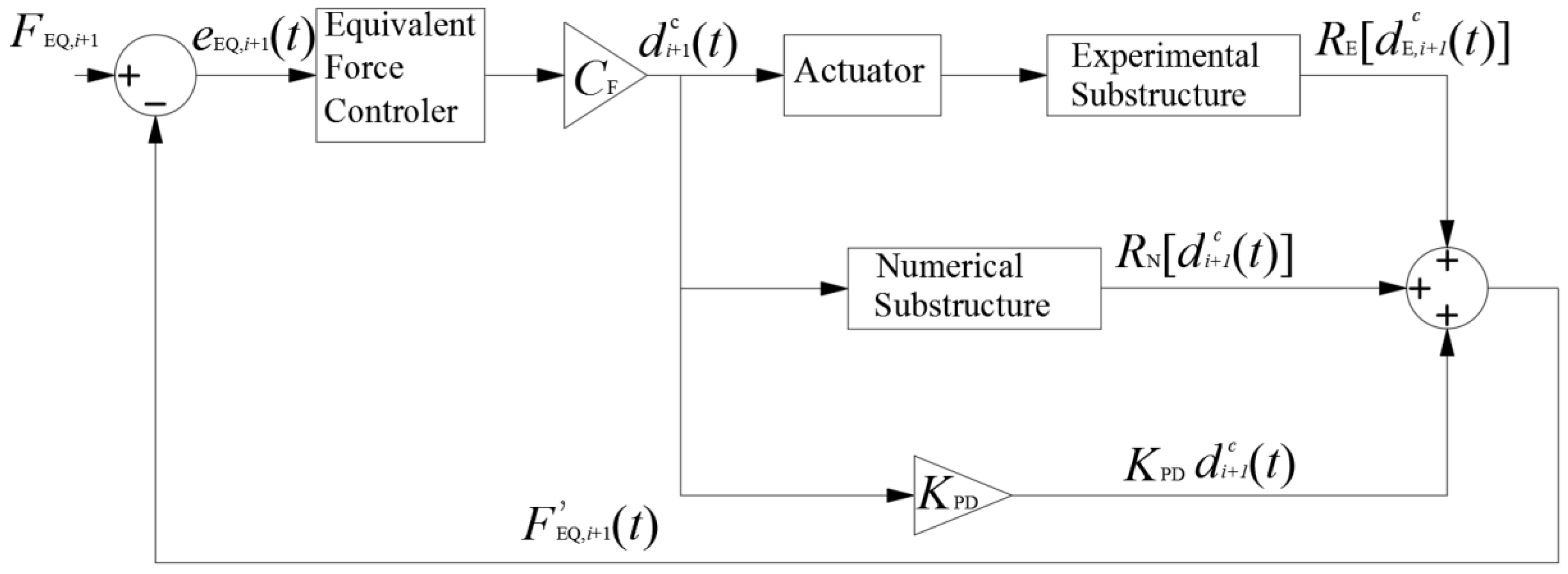
3.2. Equivalent Force Control Method
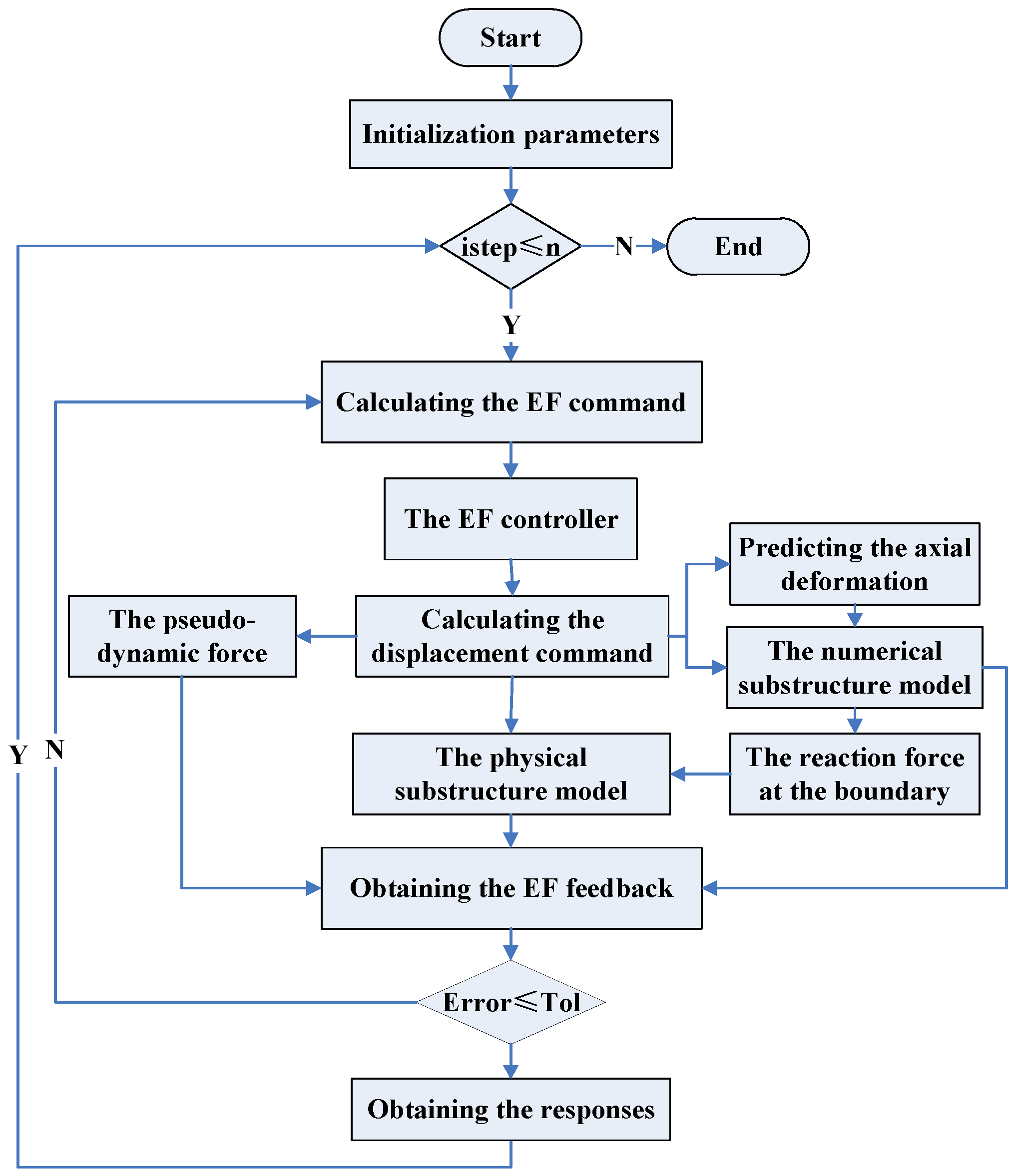
3.3. Basic Process
- Step 1: The initial stiffness matrix, the initial mass matrix, the initial damping matrix, other initial parameters, and the ground motion record are obtained. The ground motion record may be scaled in amplitude to accommodate the goal of different HS tests.
- Step 2: The EF command is calculated. The displacement command is then calculated using the force-displacement conversion matrix and the EF controller.
- Step 3: The pseudo-dynamic force is calculated using the pseudo-dynamic stiffness KPD, which can be determined from the initial parameters. Concurrently, the predicted axial deformation is obtained using Equation (1). Before the next step, all calculations are realized using Matlab. After this step, the calculated displacement command of the numerical substructure and the prediction axial deformation at the boundary is applied to the numerical substructure modeled by OpenSEES.
- Step 4: The calculated displacement command of the numerical substructure and the prediction axial deformation at the boundary are sent to the numerical substructure. Subsequently, the reaction force at the boundary is calculated. Similarly, the data calculated by OpenSEES are sent to the Matlab program and subsequently wait to receive the data calculated by Matlab for the next step.
- Step 5: The calculated reaction force in the vertical direction and the displacement command in the horizontal direction are sent to the actuator controllers for the physical substructure. Then, the reaction of the physical substructure is obtained by: (i) the sensors in the associated loading devices; or (ii) OpenSEES for the virtual test.
- Step 6: The EF feedback is obtained by summing up the pseudo-dynamic force, and the reaction of both the numerical substructure and the physical substructure. Then, compare the EF feedback with the EF command to obtain the error between them. If the error between the EF feedback with the EF command is less than the specified tolerance, go the next step. If not, repeat the steps from the third step to the sixth step.
- Step 7: The responses of the entire structure are obtained. Then, repeat the above-mentioned steps until the entire ground motion record has been processed.
4. Numerical Simulation
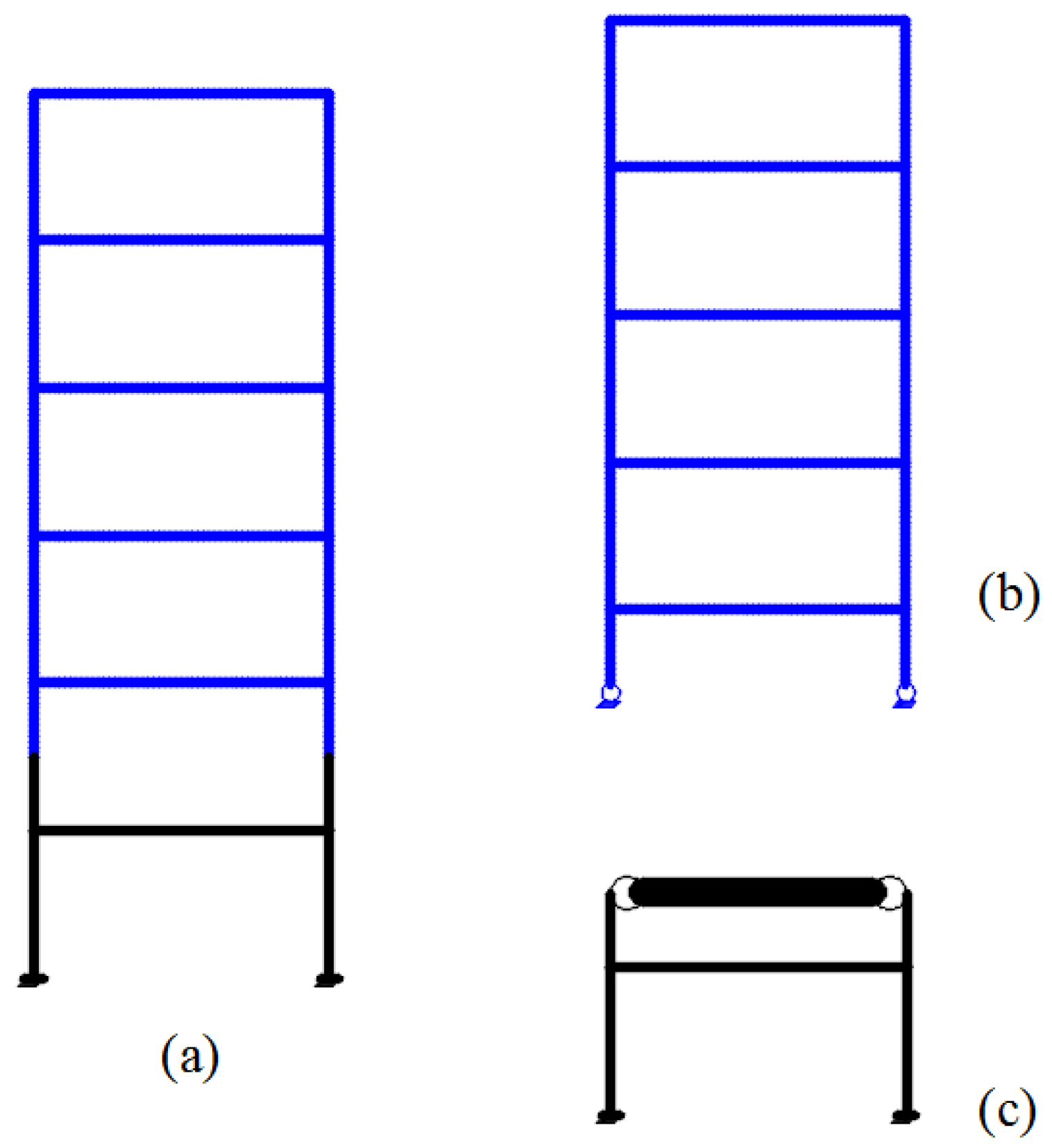
4.1. Numerical Simulation Model Based on the Uniform Design
4.2. Numerical Simulation Results Analysis
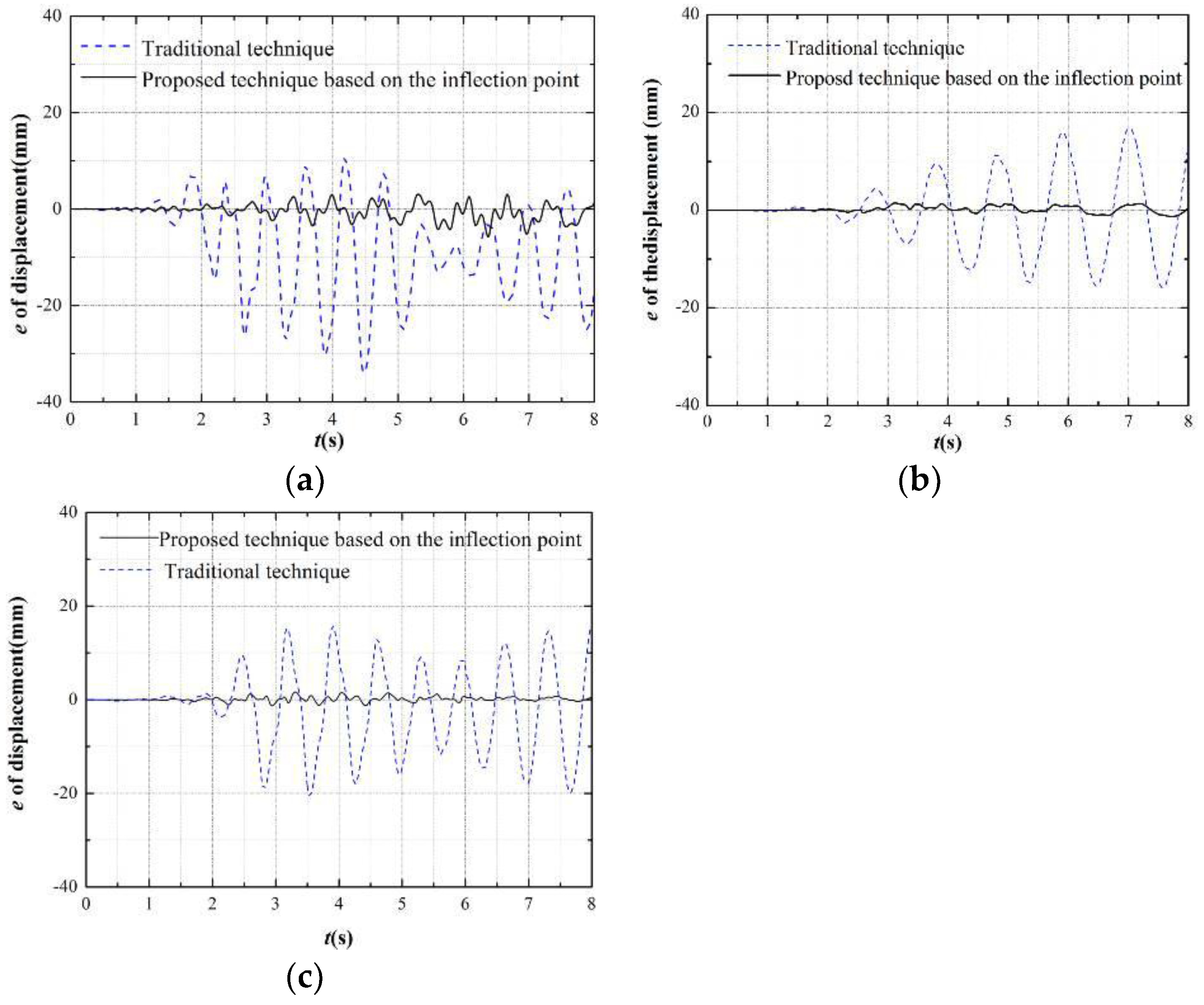
4.2.1. Displacements Analysis
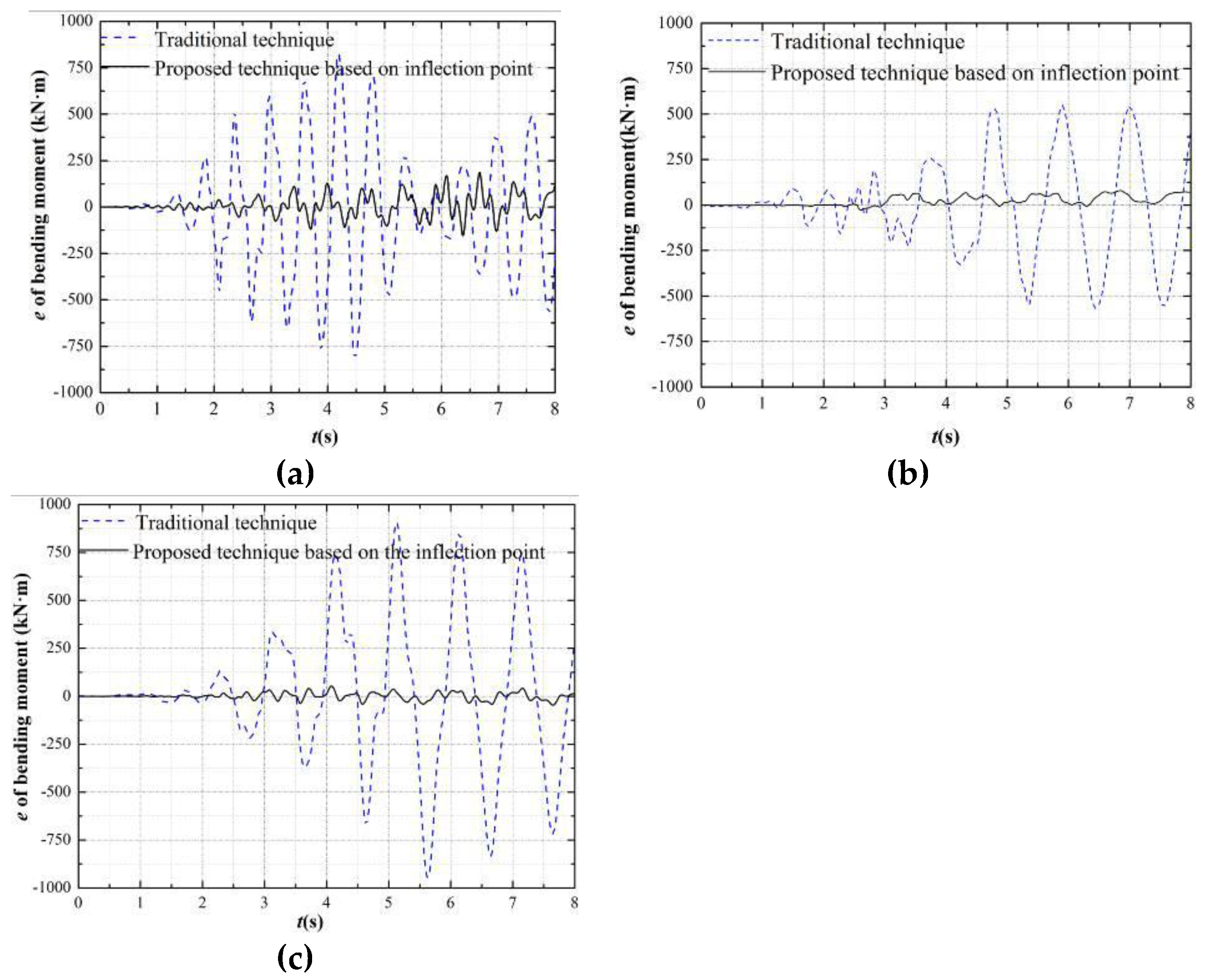
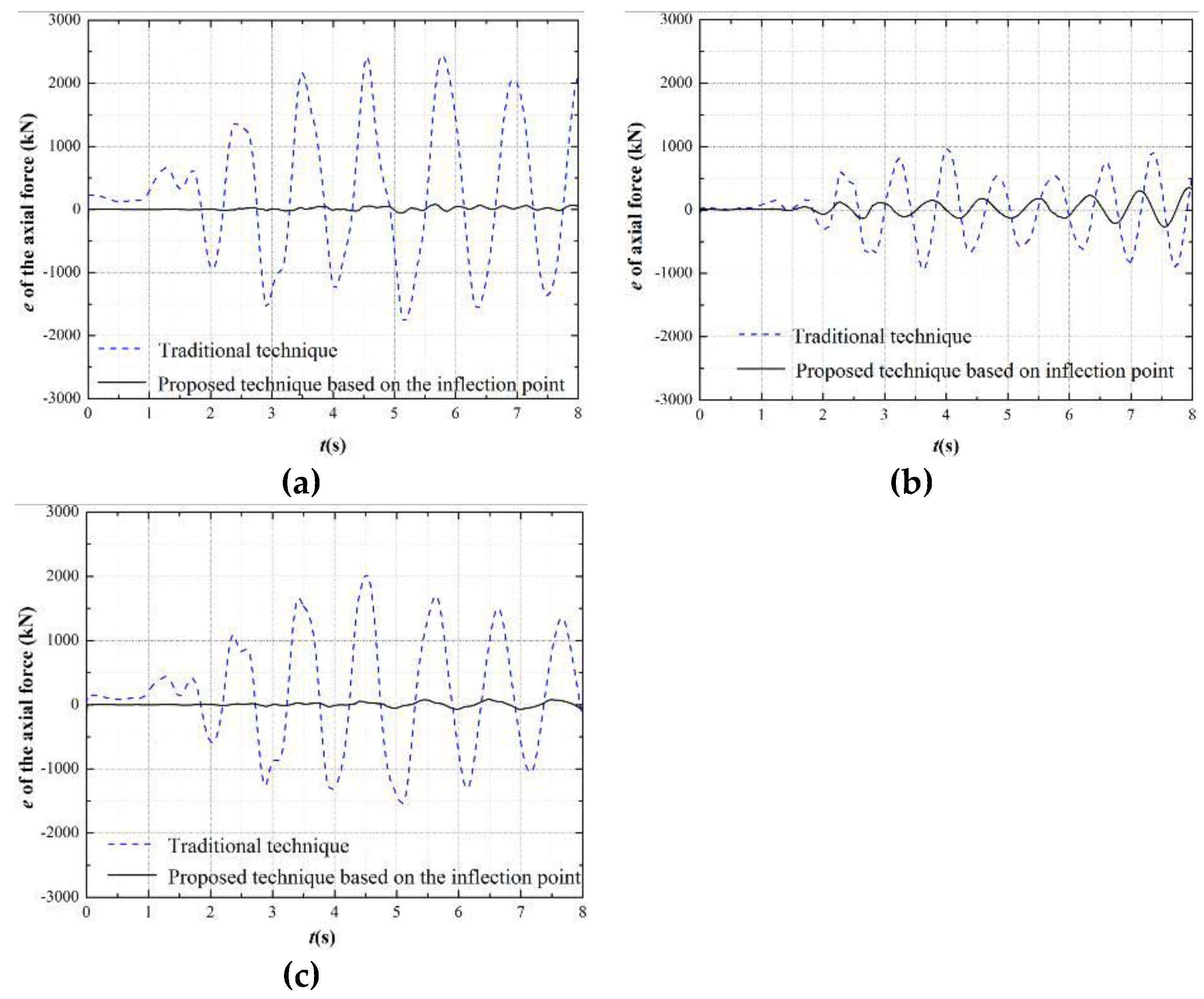
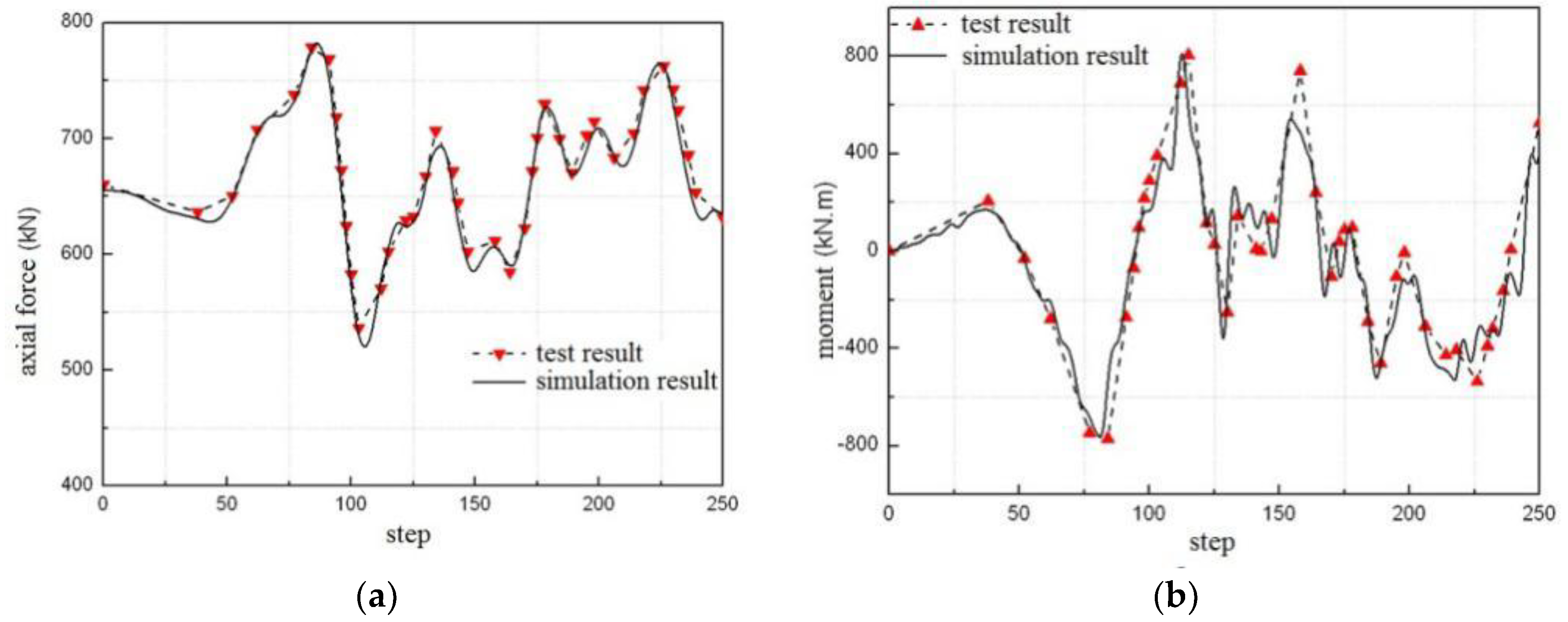
4.2.2. Internal Force Analysis
5. Experimental Validation
5.1. Test Model
5.2. Displacement–Force Mixed Control Technique
5.2.1. Vertical Loading Devices
5.2.2. Horizontal Loading devices
5.3. Arrangement of the Measurement Devices
5.3.1. Arrangement of Displacement Measuring Points
5.3.2. Arrangement of Strain Gauge
5.4. Test Results and Analysis
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hakuno, M.; Shidowara, M.; Haa, T. Dynamic destructive test of a cantilevers beam, Controlled by an analog-computer. Trans. Jpn. Soc. Civ. Eng. 1969, 171, 1–9. [Google Scholar] [CrossRef]
- Takanashi, K.; Nakashima, M. Japanese activities on online testing. J. Eng. Mech. 1987, 113, 1014–1032. [Google Scholar] [CrossRef]
- Mahin, S.A.; Shing, P.B.; Thewalt, C.R.; Hanson, R.D. Pseudodynamic test method current status and future directions. J. Struct. Eng. 1989, 115, 2113–2128. [Google Scholar] [CrossRef]
- Shing, P.B.; Nakashima, M.; Bursi, O.S. Application of psuedodynamic test method to structural research. Earthq. Spectr. 1996, 12, 29–56. [Google Scholar] [CrossRef]
- Saouma, V.; Sivaselvan, M. Hybrid Simulation: Theory, Implementation and Applications; Taylor & Francis: London, UK, 2008; ISBN 978-0-415-46568-7. [Google Scholar]
- Bursi, O.S.; Wagg, D. Modern Testing Techniques for Structural Systems: Dynamics and Control; Springer: New York, NY, USA, 2008; ISBN 978-3-211-09445-7. [Google Scholar]
- Wu, B.; Wang, Q.; Shing, P.B.; Ou, J. Equivalent force control method for generalized real-time substructure testing. Earthq. Eng. Struct. Dyn. 2007, 36, 1127–1149. [Google Scholar] [CrossRef]
- Wallace, M.I.; Sieber, J.; Neild, S.A.; Wagg, D.J.; Krauskopf, B. Stability analysis of real-time dynamic substructuring using delay differential equation models. Earthq. Eng. Struct. Dyn. 2005, 34, 1817–1832. [Google Scholar] [CrossRef]
- Ahmadizadeh, M.; Mosqueda, G.; Reinhorn, A.M. Compensation of actuator delay and dynamics for real-time hybrid structural simulation. Earthq. Eng. Struct. Dyn. 2008, 37, 21–42. [Google Scholar] [CrossRef]
- Chen, C.; Ricles, J.M.; Marullo, T.; Mercan, O. Real-time hybrid testing using the unconditionally stable explicit CR integration algorithm. Earthq. Eng. Struct. Dyn. 2009, 38, 23–44. [Google Scholar] [CrossRef]
- Amin, M.; Shirley, D.; Siamak, R.; Arun, P. Predictive stability indicator: A novel approach to configuring a real-time hybrid simulation. Earthq. Eng. Struct. Dyn. 2017, 46, 95–116. [Google Scholar]
- Ou, G.; Ozdagli, A.I.; Dyke, S.J.; Wu, B. Robust integrated actuator control experimental verification and real-time hybrid simulation implementation. Earthq. Eng. Struct. Dyn. 2015, 44, 441–460. [Google Scholar] [CrossRef]
- Phillips, B.M.; Takada, S.; Spencer, B.F.; Fujino, Y. Feedforward actuator controller development using the backwarddifference method for real-time hybrid simulation. Smart Struct. Syst. 2014, 14, 1081–1103. [Google Scholar] [CrossRef]
- Friedman, A.; Dyke, S.J.; Phillips, B.; Ahn, R.; Dong, B.; Chae, Y.; Castaneda, N.; Jiang, Z.; Zhang, J.; Cha, Y.; et al. Large-scale real-time hybrid simulation for evaluation of advanced damping system performance. J. Struct. Eng. 2015, 141, 04014150. [Google Scholar] [CrossRef]
- Gao, X.; Castaneda, N.; Dyke, S.J. Real-time hybrid simulation: From dynamic system, motion control to experimental error. Earthq. Eng. Struct. Dyn. 2013, 42, 815–832. [Google Scholar] [CrossRef]
- Takahashi, Y.; Fenves, G. Software framework for distributed experimental-computational simulation of structural systems. Earthq. Eng. Struct. Dyn. 2006, 35, 267–291. [Google Scholar] [CrossRef]
- Kwon, O.S.; Elnashai, A.S.; Spencer, B.F. UI-SIMCOR: A global platform for hybrid distributed simulation. In Hybrid Simulation: Theory, Implementation and Applications; CRC Press: Boca Raton, FL, USA, 2008; pp. 157–167. [Google Scholar]
- Pan, P.; Tomofuji, H.; Wang, T.; Nakashima, M.; Ohsaki, M.; Mosalam, K.M. Development of peer-to-peer (P2P) internet online hybrid test system. Earthq. Eng. Struct. Dyn. 2006, 35, 867–890. [Google Scholar] [CrossRef]
- Guo, Y.R.; Zhu, X.J.; Wang, Z.M.; Zhang, Z.X. A NetSLab Based Hybrid Testing Program for Composite Frame Structures with Buckling Restrained Braces. Adv. Mater. Res. 2013, 639–640, 1142–1147. [Google Scholar] [CrossRef]
- Buckle, I.; Reitherman, R. The consortium for the George E. Brown J. network for earthquake engineering simulation. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004; p. 4016. [Google Scholar]
- Stojadinovic, B.; Mosqueda, G.; Mahin, S.A. Event-driven control system for geographically distributed hybrid simulation. J. Struct. Eng. 2006, 132, 68–77. [Google Scholar] [CrossRef]
- Kim, J.K. KOCED collaboratory program. In Proceedings of the Annual Meeting: Networking of Young Earthquake Engineering Researchers and Professionals (ANCER), Hawaii, HI, USA, 2004. [Google Scholar]
- Ohtani, K.; Ogawa, N.; Katayama, T.; Shibata, H. Project ‘E-Defense’ (3-D Full-Scale Earthqyake Testing Facility). In Proceedings of the Joint NCREE/JRC Workshop on International Collaboration on Earthquake Disaster Mitigation Research, Taipei, Taiwan, 17–18 November 2003. [Google Scholar]
- Elnashai, A.S.; Spencer, B.F.; Kuchma, D.A.; Yang, G.; Carrion, J.E.; Gan, Q.; Kim, S.J. The multi-Axial full-scale sub-structured testing and simulation (MUST-SIM) facility at the University of Illinois at Urbana-Champaign. In Advances in Earthquake Engineering for Urban Risk Reduct; Kluwer Academic Publishers: Alphen aan den Rijn, The Netherlands, 2006; pp. 245–260. [Google Scholar]
- Fermandois-Cornejo, G.; Spencer, B.F. Framework development for multi-axial real-time hybrid simulation testing. In Proceedings of the 16th World Conference on Earthquake Engineering, Santiago, Santiago Metropolitan Region, Chile, 9–13 January 2017; p. 2770. [Google Scholar]
- Hashemi, M.J.; Tsang, H.-H.; Al-Ogaidi, Y.; Wilson, J.L.; Al-Mahaidi, R. Collapse Assessment of Reinforced Concrete Building Columns through Multi-Axis Hybrid Simulation. ACI Struct. J. 2017, 114, 437–449. [Google Scholar] [CrossRef]
- Gao, X.; Castaneda, N.; Dyke, S. Experimental Validation of a Generalized Procedure for MDOF Real-Time Hybrid Simulation. J. Eng. Mech. 2014, 140, 04013006. [Google Scholar] [CrossRef]
- Murray, J.A.; Sasani, M. Collapse Resistance of a Seven-Story Structure with Multiple Shear-Axial Column Failures Using Hybrid Simulation. J. Struct. Eng. 2016, 143, 04017012. [Google Scholar] [CrossRef]
- Kammula, V.; Erochko, J.; Kwon, O.; Christopoulos, C. Application of hybrid-simulation to fragility assessment of the telescoping self-centering energy dissipative bracing system. Earthq. Eng. Struct. Dyn. 2014, 43, 811–830. [Google Scholar] [CrossRef]
- Chae, Y.; Ricles, J.M.; Sause, R. Large-scale real-time hybrid simulation of a three-story steel frame building with magneto-rheological dampers. Earthq. Eng. Struct. Dyn. 2014, 43, 1915–1933. [Google Scholar] [CrossRef]
- Dong, B.; Sause, R.; Ricles, J.M. Accurate real-time hybrid earthquake simulations on large-scale MDOF steel structure with nonlinear viscous dampers. Earthq. Eng. Struct. Dyn. 2015, 44, 2035–2055. [Google Scholar] [CrossRef]
- Abbiati, G.; Bursi, O.S.; Caperan, P.; Sarno, L.D.; Molina, F.J.; Paolacci, F.; Pegon, P. Hybrid simulation of a multi-span RC viaduct with plain bars and sliding bearings. Earthq. Eng. Struct. Dyn. 2015, 44, 2221–2240. [Google Scholar] [CrossRef]
- Murray, J.A.; Sasani, M. Near-collapse response of existing RC building under severe pulse-type ground motion using hybrid simulation. Earthq. Eng. Struct. Dyn. 2016, 45, 1109–1127. [Google Scholar] [CrossRef]
- Shao, X.; Pang, W.; Griffith, C.; Ziaei, E.; van de Lindt, J. Development of a hybrid simulation controller for full-scale experimental investigation of seismic retrofits for soft-story woodframe buildings. Earthq. Eng. Struct. Dyn. 2016, 45, 1233–1249. [Google Scholar] [CrossRef]
- Kolay, C.; Ricles, J.M.; Marullo, T.M.; Mahvashmohammadi, A.; Sause, R. Implementation and application of the unconditionally stable explicit parametrically dissipative KR-alpha method for real-time hybrid simulation. Earthq. Eng. Struct. Dyn. 2015, 44, 735–755. [Google Scholar] [CrossRef]
- Hashemi, M.J.; Mosqueda, G. Innovative substructuring technique for hybrid simulation of multistory buildings through collapse. Earthq. Eng. Struct. Dyn. 2014, 43, 2059–2074. [Google Scholar] [CrossRef]
- Wang, T.; Mosqueda, G.; Jacobsen, A. Performance evaluation of a distributed hybrid test framework to reproduce the collapse behavior of a structure. Earthq. Eng. Struct. Dyn. 2012, 41, 295–313. [Google Scholar] [CrossRef]
- Mahmoud, H.N.; Elnashai, A.S.; Spencer, B.F.; Kwon, O.S.; Bennier, D.J. Hybrid simulation for earthquake response of semirigid partial-strength steel frames. J. Struct. Eng. 2013, 139, 1134–1148. [Google Scholar] [CrossRef]
- Chen, Z.X.; Xu, G.Sh.; Wu, B.; Sun, Y.; Wang, H.; Wang, F. Equivalent force control method for substructure pseudo-dynamic test of a full-scale masonry structure. Earthq. Eng. Struct. Dyn. 2014, 43, 969–983. [Google Scholar] [CrossRef]
- Fang, K.T.; Ma, C.X. The Uniform Design Method; Science Press: Beijing, China, 2001; ISBN 7-03-009189-2. [Google Scholar]


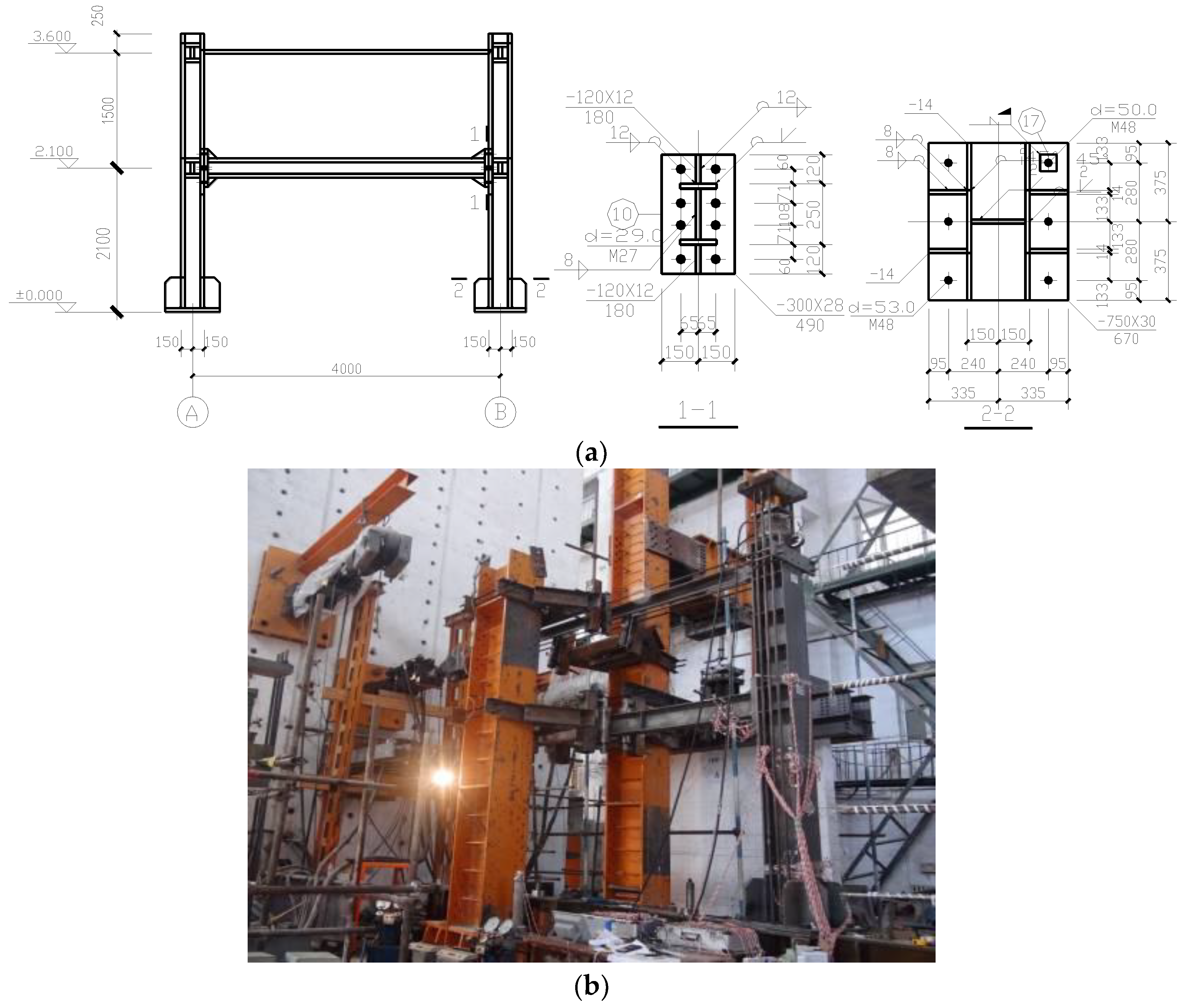
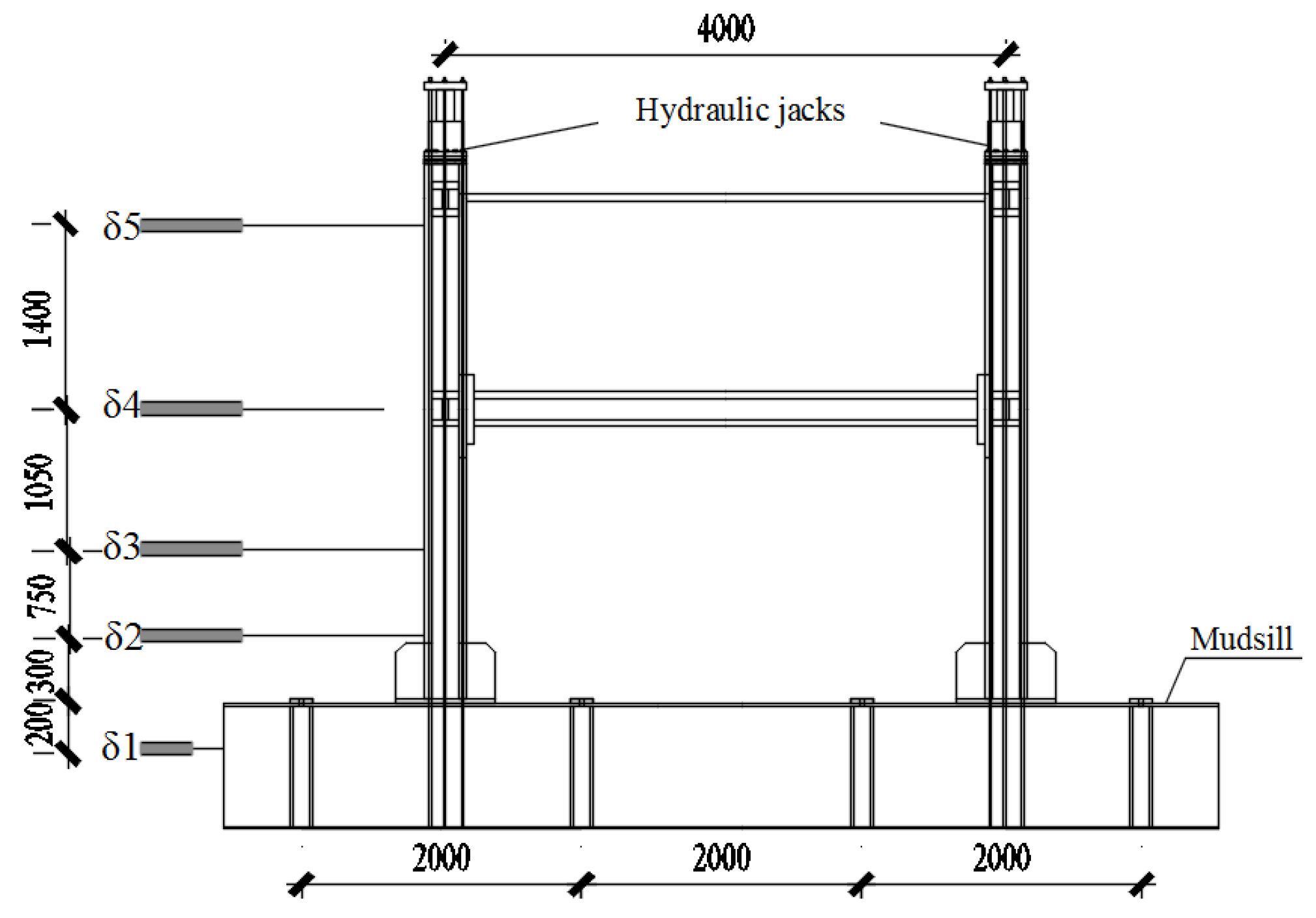




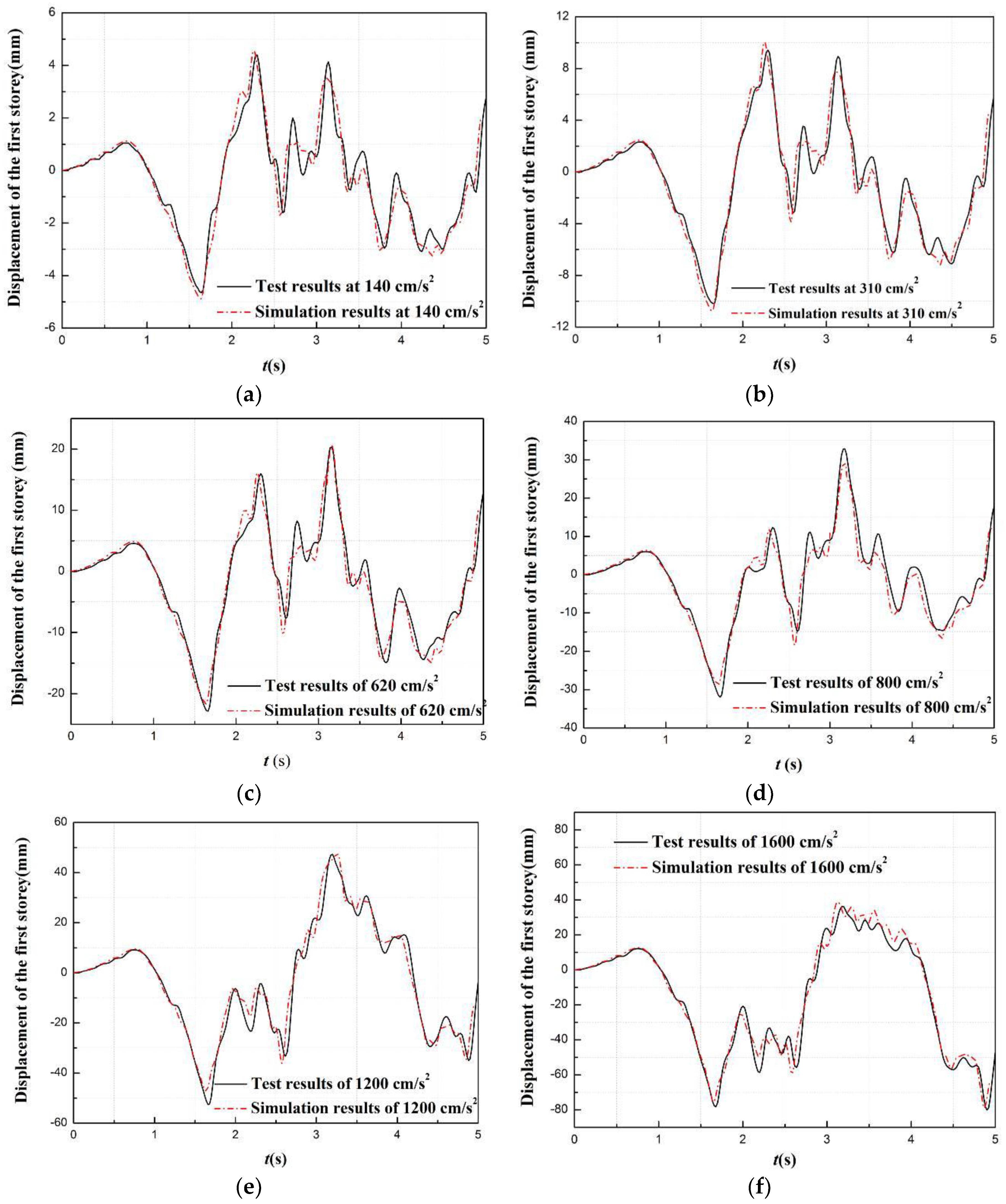

| Test Number | Number of Story | LSR of Beam–Column | PGA (cm/s2) | Number of Story for the Physical Substructure | Beam Section (mm) | Column Section (mm) |
|---|---|---|---|---|---|---|
| 1 | 3 | 0.9 | 540 | 1 | 300 × 550 × 18 × 12 | 400 × 400 × 21 × 13 |
| 2 | 4 | 1.4 | 420 | 2 | 300 × 600 × 24 × 14 | 400 × 400 × 21 × 13 |
| 3 | 5 | 1.9 | 300 | 1 | 300 × 700 × 24 × 12 | 400 × 400 × 21 × 13 |
| 4 | 6 | 0.8 | 180 | 1 | 300 × 500 × 20 × 14 | 400 × 400 × 21 × 13 |
| 5 | 7 | 1.3 | 55 | 1 | 300 × 600 × 22 × 14 | 400 × 400 × 21 × 13 |
| 6 | 8 | 1.8 | 580 | 3 | 300 × 700 × 22 × 12 | 400 × 400 × 21 × 13 |
| 7 | 9 | 0.7 | 460 | 1 | 300 × 500 × 17 × 12 | 400 × 400 × 21 × 13 |
| 8 | 10 | 1.2 | 340 | 3 | 350 × 550 × 22 × 14 | 400 × 400 × 21 × 13 |
| 9 | 11 | 1.7 | 220 | 1 | 450 × 800 × 28 × 16 | 500 × 500 × 28 × 18 |
| 10 | 12 | 0.6 | 100 | 1 | 450 × 550 × 22 × 14 | 500 × 500 × 28 × 18 |
| 11 | 13 | 1.1 | 620 | 3 | 450 × 650 × 28 × 18 | 500 × 500 × 28 × 18 |
| 12 | 14 | 1.6 | 500 | 2 | 450 × 800 × 26 × 16 | 500 × 500 × 28 × 18 |
| 13 | 15 | 0.5 | 380 | 1 | 400 × 500 × 24 × 16 | 500 × 500 × 28 × 18 |
| 14 | 16 | 1 | 260 | 1 | 450 × 600 × 31 × 18 | 500 × 500 × 28 × 18 |
| 15 | 17 | 1.5 | 140 | 1 | 450 × 800 × 24 × 16 | 500 × 500 × 28 × 18 |
| Theoretical Thickness of Steel Plate (mm) | Real Thickness of Steel Plate (mm) | Yield Strength (Mpa) | Elasticity Modulus (105 Mpa) | Ultimate Strength (Mpa) |
|---|---|---|---|---|
| 7 | 6.8 | 220.5 | 2.02 | 390.4 |
| 10 | 9.85 | 202.3 | 1.90 | 323.2 |
| 12 | 10.5 | 216.0 | 2.04 | 345.6 |
| 16 | 15.7 | 206.5 | 1.91 | 339.6 |
| Peak Acceleration (cm/s2) | Axial Force at the Bottom of the Column | Bending Moment at the Bottom of the Column | Bending Moment at the End of Beam |
|---|---|---|---|
| 310 | 2.5% | 3.7% | 6.1% |
| 620 | 6.7% | 9.3% | 4.0% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Yan, X.; Wang, H.; Zhu, X.; Spencer, B.F. Substructure Hybrid Simulation Boundary Technique Based on Beam/Column Inflection Points. Sustainability 2018, 10, 2655. https://doi.org/10.3390/su10082655
Chen Z, Yan X, Wang H, Zhu X, Spencer BF. Substructure Hybrid Simulation Boundary Technique Based on Beam/Column Inflection Points. Sustainability. 2018; 10(8):2655. https://doi.org/10.3390/su10082655
Chicago/Turabian StyleChen, Zaixian, Xueyuan Yan, Hao Wang, Xingji Zhu, and Billie F. Spencer. 2018. "Substructure Hybrid Simulation Boundary Technique Based on Beam/Column Inflection Points" Sustainability 10, no. 8: 2655. https://doi.org/10.3390/su10082655
APA StyleChen, Z., Yan, X., Wang, H., Zhu, X., & Spencer, B. F. (2018). Substructure Hybrid Simulation Boundary Technique Based on Beam/Column Inflection Points. Sustainability, 10(8), 2655. https://doi.org/10.3390/su10082655






