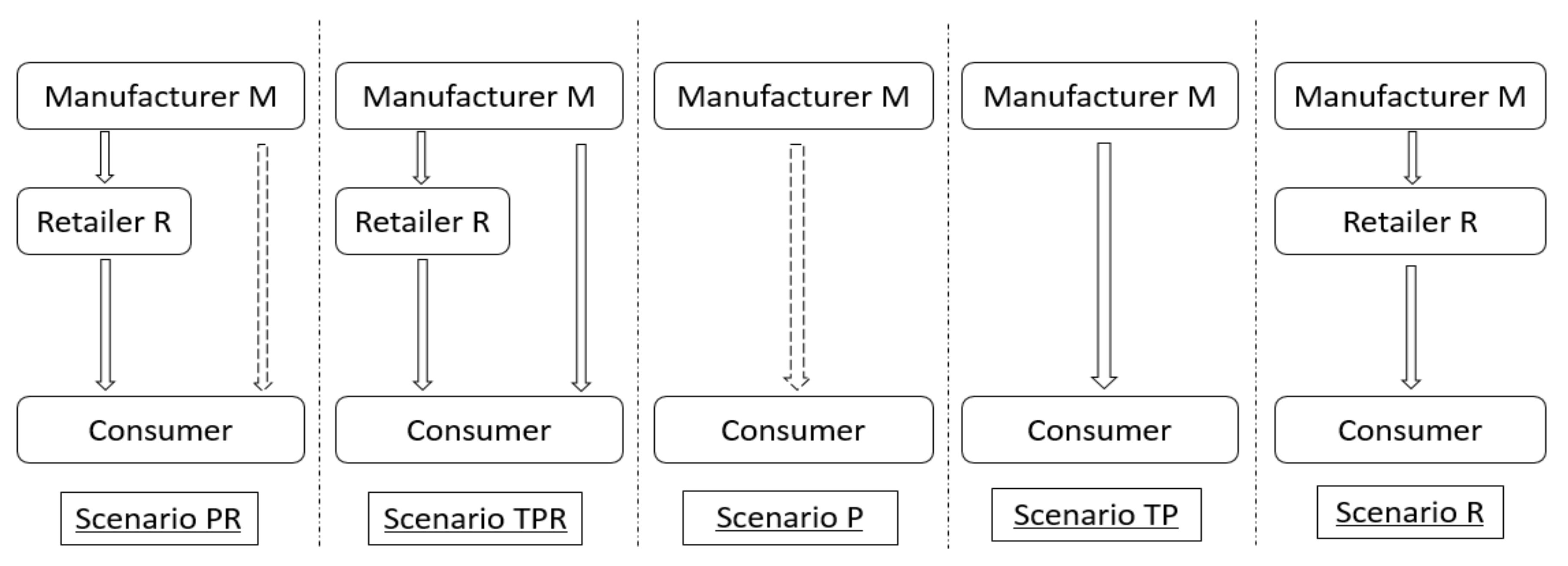
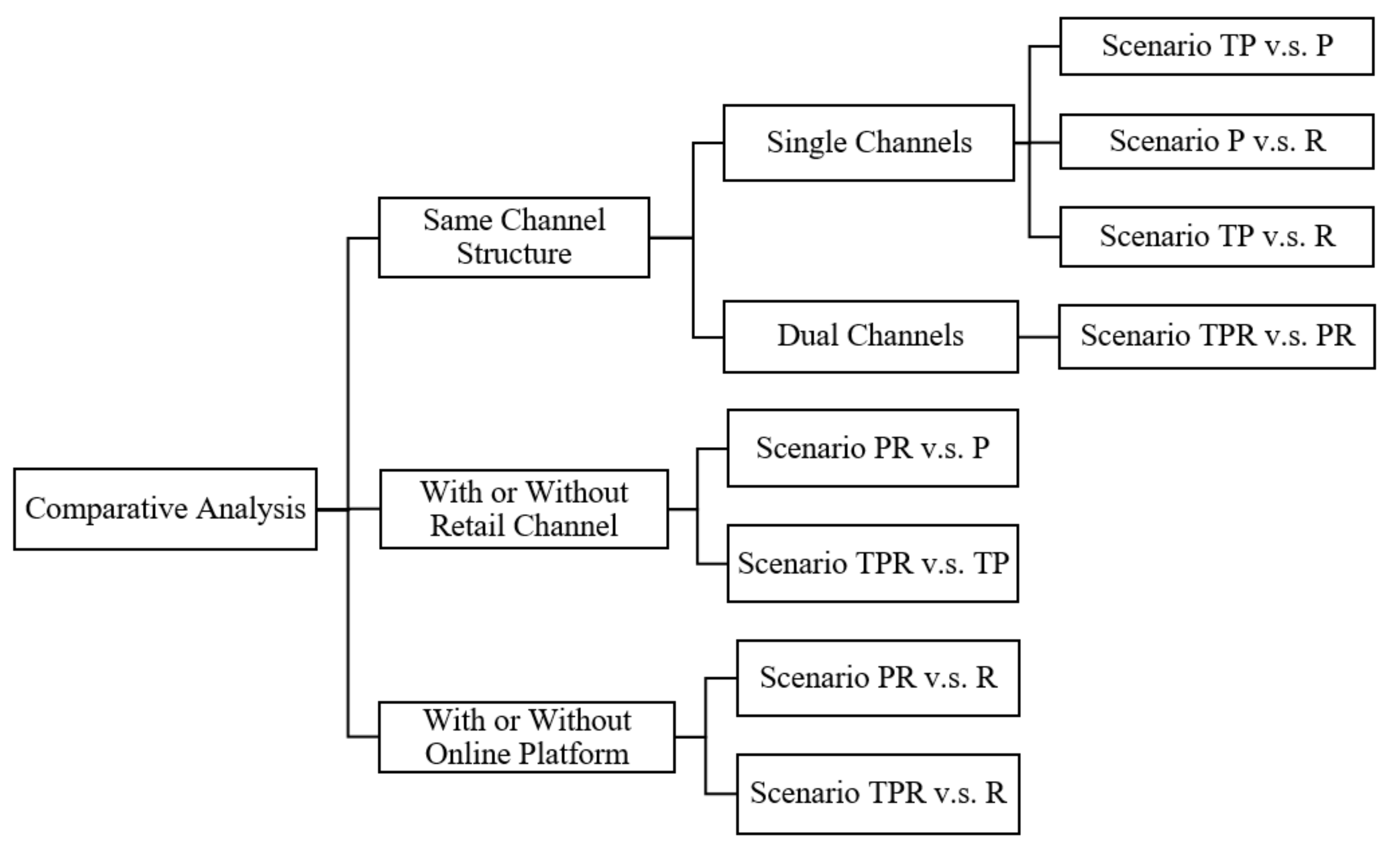
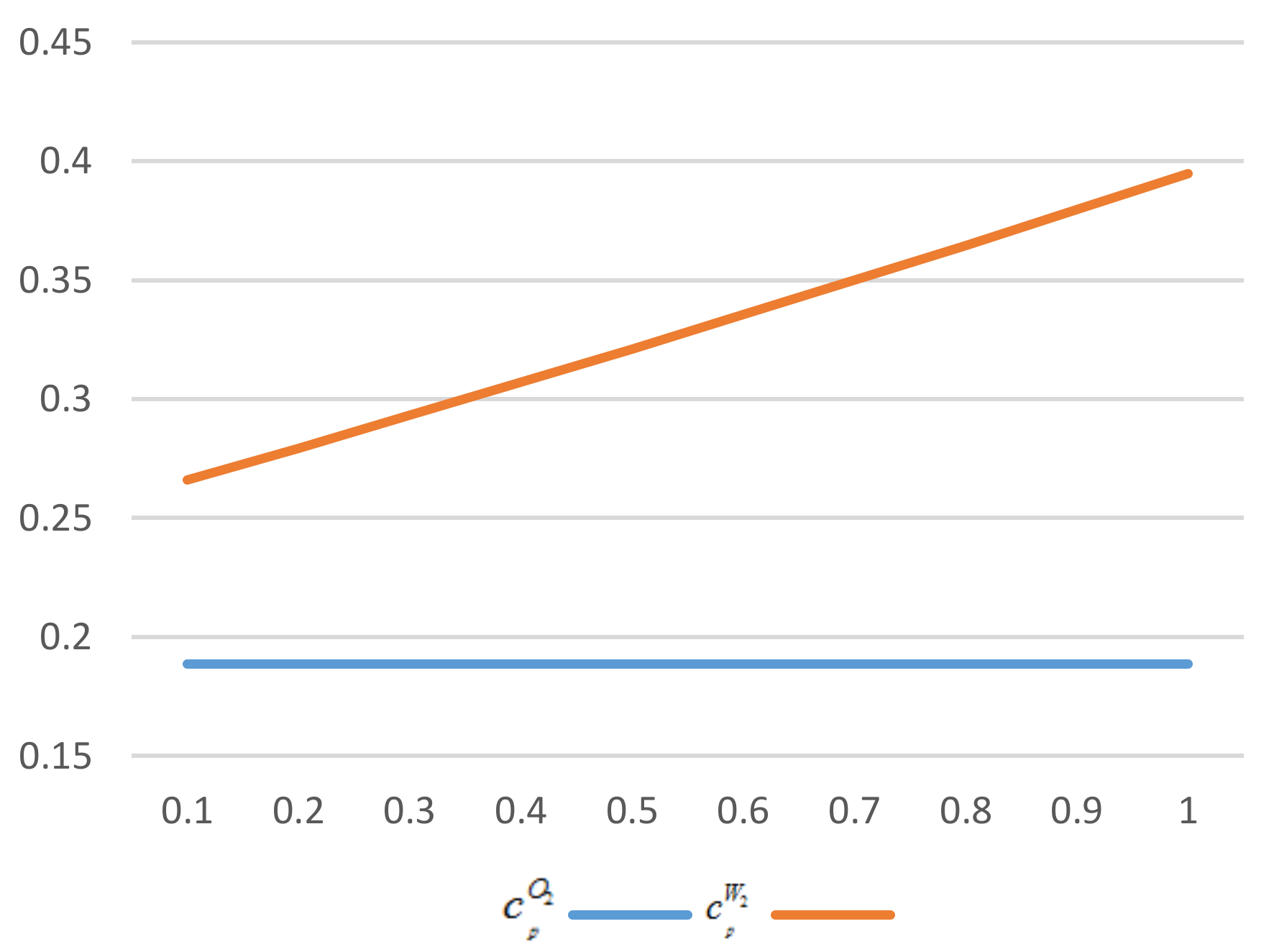We analyze the three scenarios which have the same channel structure, including single channels (TP and P, P and R, TP and R) and dual channels (PR and TPR). We further get and compare the critical conditions with or without enhancement, such as self-owned cost of a platform and revenue proportion through a third-party platform.
4.1.1. Comparisons of Single Channels
We first compare the profits of TP and P. In Scenario TP, the manufacturer pays a certain proportion of revenue to a third-party platform, while the manufacturer invests in building up and owning a platform in Scenario P. A concern over which will be more profitable arises. Comparing the two online channels, we obtain the critical construction cost of a self-owned platform.
Theorem 1. Scenario TP outperforms Scenario P with respect to profit if:
- (1)
- (2)
- (3)
If,; Otherwise,.
The first and second items of Theorem 1 provide two critical points between the profit changes of TP and P for a manufacturer. The third item shows the relationship between two critical construction costs without and with enhancement. A manufacturer benefits from having a third-party platform when is large. On the one hand, when there is no enhancement, using a third-party platform will be more profitable if the construction cost is higher than . On the other hand, when the enhancement occurs, total market demand will be higher, it is more necessary to build up a platform. A third-party platform should be chosen if the construction cost is more than . Additionally, when , which means that if the low-carbon preference is over a certain level, the critical self-owned cost with enhancement will be larger than that without enhancement.
It is reasonable that a manufacturer needs plenty of investment to build up a platform, while it just pays a fixed revenue proportion to a third-party platform. So, it depends on the construction cost. As the construction cost continues to rise, a third-party platform will be more beneficial for a manufacturer. With the enhancement of the low-carbon preference, the total demand and profit also rise. A manufacturer is encouraged to build up a platform without paying the third-party fee. Therefore, only when the construction cost becomes extremely high, TP performs better than P, so we get . When the enhancement is high, Scenario P performs better than TP.
Then we compare the profits of P and R. The manufacturer has no online platform but a retail channel in Scenario R. When there is only one single channel, we should consider whether an online or an offline channel would be better. Comparing a retail channel with a self-owned online channel, we calculate the critical cost of a self-owned platform.
Theorem 2. Scenario P outperforms Scenario R with respect to profit if:
Theorem 2 suggests two critical construction costs of Scenarios P and R. In addition, it proves that a manufacturer benefits from having a self-owned platform when is small. For one thing, if there is no enhancement, owning a platform will be more beneficial than a retail channel if the construction cost is lower than . For another, if the enhancement occurs, a self-owned platform should be used if the construction cost is less than .
It is intuitive that if the construction cost is low, a self-owned platform earns more profits than a retail channel, which depends on the construction cost. As the construction cost continues to rise, a retail channel will be more profitable even if the manufacturer offers a wholesale price. Furthermore, since the environmental coefficient in a retail channel is higher than that of a direct channel, offline demand increases more than online with enhancement. Therefore, a retail channel would become more profitable if the enhancement is large.
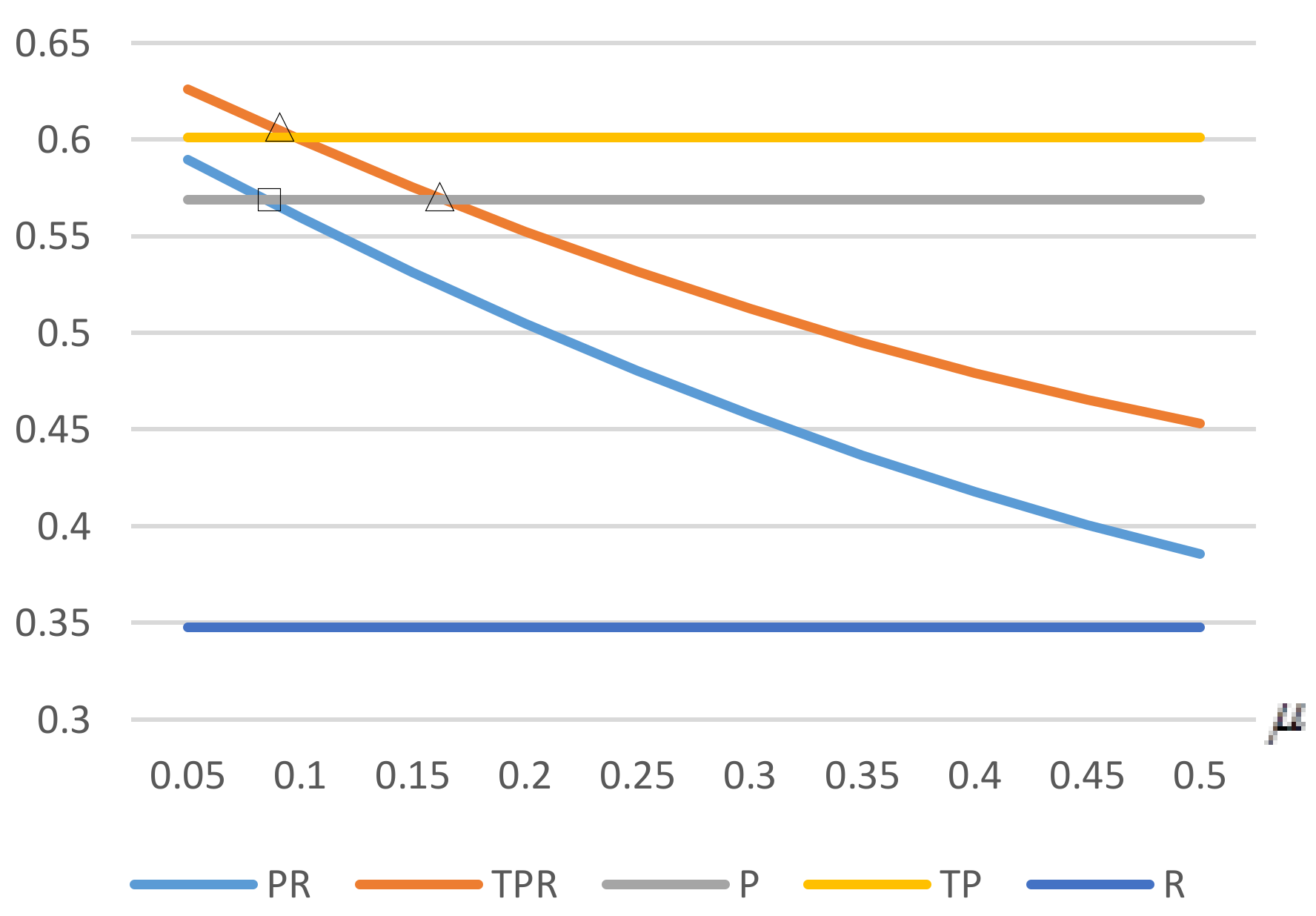
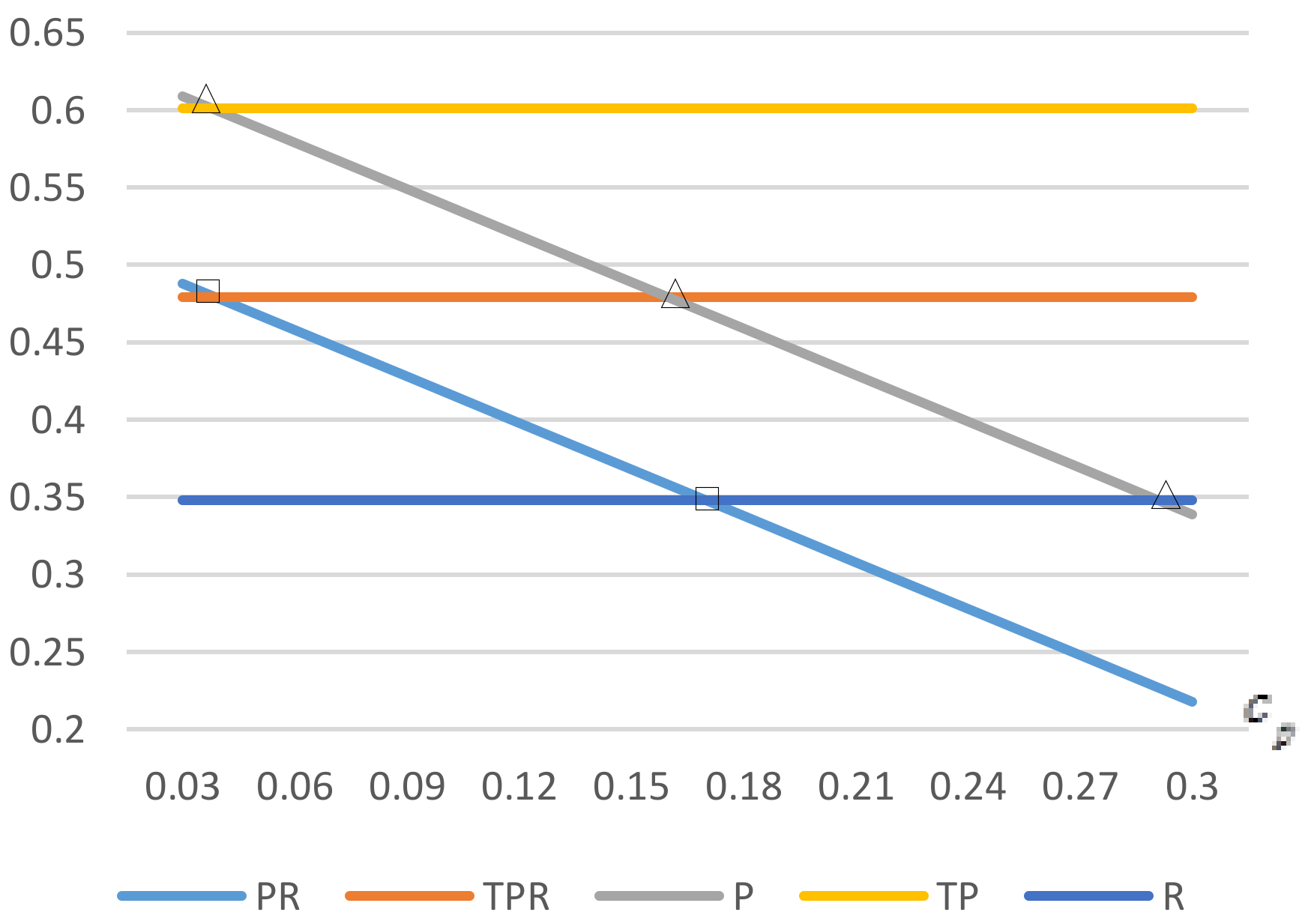
We make a comparison of the critical construction costs
between the conditions without and with enhancement. Since it is difficult to compare them by theoretical analysis, we provide numerical analysis to show their differences. We get the related parameters and specify that
,
,
,
,
,
,
, which are all used from
Figure 3 to
Figure 8. The superscript of
and
mean without and with respectively, which is also applicable from
Figure 3 to
Figure 8.
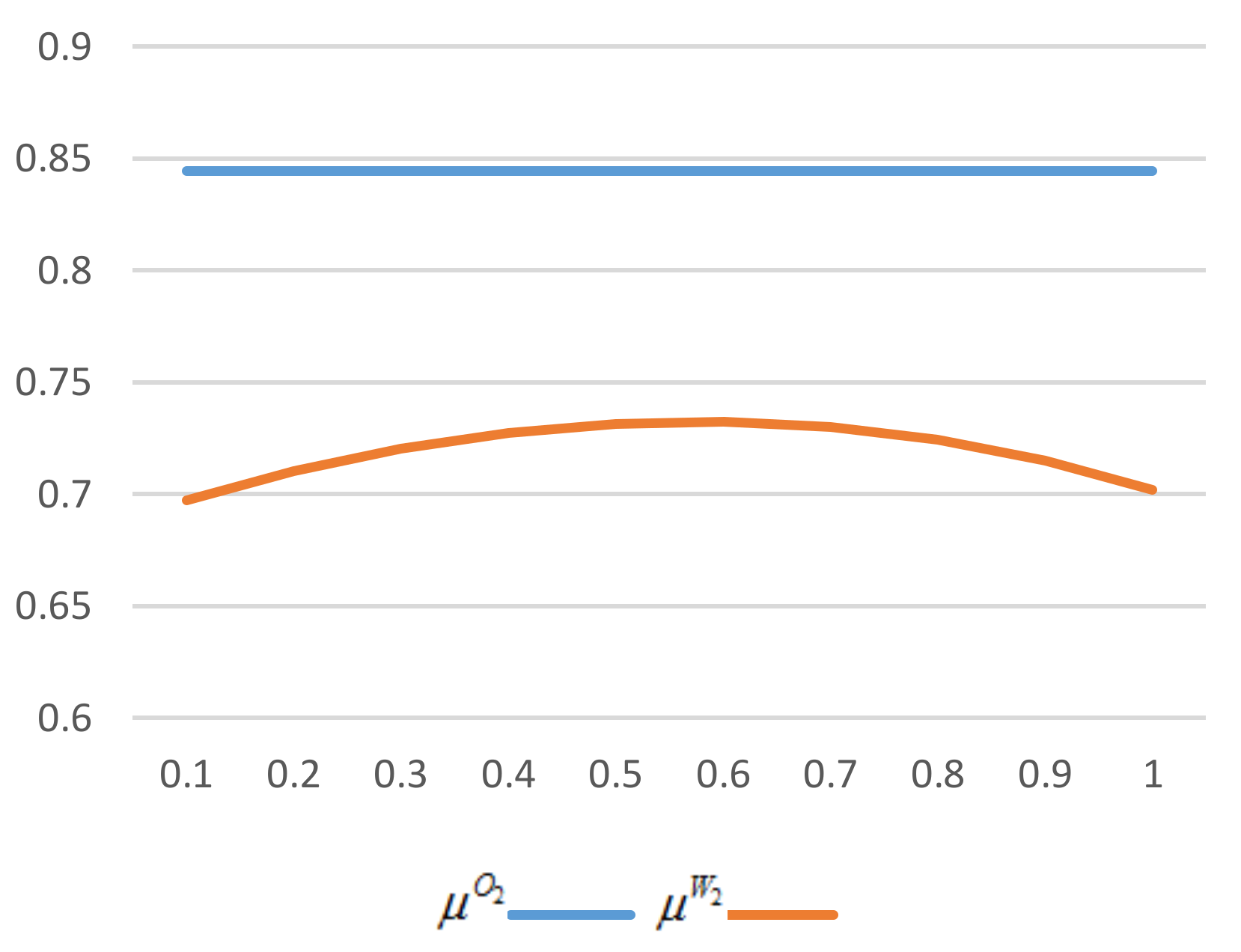
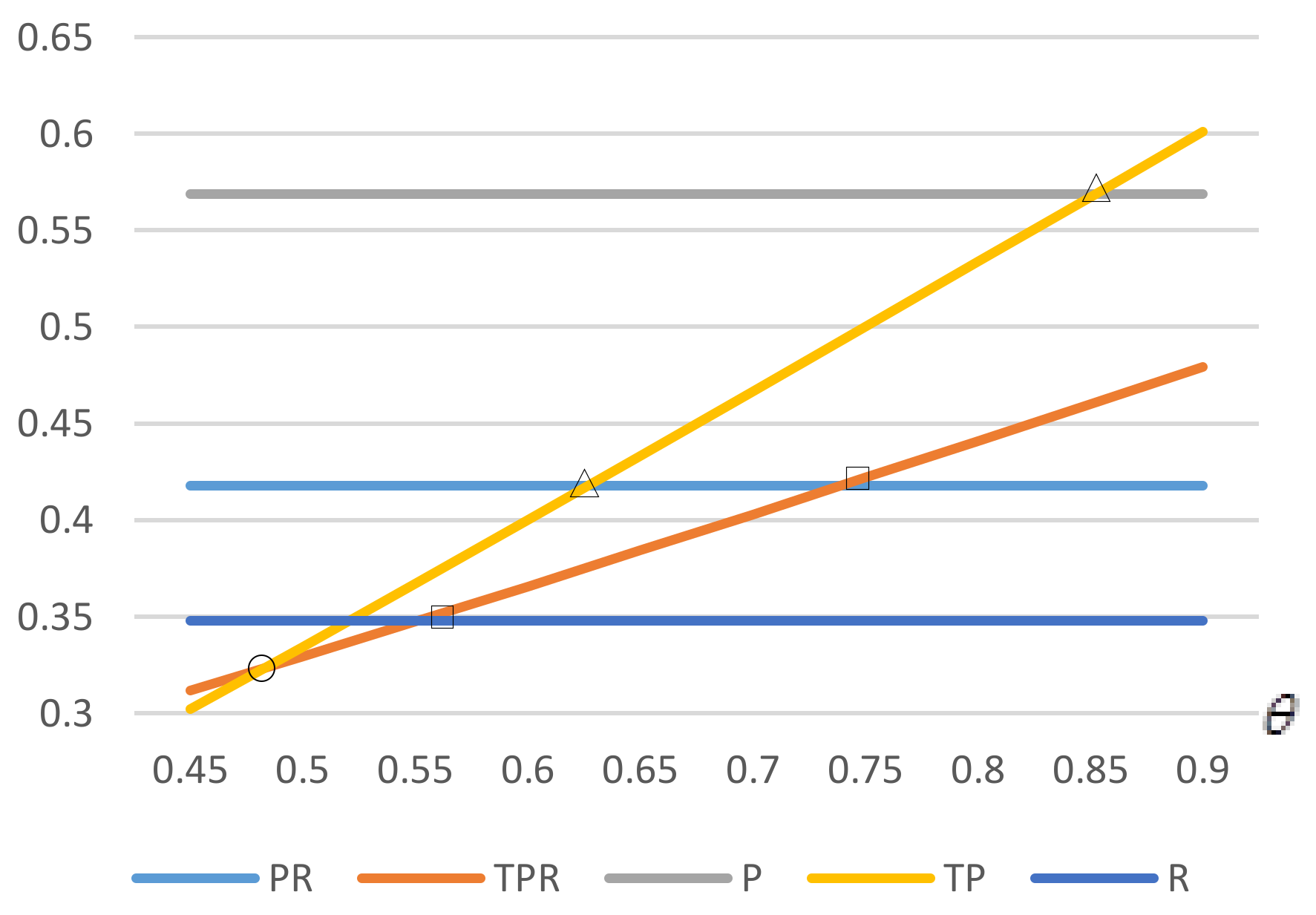
As we can see in
Figure 3, the critical construction cost with enhancement is always higher than that without enhancement. The intersection does not appear as enhancement becomes larger. It is reasonable that the enhancement increases both total demand and profit. A manufacturer would rather build up a self-owned platform than offer a wholesale price to a retailer. Therefore, Scenario P performs better than R, we get
.
Next, we compare the profits of TP and R. The platform is owned by a third party in Scenario TP, while the manufacturer has no platform but a retail channel in Scenario R. One concern is that Scenario TP or R performs better. By comparing a third-party platform with a retail channel, we get the critical proportion of manufacturer’s revenue through an online platform.
Theorem 3. Scenario TP outperforms Scenario R with respect to profit if:
- (1)
- (2)
With enhancementwhere.
Theorem 3 provides two critical revenue proportions of TP and R. Additionally, it demonstrates that if there is just a single channel, using a third-party platform will be more profitable than a retail channel when the revenue proportion is high. Without enhancement, when the proportion is larger than , a third-party platform will be more beneficial. With enhancement, a retail channel earns more if the proportion is smaller than .
When the proportion is high, it is so reasonable that owning a third-party platform can earn more without offering a wholesale price to a retailer. Therefore, if a manufacturer just considers a single channel and the proportion is small, choosing a retail channel will be more beneficial since high proportion of revenue is deprived by a third-party platform. When there is an enhancement of low-carbon preference, a retail channel gains higher demand and profit.
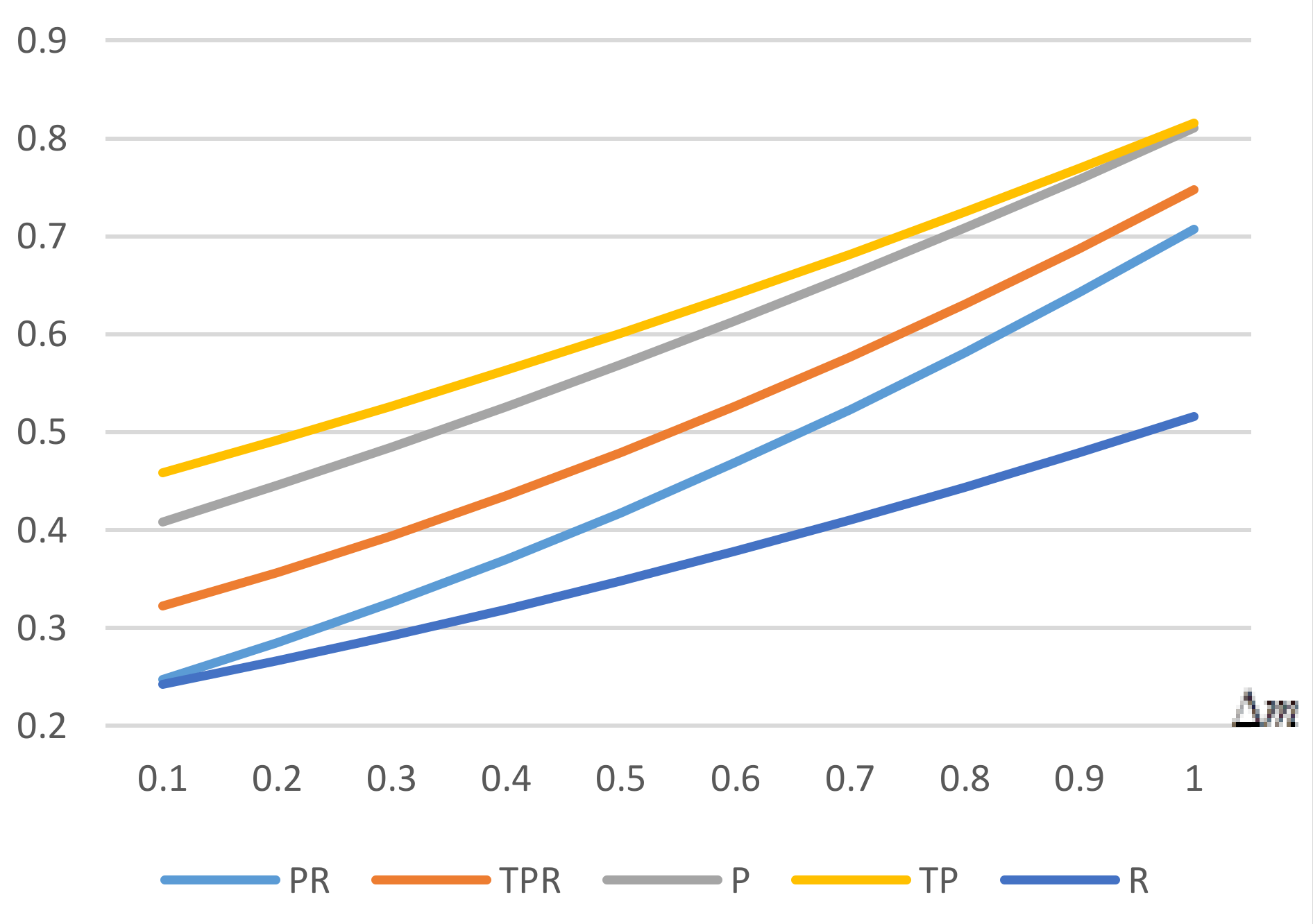
We make a comparison of the two critical revenue proportions between the conditions without and with enhancement below:
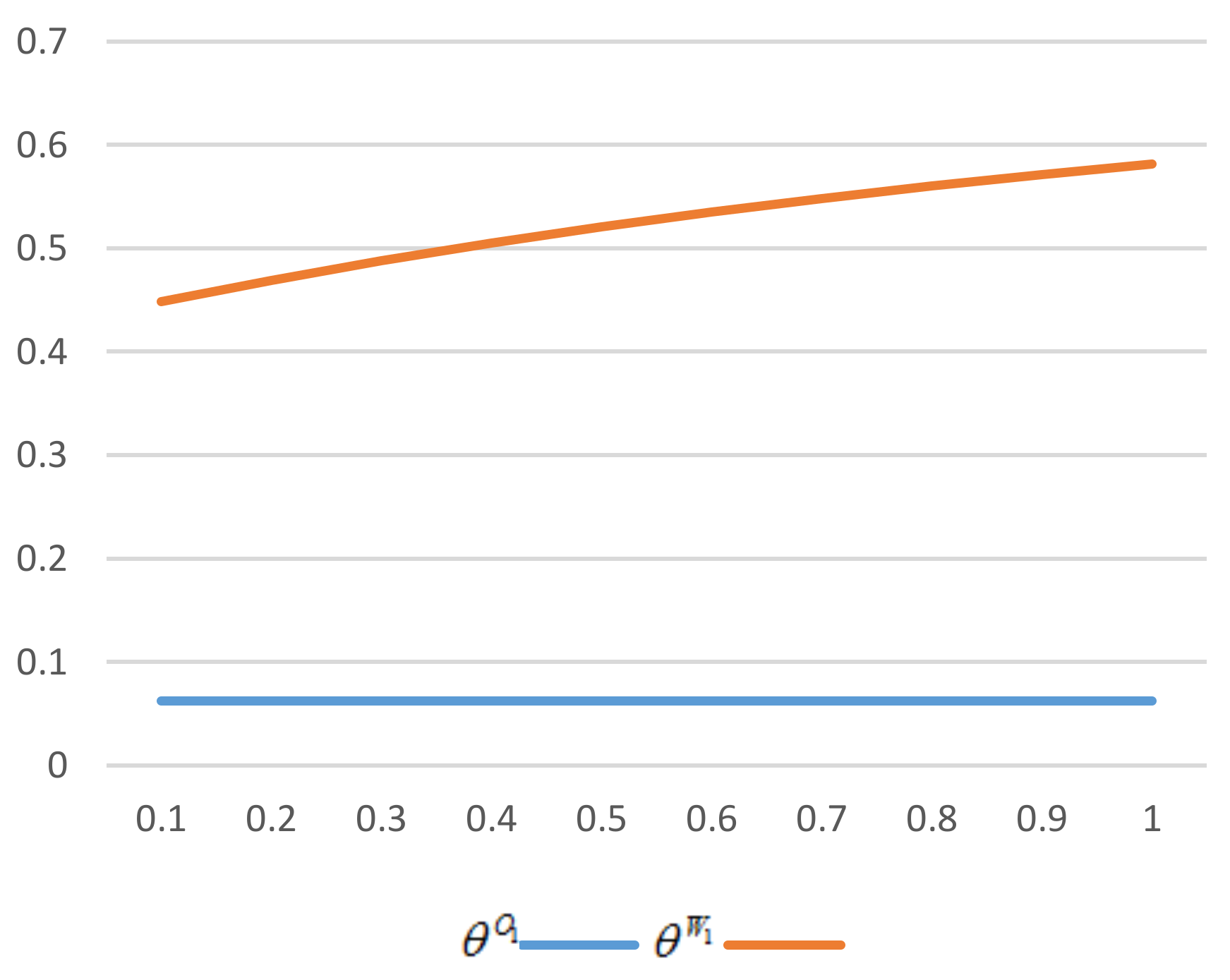
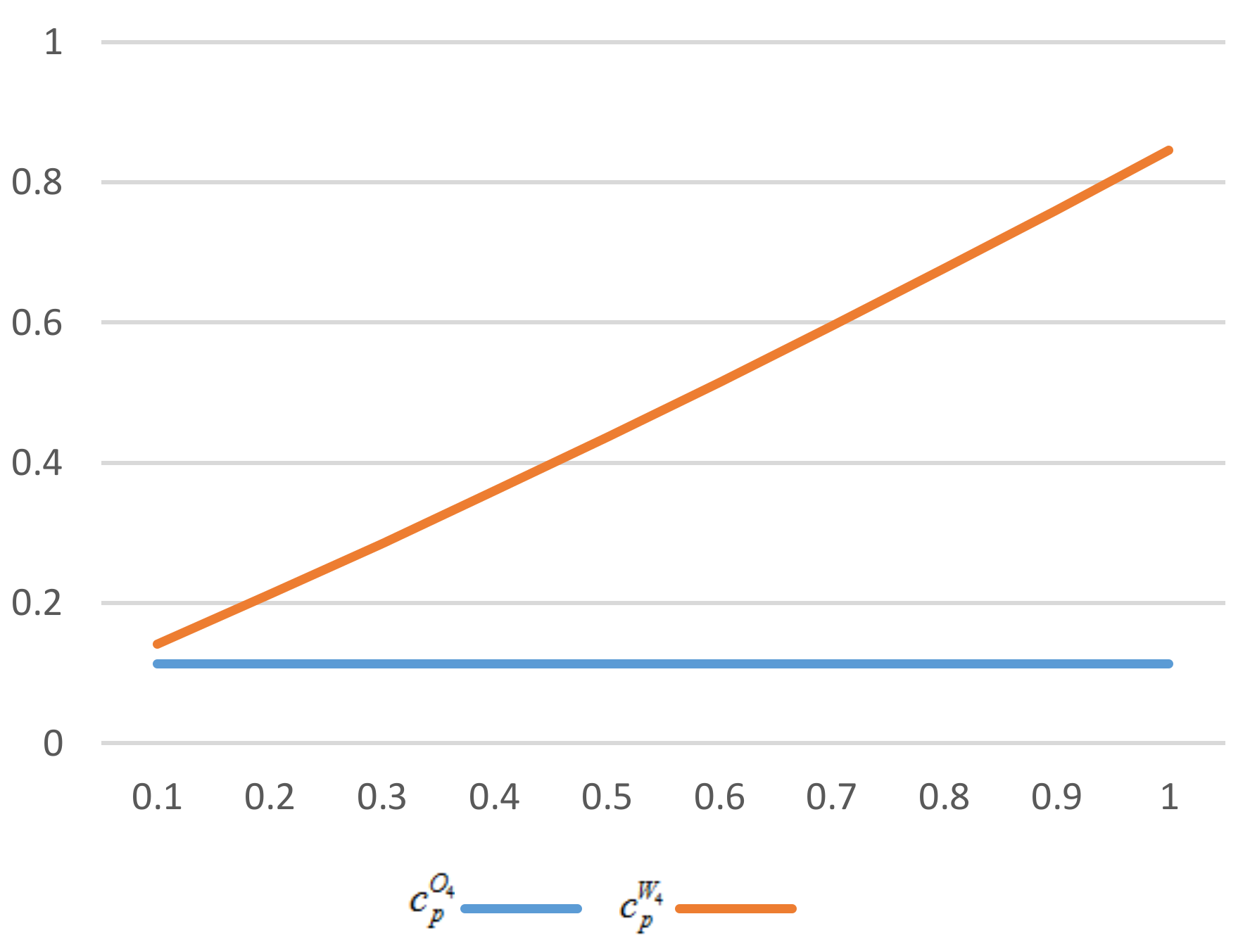
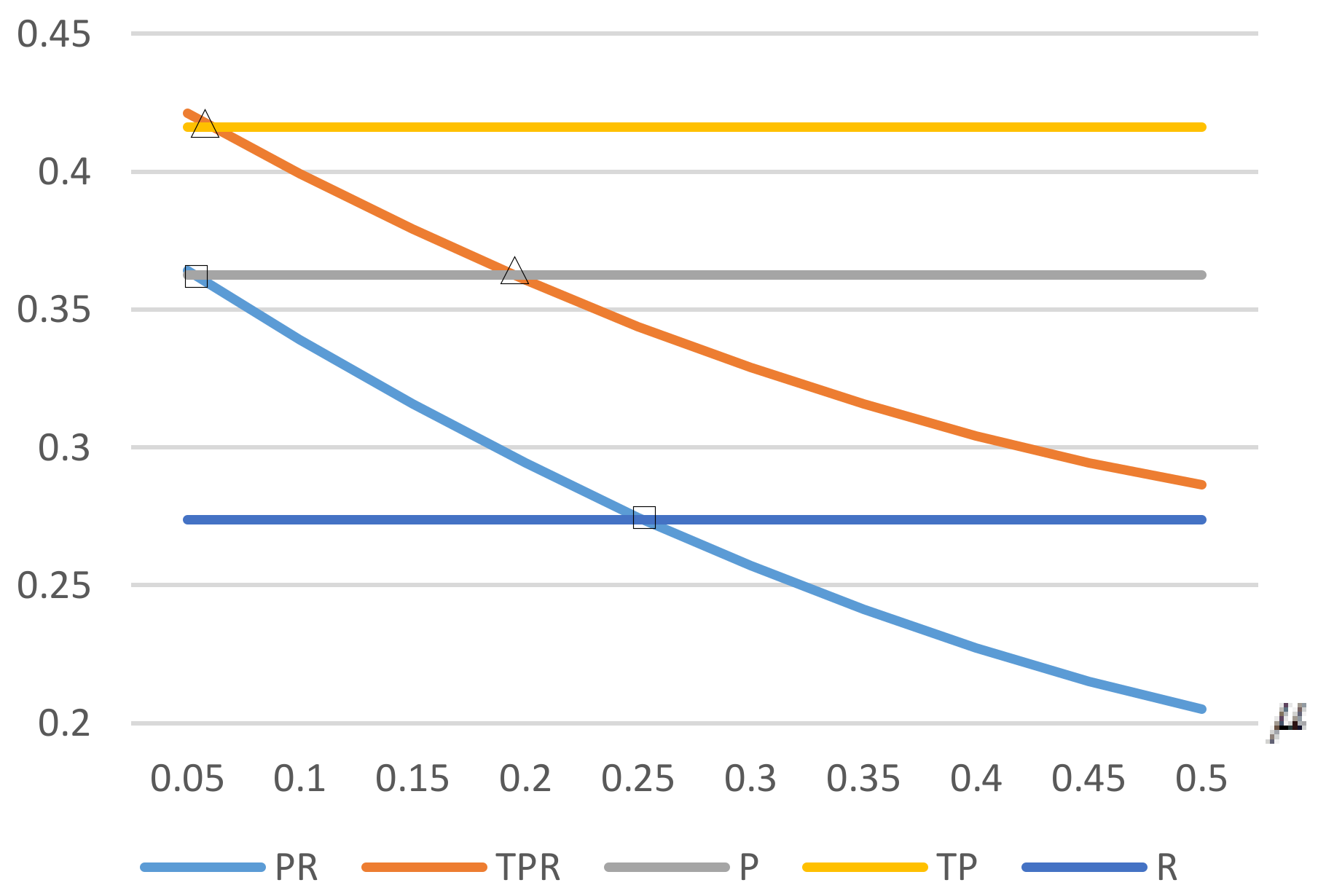
In
Figure 4, it is obvious that the critical proportion with enhancement of low-carbon preference is always higher than that without enhancement. There is no intersection between two critical points. The total demand goes up along with enhancement, but the offline demand increases more due to higher offline environmental coefficient. Thus, when there is an enhancement, a manufacturer would like to adopt a retailer channel unless it serves higher revenue proportion through a third-party platform.
4.1.2. Comparisons of Dual Channels
Compare the profits of PR and TPR. The manufacturer owns a platform and a retail channel in Scenario PR, while a third-party platform and a retail channel are possessed in Scenario TPR. Comparing these two dual channels, we get the critical construction cost.
Theorem 4. Scenario TPR outperforms Scenario PR with respect to profit if
- (1)
- (2)
- (3)
If, ; Otherwise,.
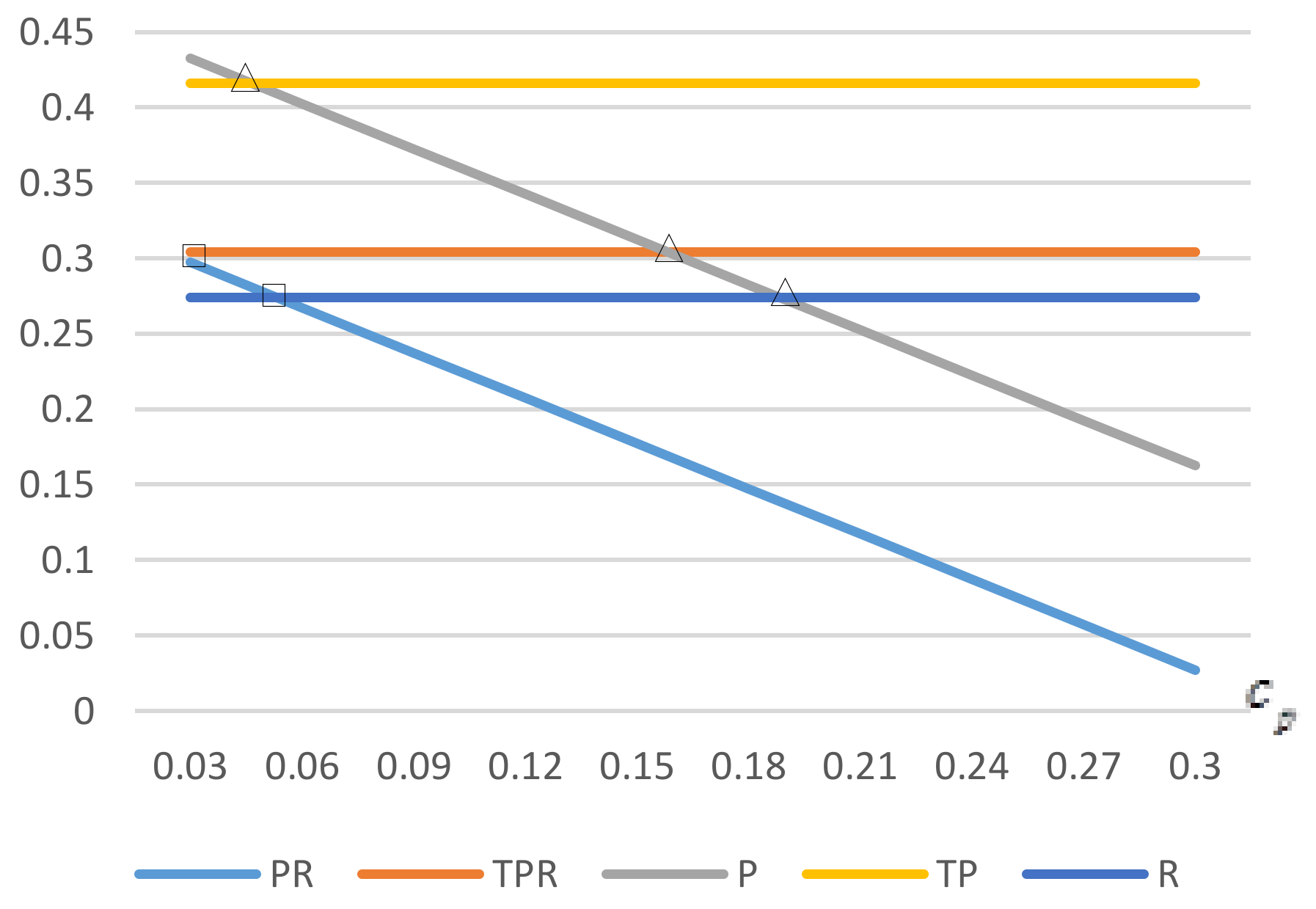
Theorem 4 comes up with two critical construction costs for profit changes between PR and TPR. On the one hand, when there is no enhancement, having a self-owned platform will be more beneficial than a third-party platform if the construction cost is lower than . On the other hand, when there is an enhancement of low-carbon preference, a self-owned platform should be used if the self-owned cost is less than . As the enhancement is larger than , the critical construction cost with enhancement is higher than that without enhancement.
As the construction cost continues to rise either without or with enhancement, a third-party platform will be more profitable for a manufacturer. Furthermore, when the enhancement becomes large, total demand goes up. Owning a platform is more worthwhile instead of paying the third-party platform fee, so PR performs better than TPR, which means that a manufacturer is likely to select a self-owned platform rather than a third-party platform. When construction cost is very high, a third-party platform would be more profitable, so we get .