Economic Impact of the High-Speed Railway on Housing Prices in China
Abstract
1. Introduction
2. Literature Review
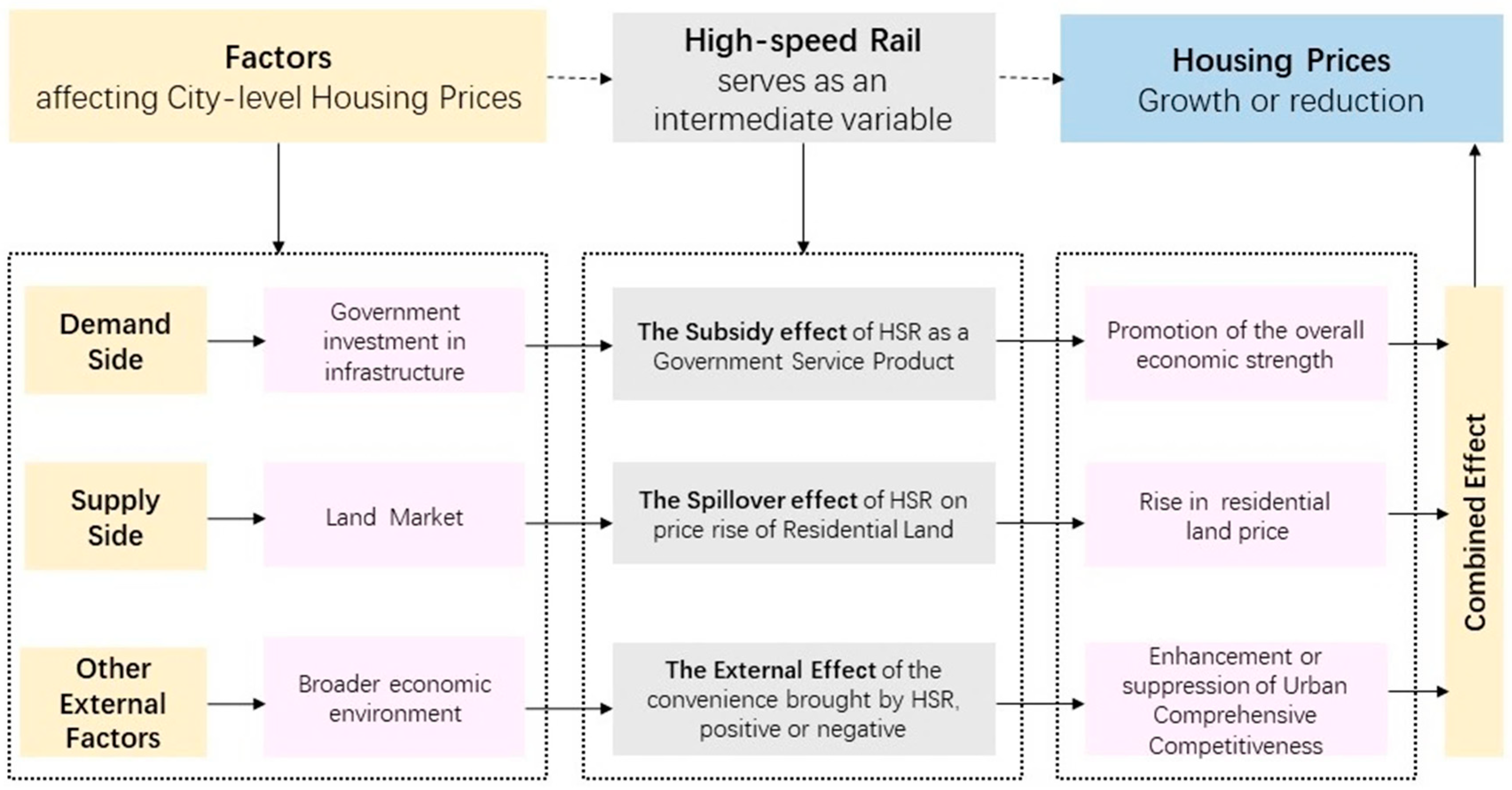
3. How the HSR Affects City-Level Housing Prices: A Theoretical Framework
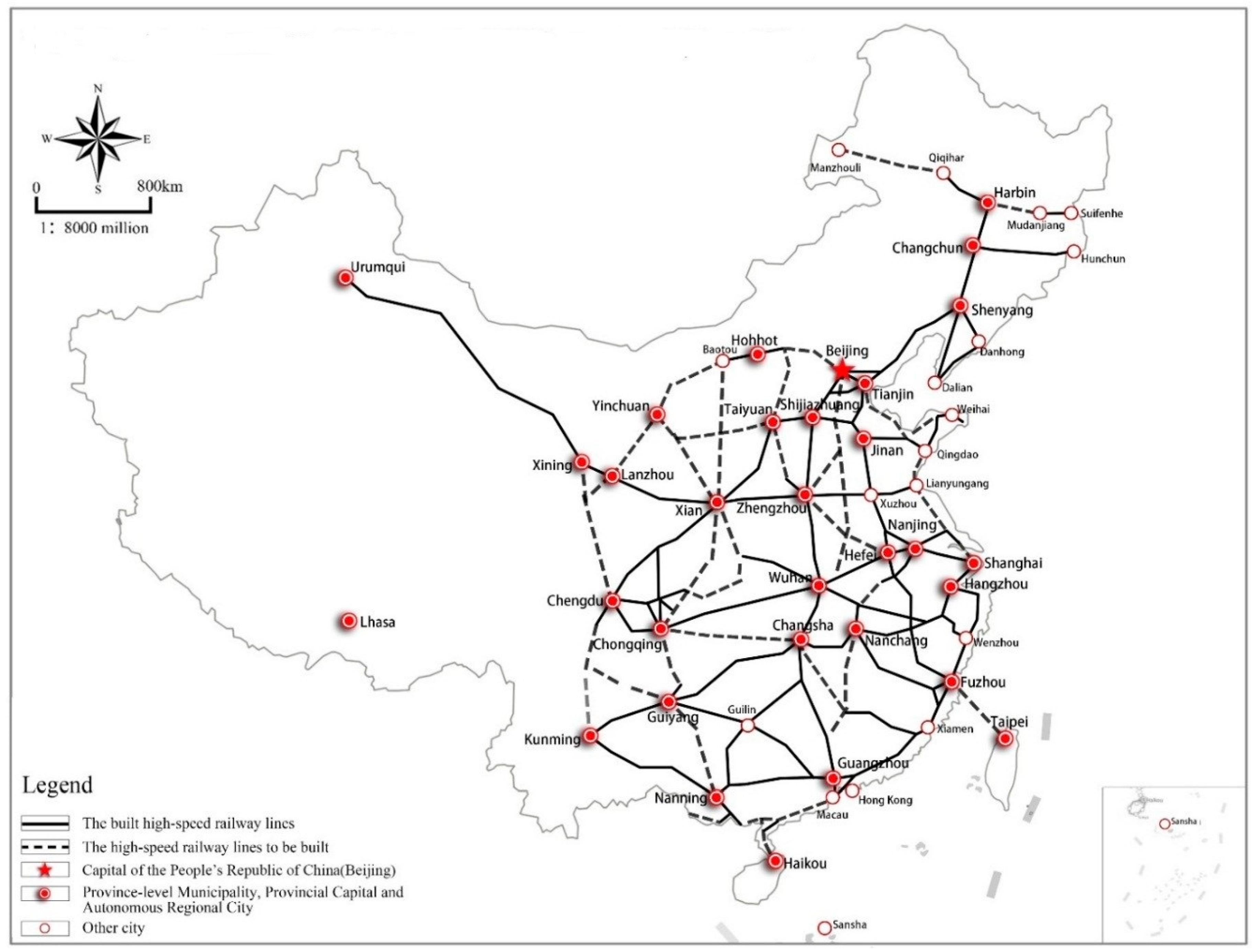
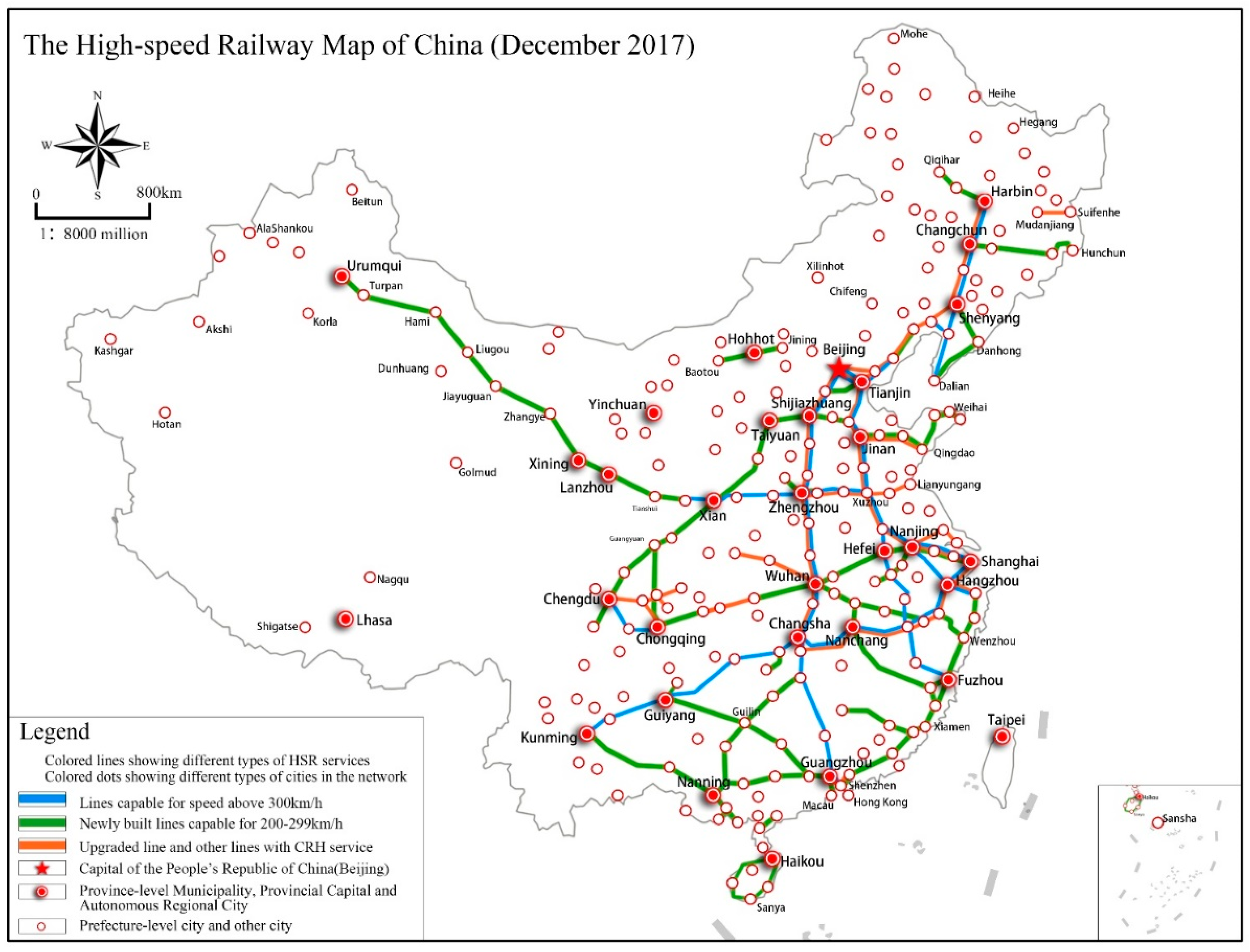
4. Variables, Data, and Methodology
4.1. Variables
4.2. Samples and Data
- (1)
- 9 national central cities (abbreviated as N), including Beijing, Tianjin, Shanghai, Guangzhou, Chongqing, Chengdu, Wuhan, Zhengzhou, and Xi’an (according to the National Urban System Plan (2010–2020), China’s highest-level strategic plan, which was jointly prepared by 19 central ministries and commissions, including the Ministry of Housing, the National Development and Reform Commission, the Health and Family Planning Commission, and the Ministry of Education);
- (2)
- 27 regional central cities (abbreviated as R), including all the provincial capital cities and Municipalities with Independent Planning Status under the National Social and Economic Development Plan (Shijiazhuang, Shenyang, Dalian, Changchun, Taiyuan, Hohhot, Harbin, Jinan, Qingdao, Nanjing, Hangzhou, Xiamen, Shenzhen, Suzhou, Ningbo, Hefei, Fuzhou, Nanchang, Changsha, Nanning, Haikou, Guiyang, Kunming, Lanzhou, Xining, Yinchuan, and Urumqi: These cities are provincial cities or “Municipalities with Independent Planning Status under the National Social and Economic Development Plan”, issued by the nation); and
- (3)
- 249 other prefecture-level cities (abbreviated as O), and these are ordinary prefecture-level cities officially announced by China’s National Government.
- (1)
- Housing price data, a 2009–2017 dataset including 285 city-level real estate prices (the commercial housing transaction price) selected from “ANJUKE (https://anjuke.com)”, one of the largest real estate internet portals in China;
- (2)
- Railway and HSR data (whether or not a certain city possessed a railway or HSR, respectively) from “National Railway Passenger Train Schedules (2009–2017)”, provided by China’s railway customer service center (according to the definition of the National Railway Administration (2014), the HSR in China includes rail lines served by G-, C-, and D-prefixed bullet trains, but in our study, we only took newly constructed HSR lines into account served by G- and C-prefixed bullet trains and excluded HSR lines sped up on ordinary rail lines, served by D-prefix bullet trains);
- (3)
- Population data (total population of municipal districts was introduced to control for heterogeneous patterns of residential characteristics among different cities) sourced from “China’s City Statistical Yearbook (2009–2017)”;
- (4)
- Financial data, GDP, savings, and loans (total savings in municipal districts, total loans in municipal districts) collected from “China’s City Statistical Yearbook (2009–2017)”; and
- (5)
- Airport data (whether or not a certain city possessed an airport) extracted from “the official Civil Aviation Industry Development Statistics Bulletin (2009–2017)”, which are published on the website of the Civil Aviation Administration of China (CAAC). It was considered to be no airport when the following two situations occurred: (1) The airport was licensed for operating permission, but there were no flights opened yet, and (2) the airport shut down for a certain year for the reason of long-term maintenance.
4.3. Methodology
4.3.1. Baseline Regression: Fixed Effect Model
4.3.2. Dynamic Panel Data Model
4.3.3. Regression Model with City Classification Dummies and Regional Dummies
5. Empirical Results
5.1. Results of Baseline Regression and Dynamic Panel Data Model
5.2. Results of City Classification Dummies and Regional Dummies (National-Scale)
5.2.1. Impacts Varied between Different City Dummies
5.2.2. The Regional Imbalance Narrowed
5.3. Subsample Estimations with More Inner-City Explanatory Variables (35 Key Cities)
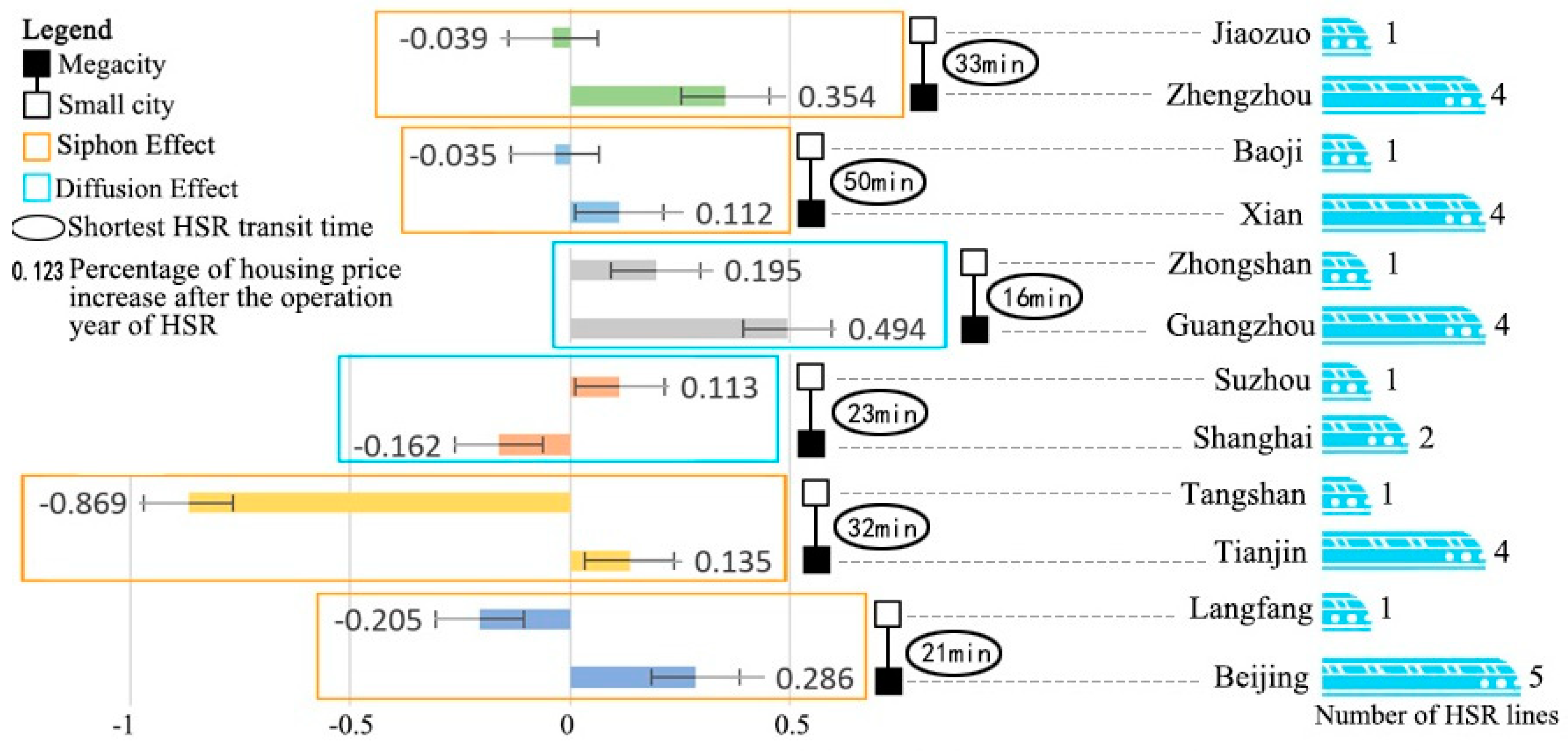
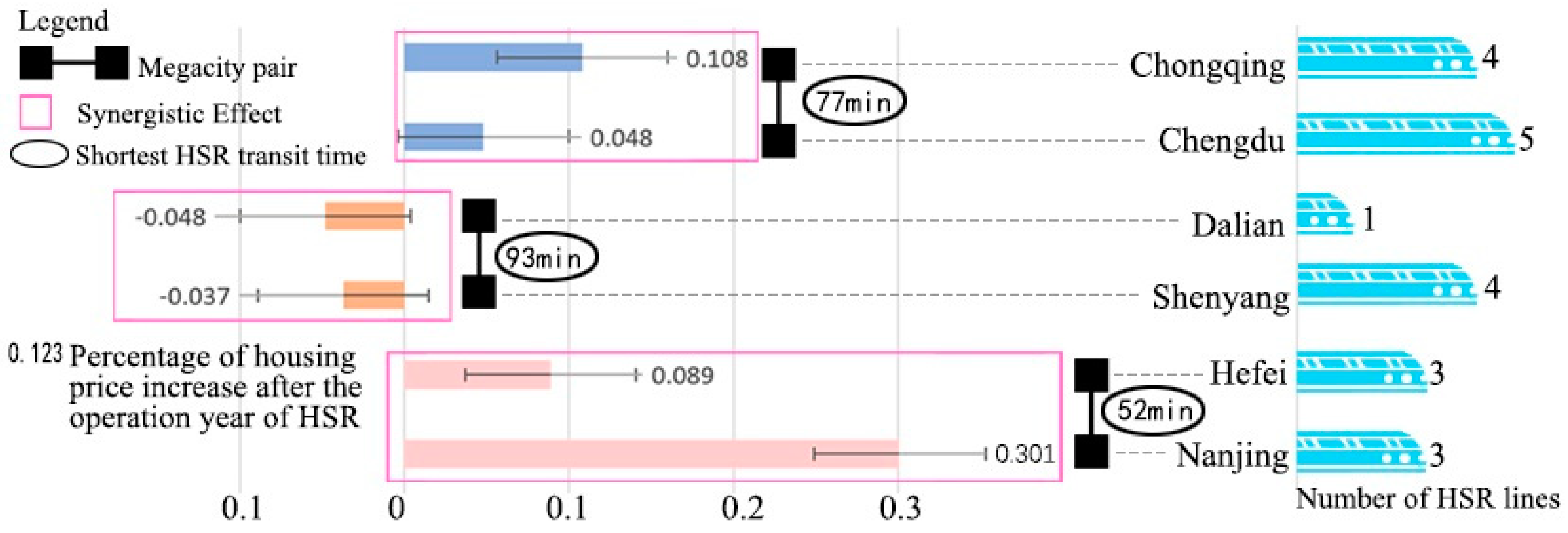
5.4. Impacts Varied between Different City Pairs (Micro-Scale)
5.4.1. Impacts between Megacity and Small City Pairs
5.4.2. Impacts between Megacity (or Central City) Pairs
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Scenario | Typical Year | Important Event |
|---|---|---|
| Period of China Railwayline being upgraded for HSR (2003–2007). | 2003 | The first upgraded line began operating. |
| 2007 | The second upgraded line operated. | |
| The sixth round of the Railway Speed-Up Campaign, during which 6849 km of CR lines were upgraded to speeds of over 200 km/h. | ||
| Period of newly built HSR lines expansion (2008–2015). | 2008 | The Mid to Long-Term Railway Network Plan of China’s Ministry of Railways (2008) was issued. |
| The first newly built HSR line, from Beijing to Tianjin, operated. | ||
| 2008–2015 | The HSR network expanded rapidly and newly built HSR lines were introduced annually and on a massive scale: | |
| 2015 | The “four north-south and four west-east corridors” national HSR network was basically completed by the end of 2015. | |
| Period of realizing a miraculous national HSR network (2016–2025). | 2016 | The Mid to Long-Term Railway Network Plan (revised in 2016). |
| 2025 | Formulating the “eight vertical and eight horizontal corridors” national HSR network. |
| HSR Lines | Construction Time | Opening Time | Length (km) | Speed (km/h) |
|---|---|---|---|---|
| Qinhuangdao–Shenyang | 01/01/1999 | 01/07/2003 | 405 | 250 |
| Hefei–Nanjing | 11/06/2005 | 19/04/2008 | 154 | 250 |
| Beijing–Tianjin | 07/04/2005 | 01/08/2008 | 120 | 350 |
| Qingdao–Jinan | 28/01/2007 | 20/12/2008 | 393 | 250 |
| Shijiazhuang–Taiyuan | 11/06/2005 | 01/04/2009 | 190 | 250 |
| Hefei–Wuhan | 01/08/2005 | 01/04/2009 | 351 | 200 |
| Dazhou–Chengdu | 01/05/2005 | 07/07/2009 | 148 | 250 |
| Ningbo–Taizhou–Wenzhou | 27/10/2005 | 28/09/2009 | 268 | 250 |
| Wenzhou–Fuzhou | 08/01/2005 | 28/09/2009 | 298 | 250 |
| Wuhan–Guanghzou | 23/06/2005 | 26/12/2009 | 968 | 350 |
| Zhengzhou–Xian | 01/09/2005 | 06/01/2010 | 455 | 350 |
| Fuzhou–Xiamen | 01/10/2005 | 26/04/2010 | 275 | 250 |
| Chengdu–Dujiangyan | 04/11/2008 | 12/05/2010 | 65 | 250 |
| Shanghai–Nanjing | 01/07/2008 | 01/07/2010 | 301 | 220 |
| Nanchang–Jiujiang | 28/06/2007 | 20/09/2010 | 131 | 350 |
| Shanghai–Hangzhou | 01/04/2009 | 26/11/2010 | 150 | 350 |
| Yichang–Wanzhou | 01/12/2003 | 22/12/2010 | 377 | 200 |
| Wuhan–Yichang | 17/09/2008 | 23/12/2010 | 293 | 250 |
| Haikou–Sanya (eastern coastal line) | 29/09/2007 | 30/12/2010 | 308 | 250 |
| Changchun–Jilin | 01/04/2008 | 30/12/2010 | 111 | 200 |
| Jiangmen–Xinhui | 18/12/2005 | 07/01/2011 | 27 | 350 |
| Beijing–Shanghai | 18/04/2008 | 30/06/2011 | 1433 | 350 |
| Guangzhou–Shenzhen | 20/08/2008 | 26/12/2011 | 116 | 200 |
| Longyan–Xiamen | 25/12/2006 | 01/07/2012 | 171 | 350 |
| Zhengzhou–Wuhan | 15/10/2008 | 28/09/2012 | 536 | 350 |
| Hefei–Bengbu | 20/05/2009 | 16/10/2012 | 132 | 350 |
| Haerbin–Dalian | 23/08/2007 | 01/12/2012 | 921 | 350 |
| Beijing–Zhengzhou | 26/12/2007 | 26/12/2012 | 693 | 350 |
| Nanjing–Hangzhou | 01/04/2009 | 01/07/2013 | 249 | 350 |
| Panjin–Yinkou | 31/05/2009 | 12/09/2012 | 89 | 350 |
| Tianjin–Qinghuangdao | 08/11/2008 | 01/12/2013 | 261 | 350 |
| Xiamen–Shenzhen | 23/11/2007 | 28/12/2013 | 502 | 250 |
| Xian–Baoji | 18/12/2009 | 28/12/2013 | 148 | 250 |
| Guangxi Coastal (Nanning–Qinzhou–Beihai) | 11/12/2008 | 28/12/2013 | 261 | 250 |
| Liuzhou–Nanning | 27/12/2008 | 28/12/2013 | 223 | 350 |
| Wuhan–Xianning | 26/03/2009 | 28/12/2013 | 90 | 250 |
| Taiyuan–Xian | 03/12/2009 | 01/07/2014 | 678 | 250 |
| Nanchang–Changsha | 26/02/2009 | 16/09/2014 | 344 | 350 |
| Hangzhou–Nanchang | 18/04/2010 | 10/12/2014 | 582 | 350 |
| Lanzhou–Wulumuqi | 01/01/2010 | 26/12/2014 | 1776 | 250 |
| Guangzhou–Nanning | 11/09/2008 | 18/04/2014 | 577 | 250 |
| Huanggang–Wuhan–Huangshi | 02/10/2009 | 18/06/2014 | 97 | 250 |
| Taiyuan(south)–Xi’an(north) | 03/12/2009 | 01/07/2014 | 579 | 250 |
| Nanchang(west)–Changsha(south) | 22/12/2009 | 16/09/2014 | 342 | 300 |
| Urumqi (south)–Hami | 04/11/2009 | 16/11/2014 | 530 | 200 |
| Hangzhou (east)–Nanchang (west) | 22/12/2009 | 10/12/2014 | 591 | 300 |
| Changsha (south)–Xinhuang (west) | 16/03/2010 | 16/12/2014 | 420 | 300 |
| Chengdu–Mianyang–Leshan | 30/12/2008 | 20/12/2014 | 319 | 200 |
| Wuzhou (south) –Guangzhou (south) | 09/11/2008 | 26/12/2014 | 249 | 200 |
| Guizhou–Guangxi | 13/10/2008 | 26/12/2014 | 861 | 250 |
| Hami–Lanzhou (west) | 04/11/2009 | 26/12/2014 | 1246 | 200 |
| Zhengzhou–Songcheng | 29/12/2009 | 28/12/2014 | 50 | 200 |
| Xinhuang (west) –Guiyang (north) | 26/03/1010 | 18/06/2015 | 286 | 300 |
| Harbin–Qiqihar | 05/07/2009 | 17/08/2015 | 286 | 250 |
| Nanjing (south)–Anqing | 28/12/2008 | 06/12/2015 | 257 | 200 |
| Nanning–Baise | 27/12/2009 | 11/12/2015 | 223 | 200 |
| Chengdu–Chongqing | 22/03/2010 | 26/12/2015 | 305 | 300 |
| Shenzhen–Futian | 20/08/2008 | 30/12/2015 | 8 | 300 |
| Zhengzhou–Xuzhou | 26/12/2 012 | 10//9/2016 | 357 | 300 |
| Chongqing (north)–Wanzhou (north) | 22/12/2010 | 28/11/2016 | 247 | 200 |
| Guiyang–Kunming | 26/03/2010 | 28/12/2016 | 461 | 300 |
| Baise–Kunming (south) | 27/12/2009 | 28/12/2016 | 487 | 200 |
| Dazhi (north)–Yangxin | 29/12/2013 | 12/06/2017 | 36 | 200–250 |
| Baoji–Lanzhou | 19/10/2010 | 09/07/2017 | 403 | 250 |
| Hohhot (east)–Wulanchabu | 16/06/2014 | 03/08/2017 | 126 | 250 |
| Yangxin–Jiujiang | 29/12/2013 | 21/09/2017 | 79 | 250 |
| Jiangyou–Xi’an | 10/11/2010 | 06/12/2017 | 509 | 250 |
| Shijiazhuang–Jinan | 08/02/2014 | 28/12/2017 | 319 | 250 |
References
- Jian, T.; Sachs, J.D.; Warner, A.M. Trends in regional inequality in China. China Econ. Rev. 1996, 7. [Google Scholar] [CrossRef]
- Zhang, Q.; Zou, H.F. Regional inequality in contemporary China. Ann. Econ. Financ. 2012, 13, 113–137. [Google Scholar]
- Chen, Z.; Haynes, K. Chinese Railway in the Era of High-Speed; Emerald Group Publishing Limited: Bingley, UK, 2015. [Google Scholar]
- Wu, Y.; Chen, Y.; Deng, X.; Hui, E.C.M. Development of Characteristic towns in China. Habitat Int. 2017, 77, 21–31. [Google Scholar] [CrossRef]
- Wang, K.; Xia, W.; Zhang, A. Should further expand its high-speed rail network? Consider the low-cost carrier factor. Transp. Res. Part A 2017, 100, 105–120. [Google Scholar] [CrossRef]
- Zheng, S.; Saiz, A. Introduction to the special issue “China’s urbanization and housing market”. J. Hous. Econ. 2016, 33, 1–3. [Google Scholar] [CrossRef]
- Cao, J.; Liu, X.C.; Wang, Y.; Li, Q. Accessibility impacts of China’s high-speed rail network. J. Transp. Geogr. 2013, 28, 12–21. [Google Scholar] [CrossRef]
- Jiao, J.; Wang, J.; Jin, F. Impacts of the high-speed rail lines on the city network in China. J. Transp. Geogr. 2017, 60, 257–266. [Google Scholar] [CrossRef]
- Zheng, S.; Kahn, M.E. China’s bullet trains facilitate market integration and mitigate the cost of megacity growth. Proc. Natl. Acad. Sci. USA 2013, 110, 1248–1253. [Google Scholar] [CrossRef]
- Bajic, V. The effects of a new subway line on housing prices in metropolitan Toronto. Urban Study 1983, 20, 147–158. [Google Scholar] [CrossRef]
- Knaap, G.J.; Ding, C.; Hopkins, L.D. Do plans matter? The effects of light rail plans on land values in station areas. J. Plan. Educ. Res. 2001, 21, 32–39. [Google Scholar] [CrossRef]
- Debrezion, G.; Pels, E.; Rietveld, P. The impact of railway stations on residential and commercial property value: A meta-analysis. J. Real Estate Financ. Econ. 2007, 35, 161–180. [Google Scholar] [CrossRef]
- Debrezion, G.; Pels, E.; Rietveld, P. The impact of rail transport on real estate prices an empirical analysis of the Dutch housing market. Urban Study 2011, 48, 997–1015. [Google Scholar] [CrossRef]
- Duncan, M. The impact of transit-oriented development on housing prices in San Diego, CA. Urban Study 2011, 48, 101–127. [Google Scholar] [CrossRef]
- Andersson, D.E.; Shyr, O.F.; Fu, J. Does high-speed rail accessibility influence residential property prices? Hedonic estimate from southern Taiwan. J. Transp. Geogr. 2010, 18, 166–174. [Google Scholar] [CrossRef]
- Zhang, M.; Meng, X.; Wang, L.; Xu, T. Transit development shaping urbanization: Evidence from the housing market in Beijing. Habitat Int. 2014, 44, 545–554. [Google Scholar] [CrossRef]
- Zhao, S.; Wu, N.; Wang, X. Impact of Feeder Accessibility on High-Speed Rail Share: Wuhan-Guangzhou Corridor, China. J. Urban Plan. Dev. 2018, 144, 04018029. [Google Scholar] [CrossRef]
- Button, K. Is there any economic justification for high-speed railways in the United States? J. Transp. Geogr. 2012, 22, 300–302. [Google Scholar] [CrossRef]
- Blum, U.; Haynes, K.E.; Karlsson, C. Introduction to the special issue: The regional and urban effects of high-speed trains. Ann. Reg. Sci. 1997, 31, 1–20. [Google Scholar] [CrossRef]
- Armstrong, R.J.; Rodriguez, D.A. An evaluation of the accessibility benefits of commuter rail in eastern Massachusetts using spatial hedonic price functions. Transportation 2006, 33, 21–43. [Google Scholar] [CrossRef]
- Rosen, S. Hedonic prices and implicit markets: Product differentiation in pure competition. J. Polit. Econ. 1974, 82, 34–55. [Google Scholar] [CrossRef]
- Billings, S.B. Estimating the value of a new transit option. Reg. Sci. Urban Econ. 2011, 41, 525–536. [Google Scholar]
- Bowes, D.R.; Ihlanfeldt, K.R. Identifying the impacts of rail transit stations on residential property values. J. Urban Econ. 2001, 50, 1–25. [Google Scholar] [CrossRef]
- Duncan, M. Comparing rail transit capitalization benefits for single-family and condominium units in San Diego, California. Transp. Res. Rec. 2008, 2067, 120–130. [Google Scholar] [CrossRef]
- Hess, D.B.; Almeida, T.M. Impact of proximity to light rail rapid transit on station-area property values in Buffalo, New York. Urban Study 2007, 44, 1041–1068. [Google Scholar] [CrossRef]
- Yan, S.; Delmelle, E.; Duncan, M. The impact of a new light rail system on single-family property values in Charlotte, North Carolina. J. Transp. Land Use 2012, 5, 60–67. [Google Scholar]
- Chalermpong, S. Rail transit and residential land use in developing countries: Hedonic study of residential property prices in Bangkok, Thailand. Transp. Res. Record 2007, 2038, 111–119. [Google Scholar] [CrossRef]
- Cervero, R.; Kang, C.D. Bus rapid transit impacts on land uses and land values in Seoul, Korea. Transp. Policy 2011, 18, 102–116. [Google Scholar] [CrossRef]
- Cervero, R.; Duncan, M. Neighbourhood Composition and Residential Land Prices: Does Exclusion Raise or Lower Values? Urban Stud. 2004, 41, 299–315. [Google Scholar] [CrossRef]
- Chen, C.L.; Hall, P. The impact of high-speed trains on British economic geography: A study of the UK’s 125/225 and its effects. J. Transp. Geogr. 2011, 19, 689–704. [Google Scholar] [CrossRef]
- Ureña, J.M.; Menerault, P.; Garmendia, M. The high-speed rail challenge for big intermediate cities: A national, regional, and local perspective. Cities. 2009, 26, 266–279. [Google Scholar] [CrossRef]
- Dupuy, G. Lurbanissme des Reséaux: Theotiésetmétgodes; Armand Collin: Paris, France, 1991. [Google Scholar]
- Spiekermann, K.; Wegener, M. Accessibility and spatial development in Europe. Sci. Reg. 2006, 5, 15–46. [Google Scholar]
- Sasaki, K.; Ohashi, T.; Ando, A. High-speed rail transit impact on regional systems: Does the Shinkansen contribute to dispersion? Ann. Reg. Sci. 1997, 31, 77–98. [Google Scholar] [CrossRef]
- Albalate, D.; Bel, G. The Economics and Politics of High-Speed Rail: Lessons from Experiences Abroad; Rowman and Littlefield Publishers: Lanham, MD, USA, 2012. [Google Scholar]
- Chen, Z.; Haynes, K. Impact of high-speed rail on regional economic disparity in China. J. Transp. Geogr. 2017, 65, 80–91. [Google Scholar] [CrossRef]
- Raturi, V.; Verma, A. Analyzing competition between High Speed Rail and Bus mode using market entry game analysis. Sci. Direct 2017, 25, 2373–2384. [Google Scholar] [CrossRef]
- Pol, P. The Economic Impact of the High-Speed Train on Urban Regions. In Proceedings of the 43rd European Regional Science Association ERSA Congress, Jyväskylä, Finland, 27–30 August 2003. [Google Scholar]
- Armando, C.; Luigi, P.; Ilaria, H. Hedonic value of high-speed services: Quantitative analysis of the students’ domestic tourist attractiveness of the main Italian cities. J. Transp. Res. Part A 2017, 100, 348–365. [Google Scholar]
- Lin, Y. Travel costs and urban specialization patterns: Evidence from China’s high speed railway system. J. Urban Econ. 2017, 98, 98–123. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, L.; Wang, S. Financial development and economic growth: Recent evidence from China. J. Comp. Econ. 2012, 40, 393–412. [Google Scholar] [CrossRef]
- Arellano, M.; Bond, S. Some tests of specification for panel data: Monte Carlo evidence and an application to employment equations. The Review of Economic Studies. 1991, 58, 277–297. [Google Scholar] [CrossRef]
- Arellano, M.; Bover, O. Another look at the instrumental variable estimation of error-components models. J. Econom. 1995, 68, 29–51. [Google Scholar] [CrossRef]
- Blundell, R.; Bond, S. Initial conditions and moment restrictions in dynamic panel data models. J. Econom. 1998, 87, 115–143. [Google Scholar] [CrossRef]
- Sun, F.; Yuri, S.M. Economic Impact of High-Speed Rail on Household Income in China; Transportation Research Board: Washington, DC, USA, 2016; pp. 71–78. [Google Scholar]
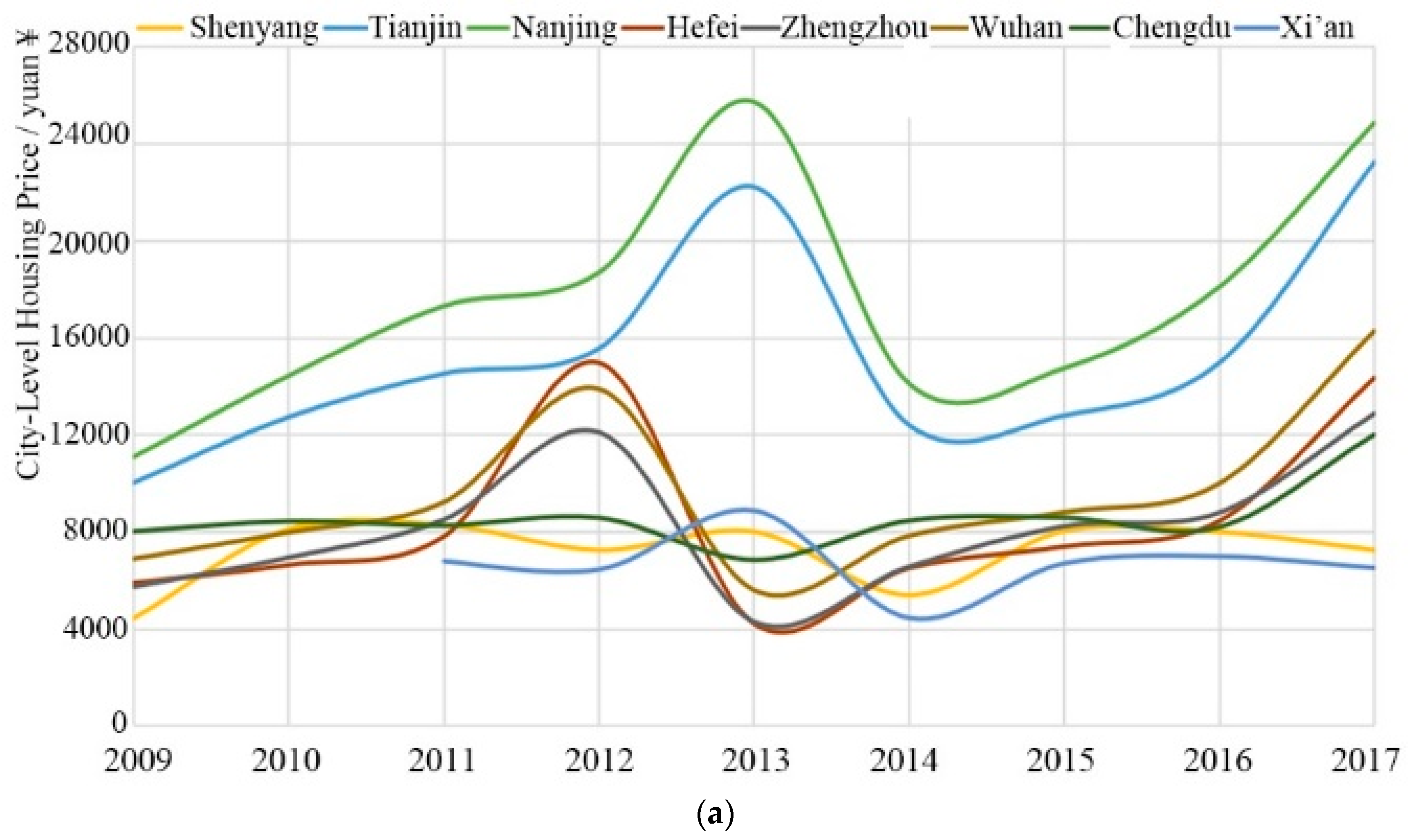
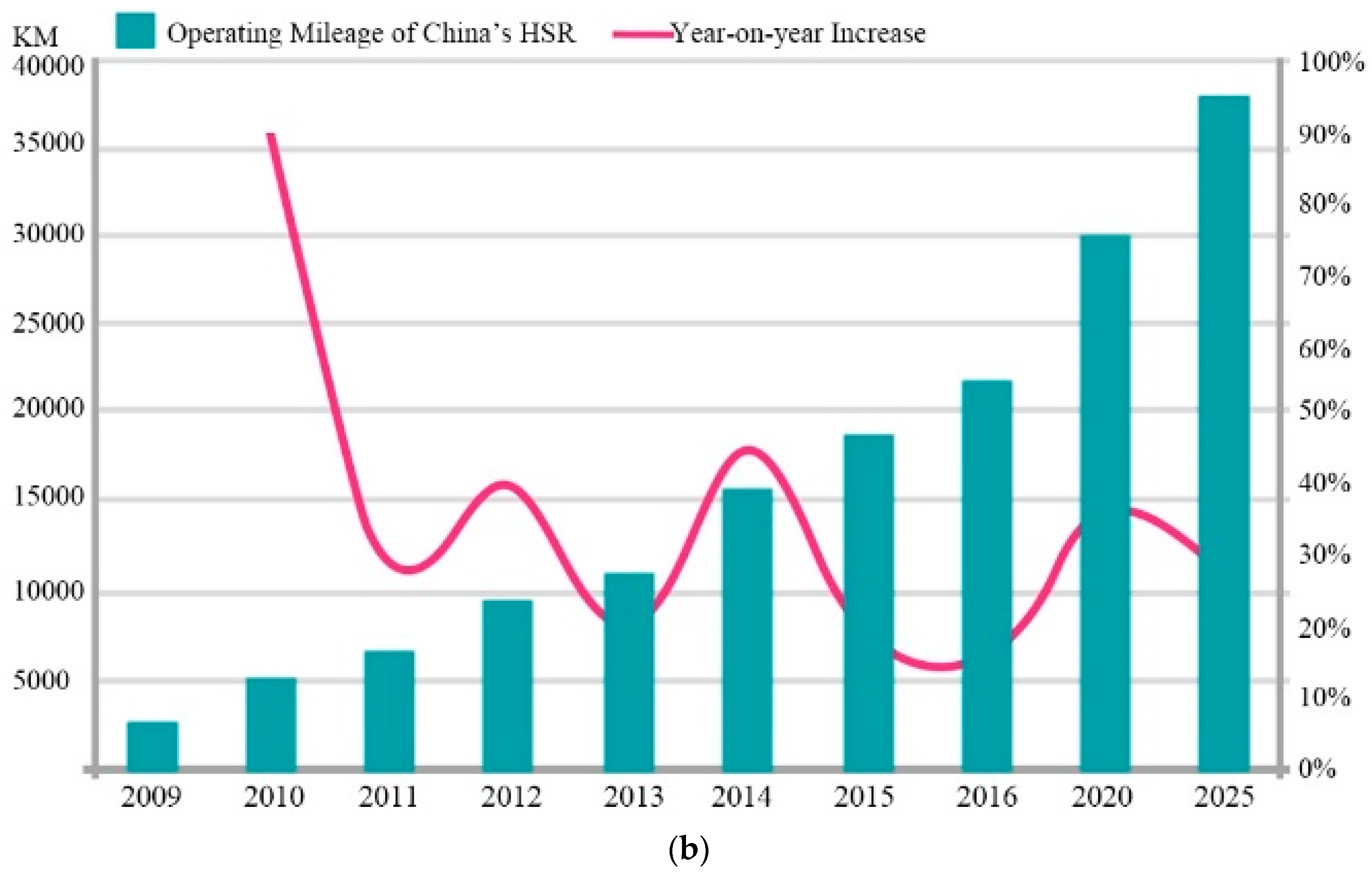
| Symbols | Definition | Minimum | Maximum | Mean | SD | Observations |
|---|---|---|---|---|---|---|
| y | ln(housing price) | 7.4697 | 10.9642 | 8.8197 | 0.4893 | 1042 |
| hsr | HSR | 0 | 1 | 0.2760 | 0.4471 | 2565 |
| pop | Ln(population) | 2.7147 | 7.8043 | 4.6103 | 0.7722 | 2565 |
| air | Airline | 0 | 1 | 0.4596 | 0.4985 | 2565 |
| rail | Railway | 0 | 1 | 0.9341 | 0.2481 | 2565 |
| save | Savings/GDP | 0.0430 | 4.1361 | 0.8454 | 0.3962 | 2515 |
| loan | Loans/GDP | 0.0623 | 84.6609 | 1.5597 | 2.2602 | 2516 |
| Baseline Regression: Fixed Effect Model | Dynamic Panel Data Model | |||
|---|---|---|---|---|
| Difference GMM | System GMM | |||
| hsri,t−1 | 0.139 *** | 0.048 * | 0.073 *** | |
| (0.204) | (0.025) | (0.024) | ||
| hsri,t | 0.185 *** | 0.072 ** | 0.086 ** | |
| (0.022) | (0.036) | (0.036) | ||
| yi,t−1 | 0.670 *** | 0.805 *** | ||
| (0.056) | (0.036) | |||
| pop | 0.382 *** | 0.491 *** | 0.361 *** | 0.185 *** |
| (0.051) | (0.053) | (0.070) | (0.053) | |
| air | −0.018 | −0.021 | 0.065 | −0.038 |
| (0.060) | (0.066) | (0.053) | (0.119) | |
| rail | 0.033 | 0.027 | −0.171 ** | −0.220 *** |
| (0.140) | (0.154) | (0.070) | (0.083) | |
| save | −0.058 | −0.064 | 0.234 *** | 0.238 *** |
| (0.053) | (0.056) | (0.076) | (0.079) | |
| loan | 0.049 *** | 0.070 *** | 0.016 ** | −0.003 |
| (0.010) | (0.010) | (0.009) | (0.011) | |
| constant | 6.803 *** | 6.189 *** | 1.027 ** | 0.864 ** |
| (0.301) | (0.320) | (0.478) | (0.341) | |
| Observations | 1000 | 1031 | 532 | 779 |
| Diagnosis | R2 = 0.3397 Hausman test (p = 0.00) | R2 = 0.3260 Hausman test (p = 0.00) | Sargan test (p = 0.00) First-order (p = 0.00) Second-order (p = 0.38) | Sargan test (p = 0.00) First-order (p = 0.00) Second-order (p = 0.28) |
| Pooled Data | Panel Data: Fixed Effect Model | |||
|---|---|---|---|---|
| Beta | Standard Errors | Beta | Standard Errors | |
| hsr | −0.003 | 0.028 | 0.049 | 0.033 |
| hsr*N | 0.600 *** | 0.078 | 0.317 *** | 0.056 |
| hsr*R | 0.349 *** | 0.061 | 0.196 *** | 0.048 |
| N | 0.087 * | 0.077 | ||
| R | 0.102 ** | 0.048 | ||
| pop | 0.122 *** | 0.021 | 0.482 *** | 0.052 |
| air | 0.083 *** | 0.027 | −0.017 | 0.065 |
| rail | 0.040 | 0.082 | 0.023 | 0.150 |
| save | −0.171 *** | 0.033 | −0.043 | 0.055 |
| loan | 0.086 *** | 0.014 | 0.061 *** | 0.010 |
| constant | 8.049 *** | 0.129 | 6.256 *** | 0.313 |
| Observations | 1031 | 1031 | ||
| Diagnosis | R2 = 0.4632 | R2 = 0.3735 Hausman test (p = 0.00) | ||
| Pooled Data | Panel Data: Fixed Effect Model | |||
|---|---|---|---|---|
| Beta | Standard Errors | Beta | Standard Errors | |
| hsr | 0.021 | 0.063 | 0.145 *** | 0.048 |
| hsr*East | 0.135 ** | 0.070 | 0.064 | 0.056 |
| hsr*Central | 0.014 | 0.073 | 0.025 | 0.064 |
| East | 0.336 *** | 0.039 | ||
| Central | 0.089 ** | 0.043 | ||
| pop | 0.211 *** | 0.016 | 0.485 *** | 0.053 |
| air | 0.140 *** | 0.026 | −0.021 | 0.066 |
| rail | −0.036 | 0.082 | 0.030 | 0.154 |
| save | −0.117 *** | 0.032 | −0.069 | 0.056 |
| loan | 0.090 *** | 0.012 | 0.070 *** | 0.010 |
| constant | 7.419 *** | 0.110 | 6.214 *** | 0.321 |
| Observations | 1031 | 1031 | ||
| Diagnosis | R2 = 0.4791 | R2 = 0.3373 Hausman test (p = 0.00) | ||
| Symbols | Definition | Minimum | Maximum | Mean | SD | Observations |
|---|---|---|---|---|---|---|
| y | Housing price (in logs) | 7.8284 | 10.7254 | 8.8189 | 0.5057 | 315 |
| hsr | HSR | 0 | 1 | 0.5302 | 0.4999 | 315 |
| pop | Population (in logs) | 5.8497 | 7.8034 | 4.4868 | 0.6756 | 315 |
| restr | Restriction | 0 | 1 | 0.3841 | 0.4872 | 315 |
| metro | Metro | 0 | 18 | 1.7683 | 3.4104 | 315 |
| rail | Railway | 0 | 1 | 0.9968 | 0.0563 | 315 |
| save | Savings/GDP | 0.0787 | 1.995 | 0.8613 | 0.2545 | 305 |
| loan | Loans/GDP | 0.0623 | 4.6291 | 0.7000 | 2.2402 | 304 |
| land | Residential Land/construction land | 0.1887 | 0.7143 | 0.3079 | 0.073 | 262 |
| (1) | (2) | (3) | ||||
|---|---|---|---|---|---|---|
| Beta | Standard Errors | Beta | Standard Errors | Beta | Standard Errors | |
| hsri,t | 0.207 *** | 0.026 | 0.147 *** | 0.024 | 0.142 *** | 0.026 |
| restri,t | 0.017 | 0.018 | ||||
| restri,t+1 | −0.039 ** | 0.019 | ||||
| pop | 0.840 *** | 0.100 | 0.501 *** | 0.098 | 0.505 *** | 0.114 |
| metro | 0.076 *** | 0.010 | 0.060 *** | 0.011 | ||
| rail | 0.000 | 0.171 | −0.047 | 0.142 | −0.030 | 0.137 |
| save | −0.194 ** | 0.076 | −0.255 *** | 0.081 | −0.208 ** | 0.082 |
| loan | 0.203 *** | 0.026 | 0.136 *** | 0.031 | 0.131 *** | 0.034 |
| land | 0.100 | 0.326 | −0.110 | 0.019 | ||
| constant | 3.511 *** | 0.640 | 5.648 *** | 0.634 | 5.686 *** | 0.734 |
| Observations | 304 R2 = 0.5785 Hausman test (p = 0.00) | 256 R2 = 0.5888 Hausman test (p = 0.00) | 226 R2 = 0.5251 Hausman test (p = 0.00) | |||
| Diagnosis | ||||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Liu, X.; Wang, F. Economic Impact of the High-Speed Railway on Housing Prices in China. Sustainability 2018, 10, 4799. https://doi.org/10.3390/su10124799
Wang Y, Liu X, Wang F. Economic Impact of the High-Speed Railway on Housing Prices in China. Sustainability. 2018; 10(12):4799. https://doi.org/10.3390/su10124799
Chicago/Turabian StyleWang, Yuxiang, Xueli Liu, and Feng Wang. 2018. "Economic Impact of the High-Speed Railway on Housing Prices in China" Sustainability 10, no. 12: 4799. https://doi.org/10.3390/su10124799
APA StyleWang, Y., Liu, X., & Wang, F. (2018). Economic Impact of the High-Speed Railway on Housing Prices in China. Sustainability, 10(12), 4799. https://doi.org/10.3390/su10124799






