Warranty Decision Model and Remanufacturing Coordination Mechanism in Closed-Loop Supply Chain: View from a Consumer Behavior Perspective
Abstract
1. Introduction
2. Problem Description and Assumptions
2.1. Problem Description
2.2. Basic Assumptions and Parameters
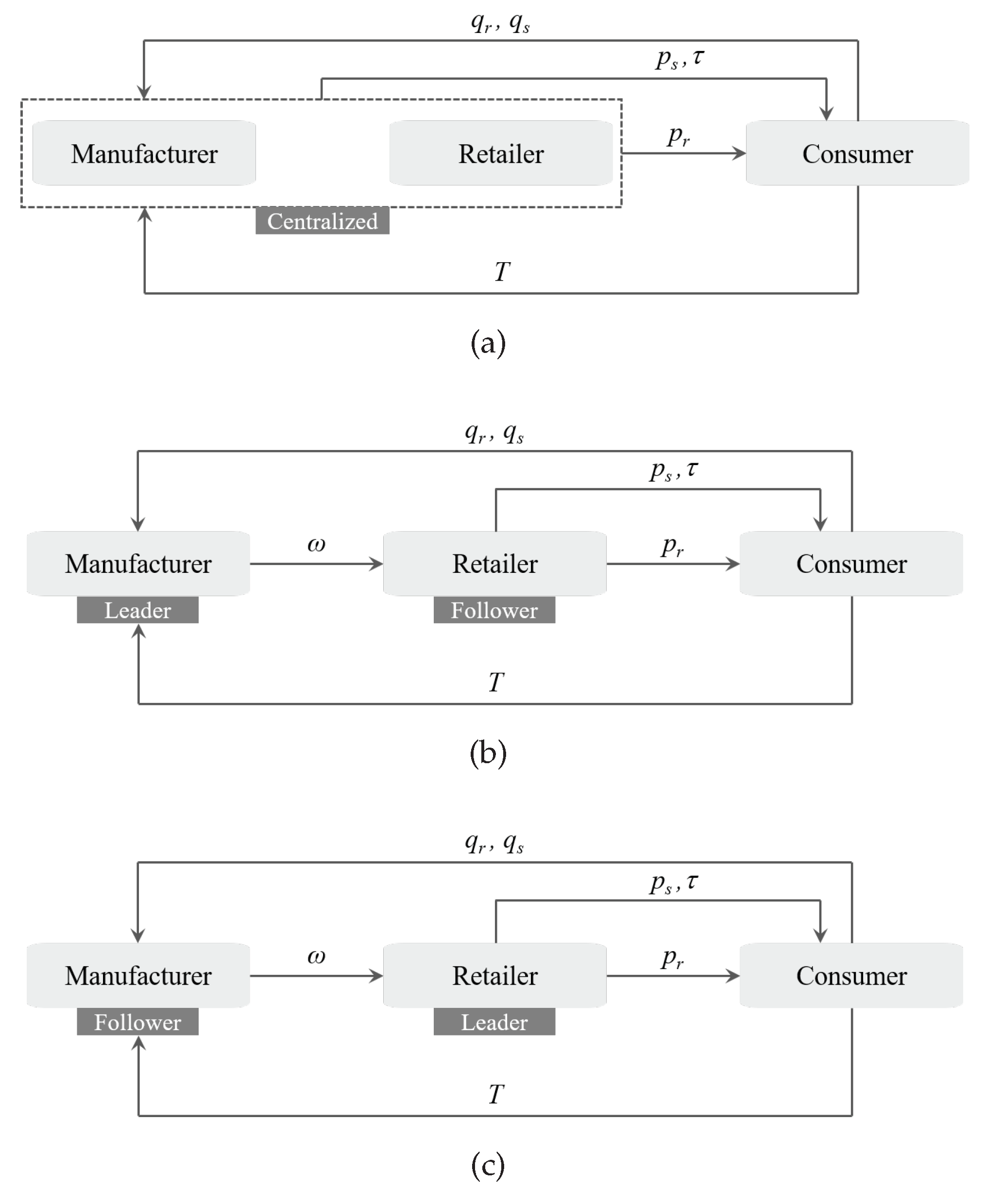
3. Closed-Loop Supply Chain Decision
3.1. Centralized Decision Making (Model C)
3.2. Decentralized Decision
3.2.1. M-R Decision (Model D1)
3.2.2. R-M Decision (Model D2)
4. Analysis of Decision-Making Properties of Closed-Loop Supply Chain
- ,
- ,
- .
5. Coordination Mechanism Design
5.1. M-R Decision: Revenue Sharing Contract (S-1 Model)
5.2. M-R Decision: Improved Revenue Sharing Contract (S-2 Model)
5.3. R-M Decision: Two Charging Contracts (T Model)
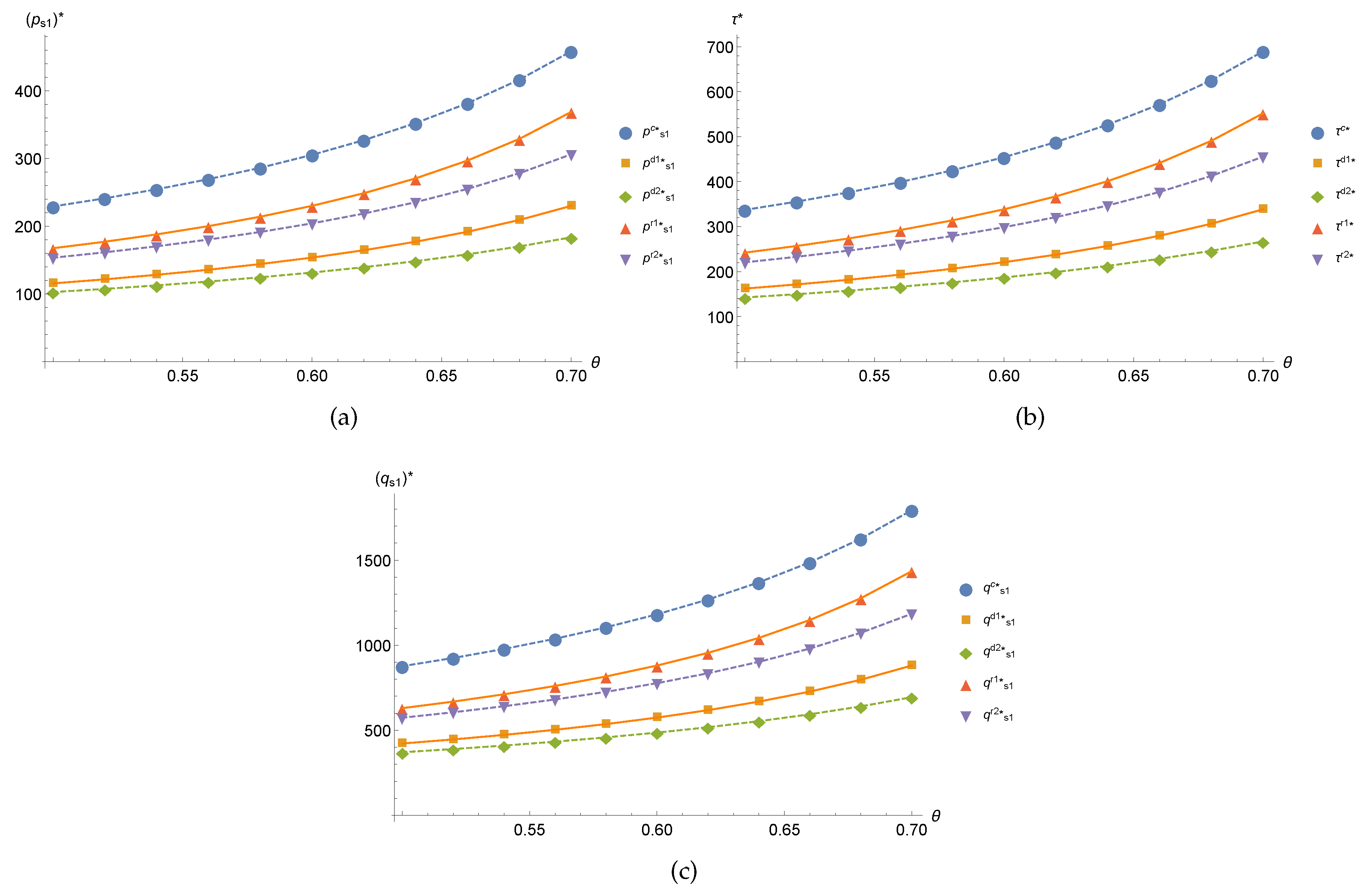
6. Numerical Simulation
6.1. Remanufacturing Closed-Loop Supply Chain Warranty Decision Model
6.2. Remanufacturing Closed-Loop Supply Chain Coordination Mechanism
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Boulding, W.; Kirmani, A. A consumer-side experimental examination of signaling theory: do consumers perceive warranties as signals of quality? J. Consum. Res. 1993, 20, 111–123. [Google Scholar] [CrossRef]
- Wei, J.; Zhao, J.; Li, Y. Price and warranty period decisions for complementary products with horizontal firms’ cooperation/noncooperation strategies. J. Clean. Prod. 2015, 105, 86–102. [Google Scholar] [CrossRef]
- Ahi, P.; Searcy, C. A comparative literature analysis of definitions for green and sustainable supply chain management. J. Clean. Prod. 2013, 52, 329–341. [Google Scholar] [CrossRef]
- Shafiee, M.; Chukova, S. Maintenance models in warranty: A literature review. Eur. J. Oper. Res. 2013, 229, 561–572. [Google Scholar] [CrossRef]
- Song, M.; Wang, S.; Sun, J. Environmental regulations, staff quality, green technology, R&D efficiency, and profit in manufacturing. Technol. Forecast. Soc. Chang. 2018, 133, 1–14. [Google Scholar]
- Li, K.; Wang, L.; Chhajed, D.; Mallik, S. The Impact of Quality Perception and Consumer Valuation Change on Manufacturer’s Optimal Warranty, Pricing, and Market Coverage Strategies. Decis. Sci. 2018. [Google Scholar] [CrossRef]
- Lan, Y.; Zhao, R.; Tang, W. A fuzzy supply chain contract problem with pricing and warranty. J. Intell. Fuzzy Syst. 2014, 26, 1527–1538. [Google Scholar]
- Du, S.; Hu, L.; Song, M. Production optimization considering environmental performance and preference in the cap-and-trade system. J. Clean. Prod. 2016, 112, 1600–1607. [Google Scholar] [CrossRef]
- Arabi, M.; Mansour, S.; Shokouhyar, S. Optimizing a warranty–based sustainable product service system using game theory. Int. J. Sustain. Eng. 2018. [Google Scholar] [CrossRef]
- Chen, C.K.; Lo, C.C.; Weng, T.C. Optimal production run length and warranty period for an imperfect production system under selling price dependent on warranty period. Eur. J. Oper. Res. 2017, 259, 401–412. [Google Scholar] [CrossRef]
- Li, N.; Li, B. A Closed-loop Supply Chain Coordination Strategy Based on Product Warranty Period. Syst. Eng. 2016, 34, 90–96. [Google Scholar]
- Mai, D.T.; Liu, T.; Morris, M.D.S.; Sun, S. Quality coordination with extended warranty for store-brand products. Eur. J. Oper. Res. 2017, 256, 524–532. [Google Scholar] [CrossRef]
- Sabbaghi, M.; Behdad, S. Consumer decisions to repair mobile phones and manufacturer pricing policies: The concept of value leakage. Resour. Conserv. Recycl. 2018, 133, 101–111. [Google Scholar] [CrossRef]
- Xu, L.; Shi, X.; Du, P.; Govindan, K.; Zhang, Z. Optimization on pricing and overconfidence problem in a duopolistic supply chain. Comput. Oper. Res. 2018, 101, 162–172. [Google Scholar] [CrossRef]
- Savaskan, R.C.; Bhattacharya, S.; Van Wassenhove, L.N. Closed-loop supply chain models with product remanufacturing. Manag. Sci. 2004, 50, 239–252. [Google Scholar] [CrossRef]
- Fleischmann, M.; Bloemhof-Ruwaard, J.M.; Dekker, R.; van der Laan, E.; van Nunen, J.A.E.E.; Van Wassenhove, L.N. Quantitative models for reverse logistics: A review. Eur. J. Oper. Res. 1997, 103, 1–17. [Google Scholar] [CrossRef]
- Xu, Z.; Peng, Z.; Yang, L.; Chen, X. An Improved Shapley Value Method for a Green Supply Chain Income Distribution Mechanism. Int. J. Environ. Res. Public Health 2018, 15, 1976. [Google Scholar] [CrossRef] [PubMed]
- Gong, Y.; Jiang, Y. Study on Pricing and Channel Selection of Closed-loop Supply Chain Hybrid Recovery Mode. Soft Sci. 2018, 32, 127–131+144. [Google Scholar]
- Kaya, O.; Bagci, F.; Turkay, M. Planning of capacity, production and inventory decisions in a generic reverse supply chain under uncertain demand and returns. Int. J. Prod. Res. 2014, 52, 270–282. [Google Scholar] [CrossRef]
- Luo, Z.; Chen, X.; Chen, J.; Wang, X. Optimal pricing policies for differentiated brands under different supply chain power structures. Eur. J. Oper. Res. 2017, 259, 437–451. [Google Scholar] [CrossRef]
- Yoo, S.H.; Kim, B.C. Joint pricing of new and refurbished items: A comparison of closed-loop supply chain models. Int. J. Prod. Econ. 2016, 182, 132–143. [Google Scholar] [CrossRef]
- Gan, S.S.; Pujawan, I.N.; Widodo, B. Pricing decision for new and remanufactured product in a closed-loop supply chain with separate sales-channel. Int. J. Prod. Econ. 2017, 190, 120–132. [Google Scholar] [CrossRef]
- Chen, X.; Li, L.; Zhou, M. Manufacturer’s pricing strategy for supply chain with warranty period-dependent demand. Omega 2012, 40, 807–816. [Google Scholar] [CrossRef]
- Gaur, J.; Subramoniam, R.; Govindan, K.; Huisingh, D. Closed-loop supply chain management: From conceptual to an action oriented framework on core acquisition. J. Clean. Prod. 2017, 167, 1415–1424. [Google Scholar] [CrossRef]
- Joshi, Y.; Rahman, Z. Factors affecting green purchase behaviour and future research directions. Int. Strateg. Manag. Rev. 2015, 3, 128–143. [Google Scholar] [CrossRef]
- Gallego, G.; Wang, R.; Ward, J.; Hu, M.; Beltran, J.L. Flexible-duration extended warranties with dynamic reliability learning. Prod. Oper. Manag. 2014, 23, 645–659. [Google Scholar] [CrossRef]
- Su, C.; Wang, X. Modeling flexible two-dimensional warranty contracts for used products considering reliability improvement actions. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2016, 230, 237–247. [Google Scholar] [CrossRef]
- Li, N.; Li, B.; Liu, Z. Research on the guaranty subject and warranty efficiency of remanufactured products. Oper. Res. Manag. 2016, 25, 249–257. [Google Scholar]
- Zhu, X.; Yu, L. Differential Pricing Decision and Coordination of Green Electronic Products from the Perspective of Service Heterogeneity. Appl. Sci. 2018, 8, 1207. [Google Scholar] [CrossRef]
- Zhou, L.; Naim, M.M.; Disney, S.M. The impact of product returns and remanufacturing uncertainties on the dynamic performance of a multi-echelon closed-loop supply chain. Int. J. Prod. Econ. 2017, 183, 487–502. [Google Scholar] [CrossRef]
- Li, K.; Mallik, S.; Chhajed, D. Design of extended warranties in supply chains under additive demand. Prod. Oper. Manag. 2012, 21, 730–746. [Google Scholar] [CrossRef]
- Cachon, G.P.; Lariviere, M.A. Supply chain coordination with revenue-sharing contracts: strengths and limitations. Manag. Sci. 2005, 51, 30–44. [Google Scholar] [CrossRef]
- Cachon, G.P. Supply chain coordination with contracts. In Handbooks in Operations Research and Management Science; Elsevier: Amsterdam, The Netherlands, 2003; Volume 11, pp. 227–339. [Google Scholar]
- Zhou, W.; Han, X.; Shen, Y. The Closed-loop Supply Chain Pricing and Service Level Decision and Coordination Considering Consumer Behavior. Comput. Integr. Manuf. Syst. 2017, 23, 2241–2250. [Google Scholar]
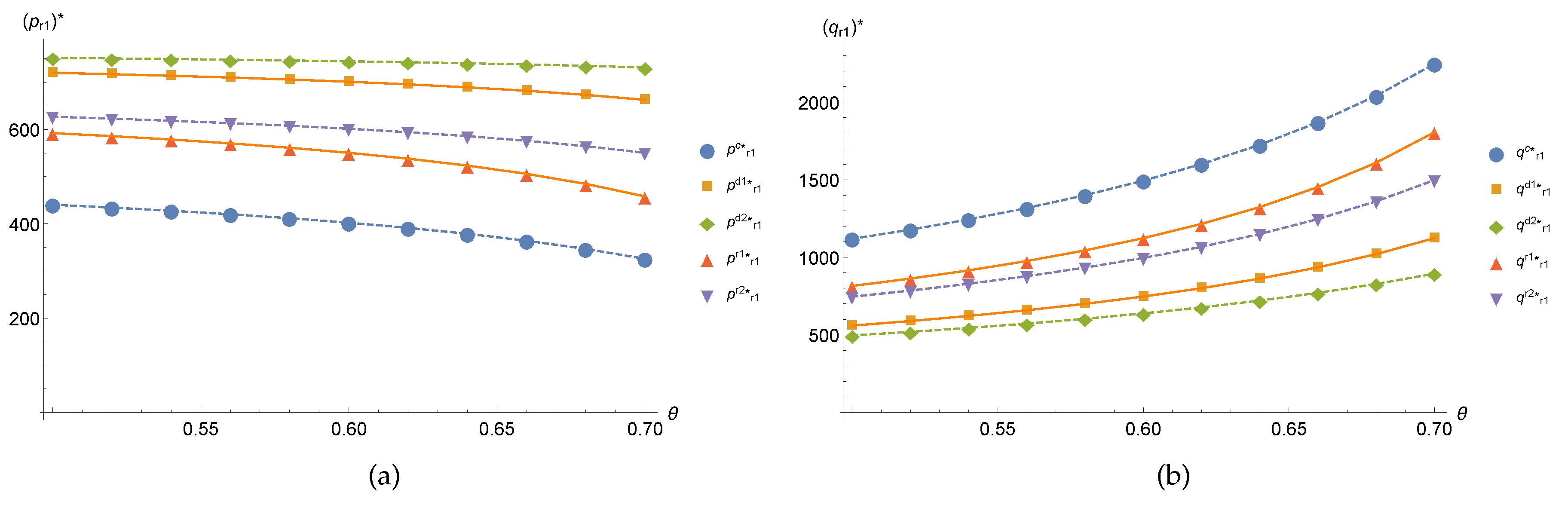
| Model C | |
| Model D1 | |
| Model D2 | |
| Centralized Decision | Decentralized M-R Decision | Decentralized R-M Decision | |||||
|---|---|---|---|---|---|---|---|
| 0.3 | 332,462 | 166,150 | 83,237.3 | 249,387.3 | 82,566.5 | 153,316 | 235,882.5 |
| 0.4 | 399,130 | 199,484 | 99,904.3 | 299,388.3 | 98,889.1 | 181,202 | 280,091.1 |
| 0.5 | 499,263 | 249,550 | 124,938 | 374,488 | 123,181 | 221,503 | 344,684 |
| 0.6 | 666,501 | 333,169 | 166,747 | 499,916 | 163,062 | 284,884 | 447,946 |
| Decentralized M-R Decision | Revenue Sharing Contract | Revenue Sharing Contract (Improved) | ||||||
|---|---|---|---|---|---|---|---|---|
| 166,150 | 83,237.3 | 249,387.3 | 212,817 | 69,047.8 | 281,864.8 | 182,334 | 83,237.3 | 265,571.3 |
| 199,484 | 99,904.3 | 299,388.3 | 263,360 | 81,419.7 | 344,779.7 | 226,779 | 99,904.3 | 326,683.3 |
| 249,550 | 124,938 | 374,488 | 341,630 | 98,862.1 | 440,492.1 | 293,535 | 124,938 | 418,473 |
| 333,169 | 166,747 | 499,916 | 479,065 | 124,442 | 603,507 | 405,027 | 166,747 | 571,774 |
| Decentralized M-R Decision | Two Charge Contracts | ||||
|---|---|---|---|---|---|
| 82,566.5 | 153,316 | 235,882.5 | 82,566.5 | 248,955 | 331,521.5 |
| 98,889.1 | 181,202 | 280,091.1 | 98,889.1 | 290,762 | 389,651.1 |
| 123,181 | 221,503 | 344,684 | 123,181 | 271,168 | 394,349 |
| 163,062 | 284,884 | 447,946 | 163,062 | 378,543 | 541,605 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, X.; Yu, L.; Zhang, J.; Li, C.; Zhao, Y. Warranty Decision Model and Remanufacturing Coordination Mechanism in Closed-Loop Supply Chain: View from a Consumer Behavior Perspective. Sustainability 2018, 10, 4738. https://doi.org/10.3390/su10124738
Zhu X, Yu L, Zhang J, Li C, Zhao Y. Warranty Decision Model and Remanufacturing Coordination Mechanism in Closed-Loop Supply Chain: View from a Consumer Behavior Perspective. Sustainability. 2018; 10(12):4738. https://doi.org/10.3390/su10124738
Chicago/Turabian StyleZhu, Xiaodong, Lingfei Yu, Ji Zhang, Chenliang Li, and Yizhao Zhao. 2018. "Warranty Decision Model and Remanufacturing Coordination Mechanism in Closed-Loop Supply Chain: View from a Consumer Behavior Perspective" Sustainability 10, no. 12: 4738. https://doi.org/10.3390/su10124738
APA StyleZhu, X., Yu, L., Zhang, J., Li, C., & Zhao, Y. (2018). Warranty Decision Model and Remanufacturing Coordination Mechanism in Closed-Loop Supply Chain: View from a Consumer Behavior Perspective. Sustainability, 10(12), 4738. https://doi.org/10.3390/su10124738




