How Does Polycentric Urban Form Affect Urban Commuting? Quantitative Measurement Using Geographical Big Data of 100 Cities in China
Abstract
1. Introduction
1.1. Literature Review and Research Gap
1.2. Reseach Questions, Aims and Innavotion
2. Materials and Methods
2.1. Variable Selection and Data Calculation
2.1.1. Commuting Variables
2.1.2. Polycentric Variables
- (1)
- Convert the raster form of Landscan to vector form to identify the spatial distribution of population.
- (2)
- Extract hot spot plots, and identify populations covered by map spots in each hot spot region by superimposing data with population spatial distribution.
- (3)
- Extract the four hot spot plots with the largest population, and calculate the urban polycentricity index according to Equation (2).
2.1.3. Control Variables
2.2. Regression Analysis
3. Result and Discussion
3.1. Polycentric Index of Study Cities
3.2. Regression Results and Analysis
3.3. Compared with Previous Studies
- (1)
- First, the study areas are inconsistent. Some of them are conducted within a city or a metropolitan area [15,18,60], While others take numerous cities rather a single city as study area [43]. Therefore, the results may or may not be the same with alternative research scales, and each result may only be applicable for the specific scale.
- (2)
- Second, part of the explanation could be the inconsistent data source even for the same indicator. For example, Gordon et al. [28] and Cervero et al. [18] found different relationships between urban spatial form and commuting efficiency even though using the same indicator. This may due partially to the inconsistent data obtained from different national surveys. Further studies are needed to predict whether the results remain the same when using the same dataset.
3.4. Reason for Polycentricity and Suggestions for Urban Planning
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- US Environmental Protection Agency. Our Built and Natural Environments: A Technical Review of the Interactions Between Land Use, Transportation and Environmental Quality (EPA 231-R-01e002); US Environmental Protection Agency: Washington, DC, USA, 2001.
- Ewing, R.; Pendall, R.; Chen, D. Measuring sprawl and its transportation impacts. J. Transp. Res. Board 2003, 1831, 175–183. [Google Scholar] [CrossRef]
- Dulal, H.B.; Brodnig, G.; Onoriose, C.G. Climate change mitigation in the transport sector through urban planning: A review. Habitat Int. 2011, 35, 494–500. [Google Scholar] [CrossRef]
- Yuan, M.; Song, Y.; Huang, Y.; Hong, S.; Huang, L. Exploring the association between urban form and air quality in China. J. Plan. Educ. Res. 2017, 38, 413–426. [Google Scholar] [CrossRef]
- Wang, M.; Madden, M.; Liu, X. Exploring the Relationship between Urban Forms and CO2 Emissions in 104 Chinese Cities. J. Urban Plan. Dev. 2017, 143, 04017014. [Google Scholar] [CrossRef]
- Parr, J. The polycentric urban region: A closer inspection. Reg. Stud. 2004, 38, 231–240. [Google Scholar] [CrossRef]
- Liu, X.; Wang, M.J.L. How polycentric is urban China and why? A case study of 318 cities. Landsc. Urban Plan. 2016, 151, 10–20. [Google Scholar] [CrossRef]
- Gordon, P.; Richardson, H.W.; Wong, H.L. The distribution of population and employment in a polycentric city: The case of Los Angeles. Environ. Plan. A 1986, 18, 161–173. [Google Scholar] [CrossRef] [PubMed]
- Anas, A.; Arnott, R.; Small, K.A. Urban spatial structure. J. Econ. Lit. 1998, 36, 1426–1464. [Google Scholar]
- Kloosterman, R.C.; Musterd, S. The polycentric urban region: Towards a research agenda. Urban Stud. 2001, 38, 623–633. [Google Scholar] [CrossRef]
- Hall, P.G.; Pain, K. The Polycentric Metropolis: Learning from Mega-City Regions in Europe; Routledge: Abingdon-on-Thames, UK, 2006. [Google Scholar]
- Vasanen, A. Functional polycentricity: Examining metropolitan spatial structure through the connectivity of urban sub-centres. Urban Stud. 2012, 49, 3627–3644. [Google Scholar] [CrossRef]
- Huang, X.; Li, Y.; Hay, I. Polycentric city-regions in the state-scalar politics of land development: The case of China. Land Use Policy 2016, 59, 168–175. [Google Scholar] [CrossRef]
- Schwanen, T.; Dieleman, F.M.; Dijst, M. Travel behaviour in Dutch monocentric and policentric urban systems. J. Transp. Geogr. 2001, 9, 173–186. [Google Scholar] [CrossRef]
- Lin, D.; Allan, A.; Cui, J. The impacts of urban spatial structure and socio-economic factors on patterns of commuting: A review. Int. J. Urban Sci. 2015, 19, 238–255. [Google Scholar] [CrossRef]
- Clark, W.A.; Kuijpers-Linde, M. Commuting in restructuring urban regions. Urban Stud. 1994, 31, 465–483. [Google Scholar] [CrossRef]
- Ewing, R. Is Los Angeles-style sprawl desirable? J. Am. Plan. Assoc. 1997, 63, 107–126. [Google Scholar] [CrossRef]
- Cervero, R.; Wu, K.-L. Sub-centring and commuting: Evidence from the San Francisco Bay area, 1980–90. Urban Stud. 1998, 35, 1059–1076. [Google Scholar] [CrossRef]
- Naess, P.; Sandberg, S.L. Workplace location, modal split and energy use for commuting trips. Urban Stud. 1996, 33, 557–580. [Google Scholar] [CrossRef]
- Jun, M.-J.; Hur, J.-W. Commuting costs of “leap-frog” newtown development in Seoul. Cities 2001, 18, 151–158. [Google Scholar] [CrossRef]
- Aguilera, A. Growth in commuting distances in French polycentric metropolitan areas: Paris, Lyon and Marseille. Urban Stud. 2005, 42, 1537–1547. [Google Scholar] [CrossRef]
- Gordon, P.; Wong, H.L. The costs of urban sprawl: Some new evidence. Environ. Plan. A 1985, 17, 661–666. [Google Scholar] [CrossRef]
- Modarres, A. Polycentricity, commuting pattern, urban form: The case of Southern California. Int. J. Urban Reg. Res. 2011, 35, 1193–1211. [Google Scholar] [CrossRef]
- Alqhatani, M.; Setunge, S.; Mirodpour, S. Can a polycentric structure affect travel behaviour? A comparison of Melbourne, Australia and Riyadh, Saudi Arabia. J. Mod. Transp. 2014, 22, 156–166. [Google Scholar] [CrossRef]
- Gordon, P.; Richardson, H.W. Are compact cities a desirable planning goal? J. Am. Plan. Assoc. 1997, 63, 95–106. [Google Scholar] [CrossRef]
- Deng, M.; Li, X.; Lin, X.H. Counter measures of transportation development in Guangzhou based analysis on characteristic of the inhabitant trip. Econ. Geogr. 2000, 20, 109–113. [Google Scholar]
- Alpkokin, P.; Cheung, C.; Black, J.; Hayashi, Y. Dynamics of clustered employment growth and its impacts on commuting patterns in rapidly developing cities. Transp. Res. Part A Policy Pract. 2008, 42, 427–444. [Google Scholar] [CrossRef]
- Gordon, P.; Richardson, H.W.; Jun, M.-J. The commuting paradox evidence from the top twenty. J. Am. Plan. Assoc. 1991, 57, 416–420. [Google Scholar] [CrossRef]
- Davoudi, S. Polycentricity: What does it mean and how is it interpreted in the ESDP. In Proceedings of the Urban and Spatial European Policies: Levels of Territorial Government, Turin, Italy, 18–20 April 2002. [Google Scholar]
- Bray, D. Space and Governance in Urban China: The Danwei System from Origins to Reform; Stanford University Press: East Palo Alto, CA, USA, 2005. [Google Scholar]
- Wang, D.; Chai, Y. The jobs–housing relationship and commuting in Beijing, China: The legacy of Danwei. J. Transp. Geogr. 2009, 17, 30–38. [Google Scholar] [CrossRef]
- Website, C.E. Beijing Is Losing about 70 Billion a Year Due to Traffic Congestion. 2014. Available online: http://finance.ce.cn/rolling/201409/28/t20140928_3614016.shtml (accessed on 28 September 2014).
- Tana, M.-P.K.; Chai, Y. Urban form, car ownership and activity space in inner suburbs: A comparison between Beijing (China) and Chicago (United States). Urban Stud. 2016, 53, 1784–1802. [Google Scholar] [CrossRef]
- Zhao, P.; Lu, B.; De Roo, G. The impact of urban growth on commuting patterns in a restructuring city: Evidence from Beijing. Pap. Reg. Sci. 2011, 90, 735–754. [Google Scholar] [CrossRef]
- Yue, W.; Liu, Y.; Fan, P. Polycentric urban development: The case of Hangzhou. Environ. Plan. A 2010, 42, 563–577. [Google Scholar] [CrossRef]
- Qin, B.; Han, S.S. Emerging polycentricity in Beijing: Evidence from housing price variations, 2001–2005. Urban Stud. 2013, 50, 2006–2023. [Google Scholar] [CrossRef]
- Yue, W.; Fan, P.; Wei, Y.D.; Qi, J. Economic development, urban expansion, and sustainable development in Shanghai. Stoch. Environ. Res. Risk Assess. 2014, 28, 783–799. [Google Scholar] [CrossRef]
- Zhao, P.; Lü, B.; De Roo, G. Urban expansion and transportation: The impact of urban form on commuting patterns on the city fringe of Beijing. Environ. Plan. A 2010, 42, 2467–2486. [Google Scholar] [CrossRef]
- Pan, H.; Shen, Q.; Zhang, M. Influence of urban form on travel behaviour in four neighbourhoods of Shanghai. Urban Stud. 2009, 46, 275–294. [Google Scholar]
- Liu, X.; Gong, L.; Gong, Y.; Liu, Y. Revealing travel patterns and city structure with taxi trip data. J. Transp. Geogr. 2015, 43, 78–90. [Google Scholar] [CrossRef]
- Song, Y.; Chen, Y.; Pan, X. Polycentric spatial structure and travel mode choice: The case of Shenzhen, China. Reg. Sci. Policy Pract. 2012, 4, 479–493. [Google Scholar] [CrossRef]
- Song, Y.; Shao, G.; Song, X.; Liu, Y.; Pan, L.; Ye, H. The relationships between urban form and urban commuting: An empirical study in China. Sustainability 2017, 9, 1150. [Google Scholar] [CrossRef]
- Sun, B.; He, Z.; Zhang, T.; Wang, R. Urban spatial structure and commute duration: An empirical study of China. Int. J. Sustain. Transp. 2016, 10, 638–644. [Google Scholar] [CrossRef]
- Bai, X.; Shi, P.; Liu, Y. Society: Realizing China’s urban dream. Nat. News 2014, 509, 158. [Google Scholar] [CrossRef]
- Dhakal, S. Urban energy use and carbon emissions from cities in China and policy implications. Energy Policy 2009, 37, 4208–4219. [Google Scholar] [CrossRef]
- Liu, Y.; Song, Y.; Song, X. An empirical study on the relationship between urban compactness and CO2 efficiency in China. Habitat Int. 2014, 41, 92–98. [Google Scholar] [CrossRef]
- Lin, D.; Allan, A.; Cui, J. Exploring differences in commuting behaviour among various income groups during polycentric urban development in China: New evidence and its implications. Sustainability 2016, 8, 1188. [Google Scholar] [CrossRef]
- Yu, L. Chinese City and Regional Planning Systems; Routledge: Abingdon-on-Thames, UK, 2017. [Google Scholar]
- Kitchin, R.J.G. The real-time city? Big data and smart urbanism. GeoJournal 2014, 79, 1–14. [Google Scholar] [CrossRef]
- Dmowska, A.; Stepinski, T.F. High resolution dasymetric model of US demographics with application to spatial distribution of racial diversity. Appl. Geogr. 2014, 53, 417–426. [Google Scholar] [CrossRef]
- Shen, J.; Wang, G. Estimating the contributions of migration factors to interprovincial migration in China 1995–2000. Ann. GIS 2012, 18, 257–266. [Google Scholar] [CrossRef]
- Liu, X.; Derudder, B.; Wang, M. Polycentric urban development in China: A multi-scale analysis. Environ. Plan. B: Urban Anal. City Sci. 2017, 45, 953–972. [Google Scholar] [CrossRef]
- Getis, A.; Ord, J.K. The analysis of spatial association by use of distance statistics. Geogr. Anal. 1992, 24, 189–206. [Google Scholar] [CrossRef]
- Ord, J.K.; Getis, A. Local spatial autocorrelation statistics: Distributional issues and an application. Geogr. Anal. 1995, 27, 286–306. [Google Scholar] [CrossRef]
- Thomas, L.; Cousins, W. The compact city: A successful, desirable and achievable urban form. In Compact City Series: The Compact City: A Sustainable Urban Form? (Volume 3); Routledge: Abingdon-on-Thames, UK, 1996; pp. 53–65. [Google Scholar]
- He, Q.; Song, Y.; Liu, Y.; Yin, C. Diffusion or coalescence? Urban growth pattern and change in 363 Chinese cities from 1995 to 2015. Sustain. Cities Soc. 2017, 35, 729–739. [Google Scholar] [CrossRef]
- Torrens, P.M.; Alberti, M. Measuring Sprawl; Working Paper, no. 27; Centre for Advanced Spatial Analysis, University College: London, UK, 2000. [Google Scholar]
- Mou, Y.; Song, Y.; Xu, Q.; He, Q.; Hu, A. Influence of Urban-Growth Pattern on Air Quality in China: A Study of 338 Cities. Int. J. Environ. Res. Public Health 2018, 15, 1805. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Liu, J.Y.; Zhuang, D.F.; Wang, L. Spatial-temporal changes of urban spatial morphology in China. Acta Geogr. Sin. 2005, 60, 392–400. [Google Scholar]
- Levinson, D.M.; Kumar, A. The rational locator: Why travel times have remained stable. J. Am. Plan. Assoc. 1994, 60, 319–332. [Google Scholar] [CrossRef]
- Sun, B.; Tu, T.; Shi, W.; Guo, Y. Test on the performance of polycentric spatial structure as a measure of congestion reduction in megacities: The case study of Shanghai. Urban Plan. Forum 2013, 2, 63–69. [Google Scholar]
- Cervero, R.; Landis, J. Suburbanization of jobs and the journey to work: A submarket analysis of commuting in the San Francisco Bay Area. J. Adv. Transp. 1992, 26, 275–297. [Google Scholar] [CrossRef]
- Burgess, R.; Jenks, M. Compact Cities: Sustainable Urban Forms for Developing Countries; Routledge: Abingdon-on-Thames, UK, 2002. [Google Scholar]
- Tian, Y.; Jim, C.Y.; Wang, H. Assessing the landscape and ecological quality of urban green spaces in a compact city. Landsc. Urban Plan. 2014, 121, 97–108. [Google Scholar] [CrossRef]
- Stevenson, M.; Thompson, J.; De Sá, T.H.; Ewing, R.; Mohan, D.; McClure, R.; Roberts, I.; Tiwari, G.; Giles-Corti, B.; Sun, X.; et al. Land use, transport, and population health: Estimating the health benefits of compact cities. The Lancet 2016, 388, 2925–2935. [Google Scholar] [CrossRef]
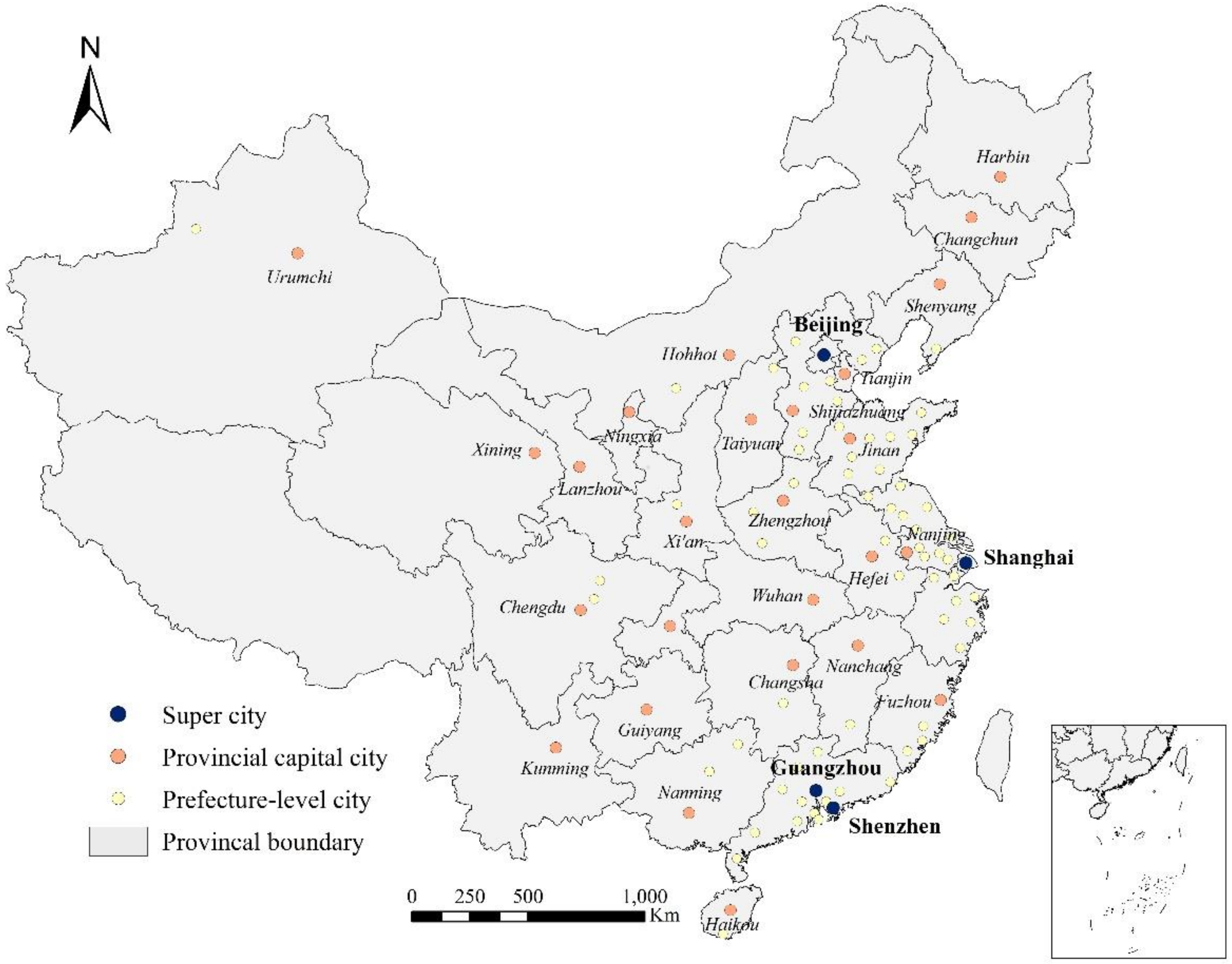
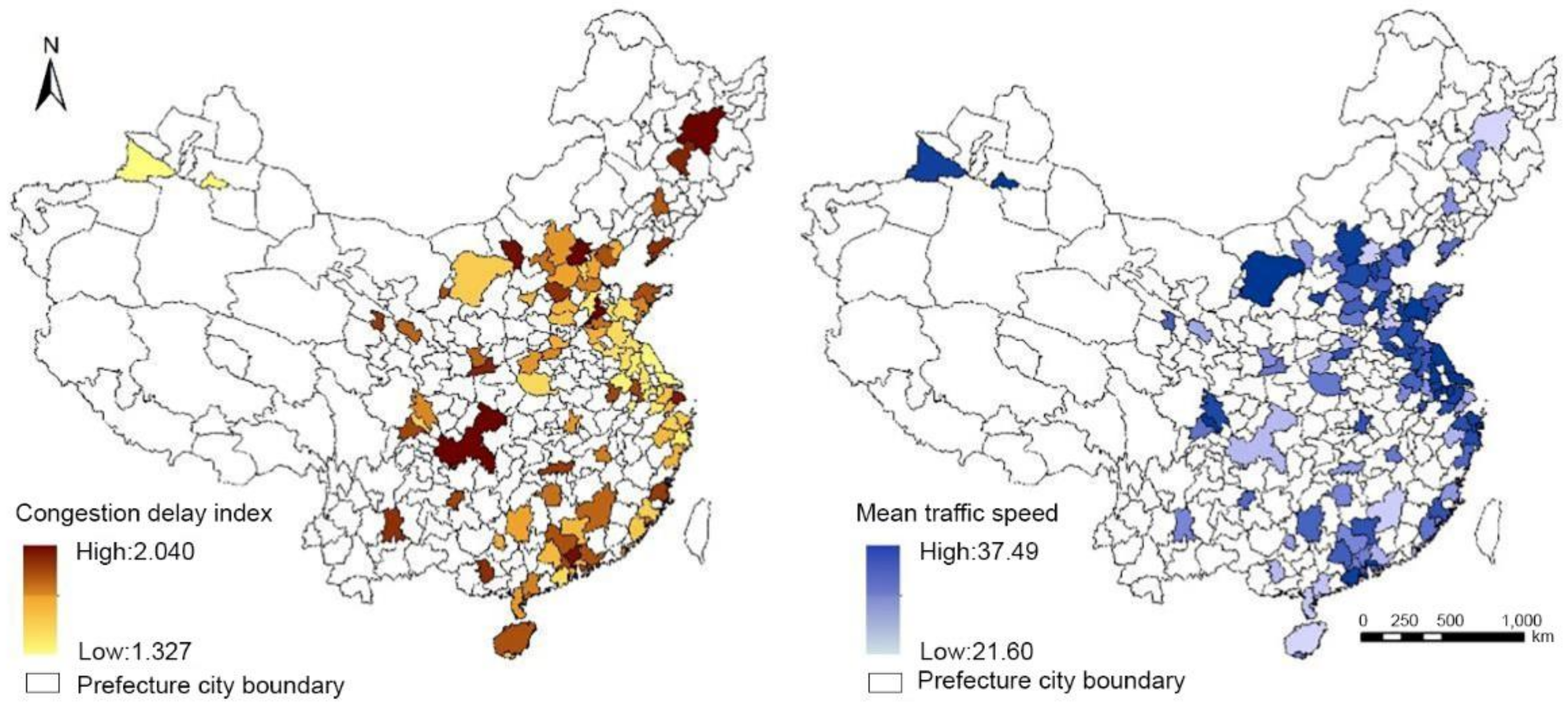
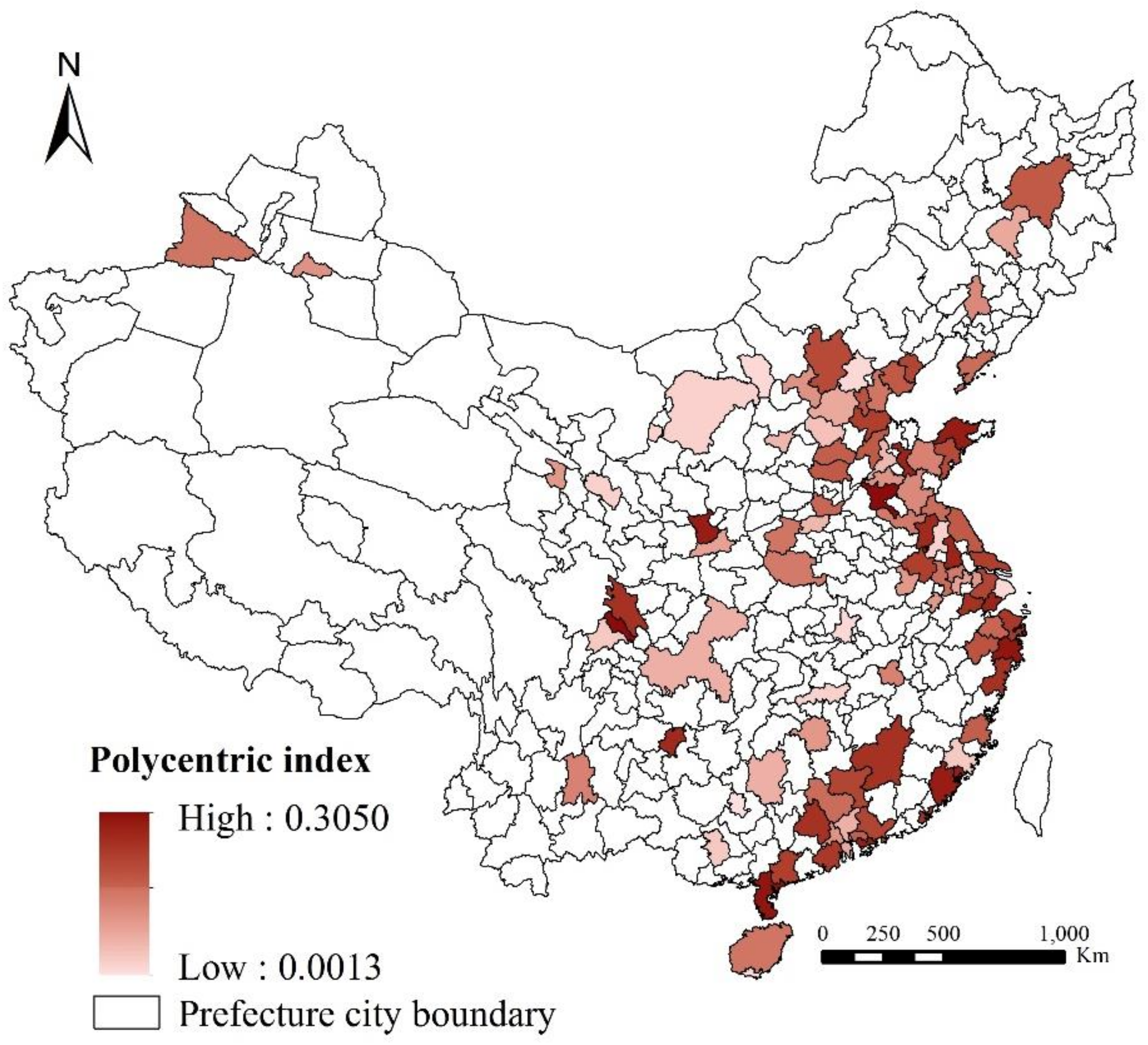
| Variable | Unit | Minimize | Maximize | Mean | Standard Deviation |
|---|---|---|---|---|---|
| CDI | N/A | 1.327 | 2.040 | 1.674 | 0.138 |
| MTS | km/h | 21.600 | 37.490 | 26.961 | 3.384 |
| Polycentricity | N/A | 0.001300 | 0.305000 | 0.054308 | 0.052873 |
| CT | N/A | 0.032 | 0.174 | 0.071 | 0.024 |
| PC | Cars/thousand persons | 18.229 | 502.611 | 103.444 | 83.851 |
| PB | Buses/thousand persons | 1.280 | 94.370 | 11.837 | 10.369 |
| PUA | m2/person | 2.270 | 72.870 | 15.868 | 8.800 |
| PD | Persons/km2 | 1914.290 | 39,871.801 | 7856.684 | 6953.921 |
| Variable | Model 1 (R2 = 0.313) | Model 2 (R2 = 0.352) | Model 3 (R2 = 0.405) | Model 4 (R2 = 0.461) | Model 5 (R2 = 0.498) | Model 6 (R2 = 0.513) |
|---|---|---|---|---|---|---|
| Polycentricity | −0.687 * | −0.697 * | −0.597 * | −0.622 * | −0.639 ** | −0.547 * |
| CT | 1.043 | 1.315 * | 1.281 * | 0.637 | 0.594 | |
| PC | 4.949 × 10−4 ** | 2.890 × 10−4 | 2.067 × 10−4 | 3.623 × 10−4 | ||
| PB | 2.655 × 10−3 | 2.916 × 10−3 | 2.783 × 10−3 | |||
| PUA | −6.42 × 10−6 *** | 5.269 × 10−5 * | ||||
| PD | 0.003 |
| Variable | Model 1 (R2 = 0.291) | Model 2 (R2 = 0.327) | Model 3 (R2 = 0.384) | Model 4 (R2 = 0.421) | Model 5 (R2 = 0.452) | Model 6 (R2 = 0.499) |
|---|---|---|---|---|---|---|
| Polycentricity | 14.218 * | 14.547 * | 14.606 * | 15.005 * | 15.446 * | 14.066 * |
| CT | −33.704 * | −33.545 * | −33.007 * | −16.394 | −15.743 | |
| PC | 2.898 × 10−4 | 0.004 | 0.006 | 0.003 | ||
| PB | −0.042 | −0.049 | −0.047 | |||
| PUA | 1.676 × 10−4 *** | −1.491 × 10−4 ** | ||||
| PD | −0.042 |
| Commuting Variables | CT | PC | PB | PUA | PD |
|---|---|---|---|---|---|
| MTS | 14.218 -> 14.547 | 14.218 -> 14.606 | 14.218 -> 14.091 | 14.218 -> 14.445 | 14.218 -> 12.274 |
| (0.309) | (0.388) | (−0.127) | (0.227) | (−1.944) | |
| CDI | −0.687 -> −0.697 | −0.687 -> −0.597 | −0.687 -> −0.661 | −0.687 -> −0.696 | −0.687 -> −0.646 |
| (−0.01) | (0.09) | (0.026) | (−0.009) | (0.041) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Mou, Y.; Wang, H.; Yin, C.; He, Q. How Does Polycentric Urban Form Affect Urban Commuting? Quantitative Measurement Using Geographical Big Data of 100 Cities in China. Sustainability 2018, 10, 4566. https://doi.org/10.3390/su10124566
Li X, Mou Y, Wang H, Yin C, He Q. How Does Polycentric Urban Form Affect Urban Commuting? Quantitative Measurement Using Geographical Big Data of 100 Cities in China. Sustainability. 2018; 10(12):4566. https://doi.org/10.3390/su10124566
Chicago/Turabian StyleLi, Xiaoyan, Yanchuan Mou, Huiying Wang, Chaohui Yin, and Qingsong He. 2018. "How Does Polycentric Urban Form Affect Urban Commuting? Quantitative Measurement Using Geographical Big Data of 100 Cities in China" Sustainability 10, no. 12: 4566. https://doi.org/10.3390/su10124566
APA StyleLi, X., Mou, Y., Wang, H., Yin, C., & He, Q. (2018). How Does Polycentric Urban Form Affect Urban Commuting? Quantitative Measurement Using Geographical Big Data of 100 Cities in China. Sustainability, 10(12), 4566. https://doi.org/10.3390/su10124566




