A Deep Learning Approach for Real-Time Intrusion Mitigation in Automotive Controller Area Networks
Abstract
1. Introduction
1.1. Related Works
1.2. Challenges in Intrusion Mitigation
- Non-linear complex data handling: CAN-bus data is highly non-linear as the different nodes communicate with each other to perform tasks that differ in functional complexity. Deep-denoising autoencoder (DDAE) models have built-in capability to handle non-linear data comfortably.
- Robust noise removal: DDAE models are designed to clean the noisy data.However, effective noise filtering is a challenging task to avoid model overfitting and underfitting that often result in loss of significant information, and failure in learning underlying data patterns to generalize well to new data.
- Gradient handling: Gradient vanishing and divergence is a big challenge in non-linear data where vanishing can slow down model learning, and divergence can accelerate weight updates causing instability in the model.
- Generalization: With the evolving nature of cyber-intrusions demonstrating new attack vector designs, it is imperative to have an adaptive model to denoise the new unseen data efficiently.
1.3. Motivation
1.4. Contributions
- Novel light-weight AM-DDAE model design: Development of a novel adaptive momentum-based deep denoising autoencoder for intrusions mitigation in smart cars, with considerably low computational cost. Additionally, Explainable AI techniques—SHAP and LIME—are incorporated to examine model’s decision-making capabilities.
- Generalization: Investigation of the proposed mechanism by employing multiple cyber-attacks for different makes of smart cars ensuring the generalizability and applicability of the proposed mechanism over various attack designs and car models.
- Efficiency and robustness: Analysis of the results revealed a comprehendible performance with 2.87 × 10−7 mean reconstruction error, less than 1% percentage error and 0.145532 sec average execution time which verifies the robustness and efficiency of the proposed mechanism. The model presented an equally strong performance when further evaluated on a new unseen attack design, and on Adversarial Machine Learning Attack. Additionally, on comparison with Generative Adversarial Networks, the proposed model demonstrated exceedingly high performance with 99 times higher accuracy in intrusions mitigation.
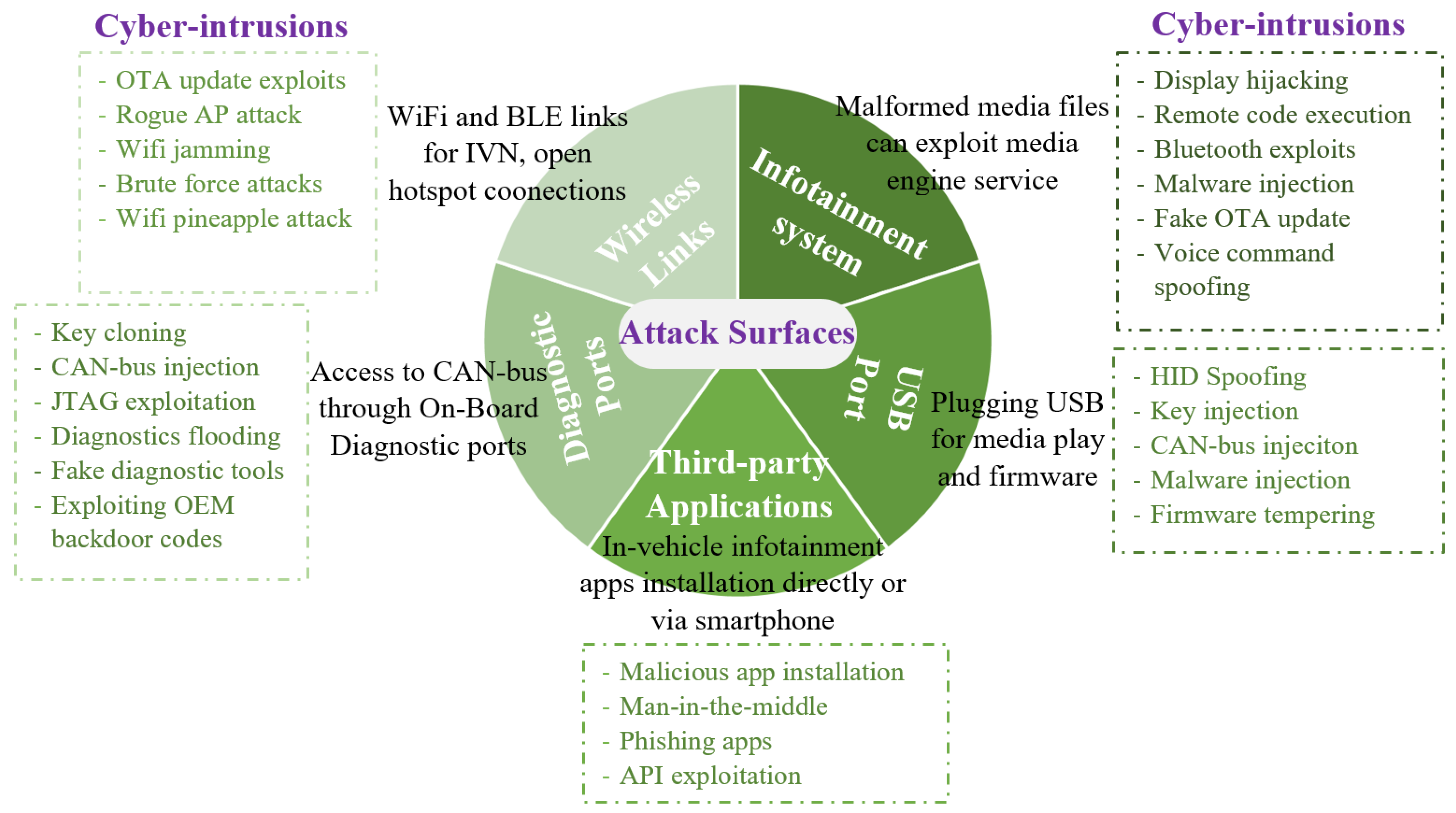
2. The Smart Cars: Potential Attack Surfaces & Cyber-Intrusions
3. Proposed Methodology
3.1. Datasets
3.2. Data Preprocessing
3.3. Attack Design
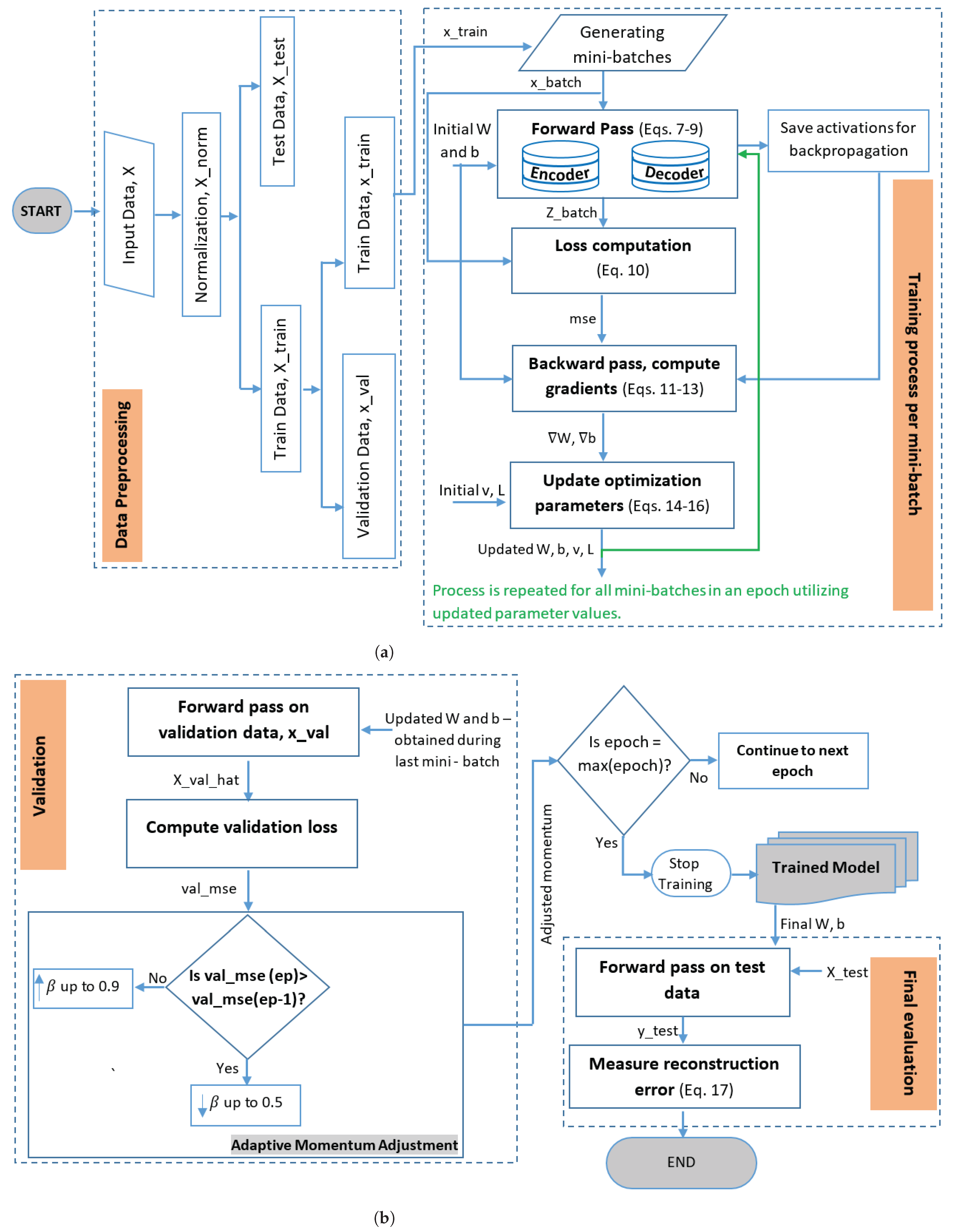
3.4. Proposed AM-Based Deep-Denoising Autoencoder
| Algorithm 1: AM-DDAE Mechanism for Intrusion Mitigation |
|
3.4.1. Working of the Proposed AM-DDAE Mechanism
3.4.2. Architecture of the Proposed AM-DDAE Mechanism
3.4.3. Error Metrics
4. Results and Discussions
4.1. Error Metrics
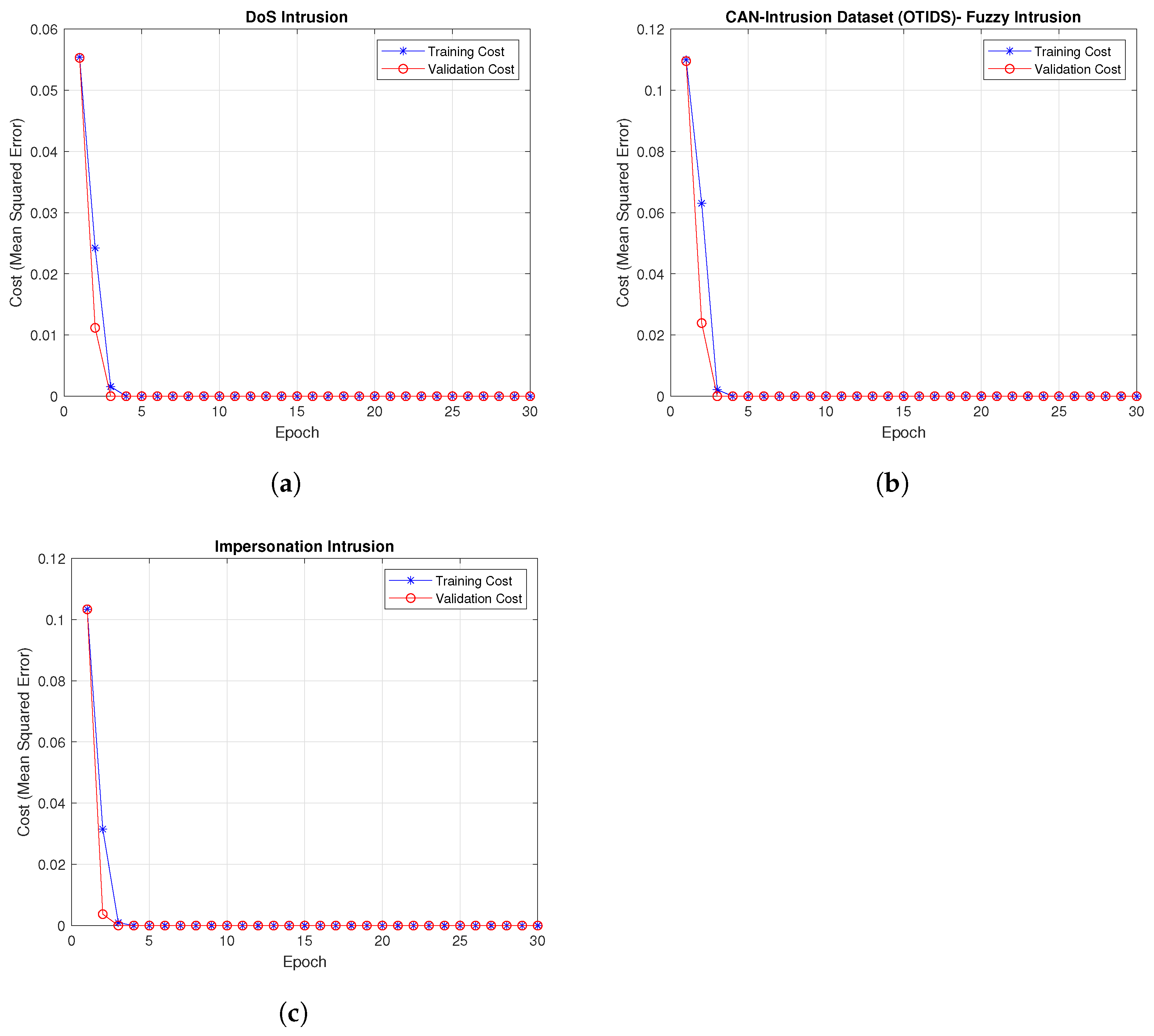
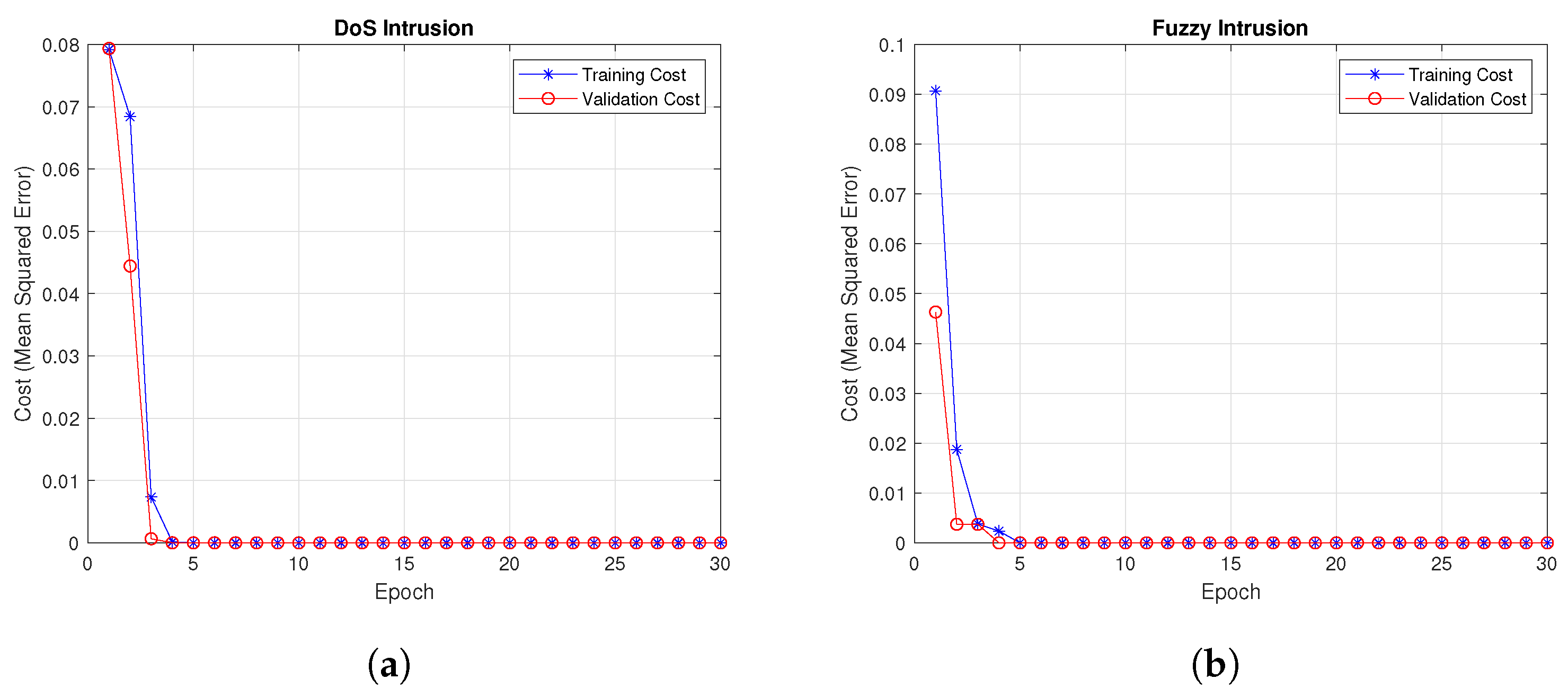
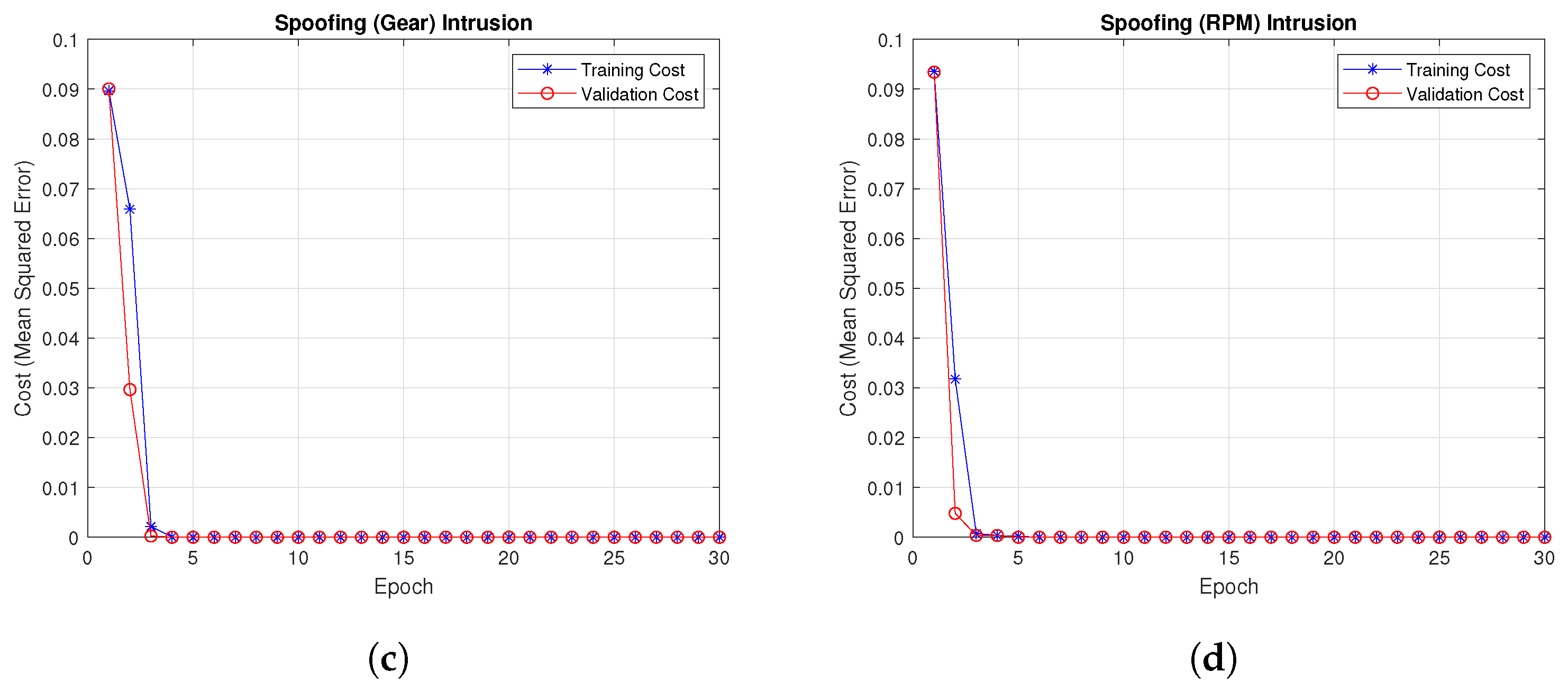
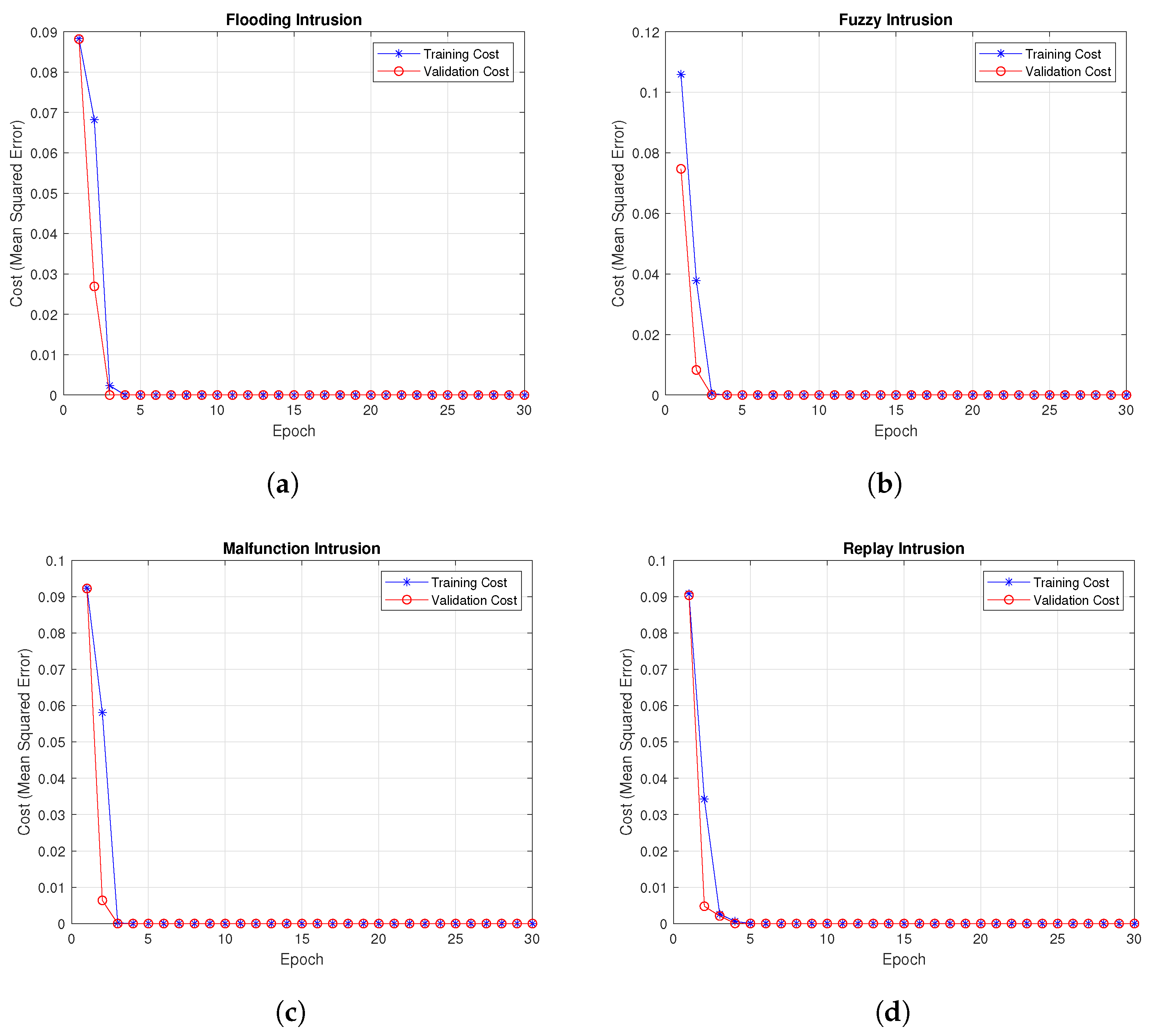
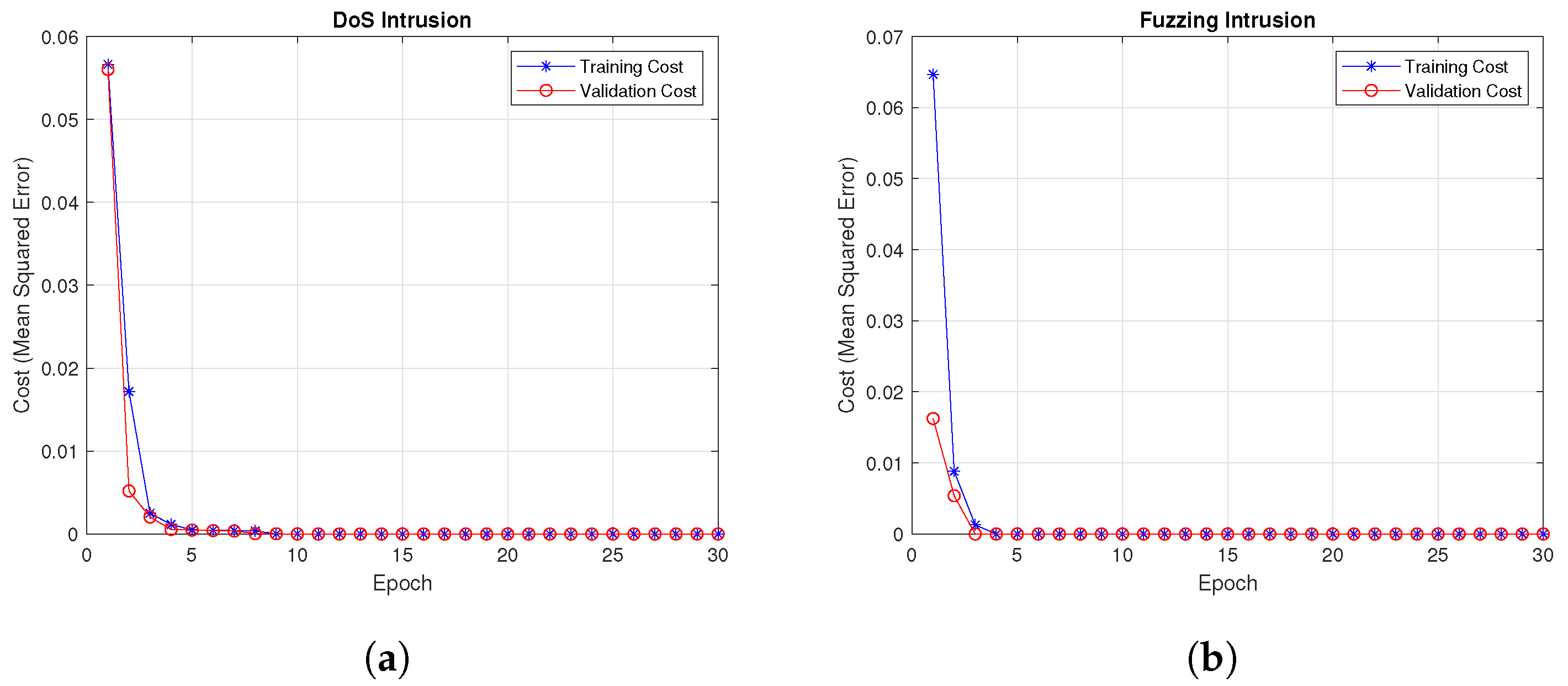
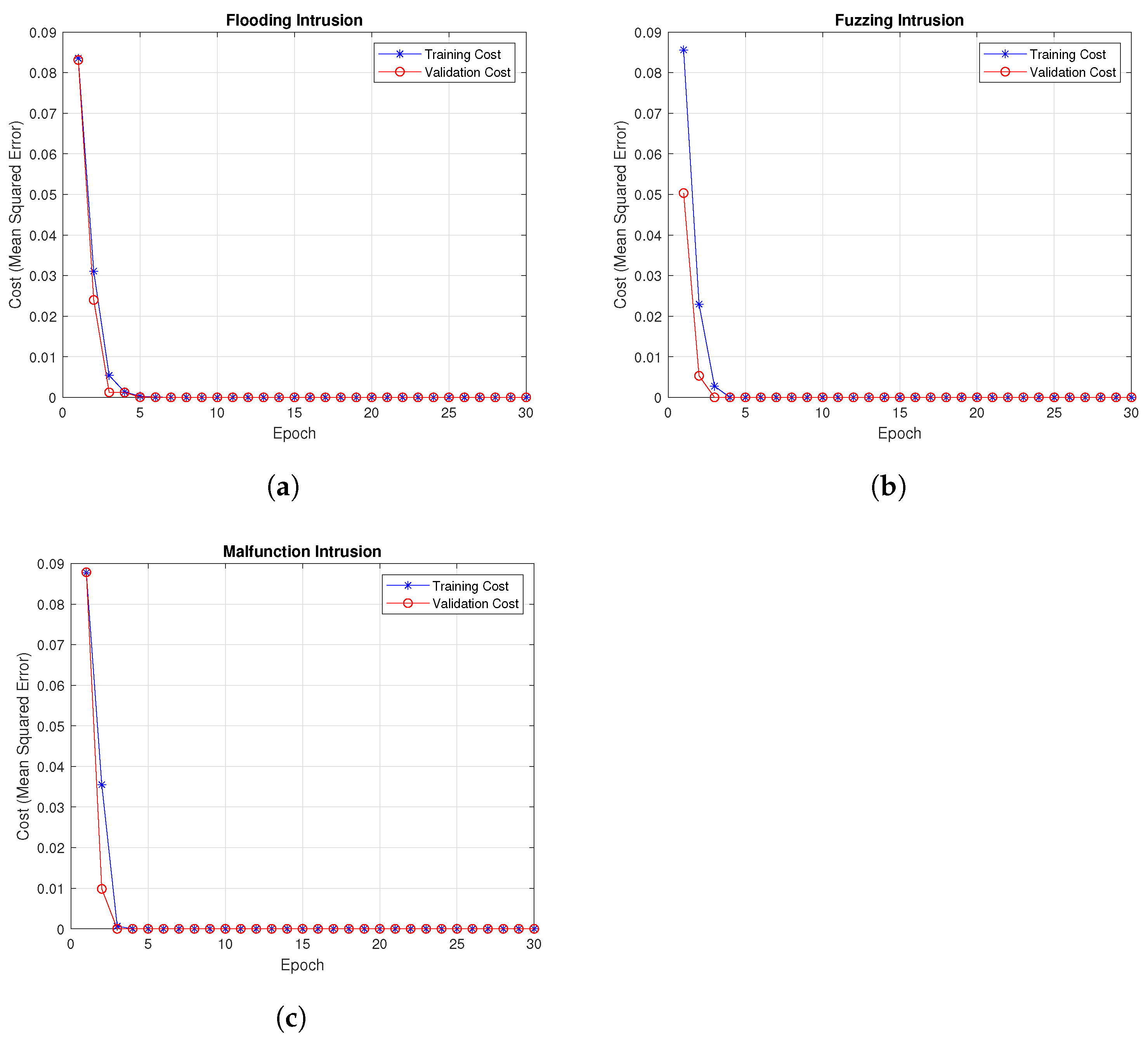
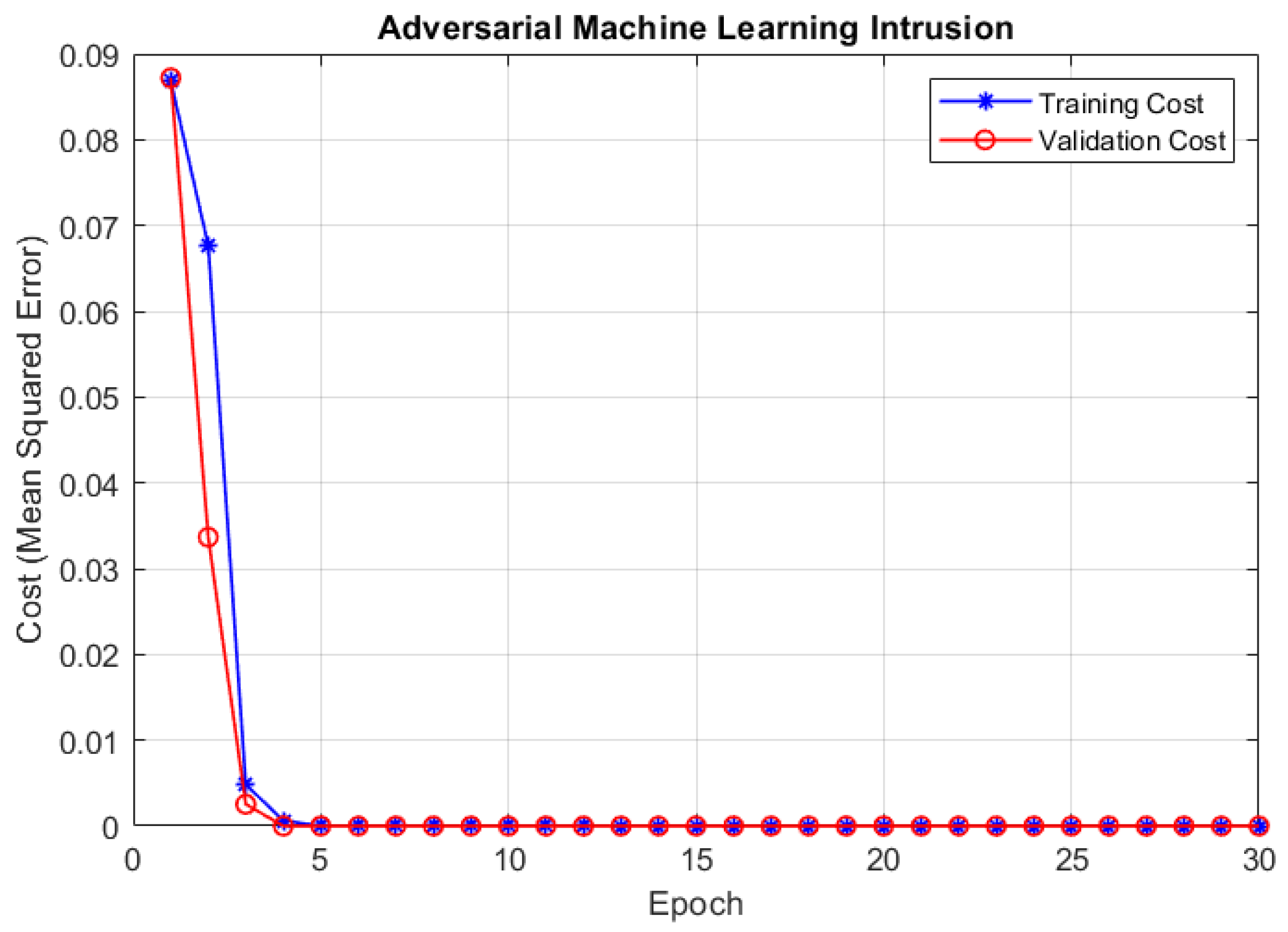
4.2. Training and Validation Cost
4.3. Computational Time
4.4. Adaptability of the Proposed AM-DDAE Model to Unseen Attack
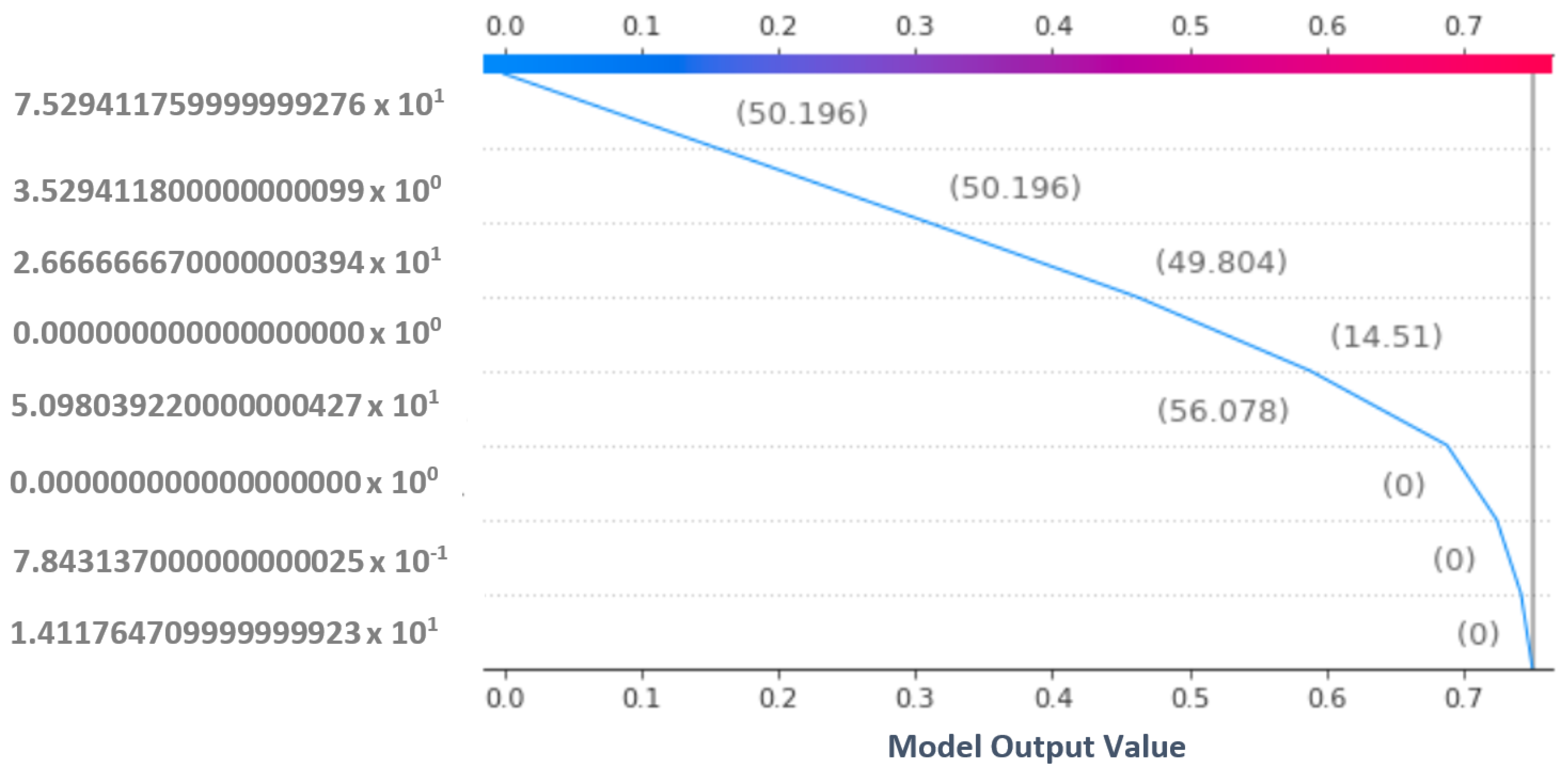
4.5. Decision-Making Process of the Proposed Model Through Explainable AI
4.6. Results and Analysis of Adversarial Machine Learning Attack
4.7. Comparison with Generative Adversarial Networks
4.8. Comparison with Existing Studies
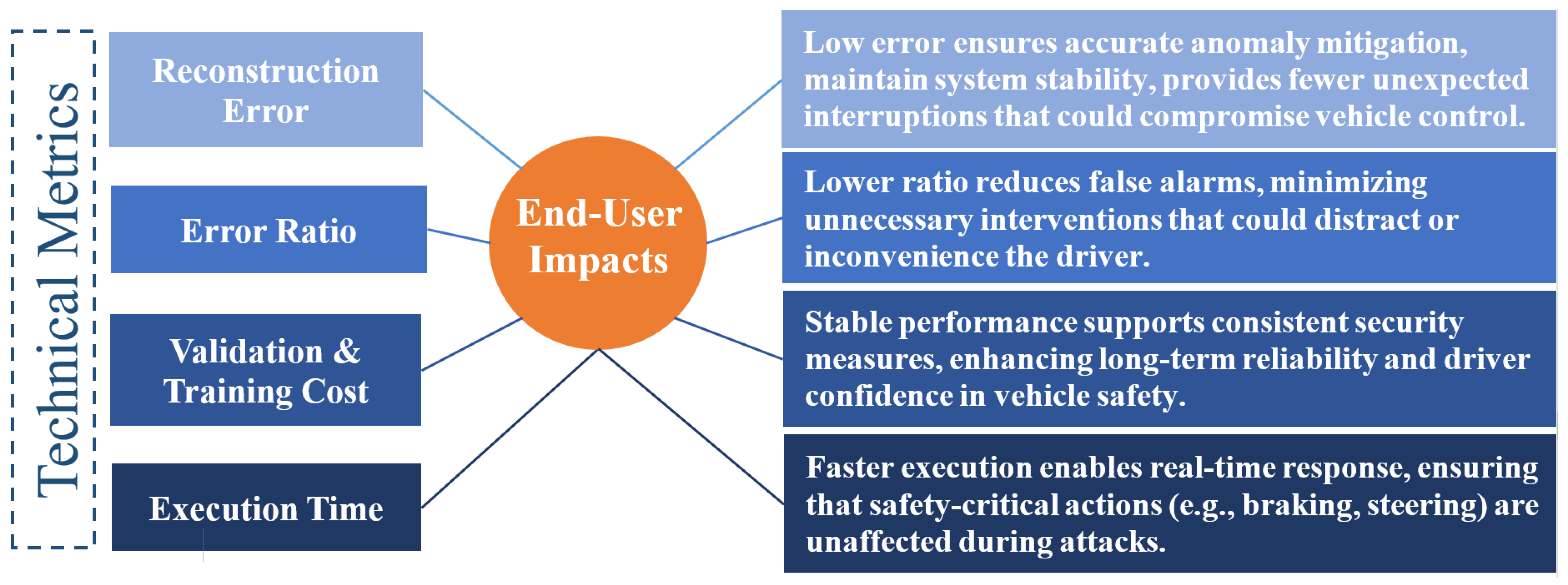
4.9. Impacts of the Proposed Mechanism on End-Users
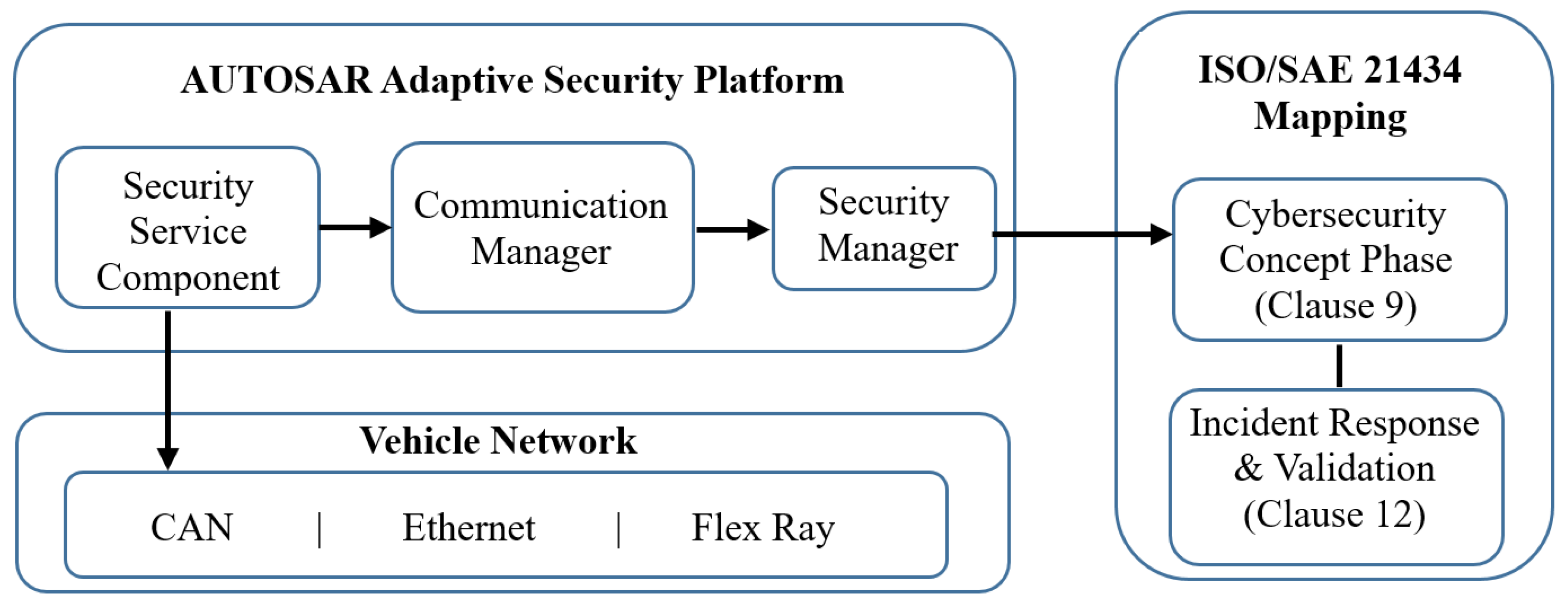
4.10. Integration of Proposed Model with Existing Security Frameworks
4.11. Advantages of the Proposed Mechanism
4.12. Limitations and Future Scope
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AM | Adaptive Momentum | AI | Artificial Intelligence |
| AP | Access Point | API | Application Programming Interface |
| CAN | Controller Area Network | CNN | Convolutional Neural Network |
| DDAE | Deep Denoising Autoencoder | DL | Deep Learning |
| DoS | Denial of Service | ECUs | Electronic Control Units |
| ETI | Event-triggered Interval | FDL | Federal Deep Learning |
| FL | Federated Learning | GAN | Generative Adversarial Network |
| GPS | Global Positioning System | HID | Human Interface Display |
| ID | Identifier | IDMS | Intrusion Detection and Mitigation System |
| IDS | Intrusion Detection System | IVN | In-Vehicular Network |
| JTAG | Joint Test Action Group | LSTM | Long-short Term Memory |
| MAC | Media Access Control | ML | Machine Learning |
| OBD | On-Board Diagnostics | OTA | Over-the-Air |
| RE | Reconstruction Error | ReLU | Rectified Linear Unit |
| RNN | Recurrent Neural Network | SCs | Smart Cars |
| SDM | Self-defence Mechanism | SerIoT | Secure and Safe Internet of Things |
| SSM | State-Space Model | SVM | Support Vector Machine |
| UIOs | Unknown Input Observers | USB | Universal Serial Bus |
References
- Alsaade, F.W.; Al-Adhaileh, M.H. Cyber attack detection for self-driving vehicle networks using deep autoencoder algorithms. Sensors 2023, 23, 4086. [Google Scholar] [CrossRef] [PubMed]
- Upstream. Upstream’s 2025 Global Automotive Cybersecurity Report Executive Summary. 2025. Available online: https://upstream.auto/ty-2025-gacr-executive-summary/ (accessed on 19 August 2025).
- Upstream. 2025 Predictions: The Future of Automotive Cybersecurity. 2025. Available online: https://upstream.auto/ty-2025-predictions/ (accessed on 19 August 2025).
- SOCRadar. Major Cyber Attacks Targeting the Automotive Industry. 2024. Available online: https://socradar.io/major-cyber-attacks-targeting-the-automotive-industry/ (accessed on 10 November 2024).
- Ionut Arghire. 16 Car Makers and Their Vehicles Hacked via Telematics, APIs, Infrastructure. 2023. Available online: https://www.securityweek.com/16-car-makers-and-their-vehicles-hacked-telematics-apis-infrastructure/ (accessed on 6 June 2024).
- SLNT. Under the Hood: The Modern Reality of Car Hacking. 2024. Available online: https://slnt.com/blogs/insights/under-the-hood-the-modern-reality-of-car-hacking (accessed on 10 November 2024).
- Zhou, X.; Wu, Y.; Lin, J.; Xu, Y.; Woo, S. A Stacked Machine Learning-Based Intrusion Detection System for Internal and External Networks in Smart Connected Vehicles. Symmetry 2025, 17, 874. [Google Scholar] [CrossRef]
- Tanksale, V. Intrusion detection system for controller area network. Cybersecurity 2024, 7, 4. [Google Scholar] [CrossRef]
- Alfardus, A.; Rawat, D.B. Machine Learning-Based Anomaly Detection for Securing In-Vehicle Networks. Electronics 2024, 13, 1962. [Google Scholar] [CrossRef]
- Bari, B.S.; Yelamarthi, K.; Ghafoor, S. Intrusion detection in vehicle controller area network (can) bus using machine learning: A comparative performance study. Sensors 2023, 23, 3610. [Google Scholar] [CrossRef] [PubMed]
- Shahriar, M.H.; Xiao, Y.; Moriano, P.; Lou, W.; Hou, Y.T. ANShield: Deep Learning-Based Intrusion Detection Framework for Controller Area Networks at the Signal-Level. IEEE Internet Things J. 2023, 10, 22111–22127. [Google Scholar] [CrossRef]
- Cheng, P.; Xu, K.; Li, S.; Han, M. TCAN-IDS: Intrusion detection system for internet of vehicle using temporal convolutional attention network. Symmetry 2022, 14, 310. [Google Scholar] [CrossRef]
- Moulahi, T.; Zidi, S.; Alabdulatif, A.; Atiquzzaman, M. Comparative performance evaluation of intrusion detection based on machine learning in in-vehicle controller area network bus. IEEE Access 2021, 9, 99595–99605. [Google Scholar] [CrossRef]
- Kavousi-Fard, A.; Dabbaghjamanesh, M.; Jin, T.; Su, W.; Roustaei, M. An evolutionary deep learning-based anomaly detection model for securing vehicles. IEEE Trans. Intell. Transp. Syst. 2020, 22, 4478–4486. [Google Scholar] [CrossRef]
- Ahmed, N. Detection, Identification, and Mitigation of False Data Injection Attacks and Faults in Vehicle Platooning. Ph.D. Thesis, Lakehead University, Thunder Bay, ON, Canada, 2023. Available online: https://knowledgecommons.lakeheadu.ca/handle/2453/5254 (accessed on 12 December 2024).
- Hassan, S.M.; Mohamad, M.M.; Muchtar, F.B. Advanced intrusion detection in MANETs: A survey of machine learning and optimization techniques for mitigating black/gray hole attacks. IEEE Access 2024, 12, 150046–150090. [Google Scholar] [CrossRef]
- Moradi, M.; Kordestani, M.; Jalali, M.; Rezamand, M.; Mousavi, M.; Chaibakhsh, A.; Saif, M. Sensor and Decision Fusion-based Intrusion Detection and Mitigation Approach for Connected Autonomous Vehicles. IEEE Sens. J. 2024, 24, 20908–20919. [Google Scholar] [CrossRef]
- Samani, M.A.; Farrokhi, M. Adverse to Normal Image Reconstruction Using Inverse of StarGAN for Autonomous Vehicle Control. IEEE Access 2025, 13, 77305–77316. [Google Scholar] [CrossRef]
- Wang, K. Leveraging Deep Learning for Enhanced Information Security: A Comprehensive Approach to Threat Detection and Mitigation. Int. J. Adv. Comput. Sci. Appl. 2024, 15, 964. [Google Scholar] [CrossRef]
- Sontakke, P.V.; Chopade, N.B. Optimized Deep Neural Model-Based Intrusion Detection and Mitigation System for Vehicular Ad-Hoc Network. Cybern. Syst. 2023, 54, 985–1013. [Google Scholar] [CrossRef]
- Hidalgo, C.; Vaca, M.; Nowak, M.P.; Frölich, P.; Reed, M.; Al-Naday, M.; Mpatziakas, A.; Protogerou, A.; Drosou, A.; Tzovaras, D. Detection, control and mitigation system for secure vehicular communication. Veh. Commun. 2022, 34, 100425. [Google Scholar] [CrossRef]
- Eric Schädlich. The Most Influential Automotive Hacks. 2024. Available online: https://dissec.to/general/the-most-influential-automotive-hacks/ (accessed on 4 February 2025).
- Majumdar, A.R.C. 42 Luxury Cars Stolen over Four Weeks in Oakville. 2021. Available online: https://www.oakvillenews.org/local-news/42-luxury-cars-stolen-over-four-weeks-oakville-ontario-8486515 (accessed on 4 February 2025).
- Khanna, H.; Kumar, M.; Bhardwaj, V. An Integrated Security VANET Algorithm for Threat Mitigation and Performance Improvement Using Machine Learning. SN Comput. Sci. 2024, 5, 1089. [Google Scholar] [CrossRef]
- Khanapuri, E.; Chintalapati, T.; Sharma, R.; Gerdes, R. Learning based longitudinal vehicle platooning threat detection, identification and mitigation. IEEE Trans. Intell. Veh. 2021, 8, 290–300. [Google Scholar] [CrossRef]
- HCRL. CAN Dataset for Intrusion Detection (OTIDS). Available online: https://ocslab.hksecurity.net/Dataset/CAN-intrusion-dataset (accessed on 1 March 2024).
- HCRL. Car-Hacking Dataset. Available online: https://ocslab.hksecurity.net/Datasets/car-hacking-dataset (accessed on 1 March 2024).
- HCRL. In-Vehicle Network Intrusion Detection Challenge. Available online: https://ocslab.hksecurity.net/Datasets/datachallenge2019/car (accessed on 1 March 2024).
- HCRL. M-CAN Intrusion Dataset. Available online: https://ocslab.hksecurity.net/Datasets/m-can-intrusion-dataset (accessed on 1 March 2024).
- HCRL. B-CAN Intrusion Dataset. Available online: https://ocslab.hksecurity.net/Datasets/b-can-intrusion-dataset (accessed on 1 March 2024).
- HCRL. CAN-FD Intrusion Dataset. Available online: https://ocslab.hksecurity.net/Datasets/can-fd-intrusion-dataset (accessed on 1 March 2024).
- Shirazi, H.; Pickard, W.; Ray, I.; Wang, H. Towards resiliency of heavy vehicles through compromised sensor data reconstruction. In Proceedings of the Twelfth ACM Conference on Data and Application Security and Privacy, Baltimore, MD, USA, 24–27 April 2022; pp. 276–287. [Google Scholar]





| Reference | Purpose | Strengths | Weaknesses | Year | Category |
|---|---|---|---|---|---|
| [7] | Stacked Machine Learning (ML) based intrusion detection system (IDS) for automotive networks | 99.99 % Detection Accuracy | Undefined car, Heavyweight | 2025 | Detection |
| [8] | ML based IDS for automotive controller area network | 0.9968 Specificity, 0.9948 Sensitivity | No description about accuracy measure and computational time | 2024 | |
| [9] | DL based IDS for automotive networks | 95 % Detection Accuracy | Limited to single attack type; no detail about computational time | 2024 | |
| [10] | ML based IDS for automotive controller area network | 99.9% Detection accuracy | Heavyweight | 2023 | |
| [11] | DL based IDS for automotive controller area network | 0.952 Area under the curve | No description about computational time, undefined car | 2023 | |
| [12] | ML based IDS for automotive controller area network | 0.9998 F1-score | Heavyweight | 2022 | |
| [13] | ML based IDS for automotive controller area network | 98.5269 % Detection accuracy | Heavyweight | 2021 | |
| [14] | GAN based IDS for automotive controller area network | 96.84 % Hit rate | Undefined car, limited to single attack type; no detail about computational time | 2020 | |
| [18] | starGAN based image reconstruction for autonomous vehcile control | 22.21 PSNR, 0.92 SSIM | Heavyweight, limited object detection | 2025 | Mitigation |
| [19] | DL based intrusion mitigation for information security in cyberspace | 95.4 % Detection accuracy; Compromised data blockade, Affected node isolation | No real-time data reconstruction | 2024 | |
| [20] | DL based IDMS for vehicular ad hoc networks | 100 % True detection rate; Affected node isolation | No real-time data reconstruction | 2023 | |
| [21] | SerIoT system for vehicular communication networks | Compromised data blockade, Deflection to decoy system | No real-time data reconstruction | 2022 | |
| [25] | DL based IDMS for vehicle platoons | 96.3 % Detection accuracy, Gap Widening between vehicles for mitigation | No real-time data reconstruction | 2021 |
| Dataset | Attack Type | Attack Injection Rate (pps) | Volume (Number of Samples) | Targets | Sample Rate (Samples/s) | |
|---|---|---|---|---|---|---|
| Attack | Normal | |||||
| 1 | DoS | - | 2,244,041 | 2,369,868 | CAN bus traffic | - |
| Fuzzy | - | |||||
| Impersonation | - | |||||
| 2 | DoS | 3333.3 | 2,331,517 | 15,226,830 | ECUs, Gear, RPM Gauge | |
| Fuzzy | 2000.0 | 2563.28 | ||||
| Spoofing (Gear) | 1000.0 | - | ||||
| Spoofing (RPM) | 1000.0 | 1922.46 | ||||
| 3 | Flooding | - | 1,253,508 | 8,114,265 | ECUs, random and specific CAN IDs | - |
| Fuzzy | - | |||||
| Malfunction | - | |||||
| Replay | - | |||||
| 4 | DoS | 4000.0 | 500,000 | 2,452,620 | Multimedia communication devices | 13,667.88 |
| Fuzzing | 10,000.0 | |||||
| 5 | DoS | 4000.0 | 500,000 | 7,530,786 | Low-speed communication devices | 5576.93 |
| Fuzzing | 10,000.0 | |||||
| 6 | Flooding | 10,000.0 | 1,630,473 | 5,490,129 | CAN bus | 1977.945 |
| Fuzzing | 5000.0 | |||||
| Malfunction | 1000.0 | |||||
| Parameters | Values |
|---|---|
| Total samples per dataset | 500,000 |
| Training Samples per dataset | 325,000 |
| Test Samples per dataset | 175,000 |
| Hidden Layers | 3 |
| Total Neurons in Hidden Layers | 104 |
| Latent Space size | 8 |
| Loss Function | mse |
| Activation Function Input/Output | relu |
| Initial Momentum | 0.89 |
| Initial Learning Rate | 0.01 |
| Number of Epochs | 30 |
| DoS Intrusion | |||||
|---|---|---|---|---|---|
| Optimal Reconstructed Data | |||||
| Original Value | 0.7529411 | 0.7607843 | 0.7647058 | 0.7490196 | 0.7568627 |
| Reconstructed Value | 0.7529412 | 0.7607844 | 0.7647061 | 0.7490192 | 0.7568622 |
| Reconstruction Error | 6.53 × 10−8 | 8.48 × 10−8 | 2.69 × 10−7 | 3.86 × 10−7 | 4.64 × 10−7 |
| Error Ratio | 8.67 × 10−8 | 1.12 × 10−7 | 3.52 × 10−7 | 5.15 × 10−7 | 6.14 × 10−7 |
| Poor Reconstructed Data | |||||
| Original Value | 0.2705882 | 0.3098039 | 0.2784313 | 0.2745098 | 0.8470588 |
| Reconstructed Value | 0.2652617 | 0.3044519 | 0.2730492 | 0.2690989 | 0.8386531 |
| Reconstruction Error | 5.32 × 10−3 | 5.35 × 10−3 | 5.38 × 10−3 | 5.41 × 10−3 | 8.41 × 10−3 |
| Error Ratio | 0.019685 | 0.017275 | 0.01933 | 0.019711 | 0.0099234 |
| Reconstruction Error ( ± ) = (1.3695± 1.7307) × 10−4 | |||||
| Fuzzy Intrusion | |||||
| Optimal Reconstructed Data | |||||
| Original Value | 0.8470588 | 0.8470588 | 0.6784313 | 0.9686274 | 0.5647058 |
| Reconstructed Value | 0.8470588 | 0.8078431 | 0.6784314 | 0.9686275 | 0.5647059 |
| Reconstruction Error | 4.23 × 10−9 | 1.34 × 10−8 | 2.54 × 10−8 | 3.20 × 10−8 | 3.43 × 10−8 |
| Error Ratio | 4.99 × 10−9 | 1.65 × 10−8 | 3.74 × 10−8 | 3.31 × 10−8 | 6.08 × 10−8 |
| Poor Reconstructed Data | |||||
| Original Value | 0.0274509 | 0.9294117 | 0.0274509 | 0.9843137 | 0.0549019 |
| Reconstructed Value | 0.0338043 | 0.9228175 | 0.0342877 | 0.9752079 | 0.0646703 |
| Reconstruction Error | 6.35 × 10−3 | 6.59 × 10−3 | 6.83 × 10−3 | 9.10 × 10−3 | 9.76 × 10−3 |
| Error Ratio | 0.23144 | 0.0070951 | 0.24905 | 0.0092509 | 0.17792 |
| Reconstruction Error ( ± ) = (1.0999 ± 0.6405) × 10−4 | |||||
| Impersonation Intrusion | |||||
| Optimal Reconstructed Data | |||||
| Original Value | 0.0509803 | 0.0431372 | 0.8549019 | 0.0627450 | 0.0078431 |
| Reconstructed Value | 0.0509803 | 0.0431373 | 0.8549018 | 0.0627452 | 0.0078429 |
| Reconstructed Error | 4.63 × 10−8 | 6.80 × 10−8 | 1.38 × 10−7 | 1.48 × 10−7 | 1.82 × 10−7 |
| Error Ratio | 9.08 × 10−7 | 1.57 × 10−6 | 1.62 × 10−7 | 2.36 × 10−6 | 2.32 × 10−5 |
| Poor Reconstructed Data | |||||
| Original Value | 0.9882352 | 0.9843137 | 0.9294117 | 0.9960784 | 0.9921568 |
| Reconstructed Value | 0.9837410 | 0.9897851 | 0.9352317 | 0.9785670 | 0.9713379 |
| Reconstruction Error | 4.49 × 10−3 | 5.47 × 10−3 | 5.82 × 10−3 | 1.75 × 10−2 | 2.08 × 10−2 |
| Error Ratio | 0.0045478 | 0.0055587 | 0.006262 | 0.01758 | 0.020983 |
| Reconstruction Error ( ± ) = (1.4127 ± 1.9858) × 10−4 | |||||
| DoS Intrusion | |||||
|---|---|---|---|---|---|
| Optimal Reconstructed Data | |||||
| Original Value | 0.0901960 | 0.9686274 | 0.0705882 | 0.9843137 | 0.9686274 |
| Reconstructed Value | 0.0901961 | 0.9686273 | 0.0705885 | 0.9843134 | 0.9686271 |
| Reconstruction Error | 1.0 × 10−7 | 1.40 × 10−7 | 2.65 × 10−7 | 2.65 × 10−7 | 2.82 × 10−7 |
| Error Ratio | 1.11 × 10−6 | 1.44 × 10−7 | 3.75 × 10−6 | 2.69 × 10−7 | 2.91 × 10−6 |
| Poor Reconstructed Data | |||||
| Original Value | 0.0627450 | 0.0862745 | 0.0941176 | 0.1058823 | 0.0823529 |
| Reconstructed Value | 0.0779733 | 0.1016976 | 0.1106752 | 0.1228766 | 0.1009537 |
| Reconstruction Error | 0.015228 | 0.015423 | 0.016558 | 0.016994 | 0.018601 |
| Error Ratio | 0.2427 | 0.17877 | 0.17592 | 0.1605 | 0.22587 |
| Reconstruction Error ( ± ) = (2.5156 ± 5.1545) × 10−4 | |||||
| Fuzzy Intrusion | |||||
| Optimal Reconstructed Data | |||||
| Original Value | 0.0941176 | 0.1333333 | 0.5882352 | 0.9803921 | 0.9490196 |
| Reconstructed Value | 0.0941176 | 0.1333333 | 0.5882352 | 0.9803921 | 0.9490196 |
| Reconstruction Error | 3.94 × 10−11 | 5.34 × 10−11 | 1.07 × 10−10 | 1.40 × 10−10 | 1.88 × 10−10 |
| Error Ratio | 4.18 × 10−10 | 4.0 × 10−10 | 1.83 × 10−10 | 1.43 × 10−10 | 1.98 × 10−10 |
| Poor Reconstructed Data | |||||
| Original Value | 0.1529411 | 0.0392156 | 0.0274509 | 0.0745098 | 0.0470588 |
| Reconstructed Value | 0.1556089 | 0.0433465 | 0.0327977 | 0.0829002 | 0.0592805 |
| Reconstruction Error | 0.0026678 | 0.0041309 | 0.0053468 | 0.0083904 | 0.012222 |
| Error Ratio | 0.017443 | 0.10534 | 0.19478 | 0.11261 | 0.25971 |
| Reconstruction Error ( ± ) = 3.9921 × 10−6 ± 4.0126 × 10−5 | |||||
| Spoofing (Gear) Intrusion | |||||
| Optimal Reconstructed Data | |||||
| Original Value | 0.0627450 | 0.0352941 | 0.1254901 | 0.0549019 | 0.0274509 |
| Reconstructed Value | 0.0627450 | 0.0352941 | 0.1254902 | 0.0549021 | 0.0274511 |
| Reconstruction Error | 1.34 × 10−10 | 2.48 × 10−8 | 7.49 × 10−8 | 1.50 × 10−7 | 1.67 × 10−7 |
| Error Ratio | 2.14 × 10−9 | 7.03 × 10−7 | 5.97 × 10−7 | 2.74 × 10−6 | 6.11 × 10−6 |
| Poor Reconstructed Data | |||||
| Original Value | 0.9921568 | 0.9960784 | 0.8980392 | 0.9647058 | 0.9686274 |
| Reconstructed Value | 0.9977037 | 1.0017604 | 0.9037346 | 0.9707119 | 0.9600952 |
| Reconstruction Error | 0.0055469 | 0.005682 | 0.0056954 | 0.0060061 | 0.0085322 |
| Error Ratio | 0.0055907 | 0.0057044 | 0.006342 | 0.0062258 | 0.0088085 |
| Reconstruction Error ( ± ) = (1.6033 ± 1.4613) × 10−4 | |||||
| Spoofing (RPM) Intrusion | |||||
| Optimal Reconstructed Data | |||||
| Original Value | 0.0431372 | 0.0352941 | 0.1254901 | 0.0980392 | 0.0745098 |
| Reconstructed Value | 0.0431373 | 0.0352941 | 0.1254902 | 0.0980392 | 0.0745097 |
| Reconstruction Error | 4.84 × 10−8 | 5.20 × 10−8 | 5.45 × 10−8 | 6.95 × 10−8 | 7.67 × 10−8 |
| Error Ratio | 1.12 × 10−6 | 1.47 × 10−6 | 4.34 × 10−7 | 7.09 × 10−7 | 1.03 × 10−6 |
| Poor Reconstructed Data | |||||
| Original Value | 0.0705882 | 0.9490196 | 0.9843137 | 0.9333333 | 1.0 |
| Reconstructed Value | 0.0663771 | 0.9446970 | 0.9793825 | 0.9333333 | 0.9946695 |
| Reconstruction Error | 0.0042111 | 0.0043225 | 0.0049312 | 0.0051985 | 0.0053304 |
| Error Ratio | 0.059657 | 0.0045547 | 0.0050098 | 0.0055698 | 0.0053304 |
| Reconstruction Error ( ± ) = (1.0828 ± 1.3339) × 10−4 | |||||
| Flooding Intrusion | |||||
|---|---|---|---|---|---|
| Optimal Reconstructed Data | |||||
| Original Value | 0.9529411 | 0.9568627 | 0.9294117 | 0.8470588 | 0.9411764 |
| Reconstructed Value | 0.9529411 | 0.9568627 | 0.9294117 | 0.8470588 | 0.9411764 |
| Reconstruction Error | 1.6 × 10−12 | 1.9 × 10−12 | 2.0 × 10−12 | 6.2 × 10−12 | 8.7 × 10−12 |
| Error Ratio | 1.7 × 10−12 | 2.0 × 10−12 | 2.1 × 10−12 | 7.3 × 10−12 | 9.2 × 10−12 |
| Poor Reconstructed Data | |||||
| Original Value | 0.9686274 | 0.0196078 | 0.0039215 | 0.0235294 | 0.9960784 |
| Reconstructed Value | 0.9686236 | 0.0196120 | 0.0039340 | 0.0235914 | 0.9944053 |
| Reconstruction Error | 3.78 × 10−6 | 4.17 × 10−6 | 1.25 × 10−5 | 6.20 × 10−5 | 1.67 × 10−3 |
| Error Ratio | 3.91 × 10−6 | 0.00021285 | 0.0031925 | 0.0026376 | 0.0016797 |
| Reconstruction Error ( ± ) = 2.871 × 10−7 ± 1.2391 × 10−5 | |||||
| Fuzzy Intrusion | |||||
| Optimal Reconstructed Data | |||||
| Original Value | 0.6078431 | 0.8470588 | 0.6901960 | 0.6274509 | 0.8666666 |
| Reconstructed Value | 0.6078431 | 0.8470588 | 0.6901960 | 0.6274509 | 0.8666666 |
| Reconstruction Error | 1.0 × 10−11 | 2.2 × 10−11 | 3.4 × 10−11 | 6.0 × 10−11 | 6.4 × 10−11 |
| Error Ratio | 1.7 × 10−11 | 2.6 × 10−11 | 4.9 × 10−11 | 9.6 × 10−11 | 7.3 × 10−11 |
| Poor Reconstructed Data | |||||
| Original Value | 0.0235294 | 0.1254901 | 0.0784313 | 0.0117647 | 0.0235294 |
| Reconstructed Value | 0.0179177 | 0.1313583 | 0.0864377 | 0.0211943 | 0.0363473 |
| Reconstruction Error | 0.012818 | 0.0094297 | 0.0080064 | 0.0058681 | 0.0056116 |
| Error Ratio | 0.54476 | 0.80152 | 0.10208 | 0.046762 | 0.23849 |
| Reconstruction Error ( ± ) = 1.1844 × 10−6 ± 9.7876 × 10−5 | |||||
| Malfunction Intrusion | |||||
| Optimal Reconstructed Data | |||||
| Original Value | 0.9215686 | 0.8705882 | 0.3294117 | 0.7647058 | 0.3764705 |
| Reconstructed Value | 0.9215686 | 0.8705882 | 0.3294117 | 0.7647058 | 0.3764705 |
| Reconstruction Error | 1.9 × 10−11 | 1.1 × 10−10 | 1.9 × 10−11 | 2.1 × 10−10 | 2.2 × 10−10 |
| Error Ratio | 2.1 × 10−11 | 1.3 × 10−10 | 5.9 × 10−11 | 2.8 × 10−10 | 5.8 × 10−11 |
| Poor Reconstructed Data | |||||
| Original Value | 0.9921568 | 0.1333333 | 0.8470588 | 0.0078431 | 0.0705882 |
| Reconstructed Value | 0.9911699 | 0.1343709 | 0.8456669 | 0.0110356 | 0.0952084 |
| Reconstruction Error | 0.00098688 | 0.0010376 | 0.0013919 | 0.0031925 | 0.02462 |
| Error Ratio | 0.00099468 | 0.0077824 | 0.0016432 | 0.40705 | 0.34879 |
| Reconstruction Error ( ± ) = 8.9644 × 10−7 ± 1.1129 × 10−4 | |||||
| Replay Intrusion | |||||
| Optimal Reconstructed Data | |||||
| Original Value | 0.0313725 | 0.0627450 | 0.0196078 | 0.2705882 | 0.0352941 |
| Reconstructed Value | 0.0313724 | 0.0627452 | 0.0196077 | 0.2705880 | 0.0352939 |
| Reconstruction Error | 8.47 × 10−8 | 1.08 × 10−7 | 1.12 × 10−7 | 1.63 × 10−7 | 1.78 × 10−7 |
| Error Ratio | 2.70 × 10−6 | 1.73 × 10−6 | 5.75 × 10−7 | 6.04 × 10−7 | 5.07 × 10−6 |
| Poor Reconstructed Data | |||||
| Original Value | 0.9921568 | 0.0431372 | 0.9960784 | 0.0745098 | 0.0156862 |
| Reconstructed Value | 0.9980645 | 0.0491685 | 1.0028459 | 0.0940016 | 0.0395505 |
| Reconstruction Error | 5.90 × 10−3 | 6.03 × 10−3 | 6.76 × 10−3 | 1.94 × 10−2 | 2.38 × 10−2 |
| Error Ratio | 0.0059544 | 0.13982 | 0.0067941 | 0.2616 | 1.5213 |
| Reconstruction Error ( ± ) = (2.8144 ± 2.9713) × 10−4 | |||||
| DoS Intrusion | |||||
|---|---|---|---|---|---|
| Optimal Reconstructed Data | |||||
| Original Value | 0.0313725 | 0.0039215 | 0.0274509 | 0.3294117 | 0.0352941 |
| Reconstructed Value | 0.0313739 | 0.0039248 | 0.0274466 | 0.3294051 | 0.0353012 |
| Reconstruction Error | 1.43 × 10−6 | 3.32 × 10−6 | 4.28 × 10−6 | 6.63 × 10−6 | 7.15 × 10−6 |
| Error Ratio | 4.57 × 10−5 | 8.47 × 10−4 | 1.55 × 10−4 | 2.01 × 10−5 | 2.02 × 10−4 |
| Poor Reconstructed Data | |||||
| Original Value | 0.0117647 | 0.0039215 | 0.9921568 | 0.0235294 | 0.9843137 |
| Reconstructed Value | 0.0141285 | 0.0011375 | 0.9954768 | 0.0298712 | 0.9959440 |
| Reconstruction Error | 0.0023639 | 0.002784 | 0.00332 | 0.0063418 | 0.01163 |
| Error Ratio | 0.20093 | 0.70993 | 0.0033462 | 0.26953 | 0.011816 |
| Reconstruction Error ( ± ) = (1.2052 ± 2.9518) × 10−4 | |||||
| Fuzzing Intrusion | |||||
| Optimal Reconstructed Data | |||||
| Original Value | 0.0392156 | 0.0196078 | 0.3647058 | 0.0980392 | 0.4274509 |
| Reconstructed Value | 0.0392156 | 0.0196078 | 0.3647058 | 0.0980392 | 0.4274510 |
| Reconstruction Error | 3.33 × 10−9 | 3.71 × 10−9 | 8.45 × 10−9 | 1.32 × 10−8 | 3.09 × 10−8 |
| Error Ratio | 8.51 × 10−8 | 1.89 × 10−7 | 2.31 × 10−8 | 1.35 × 10−7 | 7.23 × 10−8 |
| Poor Reconstructed Data | |||||
| Original Value | 0.1058823 | 0.0705882 | 0.0862745 | 0.0509803 | 0.0431372 |
| Reconstructed Value | 0.0995527 | 0.0771858 | 0.0959314 | 0.0608457 | 0.0280398 |
| Reconstruction Error | 0.0063297 | 0.0065976 | 0.0096569 | 0.0098653 | 0.015097 |
| Error Ratio | 0.05978 | 0.093466 | 0.11193 | 0.19351 | 0.34999 |
| Reconstruction Error ( ± ) = 2.6575 × 10−5 ± 1.1231 × 10−4 | |||||
| DoS Intrusion | |||||
|---|---|---|---|---|---|
| Optimal Reconstructed Data | |||||
| Original Value | 0.2 | 0.2078431 | 0.2666666 | 0.7215686 | 0.6352941 |
| Reconstructed Value | 0.1999999 | 0.2078431 | 0.2666666 | 0.7215686 | 0.6352941 |
| Reconstruction Error | 1.5 × 10−11 | 1.2 × 10−10 | 6.3 × 10−10 | 1.13 × 10−9 | 1.55 × 10−9 |
| Error Ratio | 7.3 × 10−11 | 5.6 × 10−10 | 2.36 × 10−9 | 1.56 × 10−9 | 2.44 × 10−9 |
| Poor Reconstructed Data | |||||
| Original Value | 0.1137254 | 0.01568627 | 0.0509803 | 0.4980392 | 0.2509803 |
| Reconstructed Value | 0.1161385 | 0.0183532 | 0.0562650 | 0.4920709 | 0.2346066 |
| Reconstruction Error | 0.002413 | 0.002667 | 0.0052846 | 0.0059682 | 0.016374 |
| Error Ratio | 0.021218 | 0.17002 | 0.10366 | 0.011983 | 0.065239 |
| Reconstruction Error ( ± ) = 9.9053 × 10−6 ± 4.4062 × 10−5 | |||||
| Fuzzing Intrusion | |||||
| Optimal Reconstructed Data | |||||
| Original Value | 0.0156862 | 0.4941176 | 0.0431372 | 0.0392156 | 0.2549019 |
| Reconstructed Value | 0.0156862 | 0.4941176 | 0.0431372 | 0.0392156 | 0.2549019 |
| Reconstruction Error | 7.8 × 10−10 | 1.50 × 10−9 | 2.56 × 10−9 | 3.19 × 10−9 | 3.76 × 10−9 |
| Error Ratio | 5.0 × 10−8 | 3.04 × 10−9 | 5.93 × 10−8 | 8.15 × 10−8 | 1.47 × 10−8 |
| Poor Reconstructed Data | |||||
| Original Value | 0.0039215 | 0.0117647 | 0.0039215 | 0.01568627 | 0.0274509 |
| Reconstructed Value | 0.0086751 | 0.0170816 | 0.0100046 | 0.0221609 | 0.0171910 |
| Reconstruction Error | 0.0047536 | 0.0053169 | 0.0060831 | 0.0064746 | 0.01026 |
| Error Ratio | 1.2122 | 0.45194 | 1.5512 | 0.41276 | 0.37375 |
| Reconstruction Error ( ± ) = (1.5741 ± 5.9155) × 10−5 | |||||
| Flooding Intrusion | |||||
|---|---|---|---|---|---|
| Optimal Reconstructed Data | |||||
| Original Value | 0.9372549 | 0.3960784 | 0.40 | 0.8313725 | 0.6117647 |
| Reconstructed Value | 0.9372549 | 0.3960784 | 0.3999999 | 0.8313725 | 0.6117647 |
| Reconstruction Error | 4.66 × 10−11 | 3.50 × 10−10 | 3.75 × 10−10 | 9.26 × 10−10 | 2.66 × 10−9 |
| Error Ratio | 4.97 × 10−11 | 8.83 × 10−10 | 9.39 × 10−10 | 1.11 × 10−9 | 4.35 × 10−9 |
| Poor Reconstructed Data | |||||
| Original Value | 0.1411764 | 0.1411764 | 0.0666666 | 0.3725490 | 0.8509803 |
| Reconstructed Value | 0.0271798 | 0.1466601 | 0.0731802 | 0.3830386 | 0.8329448 |
| Reconstruction Error | 0.0036504 | 0.0054836 | 0.0065136 | 0.01049 | 0.018036 |
| Error Ratio | 0.15514 | 0.038842 | 0.097704 | 0.028156 | 0.021194 |
| Reconstruction Error ( ± ) = (4.9234 ± 7.7279) × 10−5 | |||||
| Fuzzing Intrusion | |||||
| Optimal Reconstructed Data | |||||
| Original Value | 0.2039215 | 0.2274509 | 0.5960784 | 0.3411764 | 0.1019607 |
| Reconstructed Value | 0.2039215 | 0.2274509 | 0.5960784 | 0.3411764 | 0.1019607 |
| Reconstruction Error | 5.43 × 10−9 | 6.24 × 10−9 | 6.52 × 10−9 | 7.03 × 10−9 | 8.65 × 10−9 |
| ER | 2.66 × 10−8 | 2.74 × 10−8 | 1.09 × 10−8 | 2.06 × 10−8 | 8.48 × 10−8 |
| Poor Reconstructed Data | |||||
| Original Value | 0.0078431 | 0.0980392 | 0.0470588 | 0.0313725 | 0.9490196 |
| Reconstructed Value | 0.0155906 | 0.1067975 | 0.0652327 | 0.05395768 | 0.9110684 |
| Reconstruction Error | 0.0077475 | 0.0087583 | 0.018174 | 0.022585 | 0.037951 |
| Error Ratio | 0.98781 | 0.089335 | 0.3862 | 0.7199 | 0.03999 |
| Reconstruction Error ( ± ) = (5.4577 ± 1.7709) × 10−4 | |||||
| Malfunction Intrusion | |||||
| Optimal Reconstructed Data | |||||
| Original Value | 0.3372549 | 0.5921568 | 0.2705882 | 0.1176470 | 0.7450980 |
| Reconstructed Value | 0.3372549 | 0.5921568 | 0.2705882 | 0.1176470 | 0.7450980 |
| Reconstruction Error | 3.23 × 10−10 | 4.2 × 10−10 | 5.9 × 10−10 | 1.12 × 10−9 | 1.24 × 10−9 |
| Error Ratio | 9.6 × 10−10 | 7.1 × 10−10 | 2.18 × 10−9 | 9.53 × 10−9 | 1.66 × 10−9 |
| Poor Reconstructed Data | |||||
| Original Value | 0.0235294 | 0.0666666 | 0.0039215 | 0.0078431 | 0.8196078 |
| Reconstructed Value | 0.0261796 | 0.0696458 | 0.0077227 | 0.0144744 | 0.7989199 |
| Reconstruction Error | 0.0026502 | 0.0029792 | 0.0038012 | 0.0066313 | 0.020688 |
| Error Ratio | 0.11263 | 0.044688 | 0.96929 | 0.84549 | 0.025241 |
| Reconstruction Error ( ± ) = (8.7937 ± 4.3163) × 10−5 | |||||
| Dataset | Intrusions | Percentage RE (%) |
|---|---|---|
| 1 | Dos | 7.5182 × 10−5 |
| Fuzzy | 7.1871 × 10−5 | |
| Impersonation | 4.3145 × 10−5 | |
| 2 | Dos | 4.267 × 10−5 |
| Fuzzy | 9.0666 × 10−5 | |
| Spoofing (Gear) | 3.9214 × 10−5 | |
| Spoofing (RPM) | 2.2653 × 10−5 | |
| 3 | Flooding | 1.3271 × 10−5 |
| Fuzzy | 4.6938 × 10−5 | |
| Malfunction | 9.0317 × 10−5 | |
| Replay | 1.6254 × 10−5 | |
| 4 | Dos | 2.1384 × 10−5 |
| Fuzzing | 2.0139 × 10−5 | |
| 5 | Dos | 2.0518 × 10−5 |
| Fuzzing | 3.7491 × 10−5 | |
| 6 | Flooding | 1.4678 × 10−5 |
| Fuzzing | 1.7889 × 10−5 | |
| Malfunction | 7.5370 × 10−5 |
| Dataset | Intrusion | Execution Time (s) | Estimated Usage | Amortized Time (s) |
|---|---|---|---|---|
| 1 | Dos | 0.128403 | 50 | 0.002568 |
| 100 | 0.001284 | |||
| 200 | 0.000642 | |||
| Fuzzy | 0.118190 | 50 | 0.002364 | |
| 100 | 0.001182 | |||
| 200 | 0.000591 | |||
| Impersonation | 0.136582 | 50 | 0.002732 | |
| 100 | 0.001366 | |||
| 200 | 0.000683 | |||
| 2 | Dos | 0.119429 | 50 | 0.002389 |
| 100 | 0.001194 | |||
| 200 | 0.000597 | |||
| Fuzzy | 0.140763 | 50 | 0.002815 | |
| 100 | 0.001408 | |||
| 200 | 0.000704 | |||
| Spoofing (Gear) | 0.085770 | 50 | 0.001715 | |
| 100 | 0.000858 | |||
| 200 | 0.000429 | |||
| Spoofing (RPM) | 0.115697 | 50 | 0.002314 | |
| 100 | 0.001157 | |||
| 200 | 0.000578 | |||
| 3 | Flooding | 0.106050 | 50 | 0.002121 |
| 100 | 0.001061 | |||
| 200 | 0.000530 | |||
| Fuzzy | 0.118164 | 50 | 0.002363 | |
| 100 | 0.001182 | |||
| 200 | 0.000591 | |||
| Malfunction | 0.151347 | 50 | 0.003027 | |
| 100 | 0.001513 | |||
| 200 | 0.000757 | |||
| Replay | 0.117029 | 50 | 0.002341 | |
| 100 | 0.001170 | |||
| 200 | 0.000585 | |||
| 4 | Dos | 0.207910 | 50 | 0.004158 |
| 100 | 0.002079 | |||
| 200 | 0.001040 | |||
| Fuzzing | 0.132068 | 50 | 0.002641 | |
| 100 | 0.001321 | |||
| 200 | 0.000660 | |||
| 5 | Dos | 0.094069 | 50 | 0.001881 |
| 100 | 0.000941 | |||
| 200 | 0.000470 | |||
| Fuzzing | 0.148530 | 50 | 0.002971 | |
| 100 | 0.001485 | |||
| 200 | 0.000743 | |||
| 6 | Flooding | 0.145511 | 50 | 0.002910 |
| 100 | 0.001455 | |||
| 200 | 0.000728 | |||
| Fuzzing | 0.273372 | 50 | 0.005467 | |
| 100 | 0.002734 | |||
| 200 | 0.001367 | |||
| Malfunction | 0.280700 | 50 | 0.005614 | |
| 100 | 0.002807 | |||
| 200 | 0.001404 |
| Unseen-Exploits-Intrusion | |||||
|---|---|---|---|---|---|
| Best Reconstructed Data | |||||
| Original Value | 0.058823529 | 0.019607843 | 0.039215686 | 0.3333348715754 | 0.352941176 |
| Reconstructed Value | 0.058823592572301 | 0.019608034694900 | 0.039215225788863 | 0.333334871575410 | 0.352949442591866 |
| Reconstruction Error | 6.3572 × 10−8 | 1.9169 × 10−7 | 4.6021 × 10−7 | 1.5386 × 10−6 | 8.266 × 10−6 |
| Error Ratio | 1.0807 × 10−6 | 9.7764 × 10−6 | 1.1735 × 10−5 | 4.6157 × 10−6 | 2.3422 × 10−5 |
| Worst Reconstructed Data | |||||
| Original Value | 0.176470588 | 0.294117647 | 0.274509804 | 0.078431373 | 0.901960784 |
| Reconstructed Value | 0.164413727257618 | 0.281943574129103 | 0.262118984920315 | 0.092223280780675 | 0.883810436014474 |
| Reconstruction Error | 0.012057 | 0.012174 | 0.012391 | 0.013792 | 0.01815 |
| Error Ratio | 0.068322 | 0.041392 | 0.045138 | 0.17585 | 0.020123 |
| Reconstruction Error ( ± ) = 7.9501 × 10−4 ± 4.8 × 10−2 | |||||
| Parameters | Seen Data | Unseen Data |
|---|---|---|
| Mean Reconstruction Error | <1% | <1% |
| Execution Time (s) | 0.145532 | 0.058369 |
| Adversarial Machine Learning Atta | |||||
| Best Reconstructed Data | |||||
| Original Value | 0.051755242375452 | 0.010063551905973 | 0.013296405755303 | 0.010571772791250 | 0.005831583183491 |
| Reconstructed Value | 0.051755242377456 | 0.010063551430136 | 0.013296406299568 | 0.013296406299568 | 0.005831583896953 |
| Reconstruction Error | 2.0032 × 10−12 | 4.7584 × 10−10 | 5.4427 × 10−10 | 6.2462 × 10−10 | 7.1346 × 10−10 |
| Error Ratio | 3.8705 × 10−11 | 4.7283 × 10−8 | 4.0933 × 10−8 | 5.9083 × 10−8 | 1.2234 × 10−7 |
| Worst Reconstructed Data | |||||
| Original Value | 0.904889486417633 | 0.921277743274121 | 0.951833868463914 | 0.048913922043000 | 0.900990803938693 |
| Reconstructed Value | 0.903207826749840 | 0.919451094624141 | 0.949769494945811 | 0.051268595843600 | 0.897338065778924 |
| Reconstruction Error | 0.0016817 | 0.0018266 | 0.0020644 | 0.0023547 | 0.0036527 |
| Error Ratio | 0.0018584 | 0.0019827 | 0.0021688 | 0.048139 | 0.0040541 |
| Reconstruction Error ( ± ) = (4.2401 ± 7.1352) × 10−5 | |||||
| Dataset | Attack Type | Mean | RE | Difference |
|---|---|---|---|---|
| AM-DDAE (Proposed) | GANs | |||
| 1 | DoS | 0.00013695 | 0.1024 | 0.102263 |
| Fuzzy | 0.00010999 | 0.1812 | 0.18109 | |
| Impersonation | 0.00014127 | 0.1664 | 0.166259 | |
| 2 | DoS | 0.00025156 | 0.1473 | 0.147048 |
| Fuzzy | 0.000039921 | 0.2023 | 0.20226 | |
| Spoofing (Gear) | 0.00016033 | 0.1867 | 0.18654 | |
| Spoofing (RPM) | 0.00010828 | 0.1664 | 0.166292 | |
| 3 | Flooding | 0.00002871 | 0.1820 | 0.181971 |
| Fuzzy | 0.000011844 | 0.1792 | 0.179188 | |
| Malfunction | 0.00089644 | 0.1498 | 0.148904 | |
| Replay | 0.00028144 | 0.1862 | 0.185919 | |
| 4 | DoS | 0.00012052 | 0.1197 | 0.119579 |
| Fuzzing | 0.00026575 | 0.1330 | 0.132734 | |
| 5 | DoS | 0.000099053 | 0.1649 | 0.164801 |
| Fuzzing | 0.000015741 | 0.1485 | 0.148484 | |
| 6 | Flooding | 0.000049234 | 0.1672 | 0.167151 |
| Fuzzing | 0.00054577 | 0.1656 | 0.165054 | |
| Malfunction | 0.000087937 | 0.1894 | 0.189312 |
| Dataset | Attack Type | Execution | Time (s) | Difference |
|---|---|---|---|---|
| AM-DDAE (Proposed) | GANs | |||
| 1 | DoS | 0.128403 | 16.844 | 16.7156 |
| Fuzzy | 0.118190 | 13.786 | 13.66781 | |
| Impersonation | 0.136582 | 11.081 | 10.94442 | |
| 2 | DoS | 0.119429 | 11.191 | 11.07157 |
| Fuzzy | 0.140763 | 11.012 | 10.87124 | |
| Spoofing (Gear) | 0.085770 | 11.208 | 11.12223 | |
| Spoofing (RPM) | 0.115697 | 14.445 | 14.3293 | |
| 3 | Flooding | 0.106050 | 10.743 | 10.63695 |
| Fuzzy | 0.118164 | 10.913 | 10.79484 | |
| Malfunction | 0.151347 | 10.985 | 10.83365 | |
| Replay | 0.117029 | 12.500 | 12.38297 | |
| 4 | DoS | 0.207910 | 10.985 | 10.77709 |
| Fuzzing | 0.132068 | 12.382 | 12.24993 | |
| 5 | DoS | 0.094069 | 10.717 | 10.62293 |
| Fuzzing | 0.148530 | 10.816 | 10.66747 | |
| 6 | Flooding | 0.145511 | 10.690 | 10.54449 |
| Fuzzing | 0.273372 | 11.038 | 10.76463 | |
| Malfunction | 0.280700 | 10.877 | 10.5963 |
| DoS Intrusion | |||||
| Best Reconstructed Data | |||||
| Original Value | 0.003921569 | 0.019607843 | 0.011811024 | 0.015686275 | 0.007843137 |
| Reconstructed Value | 0.0039357 | 0.0196396 | 0.0117115 | 0.0155016 | 0.0074881 |
| Reconstruction Error | 0.000014093 | 0.000031763 | 0.000099567 | 0.00018467 | 0.00035506 |
| Error Ratio | 0.0035936 | 0.0016199 | 0.0084 | 0.011773 | 0.04527 |
| Worst Reconstructed Data | |||||
| Original Value | 0.984313725 | 0.976470588 | 0.976377953 | 0.980392157 | 0.996078431 |
| Reconstructed Value | 0.0118349 | 0.0037626 | 0.0025530 | 0.0039900 | 0.0050469 |
| Reconstruction Error | 0.97248 | 0.97271 | 0.97382 | 0.9764 | 0.99103 |
| Error Ratio | 0.98798 | 0.99615 | 0.99739 | 0.99593 | 0.99493 |
| Reconstruction Error ( ± ) = 0.1024 ± 0.1356 | |||||
| Fuzzy Intrusion | |||||
| Best Reconstructed Data | |||||
| Original Value | 0.019607843 | 0.615686275 | 0.298039216 | 0.31372549 | 0.635294118 |
| Reconstructed Value | 0.0196316 | 0.6157715 | 0.2977831 | 0.3134525 | 0.6355679 |
| Reconstruction Error | 0.000023804 | 0.000085197 | 0.00025608 | 0.00027301 | 0.00027379 |
| Error Ratio | 0.001214 | 0.00013838 | 0.00085921 | 0.00087021 | 0.00043096 |
| Worst Reconstructed Data | |||||
| Original Value | 0.815686275 | 0.964705882 | 0.878431373 | 0.803921569 | 0.894117647 |
| Reconstructed Value | 0.1180484 | 0.2283716 | 0.1354989 | 0.0301402 | 0.0755604 |
| Reconstruction Error | 0.69764 | 0.73633 | 0.74293 | 0.77378 | 0.81856 |
| Error Ratio | 0.85528 | 0.76327 | 0.84575 | 0.96251 | 0.91549 |
| Reconstruction Error ( ± ) = 0.1812 ± 0.0665 | |||||
| Impersonation Intrusion | |||||
| Best Reconstructed Data | |||||
| Original Value | 0.049107143 | 0.062745098 | 0.040178571 | 0.070588235 | 0.074509804 |
| Reconstructed Value | 0.0490225 | 0.0628323 | 0.0403882 | 0.0708314 | 0.0747580 |
| Reconstruction Error | 0.000084636 | 0.000087153 | 0.00020959 | 0.00024314 | 0.00024823 |
| Error Ratio | 0.0017235 | 0.001389 | 0.0052165 | 0.0034445 | 0.0033316 |
| Worst Reconstructed Data | |||||
| Original Value | 0.928571429 | 0.976470588 | 0.925490196 | 0.915178571 | 0.988235294 |
| Reconstructed Value | 0.0540381 | 0.0994046 | 0.0355721 | 0.0195887 | 0.0857598 |
| Reconstruction Error | 0.87453 | 0.87707 | 0.88992 | 0.89559 | 0.90248 |
| Error Ratio | 0.94181 | 0.8982 | 0.96156 | 0.9786 | 0.91322 |
| Reconstruction Error ( ± ) = 0.1664 ± 0.0695 | |||||
| DoS Intrusion | |||||
| Best Reconstructed Data | |||||
| Original Value | 0.007843137 | 0.04705882 | 0.004784689 | 0.019607843 | 0.003968254 |
| Reconstructed Value | 0.0075861 | 0.0465696 | 0.0037233 | 0.0183325 | 0.0024771 |
| Reconstruction Error | 0.00025706 | 0.00048924 | 0.0010614 | 0.0012754 | 0.0014912 |
| Error Ratio | 0.032775 | 0.010396 | 0.22182 | 0.065043 | 0.37578 |
| Worst Reconstructed Data | |||||
| Original Value | 0.968253968 | 0.984313725 | 0.979057592 | 0.988235294 | 0.996078431 |
| Reconstructed Value | 0.0089633 | 0.0064030 | 0.000980555 | 0.0061639 | 0.0012052 |
| Reconstruction Error | 0.95929 | 0.97791 | 0.97808 | 0.98207 | 0.99487 |
| Error Ratio | 0.99074 | 0.99349 | 0.999 | 0.99376 | 0.99879 |
| Reconstruction Error () = 0.1473 0.1349 | |||||
| Fuzzy Intrusion | |||||
| Best Reconstructed Data | |||||
| Original Value | 0.117647059 | 0.11372549 | 0.035294118 | 0.066666667 | 0.074509804 |
| Reconstructed Value | 0.1176597 | 0.1137034 | 0.0352124 | 0.0665476 | 0.0746459 |
| Reconstruction Error | 1.2592 × 10−5 | 2.2083 × 10−5 | 8.1761 × 10−5 | 1.191 × 10−4 | 1.3612 × 10−4 |
| Error Ratio | 0.00010703 | 0.00019418 | 0.0023166 | 0.0017865 | 0.0018268 |
| Worst Reconstructed Data | |||||
| Original Value | 0.980392157 | 0.949019608 | 0.929411765 | 0.945098039 | 0.976470588 |
| Reconstructed Value | 0.1312901 | 0.0984343 | 0.0726554 | 0.0552933 | 0.0850940 |
| Reconstruction Error | 0.8491 | 0.85059 | 0.85676 | 0.8898 | 0.89138 |
| Error Ratio | 0.86608 | 0.89628 | 0.92183 | 0.94149 | 0.91286 |
| Reconstruction Error () = 0.2023 0.0922 | |||||
| Spoofing (Gear) Intrusion | |||||
| Best Reconstructed Data | |||||
| Original Value | 0.004784689 | 0.019607843 | 0.178010471 | 0.004784689 | 0.062745098 |
| Reconstructed Value | 0.0046932 | 0.0197156 | 0.1781214 | 0.0045282 | 0.0623568 |
| Reconstruction Error | 9.1474 × 10−5 | 1.0777 × 10−4 | 1.1096 × 10−4 | 2.5652 × 10−4 | 3.8834 × 10−4 |
| Error Ratio | 0.019118 | 0.0054963 | 0.00062334 | 0.053613 | 0.0061891 |
| Worst Reconstructed Data | |||||
| Original Value | 0.91372549 | 0.929411765 | 0.964705882 | 0.976470588 | 0.945098039 |
| Reconstructed Value | 0.0092011 | 0.0049451 | 0.0322466 | 0.0401472 | 0.0066587 |
| Reconstruction Error | 0.90452 | 0.92447 | 0.93246 | 0.93632 | 0.93844 |
| Error Ratio | 0.98993 | 0.99468 | 0.96657 | 0.95889 | 0.99295 |
| Reconstruction Error () = 0.1867 0.0849 | |||||
| Spoofing (RPM) Intrusion | |||||
| Best Reconstructed Data | |||||
| Original Value | 0.141176471 | 0.882352941 | 0.125490196 | 0.031372549 | 0.141176471 |
| Reconstructed Value | 0.1412281 | 0.8824174 | 0.1253147 | 0.0311787 | 0.1414160 |
| Reconstruction Error | 0.000051594 | 0.00006444 | 0.00017554 | 0.00019388 | 0.00023951 |
| Error Ratio | 0.00036546 | 0.000073032 | 0.0013989 | 0.00618 | 0.0016965 |
| Worst Reconstructed Data | |||||
| Original Value | 0.980392157 | 0.956862745 | 0.984313725 | 0.988235294 | 0.996078431 |
| Reconstructed Value | 0.1335045 | 0.1035433 | 0.1278326 | 0.0753057 | 0.0731756 |
| Reconstruction Error | 0.84689 | 0.85332 | 0.85648 | 0.91293 | 0.9229 |
| Error Ratio | 0.86383 | 0.89179 | 0.87013 | 0.9238 | 0.92654 |
| Reconstruction Error () = 0.1664 0.0739 | |||||
| Flooding Intrusion | |||||
| Best Reconstructed Data | |||||
| Original Value | 0.035294118 | 0.090196078 | 0.11372549 | 0.031372549 | 0.058823529 |
| Reconstructed Value | 0.0352911 | 0.0903348 | 0.1132890 | 0.0318339 | 0.0593143 |
| Reconstruction Error | 2.979 × 10−6 | 0.00013872 | 0.00043649 | 0.00046135 | 0.00049074 |
| Error Ratio | 8.4404 × 10−5 | 0.001538 | 0.0038381 | 0.014706 | 0.0083427 |
| Worst Reconstructed Data | |||||
| Original Value | 0.976470588 | 0.94488189 | 0.925490196 | 0.878431373 | 0.933333333 |
| Reconstructed Value | 0.1155326 | 0.0826848 | 0.0591295 | 0.0064016 | 0.0128098 |
| Reconstruction Error | 0.86094 | 0.8622 | 0.86636 | 0.87203 | 0.92052 |
| Error Ratio | 0.88168 | 0.91249 | 0.93611 | 0.99271 | 0.98628 |
| Reconstruction Error ( ± ) = 0.1820 ± 0.0704 | |||||
| Fuzzy Intrusion | |||||
| Best Reconstructed Data | |||||
| Original Value | 0.11372549 | 0.235294118 | 0.011764706 | 0.11372549 | 0.074509804 |
| Reconstructed Value | 0.1138461 | 0.2354272 | 0.0119260 | 0.1135059 | 0.0747396 |
| Reconstruction Error | 0.00012063 | 0.00013307 | 0.00016134 | 0.00021959 | 0.00022975 |
| Error Ratio | 0.0010607 | 0.00056554 | 0.013714 | 0.0019309 | 0.0030835 |
| Worst Reconstructed Data | |||||
| Original Value | 0.925490196 | 0.921568627 | 0.937254902 | 0.97254902 | 0.956862745 |
| Reconstructed Value | 0.0305022 | 0.0160121 | 0.0173264 | 0.0422058 | 0.0169412 |
| Reconstruction Error | 0.89499 | 0.90556 | 0.91993 | 0.93034 | 0.93992 |
| Error Ratio | 0.96704 | 0.98263 | 0.98151 | 0.9566 | 0.9823 |
| Reconstruction Error ( ± ) = 0.1792 ± 0.0819 | |||||
| Malfunction Intrusion | |||||
| Best Reconstructed Data | |||||
| Original Value | 0.003921569 | 0.011764706 | 0.047058824 | 0.023529412 | 0.007843137 |
| Reconstructed Value | 0.0039237 | 0.0117493 | 0.0469612 | 0.0233983 | 0.0076827 |
| Reconstruction Error | 2.1172 × 10−6 | 1.545 × 10−5 | 9.7598 × 10−5 | 1.3112 × 10−4 | 1.6041 × 10−4 |
| Error Ratio | 0.00053989 | 0.0013132 | 0.002074 | 0.0055727 | 0.020453 |
| Worst Reconstructed Data | |||||
| Original Value | 0.980392157 | 0.984313725 | 0.988235294 | 0.992156863 | 0.996078431 |
| Reconstructed Value | 0.0053127 | 0.0014639 | 0.00021569 | 0.000684863 | 0.000068583 |
| Reconstruction Error | 0.97508 | 0.98285 | 0.98802 | 0.99147 | 0.99601 |
| Error Ratio | 0.99458 | 0.99851 | 0.99978 | 0.99931 | 0.99993 |
| Reconstruction Error ( ± ) = 0.1498 ± 0.1219 | |||||
| Replay Intrusion | |||||
| Best Reconstructed Data | |||||
| Original Value | 0.078431373 | 0.066666667 | 0.145098039 | 0.10980392 | 0.188235294 |
| Reconstructed Value | 0.0784392 | 0.0666569 | 0.1451117 | 0.1098243 | 0.1882974 |
| Reconstruction Error | 7.8329 × 10−6 | 9.7348 × 10−6 | 1.3626 × 10−5 | 2.0415 × 10−5 | 6.2127 × 10−5 |
| Error Ratio | 9.9869 × 10−5 | 1.4602 × 10−4 | 9.391 × 10−5 | 1.8592 × 10−4 | 3.3005 × 10−4 |
| Worst Reconstructed Data | |||||
| Original Value | 0.9372549 | 0.97254902 | 0.956862745 | 0.968253968 | 0.988235294 |
| Reconstructed Value | 0.0148576 | 0.0498330 | 0.0227760 | 0.0302223 | 0.0374357 |
| Reconstruction Error | 0.9224 | 0.92272 | 0.93409 | 0.93803 | 0.9508 |
| Error Ratio | 0.98415 | 0.94876 | 0.9762 | 0.96879 | 0.96212 |
| Reconstruction Error ( ± ) = 0.1862 ± 0.0866 | |||||
| DoS Intrusion | |||||
| Best Reconstructed Data | |||||
| Original Value | 0.003921569 | 0.007843137 | 0.023529 | 0.015686275 | 0.011764706 |
| Reconstructed Value | 0.0038629 | 0.0073847 | 0.023081 | 0.0148526 | 0.0133527 |
| Reconstruction Error | 0.000058637 | 0.00045848 | 0.00044805 | 0.00083371 | 0.001588 |
| Error Ratio | 0.014952 | 0.058456 | 0.019042 | 0.053149 | 0.13498 |
| Worst Reconstructed Data | |||||
| Original Value | 0.93333333 | 0.941176471 | 0.97254902 | 0.980392157 | 0.992156863 |
| Reconstructed Value | 0.0038465 | 0.000056349585 | 0.0053684 | 0.0025628 | 0.00071916 |
| Reconstruction Error | 0.92949 | 0.94112 | 0.95106 | 0.97783 | 0.99144 |
| Error Ratio | 0.99588 | 0.99994 | 0.9779 | 0.99739 | 0.99928 |
| Reconstruction Error ( ± ) = 0.1197 ± 0.2124 | |||||
| Fuzzing Intrusion | |||||
| Best Reconstructed Data | |||||
| Original Value | 0.015686275 | 0.066666667 | 0.011764706 | 0.078431373 | 0.039215686 |
| Reconstructed Value | 0.0157229 | 0.0665290 | 0.0119625 | 0.0786558 | 0.0396165 |
| Reconstruction Error | 0.000036624 | 0.00013769 | 0.0001978 | 0.00022444 | 0.00040083 |
| Error Ratio | 0.0023348 | 0.0020654 | 0.016813 | 0.0028617 | 0.010221 |
| Worst Reconstructed Data | |||||
| Original Value | 0.984313725 | 0.925490196 | 0.980392157 | 0.941176471 | 0.949019608 |
| Reconstructed Value | 0.0874406 | 0.0202050 | 0.0626758 | 0.0117404 | 0.0030840 |
| Reconstruction Error | 0.89687 | 0.90529 | 0.91772 | 0.92944 | 0.94594 |
| Error Ratio | 0.91117 | 0.97817 | 0.93607 | 0.98753 | 0.99675 |
| Reconstruction Error ( ± ) = 0.1330 ± 0.1266 | |||||
| DoS Intrusion | |||||
| Best Reconstructed Data | |||||
| Original Value | 0.062745098 | 0.015686275 | 0.125490196 | 0.247058824 | 0.02745098 |
| Reconstructed Value | 0.0630626 | 0.0160570 | 0.1250065 | 0.2475464 | 0.0269227 |
| Reconstruction Error | 0.0003175 | 0.00037074 | 0.00048373 | 0.00048758 | 0.00052826 |
| Error Ratio | 0.0050601 | 0.023635 | 0.0038547 | 0.0019735 | 0.019244 |
| Worst Reconstructed Data | |||||
| Original Value | 0.988235294 | 0.941176471 | 0.949019608 | 0.97254902 | 0.976470588 |
| Reconstructed Value | 0.0518627 | 0.0024055 | 0.0085331 | 0.0178499 | 0.0201059 |
| Reconstruction Error | 0.93637 | 0.93877 | 0.94049 | 0.9547 | 0.95636 |
| Error Ratio | 0.94752 | 0.99744 | 0.99101 | 0.98165 | 0.97941 |
| Reconstruction Error ( ± ) = 0.1649 ± 0.1176 | |||||
| Fuzzing Intrusion | |||||
| Best Reconstructed Data | |||||
| Original Value | 0.019607843 | 0.003921569 | 0.007843137 | 0.035294118 | 0.02745098 |
| Reconstructed Value | 0.0196479 | 0.0038376 | 0.0075930 | 0.0355900 | 0.0271260 |
| Reconstruction Error | 4.0042 × 10−5 | 8.4005 × 10−5 | 2.5012 × 10−4 | 2.9588 × 10−4 | 3.2499 × 10−4 |
| Error Ratio | 0.0020421 | 0.021421 | 0.03189 | 0.0083833 | 0.011839 |
| Worst Reconstructed Data | |||||
| Original Value | 0.976470588 | 0.952941176 | 0.949019608 | 0.941176471 | 0.996078431 |
| Reconstructed Value | 0.0588685 | 0.0346383 | 0.0145934 | 0.0025264 | 0.0112039 |
| Reconstruction Error | 0.92848 | 0.92939 | 0.93443 | 0.93865 | 0.98487 |
| Error Ratio | 0.95085 | 0.97529 | 0.98462 | 0.99732 | 0.98875 |
| Reconstruction Error ( ± ) = 0.1485 ± 0.1205 | |||||
| Flooding Intrusion | |||||
| Best Reconstructed Data | |||||
| Original Value | 0.010309278 | 0.203921569 | 0.254901961 | 0.51372549 | 0.062992126 |
| Reconstructed Value | 0.0103211 | 0.2039485 | 0.2549708 | 0.5139307 | 0.0627497 |
| Reconstruction Error | 1.1863 × 10−5 | 2.6959 × 10−5 | 6.8798 × 10−5 | 2.0519 × 10−4 | 2.4246 × 10−4 |
| Error Ratio | 1.1507 × 10−3 | 1.322 × 10−4 | 2.699 × 10−4 | 3.9941 × 10−4 | 3.849 × 10−3 |
| Worst Reconstructed Data | |||||
| Original Value | 0.925490196 | 0.996062992 | 0.968627451 | 0.968627451 | 0.994845361 |
| Reconstructed Value | 0.1642768 | 0.1514729 | 0.1238152 | 0.1041814 | 0.0170993 |
| Reconstruction Error | 0.76121 | 0.84459 | 0.84481 | 0.86445 | 0.97775 |
| Error Ratio | 0.8225 | 0.84793 | 0.87217 | 0.89244 | 0.98281 |
| Reconstruction Error ( ± ) = 0.1672 ± 0.0667 | |||||
| Fuzzing Intrusion | |||||
| Best Reconstructed Data | |||||
| Original Value | 0.050980392 | 0.48627451 | 0.007843137 | 0.003921569 | 0.482352941 |
| Reconstructed Value | 0.0510123 | 0.4863441 | 0.0079223 | 0.0038279 | 0.4824857 |
| Reconstruction Error | 3.1953 × 10−5 | 6.9589 × 10−5 | 7.9206 × 10−5 | 9.3645 × 10−5 | 1.328 × 10−4 |
| Error Ratio | 0.00062676 | 0.00014311 | 0.010099 | 0.023879 | 0.00027532 |
| Worst Reconstructed Data | |||||
| Original Value | 0.945098039 | 0.984313725 | 0.992156863 | 0.988235294 | 0.996078431 |
| Reconstructed Value | 0.0688975 | 0.0748087 | 0.0565799 | 0.0374701 | 0.0152394 |
| Reconstruction Error | 0.8762 | 0.90951 | 0.93558 | 0.95077 | 0.98084 |
| Error Ratio | 0.9271 | 0.924 | 0.94297 | 0.96208 | 0.9847 |
| Reconstruction Error ( ± ) = 0.1656 ± 0.0715 | |||||
| Malfunction Intrusion | |||||
| Best Reconstructed Data | |||||
| Original Value | 0.42745098 | 0.321568627 | 0.262745098 | 0.010152284 | 0.403921569 |
| Reconstructed Value | 0.4274471 | 0.3215783 | 0.2628300 | 0.0100435 | 0.4038029 |
| Reconstruction Error | 3.8994 × 10−6 | 9.667 × 10−6 | 8.4951 × 10−5 | 1.0877 × 10−4 | 1.1867 × 10−4 |
| Error Ratio | 9.1224 × 10−6 | 3.0062 × 10−5 | 3.2332 × 10−4 | 1.0713 × 10−2 | 2.9379 × 10−4 |
| Worst Reconstructed Data | |||||
| Original Value | 0.952941176 | 0.980392157 | 0.984313725 | 0.960784314 | 0.97254902 |
| Reconstructed Value | 0.0479626 | 0.0742492 | 0.0692697 | 0.0453411 | 0.0385420 |
| Reconstruction Error | 0.90498 | 0.90614 | 0.91504 | 0.91544 | 0.93401 |
| Error Ratio | 0.94967 | 0.92427 | 0.92963 | 0.95281 | 0.96037 |
| Reconstruction Error ( ± ) = (8.7937 ± 4.3163) × 10−5 | |||||
| Reference | System | Method | Mitigation Strategy | Performance Metrics | |
|---|---|---|---|---|---|
| Percentage Error | Execution Time (s) | ||||
| Hidalgo et al. [21] | IVN—smart intersection | GNN-MLP | Block, deflect intruder to decoy system | - | 0.0466 |
| Sontakke & Chopade [20] | Vehicular ad-hoc network | DNN-BAIT approach | Node isolation | - | - |
| Khanapuri et al. [25] | Vehicle platoon | CNN—Routh-Hurwitz Criterion | Gap widening between vehicles | - | - |
| Shirazi et al. [32] | CAN-bus | LSTM | Data Reconstruction | <6 | - |
| This study | CAN-bus | AM-DDAE | Data Reconstruction | <1 | 0.08577–0.2807 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kousar, A.; Ahmed, S.; Khan, Z.A. A Deep Learning Approach for Real-Time Intrusion Mitigation in Automotive Controller Area Networks. World Electr. Veh. J. 2025, 16, 492. https://doi.org/10.3390/wevj16090492
Kousar A, Ahmed S, Khan ZA. A Deep Learning Approach for Real-Time Intrusion Mitigation in Automotive Controller Area Networks. World Electric Vehicle Journal. 2025; 16(9):492. https://doi.org/10.3390/wevj16090492
Chicago/Turabian StyleKousar, Anila, Saeed Ahmed, and Zafar A. Khan. 2025. "A Deep Learning Approach for Real-Time Intrusion Mitigation in Automotive Controller Area Networks" World Electric Vehicle Journal 16, no. 9: 492. https://doi.org/10.3390/wevj16090492
APA StyleKousar, A., Ahmed, S., & Khan, Z. A. (2025). A Deep Learning Approach for Real-Time Intrusion Mitigation in Automotive Controller Area Networks. World Electric Vehicle Journal, 16(9), 492. https://doi.org/10.3390/wevj16090492








