Trajectory Optimization for Autonomous Highway Driving Using Quintic Splines
Abstract
1. Introduction
1.1. Components of the Path Planning
- Perception and Environment Mapping:
- -
- Sensor Data Acquisition: Collect data from sensors like LiDAR, radar, cameras, and GPS [11].
- -
- -
- Environment Mapping: Create a detailed map of the surroundings, including static and dynamic objects.
- Localization:
- Route Planning:
- -
- Global Path Planning: Determine a high-level route from the current location to the destination, considering road networks and traffic regulations [17].
- -
- Waypoints Generation: Create intermediate waypoints along the global path to guide the vehicle.
- Behavior Planning:
- Path Generation:
- Trajectory Planning:
- -
- Trajectory Optimization: Create a detailed, time-parameterized trajectory that specifies the vehicle’s position, velocity, and acceleration.
- -
- Collision Avoidance: Adjust the trajectory to avoid potential collisions with dynamic and static obstacles [21].
- Speed Profile Generation:
- Control Interface:
1.2. Background and Literature Review
1.2.1. Space Configuration
1.2.2. Path-Finders
1.2.3. Attractive and Repulsive Fields
1.2.4. Curves
1.2.5. Artificial Intelligence Schemes
1.2.6. Research Gap
- -
- High-order Smoothness: Guaranteeing continuity up to the jerk level (C3 continuity) for enhanced comfort and stability, often neglected by methods using lower-order polynomials or discrete path segments.
- -
- Real-time Performance: Maintaining low computational latency suitable for dynamic highway environments.
- -
- Kinematic Feasibility: Directly generating trajectories that respect vehicle dynamic constraints.
- -
- Integrated Decision and Planning: Cohesively linking behavioral decisions (like lane changes) with the generation of smooth, executable trajectories.
- A Novel Integrated Framework: We propose a tightly integrated architecture combining a rule-based Finite State Machine (FSM) for maneuver selection, localized quintic spline generation for C3-continuous path segments, and Model Predictive Control (MPC) for robust tracking. This addresses the integration challenge often present in modular approaches.
- Jerk-Minimized Highway Trajectories: We specifically leverage quintic splines to ensure jerk continuity, directly addressing the need for high passenger comfort and vehicle stability during high-speed highway driving, a limitation in methods offering only curvature continuity or less smooth paths.
- Computationally Efficient Localized Planning: The use of localized spline generation, triggered by the FSM and updated based on real-time sensor data, provides adaptability to dynamic environments while maintaining computational efficiency compared to global optimization or exhaustive search methods.
- Systematic Comparative Evaluation: We provide a quantitative comparison against standard benchmarks (A*, RRT, Bezier Curves) across multiple representative highway scenarios, demonstrating LSPP’s superior performance in terms of smoothness, safety metrics, and execution speed.
- -
- Employing a custom-designed FSM (detailed in Section 2.2.1, Tables 1–3), incorporating nuanced cost functions specifically for optimizing highway driving maneuvers like lane changes and overtaking.
- -
- Leveraging localized quintic spline generation (Section 2.1.2 and Section 2.2.4) triggered by the FSM. This ensures jerk continuity (C3 smoothness), critical for high-speed passenger comfort and vehicle stability, a higher standard than typically achieved with cubic or Bezier alternatives.
- -
- Tightly coupling the spline generator with the MPC tracker (Section 2.2.2) enables high-fidelity execution of these smooth, dynamically adapted trajectories while respecting vehicle kinematic limits (Equation (2)). This purpose-built integration results in a motion planner that effectively balances high-order smoothness, real-time responsiveness, and computational efficiency specifically for structured highway environments, addressing the trade-offs often found in existing approaches.
2. Methods
2.1. Foundation of Motion Planning
2.1.1. Path Planning Architecture
2.1.2. Key Characteristics of Quintic Polynomials
- Piecewise Definition: A spline is defined by multiple polynomial segments, each valid over a specific interval. For example, a quintic spline is composed of 5th-order polynomials defined piecewise between each pair of waypoints :
- The choice of quintic (5th order) polynomials is specifically motivated by the need to define a trajectory segment by specifying not only position and velocity but also acceleration at both the start and end points. This requires six boundary conditions per spatial dimension (e.g., x(0), ẋ(0), ẍ(0), x(T), ẋ(T), ẍ(T)), which perfectly matches the six coefficients available in a quintic polynomial (Equation (1)). This capability is essential for generating dynamically smooth and feasible paths for vehicles.
- Continuity and Smoothness: Splines are constructed to ensure a certain level of smoothness at the points where the polynomial pieces join (called knots). For quintic splines, the first, second, third, and fifth derivatives are usually continuous across the intervals, making the transition between segments very smooth.
- Local Control: Each segment of the spline is influenced mainly by its local data points (waypoints received from the RBLPP), allowing for localized changes in the shape of the curve without significantly affecting the entire curve.
- Boundary Conditions: When constructing splines, additional conditions are needed at the endpoints to uniquely determine the spline. Common boundary conditions include specifying the values of derivatives up to the 4th order at the endpoints, and higher order derivatives are set to zero.
2.1.3. The Proposed Motion Planner
- Interpolate waypoints for a nearby section (30 to 50 m long) of the route provided by the MPM.
- Determine the state of the egocar, including its position, orientation, velocity, and acceleration.
- Generate a set of predicted trajectories for each surrounding vehicle using data received from the ODM.
- Identify the available states for the egocar, such as “keep lane,” “change lanes to the right,” or “change lanes to the left.”
- For each available state, generate a target end state for the egocar and create multiple randomized potential trajectories by slightly perturbing elements of the target state. These “Jerk-Minimized Trajectories” (JMTs) [33] are quintic spline polynomials derived from the current initial and desired final values of position, velocity, and acceleration [34].
- Evaluate each potential trajectory using a set of cost functions that reward efficiency and penalize factors such as collisions, excessive jerks, or exceeding speed limits.
- Select the trajectory with the lowest cost.
- Assess this trajectory at the next several 20-millisecond intervals (the rate at which the data is received from the sensor fusion module) [35].
- Append these evaluations to the retained portion of the previous path.
- Send the updated path to the MPC controller for execution.
- Input Parameters:
- -
- Start: A vector of three elements [position, velocity, acceleration] representing the initial state of the vehicle.
- -
- End: A vector of three elements [position, velocity, acceleration] representing the final state of the vehicle.
- -
- T: The time duration over which the vehicle should move from the start state to the end state.
- Output:
- -
- A vector of coefficients for a 5th-degree polynomial of the form: .
- -
- These coefficients are determined to minimize jerk over the time T.
- Calculation:
- -
- A system of equations is set up using the boundary conditions provided by the start and end states.
2.2. Implementation of the LSPP
2.2.1. The Finite State Machine
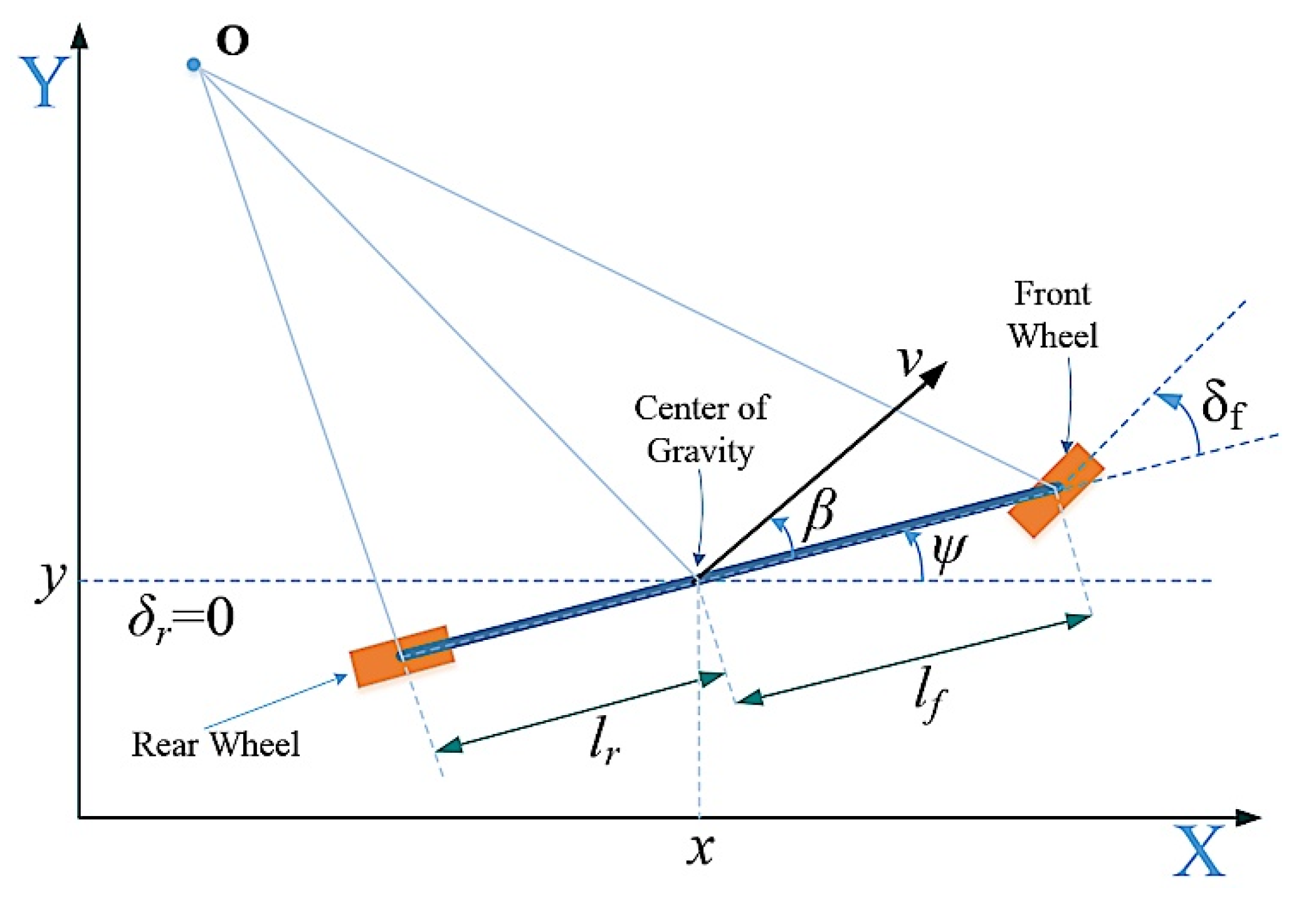
2.2.2. The Vehicle Kinematic Model
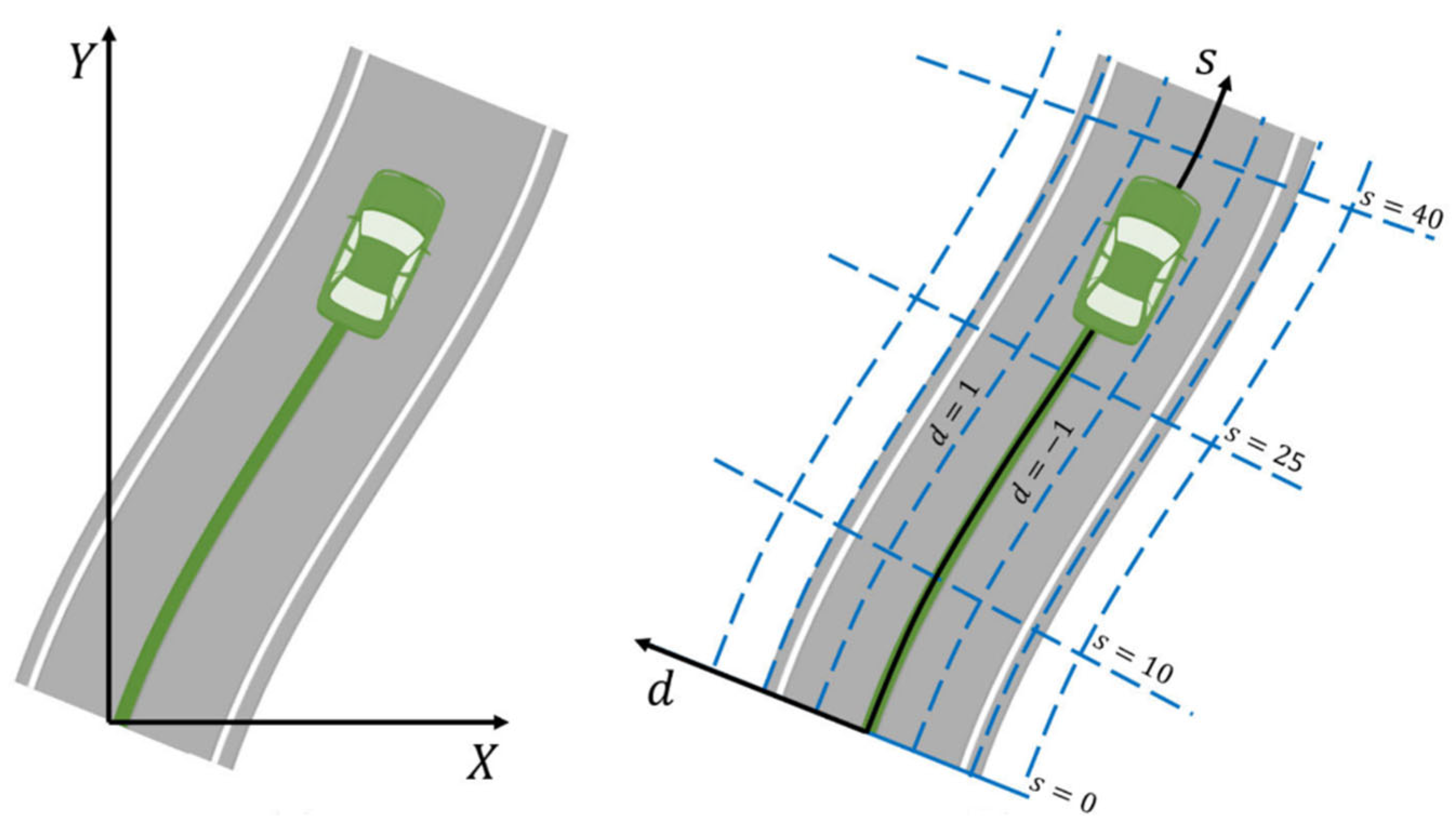
2.2.3. Frenet Coordinates for Autonomous Vehicle Motion Planning
- -
- Longitudinal Coordinate (s): The arc length along the reference path from a fixed starting point to the projection of the vehicle’s position onto the path. It represents the vehicle’s progress along the path.
- -
- Lateral Coordinate (d): The perpendicular distance from the reference path to the vehicle’s position, representing the deviation of the vehicle from the path [39].
- -
- Identify the reference point on the path: Find the point on the reference path at arc length s from the starting point, which serves as the baseline for the lateral offset.
- -
- Determine the tangent and normal vectors: calculate the tangent vector at (xref, yref) on the reference path. This can be derived from the path’s derivative or direction at s.
- -
- Apply the Lateral Offset: Move d units along the normal vector to obtain (x, y) in Cartesian coordinates:
- -
- Project the Point onto the Path: Identify the nearest point on the reference path (xref, yref) to (x, y), then calculate the arc length s along the path from the starting point to this nearest point using the following equation:
- -
- Calculate the Lateral Distance d: Compute the perpendicular distance from (x, y) to the nearest point on the path (xref, yref), giving the lateral offset d as in Equation (5). Positive or negative values of d indicate the side of the path relative to the driving direction:
2.2.4. Implementation of the Quintic Polynomial Trajectory
- -
- At (start at ):
- ○
- (Initial position)
- ○
- (Initial velocity)
- ○
- (Initial acceleration)
- -
- At (end at ):
- ○
- (Final position)
- ○
- (Final velocity)
- ○
- (Final acceleration)
- -
- : Initial state (position, heading, speed, acceleration).
- -
- : Final state (position, heading, speed, acceleration).
- -
- 2 equations for Position:
- -
- 2 equations for Velocity:
- -
- 2 equations for Acceleration:
- -
- Velocity Limit: Ensure the trajectory’s speed never exceeds the vehicle’s maximum speed . Constraint: .
- -
- Acceleration Limit: The acceleration should not exceed a threshold to ensure safety and comfort. Constraint: .
- -
- Steering Angle and Angular Velocity Limits: The trajectory must respect the maximum steering angle and the rate of change of the angle (angular velocity). Constraints: and
- -
- The curvature κ(t) along the spline influences the required steering angle. If the curvature is too high, it may exceed the vehicle’s steering capability. The curvature is calculated as:
- -
- Enforce Smooth Transitions with Jerk Constraints: The jerk (third derivative of position) calculated by Equation (7) must be limited to avoid sudden changes in acceleration, which can lead to discomfort and instability. High jerk values can also stress the actuators.
2.2.5. Putting All Together
| Algorithm 1: The LSPP Algorithm |
| Algorithm LSPP (StartState, GoalState, RoadConstraints, Obstacles, Δt, Horizon) Input: StartState // Initial position, velocity, acceleration of the egocar GoalState // Desired end position, velocity, acceleration RoadConstraints // Lane boundaries, speed limits, and kinematic limits (e.g., max steering, acceleration) Obstacles // Position and velocity of dynamic/static obstacles detected by sensor fusion Δt // Time step for trajectory update Horizon // Prediction horizon for the trajectory Output: SafePath // Smooth, collision-free trajectory to follow within the defined horizon Begin 1. Initialize Path: - Set CurrentState = StartState - Initialize SafePath as an empty list 2. Find GoalState: - Evaluate the current state of the FSM (e.g., KL, LCL, LCR) - Set GoalState = FSM State 3. Path Generation using Quintic Spline: - Calculate QuinticSpline (StartState, GoalState) based on boundary conditions: - Position, velocity, and acceleration at StartState and GoalState - Respect continuity up to the third derivative (jerk) - Store the generated spline in SafePath 4. Check Collision Avoidance and Kinematic Feasibility: - For each point P in SafePath: - If P violates any RoadConstraints (e.g., lane boundaries, speed limits, steering angles): - Mark P as unfeasible - For each obstacle O in Obstacles: - Calculate the distance d between P and O - If d < SafeBufferDistance: - Mark P as a potential collision point - Proceed to AdjustPath 5. AdjustPath for Collision Avoidance (if any potential collision points are detected): - For each marked collision point P in SafePath: - Calculate a new GoalState that adjusts the spline to avoid the obstacle (e.g., by shifting lateral distance or adjusting speed) - Generate a LocalizedSpline from CurrentState to new GoalState - Replace the segment of SafePath around P with the new LocalizedSpline segment 6. Path Smoothing and Final Check: - Ensure smoothness of SafePath by recalculating segment continuity at adjustment points - If necessary, apply a smoothing function to mitigate abrupt changes near adjusted points 7. Real-time Tracking and Execution: - Send SafePath to Model Predictive Control (MPC) for real-time tracking - Monitor vehicle state every Δt: - If a significant deviation from SafePath occurs due to dynamic changes: - Update StartState = CurrentState - Repeat from Step 2 (re-generate path based on new conditions) End Algorithm |
3. Results and Discussion
3.1. Simulation and Testing Results
3.1.1. Setting of Simulation Parameters
Vehicle Dynamics Parameters:
- -
- Vehicle Speed Limits:
- ○
- Maximum Speed: 120 km/h (33.3 m/s)
- ○
- Minimum Speed: 0 km/h (stationary), as needed for stop-and-go scenarios
- -
- Acceleration and Deceleration:
- ○
- Maximum Acceleration: 3 m/s2 to allow for efficient speed changes while maintaining passenger comfort.
- ○
- Maximum Deceleration: −5 m/s2 to ensure rapid stopping capability for emergency scenarios.
- -
- Steering Constraints:
- ○
- Maximum Steering Angle: ±25°, to limit lateral deviation within safe bounds during sharp turns.
- ○
- Maximum Steering Rate (Angular Velocity): 60°/s, enabling smooth steering transitions without abrupt turns.
- -
- Jerk Constraints:
- ○
- Maximum Jerk: 2 m/s3 to limit sudden changes in acceleration and ensure smooth trajectory transitions.
Path and Control Parameters
- -
- Lane Width: 3.5 m, consistent with standard highway lane width.
- -
- Path Planning Horizon:
- ○
- Prediction Horizon (T): 5 s (167 m for 120 km/h speed), allowing the vehicle to anticipate and respond to upcoming obstacles or turns.
- ○
- Control Time Step (Δt): 0.1 s, providing precise control updates at each step.
- -
- Curvature Constraints:
- ○
- Minimum Turning Radius: 10 m, simulating tight urban turns and curved highway segments.
Traffic and Environmental Parameters
- -
- Traffic Density:
- ○
- Sparse (Scenario 2): Limited vehicles, allowing free lane changes.
- ○
- Moderate (Scenario 1): Vehicles moving at similar speeds, with space for controlled lane changes.
- ○
- Congested (Scenario 5): High-density stop-and-go traffic to test low-speed handling and obstacle avoidance.
- -
- Obstacle Characteristics:
- ○
- Obstacle Appearance Distance: 30 m ahead, to assess emergency stopping and avoidance capabilities.
- ○
- Reaction Time for Emergency Scenarios: 1.5 s, a typical benchmark for real-time reaction in autonomous driving.
Control Algorithm-Specific Parameters for LSPP
- -
- Cost Function Weights (LSPP-specific parameters):
- ○
- Position Error Weight: 1.0, prioritizing precise path-following.
- ○
- Heading Error Weight: 0.8, to align vehicle orientation with the desired trajectory.
- ○
- Control Effort Weight: 0.5, minimizing control input variations to improve smoothness.
- -
- Trajectory Constraints:
- ○
- Lateral Deviation Limit: ±0.3 m from the centerline, allowing for safe lane positioning without abrupt lateral moves.
- -
- Safety Buffer:
- ○
- Collision Avoidance Buffer: 5 m, maintaining safe spacing to allow evasive actions if necessary.
3.1.2. Simulation Scenarios and Results
- Bezier Curve-based Planning: This method uses Bezier curves to generate smooth paths based on control points, providing smooth trajectory transitions ideal for lane changes and path following, though it lacks flexibility in complex obstacle-filled environments [47].
Scenario 1: Straight Highway with Moderate Traffic
- -
- Objective: Evaluate path-following accuracy and speed maintenance.
- -
- Metrics:
- ○
- Trajectory Smoothness (Avg. Jerk), Speed Deviation, Execution Time per cycle.
- -
- Results:
- ○
- LSPP: Avg. Jerk = 0.2 m/s3, Speed Deviation = ±2 km/h, Execution Time = 12 ms
- ○
- A* Algorithm: Avg. Jerk = 0.5 m/s3, Speed Deviation = ±6 km/h, Execution Time = 55 ms
- ○
- RRT: Jerk = 0.6 m/s3, Speed Deviation = ±4 km/h, Execution Time = 40 ms
- ○
- Bezier Curve: Jerk = 0.3 m/s3, Speed Deviation = ±3 km/h, Execution Time = 20 ms
- -
- Conclusion: LSPP demonstrates the lowest jerk and speed deviation while maintaining a short execution time, making it suitable for real-time path following.
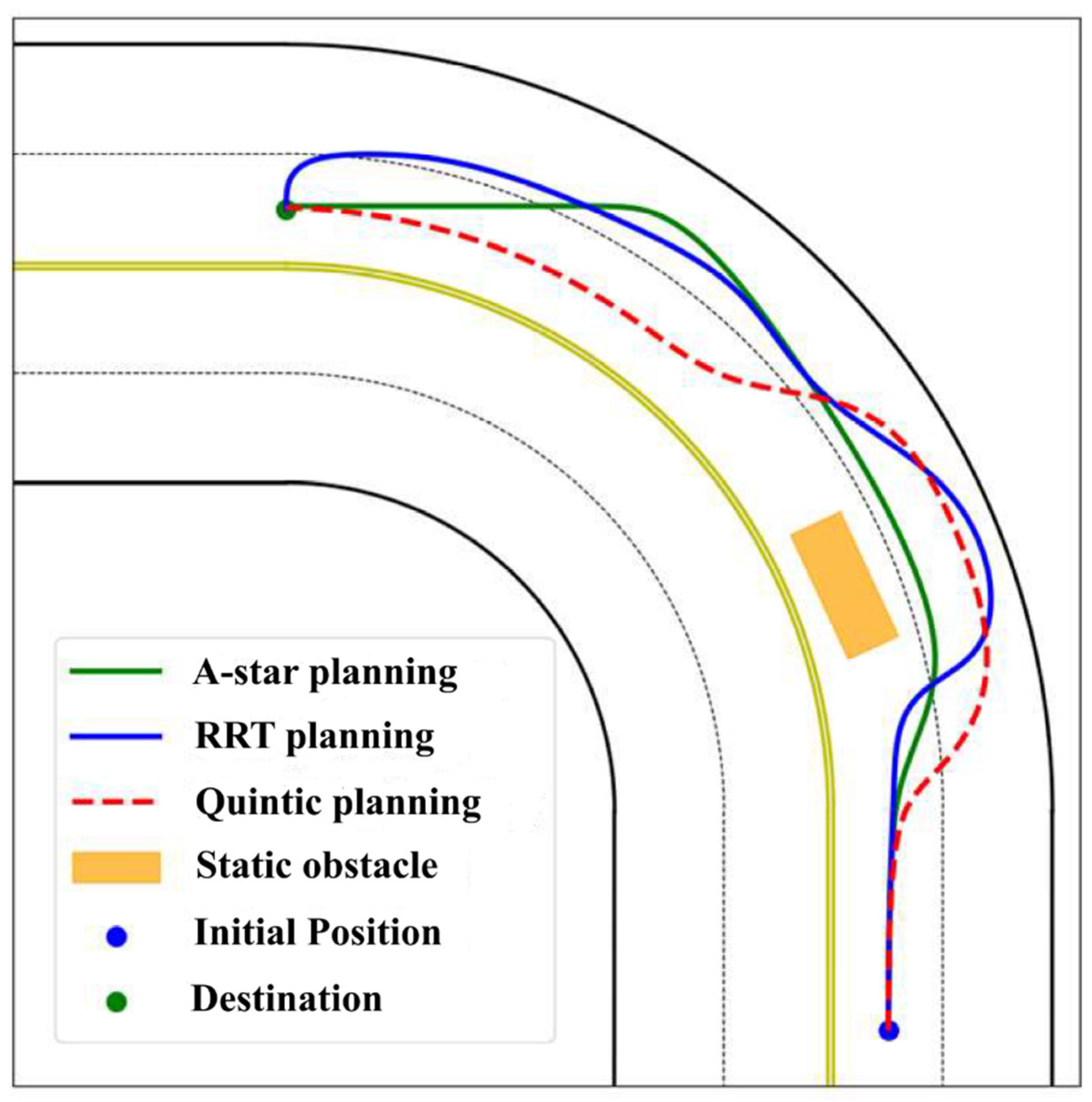
Scenario 2: Curved Highway with Lane Changes
- -
- Objective: Test lane-changing capability on curves.
- -
- Metrics:
- ○
- Lane Change Success Rate, Trajectory Smoothness (Avg. Jerk), Lateral Deviation, Execution Time.
- -
- Results:
- ○
- LSPP: Lane Change Success = 100%, Jerk = 0.3 m/s3, Max Lateral Deviation = 0.1 m, Execution Time = 15 ms
- ○
- A* Algorithm: Lane Change Success = 85%, Jerk = 0.7 m/s3, Max Lateral Deviation = 0.5 m, Execution Time = 60 ms
- ○
- RRT: Lane Change Success = 80%, Jerk = 0.8 m/s3, Max Lateral Deviation = 0.4 m, Execution Time = 50 ms
- ○
- Bezier Curve: Lane Change Success = 95%, Jerk = 0.4 m/s3, Max Lateral Deviation = 0.2 m, Execution Time = 25 ms
- -
- Conclusion: LSPP maintains optimal lane change success and lateral deviation with a shorter execution time, proving it efficient for real-time lane changes on curves (Figure 6).
Scenario 3: Emergency Stop and Obstacle Avoidance
- -
- Objective: Assess response to sudden obstacles.
- -
- Metrics:
- ○
- Collision Avoidance Rate, Stopping Distance, Trajectory Smoothness (Avg. Jerk), Execution Time.
- -
- Results:
- ○
- LSPP: Collision Avoidance = 100%, Stopping Distance = 5 m, Jerk = 0.4 m/s3, Execution Time = 10 ms
- ○
- A* Algorithm: Collision Avoidance = 70%, Stopping Distance = 2 m, Jerk = 0.9 m/s3, Execution Time = 70 ms
- ○
- RRT: Collision Avoidance = 80%, Stopping Distance = 3 m, Jerk = 0.7 m/s3, Execution Time = 55 ms
- ○
- Bezier Curve: Collision Avoidance = 90%, Stopping Distance = 4 m, Jerk = 0.5 m/s3, Execution Time = 30 ms
- -
- Conclusion: LSPP achieves a perfect collision avoidance rate with rapid execution time, demonstrating its effectiveness in emergency response scenarios.
Scenario 4: High-Speed Curved Highway with Lane-Keeping
- -
- Objective: Evaluate lane-keeping performance at high speeds.
- -
- Metrics:
- ○
- Lane Keeping Success Rate, Lateral Deviation, Trajectory Smoothness (Avg. Jerk), Execution Time.
- -
- Results:
- ○
- LSPP: Lane Keeping Success = 98%, Lateral Deviation = 0.15 m, Jerk = 0.3 m/s3, Execution Time = 15 ms
- ○
- A* Algorithm: Lane Keeping Success = 70%, Lateral Deviation = 0.5 m, Jerk = 0.7 m/s3, Execution Time = 65 ms
- ○
- RRT: Lane Keeping Success = 75%, Lateral Deviation = 0.4 m, Jerk = 0.6 m/s3, Execution Time = 52 ms
- ○
- Bezier Curve: Lane Keeping Success = 90%, Lateral Deviation = 0.3 m, Jerk = 0.4 m/s3, Execution Time = 27 ms
- -
- Conclusion: LSPP excels in lane-keeping at high speeds with minimal lateral deviation and low execution time, supporting its suitability for high-speed applications.
Scenario 5: Stop-And-Go Traffic in Congested Conditions
- -
- Objective: Assess performance in stop-and-go traffic.
- -
- Metrics:
- ○
- Comfort (Avg. Jerk) during acceleration and deceleration, Traffic Flow Efficiency, Execution Time.
- -
- Results:
- ○
- LSPP: Jerk = 0.3 m/s3, Traffic Flow Efficiency = 95%, Execution Time = 12 ms
- ○
- A* Algorithm: Jerk = 0.6 m/s3, Traffic Flow Efficiency = 80%, Execution Time = 60 ms
- ○
- RRT: Jerk = 0.5 m/s3, Traffic Flow Efficiency = 85%, Execution Time = 50 ms
- ○
- Bezier Curve: Jerk = 0.4 m/s3, Traffic Flow Efficiency = 90%, Execution Time = 22 ms
- -
- Conclusion: LSPP achieves smooth accelerations and decelerations with high traffic flow efficiency, completing computations rapidly enough for real-time stop-and-go driving.
Summary of the Simulation Results
- -
- Trajectory Smoothness (Avg. Jerk): Average jerk, measuring smoothness in acceleration and deceleration.
- -
- Speed Deviation: Difference from target speed in km/h.
- -
- Execution Time: Time taken per planning cycle (in milliseconds).
- -
- Lane Change Success Rate: Percentage of successful lane changes without collision.
- -
- Lane Keeping Success Rate: Measure the vehicle’s ability to maintain its position within a designated lane.
- -
- Max Lateral Deviation: Maximum deviation from the lane center.
- -
- Collision Avoidance Rate: Percentage of trials where collisions were avoided.
- -
- Stopping Distance: Distance from the obstacle when the vehicle halts.
- -
- Comfort (Avg. Jerk): Average jerk in stop-and-go traffic, indicative of passenger comfort.
- -
- Traffic Flow Efficiency: Percentage of traffic flow maintained without unnecessary delays.
3.2. Parameter Sensitivity Insights
3.3. Discussion
3.3.1. Execution Time
3.3.2. Collision Avoidance
3.3.3. Speed Deviation
3.3.4. Impact of Spline Order on Vehicle Dynamics, Material Wear, and Energy Efficiency
| Feature | 3rd-Order (Cubic) Spline | 5th-Order (Quintic) Spline | Sources |
|---|---|---|---|
| Continuity | C2 (Position, Velocity, Acceleration) | C3 (Adds Jerk Continuity) | [33,53] |
| Jerk Handling | Discontinuous (‘infinite jerk’ spikes) | Smooth, bounded jerk | [33,53] |
| Passenger Comfort | Moderate | High | [54,55] |
| Vibration and Mechanical Stress | High; contributes to material fatigue | Low; extends component lifespan by ~55% | [56,57] |
| Computation Load | Low | Higher (~15–30% more execution time) | [55] |
| Energy Consumption (Avg) | Slightly lower in short durations | 3–6% higher total but with 18–27% peak load savings | [58] |
| Tire Wear | Higher, uneven load distribution | Reduced by 19.19–65.20% | [59] |
| Brake Usage | Frequent due to aggressive deceleration | Reduced braking events by up to 99% | [54,64] |
| Material Impact | Increases stress on suspension, drivetrain, and tires | Reduces fatigue and wear; fewer replacements | [60,65] |
| Suitability for High-Speed | Limited due to instability under rapid transitions | Excellent due to curvature and jerk control | [18,60,66] |
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| APF | Artificial Potential Field |
| FSM | Finite State Machine |
| JMT | Jerk Minimizing Trajectory |
| ODM | Object Detection Module |
| LSPP | Localized Spline-based Path-Planning |
| MPC | Model Predictive Control |
| MPM | Mission Planner Module |
| RBLPP | Rule-Based Localized Path Planner |
| RRT | Rapidly exploring Random Tree |
| TTCs | Triggering Transitional Conditions |
References
- Alqahtani, T. Recent Trends in the Public Acceptance of Autonomous Vehicles: A Review. Vehicles 2025, 7, 45. [Google Scholar] [CrossRef]
- Teng, S.; Hu, X.; Deng, P.; Li, B.; Li, Y.; Yang, D.; Ai, Y.; Li, L.; Zhe, X.; Zhu, F.; et al. Motion Planning for Autonomous Driving: The State of the Art and Future Perspectives. IEEE Trans. Intell. Veh. 2023, 8, 3692–3711. [Google Scholar] [CrossRef]
- Farag, W. A Comprehensive Real-Time Road-Lanes Tracking Technique for Autonomous Driving. Int. J. Comput. Digit. Syst. 2020, 9, 349–362. [Google Scholar] [CrossRef] [PubMed]
- Claussmann, L.; Revilloud, M.; Gruyer, D.; Glaser, S. A Review of Motion Planning for Highway Autonomous Driving. IEEE Trans. Intell. Transp. Syst. 2020, 21, 1826–1848. [Google Scholar] [CrossRef]
- Pavitha, P.P.; Rekha, K.B.; Safinaz, S. Perception system in Autonomous Vehicle: A study on contemporary and forthcoming technologies for object detection in autonomous vehicles. In Proceedings of the 2021 International Conference on Forensics, Analytics, Big Data, Security (FABS), Bengaluru, India, 21–22 December 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Hu, J.; Wang, Y.; Cheng, S.; Xu, J.; Wang, N.; Fu, B.; Ning, Z.; Li, J.; Chen, H.; Feng, C.; et al. A Survey of Decision-making and Planning Methods for Self-driving Vehicles. Front. Neurorobotics 2025, 19, 1451923. [Google Scholar] [CrossRef] [PubMed]
- Sara, A.; Ikaouassen, H.; Kribèche, A.; Chaibet, A.; Aglzim, H. Advancing Autonomous Vehicle Control Systems: An In-depth Overview of Decision-making and Manoeuvre Execution State of the Art. J. Eng. 2023, 2023, e12333. [Google Scholar] [CrossRef]
- Patel, K.B.; Lin, H.C.; Berger, A.D.; Farag, W.; Khan, A.A. EDC Draft Force Based Ride Controller. U.S. Patent 6,196,327, 6 March 2001. [Google Scholar]
- Shao, K.; Zheng, J.; Huang, K. Robust active steering control for vehicle rollover prevention. Int. J. Model. Identif. Control 2019, 32, 70–84. [Google Scholar] [CrossRef]
- Alejandro, I.; Cervantes, I.; Francisco, J. Local Path Planning for Autonomous Vehicles Based on the Natural Behavior of the Biological Action-Perception Motion. Energies 2022, 15, 1769. [Google Scholar] [CrossRef]
- Chen, Y.; Ji, C.; Cai, Y.; Yan, T.; Su, B. Deep Reinforcement Learning in Autonomous Car Path Planning and Control: A Survey. arXiv 2024, arXiv:2404.00340. [Google Scholar] [CrossRef]
- Farag, W. Safe-driving cloning by deep learning for autonomous cars. Int. J. Adv. Mechatron. Syst. 2019, 7, 390–397. [Google Scholar] [CrossRef]
- Bacha, A.M.; Zamoum, R.B.; Lachekhab, F. Machine Learning Paradigms for UAV Path Planning: Review and Challenges. J. Robot. Control (JRC) 2025, 6, 215–233. [Google Scholar] [CrossRef]
- Koopman, P.; Wagner, M. Autonomous Vehicle Safety: An Interdisciplinary Challenge. IEEE Intell. Transp. Syst. Mag. 2017, 9, 90–96. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, K.; Gao, F.; Zhao, F. Research on Path Planning and Path Tracking Control of Autonomous Vehicles Based on Improved APF and SMC. Sensors 2025, 23, 7918. [Google Scholar] [CrossRef]
- Tjiharjadi, J.S.; Razali, S.; Sulaiman, H.A. A Systematic Literature Review of Multi-agent Pathfinding for Maze Research. J. Adv. Inf. Technol. 2022, 13, 358–367. [Google Scholar] [CrossRef]
- Farag, W. Real-Time Autonomous Vehicle Localization Based on Particle and Unscented Kalman Filters. J. Control Autom. Electr. Syst. 2021, 32, 309–325. [Google Scholar] [CrossRef]
- Reda, M.; Onsy, A.; Haikal, A.Y.; Ghanbari, A. Path Planning Algorithms in the Autonomous Driving System: A Comprehensive Review. Robot. Auton. Syst. 2024, 174, 104630. [Google Scholar] [CrossRef]
- Farag, W. Complex track maneuvering using real-time MPC control for autonomous driving. Int. J. Comput. Digit. Syst. 2020, 90, 909–920. [Google Scholar] [CrossRef]
- José, R.; Carlos, J. Path Planning for Autonomous Mobile Robots: A Review. Sensors 2020, 21, 7898. [Google Scholar] [CrossRef]
- Xu, W.; Wang, Q.; Dolan, J.M. Autonomous Vehicle Motion Planning via Recurrent Spline Optimization. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 7730–7736. [Google Scholar] [CrossRef]
- Farag, W. Complex-Track Following in Real-Time Using Model-Based Predictive Control. Int. J. Intell. Transp. Syst. Res. 2021, 19, 112–127. [Google Scholar] [CrossRef]
- Farag, W. Real-time NMPC path tracker for autonomous vehicles. Asian J. Control 2021, 23, 1952–1965. [Google Scholar] [CrossRef]
- Wen, J.; Zhang, X.; Bi, Q.; Liu, H.; Yuan, J.; Fang, Y. G2VD Planner: Efficient Motion Planning with Grid-based Generalized Voronoi Diagrams. IEEE Trans. Autom. Sci. Eng. 2024, 22, 3743–3755. [Google Scholar] [CrossRef]
- Tan, C.S.; Mohd-Mokhtar, R.; Arshad, M.R. A Comprehensive Review of Coverage Path Planning in Robotics Using Classical and Heuristic Algorithms. IEEE Access 2021, 9, 119310–119342. [Google Scholar] [CrossRef]
- Qin, P.; Liu, F.; Guo, Z.; Li, Z.; Shang, Y. Hierarchical Collision-free Trajectory Planning for Autonomous Vehicles Based on Improved Artificial Potential Field Method. Trans. Inst. Meas. Control 2023. [Google Scholar] [CrossRef]
- Siddiqi, M.R.; Milani, S.; Jazar, R.N.; Marzbani, H. Ergonomic Path Planning for Autonomous Vehicles—An Investigation on the Effect of Transition Curves on Motion Sickness. IEEE Trans. Intell. Transp. Syst. 2022, 23, 7258–7269. [Google Scholar] [CrossRef]
- Qian, X.; Navarro, I.; de La Fortelle, A.; Moutarde, F. Motion planning for urban autonomous driving using Bézier curves and MPC. In Proceedings of the 2016 IEEE 19th International Conference on Intelligent Transportation Systems (ITSC), Rio de Janeiro, Brazil, 1–4 November 2016; pp. 826–833. [Google Scholar] [CrossRef]
- Farag, W.A.; Quintana, V.H.; Lambert-Torres, G. Genetic algorithms and back-propagation: A comparative study. In Proceedings of the IEEE Canadian Conference on Electrical and Computer Engineering (Cat. No.98TH8341), Waterloo, ON, Canada, 25–28 May 1998; Volume 1, pp. 93–96. [Google Scholar] [CrossRef]
- Rucco, A.; Sujit, P.B.; Aguiar, A.P.; de Sousa, J.B.; Pereira, F.L. Optimal Rendezvous Trajectory for Unmanned Aerial-Ground Vehicles. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 834–847. [Google Scholar] [CrossRef]
- Lin, P.; Javanmardi, E.; Tsukada, M. Clothoid Curve-based Emergency-Stopping Path Planning with Adaptive Potential Field for Autonomous Vehicles. IEEE Trans. Veh. Technol. 2024, 73, 9747–9762. [Google Scholar] [CrossRef]
- Kong, J.; Pfeiffer, M.; Schildbach, G.; Borrelli, F. Kinematic and Dynamic Vehicle Models for Autonomous Driving. In Proceedings of the IEEE Intelligent Vehicles Symposium (IV), Seoul, Republic of Korea, 28 June–1 July 2015. [Google Scholar]
- Sharkawy, A.-N. Chapter 5: Minimum Jerk Trajectory Generation for Straight and Curved Movements: Mathematical Analysis. In Advances in Robotics: Reviews, Book Series; IFSA Publishing, S.L.: Barcelona, Spain, 2021; Volume 2, pp. 187–201. ISBN 978-84-09-25863-5. [Google Scholar]
- Dalle, J.; Hastuti, D.; Prasetya, M.R.A. The Use of an Application Running on the Ant Colony Algorithm in Determining the Nearest Path between Two Points. J. Adv. Inf. Technol. 2021, 12, 206–213. [Google Scholar] [CrossRef]
- Farag, W.; Nadeem, M. Enhanced real-time road-vehicles’ detection and tracking for driving assistance. Int. J. Knowl.-Based Intell. Eng. Syst. 2024, 28, 335–357. [Google Scholar] [CrossRef]
- Eigen. Available online: https://eigen.tuxfamily.org/index.php?title=Main_Page (accessed on 31 October 2024).
- Wang, X.; Qi, X.; Wang, P.; Yang, J. Decision making framework for autonomous vehicles driving behavior in complex scenarios via hierarchical state machine. Auton. Intell. Syst. 2021, 1, 10. [Google Scholar] [CrossRef]
- Werling, M.; Ziegler, J.; Kammel, S.; Thrun, S. Optimal trajectory generation for dynamic street scenarios in a Frenet Frame. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Anchorage, AK, USA, 3–8 May 2010. [Google Scholar]
- Ziegler, J.; Bender, P.; Schreiber, M.; Lategahn, H.; Strauss, T.; Stiller, C.; Dang, T.; Franke, U.; Appenrodt, N.; Keller, C.G.; et al. Making Bertha Drive—An Autonomous Journey on a Historic Route. IEEE Intell. Transp. Syst. Mag. 2014, 6, 8–20. [Google Scholar] [CrossRef]
- Kim, D.; Kim, G.; Kim, H.; Huh, K. A Hierarchical Motion Planning Framework for Autonomous Driving in Structured Highway Environments. IEEE Access 2022, 10, 20102–20117. [Google Scholar] [CrossRef]
- Paden, B.; Čáp, M.; Yong, S.Z.; Yershov, D.; Frazzoli, E. A Survey of Motion Planning and Control Techniques for Self-Driving Urban Vehicles. IEEE Trans. Intell. Veh. 2016, 1, 33–55. [Google Scholar] [CrossRef]
- González, D.; Pérez, J.; Milanés, V.; Nashashibi, F. A Review of Motion Planning Techniques for Automated Vehicles. IEEE Trans. Intell. Transp. Syst. 2016, 17, 1135–1145. [Google Scholar] [CrossRef]
- Wang, H.; Lou, S.; Jing, J.; Wang, Y.; Liu, W.; Liu, T. The EBS-A* Algorithm: An Improved A* Algorithm for Path Planning. PLoS ONE 2022, 17, e0263841. [Google Scholar] [CrossRef]
- Chang, T.; Tian, G. Hybrid A-Star Path Planning Method Based on Hierarchical Clustering and Trichotomy. Appl. Sci. 2023, 14, 5582. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, X.; Li, J.; Yang, Z.; Cao, L. Improved RRT* Algorithm for Disinfecting Robot Path Planning. Sensors 2023, 24, 1520. [Google Scholar] [CrossRef]
- Fan, Y.; Fang, X.; Gao, F.; Zhou, X.; Li, H.; Jin, H.; Song, Y. Obstacle Avoidance Path Planning for UAV Based on Improved RRT Algorithm. Discret. Dyn. Nat. Soc. 2021, 2022, 4544499. [Google Scholar] [CrossRef]
- Ling, Z.; Zeng, P.; Yang, W.; Li, Y.; Zhan, Z. BéZier Curve-based Trajectory Planning for Autonomous Vehicles with Collision Avoidance. IET Intell. Transp. Syst. 2020, 14, 1882–1891. [Google Scholar] [CrossRef]
- Dong, N.; Chen, S.; Wu, Y.; Feng, Y.; Liu, X. An enhanced motion planning approach by integrating driving heterogeneity and long-term trajectory prediction for automated driving systems: A highway merging case study. Transp. Res. Part C Emerg. Technol. 2024, 161, 104554. [Google Scholar] [CrossRef]
- Francis, S.L.; Anavatti, S.G.; Garratt, M. Real-time path planning module for autonomous vehicles in cluttered environment using a 3D camera. Int. J. Veh. Auton. Syst. 2018, 14, 40–61. [Google Scholar] [CrossRef]
- Farag, W.A.; Quintana, V.H.; Lambert-Torres, G. Neuro-fuzzy modeling of complex systems using genetic algorithms, In Proceedings of the International Conference on Neural Networks (ICNN’97). Houston, TX, USA, 9–12 June 1997; 1, pp. 444–449. [Google Scholar] [CrossRef]
- Xidias, E.; Ilias, K.; Panagiotopoulos, E.; Zacharia, P.T. An Intelligent Management System for Relocating Semi-Autonomous Shared Vehicles. Transp. Plan. Technol. 2023, 46, 93–118. [Google Scholar] [CrossRef]
- Xidias, E.; Zacharia, P.; Nearchou, A. Intelligent fleet management of autonomous vehicles for city logistics. Appl. Intell. 2022, 52, 18030–18048. [Google Scholar] [CrossRef]
- Piazzi, A.; Guarino Lo Bianco, C. Quintic G/sup 2/-splines for trajectory planning of autonomous vehicles. In Proceedings of the IEEE Intelligent Vehicles Symposium 2000 (Cat. No.00TH8511), Dearborn, MI, USA, 5 October 2000; pp. 198–203. [Google Scholar] [CrossRef]
- Lutanto, A.; Fajri, A.; Nugroho, K.C.; Falah, F. Advancements in Automotive Braking Technology for Enhanced Safety: A Review. Multidiscip. Innov. Res. Appl. Eng. 2024, 1. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, L.; Li, N. Improved Quintic Polynomial Autonomous Vehicle Lane-Change Trajectory Planning Based on Hybrid Algorithm Optimization. World Electr. Veh. J. 2025, 16, 244. [Google Scholar] [CrossRef]
- Sustainability Directory. Automotive Materials Durability. Energy Sustainability Directory. Available online: https://energy.sustainability-directory.com/term/automotive-materials-durability/ (accessed on 5 July 2025).
- Radial Tire Company. How Driving on Rough Roads Impacts Your Suspension and What You Can Do. Available online: https://www.radialtirecompany.com/About/News-Center/ArticleID/11166 (accessed on 5 July 2025).
- Szumska, E.M. Regenerative Braking Systems in Electric Vehicles: A Comprehensive Review of Design, Control Strategies, and Efficiency Challenges. Energies 2024, 18, 2422. [Google Scholar] [CrossRef]
- Hu, T.; Xu, X.; Nguyen, T.; Liu, F.; Yuan, S.; Xie, L. Tire Wear Aware Trajectory Tracking Control for Multi-axle Swerve-drive Autonomous Mobile Robots. arXiv 2025, arXiv:2506.04752. [Google Scholar] [CrossRef]
- Fiveable. 5.2 Trajectory Generation—Autonomous Vehicle Systems. Edited by Becky Bahr, Fiveable. 2024. Available online: https://library.fiveable.me/autonomous-vehicle-systems/unit-5/trajectory-generation/study-guide/UwMywl8JvwYSAmcF (accessed on 12 July 2025).
- Škugor, B.; Jure, S.; Joško, D. Analysis of Optimal Battery State-of-Charge Trajectory for Blended Regime of Plug-in Hybrid Electric Vehicle. World Electr. Veh. J. 2019, 10, 75. [Google Scholar] [CrossRef]
- Parekh, D.; Poddar, N.; Rajpurkar, A.; Chahal, M.; Kumar, N.; Joshi, G.P.; Cho, W. A Review on Autonomous Vehicles: Progress, Methods and Challenges. Electronics 2021, 11, 2162. [Google Scholar] [CrossRef]
- Autocrypt. The State of Autonomous Driving in 2025. 2025. Available online: https://autocrypt.io/state-of-autonomous-driving-2025/ (accessed on 24 July 2025).
- NHTSA. NHTSA Releases 2023 Traffic Deaths, 2024 Estimates. Available online: https://www.nhtsa.gov/press-releases/nhtsa-2023-traffic-fatalities-2024-estimates (accessed on 24 July 2025).
- Sun, H.; Zhang, W.; Yu, R.; Zhang, Y. Motion Planning for Mobile Robots—Focusing on Deep Reinforcement Learning: A Systematic Review. IEEE Access 2021, 9, 69061–69081. [Google Scholar] [CrossRef]
- Tezerjani, M.D.; Carrillo, D.; Qu, D.; Dhakal, S.; Mirzaeinia, A.; Yang, Q. Real-time Motion Planning for autonomous vehicles in dynamic environments. arXiv 2024, arXiv:2406.02916. [Google Scholar] [CrossRef]

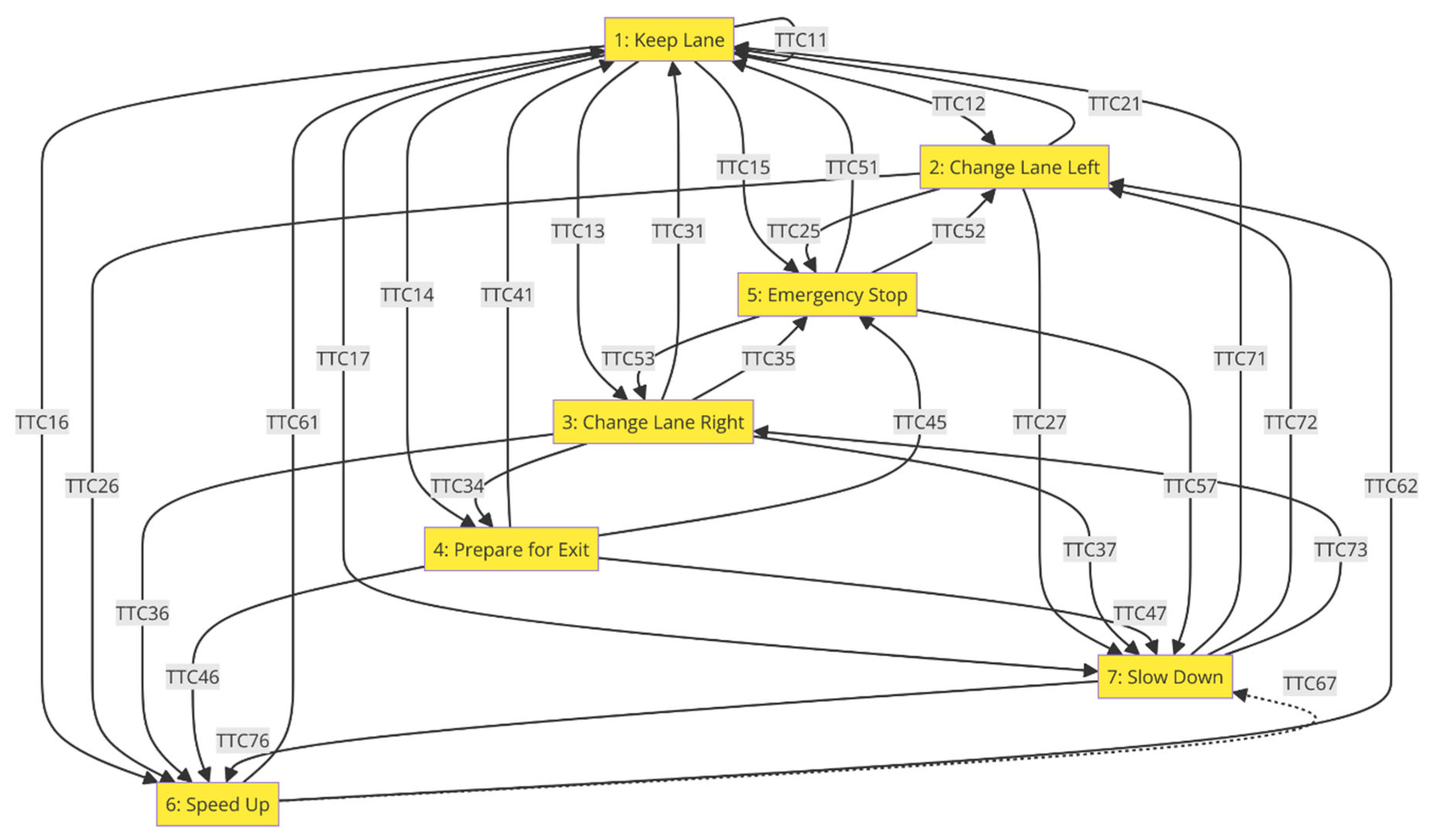

| # | Ego Car State | Description | Possible Transitions | Triggering Conditions | Relevant Cost Functions |
|---|---|---|---|---|---|
| 1 | Keep Lane | The ego car stays in its current lane, maintaining a safe distance from vehicles. |
|
|
|
| 2 | Change Lane Left | The ego car shifts to the left lane, typically to overtake a slower vehicle. |
|
|
|
| 3 | Change Lane Right | The ego car shifts to the right lane, typically to make way for faster traffic. |
|
|
|
| 4 | Prepare for Exit | The ego car prepares to leave the highway by moving into the exit lane. |
|
|
|
| 5 | Emergency Stop | The ego car decelerates rapidly to avoid a collision or stop for an obstacle. |
|
|
|
| 6 | Speed Up | The ego car increases speed to maintain the target speed or overtake other cars. |
|
|
|
| 7 | Slow Down | The ego car decreases speed to maintain safety and avoid collisions. |
|
|
|
| Cost Function | Description | Formula | States Where Applied | Purpose in Transitioning Between States |
|---|---|---|---|---|
| Speed Cost | Penalizes deviation from the target speed, either too slow or too fast. |
| Ensures the ego car maintains an optimal speed, transitioning between speeding up and slowing down as needed. | |
| Collision Cost | Assigns high penalties for potential collisions with vehicles, obstacles, or other hazards. | is the minimum distance to obstacles |
| Avoids collisions by influencing decisions to either change lanes, slow down, or stop in case of danger ahead. |
| Lane Preference Cost | Penalizes staying in undesirable lanes (e.g., slower lanes) and rewards transitions to faster lanes. | is a penalty value for staying in a less efficient lane |
| Guides lane changes based on lane desirability, either for overtaking slower vehicles or preparing for an exit. |
| Jerk Cost | Penalizes high jerk (rapid changes in acceleration) to ensure smooth driving and passenger comfort. | , over the time interval T |
| Ensures smooth transitions during lane changes, acceleration, deceleration, or emergency stops. |
| Overtaking Efficiency Cost | Rewards efficient overtaking and penalizes unnecessary or unsafe lane changes. | , is the time taken to overtake |
| Guides the ego car in making efficient lane changes when overtaking slower vehicles, avoiding unnecessary maneuvers. |
| Safety Margin Cost | Ensures the ego car maintains a safe distance from other vehicles and obstacles. | , is the safe distance |
| Promotes safe driving by guiding the ego car to slow down or stop if the distance to an obstacle becomes too small. |
| Fuel Efficiency Cost | Penalizes unnecessary acceleration or speeding, promoting fuel efficiency. | , is the car’s speed |
| Encourages energy-efficient driving by optimizing speed adjustments and minimizing excessive acceleration. |
| # | Code | Description | Description of the Triggering Transitional Conditions (TCCs) |
| 1 | TTC11 | Stay in State 1 |
|
| 2 | TTC12 | Transit from State 1 → State 2 |
|
| 3 | TTC13 | Transit from State 1 → State 3 |
|
| 4 | TTC14 | Transit from State 1 → State 4 |
|
| 5 | TTC15 | Transit from State 1 → State 5 |
|
| 6 | TTC16 | Transit from State 1 → State 6 |
|
| 7 | TTC17 | Transit from State 1 → State 7 |
|
| 8 | TTC21 | Transit from State 2 → State 1 |
|
| 9 | TTC25 | Transit from State 2 → State 5 |
|
| 10 | TTC26 | Transit from State 2 → State 6 |
|
| 11 | TTC27 | Transit from State 2 → State 7 |
|
| 12 | TTC31 | Transit from State 3 → State 1 |
|
| 13 | TTC34 | Transit from State 3 → State 4 |
|
| 14 | TTC35 | Transit from State 3 → State 5 |
|
| 15 | TTC36 | Transit from State 3 → State 6 |
|
| 16 | TTC37 | Transit from State 3 → State 7 |
|
| 17 | TTC41 | Transit from State 4 → State 1 |
|
| 18 | TTC45 | Transit from State 4 → State 5 |
|
| 19 | TTC46 | Transit from State 4 → State 6 |
|
| 20 | TTC47 | Transit from State 4 → State 7 |
|
| 21 | TTC51 | Transit from State 5 → State 1 |
|
| 22 | TTC52 | Transit from State 5 → State 2 |
|
| 23 | TTC53 | Transit from State 5 → State 3 |
|
| 24 | TTC57 | Transit from State 5 → State 7 |
|
| 25 | TTC61 | Transit from State 6 → State 1 |
|
| 26 | TTC62 | Transit from State 6 → State 2 |
|
| 27 | TTC67 | Transit from State 6 → State 7 |
|
| 28 | TTC71 | Transit from State 7 → State 1 |
|
| 29 | TTC72 | Transit from State 7 → State 2 |
|
| 30 | TTC73 | Transit from State 7 → State 3 |
|
| 31 | TTC76 | Transit from State 7 → State 6 |
|
| Parameter | Typical Value |
| Initial/Goal Velocity | 80–100 km/h (22.2–27.8 m/s) |
| Acceleration Limits | ±3 |
| Jerk Limit | 2–3 |
| Lane Width | 3.5 m |
| Max Lateral Deviation | ±0.3 m |
| Speed Limits | 60–120 km/h (16.7–33.3 m/s) |
| Steering Angle Limit | ±25 degrees |
| Safe Distance Buffer | 5 m |
| Prediction Horizon (T) | 3–5 s |
| Control Time Step (Δt) | 0.1 s |
| Detection Range for Obstacles | 50–100 m |
| Obstacle Update Rate | 10 Hz (every 0.1 s) |
| Path Adjustment Parameters for Collision Avoidance | Typical Value |
| Lateral Shift | 0.5–1.0 m |
| Speed Reduction | 10–20% decrease |
| Angle Adjustment for Lane Changes | ±2–5 degrees |
| Scenario | Metrics | LSPP | A* Algorithm | RRT | Bezier Curve |
|---|---|---|---|---|---|
| 0.2 | 0.5 | 0.6 | 0.3 | |
| Speed Deviation ± km/h | ±2 | ±6 | ±4 | ±3 | |
| Execution Time ms | 12 | 55 | 40 | 20 | |
| Lane Change Success Rate % | 100 | 85 | 80 | 95 |
| 0.3 | 0.7 | 0.8 | 0.4 | ||
| Max Lateral Deviation m | 0.1 | 0.5 | 0.4 | 0.2 | |
| Execution Time ms | 15 | 60 | 50 | 25 | |
| Collision Avoidance Rate% | 100 | 70 | 80 | 90 |
| Stopping Distance m | 5 | 2 | 3 | 4 | |
| 0.4 | 0.9 | 0.7 | 0.5 | ||
| Execution Time ms | 10 | 70 | 55 | 30 | |
| Lane Keeping Success Rate % | 98 | 70 | 75 | 90 |
| Max Lateral Deviation m | 0.15 | 0.5 | 0.4 | 0.3 | |
| 0.3 | 70 | 0.6 | 0.4 | ||
| Execution Time ms | 15 | 65 | 52 | 27 | |
| 0.3 | 0.6 | 0.5 | 0.4 | |
| Traffic Flow Efficiency% | 95 | 80 | 80 | 90 | |
| Execution Time ms | 12 | 60 | 50 | 22 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farag, W.A.; Mahmoud, M.M. Trajectory Optimization for Autonomous Highway Driving Using Quintic Splines. World Electr. Veh. J. 2025, 16, 434. https://doi.org/10.3390/wevj16080434
Farag WA, Mahmoud MM. Trajectory Optimization for Autonomous Highway Driving Using Quintic Splines. World Electric Vehicle Journal. 2025; 16(8):434. https://doi.org/10.3390/wevj16080434
Chicago/Turabian StyleFarag, Wael A., and Morsi M. Mahmoud. 2025. "Trajectory Optimization for Autonomous Highway Driving Using Quintic Splines" World Electric Vehicle Journal 16, no. 8: 434. https://doi.org/10.3390/wevj16080434
APA StyleFarag, W. A., & Mahmoud, M. M. (2025). Trajectory Optimization for Autonomous Highway Driving Using Quintic Splines. World Electric Vehicle Journal, 16(8), 434. https://doi.org/10.3390/wevj16080434






