A Methodology for Characterizing Lithium-Ion Batteries Under Constant-Current Charging Based on Spectral Analysis
Abstract
1. Introduction
- Electrochemical models;
- Equivalent circuit models;
- Performance-based models;
- Analytical models with empirical fitting;
- Statistical approaches.
2. The Methodology Based on Spectra Generation and the Experimental Setup
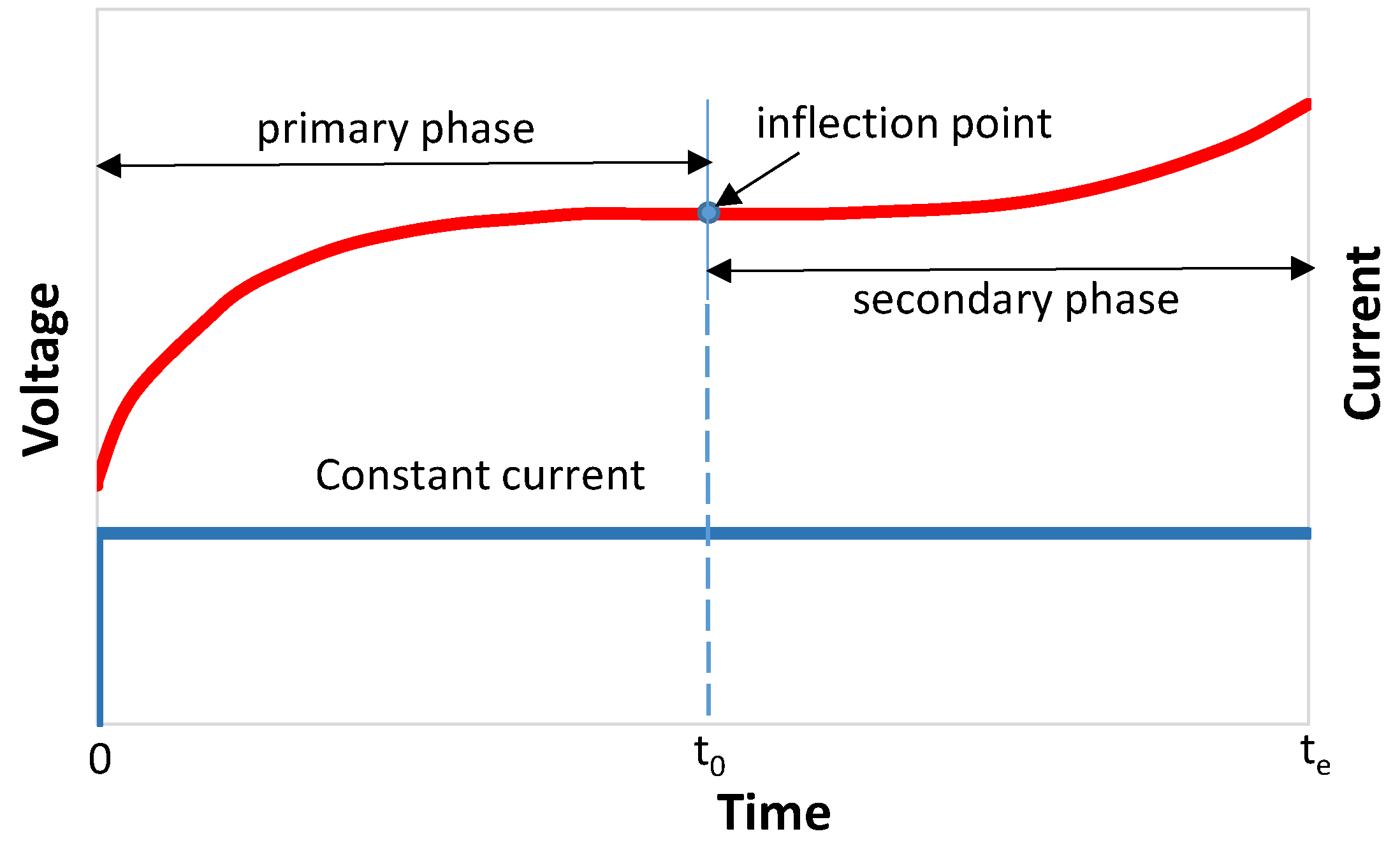
- Divide the complete voltage curve U(t) into two distinct phases (see Figure 1). The first (primary) phase includes data from the starting point up to the inflection point, while the secondary phase covers the data from the inflection point to the endpoint.
- Calculate the discrete spectrum using the experimental data from the first phase of the curve.
- Subtract the theoretically modeled curve (approximated over the entire range, from the starting point to the endpoint) from the experimental curve. This results in a monotonically increasing curve that includes data from the time range between the inflection point and the endpoint. We refer to this as the secondary curve.
- Calculate the discrete spectrum for the newly obtained curve.
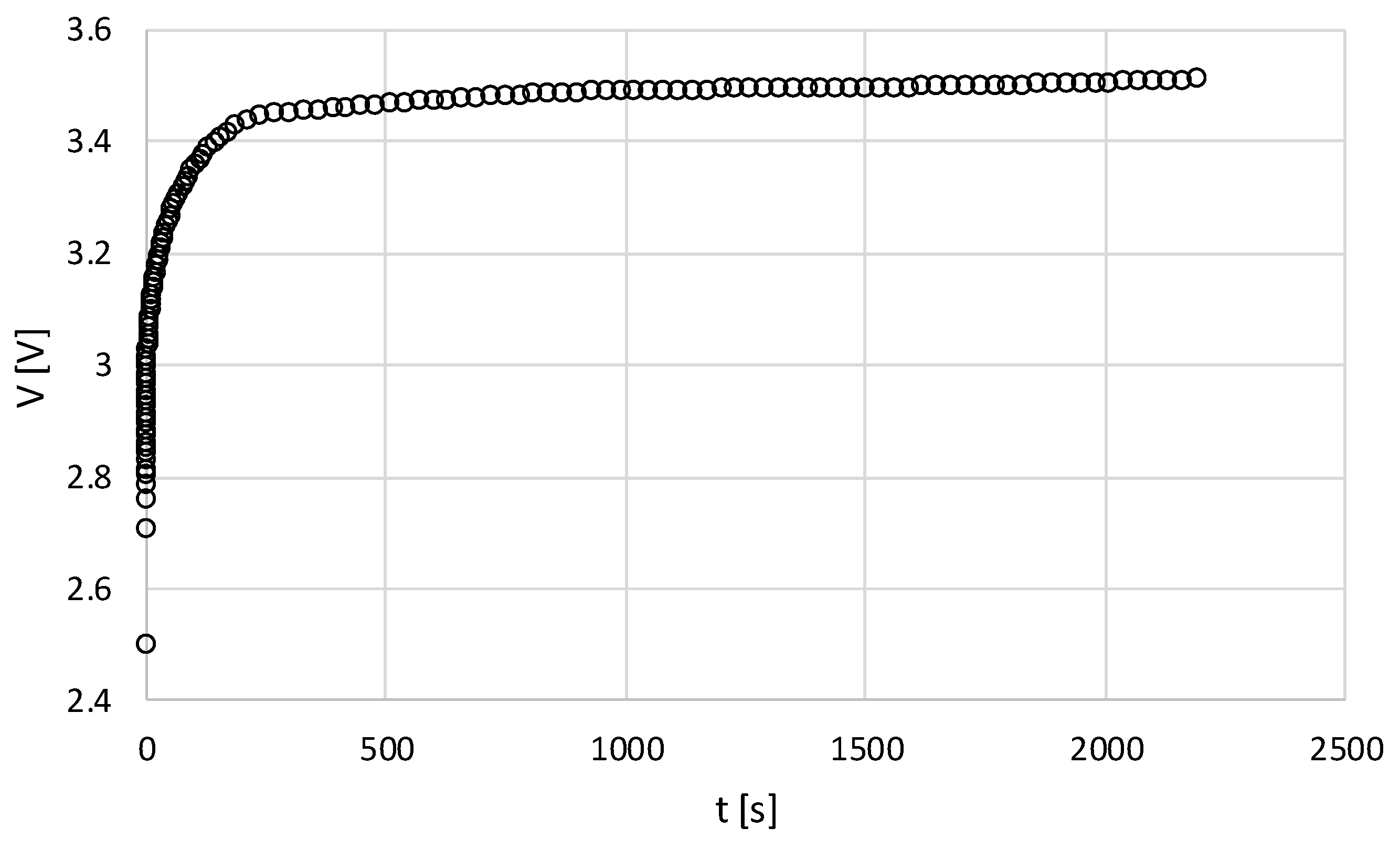
Experimental Setup
3. Numerical Calculations and Error Analysis
3.1. Fitting the Primary Phase of the Voltage Curve
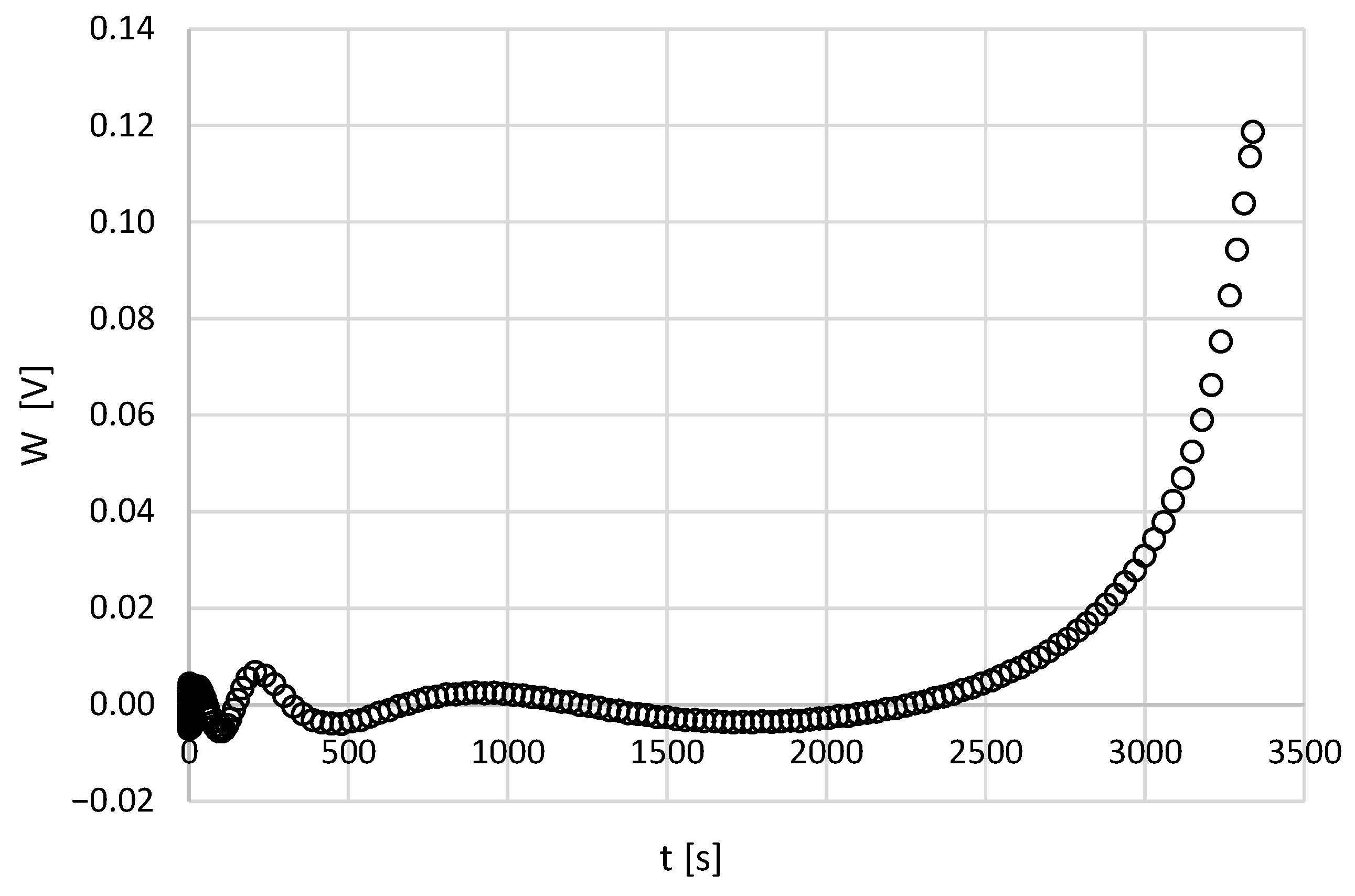
3.2. Fitting Secondary Phase of the Voltage Curve
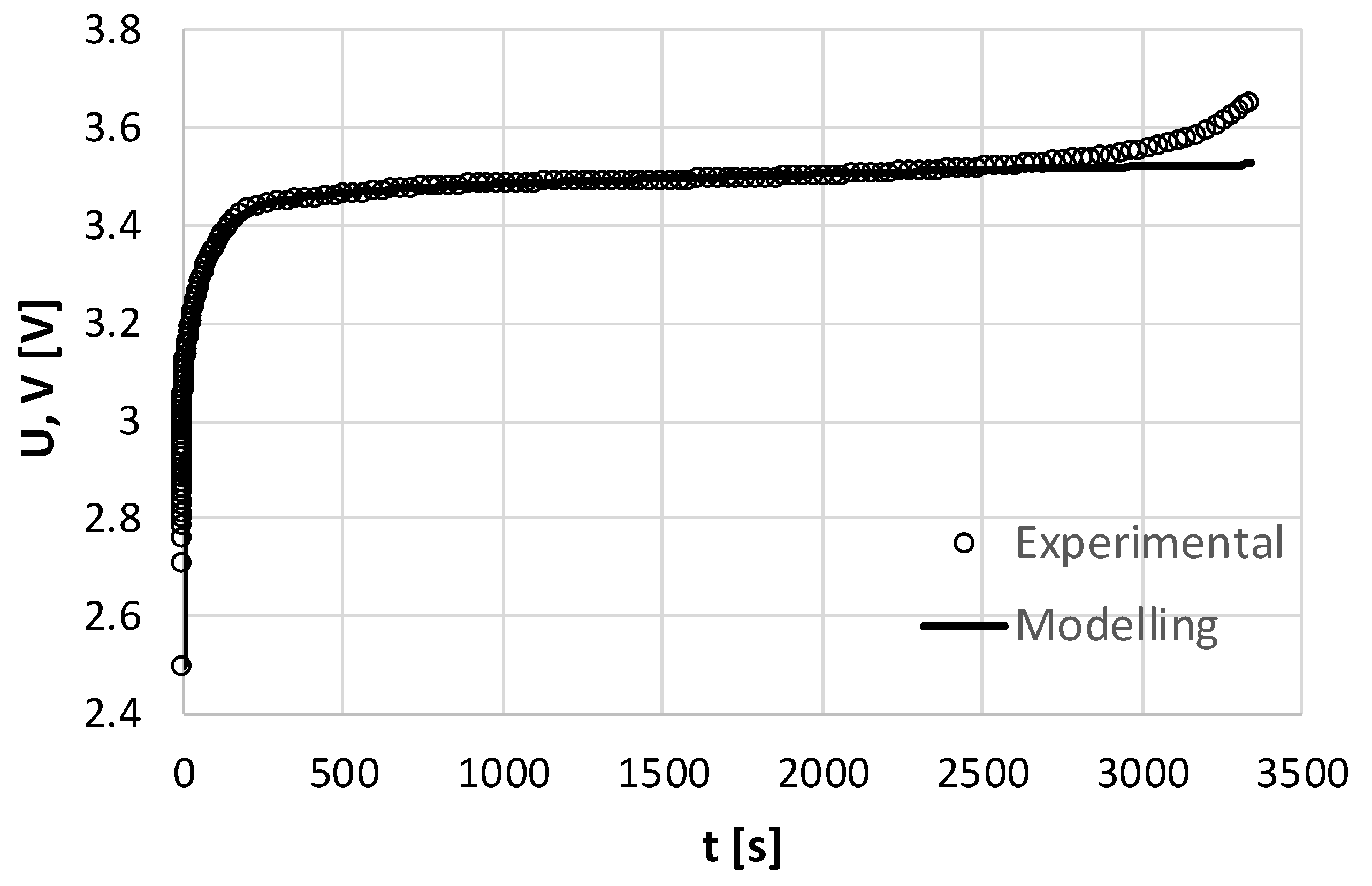
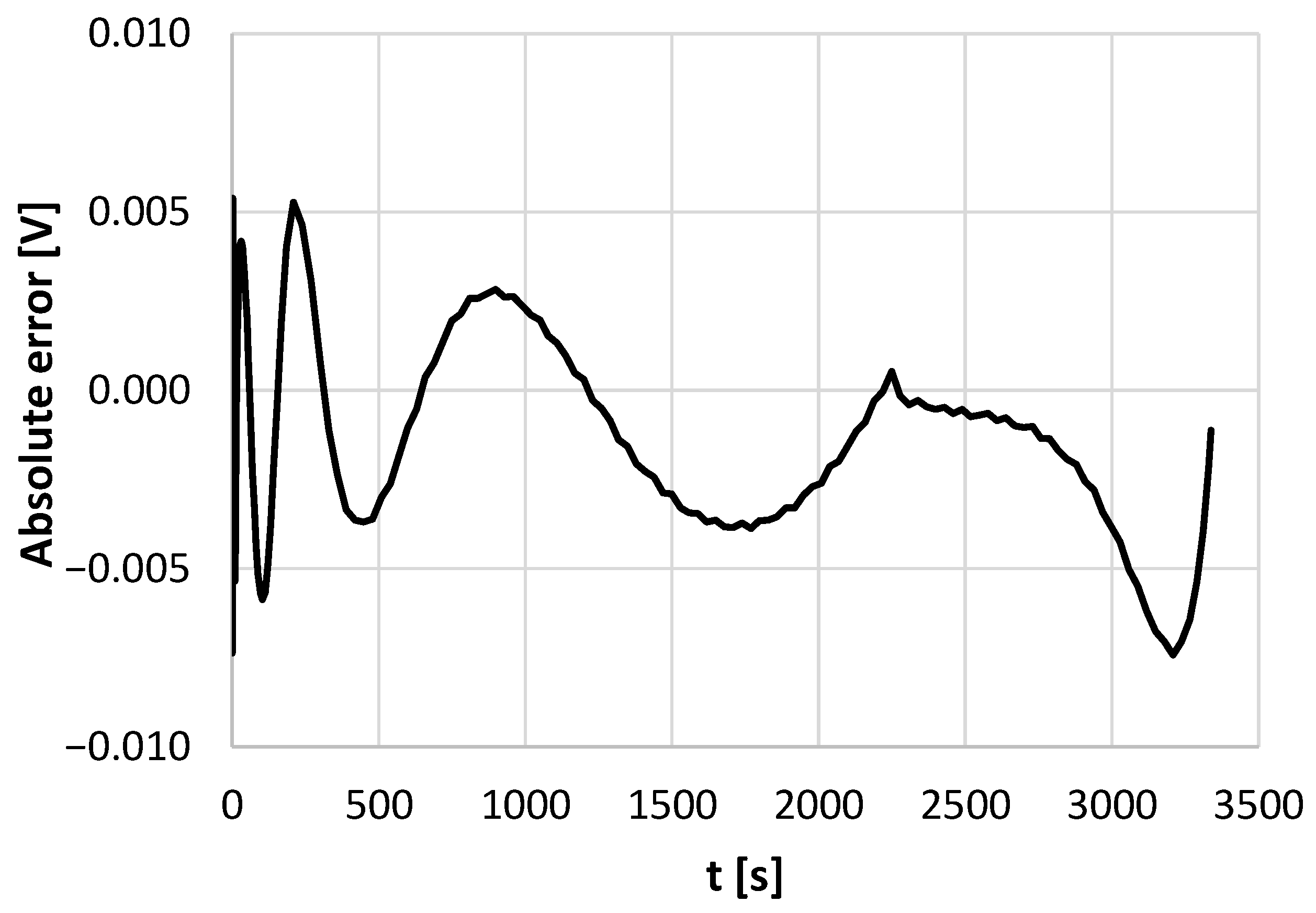
4. Final Results of the Modeling
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bayoumi, E.H.E.; De Santis, M.; Awad, H. A Brief Overview of Modeling Estimation of State of Health for an Electric Vehicle’s Li-Ion Batteries. World Electr. Veh. J. 2025, 16, 73. [Google Scholar] [CrossRef]
- Pisani Orta, M.A.; Garcia Elvira, D.; Valderrama Blavi, H. Review of State-of-Charge Estimation Methods for Electric Vehicle Applications. World Electr. Veh. J. 2025, 16, 87. [Google Scholar] [CrossRef]
- Peng, J.; Gao, Y.; Cai, L.; Zhang, M.; Sun, C.; Liu, H. State of Health Estimation for Lithium-Ion Batteries Using Electrochemical Impedance Spectroscopy and a Multi-Scale Kernel Extreme Learning Machine. World Electr. Veh. J. 2025, 16, 224. [Google Scholar] [CrossRef]
- Gu, S.; Qian, K.; Yang, Y. Optimization of Electric Vehicle Charging and Discharging Strategies Considering Battery Health State: A Safe Reinforcement Learning Approach. World Electr. Veh. J. 2025, 16, 286. [Google Scholar] [CrossRef]
- Mukhopadhyay, A.; Sheldon, B.W. Deformation and stress in electrode materials for Li-ion batteries. Prog. Mater. Sci. 2014, 63, 58–116. [Google Scholar] [CrossRef]
- Purewal, J.; Wang, J.; Graetz, J.; Soukiazian, S.; Tataria, H.; Verbrugge, M.W. Degradation of lithium ion batteries employing graphite negatives and nickel-cobalt-manganese oxide + spinel manganese oxide positives: Part 2, chemical-mechanical degradation model. J. Power Sources 2014, 272, 1154–1161. [Google Scholar] [CrossRef]
- Dubarry, M.; Qin, N.; Brooker, P. Calendar aging of commercial Li-ion cells of different chemistries—A review. Curr. Opin. Electrochem. 2018, 9, 106–113. [Google Scholar] [CrossRef]
- Han, X.; Lu, L.M.; Zheng, Y.; Feng, X.; Li, Z.; Li, J.; Ouyang, M. A review on the key issues of the lithium ion battery degradation among the whole life cycle. eTransportation 2019, 1, 100005. [Google Scholar] [CrossRef]
- Moser, F.; Fourgeot, F.; Rouget, R.; Crosnier, O.; Brousse, T. In situ X-ray diffraction investigation of zinc based electrode in NieZn secondary batteries. Electrochim. Acta 2013, 109, 110–116. [Google Scholar] [CrossRef]
- Jaiswal, A.; Chalasani, S.C. The role of carbon in the negative plate of the lead-acid battery. J. Energy Storage 2015, 1, 15–21. [Google Scholar] [CrossRef]
- Hazotte, C.; Leclerc, N.; Meux, E.; Lapicque, F. Direct recovery of cadmium and nickel from Ni-Cd spent batteries by electroassisted leaching and electrodeposition in a single-cell process. Hydrometallurgy 2016, 162, 94–103. [Google Scholar] [CrossRef]
- Zhao, R.; Liu, J.; Gu, J. A comprehensive study on Li-ion battery nail penetrations and the possible solutions. Energy 2017, 123, 392–401. [Google Scholar] [CrossRef]
- Zhang, J.; Lee, J. A review on prognostics and health monitoring of Li-ion battery. J. Power Sources 2011, 196, 6007–6014. [Google Scholar] [CrossRef]
- Tao, L.; Ma, J.; Cheng, Y.; Noktehdan, A.; Chong, J.; Lu, C. A review of stochastic battery models and health management. Renew. Sust. Energ. Rev. 2017, 80, 716–732. [Google Scholar] [CrossRef]
- Hossain Lipua, M.S.; Hannanc, M.A.; Hussaina, A.; Hoqued, M.M.; Kerc, P.J.; Saada, M.H.M.; Ayob, A. A review of state of health and remaining useful life estimation methods for lithium-ion battery in electric vehicles: Challenges and recommendations. J. Clean Prod. 2018, 205, 115–133. [Google Scholar] [CrossRef]
- Šeruga, D.; Gosar, A.; Sweeney, C.A.; Jaguemont, J.; Van Mierlo, J.; Nagode, M. Continuous modelling of cyclic ageing for lithium-ion batteries. Energy 2021, 215, 119079. [Google Scholar] [CrossRef]
- Barré, A.; Deguilhem, B.; Grolleau, S.; Gérard, M.; Suard, F.; Riu, D. A review on lithium-ion battery ageing mechanisms and estimations for automotive applications. J. Power Sources 2013, 241, 680–689. [Google Scholar] [CrossRef]
- Hu, M.; Li, Y.; Li, S.; Fu, C.; Qin, D.; Li, Z. Lithium-ion battery modelling and parameter identification based on fractional theory. Energy 2018, 165, 153–163. [Google Scholar] [CrossRef]
- Assi, M.; Amer, M. A Comparative Analysis of Lithium-Ion Batteries Using a Proposed Electrothermal Model Based on Numerical Simulation. World Electr. Veh. J. 2025, 16, 60. [Google Scholar] [CrossRef]
- Krause, T.; Nusko, D.; Rittmann, J.; Pitta Bauermann, L.; Kroll, M.; Holly, C. Synthetic Data Generation for AI-Informed End-of-Line Testing for Lithium-Ion Battery Production. World Electr. Veh. J. 2025, 16, 75. [Google Scholar] [CrossRef]
- Jaguemont, J.; Darwiche, A.; Barde, F. Model Predictive Control Using an Artificial Neural Network for Fast-Charging Lithium-Ion Batteries. World Electr. Veh. J. 2025, 16, 231. [Google Scholar] [CrossRef]
- Zhang, H.; Lai, Y.-H. Improving State-of-Health Estimation for Lithium-Ion Batteries Based on a Generative Adversarial Network and Partial Discharge Profiles. World Electr. Veh. J. 2025, 16, 277. [Google Scholar] [CrossRef]
- Painter, R.; Parthasarathy, R.; Li, L.; Embry, I.; Sharpe, L.; Hargrove, S.K. An Artificial Neural Network-Based Battery Management System for LiFePO4 Batteries. World Electr. Veh. J. 2025, 16, 282. [Google Scholar] [CrossRef]
- de Anda-Suarez, J.; Perez-Zuniga, G.; Lopez-Ramirez, J.L.; Herrera Perez, G.; Zeferino Gonzalez, I.; Verde Gomez, J.Y.; on behalf of the TecNM Energy Production and Storage Network. Lithium Battery Enhancement Through Electrical Characterization and Optimization Using Deep Learning. World Electr. Veh. J. 2025, 16, 167. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, C.; Zhang, X.; Zhou, Z. Lithium-Ion Battery SOH Estimation Method Based on Multi-Feature and CNN-BiLSTM-MHA. World Electr. Veh. J. 2024, 15, 280. [Google Scholar] [CrossRef]
- Tran, M.K.; DaCosta, A.; Mevawalla, A.; Panchal, S.; Fowler, M. Comparative study of equivalent circuit models performance in four common lithium-ion batteries: LFP NMC, LMO, NCA. Batteries 2021, 7, 51. [Google Scholar] [CrossRef]
- Han, X.; Ouyang, M.; Lu, L.; Li, J. Simplification of physics-based electrochemical model for lithium ion battery on electric vehicle. Part I: Diffusion simplification and single particle model. J. Power Sources 2015, 278, 802–813. [Google Scholar] [CrossRef]
- Hariharan, K.S.; Kumar, V.S. A nonlinear equivalent circuit model for lithium ion cells. J. Power Sources 2013, 222, 210–217. [Google Scholar] [CrossRef]
- Grandjean, T.R.B.; McGordon, A.; Jennings, P.A. Structural identifiability of equivalent circuit models for Li-Ion batteries. Energies 2017, 10, 90. [Google Scholar] [CrossRef]
- Wang, S.L.; Fernandez, C.; Zou, C.Y.; Yu, C.M.; Li, X.X.; Pei, S.J.; Xie, W. Open circuit voltage and state of charge relationship functional optimization for the working state monitoring of the aerial lithium-ion battery pack. J. Clean Prod. 2018, 198, 1090–1104. [Google Scholar] [CrossRef]
- Li, Y.; Vilathgamuwa, M.; Farrell, T.; Choi, S.S.; Tran, N.T.; Teague, J. A Physics-Based Distributed-Parameter Equivalent Circuit Model for Lithium-Ion Batteries. Electrochim. Acta 2019, 299, 451–469. [Google Scholar] [CrossRef]
- Chen, Z.; Yang, L.; Zhao, X.; Wang, Y.; He, Z. Online state of charge estimation of Li-ion battery based on an improved unscented Kalman filter approach. Appl. Math. Model. 2019, 70, 532–544. [Google Scholar] [CrossRef]
- Zhang, Q.; Shang, Y.; Li, Y.; Cui, N.; Duan, B.; Zhang, C. A novel fractional variable-order equivalent circuit model and parameter identification of electric vehicle Li-ion batteries. ISA Trans. 2020, 97, 448–457. [Google Scholar] [CrossRef]
- Chen, D.; Xiao, L.; Yana, W.; Guoa, Y. A novel hybrid equivalent circuit model for lithium-ion battery considering nonlinear capacity effects. Energy Rep. 2021, 7, 320–329. [Google Scholar] [CrossRef]
- Biju, N.; Fang, H. BattX: An equivalent circuit model for lithium-ion batteries over broad current ranges. Appl. Energy 2023, 339, 120905. [Google Scholar] [CrossRef]
- Poopanya, P.; Sivalertporn, K.; Phophongviwat, T. A Comparative Study on the Parameter Identification of an Equivalent Circuit Model for an Li-ion Battery Based on Different Discharge Tests. World Electr. Veh. J. 2022, 13, 50. [Google Scholar] [CrossRef]
- Velasco-Arellano, H.; Castillo-Magallanes, N.; Visairo-Cruz, N.; Nunez-Gutierrez, C.A.; Lazaro, I. Parametric Correlation Analysis between Equivalent Electric Circuit Model and Mechanistic Model Interpretation for Battery Internal Aging. World Electr. Veh. J. 2024, 15, 291. [Google Scholar] [CrossRef]
- Sankarkumar, R.S.; Rajasekar, N. A Novel Spotted Hyena Optimizer for the Estimation of Equivalent Circuit Model Parameters in Li-Ion Batteries. World Electr. Veh. J. 2024, 15, 431. [Google Scholar] [CrossRef]
- Tran, M.K.; Mathew, M.; Janhunen, S.; Panchal, S.; Raahemifar, K.; Fraser, R.; Fowler, M. A comprehensive equivalent circuit model for lithium-ion batteries, incorporating the effects of state of health state of charge, and temperature on model parameters. J. Energy Storage 2021, 43, 103252. [Google Scholar] [CrossRef]
- Nagode, M.; Gosar, A.; Sweeney, C.A.; Jaguemont, J.; Van Mierlo, J.; Šeruga, D. Mechanistic modelling of cyclic voltage-capacity response for lithium-ion batteries. Energy 2019, 186, 115791. [Google Scholar] [CrossRef]
- Alshawabkeh, A.; Matar, M.; Almutairy, F. Parameters Identification for Lithium-Ion Battery Models Using the Levenberg—Marquardt Algorithm. World Electr. Veh. J. 2024, 15, 406. [Google Scholar] [CrossRef]



| Genetic Algorithm | Levenberg–Marquardt | |||
|---|---|---|---|---|
| 71,914.9 [s/V] | 505,370 [s/V] | |||
| [s] | [V] | [s] | [V] | |
| 1 | 8.913004 × 10−3 | 3.033364 × 10−1 | 9.000 × 10−3 | 3.134 × 10−1 |
| 2 | 8.461603 × 10−2 | 7.481855 × 10−2 | 1.769 × 10−1 | 7.540 × 10−2 |
| 3 | 2.566468 × 100 | 1.743974 × 10−1 | 3.074 × 100 | 1.765 × 10−1 |
| 4 | 4.409065 × 101 | 2.054043 × 10−1 | 6.371 × 101 | 3.442 × 10−1 |
| 5 | 1.173434 × 102 | 2.032495 × 10−1 | 2.810 × 102 | 5.520 × 10−2 |
| 6 | 4.526886 × 103 | 4.813059 × 10−2 | 5.088 × 103 | 1.141 × 10−1 |
| SSE | 6.8 × 10−4 | 2.0 × 10−4 | ||
| Error Estimation | |||||
|---|---|---|---|---|---|
| SSE | 0.1132 | 0.0048 | 0.0034 | 0.0007 | 0.0002 |
| R-square | 0.9859 | 0.9994 | 0.9996 | 0.9999 | 1.0000 |
| RMSE | 0.0295 | 0.0061 | 0.0052 | 0.0024 | 0.0013 |
| [s] | [V] | |
|---|---|---|
| 1 | 239.5 | 1.103 × 10−3 |
| 2 | 1999 | 3.369 × 10−3 |
| 3 | 2597 | 1.4610 × 10−2 |
| 4 | 3097 | 2.585 × 10−3 |
| 5 | 3597 | 1.475 × 10−2 |
| SSE | 8.585 × 10−5 | |
| R-square | 0.9982 | |
| RMSE | 1.721 × 10−3 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nikonov, A.; Nagode, M.; Klemenc, J. A Methodology for Characterizing Lithium-Ion Batteries Under Constant-Current Charging Based on Spectral Analysis. World Electr. Veh. J. 2025, 16, 308. https://doi.org/10.3390/wevj16060308
Nikonov A, Nagode M, Klemenc J. A Methodology for Characterizing Lithium-Ion Batteries Under Constant-Current Charging Based on Spectral Analysis. World Electric Vehicle Journal. 2025; 16(6):308. https://doi.org/10.3390/wevj16060308
Chicago/Turabian StyleNikonov, Anatolij, Marko Nagode, and Jernej Klemenc. 2025. "A Methodology for Characterizing Lithium-Ion Batteries Under Constant-Current Charging Based on Spectral Analysis" World Electric Vehicle Journal 16, no. 6: 308. https://doi.org/10.3390/wevj16060308
APA StyleNikonov, A., Nagode, M., & Klemenc, J. (2025). A Methodology for Characterizing Lithium-Ion Batteries Under Constant-Current Charging Based on Spectral Analysis. World Electric Vehicle Journal, 16(6), 308. https://doi.org/10.3390/wevj16060308









