1. Introduction
The rapid proliferation of electric vehicles (EVs) into power grids in recent years presents opportunities and challenges, particularly regarding power-grid stability, load balancing, and peak demand management [
1]. Energy is a cornerstone of modern society, with energy storage systems, such as batteries and supercapacitors, playing a critical role in enabling efficient energy distribution and utilization in EVs. As EVs become an integral part of the modern grid and adoption will grow in the future, driven by decarbonization goals, their impact on the grid becomes increasingly significant, introducing a pressing need to develop advanced strategies to ensure a reliable and efficient energy ecosystem [
2]. The increase in the penetration of EVs to the power grid through the grid-to-vehicle (G2V) operation as load and vehicle-to-grid (V2G) operation as the source introduced disturbances in the power grid [
3]. These disturbances become a challenge for voltage stability, frequency regulation, and overall power quality. Therefore, we present a Machine Learning-based Model Predictive Control (MPC) strategy that is essential to mitigate the adverse effects of these disturbances and maintain power-grid stability and quality.
EVs offer a unique solution, such as mobile energy storage, due to large-capacity batteries acting as mobile energy markets through V2G and G2V interactions [
4]. The EVs support power grids using V2G interactions during grid overloading, reducing peak load and enhancing grid stability [
5]. The power grid, in return, provides economic benefits to EV users during coordinated and planned G2V operations when the grid is in low demand or high in renewable generation penetrations. Due to the unpredictable use of EVs with uncoordinated and unplanned G2V operations of a large fleet of EVs, charging demand can significantly increase peak loads and stress local distribution infrastructure [
4]. Similarly, in the V2G operation mode, EVs distribute energy resources that support the power grid through ancillary services. However, these bidirectional energy transactions also introduced disturbances due to rapid, time-varying changes in load demand and available generation. These disturbances perturb the grid voltage and frequency, and these perturbations become significant during renewable intermittent and power dynamic variations that can degrade control performance and compromise the grid stability and power quality [
6]. These factors introduce a source of nonlinear, fast, and stochastic disturbances to the power grid to maintain stable and reliable power-grid operations.
Conventional control-system design performance is degraded to maintain grid stability under high EV penetration. The traditional control design relies on primary frequency control that depends on governor response and droop-based voltage control using fixed set-point PI regulator controllers in power distribution networks. These methods work well for gradual changes. However, due to a sluggish control response, they struggle to regulate frequency oscillation and local voltage collapse in response to nonlinear, fast, and stochastic EV-induced disturbances [
7]. Similarly, static and centralized control schemes cannot accommodate a large fleet of EVs’ integration with stochastic power dynamic behavior. As EV integration increases, a learning-based advanced control design is required to avoid large swing demands from EVs that can push the power system outside the safe operating limits.
In the literature, a significant amount of work was performed regarding grid stability, load balancing, and peak demand management to optimize the EVs’ interactions with the power grid. In [
8], the researchers introduced an improved scheduling approach that applies multi-objective optimization to balance load demand by managing the uncoordinated charging of many EVs, helping maintain the stability of the power grid. Effective and advanced control strategies are required to provide a seamless, stable, EV integration with the modern power grid. A few approaches were proposed for enhancing grid flexibility, stability, and power quality, utilizing optimization and learning techniques. These strategies include machine learning, bidirectional communication, and intelligent control systems to optimize EV grid integrations. A cooperative frequency control strategy was proposed in [
9] to address the microgrid frequency regulation problem under excessive EV discharge and stochastic disturbances from distributed power load and generation. An evolutionary deep reinforcement learning control strategy was implemented to mitigate the excess EV discharge while ensuring frequency regulations. The authors in [
10] introduced reinforcement learning and support vector regression machine learning models to facilitate EV integration to maintain grid frequency, voltage, and line loading regulation.
In [
11], the authors introduced a multifunctional EV charging station integrated with the grid, enhancing power quality by employing V2G, G2V, and active-filtering modes. They developed a self-adjusting filter control strategy to reduce harmonic distortions in the grid current and ensure reliable EV battery charging. Furthermore, fuzzy logic-based autonomous controllers were utilized to regulate EV charging, addressing under-voltage problems. Meanwhile, the authors in [
12] described a scheduling approach based on charging time and energy constraints to meet EV charging requirements efficiently within specified time frames. The integration of EVS into the power grid is managed through various control structures, including centralized, decentralized, and hierarchical approaches, each with unique strengths and limitations. In [
13], a hierarchical charging control method is introduced, combining centralized control at the aggregator level to reduce overall energy costs with decentralized control strategies at the individual EV level. Extending this comparison, ref. [
14] analyzed adaptive multi-agent systems and mixed-integer linear programming (MILP) for managing large-scale EV fleets. The decentralized MAS approach, relying on independent agent decisions, offered computational efficiency but lacked the flexibility provided by the MILP method. Hierarchical control structures, integrating both centralized and decentralized elements, have been increasingly utilized to combine the advantages of each approach. For instance, a tri-level hierarchical coordination strategy based on the Stackelberg leader–follower model is proposed in [
15], effectively optimizing energy transactions across multiple control layers. Similarly, another hierarchical structure incorporated blockchain technology, enabling global optimization and peer-to-peer energy exchanges while addressing concerns like battery degradation [
16]. The user preferences and dynamic energy tariffs were integrated into hierarchical methods, aligning EV charging processes with user requirements and grid stability objectives [
17].
While several ML-based methods for load modeling and uncertainty prediction in power grids, such as those in [
10,
18], employ data-driven techniques like support vector regression or neural networks to forecast EV-induced disturbances, they often require extensive datasets and lack the integration of physical laws, leading to reduced generalizability under limited data or extreme scenarios. In contrast, the proposed PIML-MPC framework uniquely combines physics-informed neural networks, leveraging swing equations and voltage dynamics, with Model Predictive Control to achieve accurate disturbance predictions with minimal data (1000 samples) while ensuring physical consistency. Unlike the existing ML-based load modeling approaches [
10,
18], which focus solely on data-driven predictions, our method embeds physical constraints directly into the learning process, enabling robust real-time control and superior frequency regulation (97.6% RMSE reduction compared to conventional MPC), as demonstrated on the IEEE 39-bus system.
MPC is one of the promising approaches to managing EVs introduced by nonlinear and time-varying disturbances [
19]. The MPC design consists of two parts: dynamic future predictions and optimization of control actions [
20]. Due to the inherent property to handle multivariable systems with the anticipation of future events, MPC is well-suited to regulate the grid with EVs under fast fluctuations and constraints, e.g., battery limit, grid voltage bounds, etc. A distributed MPC framework is applied to coordinate the EV charging and V2G operations for grid support. The MPC can achieve voltage regulation goals and EV charging objectives [
21]. The MPC formulation allows control design to forecast the EV charging patterns and proactively regulate the frequency and voltage. MPC is critically dependent on prediction models. In practice, modeling complex EV and grid dynamics is challenging, compromising the prediction ability of the MPC framework and computing suboptimal or destabilizing control actions [
21].
Physics-Informed Machine Learning (PIML) overcomes the limitation of complex modeling for predictions. PIML is a category of machine learning models that integrates the model from physical-domain knowledge and data-driven learning algorithms. This hybrid modeling achieved high fidelity with much less data required [
18]. The physical model helps create a surrogate power system model using a swing equation and captures complex EV and renewable fluctuations without an excessive dataset containing all possible scenarios. These models can be more reliable for EV integration forecasting with limited historical data and can be generalized better to uncoordinated EV integration and avoid violating energy conservation by design [
18]. Despite the potential of MPC and PIML separately, their combined benefits for EV disturbance mitigation have not been fully explored.
Contrarily, the MPC-based control design faced scalability and accuracy issues, and pure data-driven controls required large training datasets that captured all critical system constraints and complex behaviors [
21]. According to [
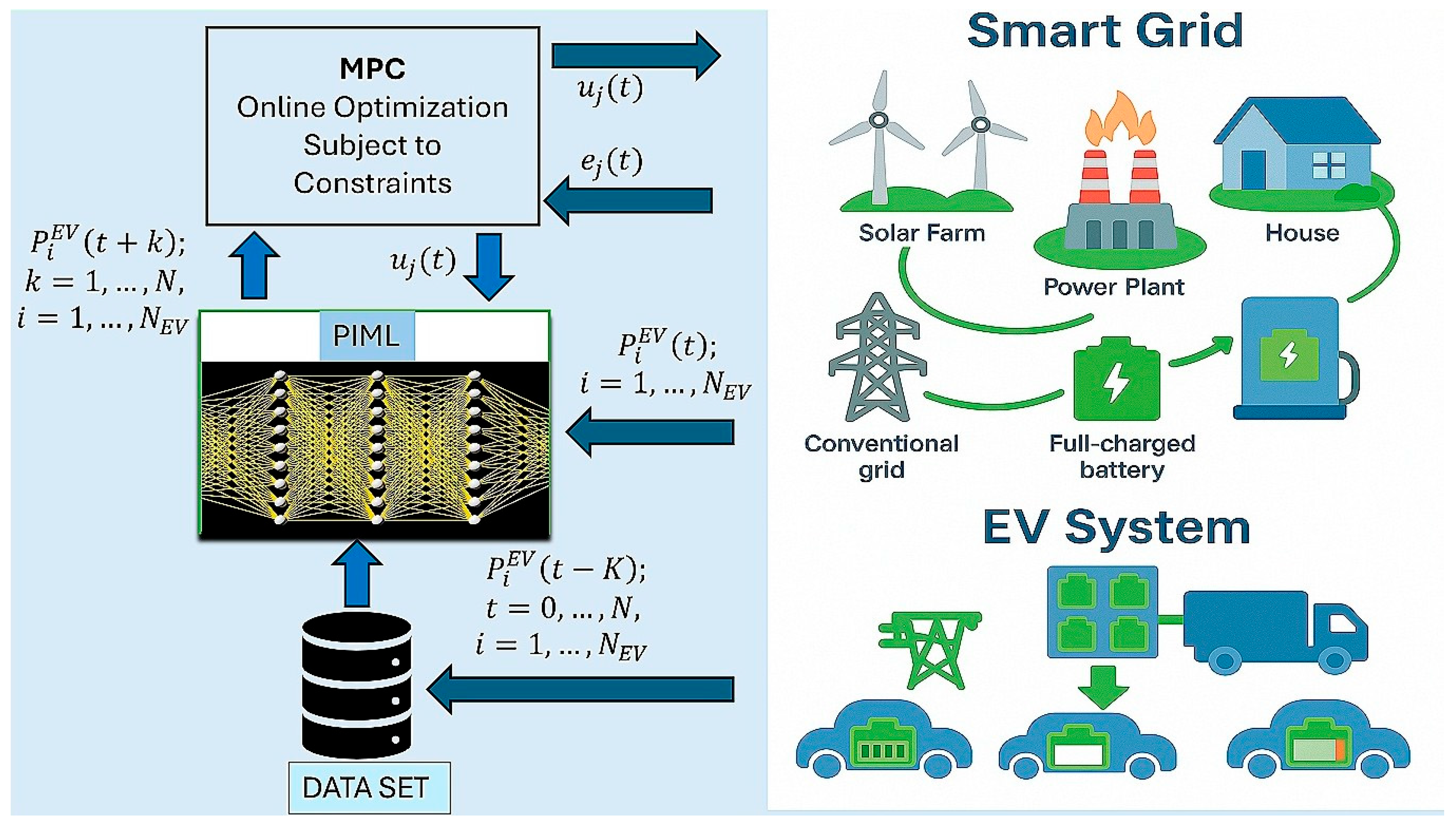
21], the real-time optimization of EV energy management by integrating machine learning is a promising direction to improve robustness and adaptability. This paper represents a combination of PIML and MPC control design, where PIML continually informs and updates the predictive model within an MPC. This hybrid control design combines the strength of data-driven adaptation and physics-based rigorous control design. The system diagram of the proposed control framework is depicted in
Figure 1, where a dataset is developed using historical data on EV power demand and supply to the grid, power-grid load demand, voltage variations, and frequency deviations. The PIML model uses EV interaction dynamics and datasets. The trained model is used for future horizon predictions of model states, and online optimization is implemented to optimize control actions. These control actions regulate the power grid and mitigate the disturbance generated by EV interactions.
This work introduces a novel integration of PIML within MPC to bolster power-grid stability amid rising EV adoption. The proposed framework utilizes physics-based ML to capture intricate interactions between electric vehicles and grid dynamics, embedding this model into an MPC for the real-time management of EV energy flows. The model maintains accurate and physically consistent predictions, even as conditions evolve, by incorporating fundamental physical principles, such as battery behavior, network limitations, and electrical flow equations. Consequently, the MPC optimizes control signals, mitigating disruptions from abrupt EV charging demands or unplanned vehicle-to-grid contributions. Compared to traditional methods and static-model MPC strategies, our approach ensures enhanced voltage and frequency stability with greater data efficiency than purely data-driven approaches. This research addresses the existing gaps by demonstrating practical, reliable AI-enabled control methods critical for resilient future smart grid operations. The key contributions of this work are as follows:
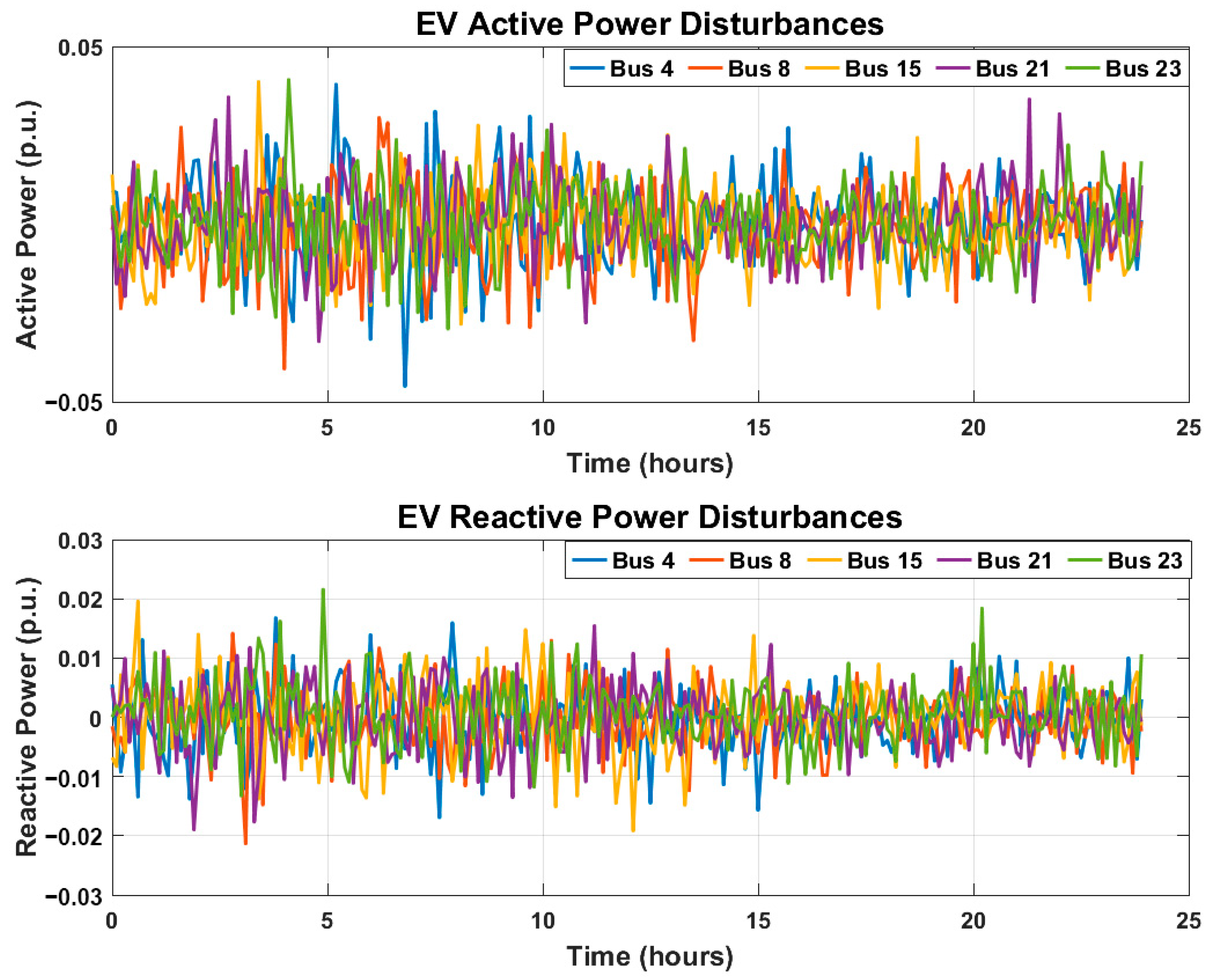
Development of a dynamic disturbance model using a PIML approach, which accurately emulates the stochastic behavior of EV plug-in and plug-out events and their impact on the power grid.
Design of an advanced MPC framework that incorporates PIML-based disturbance predictions for the real-time estimation and compensation of uncertainties, enhancing the robustness of the underlying prediction model.
Rigorous mathematical stability analysis of the proposed PIML-MPC control law, comprising two parts: (i) convergence guarantees PIML model training and (ii) closed-loop stability of the MPC formulation using Lyapunov-based techniques.
Comprehensive performance evaluation of the proposed control strategy on the IEEE 39-bus system under diverse G2V and V2G scenarios, demonstrating significant improvements in grid stability metrics.
This paper is organized as follows:
Section 2 presents the mathematical modeling of the power system dynamics.
Section 3 details the event-driven modeling of EV disturbances for plug-in and plug-out events.
Section 4 introduces the PIML model design.
Section 5 elaborates on the PIML-enhanced MPC formulation and provides mathematical stability proof for the proposed control law.
Section 6 evaluates the performance of the proposed approach using the IEEE 39 bus system. Finally,
Section 7 concludes the paper with key findings and directions for future research.
5. Physics-Informed Machine Learning Model Predictive Control Design with Disturbance Prediction
This section develops a rigorous, nonlinear MPC formulation that incorporates PIML-based disturbance predictions. The objective is to regulate grid voltage and frequency by optimizing control actions under nonlinear dynamics, EV-induced stochastic disturbances, and physical constraints. We derive the full MPC formulation, present the algorithmic implementation, and provide a Lyapunov-based stability proof of the closed-loop system.
5.1. System Dynamics and PIML Integration
The nonlinear state-space dynamics of the power grid with EV-induced disturbances shown by (10) is rewritten into power system dynamics and unknown disturbance as:
where
denotes the system state vector (consisting of rotor angles, angular velocities, and bus voltages),
is the control input (active and reactive power set-points), and
is the unknown disturbance due to EV plug-in/plug-out events. The power system dynamics are presented by nonlinear
. To enhance disturbance rejections, the disturbance
that is induced by uncoordinated EV interaction is approximated for predictions using a PIML-based neural network in (26) as discussed in
Section 4, such that:
Equation (27) represents the neural network prediction model that is parameterized by and trained on a dataset with physics-informed loss, . The prediction model within the MPC framework uses (26) and (27) to predict system dynamics and disturbance over the prediction horizon.
For the digital implementation of the MPC control law, the power system dynamics in (26) are discretized using the forward Euler method with sampling time
:
Equation (28) discretizes the dynamics using a discrete time step , and . The discretized model in (28) serves as the prediction model for MPC optimization.
5.2. Nonlinear MPC Formulation
A nonlinear optimization problem is formulated for the deviation of grid states from reference values with constraint satisfaction and disturbance rejection. For nonlinear MPC formulation, at each step, a finite-horizon optimal control problem is solved over the prediction horizon, .
We define an optimization cost function to minimize over a finite horizon
to calculate the control actions
as:
where
and
are the predicted state and control at step
based on the information at time step
. In (29),
and
are reference state and control trajectories;
are weight matrices for states, inputs, and terminal states, respectively. The terminal cost
penalizes the deviation at the horizon’s end to enhance stability.
The optimization cost function in Equation (29) is defined at time step
to minimize state and control deviations over a prediction horizon
. To extend this to the next time step,
, the cost function is reformulated as:
where
and
are the predicted states and controls at step
based on the information at time
, and
is the terminal cost matrix penalizing deviations at the end of the horizon. The terminal cost
ensures stability by enforcing a control-invariant terminal set, as described in Assumption 4. This term guides the system states toward the reference trajectory at the horizon’s end, reducing the risk of instability due to finite-horizon optimization. The shift from
maintains the receding horizon principle, where the first control inputs
, and the optimization is repeated with updated measurements.
The online MPC optimization problem formulation at time
is formulated as follows:
where
and
are compact polytopic sets defining state and control constraint sets, respectively, and
is a terminal constraint set designed to ensure stability. The disturbance predictions are computed as
using the PIML model.
The optimal control trajectory with control horizon calculated using (31) is denoted as
, where
is the control horizon. Following the receding horizon principle, the first control input
is applied. The next sample repeats the optimization with a receding horizon prediction and updated measures. The PIML-enhanced NMPC algorithm is presented in Algorithm 2.
| Algorithm 2: PIML-Enhanced Nonlinear MPC |
Input: Initial state , prediction horizon N, PIML model weighting matrices , constraint sets , sampling time .
For each time set:
1. Measure State: Obtained current state .
2. Disturbance Prediction: Compute for
3. Solve Optimization: Solve the online nonlinear optimal control problem in (31):
subject to dynamics and constraints:
4. Apply Control: Apply first control input .
5. Update: Set and return to step 1.
End. |
Algorithm 2 ensures real-time disturbance compensation by integrating PIML predictions into the MPC’s prediction formulation and enabling the regulation of power-grid frequency and voltage under stochastic EV interactions.
5.3. Stability Analysis
The closed-loop stability of Algorithm 2 is analyzed to guarantee convergence using a Lyapunov-based approach; for simplicity, a perfect disturbance prediction is assumed (
) followed by the PIML convergence proof in
Section 4.
Assumption 3. The system dynamics, i.e., is Lipschitz continuous with constants and , Assumption 4. The sets and are compact and contain their respective origins. The terminal set is control invariant, i.e., for any .
Assumption 5. The terminal cost matrix satisfies a Lyapunov condition: a control law exists:
where
.
Theorem 2 (Nominal Stability). Under Assumptions 3 to 5, the optimization problem is recursively feasible, i.e., if optimization is feasible at k = 0, it remains feasible at , and the resulting closed-loop system is asymptotically stable, i.e., as .
Proof. Theorem 1 proof is divided into recursive feasibility and Lyapunov stability.
- 1.
Recursive feasibility: Suppose the optimization is feasible at time-step
, the optimization solution yields the following optimal control sequence,
, and state trajectory,
. At time
, construct a candidate control sequence:
where
is the terminal control (using the LQR control law). The corresponding trajectory satisfies the dynamics and constraints since
, and
is control invariant according to Assumption 4. Thus,
is feasible and ensures recursive feasibility.
- 2.
Cost decrease: Compute the MPC optimization cost at
in (29):
where
.
This satisfies the Lyapunov cost-decreasing property, i.e., :
- 3.
Convergence: Since and , is non-increasing and bounded below, ; thus, , which provides asymptotic stability.□
The terminal cost in the cost function at plays a critical role in the Lyapunov-based stability proof. As shown in Theorem 2, the terminal cost satisfies the Lyapunov condition (Assumption 5), ensuring that the cost function is non-increasing and bounded below, which guarantees the asymptotic stability of the closed-loop system. The terminal cost at extends the stability properties from time , as the control-invariant terminal set ensures recursive feasibility, and the positive definite matrix penalizes terminal state deviations, reinforcing convergence to the reference state.
Robustness to Disturbance Prediction Errors: In practice, . Suppose a bounded prediction error, i.e., . The closed-loop dynamics become: .
The perturbation term is bounded by . Using the input to state stability (ISS) properties with sufficient, small , the system states remain bounded, and the tracking error is bounded by a function of . Under a sufficiently small , the system satisfies local ISS properties. The robustness is enhanced based on the PIML model’s accuracy and minimization of .
5.4. Computational Complexity of the PIML NMPC Algorithm
The computational complexity of solving the nonlinear optimization problem depends on the horizon (N) and the system’s dimensionality. Using the previous solution to ensure real-time applicability, we employed efficient solvers (e.g., interior-point methods) and warm-start techniques. The PIML model’s training was performed offline, with online evaluations being computationally lightweight due to the neural network’s feed-forward structure.
7. Conclusions and Future Work
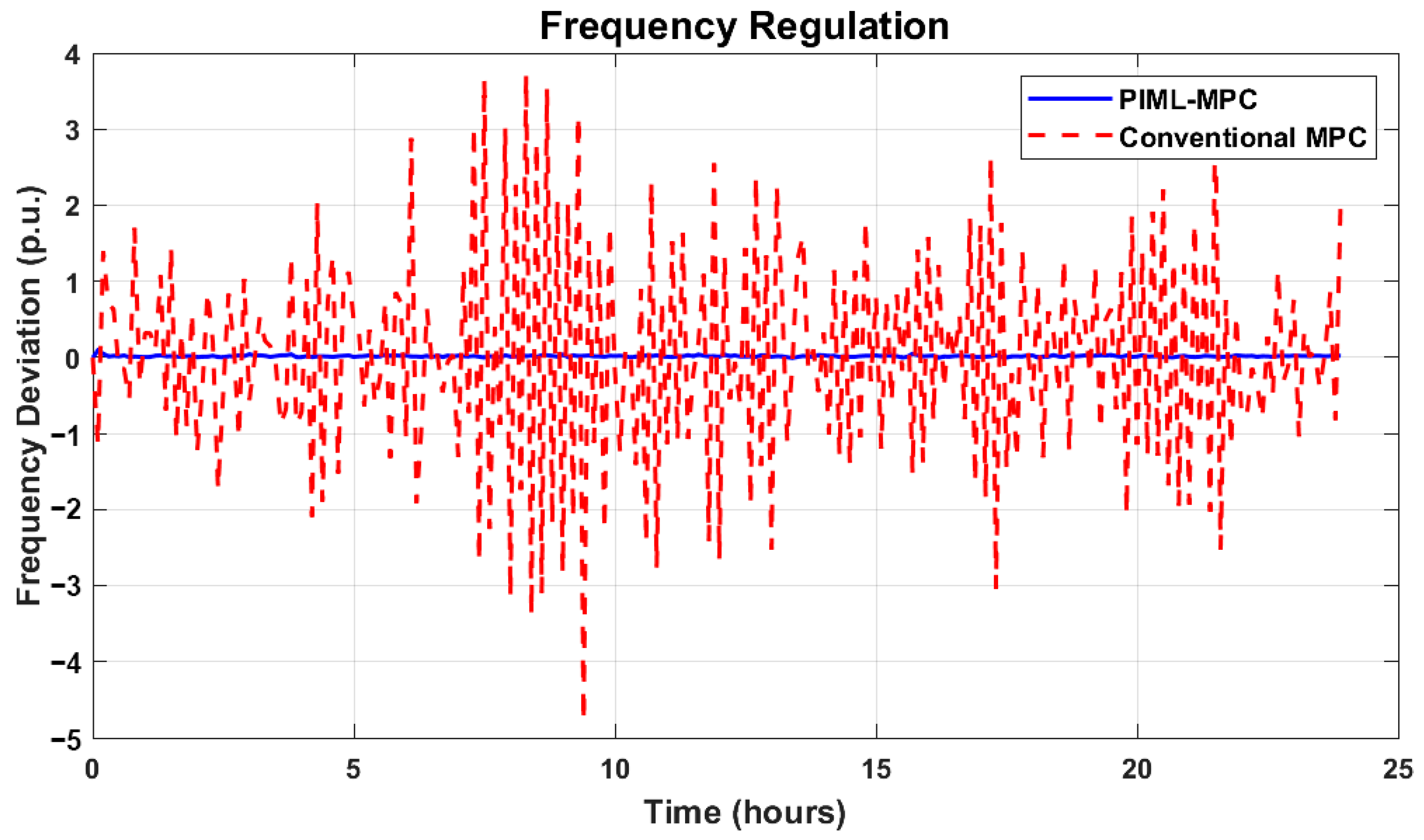
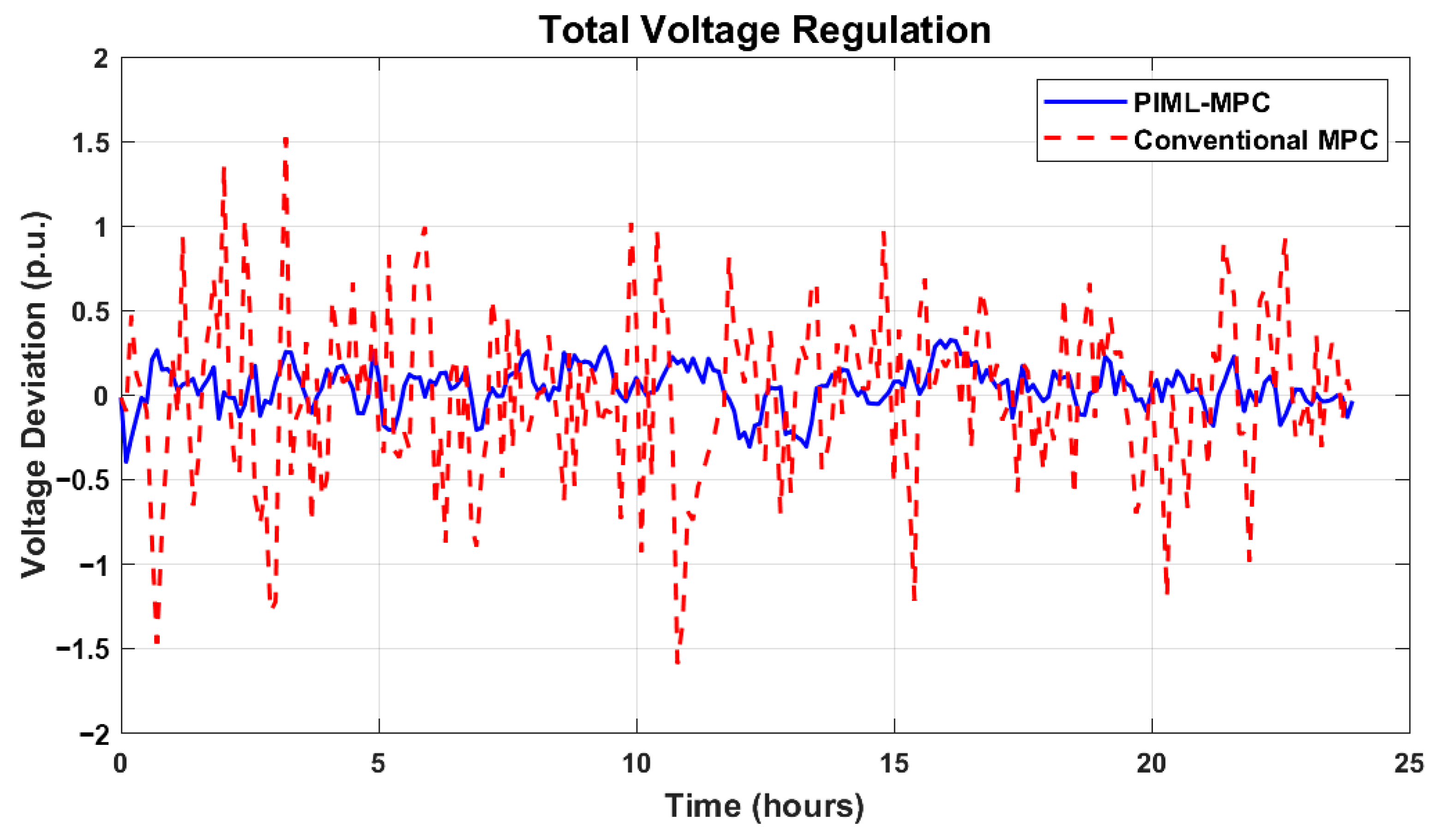
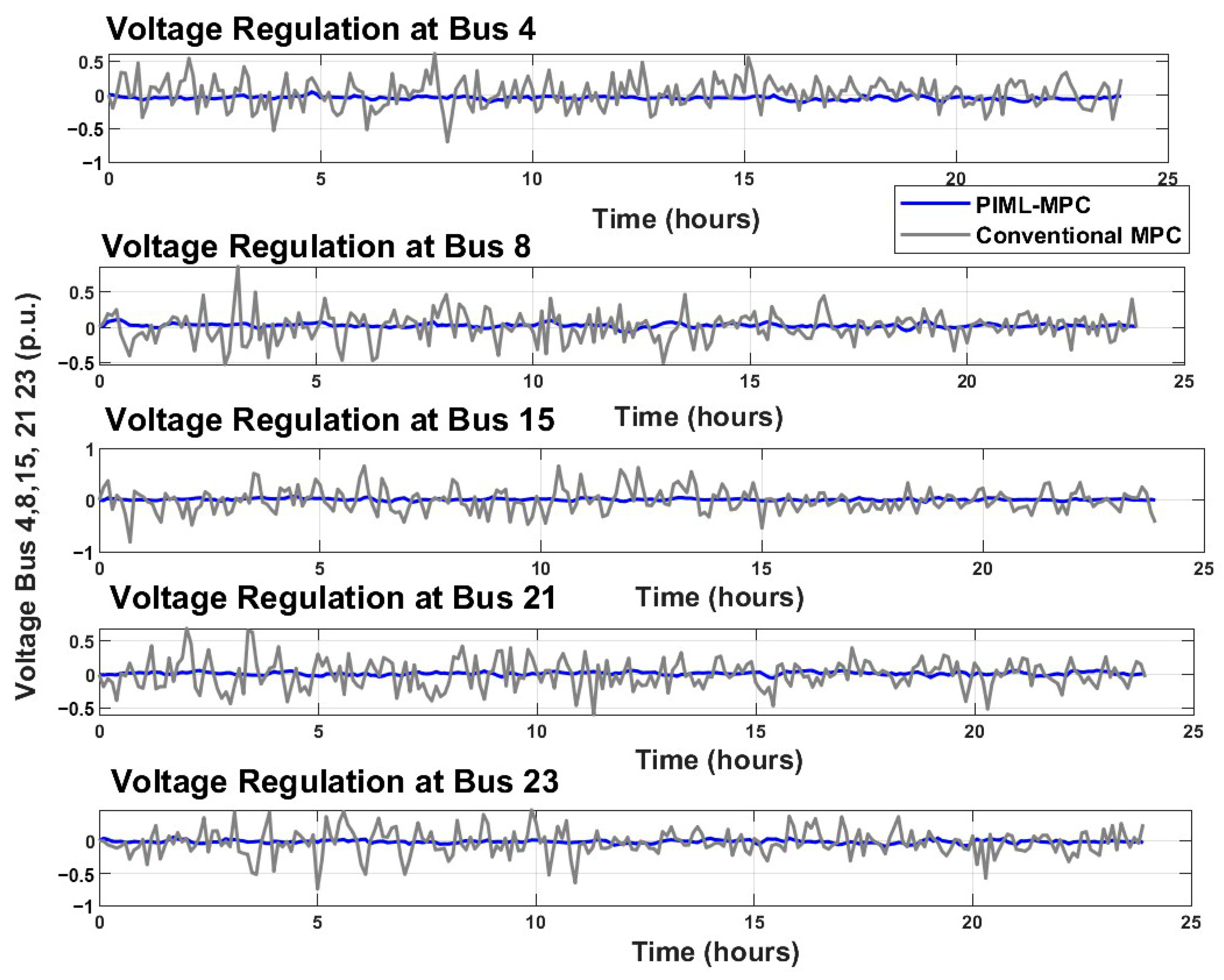
This study introduced a novel PIML-MPC framework to enhance power-grid stability under stochastic EV disturbances, with three primary contributions: (a) integrating physics-informed neural networks with MPC for accurate disturbance prediction, (b) achieving data-efficient control with minimal training data, and (c) ensuring physical consistency in predictions and control actions. The results validate these contributions on the IEEE 39-bus system over a 24 h simulation. First, the PIML model’s integration with MPC achieved precise disturbance predictions (MAE of 0.002 p.u. for active power, 0.0015 p.u. for reactive power,
Section 6.2.1), enabling proactive control that reduced frequency RMSE by 97.6% (0.0112 p.u. vs. 0.4672 p.u.) and voltage RMSE by 18.8% (0.4006 p.u. vs. 0.4932 p.u.) compared to the conventional MPC (
Section 6.2.2 and
Section 6.2.3). This outperforms other MPC methods (e.g., distributed MPC’s 0.015 p.u. and robust MPC’s 0.0138 p.u.,
Section 6.2.5), confirming the advantage of physics-informed predictions. Second, the framework’s data efficiency was demonstrated by training on only 1000 samples, 90% less than typical ML-based methods (e.g., [
9,
21],
Section 6.2.5), yet achieving a 15–25.3% RMSE improvement over reinforcement learning and distributed MPC. Third, embedding physical constraints (e.g., swing equations,
Section 4.2) ensured prediction consistency, maintaining the ROCOF within the regulatory limits (±0.3 p.u. vs. ±4 p.u. for the conventional MPC,
Section 6.2.2) and reducing voltage spikes (
Section 6.2.3). These results highlight the framework’s robustness for real-time grid stability under high EV penetration. Future work will address limitations, such as the simplified voltage dynamics model, by incorporating detailed AC power-flow representations to improve voltage regulation (
Section 6.2.3). Testing on larger systems (e.g., IEEE 118-bus,
Section 6.2.7) and real-world EV charging datasets (
Section 6.2.7) will further validate the scalability and applicability. Adaptive tuning of hyperparameters (e.g.,
,
Table 1) and distributed MPC architectures will enhance the computational efficiency and generalization.