Abstract
LiFePO4 batteries are widely used in hybrid electric tractors due to their high energy density, stable working voltage, low self-discharge rate, long cycle life, absence of memory effect, environmental friendliness, and flexible sizing. Accurate State of Charge (SOC) estimation is crucial for Battery Management Systems (BMSs). This study utilizes a LiFePO4 battery dataset from the University of Maryland to improve SOC estimation accuracy. The forgetting factor recursive least squares method was employed for parameter identification, and a temperature-dependent second-order RC equivalent circuit model was developed in MATLAB R2024a/Simulink. The proposed SAO-LSTM model demonstrated superior SOC estimation performance compared to traditional ampere-hour integration, achieving a 98.23% error reduction. Evaluation results showed 0.39% and 0.31% decreases in root mean square error and mean absolute error, respectively, confirming the model’s robustness and high estimation accuracy for LiFePO4 batteries in hybrid electric tractors.
1. Introduction
With the continuous aggravation of environmental pollution and energy crises, the hybrid electric–diesel tractor, which combines the advantages of both electric and traditional fuel-powered tractors, has become the primary choice in agricultural production. It is also a key research direction for agricultural machinery equipment development toward ecology, energy conservation, and environmental protection [1,2,3]. As one of the critical components of the tractor, the battery’s performance directly determines the safety, reliability, and operational efficiency of agricultural tasks performed by the tractor [4]. BMS is required to provide the driver with accurate battery status information in real-time, such as SOC and State of Health (SOH), to ensure the battery operates safely and reliably while the tractor performs agricultural work efficiently. Battery SOC estimation is one of the core functions of the power battery management system. Accurate SOC estimation can optimize the power battery system, effectively ensuring the efficient and safe operation of the battery system, and provides essential information for the energy management and safety management of hybrid tractors [5,6]. Existing studies mainly focus on optimizing SOC estimation algorithms, often neglecting the high sensitivity of batteries to temperature, which leads to significant errors in battery model parameter identification and SOC estimation results. Therefore, conducting SOC estimation of hybrid tractor onboard batteries with temperature considerations can effectively enhance BMS performance as well as fuel economy and work efficiency, which is of significant importance for the ecological, energy-saving, and environmentally friendly development of agricultural machinery [7].
SOC refers to the ratio of the current remaining charge to the total capacity of the battery. It cannot be directly measured by sensors and can only be indirectly obtained through parameters such as current, voltage, and temperature. To better study the charge-discharge characteristics of batteries and design reliable SOC estimation methods for optimizing the energy management system of hybrid tractors, accurate battery modeling is essential [8]. Common power battery models include electrochemical models, equivalent circuit models (ECMs), fractional-order models, and multi-model fusion. Pramanik et al. [9] established a 1-D electrochemical model based on the internal reaction mechanisms of batteries and proposed a new charging strategy for lithium-ion batteries based on the Pontryagin principle. This strategy effectively shortens the charging time within safe limits and improves battery durability. Xin Lai et al. [10] focused on lithium nickel–cobalt–manganese oxide batteries and established 11 equivalent circuit models. In-depth comparative analysis of these models showed that the first-order equivalent circuit model has good reliability, while the second-order RC (Resistor–Capacitor, RC) equivalent circuit model provides higher accuracy. The other models increased the RC order, but the identification process involved numerous unknown variables, which can lead to overfitting and decreased reliability. Rui Xiong et al. [11] developed a fractional-order model that considers the Butler–Volmer kinetic equation based on battery impedance spectroscopy, optimizing lithium-ion battery parameter identification by combining least squares and genetic algorithms. Simulation results showed that, under a wide temperature range and aging conditions, the battery SOC estimation accuracy exceeded that of traditional models. Wu Yizhou et al. [12] applied the forgetting factor recursive least squares method for online parameter identification and established a dynamic stress-induced battery capacity degradation model based on battery aging experimental data. They also used multi-model fusion for SOC estimation, but this approach is computationally intensive, requires high hardware demands, and is difficult to implement on tractors at this stage. Liu Fang et al. [13] proposed a novel multi-state online joint estimation method for lithium-ion batteries based on a new electro-thermal coupling model. By employing a dual filtering algorithm to simultaneously address thermal state estimation and battery state estimation, this approach significantly improves the accuracy of state monitoring. Studies indicate that the equivalent circuit model does not consider the internal chemical reactions of the battery but describes the voltage response of lithium-ion batteries using ideal electrical components. A constant voltage source characterizes the static voltage characteristics, while an RC network is used to represent dynamic voltage characteristics such as polarization and hysteresis, with a simple structure, concentrated parameters, and clear physical meaning. On the other hand, temperature directly affects the open-circuit voltage and capacity of the power battery, thereby impacting the accuracy of SOC estimation. Therefore, it is crucial to consider the impact of temperature on battery performance during the modeling process [14,15]. Considering the complex load variation and temperature effects in tractor operation, it is more reasonable to use a second-order RC equivalent circuit model for lithium-ion battery modeling in the research process, which accounts for the temperature influence.
The agricultural operations of tractors involve random and complex loads with significant fluctuations, making it challenging to obtain precise SOC values during operations. Currently, the commonly used battery SOC estimation methods include ampere-hour integration, parameter-based methods, model-based methods, and data-driven methods. Fengyan Yi et al. [16] proposed a matrix-based long short-term memory (LSTM) network approach to predict the lifespan of proton exchange membrane fuel cells (PEMFCs), thereby enhancing the operational safety of fuel cell vehicles. Chunchun Jia [17] developed a high-precision aging model for power batteries and introduced a learning-based model predictive approach, effectively reducing the total operating costs of electric vehicles. Xin Zhang et al. [18] proposed an improved ampere-hour integration method based on a long short-term memory (LSTM) network model for battery capacity estimation. Simulation results showed that the modified ampere-hour integration method reduced SOC estimation errors to less than 10%. Liu Su-Zhen et al. [19] applied a particle swarm optimization algorithm combined with an acoustic homogenization model to accurately estimate the mechanical characteristic parameters of lithium-ion batteries, establishing a relationship between mechanical characteristics and SOC. The average absolute error (MAE) of SOC estimation under dynamic conditions was 1.68%, and the root mean square error (RMSE) was 1.92%. Jinhao Meng et al. [20] developed a dynamic linear battery model capable of automatic parameter updates and used linear Kalman filtering to estimate the SOC of lithium iron phosphate batteries. The simulation results effectively indicated that this modeling method offers faster response and higher SOC estimation accuracy. Zhang Zhi et al. [21] applied a data-driven method to estimate the SOC of lithium-ion batteries, enhancing SOC estimation accuracy by adding a gating mechanism to a recurrent neural network and combining the unscented Kalman filter (UKF) method. Yu Zhilong et al. [22] integrated neural networks with extended Kalman filtering (EKF), using EKF to update the neural network model’s thresholds in real-time. The errors in SOC estimation under both hybrid pulse power characteristic (HPPC) and urban dynamometer driving schedule (UDDS) conditions were both under 4%. Li Hongpei et al. [23] improved the unscented Kalman filter algorithm with a forgetting factor for internal battery parameter identification and used a WOA-BP (Whale Optimization Algorithm, Back Propagation Neural Network) neural network algorithm to estimate the SOC of lithium-ion batteries. Compared to the traditional BP algorithm, the SOC estimation MAE decreased by 1.9%, and the RMSE decreased by 4.1%. Research shows that data-driven methods are less dependent on mathematical models and rely on historical charging and discharging data for SOC estimation. These methods offer high estimation accuracy, excel at handling nonlinear issues, and can effectively optimize SOC estimation accuracy using neural network algorithms. Therefore, data-driven SOC estimation based on neural network algorithms has promising applications for hybrid tractors.
In conclusion, the second-order RC equivalent circuit model considering temperature effects can accurately describe the battery’s charge–discharge characteristics. Using neural network algorithms to optimize data-driven models can effectively improve SOC estimation accuracy. In this study, we select lithium iron phosphate (LiFePO4) batteries commonly used in tractors as the research object. We establish a second-order RC equivalent circuit model for LiFePO4 batteries under the influence of temperature based on experimental data. Furthermore, we use a snowballing algorithm combined with the long short-term memory network (SAO-LSTM) to estimate the SOC of the LiFePO4 battery.
The main research content of this paper is as follows: Section 2, based on real-time measurement data (current, voltage, temperature) of lithium iron phosphate batteries from the University of Maryland, completes battery parameter identification using the Forgetting Factor Recursive Least Squares (FFRLS) method. A Simulink model of the second-order RC equivalent circuit, considering temperature effects, is established in MATLAB/Simulink. Section 3 employs the SAO-LSTM model to estimate the SOC of the LiFePO4 battery, effectively improving SOC estimation accuracy. Simulation analysis of the SOC estimation of the LiFePO4 battery under the tractor plowing conditions is performed based on the whole-machine dynamic model in MATLAB/Simulink, and the results are compared with those from the conventional ampere-hour integration method. Section 4 and Section 5 discuss and summarize the research findings and experimental results of this paper.
2. Model Construction and Parameter Identification
As one of the primary power sources for tractor drive systems, power batteries directly impact the overall operational performance of the machinery. Currently, the mainstream power batteries used in vehicles include lead-acid batteries, lithium-ion batteries, LiFePO4 batteries, and nickel–metal hydride batteries. A comparative analysis of their key performance characteristics is summarized in Table 1.

Table 1.
Performance comparison of power batteries.
In hybrid tractors, the power battery serves as an auxiliary energy source that provides supplemental power during engine power shortages and vehicle startup. This application demands rapid energy response capability from the battery to meet the vehicle’s overall dynamic performance requirements. Consequently, LiFePO4 batteries have been selected as the focus of this study.
Existing research on the estimation of the SOC of batteries mainly focuses on the room temperature (25 °C). However, the actual working environment temperature of batteries varies. Under different temperature environments, the performance and relevant parameters of the battery will change, especially in extreme temperature environments. These changes not only affect the use of the battery and the estimation accuracy of the SOC but also influence the reliability of the BMS and the normal operation of the hybrid tractor. Therefore, taking the ambient temperature into account, this paper establishes a second-order RC model of lithium iron phosphate batteries based on the battery charging and discharging test data at different temperatures to conduct the research.
2.1. Equivalent Circuit Model
The common equivalent circuit models of power batteries mainly include the Rint model, the RC model, and PNGV model, GNL (General Nonlinear, GNL) model. The performance comparison of the equivalent circuit model is shown in Table 2.

Table 2.
Performance comparison of equivalent circuit models.
Therefore, in this paper, a second-order RC model is adopted to establish the physical model of the lithium-ion battery [24]. The equivalent circuit model is shown in Figure 1.
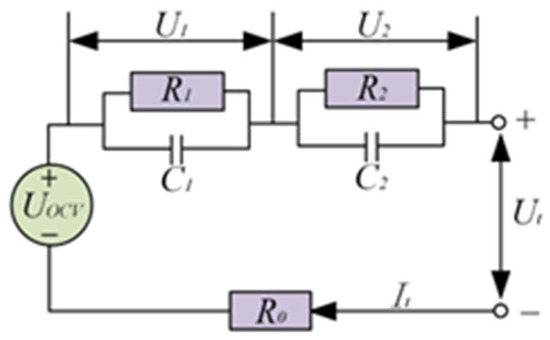
Figure 1.
Second-order RC circuit equivalent model.
This model is composed of an ideal voltage source , an ohmic internal resistance , and two RC parallel circuits. is the open-circuit voltage of the battery; is the circuit current; is the internal resistance of electrochemical polarization; is the capacitance of electrochemical polarization; is the internal resistance of concentration polarization; is the capacitance of concentration polarization; is the ohmic internal resistance; is the load voltage.
According to Kirchhoff’s voltage law and Kirchhoff’s current law, the dynamic equations of the second-order RC model are shown in Equations (1) and (2) as follows:
In these equations, represents the open-circuit voltage, and is a function of the SOC; t is the time.
2.2. OCV–SOC Characteristics at Different Temperatures
As one of the important decision-making factors for energy management, SOC plays a crucial role in the overall vehicle energy management, improving the capacity and energy utilization rate of power batteries, preventing overcharging and over-discharging of power batteries, and ensuring the safety of power battery usage. Among them, the SOC refers to the state of charge of the power battery, representing the ratio of the current power of the power battery to its total capacity:
In the formula, is the current electric capacity of the power battery, with the unit ; is the total capacity of the power battery, with the unit .
The dynamic change of SOC of the power battery is as follows:
In the formula, represents the discharging process, represents the charging process; is the coulombic efficiency of the power battery, which refers to the ratio of the discharged capacity to the charged capacity of the power battery within one cycle.
This paper conducts research by referring to the performance test data set of lithium iron phosphate batteries from the Advanced Life Cycle Engineering Center of the University of Maryland. Taking the influence of temperature into account, it models the LiFePO4 battery, aiming to better estimate the SOC of the battery, optimize the monitoring and control of the battery by BMS, and improve the overall performance of the hybrid tractor [25]. This data set conducts tests on lithium iron phosphate batteries in seven temperature environments of −10 °C, 0 °C, 10 °C, 20 °C, 30 °C, 40 °C, and 50 °C. The battery OCV—SOC—T curve is shown in Figure 2.
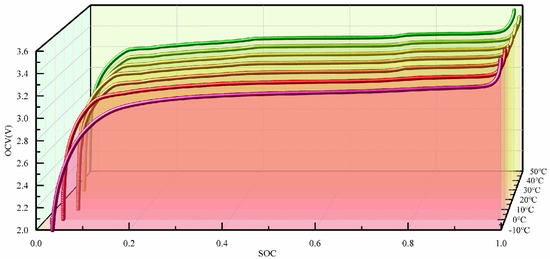
Figure 2.
LiFePO4 battery OCV—SOC—T curve.
The relevant data show that, when the battery capacity is high, the correlation decreases. Under different temperatures, there are significant differences in the charging and discharging curves of the battery. The temperature characteristics can affect the accuracy of battery modeling and the estimation of SOC. Therefore, the influence of temperature must be fully considered during the development of the algorithms for BMS.
To reduce the errors caused by the hysteresis characteristics, taking the room temperature environment of 25 °C as an example, the Curve Fitting toolbox in MATLAB is used to perform a ninth-degree polynomial fitting on the average value of OCV in the charging and discharging experiments. The fitting curve is shown in Figure 3, and the obtained polynomial function is shown in Equation (5).

Figure 3.
SOC–OCV fitting curve at room temperature (25 °C).
The SOC–OCV curves in seven temperature environments of −10 °C, 0 °C, 10 °C, 20 °C, 30 °C, 40 °C, and 50 °C are successively fitted using this method, which is convenient for subsequent calculations.
2.3. Parameter Identification of LiFePO4 Batteries Based on FFRLS
In this paper, the parameters of the power battery are identified by using data such as the real-time measured current, voltage, and temperature of the power battery based on the least squares method with a forgetting factor. The recursive least squares method is a recursive algorithm improved based on the least squares method. The recursive least squares method with a forgetting factor introduces the forgetting factor on the basis of the recursive least squares method, which effectively reduces the influence of old data in the variance matrix and can obtain more accurate identification results, so as to realize the online update of the model parameters.
The main steps of FFRLS are as follows:
- (1)
- Perform the Laplace transform on the battery model according to Equations (1) and (2), and then we have the following:
In the formula, is the Laplace operator in the complex frequency domain.
- (2)
- Use the bilinear transformation to convert it from the continuous domain to the discrete domain, and then we have the following:
In the formula, is the sampling period, in seconds; is the domain value operator of the discrete system.
Let the following be true:
In the formula, is the internal voltage drop of the battery, ; is the operating moment.
- (3)
- Inverse Laplace transformation:
The difference equation corresponding to Equation (9) in the discrete domain can be expressed as follows:
In the formula, () are the coefficients related to the model parameters.
Define the data matrix and parameter matrix of the system as follows:
Then, we have the following:
- (4)
- After arrangement, the recursive formula of the FFRLS algorithm is obtained as follows:
In the formula, is the gain matrix of the algorithm; is the covariance matrix; is the system observation matrix at the moment; is the corresponding parameter matrix; is the forgetting factor, and in this paper, .
The calculation flow chart of the FFRLS algorithm is shown in Figure 4 as follows:
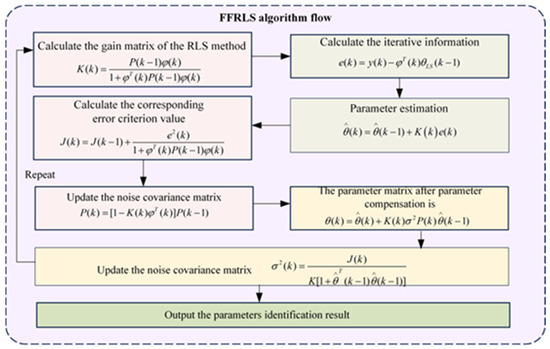
Figure 4.
Flowchart of FFRLS algorithm calculation.
The parameter identification results of LiFePO4 batteries based on FFRLS at different temperatures are as Table 3, Table 4, Table 5, Table 6 and Table 7 follows:

Table 3.
Parameter identification results of LiFePO4 batteries based on FFRLS at different temperatures.

Table 4.
Parameter identification results of LiFePO4 batteries based on FFRLS at different temperatures.

Table 5.
Parameter identification results of LiFePO4 batteries based on FFRLS at different temperatures.

Table 6.
Parameter identification results of LiFePO4 batteries based on FFRLS at different temperatures.

Table 7.
Parameter identification results of LiFePO4 batteries based on FFRLS at different temperatures.
2.4. LiFePO4 Batteries Modeling
According to the identified parameters, a Simulink model of the LiFePO4 battery is established in MATLAB/Simulink using the second-order RC equivalent circuit model, as shown in Figure 5. This model is only used for voltage simulation verification and does not calculate the battery SOC.
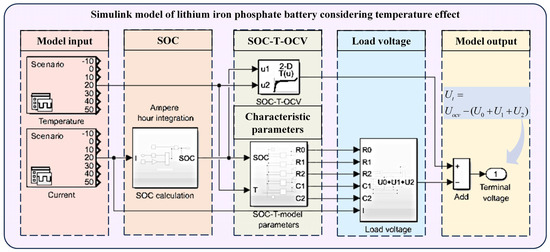
Figure 5.
Simulink model of LiFePO4 battery considering temperature effect.
3. SOC Estimation Method for Lithium Iron Phosphate Batteries Based on SAO-LSTM
Accurate estimation of SOC is a fundamental prerequisite for ensuring the safe, efficient, and reliable application of lithium iron phosphate batteries in hybrid tractors, and it is also one of the key technologies to promote the large-scale application of hybrid tractors in agricultural production. In order to improve the accuracy and reliability of the SOC estimation for lithium iron phosphate batteries, this paper proposes a SAO-LSTM method. This method can significantly enhance the accuracy of the SOC estimation for lithium iron phosphate batteries while taking into account the influence of temperature.
3.1. SAO
In traditional algorithms, the particle swarm optimization algorithm relies on the historical optimum of individuals and groups and is prone to falling into local optimum in the later stage. It has strong development ability but insufficient global search ability. Genetic algorithms rely on the randomness of crossover and mutation operations, which may lead to slow convergence speed or high resource consumption.
The Snow Ablation Optimization (SAO) algorithm mimics the sublimation and melting behavior of snow. During the melting process, snow can transform into liquid water, which then evaporates into water vapor. Meanwhile, snow can also directly turn into vapor through sublimation. The optimization can be achieved by adaptively adjusting the search range to balance global exploration and local development. The SAO algorithm divides the population into two sub-populations. One is focused on exploration, searching for new possible solutions; the other is focused on exploitation, optimizing the known solutions. This mechanism helps to discover potential excellent solutions and also enables the use of these solutions to find better results [26].
During the exploration phase, snow or the liquid water transformed from snow turns into vapor. Due to the irregularity of the movement, the search individuals show highly dispersed characteristics. Therefore, in this phase, Brownian motion is used to simulate the actual situation:
Brownian motion explores the potential regions in the search space by using dynamic and uniform step sizes, which can effectively reflect the diffusion of steam within the search space:
Among them, is the current optimal solution, and represents an individual randomly selected from a number of elite populations.
The centroid of the population is expressed as follows:
Among them, and represent the second-best and the third-best individuals in the current population, respectively. represents the centroid position of the individuals with the top 50% fitness values.
In the formula, represents the number of leaders, which is half of the total number of the entire population.
During the exploitation phase, snow transforms into liquid water through the melting process. The search individuals will develop high-quality solutions around the current best solution. The snowmelt model uses the degree–day method to reflect the snowmelt process:
In the formula, is the snowmelt rate; is the daily average temperature; is the base temperature, which is usually set to 0.
, we have the following:
Among them, is as follows:
Then the snowmelt rate can be expressed as follows:
Among them, is as follows:
Then, in the exploitation stage of the SAO algorithm, the position update can be expressed as follows:
Therefore, the complete position update of the SAO algorithm is as follows:
3.2. LSTM
The Long Short-Term Memory (LSTM) is improved from the Recurrent Neural Network (RNN) and is specifically designed to handle sequential data. It effectively solves the problems of gradient vanishing or gradient explosion that are likely to occur in the RNN during the training process. The structure of the LSTM is shown in Figure 6. The LSTM unit is composed of a forget gate, an input gate, an output gate, and a memory cell. Among them, the forget gate uses the sigmoid activation function to decide whether to forget the information of the previous memory unit, and the input gate determines which new information will be added to the storage unit. This decision is divided into two parts: first, the sigmoid activation function is used to control the weight of the added information; second, the tanh activation function is used to provide candidate values for the new information [27]. Through this process, the combination of the outputs of the forget gate and the input gate completes the update of the memory unit. Then, the output gate decides which information will be transmitted from the storage unit to the output.
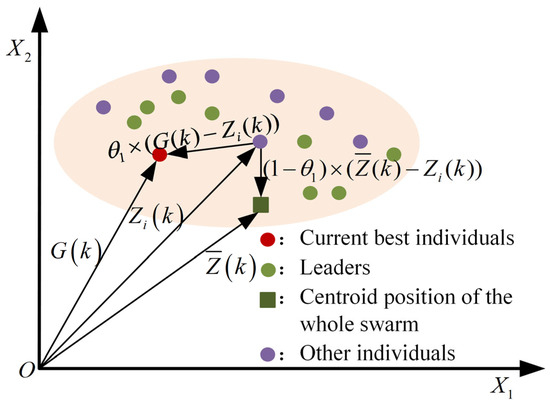
Figure 6.
SAO algorithm optimization process.
The forward propagation process of the LSTM neural network is shown in Figure 7.
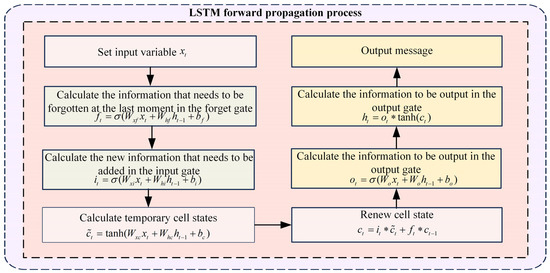
Figure 7.
LSTM forward propagation process.
Among them, , , , and represent the forget gate, input gate, output gate and memory unit, respectively. and represent the input and output of the LSTM unit at time t, respectively. and represent the interconnection weight matrix and bias parameters inside the network, respectively. The value range of the activation function is [0, 1], and this parameter can determine the degree of information transmission ability, where 0 indicates complete forgetting and 1 indicates complete retention, as described in Equation (26). Different from the function, the hyperbolic tangent function (tanh) does not control the retention or forgetting of information. It can scale the value of the input information to the range [−1, 1], which is crucial for updating the memory storage unit and generating the output value, as shown in Equation (27).
3.3. SAO LSTM
This paper proposes an SAO-LSTM method to significantly improve the accuracy of SOC estimation for lithium iron phosphate batteries while taking into account the influence of temperature. The estimation process of this method is shown in Figure 8.
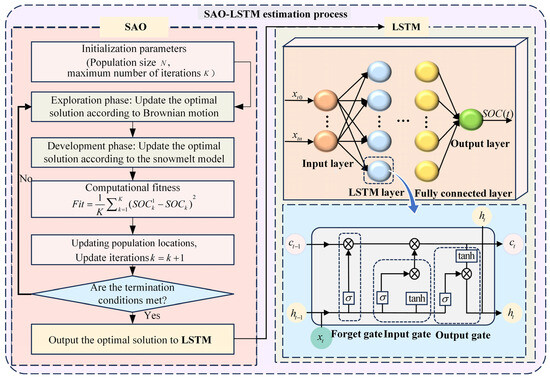
Figure 8.
SAO-LSTM estimation process.
In this study, the current data from the plowing operation process of a parallel hybrid tractor in a previous research project were used as the test dataset to carry out SOC estimation of lithium iron phosphate batteries based on SAO-LSTM [28]. The iteration curve of SAO-LSTM is shown in Figure 9, the comparison of prediction results for the test dataset is presented in Figure 10, the comparison of prediction results for the training dataset is shown in Figure 11, the prediction error of SAO-LSTM on the test dataset is displayed in Figure 12, the effect diagram of the training dataset is presented in Figure 13, and the effect diagram of the test dataset for SAO-LSTM is shown in Figure 14.
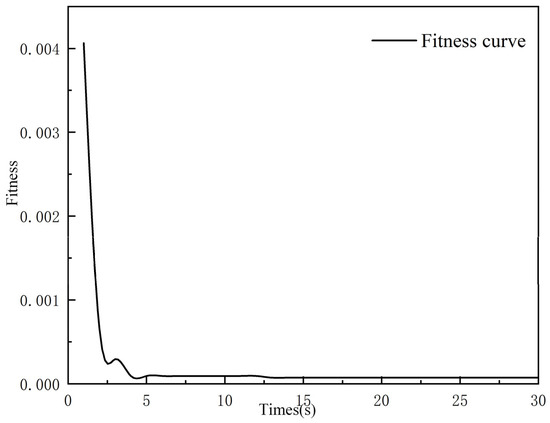
Figure 9.
SAO-LSTM iteration curve.
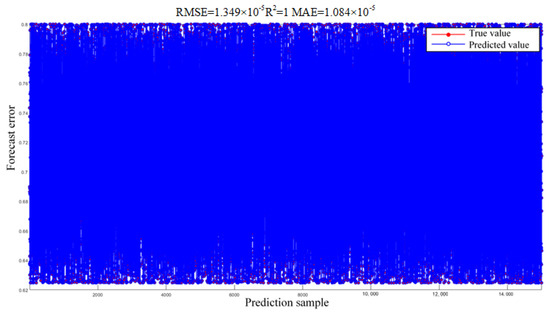
Figure 10.
Comparison of test set prediction results.
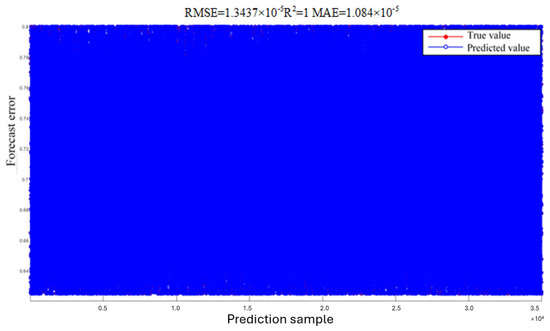
Figure 11.
Comparison of training set prediction results.
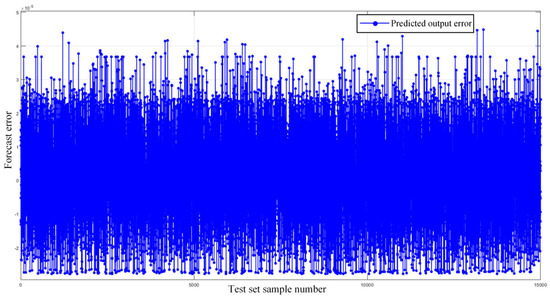
Figure 12.
SAO-LSTM test set prediction error.
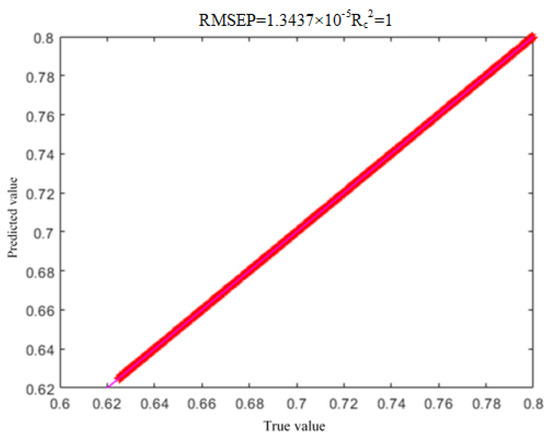
Figure 13.
Training set renderings.
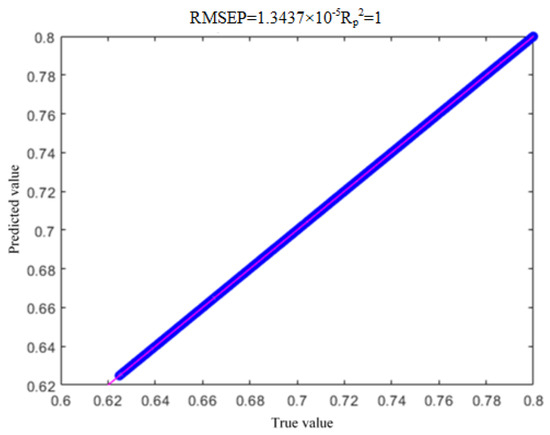
Figure 14.
Test set rendering.
4. Discussion
As can be seen from Figure 9, during the iterative process of the SAO-LSTM algorithm, the fitness value iterates from the initial to . The SAO-LSTM reduces the model error by 98.23%, indicating that this algorithm has a significant effect on improving the accuracy of SOC estimation for lithium iron phosphate batteries in hybrid tractors.
As can be observed from Figure 10 and Figure 11, the SOC predicted values optimized by SAO-LSTM have a more ideal fitting effect with the true values.
As shown in Figure 12, the prediction errors of SAO-LSTM are concentrated in , and the SOC estimation error < 0.001% meets the requirements of a high-precision BMS.
From Figure 13 and Figure 14, it can be seen that both the predicted values of the real dataset and the training dataset can achieve a good correspondence with the true values, and there is no overfitting phenomenon.
As can be seen from Table 8, for the SOC data of lithium iron phosphate batteries after being trained by SAO-LSTM, the Root Mean Squared Error (RMSE) is reduced by 0.39% compared with the original test dataset, the coefficient of determination (R2) is 1 for all cases, and the Mean Absolute Error (MAE) is reduced by 0.31%. The model has extremely strong generalization ability, effectively avoiding the overfitting phenomenon.

Table 8.
Comparison table of SOC estimation error evaluation based on SAO-LSTM.
This study employs the SAO algorithm to dynamically adjust temperature-dependent parameters (R0, R1, C1, R2, C2) in a second-order RC equivalent circuit model. By real-time recalibration of these parameters based on ambient operating temperature, the method compensates for nonlinear temperature effects on battery polarization dynamics. Simultaneously, an LSTM network is integrated to capture long-term dependencies in voltage-current sequences through its gating mechanisms, with temperature features fused into the input layer. The research results of this paper provide new ideas and methods for the SOC estimation of lithium iron phosphate batteries in hybrid tractors. However, there are still some issues worthy of further discussion. This paper mainly focuses on the influence of temperature on the SOC estimation of lithium iron phosphate batteries. However, battery aging will also lead to changes in model parameters. In the future, a multi-state joint estimation model can be constructed by combining the health state estimation of lithium iron phosphate batteries. At the same time, this paper mainly conducts SOC estimation based on current, voltage, and temperature data. In the future, by combining the battery health state estimation, a multi-state joint estimation model can be constructed, with the expectation of further improving the accuracy of the SOC estimation of lithium iron phosphate batteries [29].
5. Conclusions
This paper focuses on the problem of State of Charge (SOC) estimation of lithium iron phosphate batteries in hybrid tractors under different temperature environments and proposes an SOC estimation method based on the SAO-LSTM model. Through theoretical analysis, model construction, parameter identification, and simulation verification, the following conclusions are drawn:
- (1)
- Temperature has a significant impact on battery model parameters and SOC estimation. The analysis of the OCV–SOC curves at different temperatures and the results of parameter identification show that the open-circuit voltage, internal resistance, and polarization characteristics of the battery all change with temperature. Ignoring the temperature factor will lead to an increase in SOC estimation errors. Therefore, the influence of temperature must be considered in battery modeling and SOC estimation.
- (2)
- The second-order PNGV equivalent circuit model can well describe the dynamic characteristics of lithium iron phosphate batteries. The results of parameter identification based on the FFRLS algorithm show that this model can accurately reflect the charging and discharging behavior of the battery at different temperatures, providing a reliable model foundation for SOC estimation.
- (3)
- The SAO-LSTM model can effectively improve the accuracy of SOC estimation. By optimizing the hyperparameters of the LSTM network through the Snow Ablation Optimization (SAO) algorithm, the convergence speed and estimation accuracy of the model are significantly improved. The simulation results show that the Root Mean Squared Error (RMSE) of SAO-LSTM on both the test set and the training set is lower than 0.0000135, the coefficient of determination (R2) reaches 1, and the Mean Absolute Error (MAE) is lower than 0.0000109, verifying the superiority of this method.
- (4)
- The simulation under the actual working conditions of the tractor verifies the practicality of the method. The simulation analysis for the plowing working conditions shows that the SOC estimation results of the SAO-LSTM model are significantly better than those of the traditional ampere-hour integration method. It can adapt to complex and changeable load and temperature environments, providing reliable technical support for the energy management of hybrid tractors.
Author Contributions
Conceptualization, Y.W. and X.L.; methodology, Y.W. and X.L.; validation, J.Z. and X.L.; investigation, X.Y. and X.D.; data curation, M.L., L.W. and X.L.; writing—original draft preparation, X.L.; writing—review and editing, Y.W.; visualization, Y.W.; supervision, Y.W.; project administration, X.Y.; funding acquisition, X.Y. and Y.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Sponsored by Program for Science & Technology Innovation Talents in Universities of Henan Province, grant number 25HASTIT037; Henan Provincial Science and Technology Research Project, grant number 252102111166; State Key Laboratory of Intelligent Agricultural Power Equipment Open Project, grant number SKLIAPE 2025016; Henan Provincial Key Research and Development Program, grant number 231111112600; Henan Provincial Grant Program for Cultivating Young Key Faculty in Undergraduate institutions, grant number 2024GGJS051; The 3rd Heluo Young Talent Lift Project, grant number 2024HLTJ03; Henan Provincial Natural Science Foundation, grant number 242300420370.
Data Availability Statement
The original contributions presented in this study are included in this article; further inquiries can be directed to the corresponding author.
Conflicts of Interest
Mengnan Liu and Lin Wang were employed by Luoyang Tractor Research Institute Co., Ltd, and Xiaoxiao Du was employed by the First Tractor Company Limited. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Xie, B.; Wu, Z.; Mao, E. Development and Prospect of Key Technologies on Agricultural Tractor. Trans. Chin. Soc. Agric. Mach. 2018, 49, 1–17. [Google Scholar]
- Yang, M.; Wang, L.; Deng, X.; Lu, Y. A Review of Energy Management Strategy for Hybrid Tractors. Tract. Farm. Trans. 2024, 51, 7–15. [Google Scholar]
- Xu, L.; Zhang, J.; Yan, X.; Zhao, S.; Wu, Y.; Liu, M. Review of Research for Agricultural Equipment Electrification Technology. Trans. Chin. Soc. Agric. Mach. 2023, 54, 1–12. [Google Scholar]
- Xing, Y.; He, W.; Pecht, M.; Tsui, K.L. State of Charge Estimation of Lithium-Ion Batteries Using the Open-Circuit Voltage at Various Ambient Temperatures. Appl. Energy 2014, 113, 106–115. [Google Scholar] [CrossRef]
- Zhou, Y.; Sun, X.; Huang, L.; Lian, J. State of Health Estimation for Lithium Batteries Based on Full Life Cycle. J. Harbin Inst. Technol. 2021, 53, 55–62. [Google Scholar]
- Sun, Y.; Gong, Y.; Dong, L.; Wang, X.; Yan, Y.; Tang, X.; Dang, Y. Review of State Estimation for Battery Energy Storage Systems. J. Cent. South Univ. 2024, 55, 2320–2333. [Google Scholar]
- Wang, Y.; Tian, J.; Sun, Z.; Wang, L.; Xu, R.; Li, M.; Chen, Z. A Comprehensive Review of Battery Modeling and State Estimation Approaches for Advanced Battery Management Systems. Renew. Sustain. Energy Rev. 2020, 131, 110015. [Google Scholar] [CrossRef]
- Selvaraj, V.; Vairavasundaram, I. A Comprehensive Review of State of Charge Estimation in Lithium-Ion Batteries Used in Electric Vehicles. J. Energy Storage 2023, 72, 108777. [Google Scholar] [CrossRef]
- Pramanik, S.; Anwar, S. Electrochemical Model Based Charge Optimization for Lithium-Ion Batteries. J. Power Sources 2016, 313, 164–177. [Google Scholar] [CrossRef]
- Lai, X.; Zheng, Y.; Sun, T. A Comparative Study of Different Equivalent Circuit Models for Estimating State-of-Charge of Lithium-Ion Batteries. Electrochim. Acta 2018, 259, 566–577. [Google Scholar] [CrossRef]
- Xiong, R.; Tian, J.; Shen, W.; Sun, F. A Novel Fractional Order Model for State of Charge Estimation in Lithium Ion Batteries. IEEE Trans. Veh. Technol. 2019, 68, 4130–4139. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, Y.; Zhu, X.; Wang, Y. Adaptive SOC Estimation of Lithium-Ion Batteries Based on Multi-Model Fusion. Chin. J. Power Sources 2023, 47, 1158–1163. [Google Scholar]
- Liu, F.; Liu, X.; Su, W.; Bu, F. Online Joint Estimation Method of Key States of Lithium Batteries Based on a New Electrothermal Coupling Model. Proc. CSEE 2024, 44, 202–214. [Google Scholar]
- Wang, J.; Xiong, R.; Mu, H. Cooperative Estimation of State of Charge and Capacity for Lithium-Ion Power Batteries in Electric Vehicles Driven by Temperature and Aging Awareness Fusion. Trans. China Electrotech. Soc. 2020, 35, 4980–4987. [Google Scholar] [CrossRef]
- Jiang, S.; Chen, C.; Duan, Y.; Xiong, R. Research on Joint Estimation Method of SOC and SOH for Lithium-Ion Batteries Under Temperature and Aging Effects. J. Mech. Eng. 2024, 1, 266–275. [Google Scholar]
- Yi, F.; Shu, X.; Zhou, J.; Zhang, J.; Feng, C.; Gong, H.; Zhang, C.; Yu, W. Remaining Useful Life Prediction of PEMFC Based on Matrix Long Short-Term Memory. Int. J. Hydrogen Energy 2025, 111, 228–237. [Google Scholar] [CrossRef]
- Jia, C.; He, H.; Zhou, J.; Li, J.; Wei, Z.; Li, K.; Li, M. A Novel Deep Reinforcement Learning-Based Predictive Energy Management for Fuel Cell Buses Integrating Speed and Passenger Prediction. Int. J. Hydrogen Energy 2025, 100, 456–465. [Google Scholar] [CrossRef]
- Zhang, X.; Hou, J.; Wang, Z.; Jiang, Y. Study of SOC Estimation by the Ampere-Hour Integral Method with Capacity Correction Based on LSTM. Batteries 2022, 8, 170. [Google Scholar] [CrossRef]
- Liu, S.; Chen, D.; Yuan, L.; Xu, Z.; Jin, L.; Zhang, C. Mechanical Parameter Estimation and SOC Characterization of Lithium-Ion Batteries Based on Acoustic Homogenization Model. Proc. CSEE 2024, 44, 342–354. [Google Scholar] [CrossRef]
- Meng, J.; Stroe, D.-I.; Ricco, M.; Luo, G.; Teodorescu, R. A Simplified Model-Based State-of-Charge Estimation Approach for Lithium-Ion Battery with Dynamic Linear Model. IEEE Trans. Ind. Electron. 2019, 66, 7717–7727. [Google Scholar] [CrossRef]
- Zhang, Z.; Bai, S.; He, B.; Huang, J.; Zhang, W. SOC Estimation Technology for Lithium-Ion Power Batteries Based on Equivalent Circuit and Data-Driven Model. Technol. Innov. Appl. 2024, 14, 78–81. [Google Scholar] [CrossRef]
- Yu, Z.; Li, L.; Wei, K. SOC Estimation of Lithium Batteries Using Modified EKF Algorithm Considering Aging. J. Harbin Univ. Sci. Technol. 2022, 27, 125–132. [Google Scholar] [CrossRef]
- Li, H.; Liu, G.; Deng, W. SOC Estimation Method for Power Lithium Batteries Based on LSTM+UKF Fusion. China Meas. Test 2022, 48, 22–28. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Li, W.; Zhou, A. PNGV Equivalent Circuit Model and SOC Estimation Algorithm for Lithium Battery Pack Adopted in AGV Vehicle. IEEE Access 2018, 6, 23639–23647. [Google Scholar] [CrossRef]
- Battery Data. Center for Advanced Life Cycle Engineering. Available online: https://calce.umd.edu/battery-data (accessed on 27 November 2024).
- Deng, L.; Liu, S. Snow Ablation Optimizer: A Novel Metaheuristic Technique for Numerical Optimization and Engineering Design. Expert Syst. Appl. 2023, 225, 120069. [Google Scholar] [CrossRef]
- Chai, X.; Li, S.; Liang, F. A Novel Battery SOC Estimation Method Based on Random Search Optimized LSTM Neural Network. Energy 2024, 306, 132583. [Google Scholar] [CrossRef]
- Liu, X.; Wu, Y.; Zhang, J.; Zhao, Y.; Hu, Y.; Yan, X. Research on Energy Optimization Control Strategy for Parallel Hybrid Tractor Based on AIPSO. PLoS ONE 2025, 20, e0315369. [Google Scholar] [CrossRef]
- Zhang, L.; Hu, X.; Wang, Z.; Sun, F.; Dorrell, D.G. Fractional-Order Modeling and State-of-Charge Estimation for Ultracapacitors. J. Power Sources 2016, 314, 28–34. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).