Energy-Efficient Battery Thermal Management in Electric Vehicles Using Artificial-Neural-Network-Based Model Predictive Control
Abstract
1. Introduction
2. BTMS Control Model
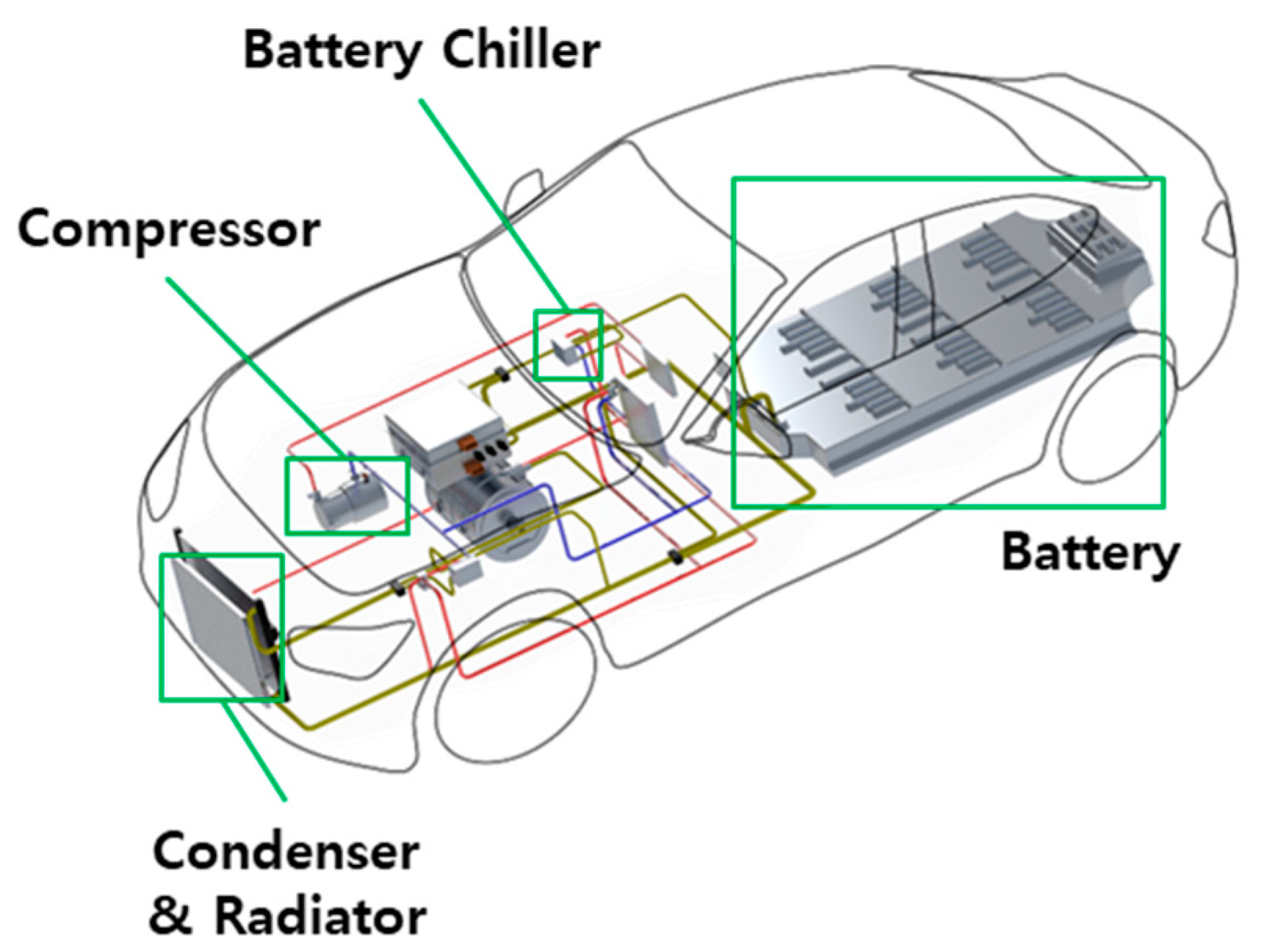
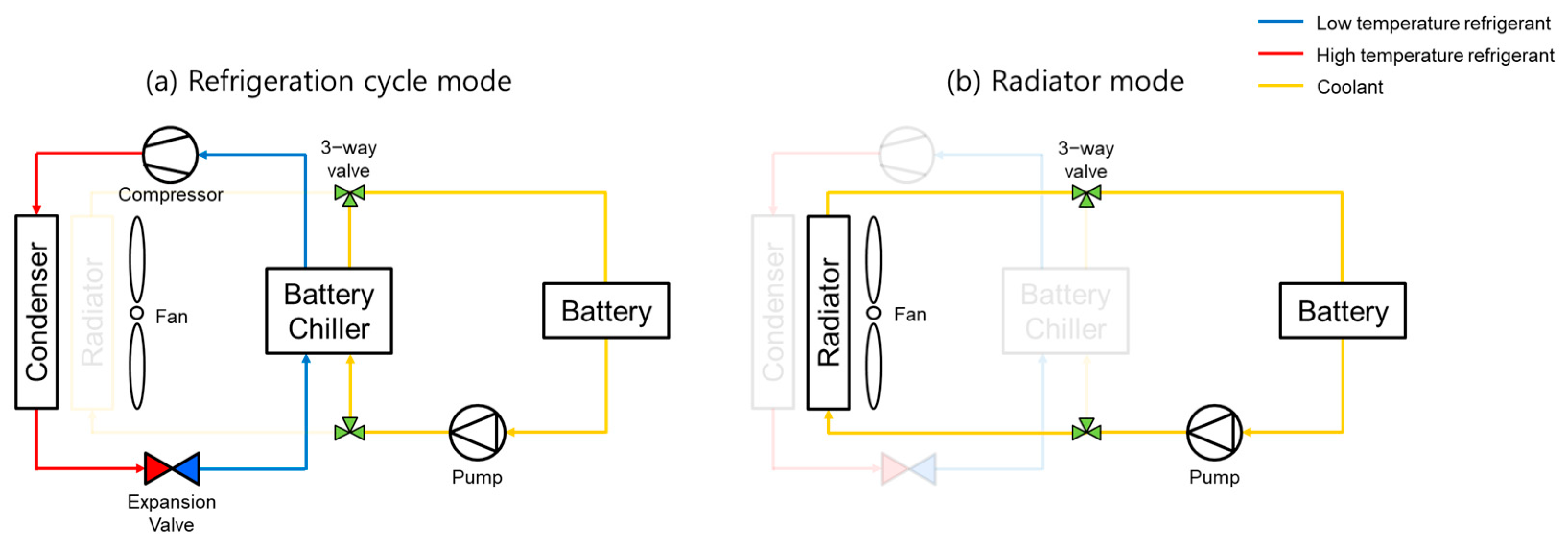
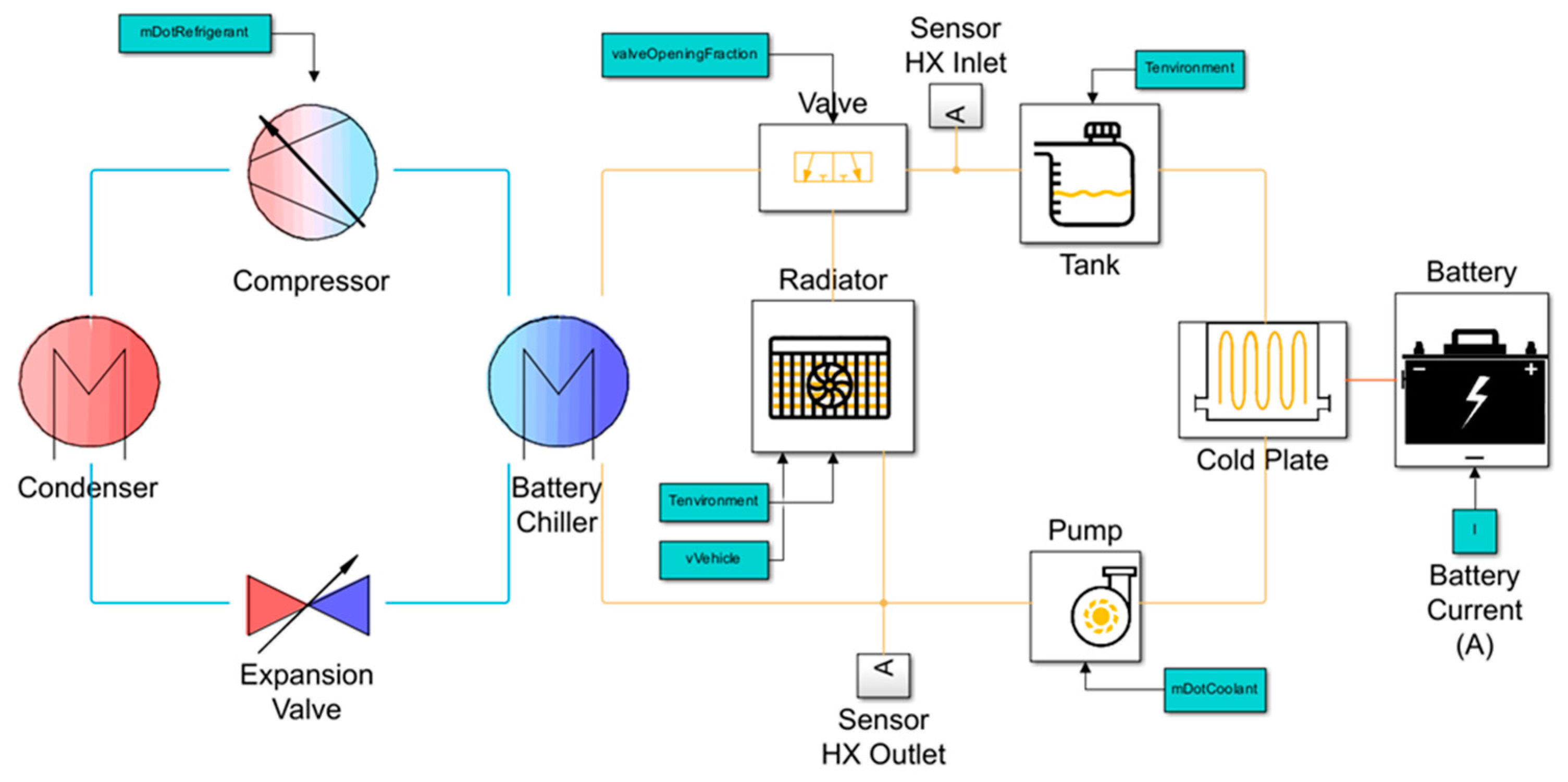
2.1. BTMS Operation
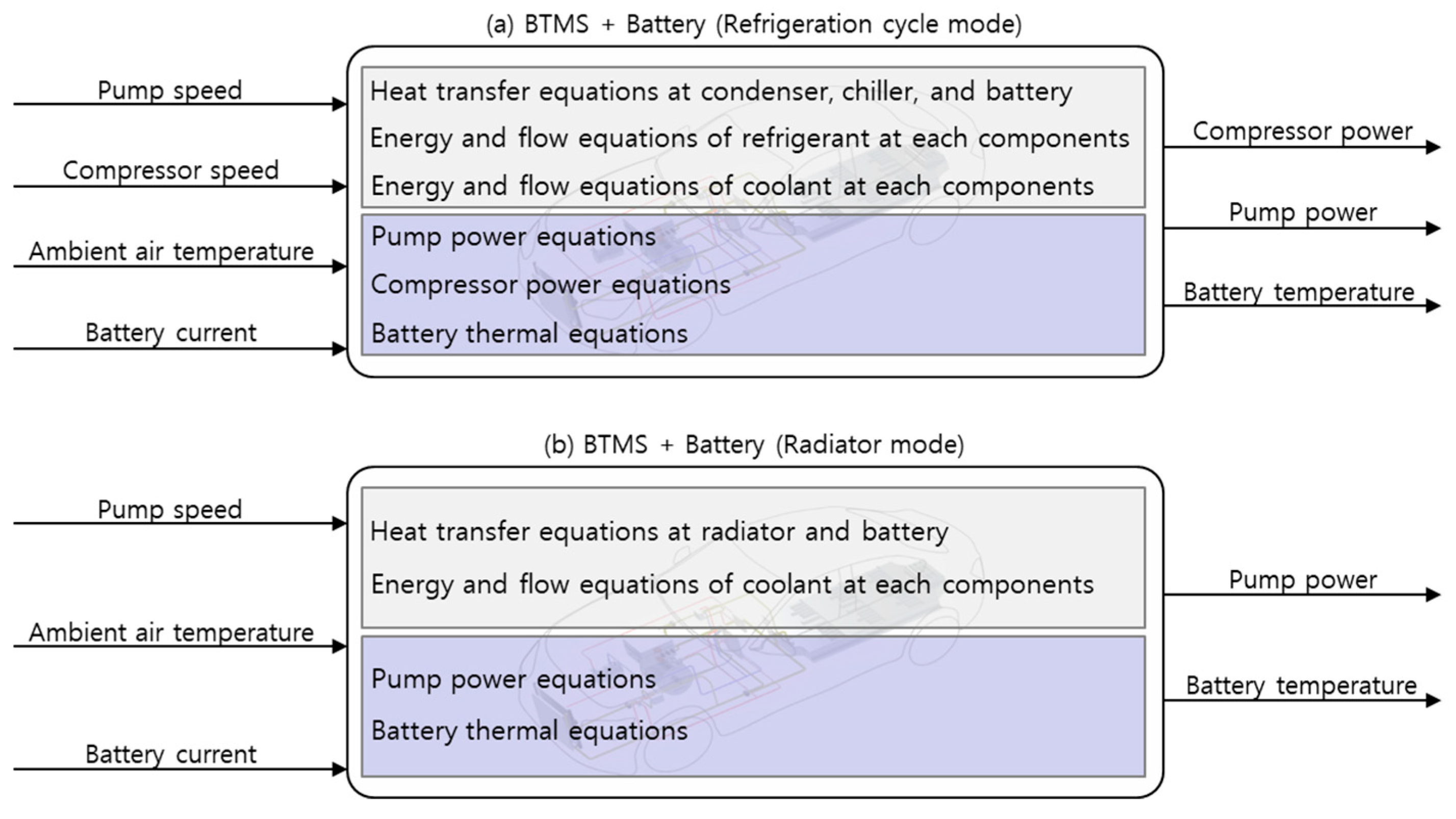
2.2. Model Structure
2.3. Model for the Refrigeration Cycle with the Coolant Cycle
2.4. Model for the Coolant Cycle
2.5. Battery Thermal Model
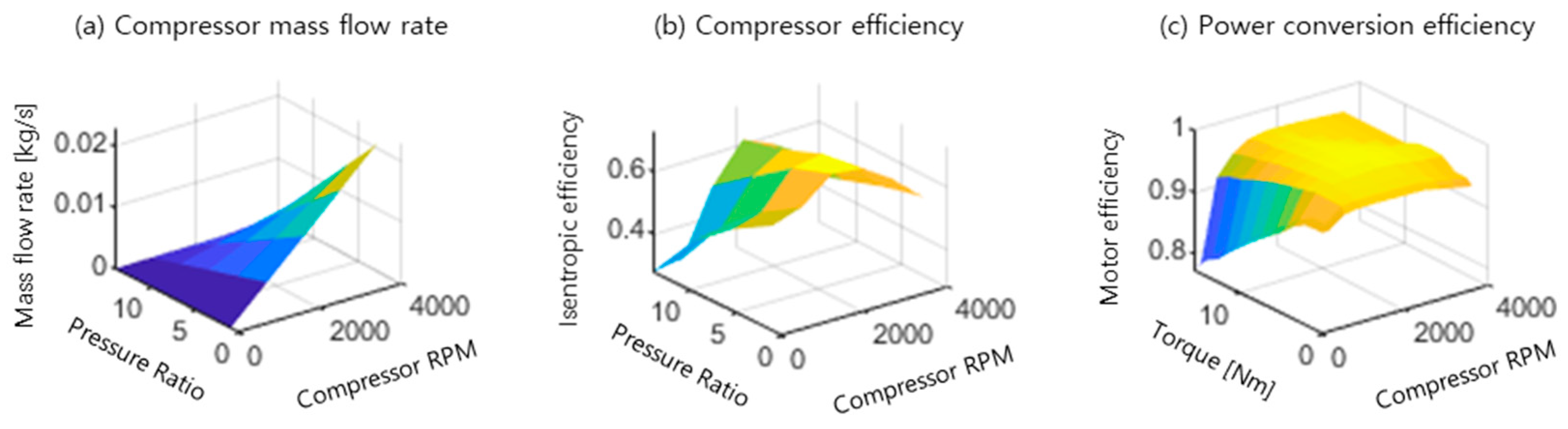
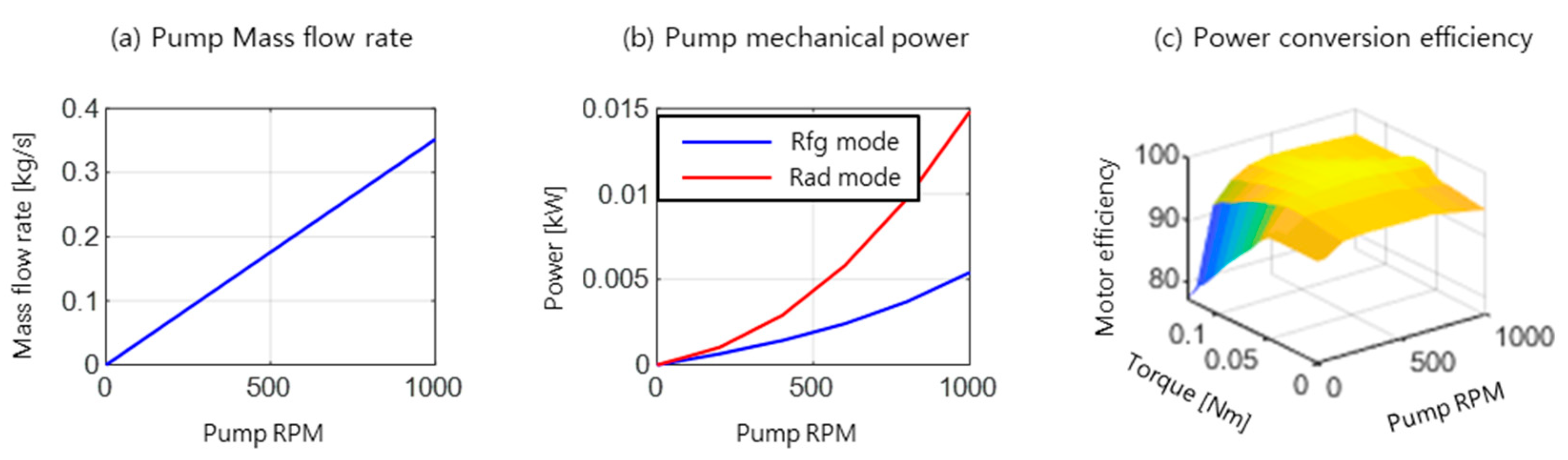
2.6. Compressor Power Model
2.7. Pump Power Model
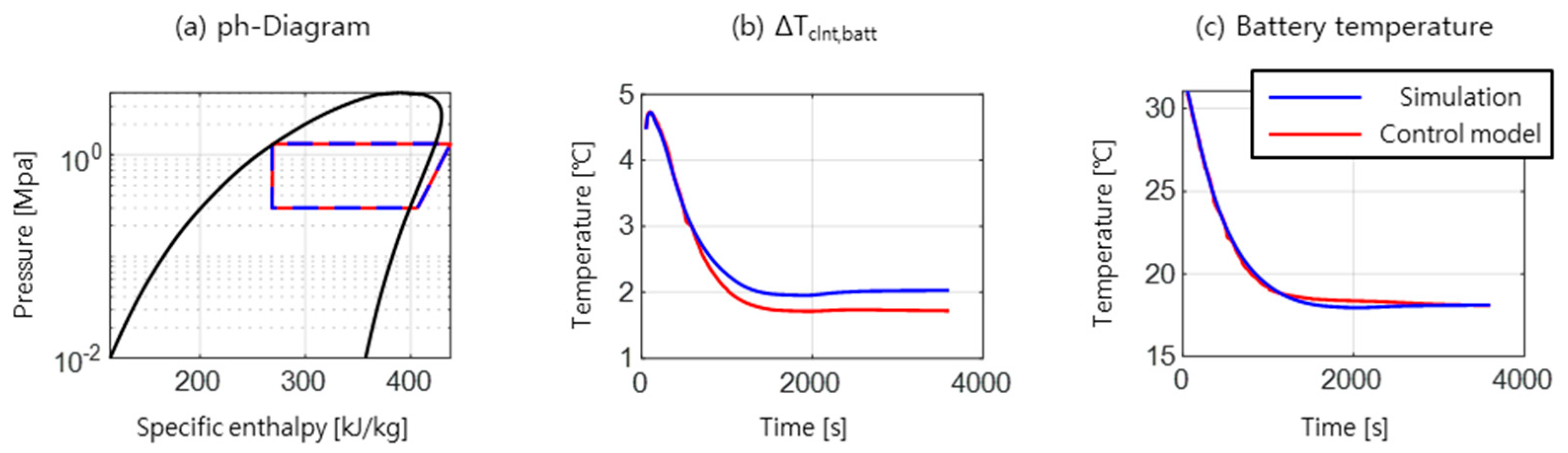
2.8. Model Training and Validation
3. Controller Design
3.1. Conventional MPC
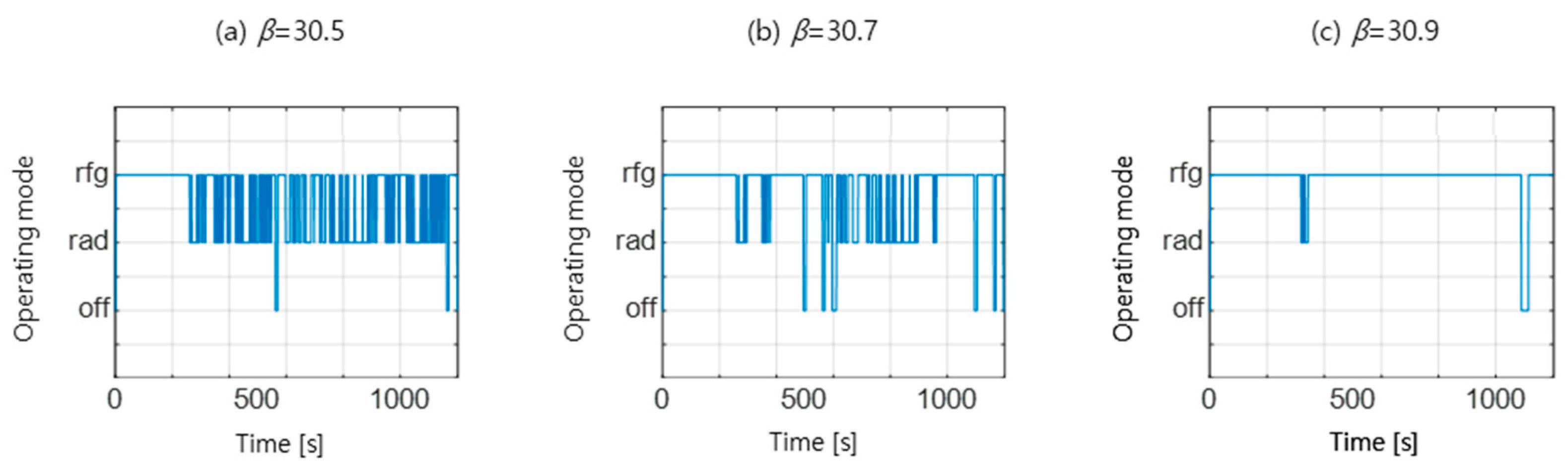
3.2. Mode Change Sensitivity in Conventional MPC
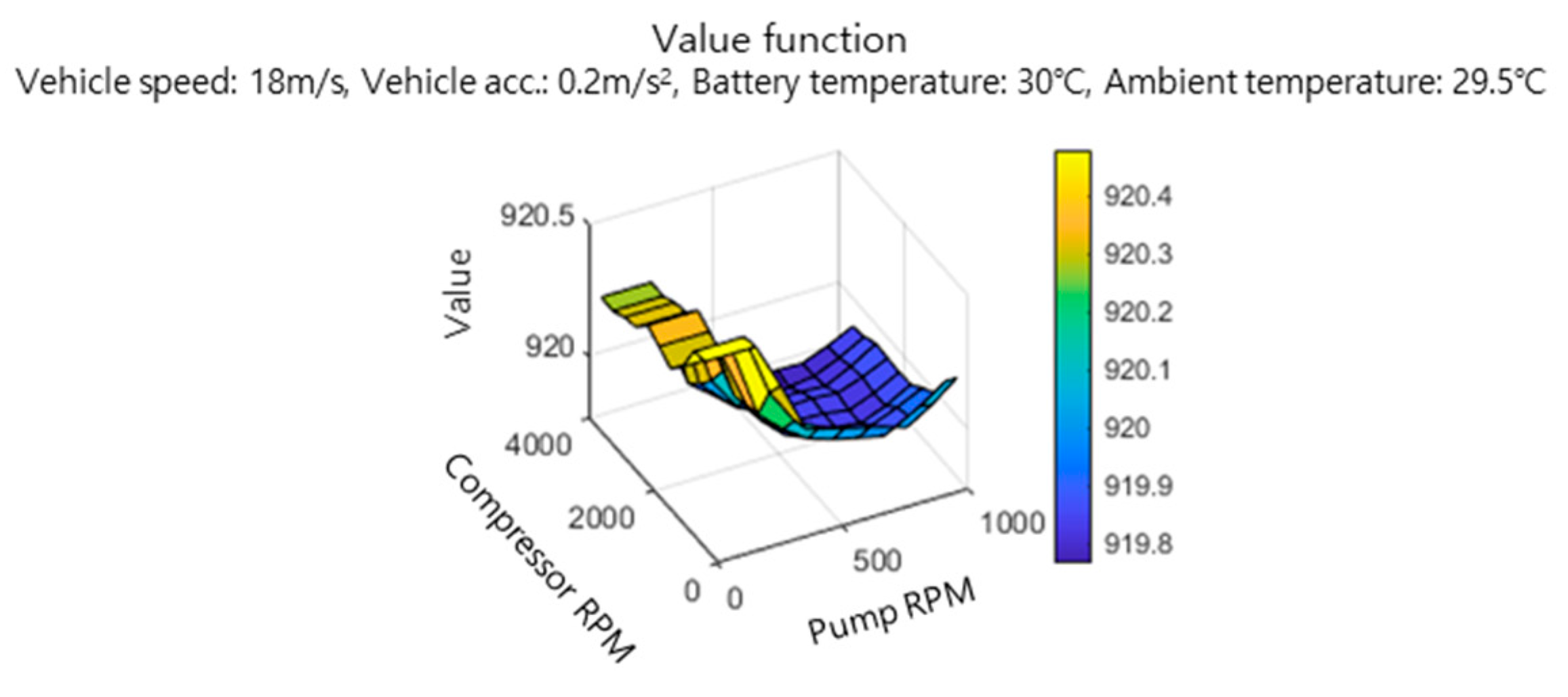
3.3. Infinity-Horizon MPC
| Algorithm 1 Value iteration |
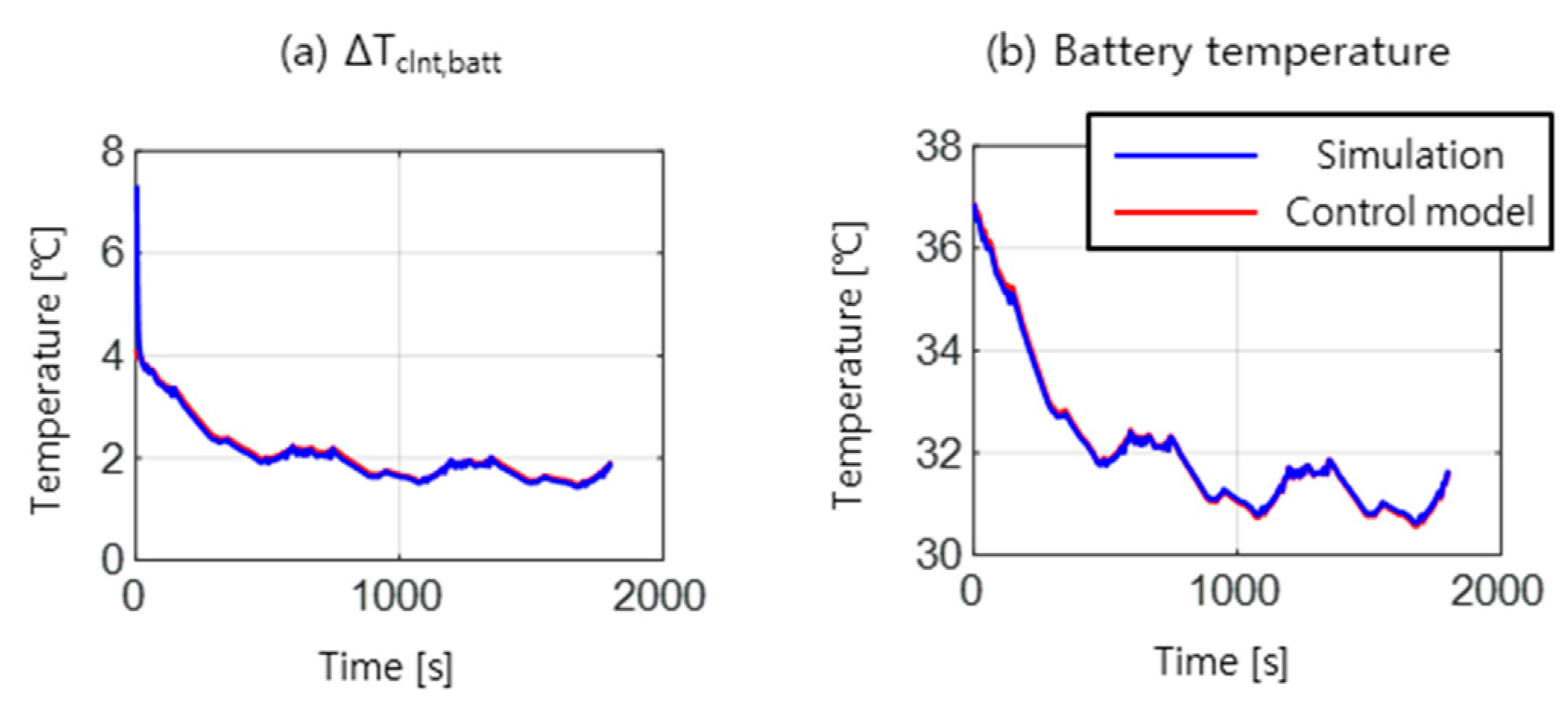
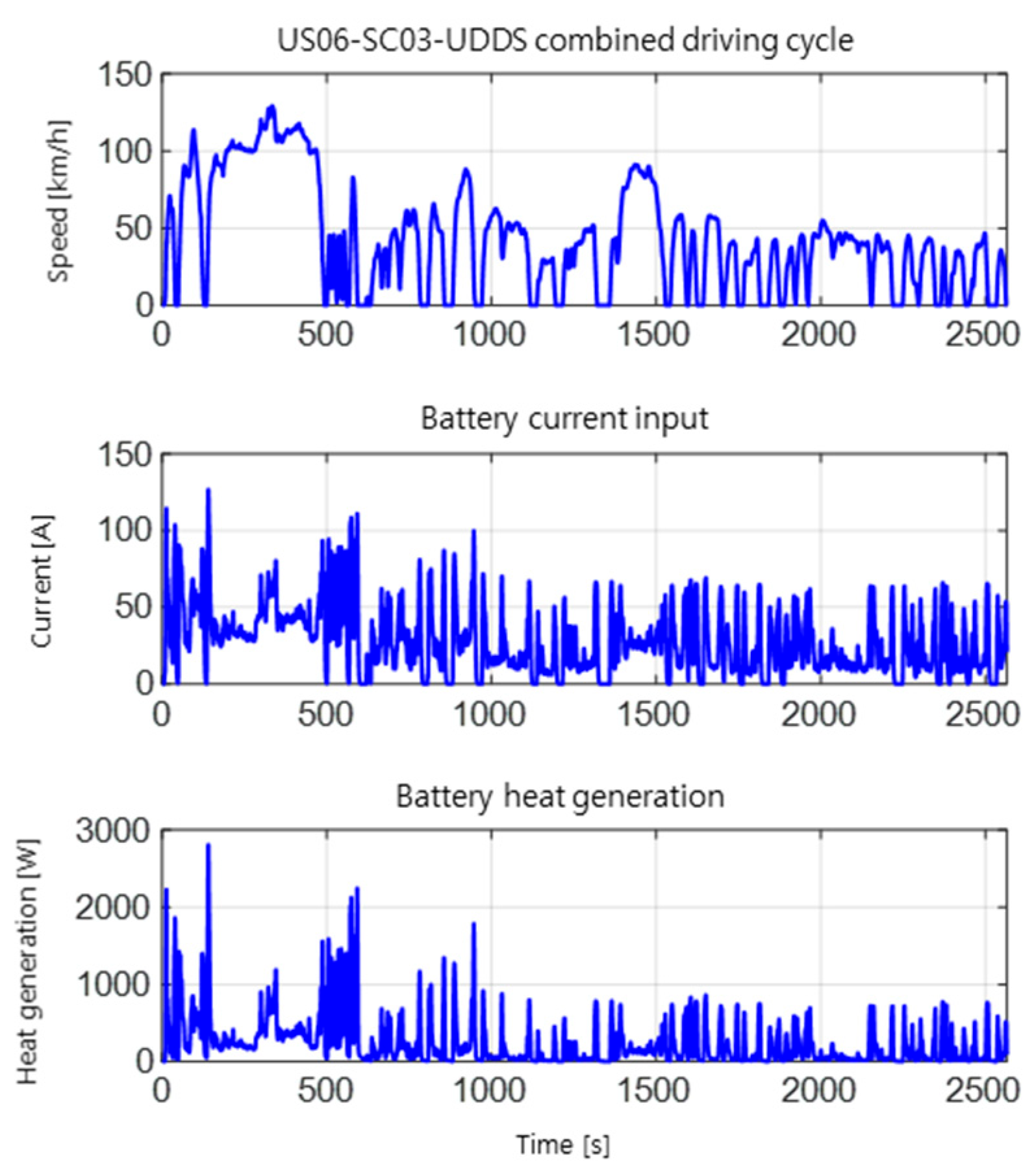
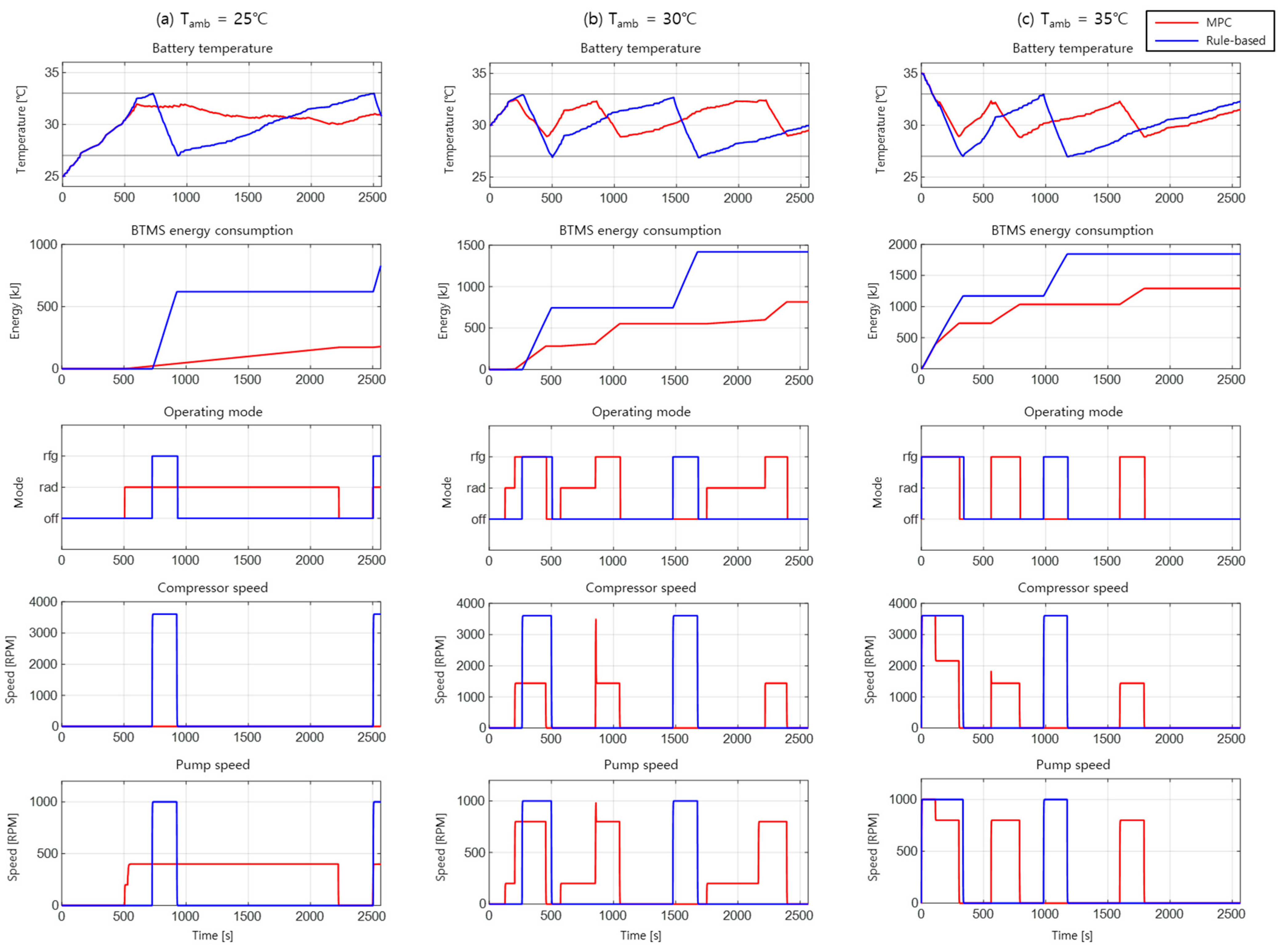
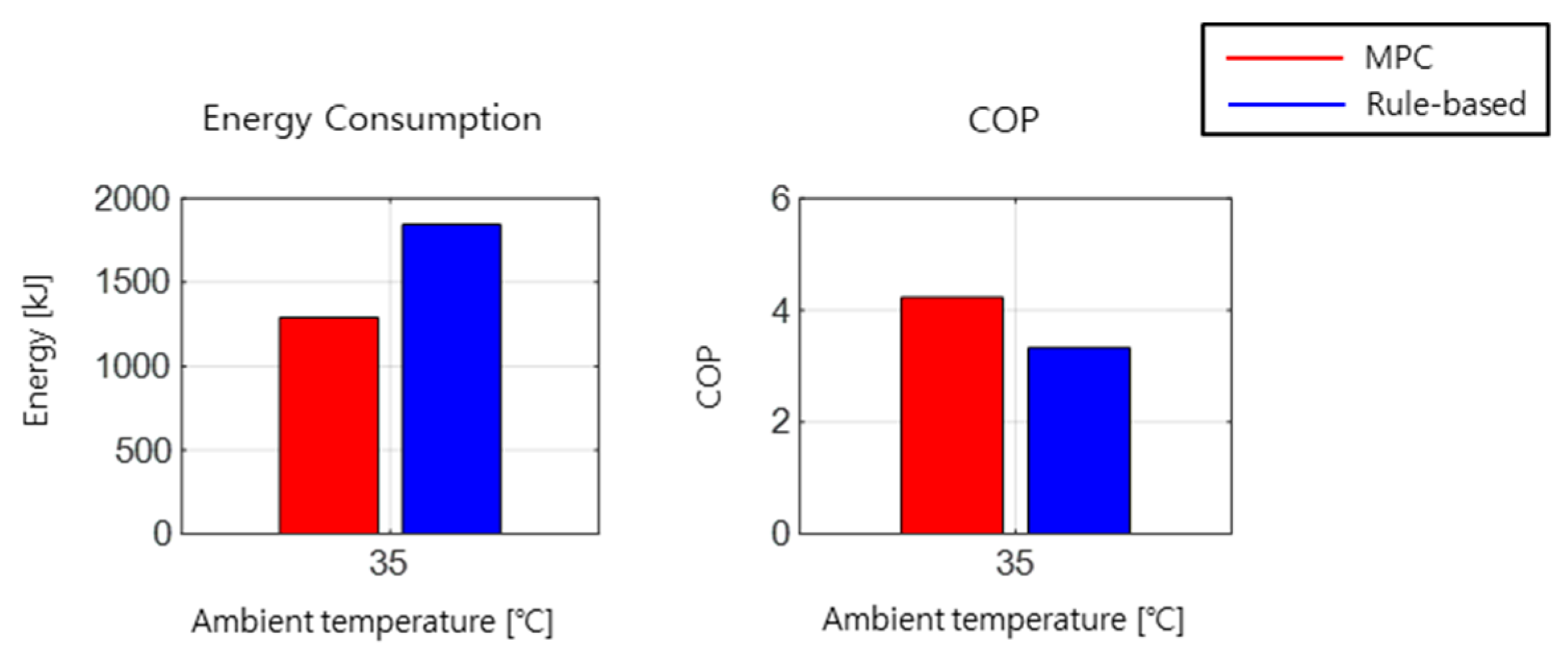
4. Controller Validation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Millo, F.; Rolando, L.; Fuso, R.; Mallamo, F. Real CO2 emissions benefits and end user’s operating costs of a plug-in Hybrid Electric Vehicle. Appl. Energy 2014, 114, 563–571. [Google Scholar] [CrossRef]
- Kim, J.; Oh, J.; Lee, H. Review on battery thermal management system for electric vehicles. Appl. Therm. Eng. 2019, 149, 192–212. [Google Scholar] [CrossRef]
- Pesaran, A.A. Battery thermal management in EV and HEVs: Issues and solutions. Battery Man 2001, 43, 34–49. [Google Scholar]
- Arora, S.; Kapoor, A.; Shen, W. A novel thermal management system for improving discharge/charge performance of Li-ion battery packs under abuse. J. Power Sources 2018, 378, 759–775. [Google Scholar] [CrossRef]
- Lei, Z.; Zhang, Y.; Lei, X. Improving temperature uniformity of a lithium-ion battery by intermittent heating method in cold climate. Int. J. Heat Mass Transf. 2018, 121, 275–281. [Google Scholar] [CrossRef]
- Lu, M.; Zhang, X.; Ji, J.; Xu, X.; Zhang, Y. Research progress on power battery cooling technology for electric vehicles. J. Energy Storage 2020, 27, 101–155. [Google Scholar] [CrossRef]
- Xu, J.M.; Zhang, C.Z.; Wan, Z.M.; Chen, X.; Chan, S.H.; Tu, Z.K. Progress and perspectives of integrated thermal management systems in PEM fuel cell vehicles: A review. Renew. Sustain. Energy Rev. 2022, 155, 111908. [Google Scholar] [CrossRef]
- Feng, X.; Ouyang, M.; Liu, X.; Lu, L.; Xia, Y.; He, X. Thermal runaway mechanism of lithium ion battery for electric vehicles: A review. Energy Storage Mater. 2018, 10, 246–267. [Google Scholar] [CrossRef]
- Kshetrimayum, K.S.; Yoon, Y.-G.; Gye, H.-R.; Lee, C.-J. Preventing heat propagation and thermal runaway in electric vehicle battery modules using integrated PCM and micro-channel plate cooling system. Appl. Therm. Eng. 2019, 159, 113797. [Google Scholar] [CrossRef]
- Chavan, S.; Venkateswarlu, B.; Prabakaran, R.; Salman, M.; Joo, S.W.; Choi, G.S.; Kim, S.C. Thermal runaway and mitigation strategies for electric vehicle lithium-ion batteries using battery cooling approach: A review of the current status and challenges. J. Energy Storage 2023, 72, 108569. [Google Scholar] [CrossRef]
- Suresh, C.; Awasthi, A.; Kumar, B.; Im, S.-k.; Jeon, Y. Advances in battery thermal management for electric vehicles: A comprehensive review of hybrid PCM-metal foam and immersion cooling technologies. Renew. Sustain. Energy Rev. 2025, 208, 115021. [Google Scholar] [CrossRef]
- Akinlabi, A.A.H.; Solyali, D. Configuration, design, and optimization of air-cooled battery thermal management system for electric vehicles: A review. Renew. Sustain. Energy Rev. 2020, 125, 109815. [Google Scholar] [CrossRef]
- Xu, J.; Guo, Z.; Xu, Z.; Zhou, X.; Mei, X. A systematic review and comparison of liquid-based cooling system for lithium-ion batteries. eTransportation 2023, 17, 100242. [Google Scholar] [CrossRef]
- Luo, J.; Zou, D.; Wang, Y.; Wang, S.; Huang, L. Battery thermal management systems (BTMs) based on phase change material (PCM): A comprehensive review. Chem. Eng. J. 2022, 430, 132741. [Google Scholar] [CrossRef]
- Gharehghani, A.; Rabiei, M.; Mehranfar, S.; Saeedipour, S.; Mahmoudzadeh Andwari, A.; García, A.; Reche, C.M. Progress in battery thermal management systems technologies for electric vehicles. Renew. Sustain. Energy Rev. 2024, 202, 114654. [Google Scholar] [CrossRef]
- Lee, J.T.; Kwon, S.; Lim, Y.; Chon, M.S.; Kim, D. Effect of air-conditioning on driving range of electric vehicle for various driving modes; SAE Technical Paper 2013-01-0040. In Proceedings of the Asia Pacific Automotive Engineering Conference, Bangkok, Thailand, 1–3 April 2013. [Google Scholar] [CrossRef]
- Huang, G.; Wang, S.; Xu, X. A robust model predictive control strategy for improving the control performance of air-conditioning systems. Energy Convers. Manag. 2009, 50, 2650–2658. [Google Scholar] [CrossRef]
- Cen, J.; Jiang, F. Li-ion power battery temperature control by a battery thermal management and vehicle cabin air conditioning integrated system. Energy Sustain. Dev. 2020, 57, 141–148. [Google Scholar] [CrossRef]
- Aprea, C.; Mastrullo, R.; Renno, C. Fuzzy control of the compressor speed in a refrigeration plant. Int. J. Refrig. 2004, 27, 639–648. [Google Scholar] [CrossRef]
- Ma, Y.; Duan, P.; Sun, Y.; Chen, H. Equalization of Lithium-Ion Battery Pack Based on Fuzzy Logic Control in Electric Vehicle. IEEE Trans. Ind. Electron. 2018, 65, 6762–6771. [Google Scholar] [CrossRef]
- Zhou, H.; Jia, F.; Jing, H.; Liu, Z.; Güvenç, L. Coordinated Longitudinal and Lateral Motion Control for Four Wheel Independent Motor-Drive Electric Vehicle. IEEE Trans. Veh. Technol. 2018, 67, 3782–3790. [Google Scholar] [CrossRef]
- Behrooz, F.; Mariun, N.; Marhaban, M.H.; Mohd Radzi, M.A.; Ramli, A.R. Review of Control Techniques for HVAC Systems—Nonlinearity Approaches Based on Fuzzy Cognitive Maps. Energies 2018, 11, 495. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, J. Self-adapting J-type air-based battery thermal management system via model predictive control. Appl. Energy 2020, 263, 114640. [Google Scholar] [CrossRef]
- Ma, Y.; Ding, H.; Mou, H.; Gao, J. Battery thermal management strategy for electric vehicles based on nonlinear model predictive control. Measurement 2021, 186, 110115. [Google Scholar] [CrossRef]
- Park, S.; Ahn, C. Computationally Efficient Stochastic Model Predictive Controller for Battery Thermal Management of Electric Vehicle. IEEE Trans. Veh. Technol. 2020, 69, 8407–8419. [Google Scholar] [CrossRef]
- He, H.; Jia, H.; Huo, W.; Yan, M. Stochastic Dynamic Programming of Air Conditioning System for Electric Vehicles. Energy Procedia 2017, 105, 2518–2524. [Google Scholar] [CrossRef]
- Tang, W.; Zhang, Y.J. A Model Predictive Control Approach for Low-Complexity Electric Vehicle Charging Scheduling: Optimality and Scalability. IEEE Trans. Power Syst. 2017, 32, 1050–1063. [Google Scholar] [CrossRef]
- Tian, Z.; Gan, W.; Zhang, X.L.; Gu, B.; Yang, L. Investigation on an integrated thermal management system with battery cooling and motor waste heat recovery for electric vehicle. Appl. Therm. Eng. 2018, 136, 16–27. [Google Scholar] [CrossRef]
- Jani, D.B.; Mishra, M.; Sahoo, P.K. Application of artificial neural network for predicting performance of solid desiccant cooling systems—A review. Renew. Sustain. Energy Rev. 2017, 80, 352–366. [Google Scholar] [CrossRef]
- Al-Waeli, A.H.A.; Sopian, K.; Yousif, J.H.; Kazem, H.A.; Boland, J.; Chaichan, M.T. Artificial neural network modeling and analysis of photovoltaic/thermal system based on the experimental study. Energy Convers. Manag. 2019, 186, 368–379. [Google Scholar] [CrossRef]
- Elsheikh, A.H.; Sharshir, S.W.; Abd Elaziz, M.; Kabeel, A.E.; Wang, G.; Zhang, H. Modeling of solar energy systems using artificial neural network: A comprehensive review. Sol. Energy 2019, 180, 622–639. [Google Scholar] [CrossRef]
- The Mathworks Inc. Electric Vehicle Thermal Management. 2021. Available online: https://www.mathworks.com/help/hydro/ug/sscfluids_ev_thermal_management.html (accessed on 9 April 2020).
- Xia, G.D.; Cao, L.; Bi, G.L. A review on battery thermal management in electric vehicle application. J. Power Sources 2017, 367, 90–105. [Google Scholar] [CrossRef]
- Park, S.; Ahn, C. Optimal Cooling Controller Design for Battery Thermal Management System of Electric Vehicle. IEEE Trans. Transp. Electrif. 2025, 11, 1529–1540. [Google Scholar] [CrossRef]
- Amini, M.R.; Kolmanovsky, I.; Sun, J. Hierarchical MPC for Robust Eco-Cooling of Connected and Automated Vehicles and Its Application to Electric Vehicle Battery Thermal Management. IEEE Trans. Control Syst. Technol. 2021, 29, 316–328. [Google Scholar] [CrossRef]
- Xie, Y.; Wang, C.; Hu, X.; Lin, X.; Zhang, Y.; Li, W. An MPC-Based Control Strategy for Electric Vehicle Battery Cooling Considering Energy Saving and Battery Lifespan. IEEE Trans. Veh. Technol. 2020, 69, 14657–14673. [Google Scholar] [CrossRef]
- Fan, Y.; Zuo, X.; Zhan, D.; Zhao, J.; Zhang, G.; Wang, H.; Wang, K.; Yang, S.; Tan, X. A novel control strategy for active battery thermal management systems based on dynamic programming and a genetic algorithm. Appl. Therm. Eng. 2023, 233, 121113. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nam, K.; Ahn, C. Energy-Efficient Battery Thermal Management in Electric Vehicles Using Artificial-Neural-Network-Based Model Predictive Control. World Electr. Veh. J. 2025, 16, 279. https://doi.org/10.3390/wevj16050279
Nam K, Ahn C. Energy-Efficient Battery Thermal Management in Electric Vehicles Using Artificial-Neural-Network-Based Model Predictive Control. World Electric Vehicle Journal. 2025; 16(5):279. https://doi.org/10.3390/wevj16050279
Chicago/Turabian StyleNam, Kiheon, and Changsun Ahn. 2025. "Energy-Efficient Battery Thermal Management in Electric Vehicles Using Artificial-Neural-Network-Based Model Predictive Control" World Electric Vehicle Journal 16, no. 5: 279. https://doi.org/10.3390/wevj16050279
APA StyleNam, K., & Ahn, C. (2025). Energy-Efficient Battery Thermal Management in Electric Vehicles Using Artificial-Neural-Network-Based Model Predictive Control. World Electric Vehicle Journal, 16(5), 279. https://doi.org/10.3390/wevj16050279






