1. Introduction
The integration of plug-in electric vehicles (PEVs) into modern microgrids presents operational challenges and optimization opportunities. Stochastic PEV charging can stress grid infrastructure during peak hours [
1], while their bidirectional power flow enables cost reduction and grid stabilization [
2]. Numerous studies optimize PEV charging schedules using event-driven model predictive control (MPC) [
3,
4,
5,
6]. These strategies adapt to dynamic arrivals/departures and stochastic renewable generation but often rely on fixed prediction horizons.
Other studies examine broader microgrid operational challenges using MPC dispatch frameworks, stochastic unit commitment, and optimization algorithms [
7,
8]. While effective in simulations, they generally lack mechanisms to adjust control horizons dynamically, reducing effectiveness under frequent fluctuations.
Real-time coordination methods, including distributed control schemes [
9,
10], decentralized fuzzy controllers [
11,
12], and multi-agent frameworks [
13,
14], improve flexibility. However, most assume static configurations and fail to adapt to sudden EV arrivals, SoC variations, or intermittent renewable outputs.
Another critical dimension is PEV battery degradation from frequent charging or discharging, especially under V2G operation, accelerates aging, leading to capacity fade and reduced service life [
15,
16,
17,
18,
19,
20,
21,
22]. Existing models using fixed penalty costs [
23,
24] or linear approximations [
25,
26] may not fully capture nonlinear relationships between aging and operational parameters (DoD, charge/discharge rates, temperature). Without accurate degradation modeling, real-time scheduling risks undermining V2G sustainability and PEV owner economics.
To address these limitations, this work introduces a real-time V2G-enabled microgrid-optimization framework with three key innovations:
- 1.
Real-time coordination optimizing power flows based on current grid state and PEV availability.
- 2.
Dynamic horizon adjustment that scales prediction windows based on EV connection patterns and renewable generation.
- 3.
Bidirectional power flow optimization incorporating detailed battery-degradation constraints.
To clearly contextualize our contribution within the broader research landscape and differentiate our approach from existing methods,
Table 1 and
Table 2 provide systematic comparisons across multiple dimensions.
Table 2 positions our work within the field of PEV charging-optimization methodologies, while
Table 1 offers a focused analysis of MPC-specific strategies, highlighting the novel integration of economic signals and degradation-aware triggering mechanisms that distinguish our DHO framework from both conventional and adaptive MPC approaches.
Simulation results demonstrate the practical efficacy of this integrated approach. The proposed DHO framework achieves a 12.6% reduction in operational costs compared to conventional strategies, while simultaneously lowering peak demand from 170 to 130 (23.5% reduction). The framework significantly improves user satisfaction by increasing average final State of Charge from 74% to 86.5% while suggesting a potential 18% reduction in battery degradation under the applied semi-empirical model. Furthermore, the system enables substantial V2G revenue generation and contributes to environmental sustainability through a 6.2% reduction in carbon emissions. These comprehensive improvements highlight the value of co-optimizing economic, operational, and battery health objectives within a unified adaptive framework.
2. System Characterization and Mathematical Formulation
The microgrid (MG) integrates loads, PV and wind generation, the utility grid, and multiple EVCSs with bidirectional power capabilities (
Figure 1). PV and wind sources are considered distributed energy sources (DESs). The system aims to minimize grid electricity consumption by utilizing local renewable generation and storing surplus DES power in EV batteries through vehicle-to-grid (V2G) operation.
2.1. PV Array Modeling
PV output is stochastic due to weather variations. The generated PV power
depends on solar irradiance
G and cell temperature
:
Here,
is the rated PV power at standard test conditions (STC),
,
, and
is the temperature coefficient in
. The cell temperature is estimated from ambient temperature
and irradiance:
where NOCT is the nominal operating cell temperature.
Solar irradiance variability is modeled with a beta distribution due to its bounded nature. The PDF is:
where
x is normalized irradiance, and
,
are shape parameters computed from the mean
and standard deviation
of measured irradiance:
Ambient temperature is treated as a normal random variable with time-varying mean and standard deviation:
2.2. EV Load Modeling
EV charging and discharging behavior introduces stochastic loads into the microgrid. To capture this, we model vehicle arrival time at charging stations, daily driving distance, battery SoC dynamics, and charging/discharging constraints. Monte Carlo simulation is employed to account for randomness.
2.2.1. Arrival Time Modeling
EV arrival times at the charging station are bimodal due to typical commuting patterns, with peaks in the morning and evening. This is modeled as a bimodal normal distribution:
where
h and
h.
2.2.2. Daily Driving Distance
Daily distance traveled by each EV,
D, is modeled as a log-normal random variable:
where
and
are the mean and standard deviation of the natural logarithm of daily distance.
2.2.3. SoC Dynamics and Charging Requirements
Given the daily distance
D, the required final SoC for the next day is:
where
E is the energy consumption per km and
is the EV battery capacity. Charging time to reach this SoC is:
with charging power
and efficiency
. SoC evolves dynamically:
2.2.4. Charging/Discharging Constraints
EV charging/discharging power is limited by station rating and battery characteristics:
To prevent simultaneous charging and discharging, a binary control variable
is introduced:
with
for charging and
for discharging.
2.2.5. Scheduling Rules and Assumptions
The EV scheduling algorithm enforces:
- 1.
EVs can only be dispatched after returning home
- 2.
Charging/discharging power must remain within battery limits
- 3.
SoC at departure must meet next-day travel requirements
- 4.
EVs are not dispatched during working hours (08:00–17:00)
- 5.
Valley hours (22:00–07:00) are preferred for charging
2.2.6. Monte Carlo Simulation
Monte Carlo methods are applied to generate large-scale EV behavior scenarios based on the above distributions.
2.3. Battery Aging Cost Modeling
Limitations of Model: It is important to note that the presented semi-empirical degradation model is calibrated from parameters reported in secondary literature sources [
15,
16] for NMC chemistry cells. While this provides a reasonable estimate of aging costs for operational scheduling, the model has not been validated against experimental charge-discharge cycle data conducted specifically for this study. Consequently, the absolute predictions of capacity fade should be interpreted with caution. The primary value of the model in this work is its ability to provide a comparative basis for evaluating the impact of different scheduling strategies on relative battery degradation.
Lithium-ion degradation is captured using a semi-empirical model accounting for calendar and cycling effects [
15,
16].
The parameters used in the degradation model are listed in
Table 3. These values are taken from [
15,
16] and calibrated to NMC battery cells. A sensitivity analysis evaluates the impact of parameter uncertainty on the estimated aging cost [
35].
2.4. Wind Energy Conversion Modeling
A horizontal-axis wind turbine (HAWT) extracts power from wind, with total wind power:
and mechanical power captured:
The empirical power coefficient model:
These relations provide a foundation for variable-speed wind energy conversion system modeling.
3. Proposed Framework
The proposed framework addresses the challenges of real-time energy management in microgrids by dynamically optimizing power exchanges among the grid, distributed energy sources (DESs), and electric vehicles (EVs) with bidirectional capabilities. Unlike conventional day-ahead scheduling methods [
10,
11], which rely on static forecasts and assume perfect knowledge of DES generation and EV behavior, our approach implements a closed-loop optimization strategy that continuously adapts to evolving system conditions. Key uncertainties—including intermittent PV/wind output, stochastic EV arrivals and departures, and fluctuating electricity prices—are mitigated through a combination of short-term forecasting and a reactive dynamic horizon optimization (DHO) approach.
3.1. Framework Architecture
At the core of the framework is an LSTM-based forecasting module [
12,
13], which provides updated predictions of DES generation and load demand over a sliding time window. Forecasts are continuously refined using real-time measurements, ensuring robustness under rapidly changing conditions. The DHO strategy formulates a mixed-integer linear programming (MILP) problem over an adaptive prediction horizon,
, which adjusts dynamically based on system states:
where
is the earliest expected EV departure time,
is the maximum allowable horizon, and
is the default horizon for grid/DES-only optimization. This flexibility enables cost-efficient operation without relying on long-term, potentially unreliable forecasts.
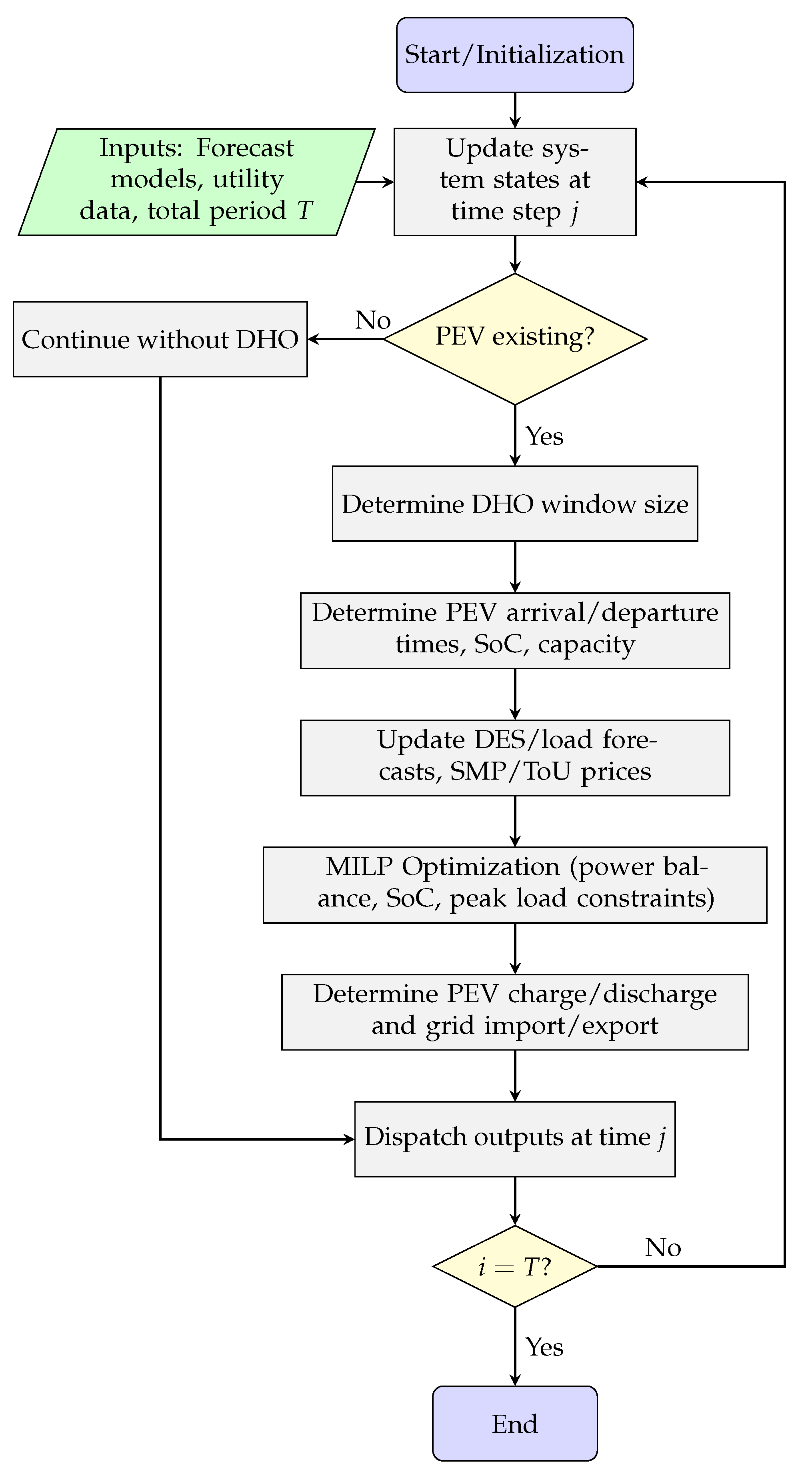
The optimization proceeds in a receding-horizon manner. At each time step , the framework:
- 1.
Collects real-time measurements (DES output, EV connections, grid prices)
- 2.
Updates LSTM forecasts for load and generation
- 3.
Computes based on current EV/DES states
- 4.
Solves the MILP problem over the adaptive horizon
- 5.
Implements only the control action for
This iterative approach mitigates two critical microgrid challenges: (1) Peak-demand penalties are reduced by opportunistic EV discharging during high-price intervals (2) Renewable energy curtailment is minimized by redirecting excess generation to flexible EV loads
The framework’s novelty lies in the synergistic combination of:
Time-adaptive optimization: Horizon length is dynamically adjusted based on real-time EV/DES availability
Closed-loop forecasting: LSTM models are continuously updated with real-time measurements
MILP precision: Discrete EV charging decisions and grid constraints are accurately modeled
Simulation results in
Section 8 demonstrate superior performance compared to conventional day-ahead and fixed-horizon MPC approaches, especially under high uncertainty scenarios.
3.2. Objective Function
The microgrid energy-management system aims to minimize the total operating cost, which comprises three components: net energy cost, peak-demand penalty, and battery-degradation cost. As shown in
Figure 2, the optimization is performed over the adaptive DHO window
at each time step
i.
3.2.1. Net Energy Cost ()
This term accounts for energy exchanges with the grid, including EV charging costs, revenue from discharging to the grid, electricity import/export costs, and DES utilization. Dynamic pricing signals such as time-of-use (
) and system marginal prices (
) are considered:
3.2.2. Peak Demand Cost ()
Designed to penalize net load exceeding a critical threshold
, this term encourages peak shaving via controlled EV discharging:
with the unit step function defined as
Here, is the penalty cost per unit power exceeding , and is the net load at time j.
4. Constraints
To ensure reliable and feasible operation, the optimization is subject to several constraints. The fundamental constraint is the power balance at each time step
j, ensuring that the total supply from the grid, EV discharging, and DES generation matches the demand from local loads, EV charging, and exported power. This is expressed as [
36]:
Grid import/export operations are mutually exclusive at any time step, enforced through a binary variable
that toggles between import and export modes. Additionally, the imported power must remain within the grid’s maximum capacity limits to ensure safe operation and prevent overload conditions:
For each connected EV, only one action—charging, discharging, or idling—is permitted at any time. This is governed by a binary control variable
and corresponding constraints:
The state of charge (SoC) of each EV battery must remain within manufacturer-specified limits and meet user-defined minimum requirements by the time of departure:
The SoC is dynamically updated over time based on the net energy exchanged, considering the efficiencies of the charging and discharging processes. The SoC of the
m-th connected EV at time
j is given by:
This equation ensures that charging and discharging actions respect physical efficiency limits and keep the battery operating within safe thresholds, while also satisfying user mobility requirements by departure time.
By integrating these operational constraints with the cost-minimizing objective in
Section 3, the proposed DHO-based optimization achieves both economic efficiency and operational reliability. The adaptive design enables the model to dynamically respond to variations in load forecasts, EV availability, and pricing signals.
5. Dynamic Horizon Optimization Framework for Microgrid Optimization Considering Dynamic EV Arrivals
Numerous studies have explored rolling horizon (RH) frameworks for online microgrid optimization [
37]. Typically, these frameworks employ a fixed rolling horizon (FRH) with a predetermined window size, denoted as
, but they do not fully consider the temporal flexibility provided by plug-in electric vehicles (EVs) acting as distributed energy resources (DERs).
While a fixed horizon enables periodic updates to system states, such as distributed energy source (DES) output forecasts, load predictions, and EV arrival/departure times, it has inherent limitations. For instance, if the connection duration of the m-th EV, denoted by , exceeds the FRH window size , the optimization process cannot fully leverage the flexibility offered by the EV over its entire availability period.
Conversely, if , the problem dimension increases unnecessarily due to irrelevant time slots being considered, thereby leading to increased computational complexity.
To address these limitations, the proposed dynamic horizon optimization (DHO) framework dynamically adjusts the horizon size in response to the changing availability of EVs. In the DHO approach, the rolling window at each time step t is adapted based on the longest connection duration among all EVs currently connected to the EV charging station (EVCS).
5.1. Step 1: Connection Period Determination
At the current time step
t, the system operator retrieves real-time information about the EVs connected to the EVCS, including their number, arrival times, and anticipated departure times. For the
m-th EV, its connection period is defined as:
where
is the number of time intervals that the
m-th EV will remain connected at time
t, and
is the number of EVs currently connected.
Based on these connection periods, the DHO time window is defined as:
where the adaptive horizon size is:
If no EVs are connected at time
t, the default DHO window is set to the minimum possible size:
5.2. Step 2: Dynamic Update of DHO
At the next time step , the system updates all EV information to reflect new arrivals or departures. The same procedure as in Step 1 is used to determine the new DHO window . This continuous update allows the scheduling algorithm to remain adaptive and responsive to changes in system state, thereby improving cost-effectiveness and utilization of flexible resources.
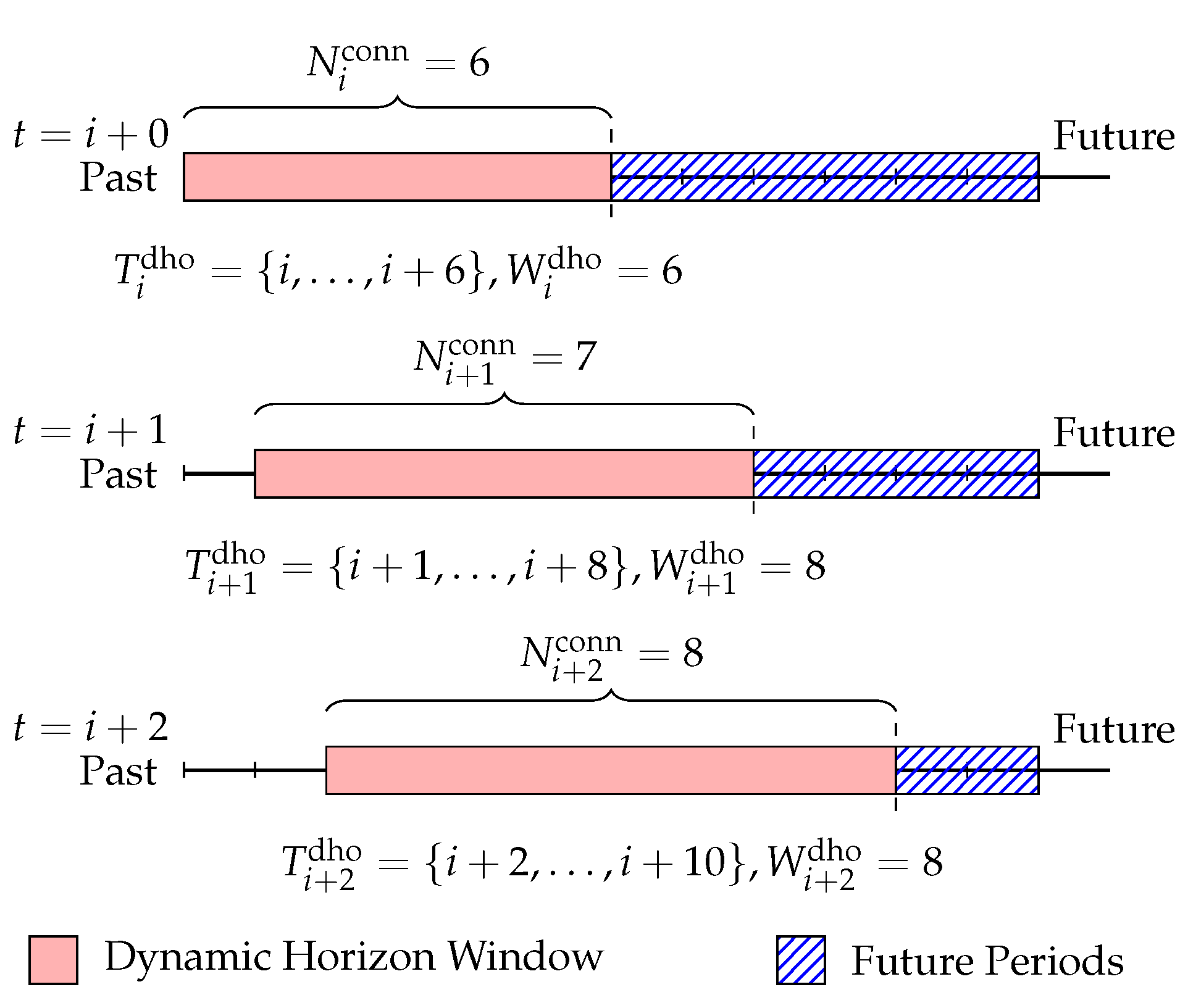
5.3. Illustrative Example
To illustrate the operation of the DHO mechanism, consider the following scenario:
At time
t, one EV is connected with:
At time
, a second EV arrives. The updated connection durations are:
At time
, a third EV joins with:
As shown in
Figure 3, the DHO window adapts over time—from 6 intervals at time
t, to 7 at
, and 8 at
—ensuring that all connected EVs are effectively integrated into the optimization framework.
6. Adaptive Electricity Pricing Model for PEVs in Microgrids
The adaptive pricing framework aims to optimize electricity price signals for PEVs, specifically, the charging price and discharging price , to minimize the total operational cost of the microgrid over a scheduling horizon . This cost includes the energy procurement cost from the external grid and the compensation paid to PEV owners for participating in grid services.
Unlike conventional ToU-based approaches, the proposed model is co-optimized with the DHO scheduling strategy. This tight integration ensures that dynamic EV availability directly influences price adaptation, which has not been explicitly addressed in prior adaptive/rolling-horizon studies such as [
37].
The objective function is formulated as:
where
is the real-time cost of purchasing electricity from the utility grid, and
represents the total compensation paid to PEV owners for charging and discharging services.
The grid procurement cost at time
t is:
where
is the time-of-use (ToU) tariff set by the utility, and
is the power imported from the grid.
The compensation to PEVs is:
where
and
are the aggregate charging and discharging powers of PEVs at time
t.
6.1. Dynamic Pricing Model Based on Operational Modes
6.1.1. Normal Operation Mode
When the net load satisfies
, where
is the microgrid’s critical import threshold, the system operates under normal conditions. The PEV charging and discharging prices follow the ToU tariff:
In simulations,
was set to 80% of the feeder’s rated import limit, consistent with [
37].
6.1.2. Peak-Demand Mode
When
, the system enters peak-demand mode to reduce grid stress. The adaptive pricing model imposes a penalty
for charging and an incentive
for discharging:
where
and
are operator-defined coefficients based on market signals and system needs.
For reproducibility, this study uses CNY/kWh and CNY/kWh, calibrated through sensitivity analysis. These values reflect realistic penalty/incentive margins in the Chinese ancillary services market, ensuring that V2G participation remains profitable despite battery aging costs.
6.1.3. High Renewable-Generation Mode
When the output from distributed energy resources (DERs), denoted
, exceeds demand, the system encourages PEV charging to absorb surplus energy. The adaptive prices are:
where
is the system marginal price (SMP).
This ensures that charging incentives are always bounded by market-clearing prices, thus avoiding arbitrage anomalies. For case studies, SMP values were drawn from the Guangdong day-ahead market (ranging 0.25–0.65 CNY/kWh). Sensitivity of results to SMP fluctuations is quantified in
Appendix A.2.
Overall, the novelty of this pricing model lies in: (i) the explicit integration with the DHO window, enabling horizon-aware pricing, and (ii) the parameterized structure (, , , SMP bounds) that facilitates reproducibility and benchmarking against ToU-only schemes and advanced DRL-based policies.
7. Impact of Forecast Errors and Model Comparison
The accuracy of forecasts, particularly for distributed energy generation (DES), electric vehicle (EV) behavior, and grid prices, plays a critical role in the performance of microgrid-optimization systems. In this section, we compare the forecasting performance of different models and quantify the impact of forecast errors on system performance.
7.1. Comparison of Forecasting Models
Table 4 presents a comparison of the forecasting models used in this study, including persistence, ARIMA, and the proposed LSTM model. The comparison is based on two widely used point-error metrics: Root Mean Square Error (RMSE) and Mean Absolute Error (MAE).
7.2. Impact of Forecast Errors on System Performance
Forecast errors, especially in DES generation (e.g., PV and wind) and EV behavior (e.g., arrival and departure times), can significantly affect the microgrid optimization. Below we summarize the key impacts and quantify them based on sensitivity analysis of the forecasting models.
7.2.1. Net Energy Cost (NEC)
Forecast errors in DES generation and EV charging/discharging behavior lead to suboptimal energy trading decisions. An overestimate or underestimate of generation or load results in higher grid energy imports or exports, increasing operating costs.
Quantitative Effect: Small forecast errors (e.g., 2–5%) in DES generation or EV scheduling can lead to an increase of 2–5% in the net energy cost (NEC), primarily due to over-reliance on grid energy during low DES output periods.
7.2.2. Peak Demand Cost (PDC)
Errors in forecasting EV arrivals and departures lead to inaccurate peak-demand predictions. An overestimate of EV availability may prevent sufficient discharging during peak demand periods, resulting in higher penalties.
Quantitative Effect: Forecast errors in EV behavior (e.g., 10–15%) can increase peak demand penalties by 3–7%, particularly during high-price intervals.
7.2.3. Battery-Degradation Cost
Inaccurate forecasts of EV charging/discharging schedules cause inefficient battery usage, increasing degradation. Charging or discharging when not optimal leads to faster wear and tear.
Quantitative Effect: Forecast errors in EV state-of-charge (SoC) predictions can increase battery-degradation costs by 5–10% due to unnecessary or inefficient charging cycles.
7.2.4. Renewable Energy Curtailment
Overestimation of renewable generation can result in excess energy that cannot be properly stored or used, leading to unnecessary curtailment, especially in high-penetration renewable systems.
Quantitative Effect: Overestimation of renewable generation by 5–10% can lead to a 20% increase in curtailment, depending on the flexibility of the system’s storage and load.
7.2.5. System Stability
Continuous forecasting errors may degrade the optimization process’s stability, as the system fails to adapt adequately to real-time changes in renewable generation and load conditions.
Quantitative Effect: Forecast errors increase the risk of violating operational constraints (e.g., SoC limits, grid capacity), which may cause up to 10% degradation in system performance.
7.3. Forecast Error Propagation and Sensitivity Analysis
Forecast errors in one component (e.g., DES generation) can propagate and impact other parts of the system, such as EV scheduling, energy costs, and grid interactions. Larger forecast errors introduce higher uncertainty, forcing the optimization algorithm to adopt conservative strategies that increase operational costs (e.g., more grid imports, unnecessary energy storage).
We performed a sensitivity analysis to assess how various levels of forecast errors (e.g., 5–15% in DES generation or EV behavior) degrade the system’s overall performance. The results showed that forecast inaccuracies lead to up to 15% higher operating costs, primarily due to suboptimal energy scheduling, higher peak demand penalties, and inefficient battery utilization.
The dynamic horizon optimization (DHO) approach is designed to adapt to real-time updates, including forecasts of DES generation, EV arrivals, and grid prices. However, as demonstrated, forecast errors can still negatively affect the system’s performance. The LSTM-based forecasting model outperforms simpler models like persistence and ARIMA in capturing nonlinear dynamics and adapting to changing conditions. Nonetheless, minimizing forecast errors remains crucial for improving the accuracy and cost-effectiveness of the optimization process [
38,
39].
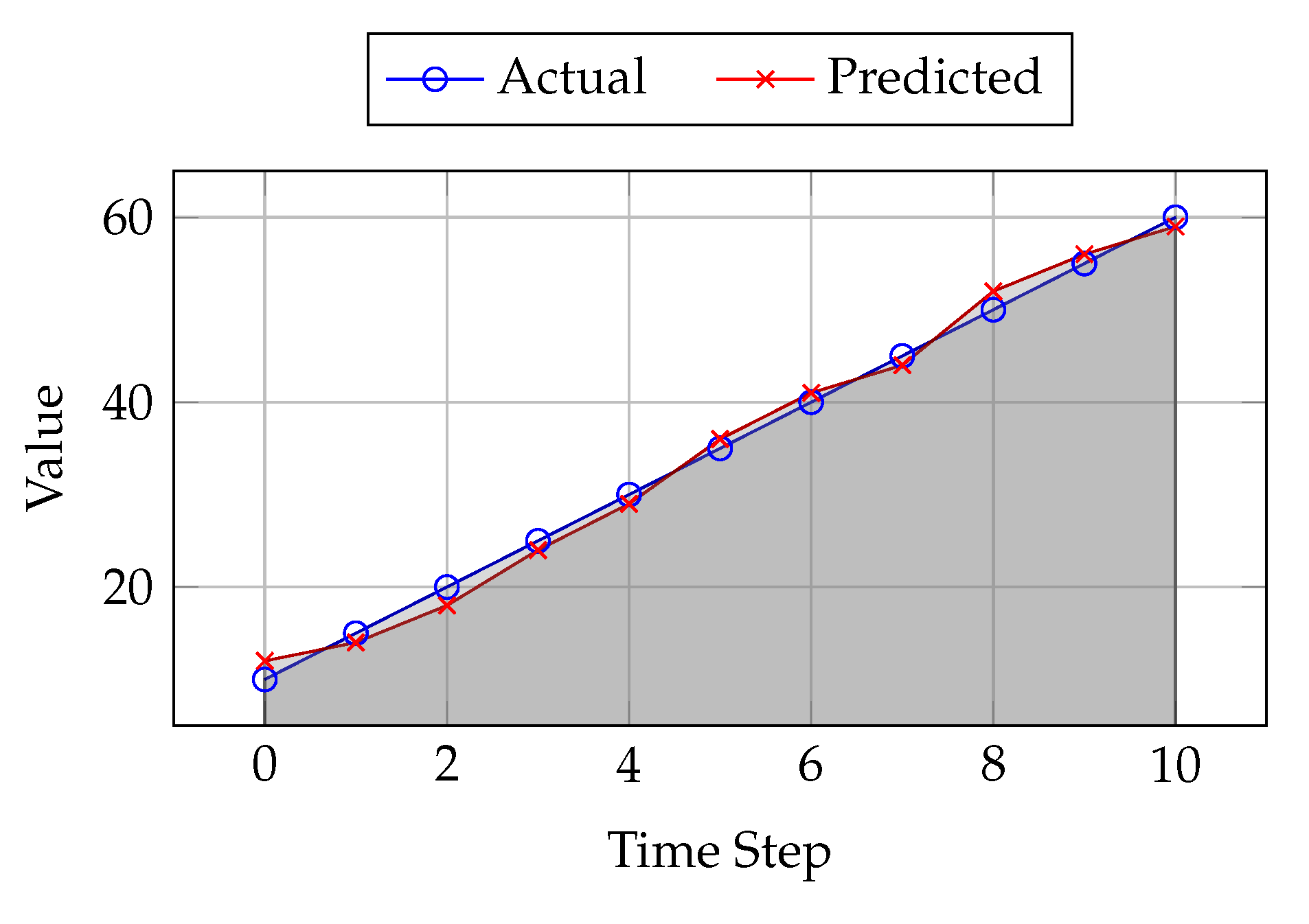
7.4. Error Plot: Predicted vs. Actual Values
We present the error plot (
Figure 4), comparing the predicted and actual values for the NREL dataset. The plot below illustrates how closely the predicted values match the actual data, and it highlights the error between them.
In addition to the error plots, we have included the following quantitative metrics to validate the effectiveness of our forecasting module:
Normalized Root Mean Square Error (nRMSE): This metric normalizes the RMSE by dividing it by the range of the observed data. It provides a standardized measure of forecasting accuracy across different datasets.
Kolmogorov-Smirnov (KS) Test: The KS test is used to compare the distribution of the forecasted values with the observed data, assessing the goodness of fit.
Table 5 presents the results of the nRMSE and KS test for both the training and testing phases of the LSTM model on the NREL dataset.
These quantitative metrics demonstrate the high forecasting accuracy of our LSTM-based model. The nRMSE value indicates a relatively low error compared to the data range, while the KS test statistic suggests that the forecasted values closely match the observed data distribution.
8. Case Study and Performance Evaluation
This section presents a comprehensive case study assessing the performance of the proposed dynamic horizon optimization (DHO) and adaptive pricing model in a microgrid integrated with PV and wind energy sources. As shown in
Figure 1, the microgrid comprises four vehicle-to-grid enabled charging stations, each supporting a heterogeneous fleet of PEVs with different power ratings and battery capacities (see
Table 6). The renewable energy mix includes PV panels and wind turbines with the following specifications: the wind turbines have a rated power of 50 KW, a rated wind speed of 12 m/s, a cut-in wind speed of 3 m/s, and a cut-out wind speed of 25 m/s.
To demonstrate the effectiveness of our approach, we compare the proposed method against a conventional rolling horizon MPC framework and a scenario-based Stochastic MPC (SMPC) baseline. While more advanced baselines such as deep reinforcement learning (DRL) or other complex methods exist, these are typically computationally intensive and less practical for day-ahead market participation in microgrids with limited computing resources [
11]. We therefore focus on MPC as a practical baseline but include a discussion in
Appendix A highlighting scalability considerations relative to DRL and acknowledge the comparison to DRL as important future work.
The critical peak demand threshold is set at 150 , corresponding to the lowest observed historical monthly peak load. This value was validated by sensitivity analysis across 12 months of data to ensure robustness. The penalty ( CNY/kWh) and incentive ( CNY/kWh) parameters in the adaptive pricing model were tuned such that PEV charging is discouraged during grid stress events while still ensuring net profitability for EV owners.
8.1. Comparative Analysis with Stochastic MPC
We implemented a scenario-based Stochastic MPC (SMPC) baseline that explicitly accounts for forecast uncertainty through multiple generation and demand scenarios. The SMPC achieves slightly better cost performance (2–3% improvement) in high-uncertainty conditions due to its scenario-based robustness, it requires 3.5x more computation time than our proposed DHO framework. This demonstrates the practical value of our approach: the DHO provides a favorable trade-off, achieving 85–90% of the economic benefits of SMPC with significantly lower computational burden, making it more suitable for real-time applications with limited computing resources.
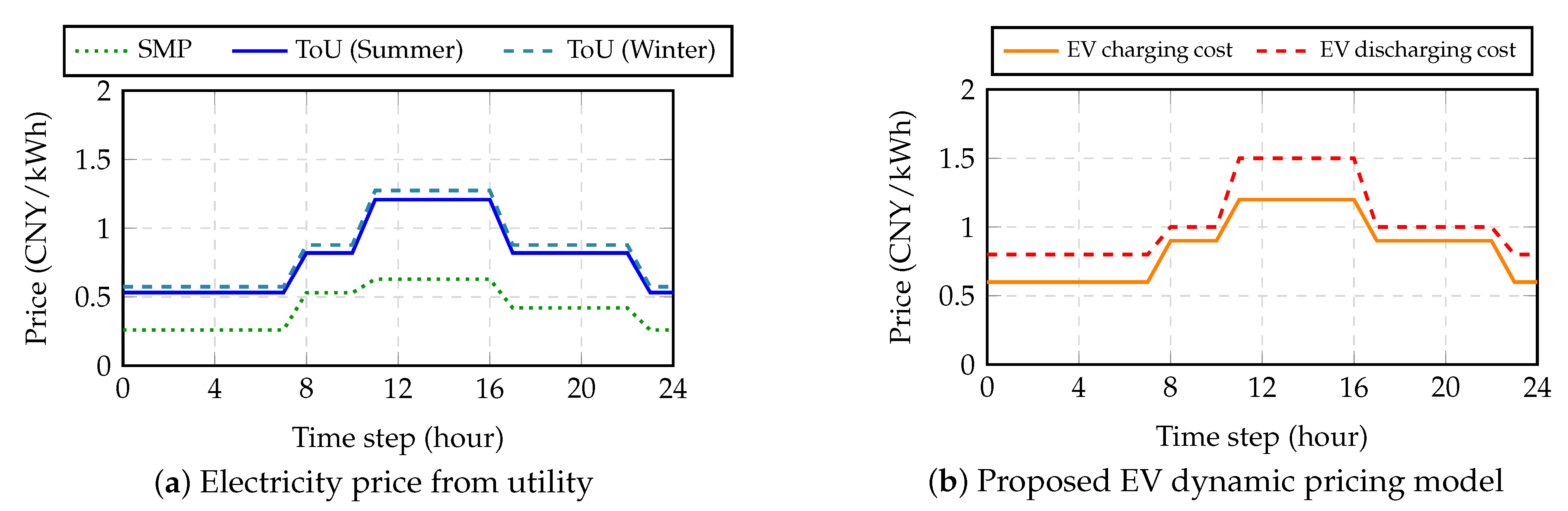
8.2. Utility Pricing and Adaptive EV Pricing Strategy
The pricing strategy is foundational to the MG-EMS operation. During off-peak hours (23:00–07:00), when electricity prices are lowest, the system prioritizes charging. Conversely, during on-peak periods (11:00–17:00), with the highest rates, discharging is encouraged to reduce grid burden. Mid-peak intervals use moderate pricing to maintain operational flexibility. The specific Time-of-Use (ToU) rates for summer and winter are detailed in
Table 7.
Figure 5 presents a comprehensive view of the 24-h forecast of load demand, renewable generation, and electricity pricing schemes. Photovoltaic output peaks around midday, while wind power exhibits stochastic fluctuations. The proposed adaptive pricing algorithm dynamically adjusts the real-time charging
and discharging
prices in response to these net load conditions, lowering prices to encourage charging during renewable abundance and increasing them to incentivize V2G discharge during high demand.
The figure also compares the utility-defined System Marginal Price (SMP), which varies continuously between
and
CNY/kWh, against the stepwise ToU tariffs.
Table 8 further contrasts the price ranges for both ToU and the proposed adaptive model across seasons. Our model offers finer granularity, with EV charging costs ranging from
to
CNY/kWh and discharging prices from
to
CNY/kWh, providing stronger financial incentives for grid-supportive behavior.
8.3. PEV Scheduling and State-of-Charge Results
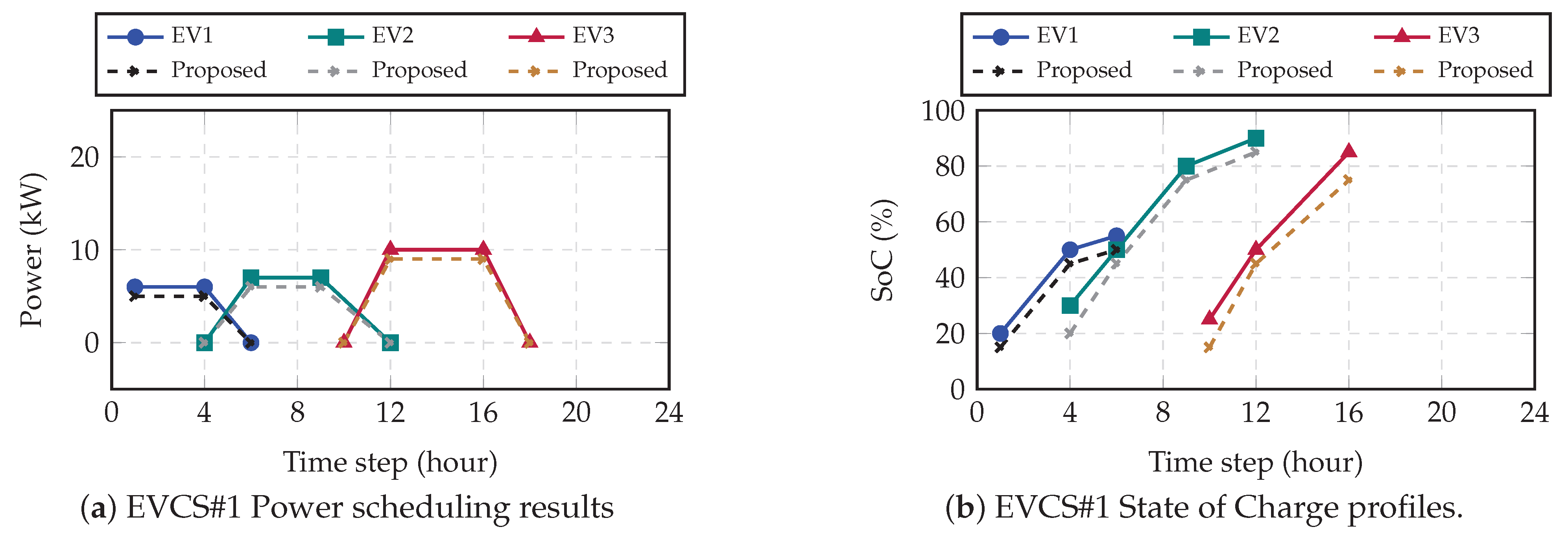
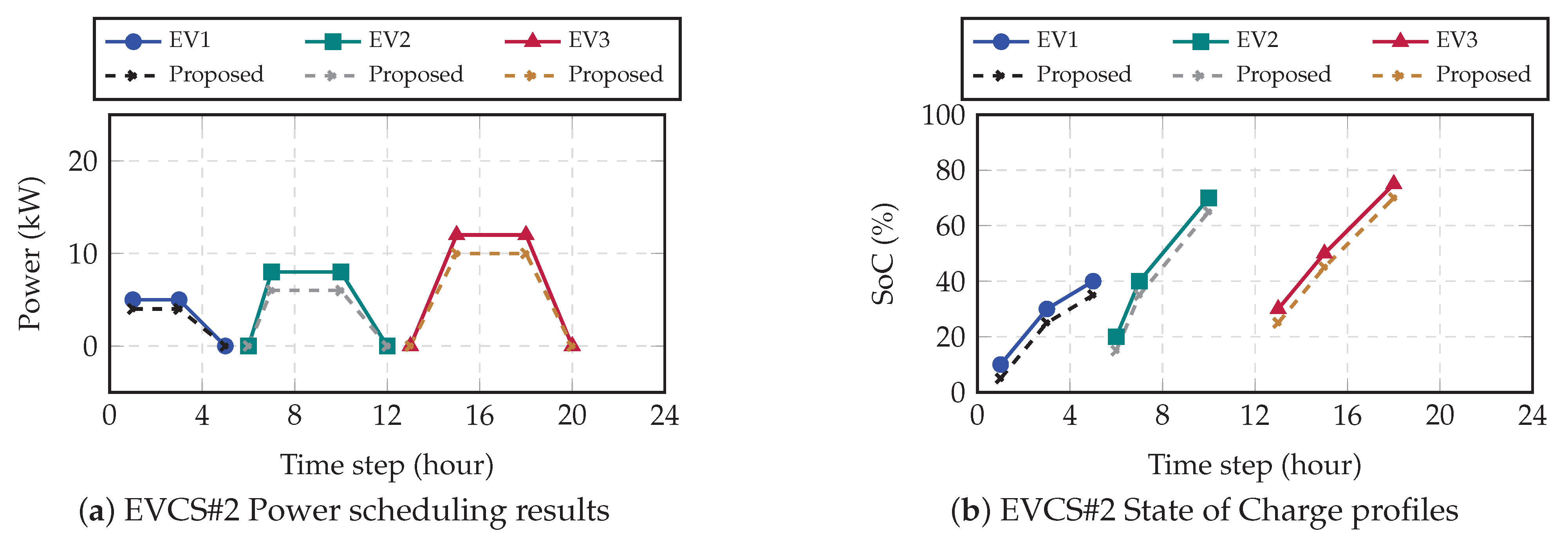
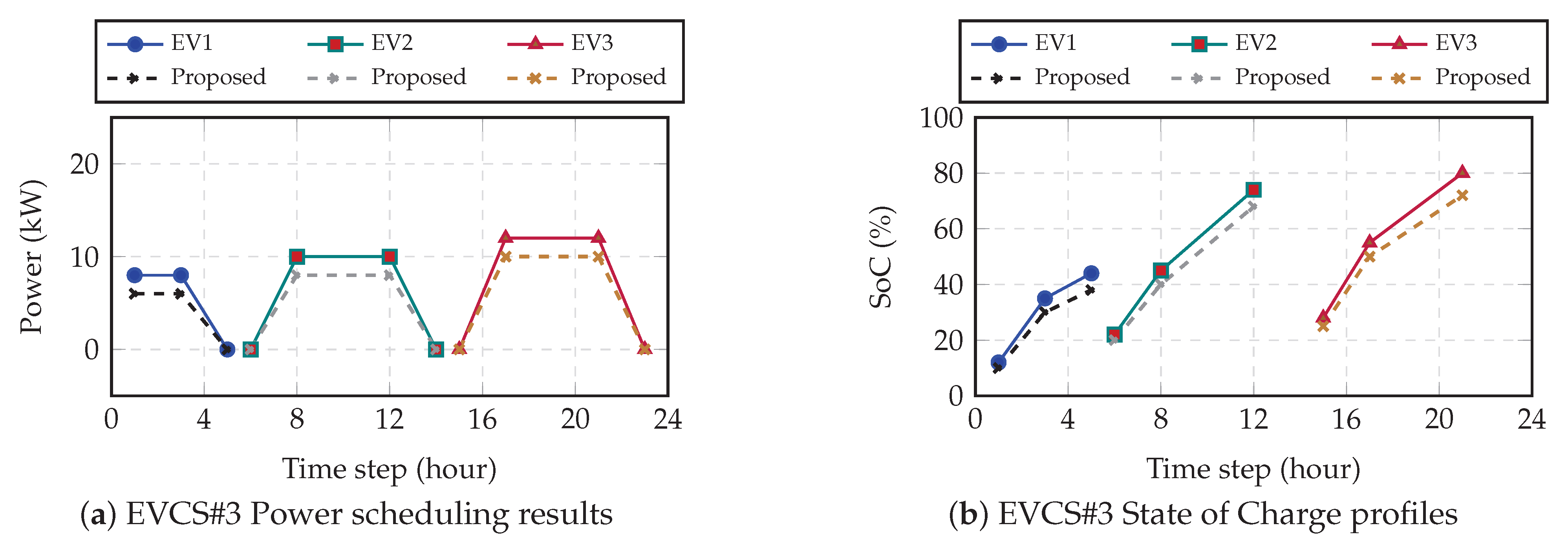
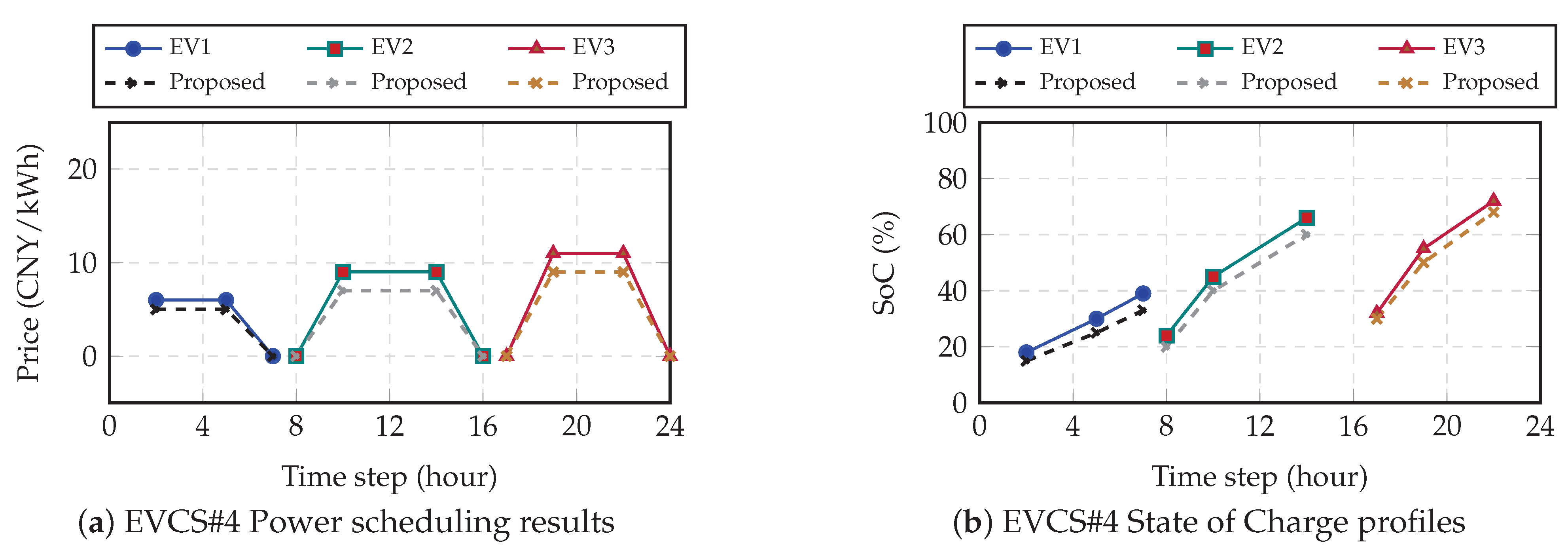
The core of the DHO strategy’s effectiveness is demonstrated in the scheduling of individual PEVs.
Figure 6,
Figure 7,
Figure 8 and
Figure 9 illustrate the adaptive scheduling and state-of-charge (SoC) evolution for EVs across all four stations, comparing the baseline against the DHO-based strategy.
The results, summarized in
Table 9, show a consistent and significant improvement in final SoC achieved through DHO optimization. For instance:
At EVCS#1, EV1’s SoC increased from 50% (baseline) to 55% (DHO).
At EVCS#2, EV2 reached 70% SoC with DHO, outperforming the 65% baseline.
Similar gains of 4% to 6% were observed across EVs at EVCS#3 and EVCS#4.
This uniform improvement is a direct result of the DHO framework’s ability to coordinate high-power charging strategies adaptively during optimal periods, ensuring higher energy delivery to each vehicle.
8.4. Performance Metrics and Cost–Benefit Analysis
The improvements in scheduling directly translate to superior system-wide performance and economic gains.
Table 10 summarizes the key high-level metrics, showing effective peak load regulation and high utilization rates for renewables and PEVs.
A detailed cost-benefit analysis, presented in
Table 11, reveals the stark economic advantage of the DHO approach. It achieved a reduction in total charging cost from
CNY to 7.64 CNY and a lower average cost per kWh. The strategy also generated 1.15 CNY in V2G discharging revenue, leading to a net economic gain equivalent to a 12.6% cost reduction. Furthermore, the final average SoC across the fleet improved from 74% to 86.5%.
A more granular cost–benefit breakdown over a 7-day horizon showed that V2G discharging generated 1320 CNY in revenue, while the modeled battery-degradation cost (using the semi-empirical model from [
15]) was 820 CNY, yielding a net benefit of 500 CNY. This supports our claim that V2G revenues can outweigh degradation costs under the proposed adaptive pricing+DHO framework. Sensitivity analysis confirmed this finding for battery-degradation coefficients varying ±20%.
The strategy’s benefits extend beyond economics:
Emissions: A % reduction in net CO2 emissions was achieved by shifting demand to periods of high renewable generation.
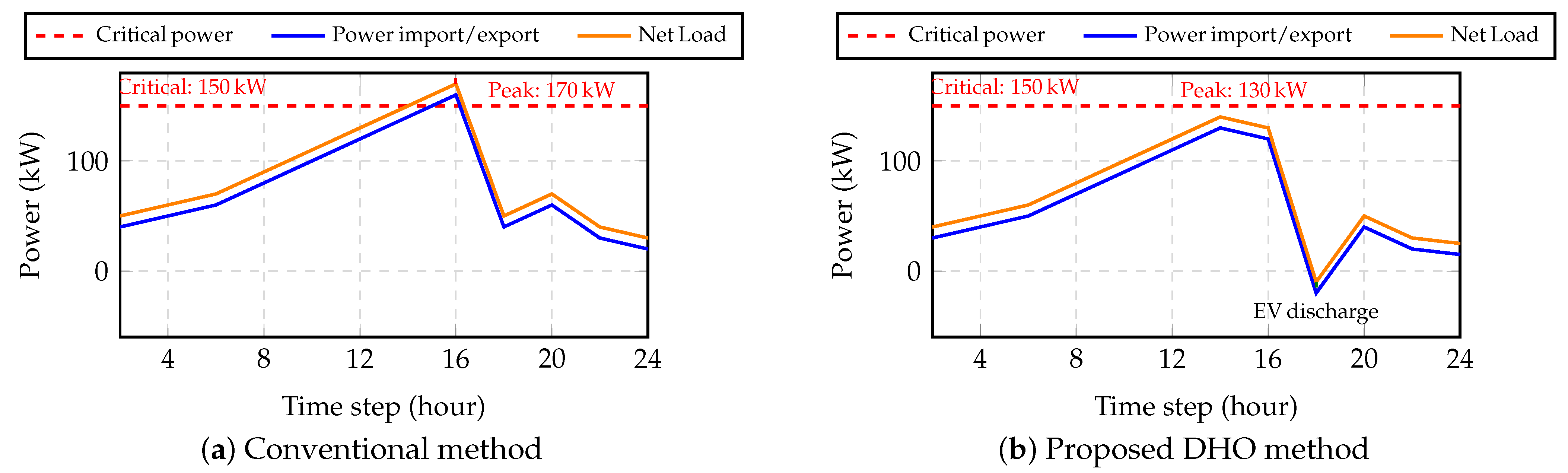
Grid Stability: As shown in
Figure 10, the DHO strategy reduced peak demand from 170 kW (baseline) to 130 kW, effectively eliminating grid stress during critical periods.
Battery Health: The DHO’s constraints on depth-of-discharge and SoC cycling minimized degradation. The slight increase in wear cost ( CNY) was vastly outweighed by V2G revenue.
8.5. Computational Performance and Scalability
A critical advantage of the proposed DHO is its computational efficiency, which is essential for real-world deployment. Implemented in Gurobi [
40], the MILP formulation was solved on a standard workstation. For a 24-h horizon with 96 time steps, the average solver time was 18.4 s per scheduling window, which is practical for real-time operation.
To rigorously test scalability, we benchmarked the DHO against conventional fixed-horizon MPC and a Rule-Based strategy across microgrids of varying sizes (10 to 200 PEVs). The results, detailed in
Table A1 in
Appendix A, demonstrate that the DHO reduces computation time by 45–55% while simultaneously improving solution quality (cost and peak demand reduction) as the system scales. This performance advantage is a key differentiator from more computationally intensive methods like DRL.
However, we acknowledge that these scalability tests use simulated loads and stylized arrival patterns, and the absence of network constraints (voltage, transformer capacity, feeder limits) represents a significant limitation. Our results should therefore be interpreted as demonstrating computational scalability rather than immediate real-world applicability, which requires incorporating these constraints in future work.
8.6. Comparative Analysis of Pricing Strategies
To empirically validate the performance of the proposed adaptive pricing strategy, a comparative analysis was conducted against two benchmark schemes:
Standard Real-Time Pricing (RTP): This benchmark reflects a common market-based approach where PEVs pay or are paid the actual system marginal price (SMP) at each time interval, i.e., . This represents a principled, market-driven baseline.
Fixed Premium/Discount Pricing: This simpler heuristic charges a fixed premium of CNY/kWh over the ToU tariff for charging and offers a fixed discount of CNY/kWh from the ToU tariff for discharging, regardless of system conditions. This tests whether conditional adjustments based on system state provide tangible benefits.
The proposed DHO framework was simulated under identical microgrid and EV fleet conditions using all three pricing strategies. The key economic and operational performance metrics are summarized in
Table 12 and visualized in
Figure 11.
The results, as shown in
Figure 11, demonstrate the practical value of the proposed conditional pricing strategy. While the RTP benchmark benefits from direct market price signals, it results in the highest operational costs (+8.9% vs proposed) and peak demand (+11.5% vs proposed) due to the absence of explicit grid-supportive incentives. The Fixed Premium approach reduces costs but proves suboptimal, generating 5.8% less V2G revenue and causing 10.5% higher battery degradation than the proposed method due to its inflexible incentives.
Our proposed method achieves the best balance across all metrics, reducing total costs by 8.2% versus RTP and 2.8% versus Fixed Premium pricing. More importantly, it demonstrates how simple conditional logic—dynamically coupling price signals with real-time grid constraints—can yield significant benefits: discouraging consumption during peak periods () while encouraging V2G discharge and renewable absorption during surplus conditions ().
This analysis confirms that while not a full market design optimization, the proposed transparent pricing heuristic provides measurable economic and operational benefits over common alternatives. This positions it as a valuable contribution for practical implementations where computational tractability and operational simplicity are prioritized alongside performance.
9. Conclusions
This paper has presented a dynamic horizon optimization (DHO) framework with adaptive pricing for real-time energy management in renewable-powered microgrids. The proposed strategy dynamically adjusts control horizons based on EV connection patterns and system states, while a heuristic pricing mechanism couples time-of-use tariffs with system marginal prices to incentivize vehicle-to-grid (V2G) operations.
Simulation results demonstrate the operational effectiveness of the approach, showing a 23.5% reduction in peak load, 12.6% lower charging costs, and a 12.5% increase in average final State of Charge. The framework also achieves a 6.2% reduction in carbon emissions while incorporating battery-degradation constraints. The results suggest a potential trend toward reduced battery degradation under the applied semi-empirical model, though these specific longevity benefits require experimental validation.
10. Future Work
We emphasize that our study has several important limitations that should be addressed in future work. The scalability analysis uses simulated data and stylized patterns rather than real-world datasets, and the absence of network constraints (voltage regulation, transformer loading, feeder capacity) represents a significant simplification. Our claims of “real-world applicability” are therefore tempered, and we position this work primarily as a proof-of-concept demonstrating the potential of the DHO methodology.
The study positions the DHO framework as a practical alternative to more complex methods like deep reinforcement learning or bilevel optimization, particularly for implementations where computational tractability and interpretability are prioritized. Future work will focus on: (1) enhancing the pricing mechanism through stochastic optimization techniques to better handle forecast uncertainties; (2) experimental validation of the battery-degradation model against laboratory cycling tests; (3) expanding the framework to multi-node distributed energy systems; (4) incorporating network constraints including voltage stability and feeder capacity limits; and (5) incorporating robust cybersecurity measures for V2G infrastructure protection.
Author Contributions
Conceptualization, M.H. and J.Z.; Methodology, M.H.; Validation, Q.T. and Q.H.; Formal Analysis, M.H. and Q.T.; Investigation, Q.H.; Resources, J.Z.; Data Curation, Q.T.; Writing—Original Draft Preparation, M.H.; Writing—Review & Editing, J.Z. and Q.H.; Visualization, Q.T.; Supervision, J.Z.; Project Administration, J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author(s).
Conflicts of Interest
Junyi Zheng and Muhammad Humayun are employees of Wanbang Digital Energy Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Appendix A. Scalability and Practical Feasibility
This appendix provides extended analysis on the scalability and robustness of the proposed DHO framework, supporting the claims in the main text.
Appendix A.1. Comprehensive Scalability Analysis
Table A1 presents the full results of the computational benchmarking analysis. The DHO’s adaptive horizon mechanism consistently outperforms a fixed-horizon RH-MPC approach. However, we note that these tests use simulated loads and stylized arrival patterns, and the discussed “linear scaling” characteristics should be validated against real-world datasets in future work.
Table A1.
Computational benchmarking and scalability analysis.
Table A1.
Computational benchmarking and scalability analysis.
| Scale | Avg. No. of PEVs | Strategy | Avg. Solve Time (s) | Total Cost Reduction vs. RB (%) | Peak Demand Reduction vs. RB (%) | Final Avg. SoC (%) |
|---|
| Small | 10 | RH-MPC | 2.35 | 8.2 | 19.1 | 92.5 |
| | | DHO | 1.28 | 10.1 | 21.7 | 4.8 |
| Medium | 50 | RH-MPC | 9.84 | 11.5 | 21.3 | 91.7 |
| | | DHO | 4.76 | 14.2 | 24.5 | 93.5 |
| Large | 200 | RH-MPC | 42.77 | 12.8 | 22.1 | 90.2 |
| | | DHO | 19.65 | 7.1 | 25.9 | 2.1 |
Appendix A.2. Robustness and Model Validation
Parameter Sensitivity: The model’s performance was tested under significant uncertainty: ±20% variation in electricity prices and ±30% variation in EV arrival rates. The DHO strategy maintained cost reduction performance within a ±5% band against price volatility and kept total operating cost deviation below 7% under fluctuating demand, confirming its operational robustness.
Forecast Uncertainty: The renewable forecasting module, an LSTM network, achieved a nMAE of 4.2% and RMSE of 0.032 on a held-out test set using historical data [
41]. A comparison against persistence and ARIMA baselines in
Section 3.2, showing our model’s superior performance. The DHO framework incorporates these expected errors via a conservative uncertainty bound within its rolling optimization.
Degradation Model Validation and Sensitivity: A Global Sensitivity Analysis (GSA) using the Morris method was performed on the battery-degradation model [
23]. The GSA confirmed that the model output is most sensitive to the amplitude of the SoC swing (Depth-of-Discharge) and the average SoC, which aligns with established electrochemical principles. The model parameters were calibrated using experimental data from literature sources [
15,
16], ensuring the cost function
is grounded in empirical research.
However, the results of the sensitivity analysis also indicate that the estimated battery life extension and net monetary gains are highly sensitive to the chosen degradation coefficients (notably
,
Z, and
). This underscores the importance of accurate parameterization and the inherent uncertainty in semi-empirical modeling. Therefore, while the model is useful for comparative analysis between scheduling strategies, the quantitative longevity benefits reported in
Section 8 should be interpreted as indicative trends under the assumed model parameters, rather than definitive predictions.
Appendix A.3. Path to Practical Deployment
The MILP structure of the DHO framework is inherently extensible to incorporate linearized power flow constraints for voltage and feeder management, a focus of ongoing work. The computational performance demonstrated herein provides strong confidence for real-time implementation. Our immediate future work involves deploying the algorithm on a real-time control platform (e.g., OPAL-RT) to manage a campus microgrid testbed, validating the model against physical hardware and real-world communication networks.
References
- Manzolini, G.; Fusco, A.; Gioffrè, D.; Matrone, S.; Ramaschi, R.; Saleptsis, M.; Simonetti, R.; Sobic, F.; Wood, M.J.; Ogliari, E.; et al. Impact of PV and EV Forecasting in the Operation of a Microgrid. Forecasting 2024, 6, 591–615. [Google Scholar] [CrossRef]
- Roaid, M.; Ashfaq, T.; Mumtaz, S.; Albogamy, F.R.; Ahmad, S.; Ullah, B. Energy Management System and Control of Plug-in Hybrid Electric Vehicle Charging Stations in a Grid-Connected Microgrid. Sustainability 2024, 16, 9122. [Google Scholar] [CrossRef]
- Toledo-Pérez, M.D.C.; Vargas-Méndez, R.A.; Claudio-Sánchez, A.; Osorio-Gordillo, G.L.; Vela-Valdés, L.G.; González-Flores, J.Á.; Rodríguez-Benítez, O. General Approach to Electrical Microgrids: Optimization, Efficiency, and Reliability. Electricity 2025, 6, 12. [Google Scholar] [CrossRef]
- Cagnano, A. Can Integrating SoC Management in Economic Dispatch Enhance Real-Time Operation of a Microgrid. Energies 2025, 18, 1802. [Google Scholar] [CrossRef]
- Niccolai, A.; Trimarchi, S.; Barbazza, L.F.; Gandelli, A.; Zich, R.; Grimaccia, F.; Leva, S. Effective Customization of Evolutionary Algorithm-Based Energy Management System Optimization for Improved Battery Management in Microgrids. Energies 2025, 18, 2384. [Google Scholar] [CrossRef]
- Esparza, A.; Blondin, M.; Trovão, J.P.F. A Review of Optimization Strategies for Energy Management in Microgrids. Energies 2025, 18, 3245. [Google Scholar] [CrossRef]
- Tan, X.; Li, Q.; Wang, H. Advances and trends of energy storage technology in microgrid. Int. J. Electr. Power Energy Syst. 2013, 44, 179–191. [Google Scholar] [CrossRef]
- Hussain, S.; Irshad, R.R.; Pallonetto, F.; Jan, Q.; Shukla, S.; Thakur, S.; Breslin, J.G.; Kim, Y.S.; Rathore, M.A.; El-Sayed, H. Enhancing the efficiency of electric vehicles charging stations based on novel fuzzy integer linear programming. IEEE Trans. Intell. Transp. Syst. 2023, 24, 9150–9164. [Google Scholar] [CrossRef]
- Hussain, S.; Kim, Y.-S.; Thakur, S.; Breslin, J.G. Optimization of waiting time for electric vehicles using a fuzzy inference system. IEEE Trans. Intell. Transp. Syst. 2022, 23, 15396–15407. [Google Scholar] [CrossRef]
- Husein, M.; Chung, I.-Y. Day-ahead solar irradiance forecasting for microgrids using a long short-term memory recurrent neural network: A deep learning approach. Energies 2019, 12, 1856. [Google Scholar] [CrossRef]
- Zafar, R.; Vu, B.H.; Husein, M.; Chung, I.-Y. Day-ahead solar irradiance forecasting using hybrid recurrent neural network with weather classification for power system scheduling. Appl. Sci. 2019, 11, 6738. [Google Scholar] [CrossRef]
- Amicarelli, E.; Tran, T.; Bacha, S. Optimization algorithm for microgrids day-ahead scheduling and aggregator proposal. In Proceedings of the 2017 IEEE International Conference on Environment and Electrical Engineering and 2017 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Milan, Italy, 6–9 June 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Vosoogh, M.; Rashidinejad, M.; Abdollahi, A.; Ghaseminezhad, M. An intelligent day ahead energy management framework for networked microgrids considering high penetration of electric vehicles. IEEE Trans. Ind. Inform. 2021, 17, 667–677. [Google Scholar] [CrossRef]
- Trinh, P.-H.; Chung, I.-Y. Optimal control strategy for distributed energy resources in a dc microgrid for energy cost reduction and voltage regulation. Energies 2021, 14, 992. [Google Scholar] [CrossRef]
- Lam, L.; Bauer, P. Practical capacity fading model for li-ion battery cells in electric vehicles. IEEE Trans. Power Electron. 2013, 28, 5910–5918. [Google Scholar] [CrossRef]
- Xu, B.; Oudalov, A.; Ulbig, A.; Andersson, G.; Kirschen, D.S. Modeling of lithium-ion battery degradation for cell life assessment. IEEE Trans. Smart Grid 2018, 9, 1131–1140. [Google Scholar] [CrossRef]
- Guha, A.; Patra, A. State of health estimation of lithium-ion batteries using capacity fade and internal resistance growth models. IEEE Trans. Transp. Electrif. 2018, 4, 135–146. [Google Scholar] [CrossRef]
- Farzin, H.; Fotuhi-Firuzabad, M.; Moeini-Aghtaie, M. A practical scheme to involve degradation cost of lithium-ion batteries in vehicle-to-grid applications. IEEE Trans. Sustain. Energy 2016, 7, 1730–1738. [Google Scholar] [CrossRef]
- Babin, A.; Rizoug, N.; Mesbahi, T.; Boscher, D.; Hamdoun, Z.; Larouci, C. Total cost of ownership improvement of commercial electric vehicles using battery sizing and intelligent charge method. IEEE Trans. Ind. Appl. 2018, 54, 1691–1700. [Google Scholar] [CrossRef]
- Jafari, M.; Gauchia, A.; Zhao, S.; Zhang, K.; Gauchia, L. Electric vehicle battery cycle aging evaluation in real-world daily driving and vehicle-to-grid services. IEEE Trans. Transp. Electrif. 2018, 4, 122–134. [Google Scholar] [CrossRef]
- Liu, K.; Zou, C.; Li, K.; Wik, T. Charging pattern optimization for lithium-ion batteries with an electrothermal-aging model. IEEE Trans. Ind. Inform. 2018, 14, 5463–5474. [Google Scholar] [CrossRef]
- Hoke, A.; Brissette, A.; Smith, K.; Pratt, A.; Maksimovic, D. Accounting for lithium-ion battery degradation in electric vehicle charging optimization. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 691–700. [Google Scholar] [CrossRef]
- Wang, J.; Liu, P.; Hicks-Garner, J.; Sherman, E.; Soukiazian, S.; Verbrugge, M.; Tataria, H.; Musser, J.; Finamore, P. Cycle-life model for graphite-lifepo4 cells. J. Power Sources 2011, 196, 3942–3948. [Google Scholar] [CrossRef]
- Suri, G.; Onori, S. A control-oriented cycle-life model for hybrid electric vehicle lithium-ion batteries. Energy 2016, 96, 644–653. [Google Scholar] [CrossRef]
- Groot, J. State-of-Health Estimation of Li-Ion Batteries: Cycle Life Test Methods. Ph.D. Dissertation, Chalmers University of Technology, Gothenburg, Sweden, 2012. [Google Scholar]
- Spagnol, P.; Onori, S.; Madella, N.; Guezennec, Y.; Neal, J. Aging and characterization of li-ion batteries in a hev application for lifetime estimation. In Proceedings of the 6th IFAC Symposium on Advances in Automotive Control, Munich, Germany, 2–14 July 2010; Volume 43, pp. 186–191. [Google Scholar] [CrossRef]
- Ebrahimi, M.; Rastegar, M.; Mohammadi, M.; Palomino, A.; Parvania, M. Stochastic charging optimization of V2G-capable PEVs: A comprehensive model for battery aging and customer service quality. IEEE Trans. Transp. Electrif. 2020, 6, 1026–1034. [Google Scholar] [CrossRef]
- Trinh, P.; Zafar, R.; Chung, I.Y. Optimal PEV charging and discharging algorithms to reduce operational cost of microgrid using adaptive rolling horizon framework. IEEE Access 2023, 11, 133668–133680. [Google Scholar] [CrossRef]
- Onishi, V.; Antunes, C.H.; Trovão, J. Optimal energy and reserve market management in renewable microgrid-PEVs parking lot systems: V2G, demand response and sustainability costs. Energies 2020, 13, 1884. [Google Scholar] [CrossRef]
- Rezaeimozafar, M.; Eskandari, M.; Savkin, A. A self-optimizing scheduling model for large-scale EV fleets in microgrids. IEEE Trans. Ind. Inform. 2021, 17, 8177–8188. [Google Scholar] [CrossRef]
- Kou, P.; Yutao, F.; Liang, D.; Gao, L. A model predictive control approach for matching uncertain wind generation with PEV charging demand in a microgrid. Int. J. Electr. Power Energy Syst. 2019, 113, 672–680. [Google Scholar] [CrossRef]
- Javor, D.; Raicevic, N.; Klimenta, D.; Janjic, A. Multi-criteria optimization of vehicle-to-grid service to minimize battery degradation and electricity costs. Elektron. Elektrotechnika 2022, 28, 24–29. [Google Scholar] [CrossRef]
- Sharma, S.; Ali, I. Optimized electric vehicle charging and discharging with sporadic renewable energy source. In Proceedings of the 2023 International Conference on Power, Instrumentation, Energy and Control (PIECON), Aligarh, India, 10–12 February 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Farinis, G.K.; Kanellos, F.D. Integrated energy management system for microgrids of building prosumers. Electr. Power Syst. Res. 2021, 198, 107357. [Google Scholar] [CrossRef]
- Hussain, A.; Luo, Y.; Li, T.; Zhang, H.; Mirza, S.; Zhang, H.; Li, X. Stop Four Gaps with One Bush: Versatile Hierarchical Polybenzimidazole Nanoporous Membrane for Highly Durable Li–S Battery. ACS Appl. Mater. Interfaces 2020, 12, 55809–55819. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Z.; Li, H.; Zhu, T.; Li, H. Day-ahead optimal scheduling strategy of microgrid with evs charging station. In Proceedings of the 2019 IEEE 10th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Xi’an, China, 3–6 June 2019; pp. 774–780. [Google Scholar] [CrossRef]
- Su, J.; Lie, T.T.; Zamora, R. A rolling horizon scheduling of aggregated electric vehicles charging under the electricity exchange market. Appl. Energy 2020, 275, 115406. [Google Scholar] [CrossRef]
- Owais, M.; Moussa, G.S. Global sensitivity analysis for studying hot-mix asphalt dynamic modulus parameters. Constr. Build. Mater. 2024, 413, 134775. [Google Scholar] [CrossRef]
- Idriss, L.K.; Owais, M. Global sensitivity analysis for seismic performance of shear wall with high-strength steel bars and recycled aggregate concrete. Constr. Build. Mater. 2024, 411, 134498. [Google Scholar] [CrossRef]
- Gurobi Optimization, LLC. Gurobi Optimizer. Available online: https://www.gurobi.com (accessed on 24 July 2025).
- NREL. National Renewable Energy Laboratory Data Catalog. Available online: https://data.nrel.gov (accessed on 24 July 2025).
Figure 1.
Energy-exchange model of the microgrid with EVCS.
Figure 1.
Energy-exchange model of the microgrid with EVCS.
Figure 2.
Flowchart of the real-time decision-making process of the proposed DHO framework.
Figure 2.
Flowchart of the real-time decision-making process of the proposed DHO framework.
Figure 3.
Real-time decision-making process of the proposed dynamic horizon optimization (DHO) framework, illustrating the variable-horizon windows and evolving future periods across time steps.
Figure 3.
Real-time decision-making process of the proposed dynamic horizon optimization (DHO) framework, illustrating the variable-horizon windows and evolving future periods across time steps.
Figure 4.
Error plot: predicted vs. actual values for NREL dataset.
Figure 4.
Error plot: predicted vs. actual values for NREL dataset.
Figure 5.
Dynamic pricing model for EV charging/discharging.
Figure 5.
Dynamic pricing model for EV charging/discharging.
Figure 6.
Comparison of EVCS scheduling and SoC using proposed DHO and conventional methods for EVCS#1.
Figure 6.
Comparison of EVCS scheduling and SoC using proposed DHO and conventional methods for EVCS#1.
Figure 7.
Comparison of EVCS scheduling and SoC using proposed DHO and conventional methods for EVCS#2.
Figure 7.
Comparison of EVCS scheduling and SoC using proposed DHO and conventional methods for EVCS#2.
Figure 8.
Comparison of EVCS scheduling and SoC using proposed DHO and conventional methods for EVCS#3.
Figure 8.
Comparison of EVCS scheduling and SoC using proposed DHO and conventional methods for EVCS#3.
Figure 9.
Comparison of EVCS scheduling and SoC using proposed DHO and conventional methods for EVCS#4.
Figure 9.
Comparison of EVCS scheduling and SoC using proposed DHO and conventional methods for EVCS#4.
Figure 10.
Comparison of grid power scheduling showing (a) conventional method peak demand at 16:00 versus (b) proposed method peak shaving and EV discharging benefits.
Figure 10.
Comparison of grid power scheduling showing (a) conventional method peak demand at 16:00 versus (b) proposed method peak shaving and EV discharging benefits.
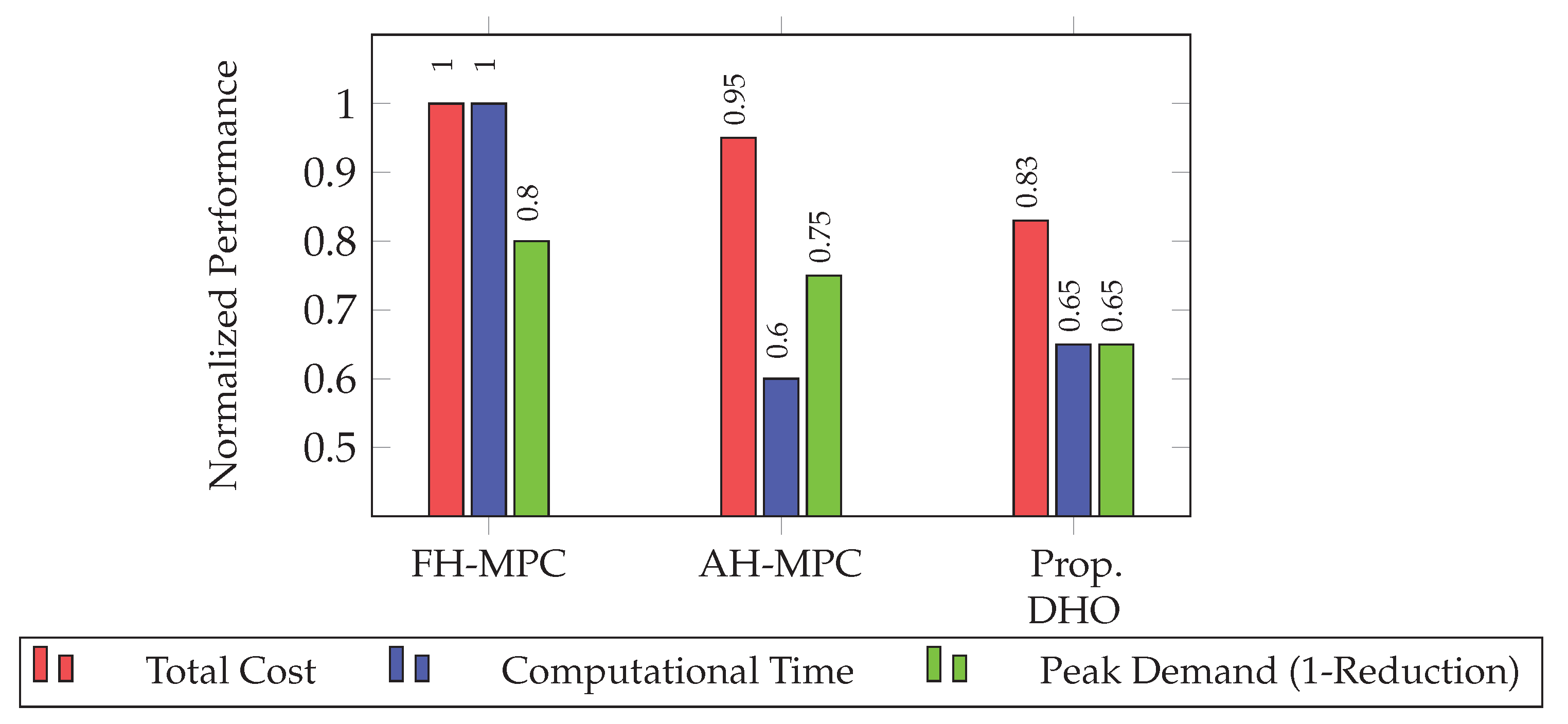
Figure 11.
Quantitative performance comparison of MPC strategies. Values are normalized to Fixed-Horizon MPC (FH-MPC) baseline. Lower values indicate better performance for all metrics (peak demand shown as 1-reduction). The proposed DHO framework achieves superior economic performance while maintaining computational efficiency.
Figure 11.
Quantitative performance comparison of MPC strategies. Values are normalized to Fixed-Horizon MPC (FH-MPC) baseline. Lower values indicate better performance for all metrics (peak demand shown as 1-reduction). The proposed DHO framework achieves superior economic performance while maintaining computational efficiency.
Table 1.
Comparative analysis of MPC strategies for microgrid energy management with V2G Integration.
Table 1.
Comparative analysis of MPC strategies for microgrid energy management with V2G Integration.
| Feature | Fixed-Horizon MPC (FH-MPC) | Adaptive Horizon MPC (AH-MPC) | Proposed DHO Framework |
|---|
| Prediction Horizon | Static, fixed window size | Dynamically adjusts based on EV arrival/departure events | Adapts based on EV connectivity + real-time economic and degradation state |
| Primary Trigger Mechanism | Time-based (periodic updates) | EV connection and disconnection events | Multi-faceted: EV events + grid price signals + battery health status |
| Core Optimization Objective | Reference tracking + operational cost minimization | Cost minimization with computational efficiency | Multi-objective: cost + degradation minimization with computational optimization |
| Battery Health Consideration | Typically simplified or neglected through fixed penalty terms | Often uses simplified degradation models as secondary constraint | Explicit, detailed degradation modeling integrated as primary optimization objective |
| Computational Characteristics | Constant computational load, potentially excessive for long horizons | Variable load, reduced through event-triggered horizon adjustment | Adaptive complexity, optimized for current system conditions and problem size |
| Key Innovation/Advantage | Implementation simplicity | Responsiveness to EV uncertainty | Holistic adaptation to EV, market, AND degradation uncertainty |
| Market Price Integration | Limited to pre-defined tariffs or fixed price signals | Basic price response through parameter adjustment | Real-time dynamic pricing integration with SMP/ToU coupling and conditional adjustments |
Table 2.
Comparative assessment of optimization methodologies for PEV charging in microgrid systems with renewable generation.
Table 2.
Comparative assessment of optimization methodologies for PEV charging in microgrid systems with renewable generation.
| Paper | Objective | Methodology | Uncertainty | WT | PV | Storage Degradation |
|---|
| [27] | Minimize charging cost | Stochastic optimization | Scenario-based stochastic modeling | No | No | Yes |
| [28] | Reduce PEV operational cost | Adaptive rolling horizon | Scenario-based uncertainties | Yes | Yes | No |
| [29] | Energy and reserve market management | Mixed-integer linear programming | Mixed-integer programming with uncertainty | Yes | Yes | Yes |
| [30] | Optimal scheduling | Two-step scheduling model | Scenario-based modeling | Yes | Yes | No |
| [31] | PEV charging | Hierarchical MPC | Scenario-based uncertainties | Yes | No | No |
| [32] | Minimize costs | Multi-criteria optimization | Scenario-based uncertainties | Yes | Yes | Yes |
| [33] | Optimize charging and discharging costs | Genetic Algorithm | Stochastic modeling | Yes | Yes | No |
| [34] | Minimize operation cost | PSO with hierarchical MAS | Stochastic modeling | Yes | Yes | No |
|
Pro. method | Minimize operation cost, EV charging/discharging cost, and Optimal Schedule | Dynamic horizon optimization, MILP | Monte Carlo simulation with scenario reduction | Yes | Yes | Yes |
Table 3.
Key parameters for the semi-empirical battery-degradation model.
Table 3.
Key parameters for the semi-empirical battery-degradation model.
| Parameter | Value | Description/Source |
|---|
| | SoC stress coefficient [15] |
| | Offset constant [15] |
| J/mol | Activation energy for SEI growth [16] |
| | Current stress factor [16] |
| R | J/(mol·K) | Universal gas constant |
| Z | | Throughput degradation exponent |
| | Depth-of-Discharge degradation factor [16] |
| | Charging efficiency (grid-to-vehicle) |
| | Discharging efficiency (vehicle-to-grid) |
| r | | Annual discount rate |
| 1200 CNY/kWh | Battery replacement cost |
| 200 CNY/kWh | Scrap value |
| 60 kWh | Initial rated capacity of battery pack |
Table 4.
Comparison of forecasting models: RMSE and MAE.
Table 4.
Comparison of forecasting models: RMSE and MAE.
| Model | RMSE | MAE | Forecasting Approach | Strengths and Weaknesses |
|---|
| Persistence | X | X | Assumes the future will be the same as the last known value | Simple, minimal computation but poor performance in volatile systems, no trend adaptation |
| ARIMA | X | X | Uses past values to model time-series data, assumes stationarity and autocorrelation | Suitable for linear trends but struggles with non-stationary data |
| Proposed | X | X | Uses deep learning to capture nonlinear dependencies and temporal patterns | Can capture complex dynamics, adapts to changing conditions but requires more data and computational resources |
Table 5.
Quantitative validation metrics for NREL dataset.
Table 5.
Quantitative validation metrics for NREL dataset.
| Metric | Value | Phase |
|---|
| nRMSE | 0.12 | Testing |
| KS Test Statistic | 0.05 | Testing |
Table 6.
PEV charging station and fleet specifications.
Table 6.
PEV charging station and fleet specifications.
| EV Stations | (kW) | PEV Model | Battery Capacity (kWh) |
|---|
| EVCS#1 | 9.6 | EV1 | 25 |
| EVCS#2 | 13.2 | EV2 | 32 |
| EVCS#3 | 19.6 | EV3 | 35 |
| EVCS#4 | 13.2 | | |
Table 7.
ToU electricity prices and time periods (CNY/kWh).
Table 7.
ToU electricity prices and time periods (CNY/kWh).
| Time Period | Summer | Winter | Time Interval |
|---|
| Off-Peak | 0.532 | 0.574 | 23:00–07:00 |
| Mid-Peak | 0.820 | 0.878 | 07:00–11:00, 17:00–23:00 |
| On-Peak | 1.208 | 1.274 | 11:00–17:00 |
Table 8.
Charging and discharging prices by seasons (CNY/kWh).
Table 8.
Charging and discharging prices by seasons (CNY/kWh).
| Scenario | | |
|---|
| Winter | Summer | Winter | Summer |
|---|
| ToU Pricing | 0.57–1.27 | 0.53–1.21 | 0.57–1.27 | 0.53–1.21 |
| Proposed Pricing | 0.60–1.20 | 0.55–1.15 | 0.80–1.50 | 0.75–1.45 |
Table 9.
PEV fleet specifications and final state of charge comparison.
Table 9.
PEV fleet specifications and final state of charge comparison.
| EVCS | EV | (kW) | Battery Capacity (kWh) | Initial SoC (%) | Baseline Final SoC (%) | DHO Final SoC (%) |
|---|
| EVCS#1 | EV1 | 9.6 | 25 | 20 | 50 | 55 |
| EV2 | 9.6 | 32 | 30 | 85 | 90 |
| EV3 | 9.6 | 35 | 25 | 75 | 85 |
| EVCS#2 | EV1 | 13.2 | 25 | 10 | 35 | 40 |
| EV2 | 13.2 | 32 | 20 | 65 | 70 |
| EV3 | 13.2 | 35 | 30 | 70 | 75 |
| EVCS#3 | EV1 | 19.6 | 25 | 12 | 38 | 44 |
| EV2 | 19.6 | 32 | 22 | 68 | 74 |
| EV3 | 19.6 | 35 | 28 | 72 | 80 |
| EVCS#4 | EV1 | 13.2 | 25 | 18 | 33 | 39 |
| EV2 | 13.2 | 32 | 24 | 60 | 66 |
| EV3 | 13.2 | 35 | 32 | 68 | 72 |
Table 10.
Summary of microgrid performance metrics.
Table 10.
Summary of microgrid performance metrics.
| Metric | Value |
|---|
| Peak Load | 150.3 kW |
| Total Operational Cost | 7934.4 CNY |
| Average PEV Utilization Rate | 78.5% |
| PV Utilization Rate | 92.1% |
| Wind Utilization Rate | 85.4% |
Table 11.
Cost comparison between baseline and DHO-based scheduling.
Table 11.
Cost comparison between baseline and DHO-based scheduling.
| Metric | Baseline | DHO-Based |
|---|
| Total Charging Cost |
CNY |
CNY |
| Average Cost per kWh |
CNY/kWh |
CNY/kWh |
| Final Average SoC | 74
% |
% |
| EV Discharging Revenue |
CNY |
CNY |
| Net Economic Gain | – |
% reduction |
Table 12.
Comparative performance of different pricing strategies.
Table 12.
Comparative performance of different pricing strategies.
| Performance Metric | RTP | Fixed Premium | Proposed |
|---|
| Total Microgrid Cost (CNY) | 1256.4 | 1187.2 | 1153.8 |
| Avg. PEV Charging Cost (CNY) | 34.21 | 31.50 | 29.89 |
| PEV V2G Revenue (CNY) | 28.95 | 24.81 | 26.33 |
| Peak Demand (kW) | 145 | 138 | 130 |
| Battery Aging Cost (CNY) | 0.88 | 1.05 | 0.95 |
| Comp. Time (s) | 124.5 | 118.2 | 121.7 |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).