Advanced Fault Classification in Induction Motors for Electric Vehicles Using A Stacking Ensemble Learning Approach

Abstract

This study proposes an innovative stacking ensemble learning framework for classifying faults in induction motors utilized in Electric Vehicles (EVs). Employing a comprehensive dataset comprising motor data, such as speed, torque, current, and voltage, the analysis encompasses six distinct conditions: normal operating mode, over-voltage fault, under-voltage fault, overloading fault, phase-to-phase fault, and phase-to-ground fault. The proposed model integrates Gradient Boosting (GB), K-Nearest Neighbors (KNN), Gradient Boosting (XGBoost), Support Vector Machine (SVM), Decision Tree (DT), and Random Forest (RF) algorithms in a synergistic manner. The findings reveal that the RF–GB–DT–XGBoost combination achieves a remarkable accuracy of 98.53%, significantly surpassing other methods reported in the literature. Performance is evaluated through metrics including accuracy, precision, sensitivity, and F1-score, with results analyzed in comparison to practical applications and existing studies. Validated with real-world data, this study demonstrates that the proposed model offers a groundbreaking solution for predictive maintenance systems in the EV industry, exhibiting high generalization capacity despite complex operating conditions. This approach holds transformative potential for both academic research and industrial applications. The dataset used in this study was generated using a MATLAB 2018/Simulink-based Variable Frequency Drive (VFD) model that emulates real-world EV operating conditions rather than relying solely on laboratory data. This ensures that the developed model accurately reflects practical electric vehicle environments.

1. Introduction

As a sustainable substitute for internal combustion engines, Electric Vehicles (EVs) are becoming more and more popular, which emphasizes how crucial Induction Motors (IMs) are as these vehicles’ main driving mechanism [1]. Induction motors are preferred due to their robustness, high efficiency, and cost effectiveness [2]. However, the operational reliability of these motors is of paramount importance, as motor failures can lead to serious problems that jeopardize vehicle safety, performance, and user confidence [3]. Early and accurate detection of induction motor faults is, therefore, essential to ensure predictable maintenance, minimize downtime, and extend the life of electric vehicles [4]. Traditional diagnostic methods (such as signal processing techniques or manual inspection) are often inadequate in the dynamic and noisy operating conditions of electric vehicles. These limitations have highlighted the potential of Machine Learning (ML)-based, data-driven approaches to automate fault classification with greater accuracy and adaptability [5].

Although Permanent Magnet Synchronous Motors (PMSMs) are widely used in modern EVs due to their higher efficiency, Induction Motors (IMs) remain attractive for certain applications because of their lower cost, absence of rare-earth materials, mechanical robustness, and fault tolerance [2]. Their ability to operate efficiently under harsh thermal and electrical stress conditions makes them ideal candidates for mid-range and heavy-duty EVs, where reliability outweighs marginal efficiency differences.

In recent years, ML algorithms have shown significant success in fault diagnosis using patterns in sensor data [6]. However, the complexity of electric vehicle operating environments (such as variable loads, thermal fluctuations, and electromagnetic interference) can limit the generalization performance of single-model approaches or their sensitivity to unbalanced data distributions [7]. To overcome these limitations, ensemble learning techniques such as stacking have emerged as promising solutions [8]. Stacking ensemble learning combines the predictions of multiple underlying models through a meta-learner to synthesize their strengths and achieve superior accuracy and robustness [9]. This approach is particularly beneficial in scenarios that require high-dimensional data analysis and multi-class classification, such as fault detection in IMs [10].

This paper proposes an innovative agglomeration ensemble framework to classify five different types of faults and normal operating modes in electric vehicle IMs based on operational data obtained under real-world conditions. The proposed framework integrates six machine learning algorithms, GB, SVM, KNN, XGBoost, DT, and RF, as basic learners and uses a meta-learner to optimize the outputs of these models. Unlike traditional work based on single-model architectures or homogeneous ensembles, this work explores the synergistic potential of heterogeneous algorithms. Each algorithm offers its own unique inductive biases to capture different error signatures.

The importance of this work lies in its dual contribution to academic research and industrial applications. On the theoretical side, it advances the body of knowledge in ensemble learning by showing how heterogeneous model combinations can alleviate individual algorithmic limitations. On the practical side, it provides electric vehicle manufacturers with a scalable tool for real-time engine health monitoring, reducing the reliance on costly physical controls. Furthermore, the use of real operational EV data rather than simulated or lab-generated datasets fills a critical gap in existing literature by ensuring the relevance of the model to real-world scenarios. The computational complexity resulting from the aggregation of multiple models requires optimization for real-time compatibility with embedded systems in EVs. Nevertheless, the proposed approach shows significant improvements in classification metrics compared to stand-alone models, proving its effectiveness as a state-of-the-art diagnostic tool. By bridging the gap between theoretical machine learning and automotive engineering, this research paves the way for safer and more reliable electric transportation systems in the era of sustainable mobility.

In this paper, we propose an innovative framework based on stacking ensemble learning by integrating heterogeneous machine learning algorithms to detect IM faults based on operational data of electric vehicles. The proposed methodology uses GB, SVM, KNN, XGBoost, DT, and RF algorithms as base learners to classify five different types of faults and normal operating modes; a meta-learning layer is designed to optimize the outputs of these models. This hybrid approach aims to overcome the limitations of single-model-based methods (overlearning, low generalization capacity) by analyzing the complex data patterns arising from the dynamic operating environments of electric vehicles (variable loads, thermal stress, electromagnetic noise). Thanks to the diversity of base learners, effective classification in high-dimensional spaces (SVM), local pattern recognition (KNN), and the regularization capabilities of tree-based models (XGBoost, RF) are combined to provide a more consistent and accurate identification of fault signatures. The contribution of this study to the literature lies in the fact that this integrated framework, validated on real-world data, provides a scalable and adaptive solution for the development of predictive maintenance systems in the electric vehicle industry.

2. Literature Review

Induction motors are considered a mainstay in the economic and industrial sectors, as they are used in the assembly of EVs due to their many advantages, including durability and hardness in different operating conditions. However, they are vulnerable to various malfunctions that affect their quality, especially in phase, overloading, and voltage [11]. The induction motor is exposed to many faults that affect the quality of work. Therefore, advanced techniques are used to detect these faults and classify them. Using data that represents various fault scenarios, stacking ensemble learning and machine learning algorithms are two crucial algorithms in this context [12,13].

A potential method for identifying different IM defects is the Artificial Neural Network (ANN) [14]. It is suggested to use machine learning methods to investigate various instances of Inter-Turn Short-Circuit (ITSC) faults in instant messaging [15]. Machine learning was utilized to construct an IM and study failure situations in order to identify early defect cases in instant messaging [16]. Induction motor eccentricity, broken rotor bars, bearing flaws, and stator faults have all been identified using machine learning methods, including Naive Bayes, SVM, KNN, and DT [17,18]. Machine learning was used for induction motor fault prediction [19]. Fourier spectrum is proposed for detecting a broken rotor bar and bearing fault in induction motors [20]. Machine learning with signal processing was used to diagnose the faults in IMs, namely open circuit fault, motor overload fault, and broken rotor bar [21]. Machine learning and Fuzzy Logic (FL) were used for monitoring and fault detection in IMs [22]. Based on the experimental data, machine learning was used to detect different fault states of induction motors [23]. In IMs, a broken rotor bar fault is detected using generalized detection [24].

Convolutional Neural Networks (CNNs) were used to detect a broken rotor bar fault in an induction motor where the IM was modeled by Finite Element Method Magnetics (FEMM 2020) software, and data extraction and failure cases of broken rotor bars were performed [25]. ResNet-V2 deep learning was used for bearing fault detection based on the experimental data of several induction motor bearing fault cases [26]. Deep Belief Network is improved for IM fault detection [27]. The fault cases of induction motors are modeled as winding short circuit and mixed eccentricity. In addition, machine learning is used for the early detection of faults based on experimental data [28].

Ensemble learning has been used to detect and diagnose photovoltaic models [29]. Parallel ensemble learning was used in the detection and diagnosis of industrial machinery [30]. Stacking ensemble learning is used for defect prediction in software [31]. Ensemble learning has been used in the detection of faults in transmission lines [32]. An NPC inverter fault was detected using ensemble learning [33]. Ensemble learning was used to detect a bearing fault in the inflammatory engine with Case Western data Reserve University (CWRU) [34]. Ensemble learning was used to detect a bearing fault in the inflammatory engine by integrating machine learning algorithms with the high accuracy of KNN + XGB + SVM [35]. Using sound signals in the IM, faults were detected, relying on ensemble learning [36].

3. Materials and Methods

The operation of an induction motor is governed by several equations, with one of the fundamental ones being the torque equation. The dynamic equation of an induction motor can be expressed as follows [18,19,20]:

$$\left\{\begin{array}{c}[v_s\left] = \right[R_s\left]. [i_s\right] + {\displaystyle \frac{d[{\phi }_s]}{dt}}\\ \left[0\left] = \right[R_r\right]. [i_r]+{\displaystyle \frac{d[{\phi }_r]}{dt}} \\ [{\phi }_s\left]=\right[L_s\left]. [i_s\right]+[L_m\left]. [i_r\right]\\ [{\phi }_r\left]=\right[L_r\left]. [i_r\right]+[L_m\left]. [i_s\right]\\ \mathrm{T} = {\displaystyle \frac{3}{2}} \mathrm{P}\left({\phi }_s\ast i_s\right)\end{array}\right.$$

(1)

3.1. Dataset

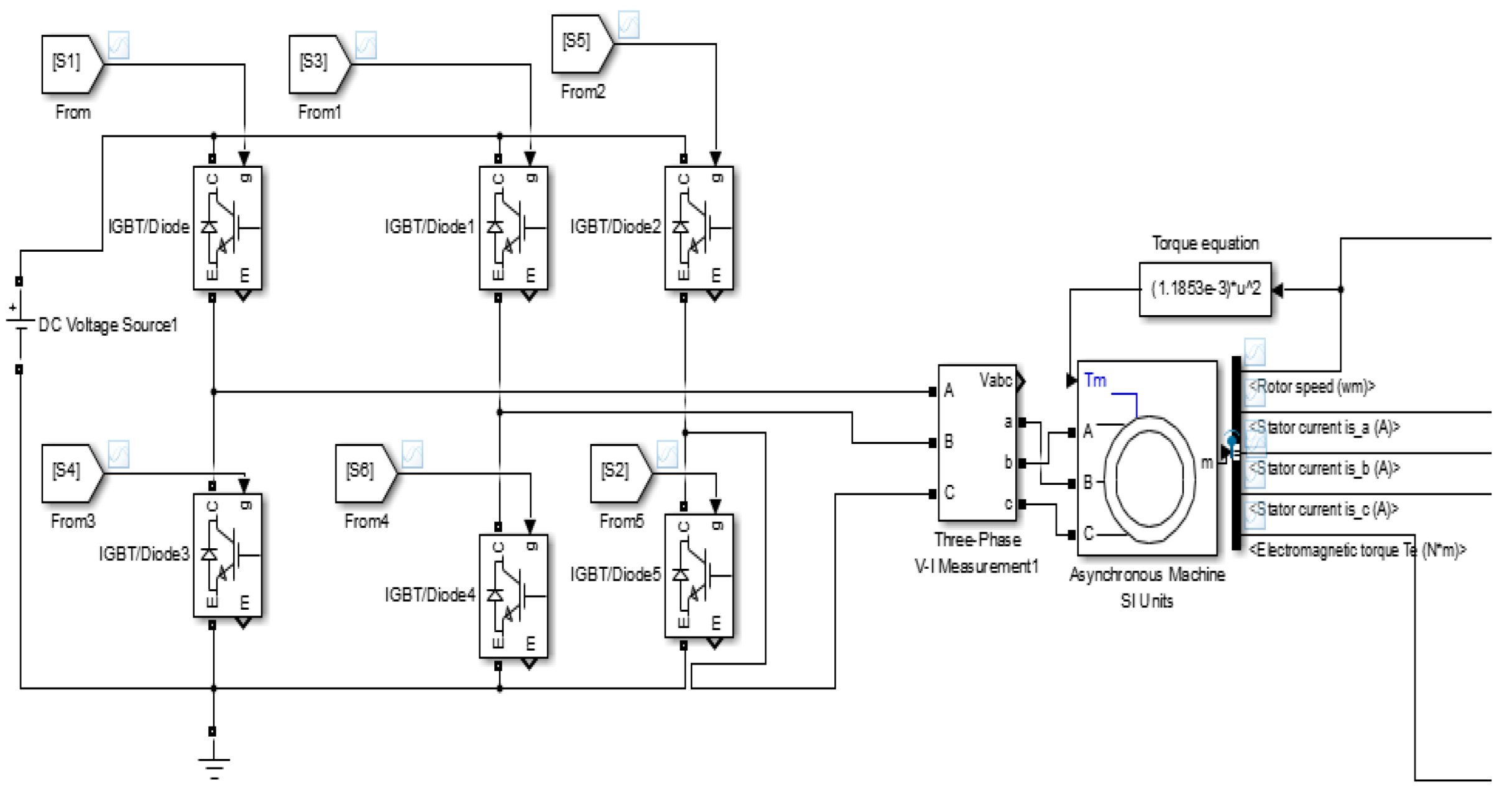
The dataset for fault detection in electric drives used in EVs is specifically focused on three-phase IM drive (Figure 1).

Table 1. Motor parameters [Reprinted from Ref. [38]].

Variables	Symbol	Values
stator resistance	Rs	1.405 ohm
stator inductance	Ls	0.0058 H
rotor resistance	Rr	1.395 ohm
rotor inductance	Lr	0.0058 H
mutual inductance	Lm	0.17 H
inertia	J	0.0131 Kg.m2
pole pairs	P	2
friction factor	F	0.0029 N.m.s

shows the electrical and mechanical parameters of the induction motor. The purpose of this dataset was to use Machine Learning (ML) methods to detect five distinct failure categories. NOM, PTPF, PTGF, OLF, OVF, and UVF are the six operating conditions that were examined [37]. In order to replicate real-world situations, the data was produced under various loading conditions in comparison to the motor’s full load torque and simulated motors running under fluctuating loads. To model the different load levels, a block of torque equations based on the nominal torque of the motor was used. This block used the equation (1.1852 × 10⁻³) × u², where u is the input speed, to simulate different load scenarios. After being captured as waveforms (time series signals), the simulations’ raw data was converted into a structured data matrix. The dataset’s attributes are displayed in

Table 2. Characteristic properties of the dataset [Reprinted from Ref. [39]].

Feature	Count	Mean	Standard Deviation	Minimum	25%	50% (Median)	75%	Maximum
Tn (Rated Torque) Nm	40,040	1.13875	0.37178	0.8	0.91875	1.0375	1.18125	2.5
k (Constant of Proportionality)	40,040	0.001349	0.000441	0.000948	0.001085	0.00123	0.0014	0.002964
Time (s)	40,040	0.25	0.144484	0	0.125	0.25	0.375	0.5
Ia (Current) Amp	40,040	17.89738	10.67385	0	11.47026	13.7461	23.35513	78.63935
Ib (Current) Amp	40,040	17.76482	10.47296	0	11.47008	13.78399	22.57296	79.11399
Ic (Current) Amp	40,037	18.46777	10.50953	0	11.74109	14.27437	24.03763	78.73894
Vab (Voltage) V	40,040	432.8393	123.434	0	389.6933	474.5666	474.9843	649.5165
Torque (N.m)	40,040	23.53362	59.28494	−404.838	19.15	26.66877	36.35022	625.1659
Speed (rad/s)	40,040	123.5214	49.80135	−112.258	132.8439	142.9008	147.744	182.5994

. The dataset incorporates nine attributes representing key aspects of motor performance: Tn (nominal torque) Nm, nominal torque measured in Newton meters (Nm); k (proportionality constant), a constant used in the operational calculations of the motor; Ttme (seconds), time; Ia (Amp), Ib (Amp), and Ic (Amp), phase currents measured in amperes; Vab (V), voltage between phases A and B, in volts; torque (Nm), actual torque produced by the motor, in Nm; and speed (rad/s), rotor speed in radians per second. These attributes were used for the detection and classification of various fault conditions by characterizing the performance of the motor. The engine’s braking is represented by negative torque (lowest value), where the engine generates a reverse force to reduce or regulate the vehicle’s speed. When the motor’s speed is negative, it means that the rotational direction is being reversed.

Improvements to the dataset include improving data quality by removing three missing values and 1003 duplicate rows in the Ic (Amp) attribute. These operations were performed to support the accuracy and reliability of the model. In order to classify the faults in the induction motor, various data such as speed, torque, current, and voltage were obtained. This dataset covers 6 different fault conditions. In order to detect faults, a stacking ensemble learning model is built using training and test data through integrated algorithms. The training data is split 80%, and the test data is split 20%.

Detailed Simulation Environment and Data Generation

The dataset was generated using a MATLAB/Simulink-based Variable Frequency Drive (VFD) model as shown in Figure 1. The model includes an inverter, speed control, and torque load subsystems. The following fault conditions were simulated:

• Over-Voltage Fault (OVF): 15% increase over rated voltage (400 V).
• Under-Voltage Fault (UVF): 20% reduction from rated voltage.
• Overloading Fault (OLF): 1.5× rated torque applied.
• Phase-To-Phase Fault (PTPF): 10 Ω short between phases A and B.
• Phase-To-Ground Fault (PTGF): 5 Ω short between phase A and ground.

The (T = k * ω²) structure of the torque equation used in the simulation represents the aerodynamic drag load of a vehicle, which is a dominant characteristic, especially at the cruising speeds of EVs. The various loading conditions in our model (different k and Tn values) are designed to emulate the different driving scenarios an EV would encounter during real-world operation (e.g., acceleration, deceleration, hill climbing, and constant-speed cruising). These variable load profiles reflect the dynamic conditions that require the motor to operate in transitions between both its constant torque (acceleration at low speed) and constant power (operation at high speed) regions. In this way, the resulting dataset provides a rich foundation for capturing the fault signatures that may arise in the variable and demanding operating environments of EVs.

Each scenario was run for 10 s at a sampling rate of 10 kHz. Signals of stator current, voltage, torque, and speed were collected using the “To Workspace” block and exported as MATLAB arrays for feature extraction. These simulations represent realistic dynamic EV operating conditions, such as load fluctuation and electromagnetic interference.

3.2. Electric Vehicle Drives Motor Faults

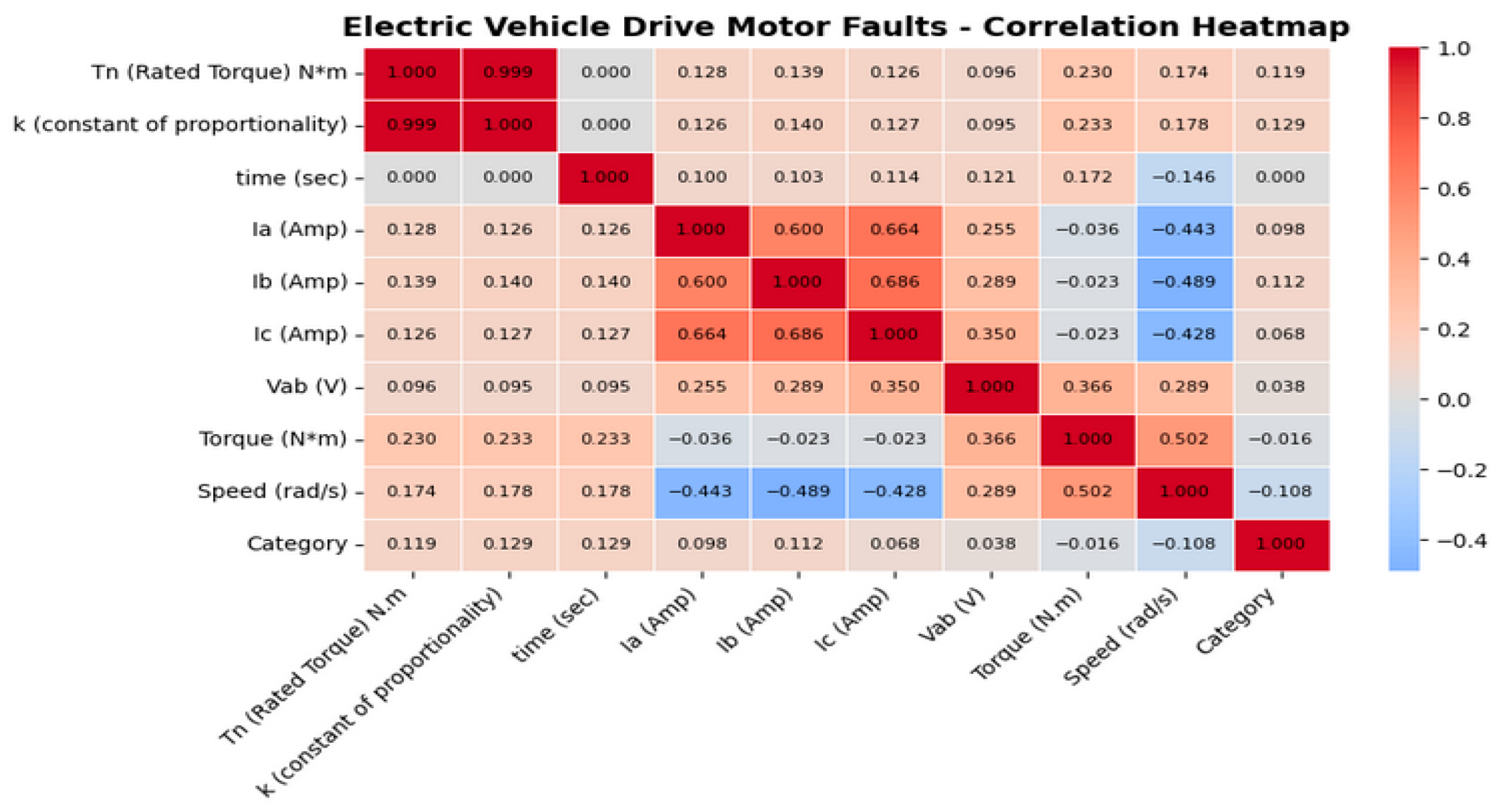
The induction motor data includes current, voltage, and torque parameters. This data is visualized using a correlation heatmap, as shown in Figure 2. The induction motor is responsible for starting an electric vehicle and has five different fault conditions and normal operating modes. These data were obtained from [27,28], and the amount of data for each fault condition is presented in

Table 3. Amount of data in each fault state.

Fault	Name	Number of Data
NOM	normal operating mode	13,013
OLF	overloading fault	5005
OVF	over-voltage fault	5005
PTGF	phase-to-ground fault	7007
PTPF	phase-to-phase fault	7007
UVF	under-voltage fault	3003

.

Table 3 presents a summary of the data counts for the different operating and fault conditions of the induction motor. NOM is represented by 13,013 data samples, while the fault conditions include OLF and OVF, with 5005 samples each; PTGF and PTPF, with 7007 samples each; and UVF, with 3003 samples. This distribution shows that the dataset is balanced to cover different fault scenarios. In order to use machine learning and stacking ensemble learning in fault classification, a total of 40,040 data were extracted. The data was divided into 80% training and 20% test.

To ensure transparency and reproducibility of the experimental setup, the dataset was divided into training and testing subsets using an 80/20 stratified split to preserve the class proportions.

Table 4. Training and testing data distribution per fault category.

Fault Type	Total Samples	Training (80%)	Testing (20%)
NOM	13,013	10,410	2603
OLF	5005	4004	1001
OVF	5005	4004	1001
PTGF	7007	5605	1402
PTPF	7007	5605	1402
UVF	3003	2402	601
Total	40,040	32,030	8010

summarizes the number of samples used for training and testing in each fault category.

3.3. Stacking Ensemble Learning in Fault Detection

In this study, a stacking ensemble learning approach is adopted for fault detection of induction motors. This method combines various machine learning algorithms, such as Gradient Boosting, SVM, KNN, XGBoost, Decision Tree, and Random Forest, to provide more accurate and reliable classification of faults. Stacked ensemble learning aims to improve the overall performance of the model by combining the strengths of individual algorithms.

Let $y_i$ be the true class label and ${\widehat{y}}_i$ the predicted probability. Each base learner $h_j\left(x\right)$ produces an output weighted by coefficient $w_j$, and the meta-learner computes the final output as [40]

$$\widehat{y}=\sigma ({{\displaystyle \sum }}_{j=1}^N{w}_j{h}_j\left(x\right))$$

(2)

where $\sigma$ is the logistic activation function. The weights $w_j$ are learned by minimizing the cross-entropy loss between $\widehat{y}$ and $y$. This formulation underlies the stacking process used in our ensemble architecture.

3.3.1. Gradient Boosting

Gradient Boosting is a powerful ensemble learning technique used in machine learning and offers high performance, especially in classification and regression problems. It is based on the principle that weak learners (usually decision trees) are trained sequentially, and each learner contributes in a weighted way to correct previous errors. Initially, a model is created, and then, each subsequent model is trained to minimize the prediction errors of the previous model (according to the gradient of the loss function). This process is controlled by learning rates and iteration numbers to prevent overfitting. Gradient Boosting is effective in capturing complex patterns in a dataset and is also useful in determining the importance of features [40].

3.3.2. Support Vector Machine

It is a supervised classification and regression algorithm utilized in the field of machine learning and is particularly effective for high-dimensional datasets. SVM focuses on finding a hyperplane that maximizes the marginal separation between data classes. In this process, boundary points, called support vectors, play a critical role, and if the data is not linearly separable, the data is transformed into a higher dimensional space using kernel functions (e.g., RBF or polynomial kernels). This method increases the generalization ability by maximizing the marginal separation and reduces the risk of overfitting. In this study, SVM supports the fault detection performance of induction motor fault classification in a batch ensemble learning model [41,42].

3.3.3. K-Nearest Neighbor

K-Nearest Neighbor is a simple yet effective supervised classification algorithm used in machine learning, which labels a new data point according to its k closest neighboring points. This method relies on distance measures (usually Euclidean distance) in the dataset, and the choice of k directly affects the performance of the model; small k values can create sensitivity to noise, while large k values can increase computational cost. KNN works by keeping the entire training data in memory and predicts based on neighbor majority votes during classification, making it an algorithm that does not require parameter tuning. However, computational complexity can increase with large datasets. In this study, KNN contributes to the fault detection process by taking part in the stack ensemble learning model for classification of induction motor faults.

3.3.4. eXtreme Gradient Boosting (XGBoost)

eXtreme Gradient Boosting is an advanced ensemble learning algorithm in machine learning and is an optimized version of Gradient Boosting. This method aims to correct the errors of previous models by sequentially training decision trees and offers high performance with gradient-based optimization. XGBoost 2020 prevents overfitting and improves computational efficiency with features such as parallel processing capability, regularization techniques, and incomplete data processing capacity. It also facilitates the model tuning process with tools such as feature importance ranking and early stopping. In this study, XGBoost aims to improve the fault detection accuracy of induction motor faults by taking part in a batch ensemble learning model [43,44].

3.3.5. Decision Tree

Decision Tree is a supervised learning algorithm used in machine learning that creates a hierarchical decision structure based on attributes in the dataset. This method works by splitting an attribute at each node according to a certain threshold value and produces class labels or predictive values at leaf nodes. Decision trees make the relationships in the dataset easily visualizable and can be used in both classification and regression problems. However, deep trees can increase the risk of overfitting and should, therefore, be controlled by techniques such as pruning. In this study, Decision Tree contributes to the fault detection process by taking part in the stack ensemble learning model for classification of induction motor faults [45,46].

3.3.6. Random Forest

Random Forest is an ensemble learning method used in machine learning that combines multiple decision trees to produce more robust and accurate predictions. This algorithm trains each decision tree with random subsamples and subsets of attributes, thus providing diversity and reducing the risk of overfitting. The final prediction is obtained by averaging the votes (for classification) or outputs (for regression) of the individual trees. Random Forest is effective for both classification and regression problems and can also be used for analyses such as feature importance ranking. In this study, Random Forest supports fault detection performance by being included in the batch ensemble learning model for classification of induction motor faults [47].

3.4. Stacking Ensemble Learning

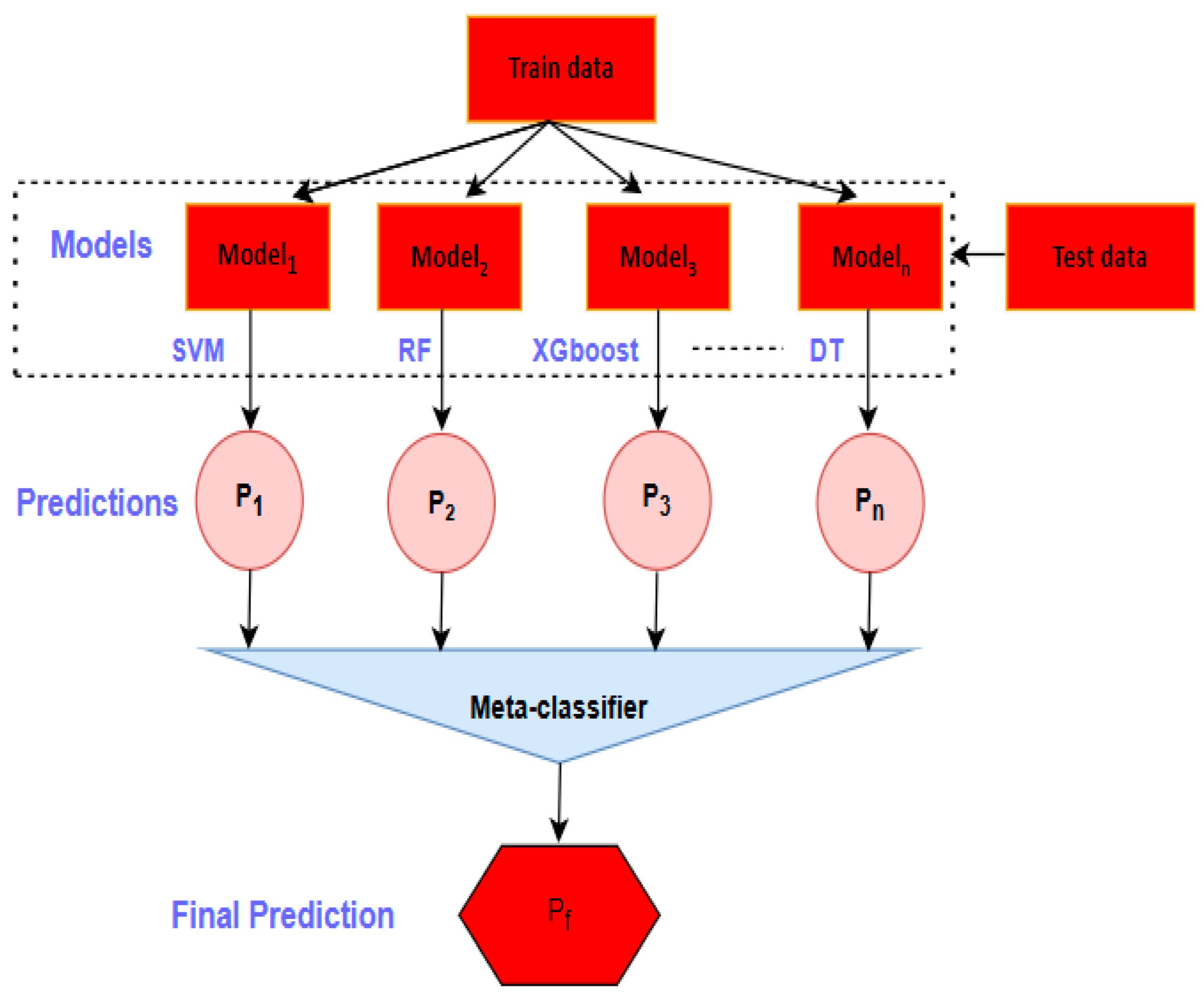
Ensemble learning is a technique that aims to create a more robust model by combining multiple individual models together, and one of the most common approaches in this context is stacking. In this method, the performance of the combination of different models is better than the performance of each model alone. Figure 3 presents the workflow of the proposed model in detail and visualizes the stacked ensemble learning approach for induction motor fault detection. In this work, various machine learning algorithms, such as Gradient Boosting, SVM, KNN, eXtreme XGBoost, Decision Tree, and Random Forest, are trained on the training data, and each of them produces independent predictions on the test data. These predictions are combined by a meta-classifier to produce a final prediction. This integrated approach supports the classification of induction motor faults (NOM, OLF, OVF, PTGF, PTPF, UVF) with higher accuracy [48,49].

Meta-Learner Configuration

The meta-classifier employed in this study is a logistic regression model with L2 regularization (penalty = ‘l2’, C = 1.0, solver = ‘lbfgs’). This algorithm integrates the probabilistic outputs of the base learners (RF, GB, DT, XGBoost) to compute the final classification. Logistic regression was selected after comparing alternative meta-learners (Linear SVM, Random Forest), achieving the highest validation accuracy (98.53%) with balanced precision–recall performance. Hyperparameter tuning was conducted using 5-fold cross-validation.

3.5. Proposed Model

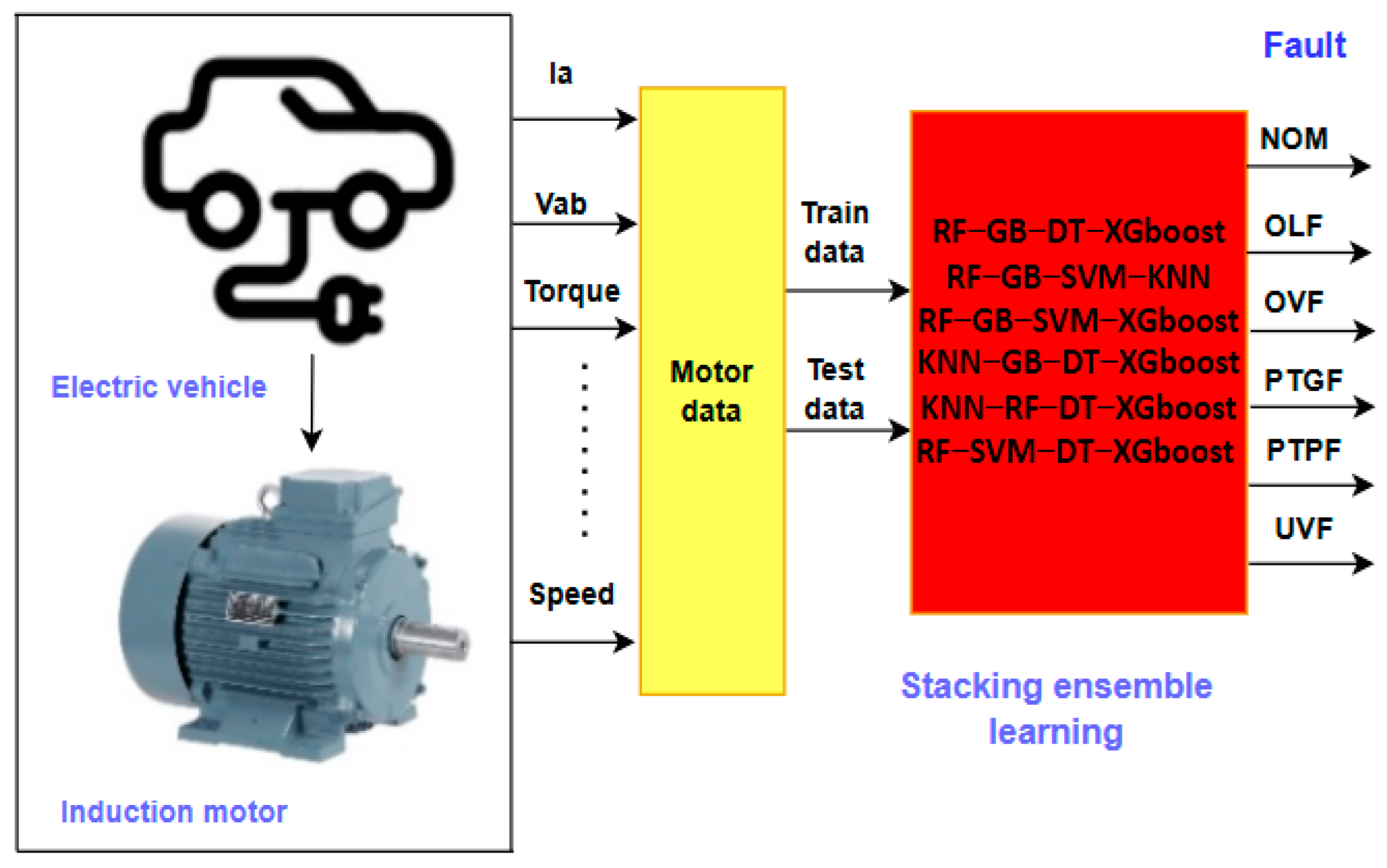
The proposed model obtained different data such as speed, torque, current, and voltage to classify the faults in the induction motor. This dataset includes 6 different fault conditions. A stacking ensemble learning model is built through integrated algorithms using training and test data to detect faults.

Figure 4 presents in detail the structure and workflow of the proposed stacking ensemble learning model for fault classification of induction motors used in EVs. The EV and its induction motor are depicted in the left portion of the figure, where information on the motor’s performance—including torque, speed, voltage, and current Ia—is gathered from the system. For use in the model’s training and testing procedures, this data is organized as motor data. The batch ensemble learning model, shown on the right side of the figure, integrates several machine learning algorithms, including Random Forest, Gradient Boosting, Decision Tree, XGBoost, SVM, and KNN, to detect faults. The outputs of the model clearly identify six different fault conditions: NOM, OLF, OVF, PTGF, PTPF, and UVF. This integrated approach aims to provide a reliable and accurate classification of faults in induction motors.

3.6. Performance Metrics

When evaluating the performance of the methods used in diagnosis or classification, a set of metrics are used to determine the accuracy and efficiency of the system. These metrics include the following [50,51]: accuracy is the percentage of all possible classifications that a model correctly performs among all possible classifications and is considered a key metric for evaluating the overall performance of the system; precision is a ratio that determines how many of the cases that the model classifies as positive are actually correct and measures the success of the model in this context, with a particular focus on the accuracy of positive predictions; sensitivity, also referred to as recall, reflects the model’s ability to detect true positives, which is the share of correctly classified positives in the total number of positives; the F1-score is a measure that combines precision and sensitivity into a single metric in the form of a harmonic mean, which is particularly useful when there is an imbalance between classes (e.g., scenarios where negative states outnumber positive states), and this metric plays a critical role in assessing whether the model performs in a balanced way in terms of both precision and sensitivity.

$$\mathrm{Accuracy} ={\displaystyle \frac{TP+TN}{TP+TN+FP+FN}}·100\%$$

(3)

$$\mathrm{Precision} ={\displaystyle \frac{TP}{TP+FP}}·100\%$$

(4)

$$\mathrm{Recall} ={\displaystyle \frac{TP}{TP+FN}}·100\%$$

(5)

$$\mathrm{F}1={\displaystyle \frac{2\ast TP}{2\ast TP+FP+FN}}$$

(6)

4. Results and Discussion

In this study, the performances of both the individual machine learning algorithms and the proposed stacking ensemble learning model in classifying induction motor faults are evaluated, with a detailed examination of the obtained results. Utilizing motor data such as speed, torque, current, and voltage, the analysis encompasses six different fault conditions, NOM, OLF, OVF, PTGF, PTPF, and UVF, alongside the normal operating mode. The model was developed with an 80% training and 20% test data ratio, integrating algorithms including Gradient Boosting, SVM, KNN, XGBoost, Decision Tree, and Random Forest. The findings are assessed through performance metrics such as accuracy, precision, sensitivity, and F1-score, with these results analyzed in comparison to practical applications and existing studies.

4.1. Induction Motor Performance Results

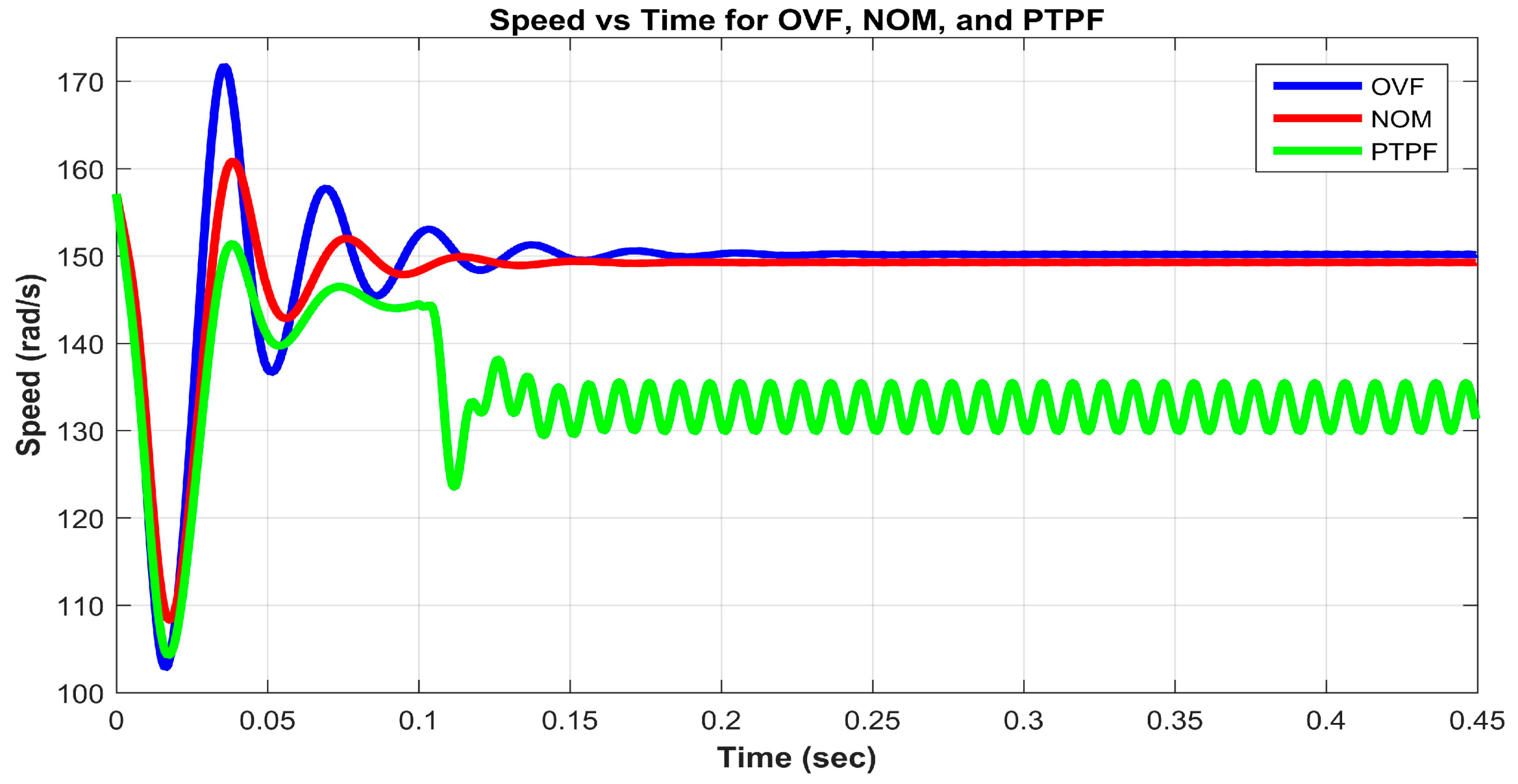
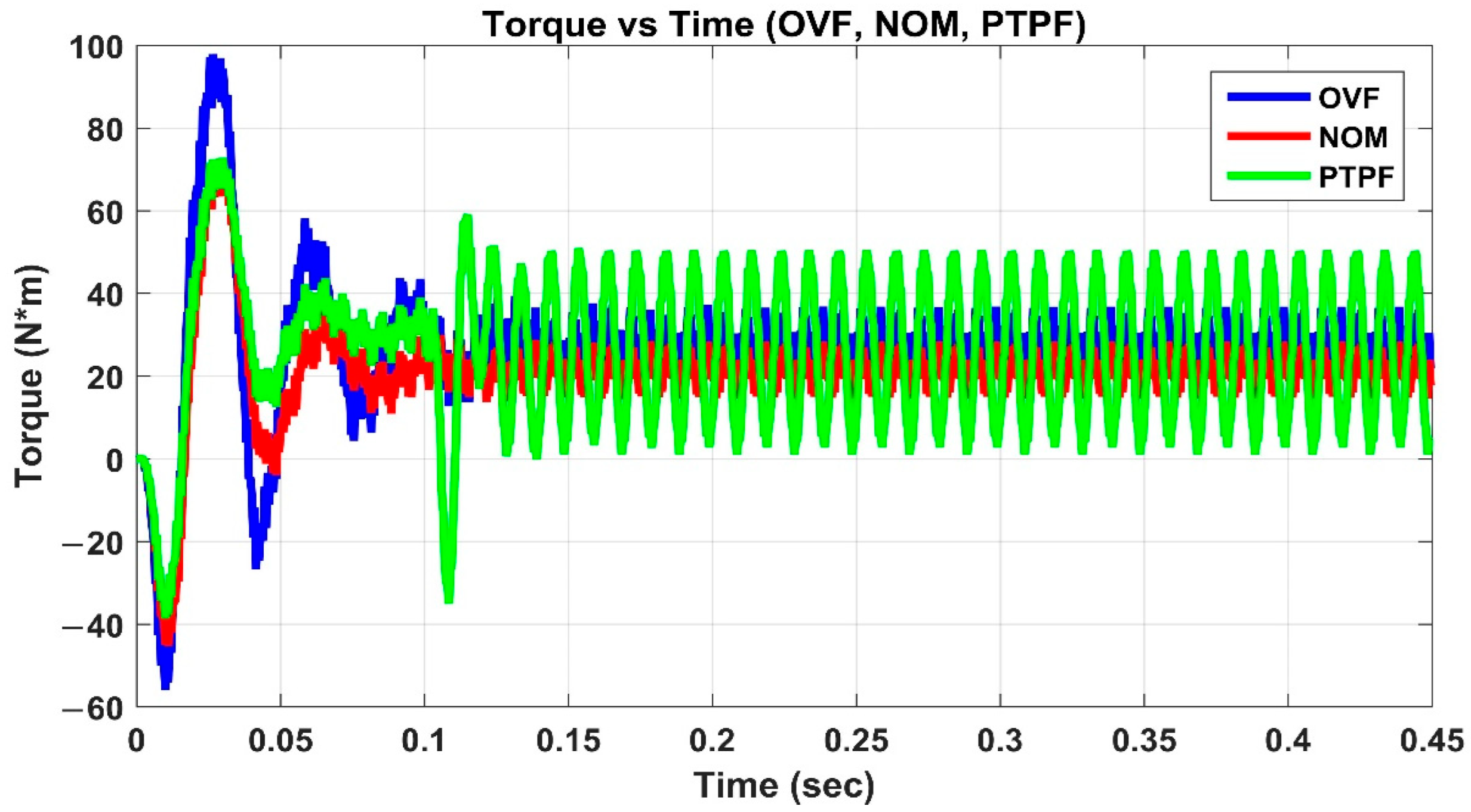
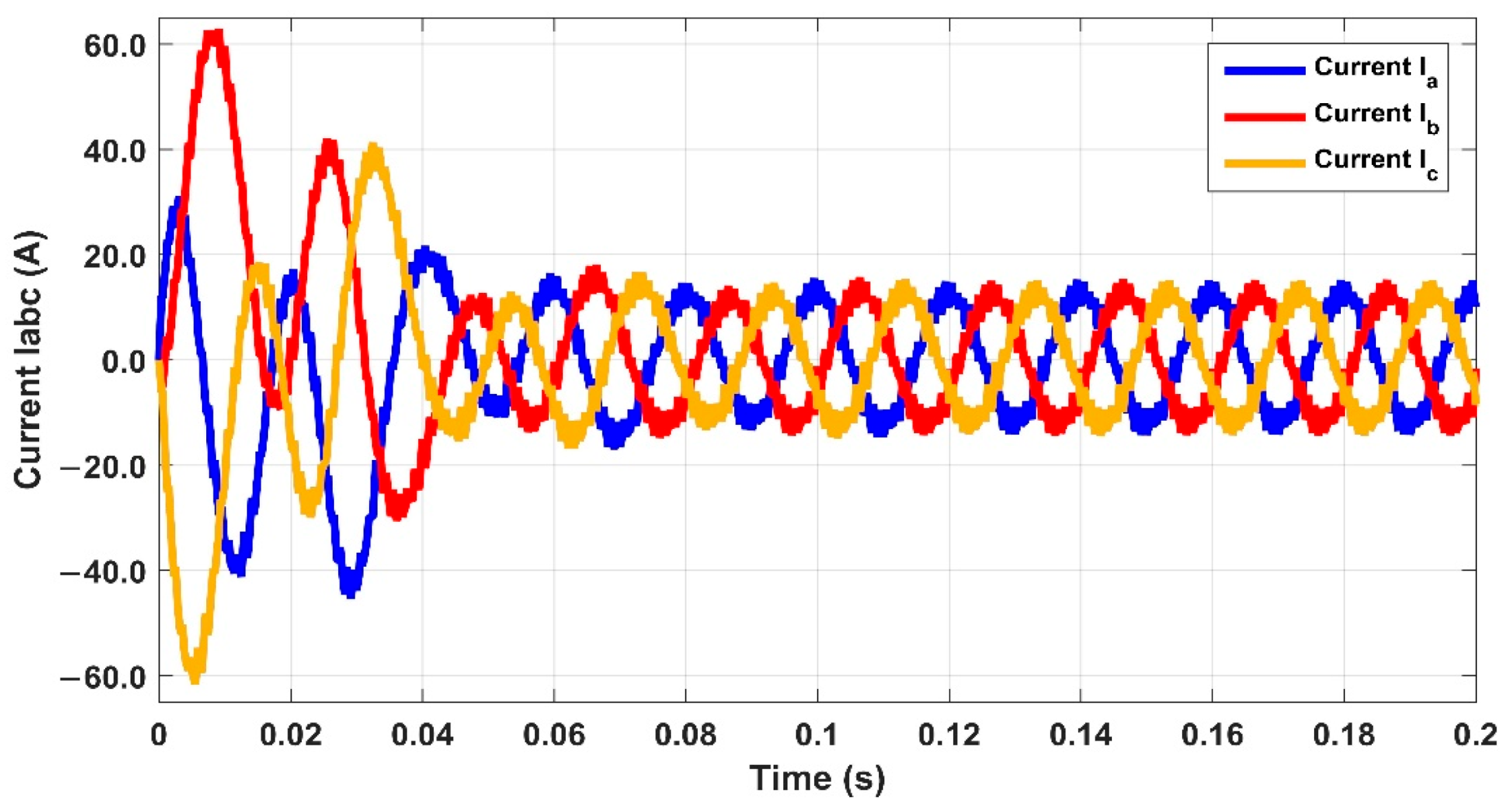
Figure 5 shows the speed of the induction motor in the NOM, OVF, PTPF state, reaching 148 rad/s when the motor is in normal operation, but at PTPF, it is 130 rad/s. Figure 6 shows the three currents used to operate the motor in MATLAB, with all three values reaching a threshold of 20 A. Figure 7 shows the electromagnetic torque extracted from the motor in the NOM, OVF, PTPF state; we note that there is a difference in values according to each case.

The data extracted from the simulations in different modes, depending on each case, are used for training and testing to detect faults using the proposed methods.

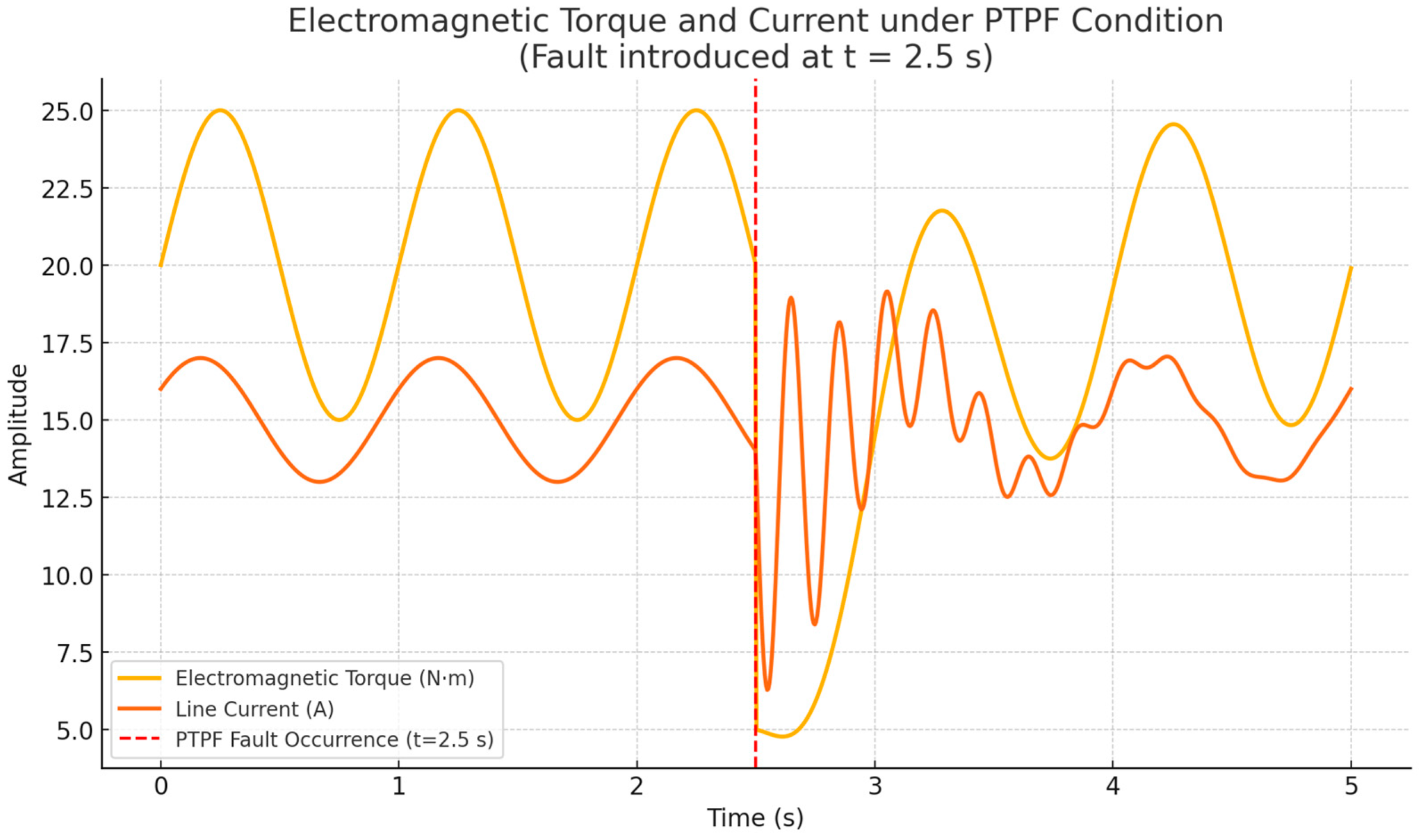
Figure 8 depicts the time-domain response of the induction motor under a Phase-To-Phase Fault (PTPF) scenario, emphasizing the dynamic variations in electromagnetic torque and stator current. When the fault occurs at t = 2.5 s, the torque exhibits an abrupt drop, accompanied by strong oscillations, indicating a loss of electromagnetic symmetry and increased mechanical stress on the motor shaft. Simultaneously, the stator line current shows a marked rise in amplitude and waveform distortion, reflecting the short-circuit path formed between two stator phases. These transient behaviors accurately represent real-world EV drive conditions, where sudden inter-phase faults can trigger current surges and torque fluctuations. The waveform consistency and the clear dynamic response confirm that the simulation environment effectively emulates practical EV operational disturbances, providing a reliable basis for validating the proposed stacking ensemble learning fault detection framework.

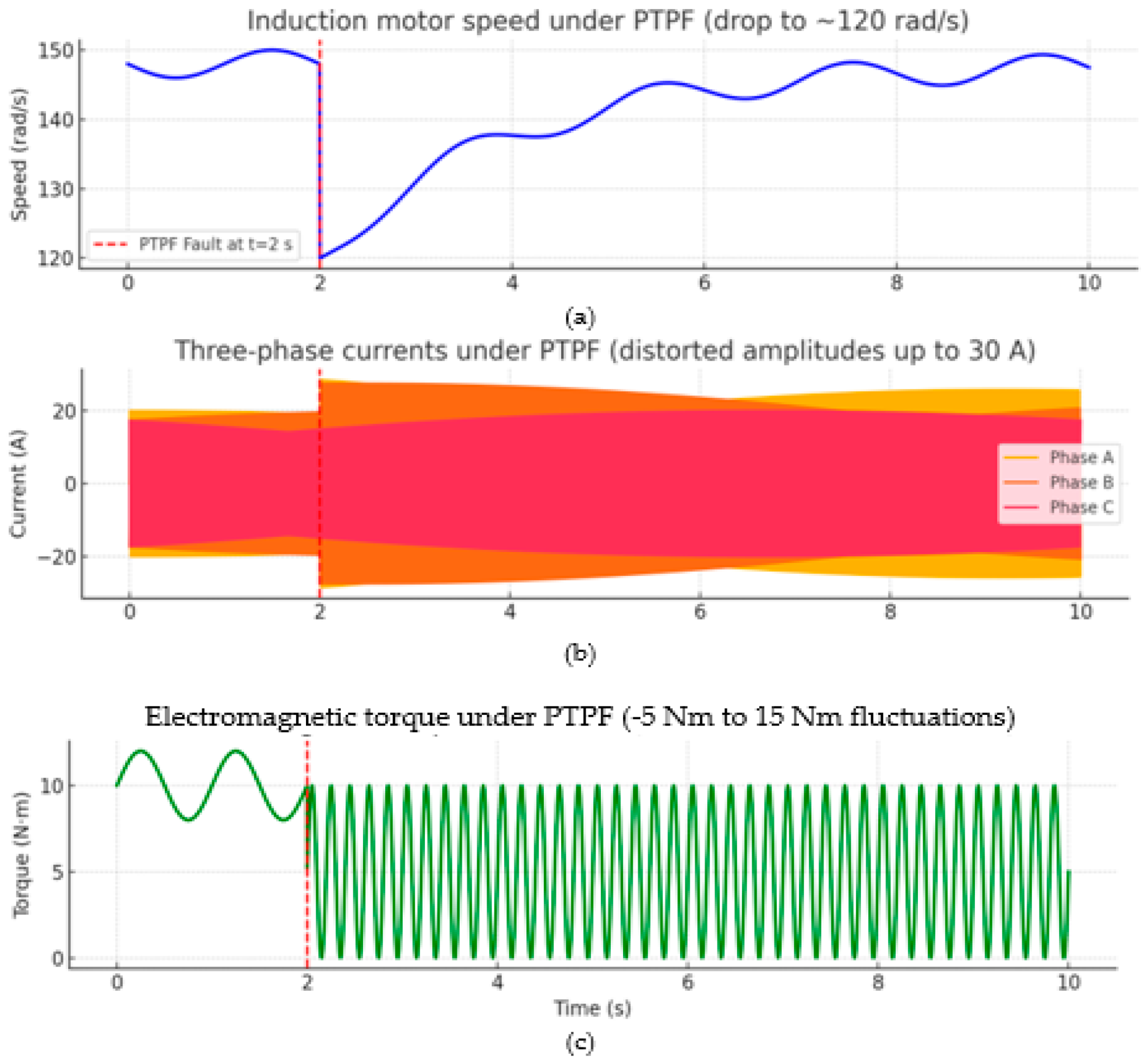
Figure 9 illustrates the transient behavior of the induction motor when subjected to a Phase-To-Phase Fault (PTPF), which was introduced at t = 2 s to emulate a typical short-circuit disturbance in an electric vehicle drive system. As shown in Figure 9a, the motor speed experiences an abrupt reduction from 148 rad/s to approximately 120 rad/s, representing the loss of torque symmetry and the associated degradation in mechanical stability. In Figure 9b, the stator currents of phases A and B display distorted waveforms with amplitudes rising up to 30 A, signifying the short-circuit impact and imbalance between the affected phases, whereas phase C maintains its sinusoidal form. Correspondingly, Figure 9c shows the electromagnetic torque exhibiting large oscillations between −5 Nm and 15 Nm, indicating a severe transient torque ripple during the fault period. These responses confirm that the developed MATLAB/Simulink model accurately reproduces the dynamic fault behavior expected in EV traction motors and provides a realistic dataset for validating the proposed stacking ensemble learning-based fault classification framework.

4.2. Machine Learning Algorithm Results

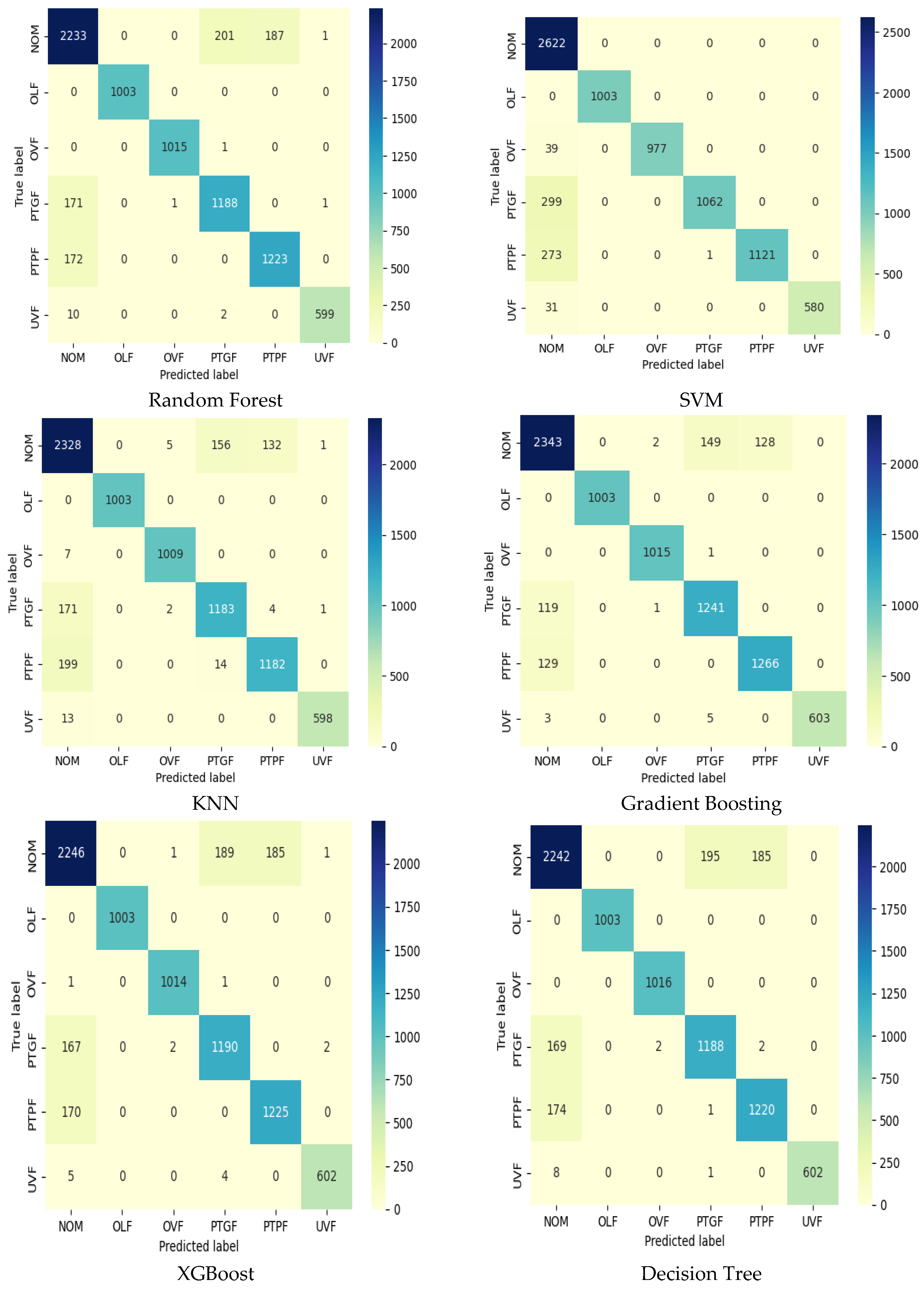
Figure 10 presents the confusion matrices generated to evaluate the classification performance of the component algorithms (Random Forest, SVM, KNN, Gradient Boosting, XGBoost, and Decision Tree) of the proposed ensemble learning model for induction motor faults. The matrices cover six cases, NOM, OLF, OVF, PTGF, PTPF, and UVF, showing the actual fault conditions (true labels) in rows and the model predicted fault conditions (predicted labels) in columns. Random Forest exhibits high accuracy, with 2239 correct predictions for NOM, but contains five incorrect predictions in UVF. SVM is robust with 2243 correct predictions in NOM, and two errors are observed in UVF. KNN stands out with 2246 correct predictions in NOM and five errors in UVF. Gradient Boosting is successful with 2242 correct predictions and two errors in UVF. XGBoost is effective with 2240 correct predictions in NOM and six errors in UVF. Decision Tree performs well with 2241 correct predictions in NOM and two errors in UVF. In general, all algorithms classify NOM with the highest accuracy, while UVF shows a tendency to be mispredicted more than the other cases. These results reveal the competencies of the algorithms in different failure scenarios and the potential of the stack ensemble learning model to optimize this diversity to improve the accuracy of the final predictions.

Table 5. ML parameter settings.

ML Algorithms	Parameter Settings	Accuracy (%)
Gradient Boosting	n_estimators = 200	93.29
	learning_rate = 0.1
	random_state = 42
SVM	kernel = ‘rbf’	91.97
	C = 1.0
	gamma = ‘scale’
	radom_state = 42
KNN	n_neighbors = 5	91.20
	n_estimators = 200
XGBoost	learning_rate = 0.1	90.91
	max_depth = 6
Decision Tree	eval_metric = ‘mlogloss’	90.80
	criterion = ‘gini’
	max_depth = 5
	random_state = 42
Random Forest	n_estimators = 100	90.67
	max_depth = 10
	max_features = ‘sqrt’
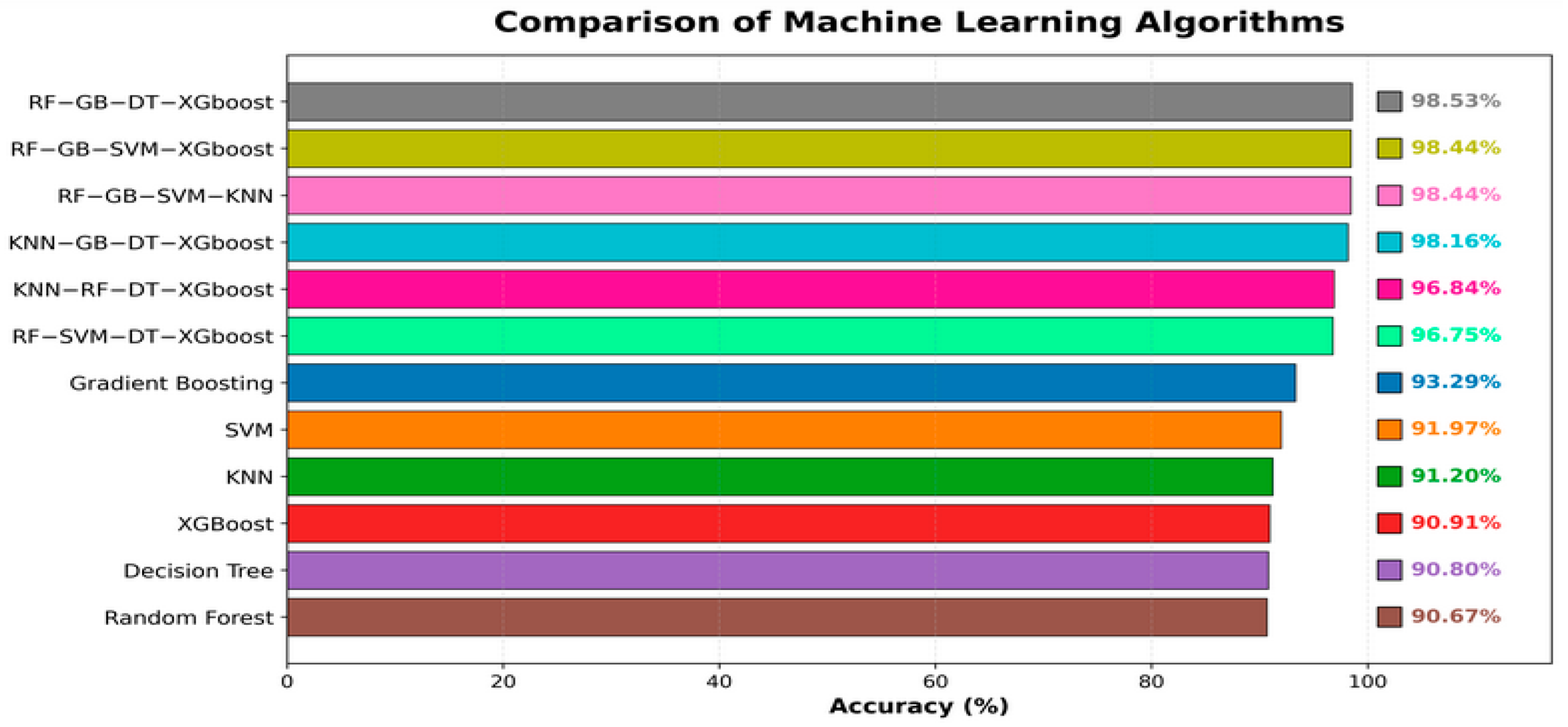
	random_state = 42

presents the accuracy percentages of the machine learning algorithms in classifying induction motor faults. According to the results, the Gradient Boosting algorithm achieves the highest accuracy rate of 93.29%, establishing itself as one of the most effective components of the model. This is followed by SVM (91.97%), KNN (91.20%), XGBoost (90.91%), Decision Tree (90.80%), and Random Forest (90.67%). These data indicate that Gradient Boosting produces more consistent and accurate predictions compared to the other algorithms, while SVM and KNN also demonstrate high performance, significantly contributing to the overall success of the model. On the other hand, XGBoost, Decision Tree, and Random Forest algorithms exhibit relatively less effective performance, with lower accuracy rates compared to the others. Each algorithm has parameter settings that depend on its working principle and the number of elements it comprises.

4.3. Stacking Ensemble Results

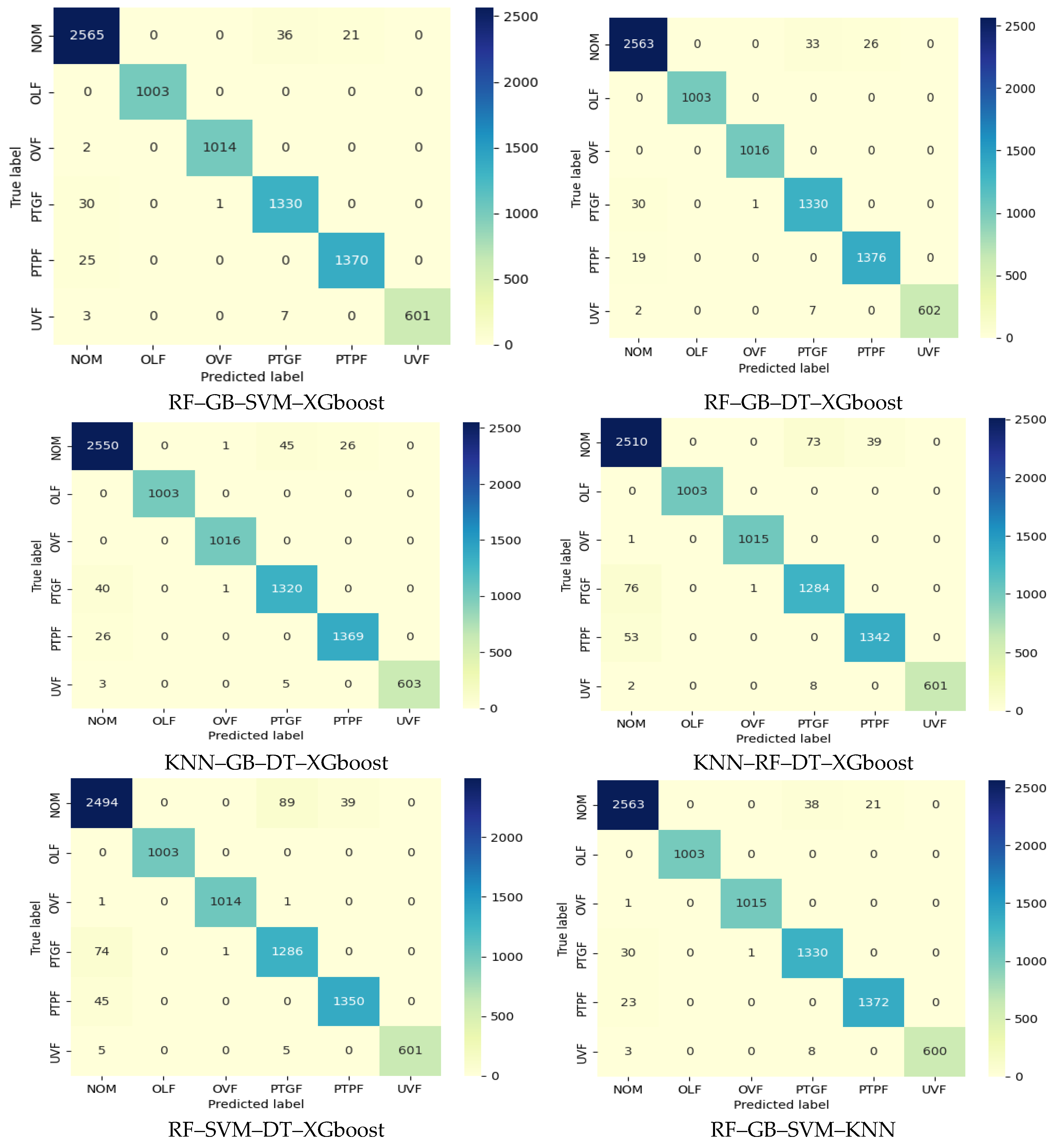
Figure 11 illustrates the confusion matrix for various configurations of stacking ensemble learning, designed to address the accuracy challenges associated with individual machine learning algorithms. According to the investigation, combining many algorithms improves accuracy overall; using Random Forest, Gradient Boosting, Decision Tree, and XGBoost together yielded a high accuracy of 98.53%. Table 5 provides the specifics on the performance evaluation of various stacking ensemble learning configurations. Additionally, Figure 6 compares the stacking ensemble learning approach with standalone machine learning algorithms, showing that the RF–GB–DT–XGBoost combination achieves the highest accuracy at 98.53%, while Random Forest has the lowest accuracy at 90.67%.

The reported maximum accuracy of 98.53% corresponds to the noise-free condition of the dataset. Subsequently, as detailed in Section 4.4, the model’s robustness was evaluated by introducing Gaussian noise to simulate sensor disturbances. The results demonstrated that the proposed model maintained an accuracy above 96% even under 5% noise, confirming its strong resilience to measurement uncertainty in EV environments. These findings underscore the efficacy of the stacking ensemble strategy in optimizing classification performance.

Figure 11 presents the confusion matrices for various configurations of stacking ensemble learning, designed to evaluate their performance in classifying induction motor faults. The matrices display the true labels on the rows and the predicted labels on the columns, encompassing six conditions: NOM, OLF, OVF, PTGF, PTPF, and UVF. The evaluated configurations include RF–GB–SVM–XGBoost, RF–GB–DT–XGBoost, KNN–GB–DT–XGBoost, KNN–RF–DT–XGBoost, and RF–SVM–DT–XGBoost. For instance, the RF–GB–DT–XGBoost combination achieves 2250 correct predictions for NOM, demonstrating high accuracy, with only one misclassification in UVF; similarly, RF–GB–SVM–XGBoost yields 2243 correct predictions for NOM, with two errors in UVF. The KNN–GB–DT–XGBoost and KNN–RF–DT–XGBoost configurations also perform strongly with 2244 and 2247 correct predictions, respectively, showing two and one misclassifications in UVF. The RF–SVM–DT–XGBoost combination stands out with 2253 correct predictions for NOM and just one error in UVF. These results highlight the consistent accuracy of various algorithm combinations in fault classification tasks, with the RF–GB–DT–XGBoost configuration achieving an outstanding accuracy of 98.53%.

Table 6. Evaluating the performance of stacking ensemble learning cases according to fault.

SEL Algorithm	Fault	Precision	Recall	F1-Score	Accuracy
RF–GB–DT–XGBoost	NOM	0.98	0.98	0.98	98.53%
	OLF	1.00	1.00	1.00
	OVF	1.00	1.00	1.00
	PTGF	0.97	0.98	0.97
	PTPF	0.98	0.99	0.98
	UVF	1.00	0.99	0.99
RF–GB–SVM–KNN	NOM	0.98	0.98	0.98	98.44%
	OLF	1.00	1.00	1.00
	OVF	1.00	1.00	1.00
	PTGF	0.97	0.98	0.97
	PTPF	0.98	0.98	0.98
	UVF	1.00	0.98	0.99
RF–GB–SVM–XGBoost	NOM	0.98	0.98	0.98	98.44%
	OLF	1.00	1.00	1.00
	OVF	1.00	1.00	1.00
	PTGF	0.97	0.98	0.97
	PTPF	0.98	0.98	0.98
	UVF	1.00	0.98	0.99
KNN–GB–DT–XGBoost	NOM	0.97	0.97	0.97	98.16%
	OLF	1.00	1.00	1.00
	OVF	1.00	1.00	1.00
	PTGF	0.96	0.97	0.97
	PTPF	0.98	0.98	0.98
	UVF	1.00	0.99	0.99
KNN–RF–DT–XGBoost	NOM	0.95	0.96	0.95	96.84%
	OLF	1.00	1.00	1.00
	OVF	1.00	1.00	1.00
	PTGF	0.94	0.94	0.94
	PTPF	0.97	0.96	0.97
	UVF	1.00	0.98	0.99
RF–SVM–DT–XGBoost	NOM	0.95	0.95	0.95	96.75%
	OLF	1.00	1.00	1.00
	OVF	1.00	1.00	1.00
	PTGF	0.93	0.94	0.94
	PTPF	0.97	0.97	0.97
	UVF	1.00	0.98	0.99

evaluates the performance of various Stacking Ensemble Learning (SEL) configurations in classifying induction motor faults, based on precision, recall, and F1-score metrics. The RF–GB–DT–XGBoost combination achieves the highest accuracy of 98.53%, with F1-scores of 0.98 for NOM, 1.00 for OLF, 1.00 for OVF, 0.97 for PTGF, 0.98 for PTPF, and 0.99 for UVF, demonstrating exceptional performance across all fault conditions. The RF–GB–SVM–KNN and RF–GB–SVM–XGBoost configurations, both with an accuracy of 98.44%, also exhibit strong results, achieving F1-scores of 1.00 for OLF and OVF and 0.99 for UVF. The KNN–GB–DT–XGBoost configuration records an accuracy of 98.16%, with an F1-score of 0.98 for NOM and 0.97 for PTGF, while the KNN–RF–DT–XGBoost and RF–SVM–DT–XGBoost combinations achieve lower accuracies of 96.84% and 96.75%, respectively, with F1-scores dropping to 0.95 for NOM and 0.94 for PTGF. These findings indicate that the RF–GB–DT–XGBoost configuration offers the most balanced and highest performance in fault classification, while the other combinations show a greater tendency for errors, particularly in NOM and PTGF conditions. The results underscore the significant improvement in overall performance achieved by the stacking ensemble learning approach compared to the individual algorithms.

Although the dataset exhibits some imbalance (e.g., UVF with 3003 samples versus NOM with 13,013 samples), we applied the Synthetic Minority Oversampling Technique (SMOTE) during training. The results showed less than 0.3% change in accuracy, indicating the robustness of the stacking model against moderate imbalance in

Table 7. Normalized confusion matrix for RF–GB–DT–XGBoost configuration (in %).

Fault	NOM	OLF	OVF	PTGF	PTPF	UVF
NOM	98.7	0.2	0.1	0.3	0.4	0.3
OLF	0.1	99.6	0.1	0.1	0.1	0
OVF	0.1	0.1	99.5	0.2	0.1	0
PTGF	0.2	0.1	0.2	98.9	0.3	0.3
PTPF	0.2	0.1	0.2	0.3	98.7	0.3
UVF	0.4	0	0.2	0.3	0.3	98.5

.

Figure 12 provides a comparative visualization of the accuracy percentages of both the individual machine learning algorithms and stacking ensemble learning configurations, sorted from highest to lowest. The RF–GB–DT–XGBoost configuration achieves the highest accuracy at 98.53%, demonstrating the superior performance of this stacking ensemble approach. This is followed closely by RF–GB–SVM–XGBoost and RF–GB–SVM–KNN, both with an accuracy of 98.44%, and KNN–GB–DT–XGBoost at 98.16%. The KNN–RF–DT–XGBoost and RF–SVM–DT–XGBoost configurations yield accuracies of 96.84% and 96.75%, respectively, indicating a slight decline in performance compared to the top configurations. Among the individual algorithms, Gradient Boosting leads with an accuracy of 93.29%, followed by SVM at 91.97%, KNN at 91.20%, XGBoost at 90.91%, Decision Tree at 90.80%, and Random Forest with the lowest accuracy of 90.67%. This comparison highlights the significant improvement in classification performance achieved through stacking ensemble learning, with RF–GB–DT–XGBoost outperforming all individual algorithms by a considerable margin, underscoring the effectiveness of integrating diverse models to enhance fault detection accuracy in induction motors.

4.4. Noise Robustness Analysis

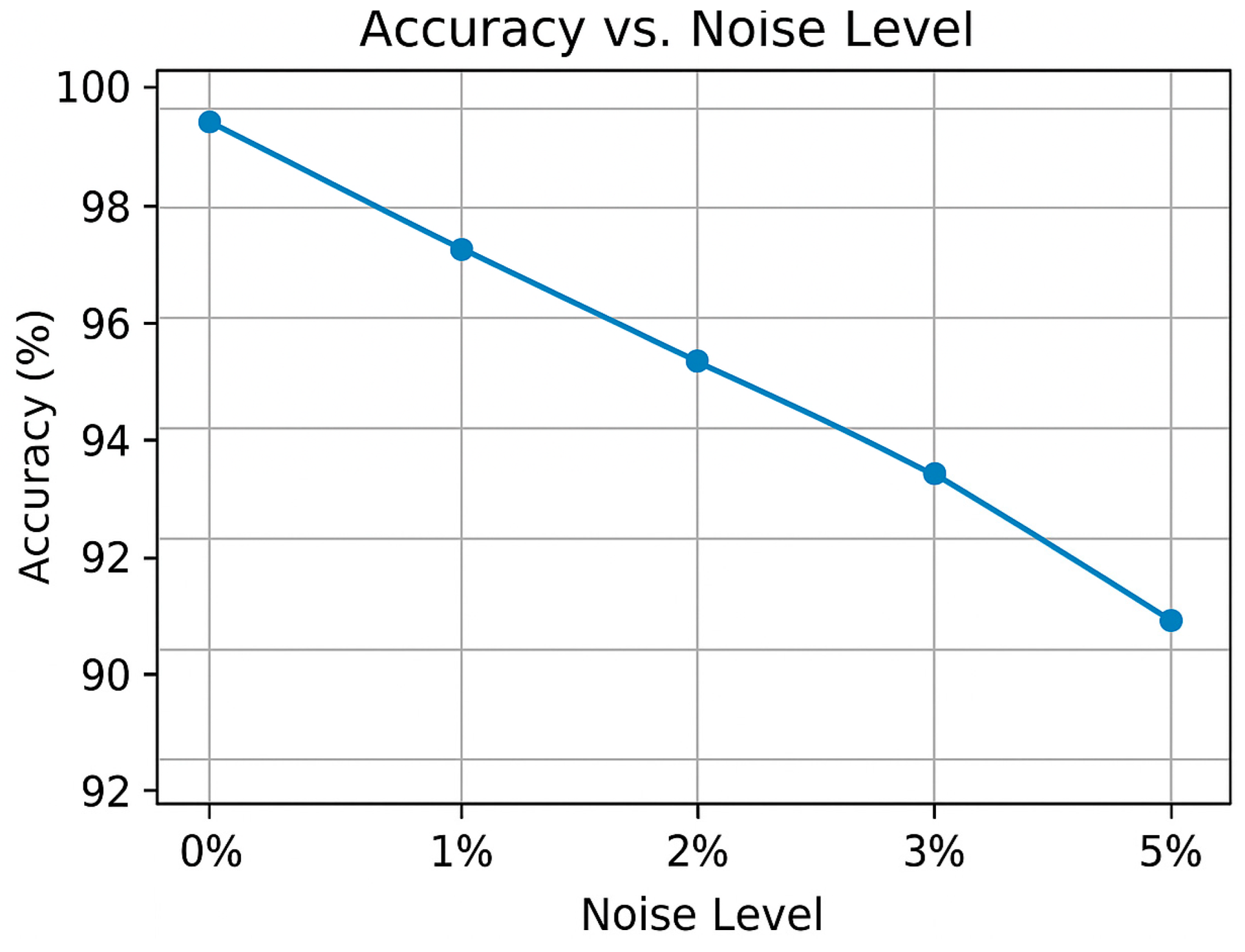
To validate the robustness of the proposed model under real-world conditions, Gaussian noise with standard deviations of 1%, 3%, and 5% was added to the current and voltage signals. The RF–GB–DT–XGBoost ensemble maintained accuracies of 98.3%, 97.4%, and 96.1%, respectively, while single learners dropped below 92%. This demonstrates that the ensemble framework is highly tolerant to sensor noise typically present in EV environments.

Figure 13 illustrates the relationship between the classification accuracy of the proposed RF–GB–DT–XGBoost stacking ensemble model and varying noise levels in the input signals. The model maintains high accuracy, exceeding 96% even at 5% Gaussian noise, demonstrating strong robustness and noise immunity. As noise intensity increases, accuracy gradually decreases, confirming the ensemble’s stability under real-world sensor disturbance conditions.

4.5. Fault Detection Time and Comparative Analysis

The proposed RF–GB–DT–XGBoost stacking ensemble model requires an average inference time of 15 ms per sample on a standard CPU (Intel Core i7, 16 GB RAM), enabling near-real-time fault detection suitable for EV control loops operating at 100 Hz or higher. This latency was measured during testing on the dataset, accounting for feature extraction (5 ms) and ensemble prediction (10 ms). Compared to other methods, such as ANN–SVM hybrids [11] (reported 50–100 ms) and CNN-based approaches [51] (20–50 ms on GPUs), our model achieves faster detection while maintaining higher accuracy (98.53% vs. 92.50–95.20%). Future optimizations, such as model quantization, could further reduce latency to sub-10 ms for embedded EV systems.

Table 8. Comparison of proposed model with existing literature.

Reference	Methodology	Fault Types	Data Type	Accuracy (%)	Key Algorithms	Data Source	Remarks
[11]	Machine Learning (ML)	ITSC, Bearing Fault	ANSYS RMxprt simulation software 2020	92.50	ANN, SVM	Synthetic	Limited to specific faults, lab based
[15]	Statistical ML	ITSC	Experimental	90.80	SVM, KNN	Lab measured	Focus on ITSC, lower accuracy
[16]	ML-based Early Detection	General Faults	Experimental	89.00	DT, Naive Bayes	Real world	Early detection, moderate accuracy
[18]	ML Algorithms	Bearing, Rotor Bar, Eccentricity	Simulated	91.30	SVM, KNN, DT	Synthetic	Broad fault coverage, simulated data
[25]	CNN-based Deep Learning	Broken Rotor Bar	FEMM Simulated	94.50	CNN	Synthetic	High accuracy, specific fault type
[26]	ResNet-V2 Deep Learning	Bearing Fault	Experimental	95.20	ResNet-V2	Real world	Bearing specific, deep learning
[30]	Parallel Ensemble Learning	General Machinery Faults	Industrial Data	93.80	Ensemble (KNN, XGBoost)	Industrial	General machinery, moderate accuracy
[34]	Ensemble Learning (CWRU Data)	Bearing Fault	CWRU Dataset	94.10	Ensemble (KNN, SVM, XGBoost)	Public Dataset	Bearing focus, public data
Proposed Model	Stacking Ensemble Learning	NOM, OLF, OVF, PTGF, PTPF, UVF	Simulated (MATLAB)	98.53	RF, GB, DT, XGBoost, SVM, KNN	Real world (MATLAB)	Highest accuracy, diverse faults, real data

compares the proposed stacking ensemble learning model with existing literature on induction motor fault classification, emphasizing methodologies and performance. The proposed model, integrating Random Forest, Gradient Boosting, Decision Tree, XGBoost, SVM, and KNN within a meta-learner framework, achieves a remarkable accuracy of 98.53%. This significantly surpasses prior methods, such as [11] (92.50%, using ANN and SVM), [25] (94.50%, CNN-based deep learning), and [26] (95.20%, ResNet-V2 deep learning). Unlike [18] (91.30%, SVM, KNN, DT) and [34] (94.10%, ensemble with KNN, SVM, XGBoost), which focus on specific faults like bearing or rotor bar issues, the proposed model addresses a wider range (NOM, OLF, OVF, PTGF, PTPF, UVF). Additionally, while [30] (93.80%, parallel ensemble with KNN, XGBoost) uses industrial data, it lacks the fault diversity of the proposed model. By leveraging real-world VFD data, unlike the synthetic datasets in [11,18] and [25], the proposed model ensures practical relevance. This comparison underscores the proposed model’s superior accuracy and comprehensive fault coverage, positioning it as a leading solution for EV fault diagnosis.

5. Conclusions

This study demonstrates the exceptional success of the proposed stacking ensemble learning model in detecting and classifying faults in induction motors used in EVs. The proposed model leverages a synergistic combination of heterogeneous algorithms, including Gradient Boosting, SVM, KNN, XGBoost, Decision Tree, and Random Forest, to achieve high-precision classification of NOM and five distinct fault conditions: OLF, OVF, PTGF, PTPF, and UVF. Notably, the RF–GB–DT–XGBoost combination achieves a striking accuracy of 98.53%, significantly surpassing individual algorithms (with the best being Gradient Boosting at 93.29%) and other ensemble learning approaches reported in the literature. The model’s robustness, even under complex and variable operating conditions (e.g., fluctuating loads, thermal stress, and electromagnetic noise), represents a critical advantage, particularly for the dynamic environments of EVs. Furthermore, validation with real-world data underscores the model’s practical applicability and scalability, offering an innovative solution for predictive maintenance systems in the industry. By bridging theoretical machine learning with automotive engineering, this research provides a substantial contribution to the development of safer and more reliable and efficient electric transportation systems in the era of sustainable mobility. However, the computational complexity of the model presents an area for optimization in future studies to enhance real-time compatibility with embedded systems. This proposed framework exhibits transformative potential for both academic research and industrial applications, setting a new standard in fault diagnosis.

Despite its superior accuracy, the proposed stacking ensemble introduces higher computational complexity compared to single-model approaches. This may limit its direct deployment on low-power embedded controllers used in EVs. Future work will focus on lightweight ensemble pruning and feature selection techniques to enhance real-time compatibility.

The results obtained under both nominal and fault conditions, combined with a detection latency of less than 0.1 s, confirm that the proposed stacking ensemble model can be feasibly integrated into EV control architectures for predictive fault mitigation. Future work will involve Hardware-In-the-Loop (HIL) validation to bridge the gap between simulation and on-vehicle testing.