Parameter Compensation for the Predictive Control System of a Permanent Magnet Synchronous Motor Based on Bacterial Foraging Optimization Algorithm
Abstract
1. Introduction
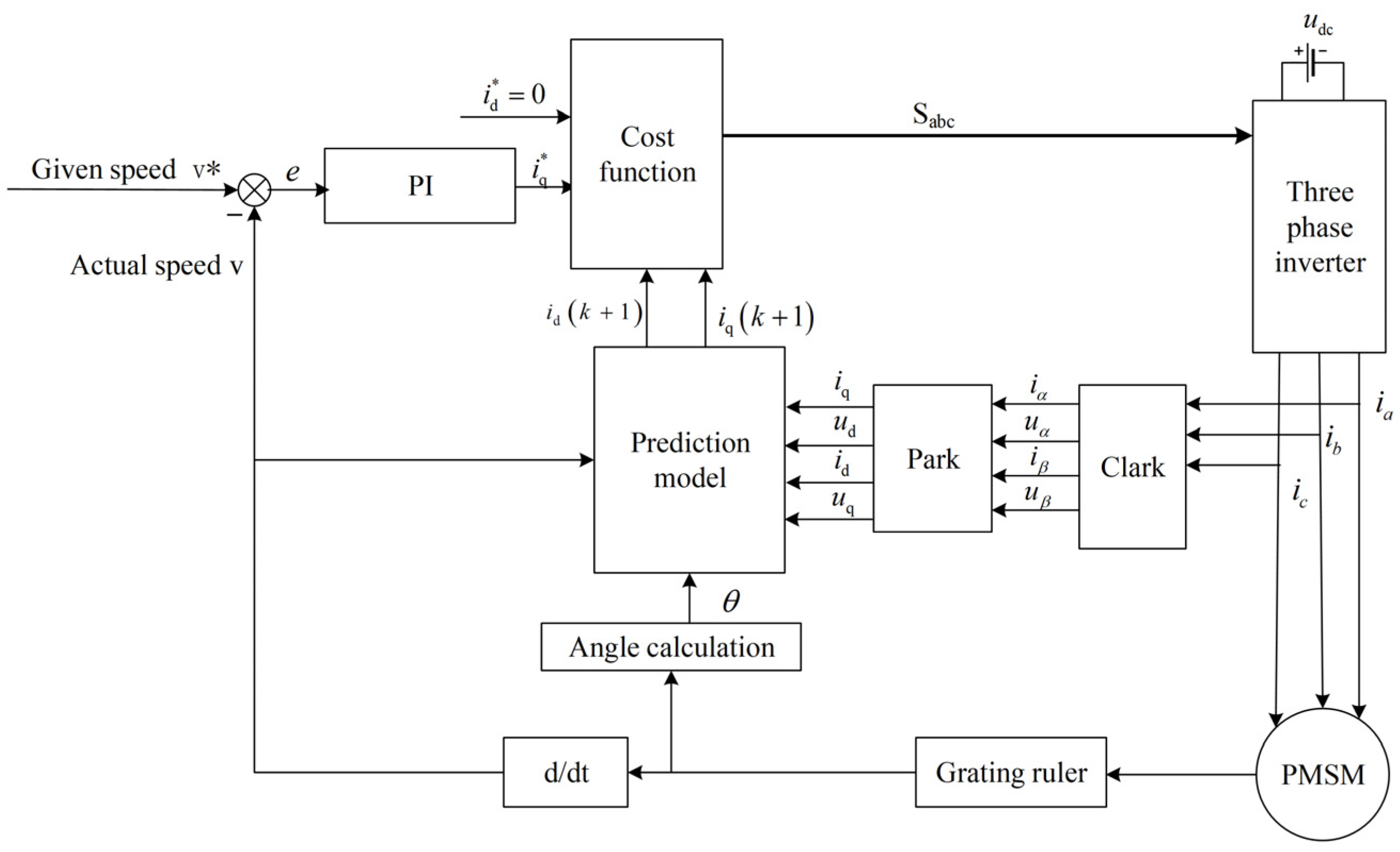
2. FCS-MPCC Theory and Model
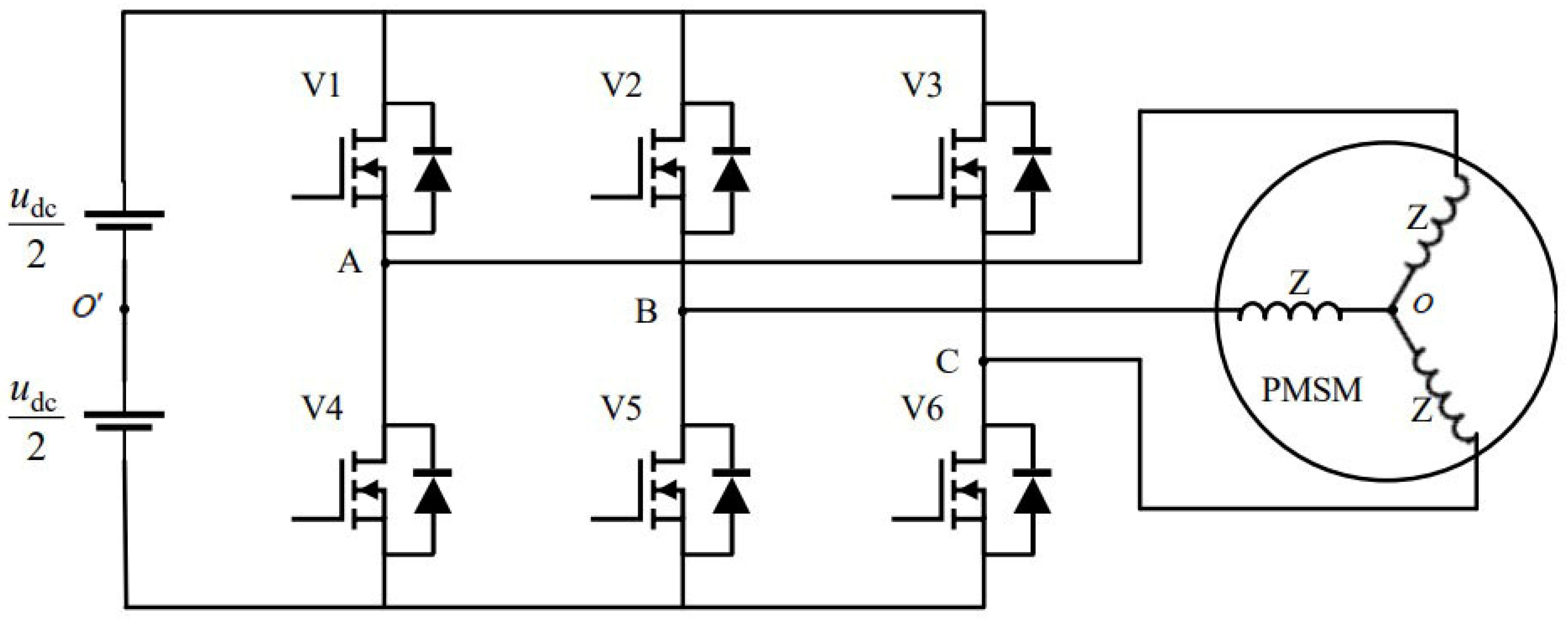
2.1. PMSM Model
2.2. FCS-MPCC Theory
3. Analysis and Compensation of Parameter Distortion
3.1. Predicted Current Deviation
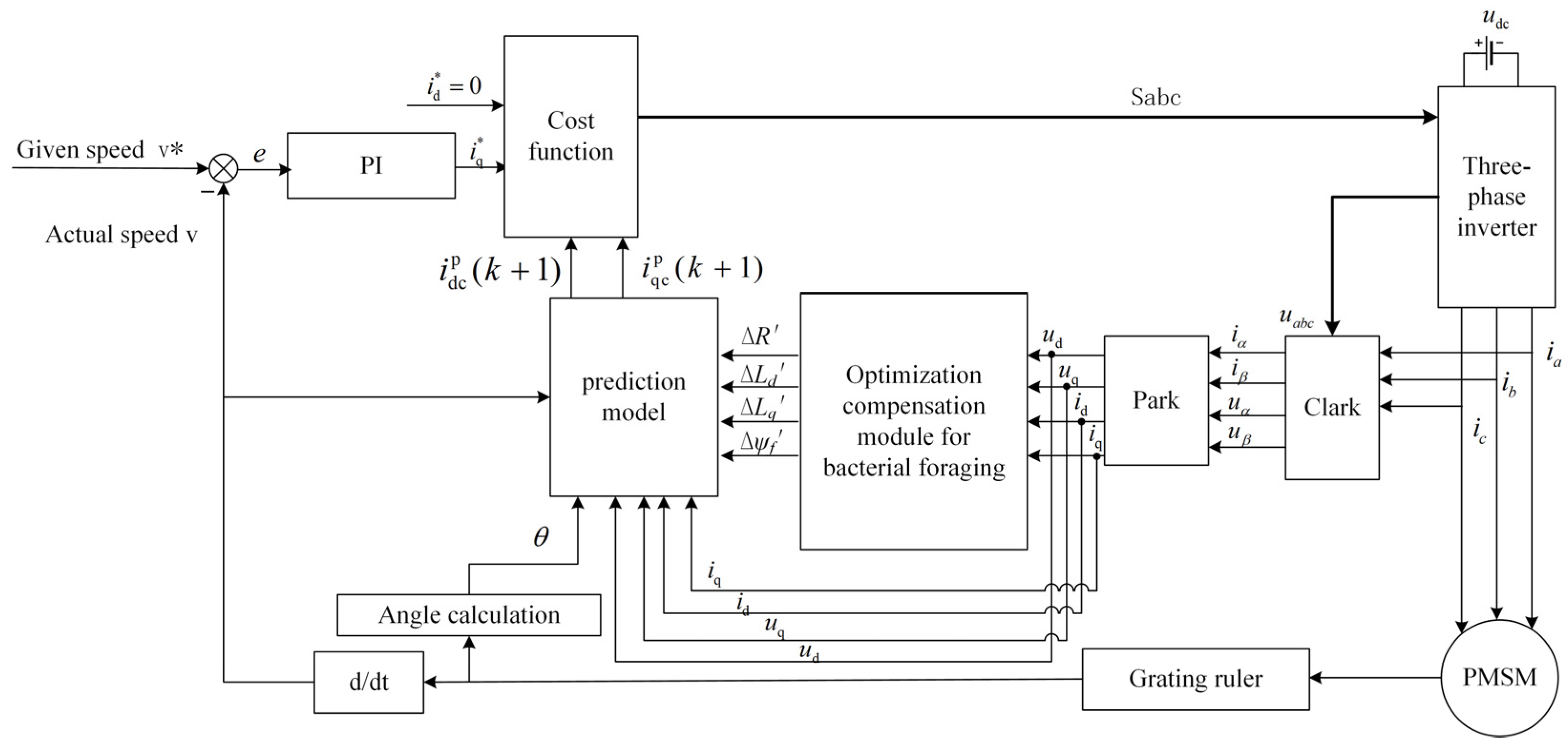
3.2. Parameter Compensation
4. BFOA Principle and Application
4.1. Principle of BFOA
- After the chemotactic action of bacteria i, the position update can be expressed as follows:
- represents the position information after the j-th chemotaxis step, the k-th replication step, and the l-th dispersion step; is the unit of step length during bacterial swimming, and is greater than 0; is the random direction selected for rolling, and specifically:
- is a randomly generated vector, and .
- In the reproductive stage of bacteria, the fitness function is sorted based on the individual’s position, and half of the individuals with good fitness are self-replicated, while the remaining half are eliminated. At this point, the bacterial population contains individuals with twice as good fitness.
- The dispersal action of bacteria can be simulated using the migration probability . Once a bacterial individual meets the probability of migration, a new bacterial individual is randomly generated at any location in space while the individual disappears. New and old bacterial individuals have different positions, namely different fitness, which enables some individuals in the population to jump out of their original positions and swim and flip, with stronger global search ability.
4.2. BFOA Generation Compensation Parameters
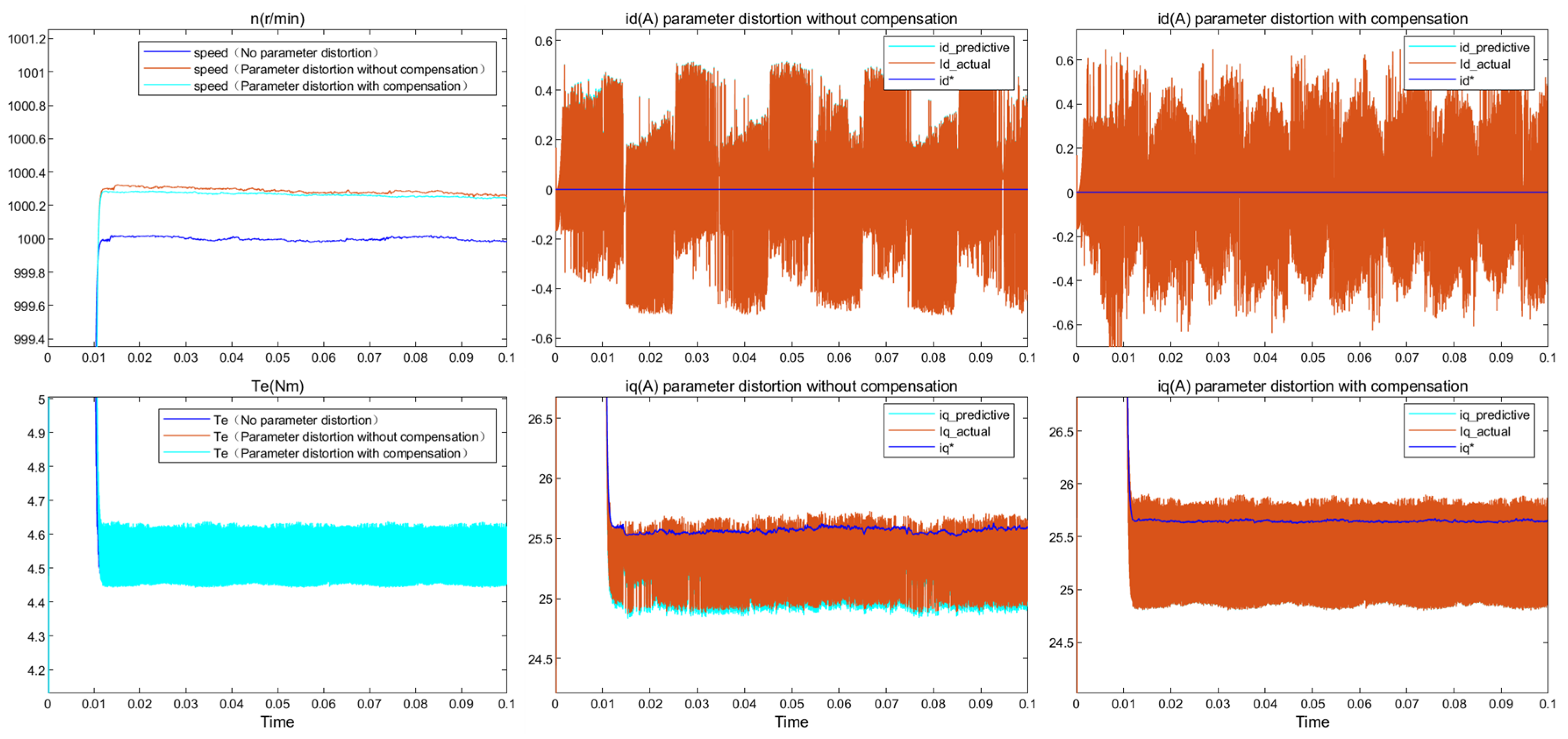
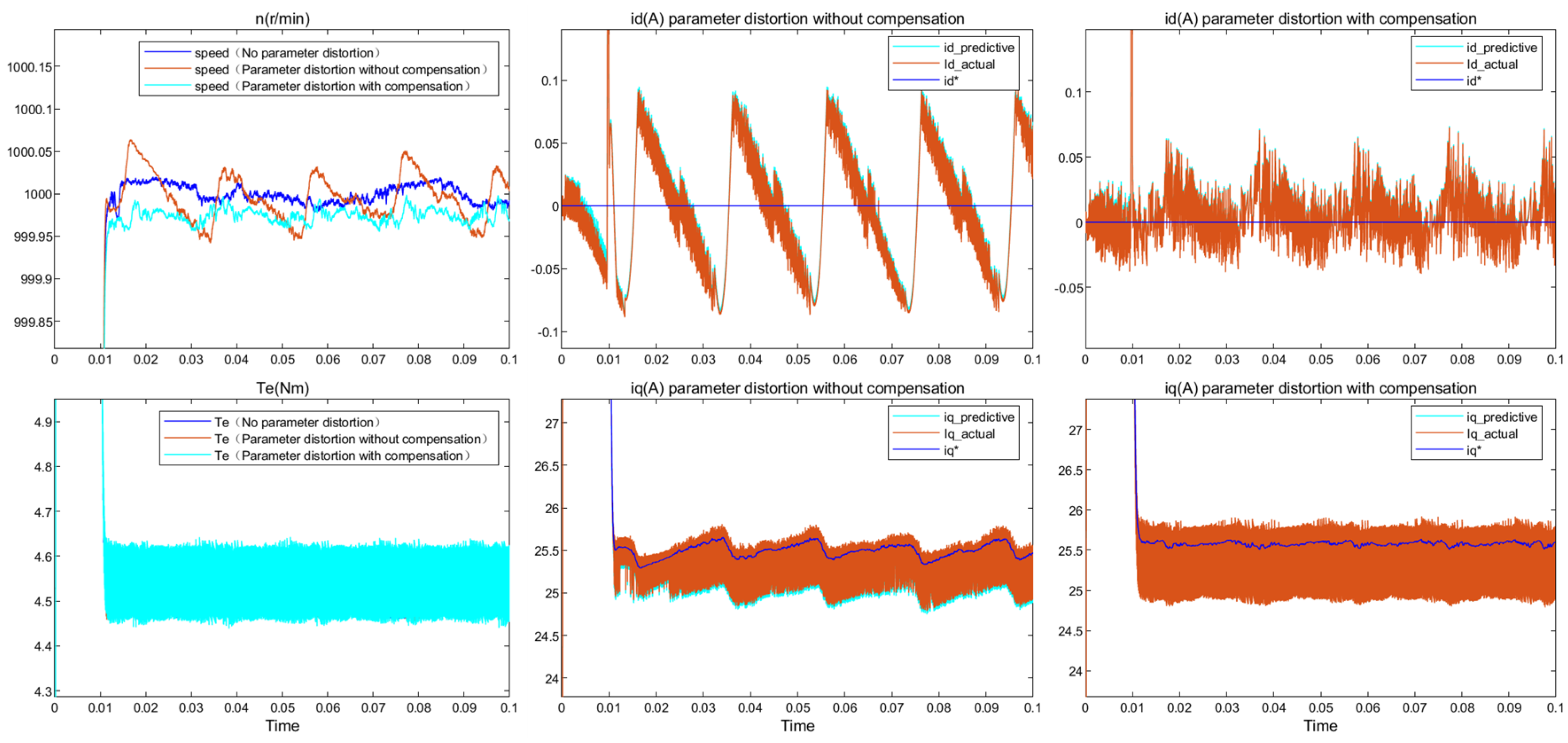
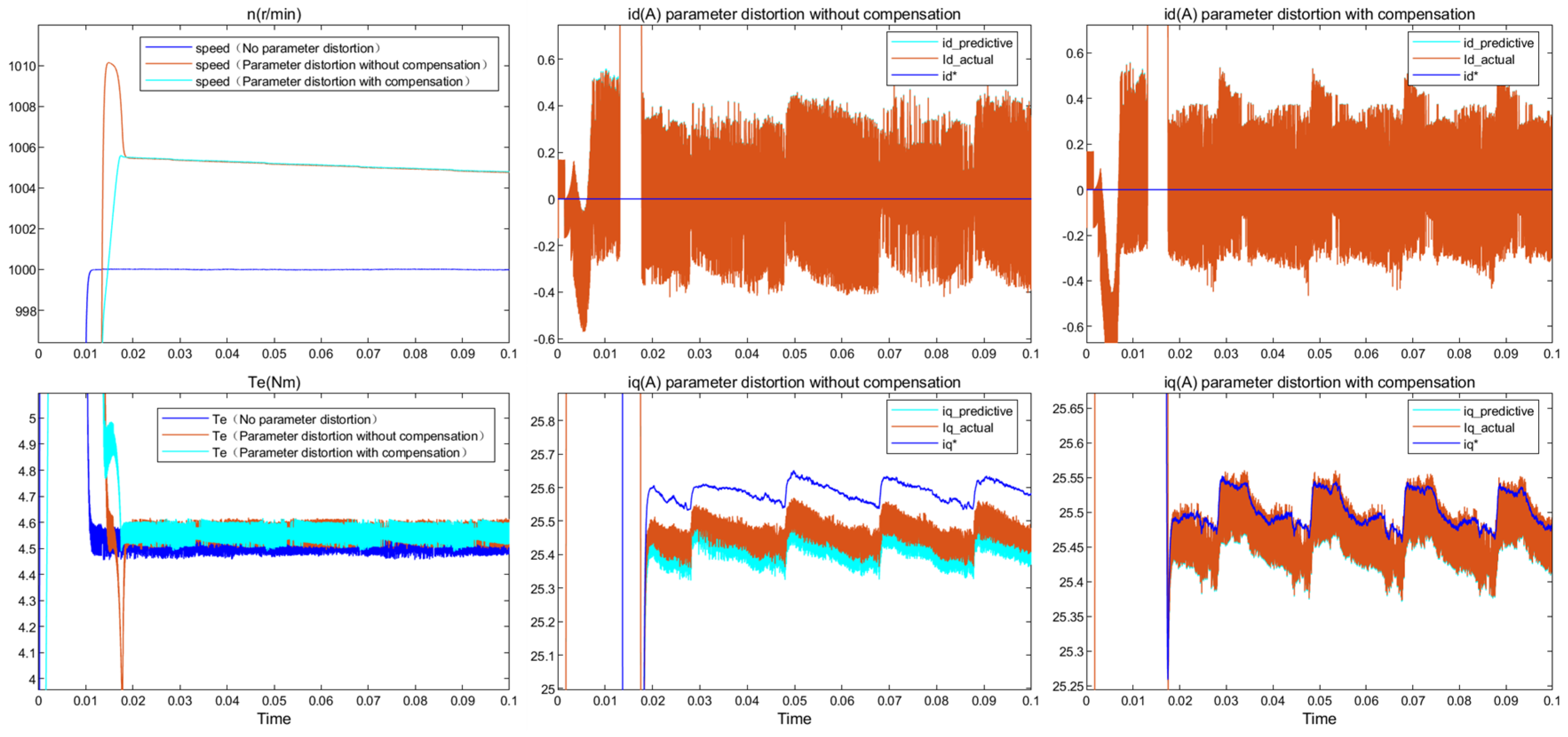
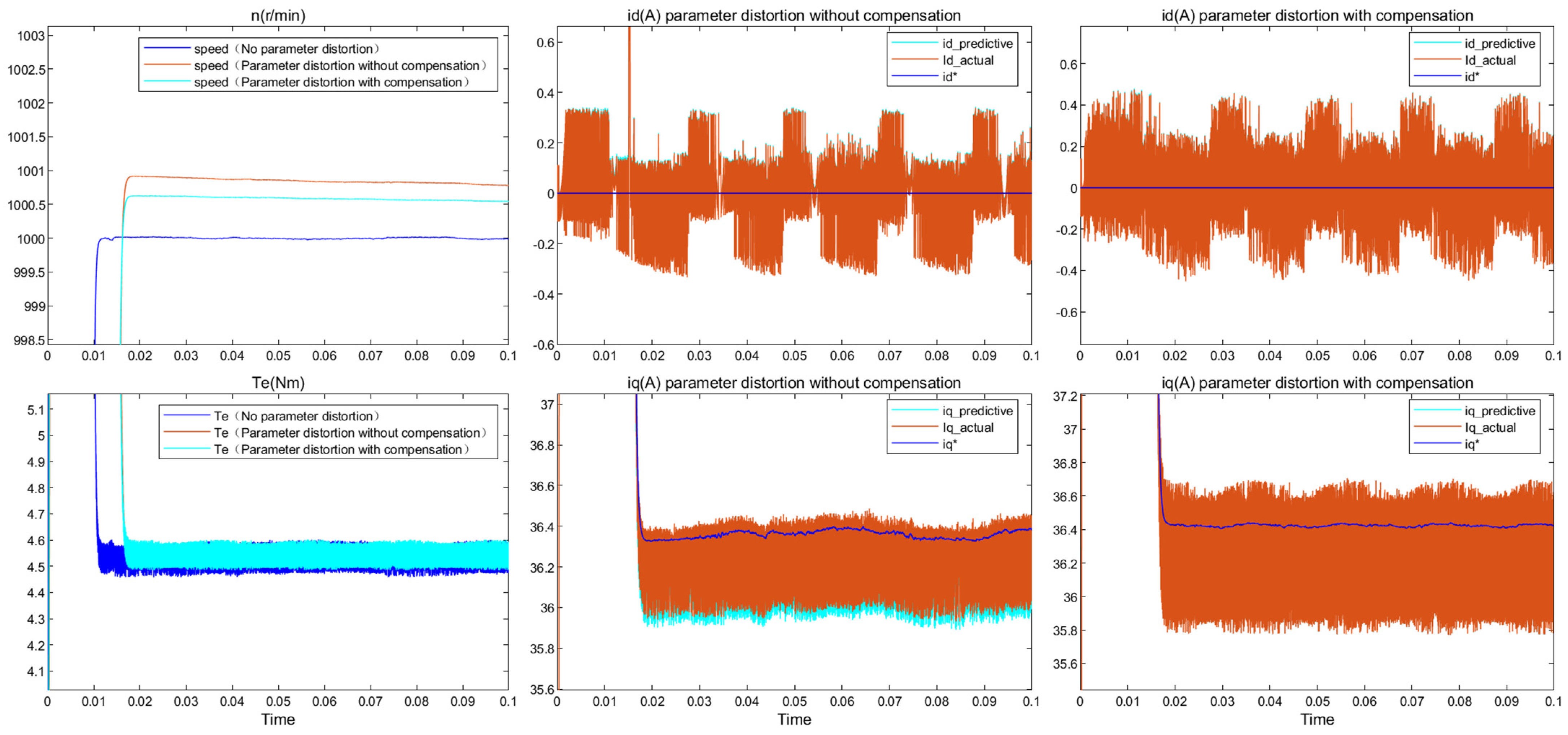
5. Simulation and Verification
- ;
- ;
- ;
- ;
- ;
- Change the calibration parameters in the simulation motor to simulate parameter distortion. The first four sets of experiments will change individual parameters to simulate distortion, and the last set of experiments will cause distortion of all four sets of parameters simultaneously.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Parameter | Value |
| Stator three-phase voltages | |
| Stator three-phase currents | |
| Three-phase winding flux linkage | |
| Stator resistance | |
| Direct axis and quadrature axis voltage | |
| Direct axis and quadrature axis current | |
| Direct axis and quadrature axis flux linkage | |
| Sampling time | |
| Inverter DC voltage source | |
| Present value of Direct axis and quadrature axis current | |
| Future value of Direct axis and quadrature axis current | |
| Cost function/Fitness function | |
| Reference value of Direct axis and quadrature axis current | |
| Theoretical value of predicted current for d and q axis | |
| Model values without distortion of motor parameters | |
| Actual value of predicted current for d and q axis | |
| , , , | Actual values with distortion of motor parameters |
| , , , | Distortion value of corresponding parameters |
| , | Predicted current values of d and q axes after compensation |
| Compensation values of corresponding parameters | |
| , | D-axis predicted the current deviation component |
| Q-axis predicted the current deviation component | |
| Location information of bacteria i | |
| Unit of step length during bacterial swimming | |
| Randomly generated direction vector | |
| Number of swimming steps | |
| Chemotaxis frequency | |
| Reproduction frequency | |
| Number of dispersion times | |
| The corresponding goodness of the position information | |
| * The bold font in the table represents the matrix. | |
Appendix A
| MATLAB code examples for optimizing PID parameters using BFOA. |
| Nc = 50; % Chemotaxis frequency Ns = 4; % Swimming frequency Nre = 4; % Copy count Ned = 2; % Disperse (migrate) times sizepop = 20; % Population size Sr = sizepop/2; % Number of copies (splits) nvar = 3; % 3 unknown quantities Ped = nvar/12; % Probability of bacterial dispersal (migration) popmin = [0,0,0]; % x min popmax = [30,30,30]; % x max Cmin = [−2,−2,−2]; % Minimum step size Cmax = [2,2,2]; % Maximum step size C(:,:) = 0.001*ones(sizepop,nvar); % After selecting the flipping direction, the step size of a single bacteria moving forward %% The cost function, which is our objective function fun = @(x)PID_Fun_1(x); %% Initialize population for I = 1:sizepop pop(i,:) = popmin + (popmax-popmin).*rand(1,nvar); % Initialize individual fitness(i) = fun( pop(i,:) ); % Initialize fitness value C(i,:) = Cmin + (Cmax-Cmin).*rand(1,nvar); % Initialization step size end %% Record a set of optimal values [bestfitness,bestindex] = min(fitness); % Take the minimum fitness value zbest = pop(bestindex,:); % Global best bacterial individual fitnesszbest = bestfitness; % Global optimal fitness value %% Iterative optimization for i = 1:Ned % Disperse (migrate) times for k = 1:Nre % Copy count for m = 1:Nc % Chemotaxis frequency for j = 1:sizepop % population % Flip delta = 2*rand(1,nvar)-0.5; pop(j,:) = pop(j,:) + C(j,:).*delta./(sqrt( delta*delta’ )); % Value range constraint pop(j,:) = 1b_ub(pop(j,:), popmin, popmax); % Update the current fitness value fitness(j) = fun(pop(j,:)); % Fitness update % Comparison between bacterial individuals if fitness(j) < fitnesszbest fitnesszbest = fitness(j); zbest = pop(j,:); end end end % Copy operation [maxF,index] = sort(fitness,‘descend’); % Sort in descending order for Nre2 = index:Sr % Update half of the population with higher fitness values pop(Nre2,:) = popmin + (popmax-popmin).*rand(1,nvar); fitness(Nre2) = fun(pop(Nre2,:)); C(Nre2,:) = Cmin + (Cmax-Cmin).*rand(1,nvar); % Update step size % Comparison between bacterial individuals if fitness(Nre2) < fitnesszbest fitnesszbest = fitness(Nre2); zbest = pop(Nre2,:); end end end % Disperse (migrate) operation for j = 1:sizepop if Ped > rand pop(j,:) = popmin + (popmax-popmin).*rand(1,nvar); fitness(j) = fun(pop(j,:)); % Comparison between bacterial individuals if fitness(j) < fitnesszbest fitnesszbest = fitness(j); zbest = pop(j,:); end end end end function BsJ = PID_Fun_1(Kpidi) ts = 0.001; sys = tf([1.0],[1 1],‘ioDelay’,0.2); dsys = c2d(sys,ts,‘z’); [num,den] = tfdata(dsys,‘v’); u_1 = 0.0; y_1 = 0.0; x = [0,0,0]’; B = 0; error_1 = 0; s = 0; P = 1000; for k = 1:1:P timef(k) = k*ts; r(k) = 1; u(k) = Kpidi(1)*x(1) + Kpidi(2)*x(3) + Kpidi(3)*x(2); if u(k)> = 10 u(k) = 10; end if u(k)< = −10 u(k) = −10; end yout(k) = -den(2)*y_1 + num(2)*u_1; error(k) = r(k)-yout(k); %-------------------Return of PID parameters---------------- u_1 = u(k); y_1 = yout(k); x(1) = error(k); % Calculating P x(2) = (error(k)-error_1)/ts; % Calculating D x(3) = x(3) + error(k)*ts; % Calculating I error_1 = error(k); if s==0 if yout(k) > 0.95 && yout(k) < 1.05 tu = timef(k); s = 1; end end end for i = 1:1:P Ji(i) = 0.999*abs(error(i)) + 0.01*u(i)^2*0.1; B = B+Ji(i); if i > 1 erry(i) = yout(i)-yout(i-1); if erry(i) < 0 B = B + 100*abs(erry(i)); end end end BsJ = sum(abs(error)); end |
References
- Development and Reform Commission Energy Bureau. The 14th Five Year Plan for Modern Energy System [Z]. The Central People’s Government of the People’s Republic of China Website. Available online: https://www.gov.cn/zhengce/zhengceku/2022-03/23/content_5680759.htm (accessed on 29 January 2022).
- CRRC Yunshang Information Technology Co., Ltd.; Guangdong Lingtai Education Resources Co., Ltd. New Energy Vehicle Drive Motor Technology; Mechanical Industry Press: Beijing, China, 2023. [Google Scholar]
- Xiao, Z.; Hu, M.; Shi, L.; Zhou, A. Online estimation of rotor temperature for built-in permanent magnet synchronous motors in electric vehicles. J. Mech. Eng. 2023, 11, 1–14. [Google Scholar]
- Xie, Y.; Sun, C.; Cai, W.; Ren, S.; Sun, C. Study on the loss of excitation mechanism and selected area heavy rare earth infiltration of permanent magnet synchronous motors for electric vehicles. J. Electr. Mach. Control. 2023, 5, 1–9. [Google Scholar]
- Xie, Y.; He, P.; Cai, W.; Liu, H. Design and optimization of permanent magnet synchronous motors with hairpin winding for vehicles. J. Electr. Mach. Control. 2021, 25, 36–45. [Google Scholar]
- Qi, X.; Su, T.; Zhou, K.; Yang, J.; Gan, X.; Zhang, Y. Overview of the Development of Model Predictive Control Strategies for AC Motors. Chin. J. Electr. Eng. 2021, 41, 6408–6419. [Google Scholar]
- Rodriguez, J.; Cristian, G.; Andres, M.; Freddy, F.-B.; Pablo, A.; Mateja, N.; Yongchang, Z.; Luca, T.; Alireza, D.; Zhenbin, Z. Latest advances of model predictive control in electrical drives—Part I: Basic concepts and advanced Strategies. IEEE Trans. Power Electron. 2022, 37, 3927–3942. [Google Scholar] [CrossRef]
- Yao, X.; Huang, C.; Wang, J.; Ma, H.; Liu, T.; Zhang, G. Dual vector model predictive current control for permanent magnet synchronous motors with parameter identification function. Chin. J. Electr. Eng. 2022, 10, 1–13. [Google Scholar]
- Peng, J.; Yao, M. Overview of Predictive Control Technology for Permanent Magnet Synchronous Motor Systems. Appl. Sci. 2023, 13, 6255. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, J.; Yang, X.; Zheng, Z.; Zhang, X.; Wang, L. Robust Deadbeat Predictive Current Regulation for Permanent Magnet Synchronous Linear Motor Drivers with Parallel Parameter Disturbance and Load Observer. IEEE Trans. Power Electron. 2022, 37, 7834–7845. [Google Scholar] [CrossRef]
- Sun, X.; Zhang, Y.; Lei, G.; Guo, Y.; Zhu, J. An improved deadbeat predictive stator flux control with reduced-order disturbance observer for in-wheel PMSMs. IEEE/ASME Trans. Mechatron. 2021, 27, 690–700. [Google Scholar] [CrossRef]
- Li, Z.; Feng, G.; Lai, C.; Banerjee, D.; Li, W.; Kar, N.C. Current injection-based multi-parameter estimation for dual three-phase IPMSM considering VSI nonlinearity. IEEE Trans. Transp. Electrif. 2019, 5, 405–415. [Google Scholar] [CrossRef]
- Li, X.; Kennel, R. General formulation of kalman-filter-based online parameter identification methods for VSI-Fed PMSM. IEEE Trans. Ind. Electron. 2021, 68, 2856–2864. [Google Scholar] [CrossRef]
- An, X.; Liu, G.; Chen, Q.; Zhao, W.; Song, X. Adjustable model predictive control for IPMSM drives based on online stator inductance identification. IEEE Trans. Ind. Electron. 2022, 69, 3368–3381. [Google Scholar] [CrossRef]
- Boileau, T.; Leboeuf, N.; Nahid-Mobarakeh, B.; Meibody-Tabar, F. Online identification of PMSM parameters: Parameter identify-ability and estimator comparative study. IEEE Trans. Ind. Appl. 2011, 47, 1944–1957. [Google Scholar] [CrossRef]
- Zhou, M.; Jiang, L.; Wang, C. Real-Time Multiparameter Identification of a Salient-Pole PMSM Based on Two Steady States. Energies 2020, 13, 6109. [Google Scholar] [CrossRef]
- Yu, Y.; Huang, X.; Li, Z.; Wu, M.; Shi, T.; Cao, Y.; Yang, G.; Niu, F. Full Parameter Estimation for Permanent Magnet Synchronous Motors. IEEE Trans. Ind. Electron. 2022, 69, 4376–4386. [Google Scholar] [CrossRef]
- Zhang, Y.G.; Yin, Z.G.; Sun, X.D.; Zhong, Y.R. On-line identification methods of parameters for permanent magnet synchronous motors based on cascade MRAS. In Proceedings of the 2015 9th International Conference on Power Electronics and ECCE Asia (ICPE 2015-ECCE Asia), Seoul, Republic of Korea, 1–5 June 2015. [Google Scholar]
- Feng, G.; Lai, C.; Mukherjee, K.; Kar, N.C. Current Injection-Based Online Parameter and VSI Nonlinearity Estimation for PMSM Drives Using Current and Voltage DC Components. IEEE Trans. Transp. Electrif 2016, 2, 119–128. [Google Scholar] [CrossRef]
- Liu, Z.; Wei, H.; Zhong, Q.; Liu, K.; Li, X.H. GPU implementation of DPSO-RE algorithm for parameters identification of surface PMSM considering VSI nonlinearity. Emerging Sel. Top. Power Electron 2017, 5, 1334–1345. [Google Scholar] [CrossRef]
- Liu, Z.H.; Zhang, J.; Zhou, S.W.; Li, X.H.; Liu, K. Coevolutionary particle swarm optimization using AIS and its application in multiparameter estimation of PMSM. IEEE Trans. Cybern 2013, 43, 1921–1935. [Google Scholar] [CrossRef]
- Liu, L.; Liu, W.X.; Cartes, D.A. Permanent magnet synchronous motor parameter identification using particle swarm optimization. Comput. Intell. Res. 2008, 4, 211–218. [Google Scholar] [CrossRef]
- Kou, P.; Zhou, J.; Li, C.; He, Y.; He, H. Identification of hydraulic turbine governor system parameters based on Bacterial Foraging Optimization Algorithm. In Proceedings of the 2010 Sixth International Conference on Natural Computation, Yantai, China, 10–12 August 2010; pp. 3339–3343. [Google Scholar]
- Niu, B.; Liu, J.; Wu, T.; Chu, X.; Wang, Z.; Liu, Y. Coevolutionary Structure-Redesigned-Based Bacterial Foraging Optimization. IEEE/ACM Trans. Comput. Biol. Bioinform. 2018, 15, 1865–1876. [Google Scholar] [CrossRef]
- Wang, D.; Qian, X.; Ban, X.; Ma, B.; Ma, Y.; Lv, Z. Enhanced Bacterial Foraging Optimization Based on Progressive Exploitation Toward Local Optimum and Adaptive Raid. IEEE Access 2019, 7, 95725–95738. [Google Scholar] [CrossRef]
- Holtz, J.; Stadtfeld, S. A predictive controller for the stator current vector of AC machines fed from a switched voltage source. In Proceedings of the International Power Electronics Conference (IPEC), Tokyo, Japan, 27–31 March 1983; pp. 1665–1675. [Google Scholar]
- Tang, J.; Liu, G.; Pan, Q. A Review on Representative Swarm Intelligence Algorithms for Solving Optimization Problems: Applications and Trends. IEEE/CAA J. Autom. Sin. 2021, 8, 1627–1643. [Google Scholar] [CrossRef]
- Dong, H.K.; Cho, C.H. Bacteria Foraging Based Neural Network Fuzzy Learning. In Proceedings of the 2nd Indian International Conference on Artificial Intelligence, Pune, India, 20–22 December 2005. [Google Scholar]
- Kim, D.H.; Abraham, A.; Cho, J.H. A hybrid genetic algorithm and bacterial foraging approach for global optimization. Inf. Sci. 2007, 177, 3918–3937. [Google Scholar] [CrossRef]
- Chen, D.; Zhang, G.; Yao, C.; Zhang, R. Optimization algorithm for bacterial foraging and application of PID parameter optimization. China Mech. Eng. 2014, 25, 59–64. [Google Scholar] [CrossRef]


| Parameter | Value |
|---|---|
| Stator resistance / | 0.0485 |
| D-axis inductance / | 0.000395 |
| Q-axis inductance / | 0.000395 |
| Permanent magnet flux chain / | 0.1194 |
| Rotational inertia / | 0.0027 |
| DC voltage source / | 220 |
| Load torque | 1.27 |
| Given speed | 1000 |
| Population size | 5000 |
| Swimming steps | 25 |
| Chemotaxis frequency | 50 |
| Reproduction frequency | 2 |
| Migration probability | 0.25 |
| Dispersion frequency | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Shen, Y.; Tan, Y. Parameter Compensation for the Predictive Control System of a Permanent Magnet Synchronous Motor Based on Bacterial Foraging Optimization Algorithm. World Electr. Veh. J. 2024, 15, 23. https://doi.org/10.3390/wevj15010023
Yang J, Shen Y, Tan Y. Parameter Compensation for the Predictive Control System of a Permanent Magnet Synchronous Motor Based on Bacterial Foraging Optimization Algorithm. World Electric Vehicle Journal. 2024; 15(1):23. https://doi.org/10.3390/wevj15010023
Chicago/Turabian StyleYang, Jiali, Yanxia Shen, and Yongqiang Tan. 2024. "Parameter Compensation for the Predictive Control System of a Permanent Magnet Synchronous Motor Based on Bacterial Foraging Optimization Algorithm" World Electric Vehicle Journal 15, no. 1: 23. https://doi.org/10.3390/wevj15010023
APA StyleYang, J., Shen, Y., & Tan, Y. (2024). Parameter Compensation for the Predictive Control System of a Permanent Magnet Synchronous Motor Based on Bacterial Foraging Optimization Algorithm. World Electric Vehicle Journal, 15(1), 23. https://doi.org/10.3390/wevj15010023





