Abstract
In recent years, with the intensification of global warming, extreme weather has become more frequent, intensifying the uncertainty of new energy output and load power, and seriously affecting the safe operation of power systems. Scene generation is an effective method to solve the uncertainty problem of stochastic planning of integrated systems of new energy generation. Therefore, this paper proposes a scenario generation and scenario reduction model of photovoltaic (PV) output and electric vehicle (EV) load power under extreme weather based on the copula function. Firstly, the non-parametric kernel density estimation method is used to fit a large number of sample data. The kernel density estimation expressions of PV and EV powers under extreme weather conditions are obtained and the corresponding goodness of fit tests are carried out. Then, a variety of joint distribution models based on the copula function are established to judge the goodness of fit of each model, and the optimal copula function is selected as the joint probability distribution function by combining the Kendall and Spearman correlation coefficients of each model. Finally, the optimal copula joint probability distribution is used to generate PV and EV power scenarios. The data of extremely hot weather in a certain province were selected for an example analysis. The results show that the output scenario obtained conforms to the correlation under this extreme weather, and has higher accuracy in reflecting the actual PV output and load power in this province under this extreme weather, which can provide a reference for reliability analyses of power systems and power grid planning.
1. Introduction
With the continuous increase in the installed proportion of new energy power generation in the power grid, wind power and photovoltaic, as the main forms, are highly susceptible to the influence of external meteorological factors, and the power generation is characterized by intermittency and volatility [1]. In the conventional meteorological environment, the new energy output can be predicted more accurately based on the weather forecast value. However, in recent years, global climate change and the intensification of the greenhouse effect have caused a significant increase in the frequency and intensity of extreme weather, and the impact of different types of extreme weather on new energy output will correspondingly show different time scales, which will lead to large-scale shutdown and output loss in the power grid, and seriously threaten the safe and stable operation of the power grid [2].
On 25 March 2020, a large range of snowfall occurred in north China. Because photovoltaic power stations did not consider the impact of snowfall on the active power output in the power forecast, the maximum active power output of photovoltaic power stations was predicted to reach 2600 MW, while the actual maximum active power output was only 1050 MW, with a large difference between the two. On 15 March and 27 March 2021, the strongest dust storm in several years occurred at a provincial power plant. Power waves of photovoltaic power plants (installed capacity of 100 MW) in this area are more obvious. After being covered by sand and dust on 15 March, the power station output showed a strong short-term fluctuation characteristic, and the maximum output was 51.81 MW. However, on 27 March, when the dust front passed through the power station, the power station output had a large drop, and after being completely covered by sand and dust, the output maintained at a low level. On 7 August 2018, the highest temperature in some parts of Zhejiang Province reached 41 °C. According to previous forecasts, Zhejiang Province has prioritized power demand response measures to alleviate the severe pressure on supply and demand. In August 2020, California, in the United States, had continuous hot weather, the highest temperature reached 49 °C, the load increased by 14% over the same period, while the external power supply decreased by 30%, resulting in the independent operator of the California power system being forced to implement two outages of more than 1 h; more than 1 million power users were affected. Therefore, in order to ensure the safe and stable operation of the power grid under extreme weather and improve the robustness of the power system, it is crucial to predict the load and renewable energy output data under low probability and high impact events [3]. Joint scenario generation of load power and renewable energy output (for example, in the environment of the increasing popularity of new energy vehicles, especially the correlation between PV output and EV load powers) under extreme weather conditions helps operators and dispatchers make correct and effective decisions for power system planning in the face of the randomness and uncertainty in power systems [4]. At the same time, highly accurate scene generation technology can transform the “passive response” into “active regulation” in the power system, and also provide theoretical support for the optimal operation and risk assessment of the power system.
PV and EV power data forecasting based on scenario generation technology is an important process in power industry planning, which mainly forecasts and calculates the EV load power in the future period through historical EV power data and other related factors. At present, the research methods of EV load power scenario generation technology are mainly divided into three categories. The first is the traditional methods of time-series analysis, regression analysis, and gray prediction models. Ref. [5] integrates the adaptive advantages of the Kalman filter algorithm to obtain a relatively accurate equation of state and observation equation, which improves the accuracy of short-term EV load power prediction, but this method takes less consideration of uncertain factors such as extreme weather. Ref. [6] established a blind numerical regression model for EV load power forecasting to improve the accuracy of EV load power forecasting by analyzing the EV load power demand and development trend in each production link of offshore oil fields. However, this method has high requirements for historical data and fails to take a large number of influential factors into account. Secondly, support-vector-machine- and decision-tree-based machine learning methods can effectively solve the nonlinear problems in output EV load power data generation. Ref. [7] optimizes the parameter selection process of support vector machine through the chaotic electromagnetics algorithm, and the algorithm’s convergence efficiency and optimization ability are improved, which is suitable for short-term EV load power prediction. Ref. [8] proposed a similarity calculation method based on local similarity minimization and a weighted similarity loss function, and improved the gradient-lifting decision tree learning algorithm to improve the performance of EV load power prediction. Finally, the deep learning method used a neural network as the parameter structure to optimize. Currently, neural networks widely used in EV load power prediction include back propagation neural networks, convolutional neural networks, recurrent neural networks, and the emerging Transformer model.
Similarly, the prediction of renewable energy generation power based on scenario generation technology also approximates the probability distribution mainly by simplifying a large number of data, which is essentially a stochastic programming problem. At present, the scenario generation technology for renewable energy power generation is also mainly divided into three categories. The first is the sampling-based method based on the Monte Carlo method and Latin hypercube sampling method. However, such methods usually require certain assumptions about the probability distribution of the sample data and involve large sets of scenarios. Secondly, the predictive method is based on an auto-regressive moving average model and a generative adversarial neural network. A predictive model is trained on a large amount of historical observation data to generate scenarios without considering statistical assumptions. Ref. [9] proposes a random wind power model based on ARIMA, which takes into account the non-stationary characteristics of wind power generation, but is unable to deal with the complex nonlinear relationship between multiple wind farms. Ref. [10] uses a conditionally improved Wasserstein generative adversarial network to generate wind power scenarios that capture the spatiotemporal relationships of multiple wind farms, but this requires high-quality historical observation samples and training parameters. Finally, the optimized method based on distance matching is adopted. However, this method is computationally inefficient for processing medium- and large-scale scenes, and it cannot capture extreme scenes in sample data.
However, few papers consider the combination of the generation of renewable energy output (PV) and load power (EV) scenarios in extreme weather environments, and most papers only predict the power of the power supply side or the EV load side of the power system, while in real life, it is more necessary to consider the correlation between PV and EV in extreme environments. To solve the above problems, the structure of the remaining part of this paper is arranged as follows. In Section 2, the non-parametric kernel density estimation method is used to fit the actual data. The kernel density expressions of PV and EV power at high temperature are obtained by goodness of fit and a precision test. In Section 3, based on the copula function, a joint distribution model of the output of various photoelectric fields and the load of electric vehicles is established. Combining the Kendall and Spearman correlation coefficients of each model, the copula distribution function is compared with the empirical copula function, and the Euclidean distance between them is determined. The optimal copula function is selected as the joint probability distribution of PV and EV power in extreme weather, and a typical scenario of PV and EV in high-temperature weather is generated. In Section 4, an example analysis shows that the PV and EV scenarios generated by this method are in line with the correlation, and can accurately reflect the actual power of PV and EV under extreme high-temperature weather in this region.
2. Kernel Density Estimation and Model Testing Methods
Research on the distribution of sample data of PV and EV power under extreme high-temperature weather is mainly divided into two categories. One is the parameter estimation method, which assumes that the data conform to a certain distribution according to experience, and then estimates the corresponding parameters of the population by sampling samples. However, this method needs to specify the specific distribution in advance. To a certain extent, the characteristics of the PV and EV power curves are ignored, resulting in the results obtained by the fitting of the parameter distribution model greatly deviating from the actual distribution of the data [11]. The other kind of non-parametric method does not have any prior assumptions about the population distribution, and studies the characteristics of the data distribution entirely from the sampled samples, and kernel density estimation belongs to this strategy.
2.1. Kernel Density Estimation Method
When the kernel density estimation method is used, the distance of each point to in the neighborhood of can be calculated to analyze the degree of distance of each point to , and then the contribution degree of these points to the estimate can be determined. Let the independent equally distributed samples drawn from be ; is the density function of coincidence, it is an unknown function, , it is necessary to calculate the estimated value of the probability density function at the point as shown in Formula (1):
where represents the number of samples, represents the window width, and represents the kernel function. The kernel function name and formula [12] used to estimate the density function are shown in Table 1.

Table 1.
Kernel functions used for estimating density function.
2.2. Model-Checking Method
2.2.1. Goodness of Fit Test
After completing the fitting of the probability density, it is necessary to test the effect of the fitting. By testing the fitting effect, we can measure the fitting degree of each fitting method to the original data, so as to select the best fitting function. There are two commonly used test methods [9], which are classified as Pearson and Kolmogorov–Smirnov.
- (1)
- Pearson
Suppose is a sample of samples extracted from the population . follows a probability density function of , and its probability distribution function is . The large interval is divided into subintervals, and there is no overlap between each subinterval. The number of samples falling into each subinterval was calculated, and the Pearson statistic was calculated using Equation (2).
where is the number of samples in the interval; is the theoretical value for which it falls in the interval.
As approaches positive infinity, the distribution of converges to . If the confidence level a is given, then a subpoint of is Equation (3).
where represents the probability of the event occurring. If the test statistic satisfies , then it means that the probability distribution at the confidence level satisfies the requirement.
- (2)
- Kolmogorov–Smirnov
The Pearson needs to divide the sample space into subspaces, which results in the variation in test results with the selection of intervals, and the Kolmogorov–Smirnov test has good applicability [13].
Suppose is the samples extracted from the population . The probability density function of is , and its probability distribution function is . The data of the samples are arranged from small to large, such that .
Based on the original samples, the empirical cumulative distribution function is obtained and calculated as shown in Equation (4).
The maximum vertical gap between the theoretical cumulative distribution and the empirical cumulative distribution is defined as the test statistic , calculated using Equation (5).
where denotes the i-th sampling interval.
The parameters of the theoretical distribution model can be obtained from actual historical data, and in this case, when a theoretical distribution is rejected in the test, the error generated by the K-S test is relatively small.
2.2.2. Test of Fitting Accuracy
The fitting accuracy test is to measure the difference between the probability model of the scenery output and the frequency distribution curve of the actual output from a quantitative point of view. The mean absolute percentage error (MAPE) and root mean square error (RMSE) are used to measure the fitting accuracy of the model [14].
where is the number of intervals; and are the density distribution of orthogonal series of standardized output power of EV and PV and the probability of histogram in the i-th interval, respectively.
3. Correlation Modeling and Scene Generation of PV and EV Power under High-Temperature Weather Based on Copula Theory
3.1. Copula-Related Theory
3.1.1. Copula Functions and Classification
The copula function is a kind of connection function that connects the joint distribution function of random vectors with the respective edge distribution function, that is, there is a copula function C that makes Formula (8) true.
where is the number of variables, is the edge distribution function of a single variable, is the copula connection function and is the joint distribution function of variables.
There are two common copula families, the Archimedes copula and the elliptic copula. The three most common types of Archimedes copula functions are Gumbel copula, Clayton copula, and Frank copula, and elliptic copula functions mainly include the normal copula and t-copula. Because fitting multidimensional random variables with the t-copula is extremely time-consuming, and the Gumbel copula form is complex, only the remaining three copula functions are considered in this paper. The coupling relationship between two or more variables can be described by selecting the optimal copula function, as shown in Figure 1 [15].
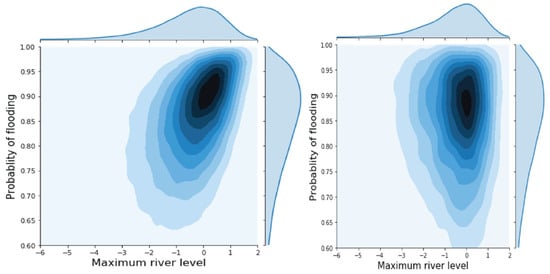
Figure 1.
Diagram of the action of the copula function.
3.1.2. PV Systems and EV Modeling
- (1)
- PV Modeling
The output power of a PV system is often calculated using the formula
where A is the area of the PV panels, S is the solar irradiance as a function of temperature T and sunshine, and (T) is the efficiency of the panels related to the temperature T.
- (2)
- EV Modeling
Assume that is the power output or efficiency of the EV under standard conditions in the area considered. EV battery charging and discharging can be modeled using
where is the output power of the EV system, is the average temperature under normal conditions, is the temperature coefficient indicating the sensitivity of EV demand to temperature changes, and is a function representing the impact of the state of charge on the EV’s efficiency or performance.
The detailed characteristics of PV plants and EVs are given in the Appendix A.
3.1.3. Optimal Choice of Copula Function
- (1)
- Joint scenario generation and reduction of PV and EV power
Because there are many types of copula functions, it is impossible to select the optimal copula directly, so it is necessary to distinguish the goodness of fit and select the optimal function. The commonly used methods include functional image discrimination, correlation coefficient discrimination, and Euclidean distance discrimination [16].
- ①
- Functional image discrimination is to compare the probability density function images of each copula function with the probability density function of the sample data, and the closest image is the optimal copula function.
- ②
- Correlation coefficient discrimination method is to judge the goodness of fit using the Kendall rank correlation coefficient and Spearman rank correlation coefficient. The rank correlation coefficients of various copula functions are compared with the rank correlation coefficients of sample data. The closer the data are, the better the goodness of fit is, and the corresponding copula function is the best.
Let the PV and EV powers with correlation be and , respectively. and are any two sample observations of the power , and the two values are independent of each other. If , it is said that and are consistent; If , then and are said to be inconsistent.
The calculation formulas of the Kendall rank correlation coefficient and Spearman rank correlation coefficient are shown in Formulas (11) and (12), respectively.
where is the logarithm of samples with consistent output in ; is the logarithm of samples with inconsistent output in ; and is the total number of sampling points. In this paper, is 24, that is, the step length is 1 h. is in in the rank; is in in the rank.
- ③
- The Euclidean distance discrimination method is to compare the Euclidean distance of each copula function with the empirical copula function of the sample data. The smaller the Euclidean distance is, the better the goodness of fit of the copula function is.
Let be the sample of the two-dimensional variable , and and are the empirical cumulative distribution functions of the two-dimensional variable , respectively. The empirical copula function calculation formula of the samples can be expressed as in Equation (14).
where is an indicator function. If , there exists , otherwise . The same is true for .
The optimal copula function is selected by using the squared Euclidean distance. The squared Euclidean distance is defined by Formula (15).
where is the empirical copula function. The size of the chosen squared Euclidean distance can reflect the closeness of various copula function models to the empirical copula function. The smaller is, the better the fitting performance of the function is [17].
- (2)
- Scenario generation based on cubic spline interpolation
The joint distribution function of each period is sampled, and the cubic spline polynomial on its cumulative probability interval is solved by means of the cubic spline interpolation method. Then, the PV and EV powers corresponding to each period can be calculated by substituting any sampling cumulative probability value into Equation (17).
where and are the coefficients of the polynomials in the cubic spline interpolation method.
- (3)
- Scenario reduction based on k-means clustering algorithm
The k-means clustering algorithm has the advantages of a simple principle and fast clustering speed, and is one of the most widely used clustering algorithms at present [18]. Therefore, the k-means clustering algorithm is selected as the scene reduction algorithm in this paper. The clustering steps are as follows [19,20,21]:
According to the preset clustering number K, K scenarios are randomly selected from all the combined PV and EV power scenarios as the initial clustering centers for each category.
Calculate the distance between each scene and the cluster center of each category, and classify each scene into the category with the closest distance to it.
Calculate the cluster center of each category again to obtain the new cluster center corresponding to each category.
Determine whether the convergence condition is met; if so, the clustering ends, otherwise, return to step (2).
4. Case Study
According to the journal Meteorology published by the National Meteorological Center, with the continuous westward extension and strengthening of the subtropical high, under the influence of factors such as atmospheric clear sky radiation and sinking warming, a total of two high-temperature weather processes occurred in July 2022 across the country. The first stage was 5–17 days; in the second stage, from 21 to 31 days, some areas in Jiangsu, Shanghai, Zhejiang, Fujian, Jiangxi, Anhui, southern Henan, and southern Xinjiang Basin experienced high-temperature weather of more than 40 °C. The daily maximum gas temperature approached or broke through the historical extreme value of the same period. At this stage, the high-temperature weather included several provinces. Taking one day as the time scale, we selected the PV and EV data of Jiangsu Province (denoted as province A) and Xinjiang Province (denoted as province B), which were in the same high-temperature weather (namely, 26 July), for comparison. In addition, the PV and EV data of Jiangsu Province (denoted as province A) under normal weather (that is, 26 May) were selected as controls. Line charts are drawn of the time dimension and space dimension on the influence of extreme high-temperature weather on PV and EV, as shown in Figure 2. The three curves in the two graphs in Figure 2 compare the data of different provinces in the same month under extreme heat weather and the data of different weather conditions in different months in the same province. The left plot represents EV data, and the right plot represents PV data. It can be seen that (1) compared with normal weather conditions, under the influence of extreme high-temperature weather, the light intensity is enhanced, and the PV output of province A is increased compared with the PV output of normal weather in the province, and the electricity load data is also increased in the extreme high-temperature weather. (2) Under the same extreme high-temperature weather condition, the dimension of province B is lower than that of province A, and the light is stronger under the same temperature condition, so the PV output data are higher. Compared with province B, province A is more developed in population and economy, and has a higher penetration rate of electric vehicles. Therefore, under the same weather conditions, province A has a greater demand for electricity load.
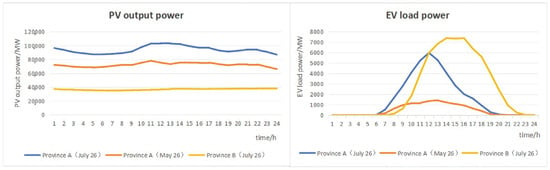
Figure 2.
Comparison of PV and EV data in time and space and weather dimensions.
In this paper, copula joint output modeling and typical scene generation were carried out based on the measured power data of 10 days from 21 July to 31 July 2022, under extreme hot weather in a certain province (generally defined as the daily maximum temperature reaching or exceeding 35 degrees Celsius in Chinese meteorology) [22,23,24,25], and the EV load and PV output power data are and , respectively.
Firstly, the copula force correlation model is established by using the historical force data at all times to illustrate the process of copula model establishment. The edge distribution function of PV and EV powers under extreme hot weather in this province is estimated using non-parametric kernel density. Then, four kinds of copula functions are constructed; unknown functions in copula functions are obtained through parameter estimation. Different copula functions are selected to combine the edge distribution functions of PV and EV, and the optimal copula function is selected according to Section 3.1.3. The Kendall rank correlation coefficient, Spearman rank correlation coefficient and squared Euclidean distance of each copula function are shown in Table 2. Table 2 reveals that the correlation coefficients calculated using the Frank copula method closely approximate those obtained from the sample data. Moreover, the Euclidean distance between the Frank copula and empirical copula is the smallest among all the results. Finally, we can obtain the joint probability distribution of PV and EV under extreme high-temperature weather, as shown in Figure 3.

Table 2.
Correlation coefficient and squared Euclidean distance of each copula function.
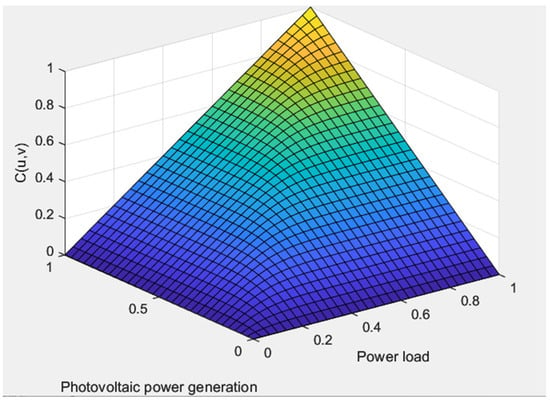
Figure 3.
Binary Frank copula distribution function diagram.
Since the PV and EV distribution functions at each time are not exactly the same, the typical scene generation through only one copula model ignores the differences in the PV and EV distribution functions at different times, and the generated output scene has a large gap to the actual situation. Therefore, copula models are established for 24 moments in the scheduling cycle, and typical joint output scenarios considering the differences of PV and EV time-series distribution functions are obtained through scene generation and reduction.
The copula model at 24 moments is sampled according to probability, and the power output scenes at 24 moments are spliced into the joint power output scenes of complete moments, which are reduced using the k-means clustering algorithm. In order to consider the difference of the PV and EV time-series distribution function, the typical joint power output scenes of the PV and EV time series are shown in Figure 4. The two color graphs in the top half of Figure 4 show the power corresponding to the changes over time of 500 scenes generated by PV and EV, respectively. The two line charts composed of green, purple, yellow, red, and blue in the bottom half of Figure 4 show the corresponding PV and EV power, respectively, generated by the clustering method over time after the scenes are reduced to five scenes. As can be seen from the two line graphs in the lower part of Figure 4, the variation in PV output with time and the variation in EV load power with time are similar under extreme high-temperature weather. The curve of PV output with time is parabolic, reaching the maximum value at noon of a day, that is, when the light is the strongest, which is in line with reality. The curve of electric vehicle load with time is relatively tortuous, and the electricity load reaches its highest value in the afternoon and evening.
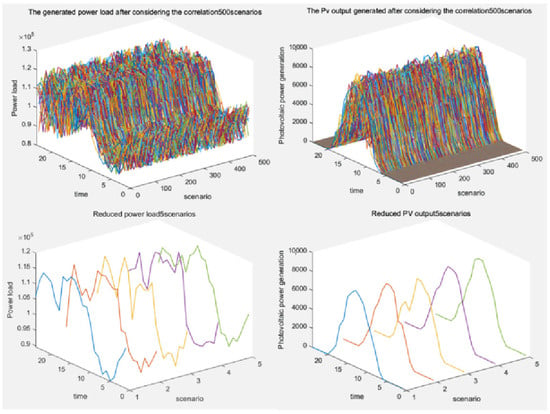
Figure 4.
Joint scenario generation and scene reduction comparison diagram.
After scenario reduction, the corresponding probability distribution for each scenario is shown in Figure 5. Comparing the probability distribution maps generated based on different copula functions with the original data can also verify again that the scenes generated based on the Frank copula are closer to the original data, and the model is more accurate.
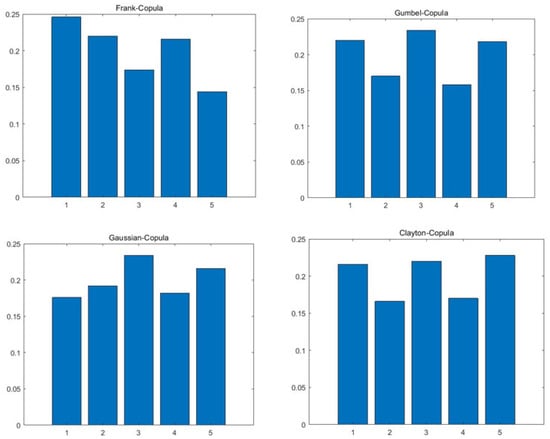
Figure 5.
Probability distribution plots after reduction of scenarios under different copula functions.
5. Conclusions
On the basis of considering the difference of PV and EV output distribution function at different moments, this paper uses copula function to establish the joint output model of PV and EV time series, and uses density function image discriminant method, correlation coefficient discriminant method and European distance discriminant method to judge the goodness of fit, and selects the optimal copula model at each moment. Finally, the optimal copula model at each moment is sampled, spliced and reduced according to probability to obtain the typical scenario of time-series joint output. The proposed model is verified by taking the measured PV and EV output data of a province for 10 days under extreme high-temperature weather as an example. The analysis results show that the typical scenario of the joint output of PV and EV power in extreme high-temperature weather can better reflect the influence of high-temperature weather on PV and EV data in this province, which can be applied to the power system optimization model, and can improve the accuracy and effectiveness of the power system optimization operation strategy. At the same time, the difference coefficient CV is used to measure the probability of the generation of five scenarios of PV and EV, which can better reflect the complementary characteristics of the two. It is worth pointing out that in terms of mathematical model, this paper only established the scenario generation and scenario reduction model of photovoltaic output and electric vehicle load power under extreme environment based on binary copula function. However, at this stage, the installed capacity of new energy continues to increase, especially for a variety of new energy types such as wind power and photovoltaic. At the same time, in the system planning cycle, it is easy to be affected by uncertain factors such as extreme environment. Therefore, how to consider the scenario generation technology of combined output and power load of various new energy in extreme environment in planning and operation will be one of the future work of this paper. Another future work will be to study and forecast the correlation of other kinds of loads and other kinds of renewable energy under extreme high-temperature weather.
Author Contributions
Methodology, X.L. and C.L.; software, X.L. and C.L.; writing—original draft preparation, X.L. and C.L.; writing—review and editing, C.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by the Science and Technology Project of SGCC “Research on Quantitative Assessment and Defense Technology of Power Supply Risk of Renewable Energy Power System for Extreme Scenarios” (5100-202255338A-2-0-SY).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article and Appendix A.
Conflicts of Interest
Xiaofei Li and Chi Li are employees of the National Key Laboratory of Renewable Energy Grid-Integration (China Electric Power Research Institute); Chen Jia is an employee of the State Grid Liaoning Electric Power Research Institute. The paper reflects the views of the scientists and not the company. The authors declare no conflicts of interest.
Appendix A
The tables describing the characteristics of PV plants and EVs are given below.

Table A1.
PV plant power output curve characteristics.
Table A1.
PV plant power output curve characteristics.
| Description | |
|---|---|
| Diurnal Variation Curve | The diurnal variation curve of a photovoltaic power station illustrates the change in power generation over the course of a day. Typically, power generation gradually increases at sunrise, may reach its peak around noon, and then gradually decreases until sunset. |
| Seasonal Variation | The power generation of a photovoltaic power station is influenced by seasonal changes. Summer, with longer sunlight hours and a higher solar zenith angle, may result in higher peak power during this season. |
| Weather Impact | Weather conditions, such as clear, cloudy, or overcast skies, directly affect the output of a photovoltaic power station. Cloudy weather can lead to fluctuations and a reduction in power generation. |
| Shadow Effect | If the photovoltaic power station is affected by shadows from buildings, trees, or other objects, irregular fluctuations may appear on the curve, known as the shadow effect. |
| Start and End Times | The times when a photovoltaic power station begins and ends its power generation, influenced by sunrise and sunset times. |
| Peak Power | The highest power generation of the photovoltaic power station during the day, typically occurring at noon when the solar zenith angle is at its maximum. |
| Power Fluctuations | The fluctuation in power on the power curve of the photovoltaic power station, representing instantaneous changes in power, potentially influenced by shadows, cloud cover, and other weather factors. |

Table A2.
EV power output curve characteristics.
Table A2.
EV power output curve characteristics.
| Description | |
|---|---|
| Charging Peak Period | Electric vehicles may experience a charging peak at night or during specific time periods, indicating users’ tendency to charge during low electricity price periods. |
| Driving Peak Period | Daytime may witness a driving peak, signifying higher usage demand for electric vehicles during the day. |
| Charging Efficiency Variations | The charging curve may reflect variations in charging efficiency at different charging power levels, influenced by battery and charging equipment performance. |
| Charging Time Distribution | Describes the distribution of time required for electric vehicle charging, including short “top-up” charges and longer “full-charge” durations. |
| Load Fluctuations: | Reflects the variability in electric vehicle power demand, with certain periods exhibiting significant power fluctuations. |
| Charging Behavior Response | Describes whether electric vehicles respond to power system demand signals or price signals, adjusting their charging behavior accordingly. |
| Usage Patterns | Distinguishes between weekdays and weekends, as well as different usage patterns during daytime and nighttime. |
References
- Tan, J.; Wu, Q.; Hu, Q.; Wei, W.; Liu, F. Adaptive robust energy and reserve co-optimization of integrated electricity and heating system considering wind uncertainty. Appl. Energy 2020, 260, 114230. [Google Scholar] [CrossRef]
- Zhang, F.; Bieber, L.; Zhang, Y.; Li, W.; Wang, L. A Multi-port DC Power Flow Controller Integrated with MMC Stations for Offshore Meshed Multi-terminal HVDC Grids. IEEE Trans. Sustain. Energy 2023, 14, 1676–1691. [Google Scholar] [CrossRef]
- Yan, J.; Liu, Y.; Han, S.; Wang, Y.; Feng, S. Reviews on uncertainty analysis of wind power forecasting. Renew. Sustain. Energy Rev. 2015, 52, 1322–1330. [Google Scholar] [CrossRef]
- Lee, D.; Baldick, R. Load and wind power scenario generation through the generalized dynamic factor model. IEEE Trans. Power Syst. 2016, 32, 400–410. [Google Scholar] [CrossRef]
- Ahmad, N.; Ghadi, Y.; Adnan, M.; Ali, M. Load forecasting techniques for power system: Research challenges and survey. IEEE Access 2022, 10, 71054–71090. [Google Scholar] [CrossRef]
- Hu, Q.; Li, F.; Fang, X.; Bai, L. A framework of residential demand aggregation with financial incentives. IEEE Trans. Smart Grid 2016, 9, 497–505. [Google Scholar] [CrossRef]
- Dong, X.; Deng, S.; Wang, D. A short-term power load forecasting method based on k-means and SVM. J. Ambient. Intell. Humaniz. Comput. 2022, 13, 5253–5267. [Google Scholar] [CrossRef]
- Fang, X.; Hu, Q.; Li, F.; Wang, B.; Li, Y. Coupon-based demand response considering wind power uncertainty: A strategic bidding model for load serving entities. IEEE Trans. Power Syst. 2015, 31, 1025–1037. [Google Scholar] [CrossRef]
- Hu, Q.; Li, F. Hardware design of smart home energy management system with dynamic price response. IEEE Trans. Smart Grid 2013, 4, 1878–1887. [Google Scholar] [CrossRef]
- Chen, P.; Pedersen, T.; Bak-Jensen, B.; Chen, Z. ARIMA-based time series model of stochastic wind power generation. IEEE Trans. Power Syst. 2009, 25, 667–676. [Google Scholar] [CrossRef]
- Zhang, Y.; Ai, Q.; Xiao, F.; Hao, R.; Lu, T. Typical wind power scenario generation for multiple wind farms using conditional improved Wasserstein generative adversarial network. Int. J. Electr. Power Energy Syst. 2020, 114, 105388. [Google Scholar] [CrossRef]
- Qiu, Y.; Li, Q.; Pan, Y.; Yang, H.; Chen, W. A scenario generation method based on the mixture vine copula and its application in the power system with wind/hydrogen production. Int. J. Hydrogen Energy 2019, 44, 5162–5170. [Google Scholar] [CrossRef]
- Zhang, Y.; Qian, W.; Ye, Y.; Li, Y.; Tang, Y.; Long, Y.; Duan, M. A novel non-intrusive load monitoring method based on ResNet-seq2seq networks for energy disaggregation of distributed energy resources integrated with residential houses. Appl. Energy 2023, 349, 121703. [Google Scholar] [CrossRef]
- Arik, I.; Kantar, Y.M.; Usta, I. The new odd-Burr Rayleigh distribution for wind speed characterization. Wind Struct. 2019, 28, 369–380. [Google Scholar]
- Zhang, W.; Xu, Y. Distributed optimal control for multiple microgrids in a distribution network. IEEE Trans. Smart Grid 2019, 10, 3765–3779. [Google Scholar] [CrossRef]
- Goh, H.H.; Peng, G.; Zhang, D.; Dai, W.; Kurniawan, T.A.; Goh, K.C.; Cham, C.L. A new wind speed scenario generation method based on principal component and R-Vine copula theories. Energies 2022, 15, 2698. [Google Scholar] [CrossRef]
- Zhang, Y.; Shotorbani, A.M.; Wang, L.; Li, W. A Combined Hierarchical and Autonomous DC Grid Control for Proportional Power Sharing with Minimized Voltage Variation and Transmission Loss. IEEE Trans. Power Deliv. 2021, 37, 3213–3224. [Google Scholar] [CrossRef]
- Zhang, S.; Yang, Q.; Gao, Y.; Gao, D. Real-time fire detection method for electric vehicle charging stations based on machine vision. World Electr. Veh. J. 2022, 13, 23. [Google Scholar] [CrossRef]
- Lu, S.; Feng, X.; Lin, G.; Wang, J.; Xu, Q. Non-Intrusive Load Monitoring and Controllability Evaluation of Electric Vehicle Charging Stations Based on K-Means Clustering Optimization Deep Learning. World Electr. Veh. J. 2022, 13, 198. [Google Scholar] [CrossRef]
- Li, H.; Gao, L.; Cai, X.; Zheng, T. Personalized Collision Avoidance Control for Intelligent Vehicles Based on Driving Characteristics. World Electr. Veh. J. 2023, 14, 158. [Google Scholar] [CrossRef]
- Sun, M.; Feng, C.; Zhang, J. Probabilistic solar power forecasting based on weather scenario generation. Appl. Energy 2020, 266, 114823. [Google Scholar] [CrossRef]
- Rocchetta, R.; Li, Y.; Zio, E. Risk assessment and risk-cost optimization of distributed power generation systems considering extreme weather conditions. Reliab. Eng. Syst. Saf. 2015, 136, 47–61. [Google Scholar] [CrossRef]
- Trakas, D.N.; Hatziargyriou, N.D. Resilience constrained day-ahead unit commitment under extreme weather events. IEEE Trans. Power Syst. 2019, 35, 1242–1253. [Google Scholar] [CrossRef]
- Ma, S.; Su, L.; Wang, Z.; Qiu, F.; Guo, G. Resilience enhancement of distribution grids against extreme weather events. IEEE Trans. Power Syst. 2018, 33, 4842–4853. [Google Scholar] [CrossRef]
- Poudyal, A.; Poudel, S.; Dubey, A. Risk-based active distribution system planning for resilience against extreme weather events. IEEE Trans. Sustain. Energy 2022, 14, 1178–1192. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).