Abstract
Electric vehicle (EV) customers are expected to charge EV batteries at a rapid EV charging station or via on-road wireless EV charging systems when possible, as per their charging needs to successfully complete any remaining trips and reach their destination. When on-road wireless EV charging systems are considered as an alternative charging method for EVs, this can affect the load of a rapid EV charging station in terms of time and magnitude. Hence, this paper presents a probabilistic framework for estimating the arrival rate of EVs at an EV rapid charging station, considering the availability of on-road wireless charging systems as an alternative charging method. The proposed model incorporates an Electric Vehicle Decision Tree that predicts the times when EVs require rapid charging based on realistic transportation data. A Monte Carlo simulation approach is used to capture uncertainties in EV user decisions regarding charging types. A queuing model is then developed to estimate the charging load for multiple EVs at the charging station, with and without the consideration of on-road EV wireless charging systems. A case study and simulation results considering a 32-bus distribution system and the US National Household Travel Survey (NHTS) data are presented and discussed to demonstrate the impact of on-road wireless EV charging on the loads of an rapid EV charging station. It is observed that having on-road wireless EV charging as complementary charging to EV charging stations helps to significantly reduce the peak load of the charging station, which improves the power system capacity and defers the need for system upgrades.
1. Introduction
Electric vehicles (EVs) have been receiving significant attention in recent years due to the growing concerns of global warming and the depletion of petroleum resources [1]. It is recognized that the existence of EV charging stations and on-road wireless charging systems is vital for facilitating EV penetration and public acceptance [2,3]. Plug-in charging and wireless charging are two popular methods for charging EVs [4,5,6]. Plug-in charging involves physically connecting the EV to an external power source using a charging cable, while wireless charging transfers electrical energy wirelessly from a charging pad to the EV’s receiver pad.
Three levels of EV charging are available and commonly used [7]: Level-1 charging uses a standard household outlet and is relatively slow, adding around 4–5 miles of range per one hour of charging. Level-2 charging, which uses a higher-voltage power source, provides faster charging times and adds around 25–30 miles of range per one hour of charging. DC fast charging is the fastest option, allowing significant range additions in just a few minutes, making it suitable for long-distance travel.
On the other hand, wireless charging eliminates the need for physical cables and connectors. It consists of a charging pad installed in a parking space and a receiver pad integrated into the EV. When the EV is parked over the charging pad, electricity is transferred wirelessly through electromagnetic induction. However, wireless charging is currently slower than plug-in charging, and it is commonly used for convenient top-up charging at home or in parking lots. The choice between plug-in charging and wireless charging depends on several factors, such as the availability of charging infrastructure and the charging capabilities of the EV. Plug-in charging offers faster options, including DC fast charging for long-distance travel, whereas wireless charging provides convenience for frequent top-up charging in specific locations. Considering on-road wireless EV charging systems as an alternative charging method for EVs, this will affect the loads of rapid EV charging stations. It is necessary to predict EV charging loads and their distribution in space and time, considering both the EV charging station and on-road wireless EV charging, which is the primary objective of this paper.
Considerable efforts have been made in modeling EV charging loads and investigating their impacts on the power grid given their uncertain charging demand. A method was developed in [8] to study the plug-in charging infrastructure considering price and drivers’ behavior, with the objective of predicting the energy demand of given EVs and matching it with the available supply. The developed method considers the initial state of charge (SOC) of the EVs among other factors in planning the charging stations. A framework was designed in [9] aiming to reach a certain level of user satisfaction considering different types of demands with EVs charging and different sources of energy, including renewable generation with its uncertain delivery. The developed community-integrated energy system, which served as an energy internet system, coordinated the response to varying loads of EV charging according to the available renewable energy. With the diversity of electrical energy sources, the coordination between these sources helped increase the efficiency of resources use, reduce the chances of a deficit in energy transfer, optimize energy transfer strategies, and reduce peak periods. The authors of [10] modeled energy transfer through different facilities, including renewable energy sources, and determined the ratio of each facility. The impact of wireless charging load on the location marginal price and retail price, considering the social welfare of the electricity market, was studied and presented in [11]. A queuing network along with statistical traffic data was considered to determine the dynamics of the spatial locations of EVs, including their state of charge, so that a wireless charging load pattern could be obtained. The interrelation between charging at wireless charging stations and the transportation network was studied in [12], aiming to control charging loads at wireless charging stations in conjunction with transportation networks to level the total travel costs for all EVs. A method based on forecasting the electricity prices on the next day was developed in [13] to determine the reserved periods and quantity the electricity needed to wirelessly charge public transport buses. The studies objective was to balance the electricity loads and reduce costs. Inductive charging of electric buses in a bus network in conjunction with microwave charging of nearby EVs was presented in [14]. Wireless charging of EVs was established through a microwave link directed from a transmitting antenna mounted on a bus and a receiving antenna on the roof of an EV. A new algorithm was proposed in [15] to obtain a day ahead strategy of charging EV batteries based on the history of their combined charging states.
An optimization algorithm was proposed in [16] to wirelessly charge EVs through lanes dedicated for wireless charging other than normal traffic lanes, with the objective of managing the wireless charging policy to reduce the energy costs and pressure on the power grid. The technical issues pertaining to the design of wireless charging pads, the coils and the frequency of their energizing currents were presented in [17]. Safety issues, standards, social, and economic aspects were also included and discussed. The authors of [18] presented a comparison between the capacitive and inductive wireless charging of EVs, considering different battery types and their models. A review of different design issues, such as communication between transmitting and receiving sides, misalignment between transmitting and receiving coils, and the inclusion of compensating capacitors in charging circuits, were also provided. Battery swapping stations are an alternative method for reducing the impact of EV load on the grid at peak hours [19,20]. A battery swapping station as a solution to homogenize the load on the grid was presented in [21]. Given the distribution of EVs in space and time and considering road topology, the size and location of a centralized battery swapping station was determined. A framework was proposed in [22] to determine a dynamic strategy of wireless charging to reduce the cost and peak-to-average ratio benefiting from vehicle-to-grid ancillary services. It was observed that the level of difficulty to obtain reliable statistical data increased with the increase in the number of EVs. Because a certain number of wireless charging facilities are required to cover a given area, a model was developed in [23] to maximize the traffic flow and reduce travel time by determining the optimum locations of these facilities. A model based on data collected by one million days of travel was developed in [24] to determine the fast charging station load and service quality.
The aforementioned literature review revealed that none of the existing studies have considered the impact of on-road EV wireless charging on rapid EV charging station load. Therefore, a probabilistic framework is proposed to estimate the EV arrival rate at an rapid EV charging station, considering the possibility of on-road EV wireless charging as an alternative charging option for EVs in the distribution system.
The present paper provides the following summary of its main contributions:
- Development of an Electric Vehicle Decision Tree (EVDT) to predict the timing and probability of EVs requiring rapid charging based on realistic transportation data.
- A Monte Carlo simulation (MCS) approach is employed to capture uncertainties in EV user decisions regarding charging type, enabling the robust analysis of different charging scenarios.
- Development of a queuing model to estimate the charging load for multiple EVs served at an EV charging station, with and without on-road wireless charging.
- Investigation of the impact of on-road EV wireless charging systems as an alternative charging method for EVs on the expected loads of a rapid EV charging station.
The remainder of this paper is organized as follows. Section 2 presents and discusses the proposed framework and associated mathematical model. Section 3 presents the input and simulation data, followed by analysis and discussion of the findings in Section 4 to demonstrate the effectiveness of the proposed framework. In Section 5, the conclusions are drawn.
2. Proposed Framework
2.1. Electric Vehicle Decision Tree and Monte Carlo Simulation Approach for Modeling an EV Charging Station, Considering an On-Road Wireless Charging System
The Electric Vehicle Decision Tree (EVDT) proposed in [25] was developed in this work and extended to model the probability of EV arrival per hour at an EV charging station, considering on-road EV wireless charging systems. The EVDT considers realistic detailed transportation data [26], including distances traveled during trips, the distribution of trips throughout the day, and the number of trips per vehicle, to predict the period of time needed for the rapid charging of EVs.
The flow chart of the developed EVDT is presented in Figure 1. For each trip, the EV’s SOC is checked based on distance-driven mileage. If the EV’s battery depletes its SOC before completion of the trip, the trip’s start time is recorded for fast charging. On the other hand, if the trip is completed before depletion of battery’s charge, the time at which the trip is completed is recorded. This strategy minimizes disruptions during trips. However, due to the lack of geospatial data relating to the distance between EVs and a central charging facility, the EVDT results indicate the probability of an EV requesting charging rather than the actual arrival of vehicles at the EV charging station. To address the lack of a distance correlation, two factors are taken into account:
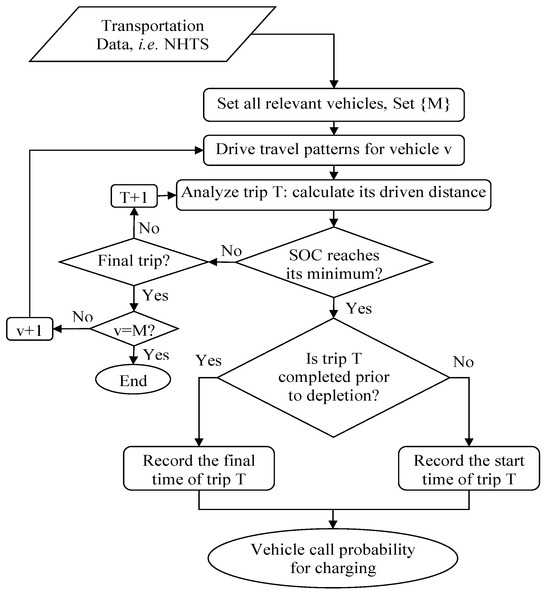
Figure 1.
Flow chart of the developed Electric Vehicle Decision Tree (EVDT).
- Point-a: The precise duration between when an EV initiates a fast charging request and its arrival at the EV charging station depends solely on the spatial distance separating the EV’s location when calling for fast charging and the EV charging station. Hence, the hour of the fast charging call is used to estimate the hourly probability of EV arrival, assuming that the EV is expected to arrive at the nearby EV charging station within a designated one-hour timeframe.
- Point-b: It is assumed that one EV charging station can cater to the needs of a few hundred EVs, based on the fact that the United States (US) gasoline fueling facilities numbered nearly 160,000 [27], or about one facility for every 1500 vehicles. Each EVCF is designed to accommodate a portion of the total forecasted vehicles in the distribution system, specifically targeting approximately 20% of the forecasted vehicles.
The EVDT incorporates point-a to estimate the timing of charging demand per hour, while incorporating both point-a and point-b plays a crucial role in determining the hourly arrival rate of EVs, which is then used as an input to generate a random decision of EV users regarding the choice of EV charging station or on-road wireless EV charging system, as presented in Figure 2.
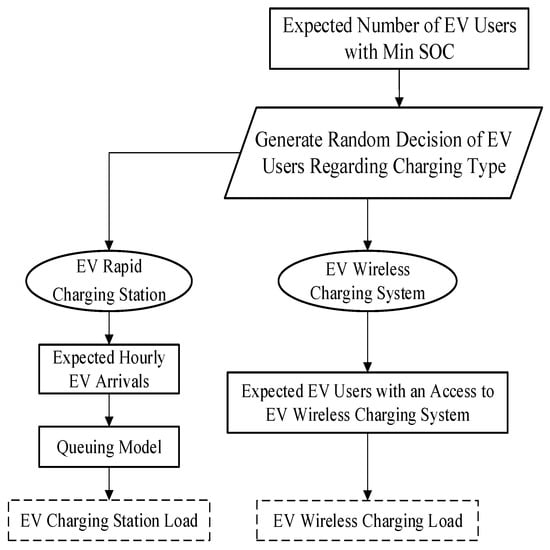
Figure 2.
Proposed Monte Carlo simulation approach for modeling an EV charging station, considering an on-road wireless charging system.
The EV arrival rate at an EVCS is affected by the customer’s choice between a rapid charging station or an on-road wireless charging system. As the on-road wireless EV charging system is considered to be complementary to EVCS in this paper, the number of EVs that prefer on-road wireless charging and the number of EVs that prefer rapid charging must be equal to the number of EVs that arrive each hour at the EVCS, in the absence of on-road wireless charging systems. This relationship is represented by the following equation:
where represents the number of EVs that select the on-road wireless charging system at an hour k; denotes the number of EVs that choose the EVCS at an hour k; and is the EV arrive rate at the EVCS in the absence of on-road wireless charging systems at an hour k. Using the EVDT, the EV arrival rate () is estimated at the EVCS without on-road wireless EV charging systems. In order to address uncertainties in EV user decisions regarding charging types, rapid charging or on-road wireless charging, the MCS is employed to generate a large set of scenarios by varying at an EVCS for each hour and each location from [0–].
These results are then incorporated into the queuing model (QM) to evaluate the demand for charging EVs, aiding in the planning of EV charging stations and informing EV investors.
2.2. Queuing Model
The queuing model describes the charging process of several EVs at a facility designated for fast charging. At a charging station, EVs can be considered as customers in a queue who have to wait their turn to charge their batteries. The EV charging station operates under the following assumed conditions [28,29]:
- The time between the arrival of EVs (inter-arrival times) is independent and follows an exponential distribution, meaning the arrival of one EV does not affect the arrival of another, resembling a Poisson process.
- Similarly, the hourly charging rates for EVs at the EV charging station are independent and exponentially distributed, also representing a Poisson process.
- The EV charging station is equipped with c identical fast chargers.
- Charging EVs follows a first-come-first-served rule; upon arrival at the EV charging station, EVs form a single queue. These assumptions enable us to model the process of charging at the EV charging station utilizing an M/M/c queuing model.
According to the formulation of the queuing model [30], the system is considered stable provided that the occupation rate of the fast chargers remains below one, which is determined by calculating the probability of a fast charger being in use. This probability () is obtained by dividing the anticipated rate at which EVs are expected to arrive at the EV charging station by the number of fast chargers that are identical in capacity and by the rate at which the charging service is provided. This can be expressed as follows:
Using Equation (2) and a sufficient condition for the stability of the queuing model, the minimum number of fast chargers required to maintain a stable queuing system at the EV charging station should satisfy the inequality given as [31]
The expected number of occupied fast chargers relies on a limiting-state probability that “n” discharged EVs are present at the EV charging station, and this is determined as follows [31]:
In this equation, is defined as
If n discharged EVs are present at the charging station, the number of occupied fast chargers is determined by taking the minimum value between n and c. The expected number of occupied fast chargers, represented as , is
Finally, to obtain an estimation of the power demand of the charging station (), the average power per fast charger is multiplied by the expected number of occupied fast chargers.
The proposed framework is programmed using the General Algebraic Modeling System (GAMS) environment [32].
3. Input and Simulation Data
The 32-bus radial distribution system presented in [33] is employed in this study. The system peak demand is 3.8 MW, with a base voltage of 12.66 kV. Profiles of the system loads are from the IEEE Reliability Test System [34], and it is also assumed that all loads are residential loads. The house peak load is assumed to be 2.08 kW [35] to calculate the number of houses at each bus. Based on data from the NHTS [26], the study estimates the average number of vehicles per household to be 1.9. Taking into account the level of EV penetration, the total number of houses in the distribution system, and the average number of vehicles per household, the number of EVs in the system is estimated. It should be mentioned that the location of the EVCS is determined from a detailed planning analysis that includes technical, environmental, and economic studies, the results of which are assumed as the input and are beyond the scope of this paper. Otherwise, spatial components of the EV trips cannot be ignored. This work does not consider optimal siting of EVCSs, and EVCS locations are considered, for example, at locations 14, 21, 24, and 30; each feeder of the distribution system has one EVCS location to cater to a maximum of 20% of the total estimated number of EVs in the distribution system on a typical day [25]. Hence, four EV charging stations collectively serve 80% of the EVs in the distribution system, while the remaining 20% are assumed to charge at alternative locations such as workplaces or commercial buildings adopting a Level-2 charging infrastructure. This assumption is deemed reasonable since the fast charging infrastructure is not yet widespread and cannot meet the charging demands of all EVs in the distribution system.
The estimation of is based on the following additional assumptions:
- State of Charge (SOC) Window: EVs are assumed to operate within an SOC window of 70%, ranging from 20% to 90%. This range ensures an appropriate balance between battery utilization and availability for charging.
- Home charging: It is assumed that EVs are fully charged at home before starting a trip with no additional charges required before the trip, except for overnight charging at home. This assumption positions fast charging as a complementary method to home charging.
- NHTS data selection: The study utilizes NHTS data, which reportedly includes 1,000,000 trips and 300,000 vehicles. However, to enhance the accuracy of the analysis, the study focuses on specific vehicle types (i.e., automobiles, sports vehicles, vans, and pickup trucks) and excludes any missing data. Consequently, 850,000 trips and 150,000 vehicles are considered for this particular investigation.
- EV battery types: The study primarily considers fully charged EV20, EV40, and EV60 vehicles, representing compact sedans with battery capacities of 6.51 kWh, 10.4 kWh and 15.6 kWh, respectively, enabling ranges of up to 20, 40 and 60 miles on electricity.
- Exclusion of low-mileage vehicles: To optimize computational efficiency, the analysis initially excludes vehicles with total distance covered throughout a day, considering all individual trips made, less than 20 miles as they do not require fast charging. Their inclusion would not significantly impact the charging demand.
By incorporating these assumptions and considerations into this work, a comprehensive analysis of EV charging station demand can be conducted while accounting for various real-world factors and potential scenarios.
4. Results and Discussion
To assess the expected demand for EV charging, it is essential to determine the arrival rate of EVs at a charging station. Using the developed EVDT method and MCS approach, the expected number of EVs arriving at a charging station, or using on-road wireless charging, considering different locations, is presented in Figure 3, Figure 4, Figure 5 and Figure 6.
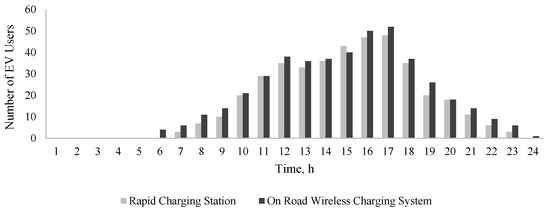
Figure 3.
Averaged EVs charged using the rapid charging station at location-14 or via on-road wireless charging.
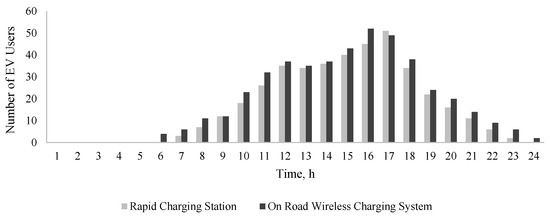
Figure 4.
Averaged EVs charged using the rapid charging station at location-21 or via on-road wireless charging.
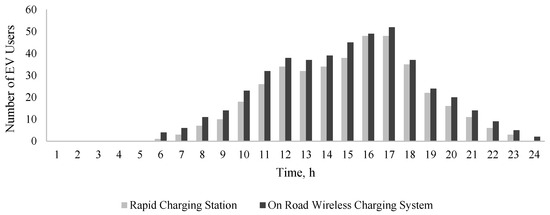
Figure 5.
Averaged EVs charged using the rapid charging station at location-24 or via on-road wireless charging.
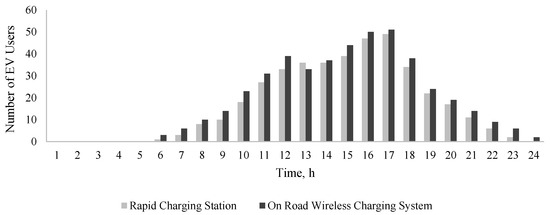
Figure 6.
Averaged EVs charged using the rapid charging station at location-30 or via on-road wireless charging.
The average number of EVs charged at either an EV charging station or via on-road wireless EV charging varies from one hour to another, depending on when the SOC of the EVs reaches is depleted, and thus require battery charging. Uncertainties in EV user decisions are addressed using the MCS approach, enabling a robust analysis of charging scenarios.
The expected arrival rate, in conjunction with the developed queuing model, gives an estimation of the expected demand for the charging process, as presented in Figure 7, Figure 8, Figure 9 and Figure 10, considering different locations with/without on-road wireless charging. The load of the EV charging station is similar in all locations, assuming a similar arrival rate at these locations.
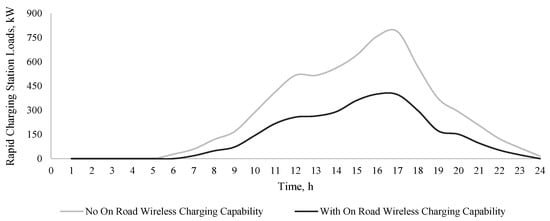
Figure 7.
EV expected charging station loads at location 14, with and without on-road wireless charging capability.
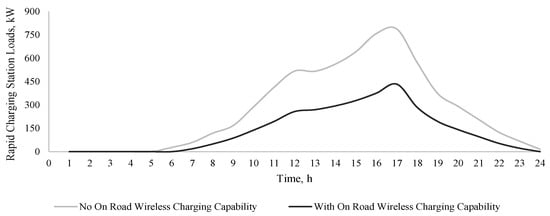
Figure 8.
EV expected charging station loads at location 21 with and without on-road wireless charging capabilities.
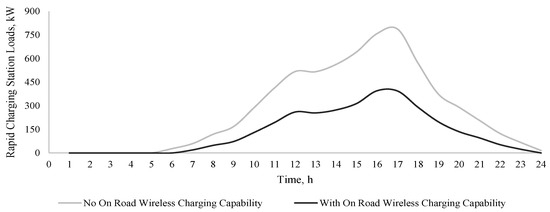
Figure 9.
EV expected charging station loads at location 24 with and without on-road wireless charging capabilities.
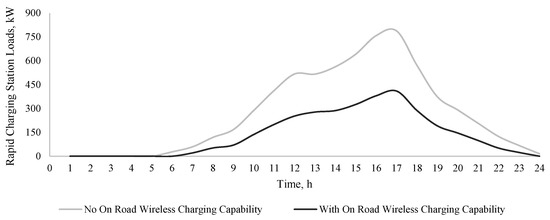
Figure 10.
EV expected charging station loads at location 30 with and without on-road wireless charging capabilities.
When applying the queuing model, it is observed that the charging station experiences maximum capacity utilization from hour 12 to hour 18, accommodating the highest number of EVs, especially when on-road wireless charging systems are not available. The increased charging station load most frequently occurs during the evening, often coinciding with peak demand of the power grid. When considering on-road wireless charging, the peak load of the charging station reduces significantly, and hence does not coincide with the system peak demand. This helps ensure grid availability when accommodating for EV charging station loads without putting stress on the system or prompting the need for system upgrades.
The expected loads of the on-road EV wireless charging system, considering different locations in the distribution system, are presented in Figure 11, Figure 12, Figure 13 and Figure 14. These loads are determined based on the average number of EVs using on-road wireless charging to charge their EV batteries, and hence they vary from one location to another. However, these EV loads do not significantly vary from one location to another due to the fact that a large set of scenarios, i.e., 100 scenarios, are generated using the MCS to address uncertainties in the choice of EV users between rapid charging station or on-road wireless charging. The load of the on-road wireless charging system is assumed to be supplied by a hybrid solar energy system, such as rooftop photovoltaic (PV) generation and battery energy storage systems (BESSs). As an increased load of the on-road wireless charging system may occur during the evening (Figure 11, Figure 12, Figure 13 and Figure 14), the rooftop PV generation system alone is not enough to support such a load, and therefore the inclusion of a BESS is necessary.
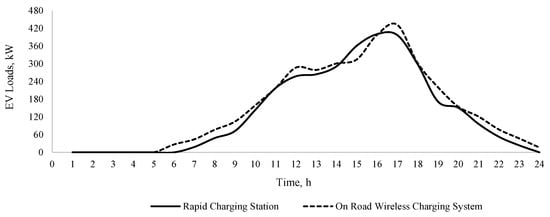
Figure 11.
Expected load of the on-road EV wireless charging system at location 14.
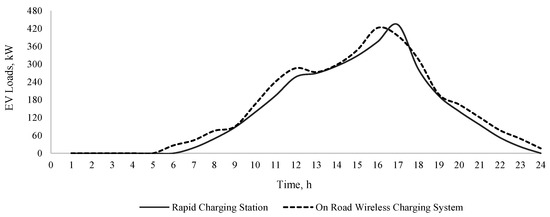
Figure 12.
Expected load of the on-road EV wireless charging system at location 21.
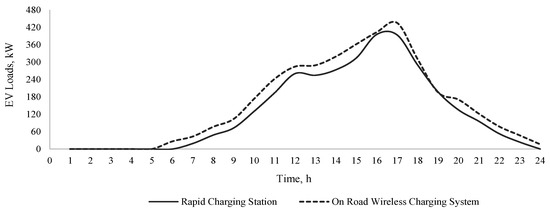
Figure 13.
Expected load of the on-road EV wireless charging system at location 24.
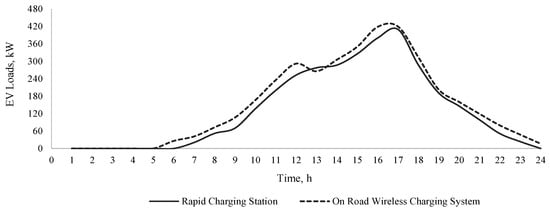
Figure 14.
Expected load of the on-road EV wireless charging system at location 30.
It can be concluded that a complementary on-road wireless charging system as an alternative charging method for EVs, with loads met by a hybrid solar energy system, the EV charging station load can be noticeably reduced, thus mitigating its impacts on the power grid.
5. Conclusions
The paper presents a probabilistic framework for estimating the charging demand of EVs, taking into account the availability of on-road wireless charging systems as an alternative charging method. The developed EVDT accurately predicted the timing of EVs requiring rapid charging based on realistic transportation data, enabling effective planning of charging infrastructure. The MC simulation approach addressed uncertainties in EV user decisions, providing a robust analysis of charging scenarios. The queuing model effectively estimated the charging load at EV charging stations, considering the EV arrival rate and ensuring system stability. The results and discussions highlighted the importance of considering on-road wireless charging systems while determining EV charging station loads. It was found that when on-road EV wireless charging systems were considered as an alternative charging option in the distribution system, the peak loads of EV charging stations were significantly reduced and did not coincide with the system’s peak loads, thus enhancing the system’s capacity and power grid to accommodate the expected EV charging station loads without system upgrades, particularly when the load of on-road wireless charging systems are supplied by rooftop PV generation.
This work contributes to the understanding of EV charging dynamics and provides valuable insights for policymakers, EV charging station operators, and investors. The proposed framework offers a robust methodology for estimating charging demand and informing decision-making processes related to the deployment of charging infrastructure. Future research can explore additional factors such as renewable energy integration, grid impact, and cost analysis to enhance the sustainability and economic viability of EV charging systems. This study significantly contributes to the advancement of EV charging infrastructure planning, supporting the widespread adoption of EVs and facilitating the transition to a more sustainable transportation system.
Author Contributions
Conceptualization, W.A. and F.A.; methodology, W.A., M.S. and F.A.; software, W.A.; validation, W.A., M.S. and F.A.; formal analysis, W.A. and M.S.; investigation, W.A., M.S. and F.A.; resources, W.A. and M.S.; data curation, W.A. and F.A.; writing—original draft preparation, W.A., M.S. and F.A.; writing—review and editing, W.A. and M.S.; visualization, W.A. and F.A.; supervision, W.A. All authors have read and agreed to the published version of the manuscript.
Funding
The authors extend their appreciation to the Deanship of Scientific Research, Imam Mohammad Ibn Saud Islamic University (IMSIU), Saudi Arabia, for funding this research work through Grant No. (221414012).
Data Availability Statement
The data presented in this study are openly available in Ref. [26] in the paper, which is “U.S. Department of Transportation. National Household Travel Survey. Available online: http://nhts.ornl.gov (accessed on 15 May 2022)”.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sbordone, D.; Bertini, I.; Di Pietra, B.; Falvo, M.C.; Genovese, A.; Martirano, L. EV fast charging stations and energy storage technologies: A real implementation in the smart micro grid paradigm. Electr. Power Syst. Res. 2015, 120, 96–108. [Google Scholar] [CrossRef]
- Conti, J.; Holtberg, P.; Diefenderfer, J.; LaRose, A.; Turnure, J.T.; Westfall, L. International Energy Outlook 2016 with Projections to 2040; Technical Report; USDOE Energy Information Administration (EIA): Washington, DC, USA, 2016. [Google Scholar]
- Colombo, C.G.; Miraftabzadeh, S.M.; Saldarini, A.; Longo, M.; Brenna, M.; Yaici, W. Literature Review on Wireless Charging Technologies: Future Trend for Electric Vehicle? In Proceedings of the 2022 Second International Conference on Sustainable Mobility Applications, Renewables and Technology (SMART), Cassino, Italy, 23–25 November 2022; pp. 1–5. [Google Scholar]
- Rotering, N.; Ilic, M. Optimal charge control of plug-in hybrid electric vehicles in deregulated electricity markets. IEEE Trans. Power Syst. 2010, 26, 1021–1029. [Google Scholar] [CrossRef]
- Lee, K.B.; A. Ahmed, M.; Kang, D.K.; Kim, Y.C. Deep reinforcement learning based optimal route and charging station selection. Energies 2020, 13, 6255. [Google Scholar] [CrossRef]
- Zhang, J.; Yan, J.; Liu, Y.; Zhang, H.; Lv, G. Daily electric vehicle charging load profiles considering demographics of vehicle users. Appl. Energy 2020, 274, 115063. [Google Scholar] [CrossRef]
- Tuttle, D.P.; Baldick, R. The evolution of plug-in electric vehicle-grid interactions. IEEE Trans. Smart Grid 2012, 3, 500–505. [Google Scholar] [CrossRef]
- Chaudhari, K.; Kandasamy, N.K.; Krishnan, A.; Ukil, A.; Gooi, H.B. Agent-based aggregated behavior modeling for electric vehicle charging load. IEEE Trans. Ind. Inform. 2018, 15, 856–868. [Google Scholar] [CrossRef]
- Li, Y.; Han, M.; Yang, Z.; Li, G. Coordinating flexible demand response and renewable uncertainties for scheduling of community integrated energy systems with an electric vehicle charging station: A bi-level approach. IEEE Trans. Sustain. Energy 2021, 12, 2321–2331. [Google Scholar] [CrossRef]
- Infante, W.; Ma, J. Coordinated management and ratio assessment of electric vehicle charging facilities. IEEE Trans. Ind. Appl. 2020, 56, 5955–5962. [Google Scholar] [CrossRef]
- Ou, C.H.; Liang, H.; Zhuang, W. Investigating wireless charging and mobility of electric vehicles on electricity market. IEEE Trans. Ind. Electron. 2014, 62, 3123–3133. [Google Scholar] [CrossRef]
- Manshadi, S.D.; Khodayar, M.E.; Abdelghany, K.; Üster, H. Wireless charging of electric vehicles in electricity and transportation networks. IEEE Trans. Smart Grid 2017, 9, 4503–4512. [Google Scholar] [CrossRef]
- Yang, C.; Lou, W.; Yao, J.; Xie, S. On charging scheduling optimization for a wirelessly charged electric bus system. IEEE Trans. Intell. Transp. Syst. 2017, 19, 1814–1826. [Google Scholar] [CrossRef]
- Jin, Y.; Xu, J.; Wu, S.; Xu, L.; Yang, D. Enabling the wireless charging via bus network: Route scheduling for electric vehicles. IEEE Trans. Intell. Transp. Syst. 2020, 22, 1827–1839. [Google Scholar] [CrossRef]
- Islam, M.S.; Mithulananthan, N.; Hung, D.Q. A day-ahead forecasting model for probabilistic EV charging loads at business premises. IEEE Trans. Sustain. Energy 2017, 9, 741–753. [Google Scholar] [CrossRef]
- Shi, J.; Gao, H.O. Efficient energy management of wireless charging roads with energy storage for coupled transportation–power systems. Appl. Energy 2022, 323, 119619. [Google Scholar] [CrossRef]
- Ahmad, A.; Alam, M.S.; Chabaan, R. A comprehensive review of wireless charging technologies for electric vehicles. IEEE Trans. Transp. Electrif. 2017, 4, 38–63. [Google Scholar] [CrossRef]
- Amjad, M.; Farooq-i Azam, M.; Ni, Q.; Dong, M.; Ansari, E.A. Wireless charging systems for electric vehicles. Renew. Sustain. Energy Rev. 2022, 167, 112730. [Google Scholar] [CrossRef]
- Du, J.; Ouyang, M. Review of electric vehicle technologies progress and development prospect in China. In Proceedings of the 2013 World Electric Vehicle Symposium and Exhibition (EVS27), Barcelona, Spain, 17–20 November 2013; pp. 1–8. [Google Scholar]
- Bobanac, V.; Pandzic, H.; Capuder, T. Survey on electric vehicles and battery swapping stations: Expectations of existing and future EV owners. In Proceedings of the 2018 IEEE International Energy Conference (ENERGYCON), Limassol, Cyprus, 3–7 June 2018; pp. 1–6. [Google Scholar]
- He, C.; Zhu, J.; Lan, J.; Li, S.; Wu, W.; Zhu, H. Optimal planning of electric vehicle battery centralized charging station based on EV load forecasting. IEEE Trans. Ind. Appl. 2022, 58, 6557–6575. [Google Scholar] [CrossRef]
- Zhang, S.; James, J. Electric vehicle dynamic wireless charging system: Optimal placement and vehicle-to-grid scheduling. IEEE Internet Things J. 2021, 9, 6047–6057. [Google Scholar] [CrossRef]
- Riemann, R.; Wang, D.Z.; Busch, F. Optimal location of wireless charging facilities for electric vehicles: Flow-capturing location model with stochastic user equilibrium. Transp. Res. Part C Emerg. Technol. 2015, 58, 1–12. [Google Scholar] [CrossRef]
- Ucer, E.; Koyuncu, I.; Kisacikoglu, M.C.; Yavuz, M.; Meintz, A.; Rames, C. Modeling and analysis of a fast charging station and evaluation of service quality for electric vehicles. IEEE Trans. Transp. Electrif. 2019, 5, 215–225. [Google Scholar] [CrossRef]
- Alharbi, W.; Bhattacharya, K. Electric Vehicle Charging Facility as a Smart Energy Microhub. IEEE Trans. Sustain. Energy 2017, 8, 616–628. [Google Scholar] [CrossRef]
- U.S. Department of Transportation. National Household Travel Survey. Available online: http://nhts.ornl.gov (accessed on 15 May 2022).
- Puget Sound Regional Council. Traffic Choices Study—Summary Report; Prepared for the Value Pricing Pilot Program; Federal Highway Administration: Washington, DC, USA, 2008. [Google Scholar]
- Li, G.; Zhang, X.P. Modeling of plug-in hybrid electric vehicle charging demand in probabilistic power flow calculations. IEEE Trans. Smart Grid 2012, 3, 492–499. [Google Scholar] [CrossRef]
- Liu, Z.; Wen, F.; Ledwich, G. Optimal planning of electric-vehicle charging stations in distribution systems. IEEE Trans. Power Deliv. 2013, 28, 102–110. [Google Scholar] [CrossRef]
- Kendall, D.G. Stochastic processes occurring in the theory of queues and their analysis by the method of the imbedded Markov chain. Ann. Math. Stat. 1953, 24, 338–354. [Google Scholar] [CrossRef]
- Kulkarni, V.G. Modeling, Analysis, Design, and Control of Stochastic Systems, 1st ed.; Springer: New York, NY, USA, 1999; Volume 362. [Google Scholar]
- General Algebraic Modeling System (GAMS) Software; GAMS Development Corporation: Fairfax, VA, USA, 2023.
- Baran, M.E.; Wu, F.F. Network reconfiguration in distribution systems for loss reduction and load balancing. IEEE Power Eng. Rev. 1989, 9, 101–102. [Google Scholar] [CrossRef]
- Pinheiro, J.; Dornellas, C.; Schilling, M.T.; Melo, A.; Mello, J. Probing the new IEEE reliability test system (RTS-96): HL-II assessment. IEEE Trans. Power Syst. 1998, 13, 171–176. [Google Scholar] [CrossRef]
- Alharbi, W.; Bhattacharya, K. Incentive design for flexibility provisions from residential energy hubs in smart grid. IEEE Trans. Smart Grid 2021, 12, 2113–2124. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).