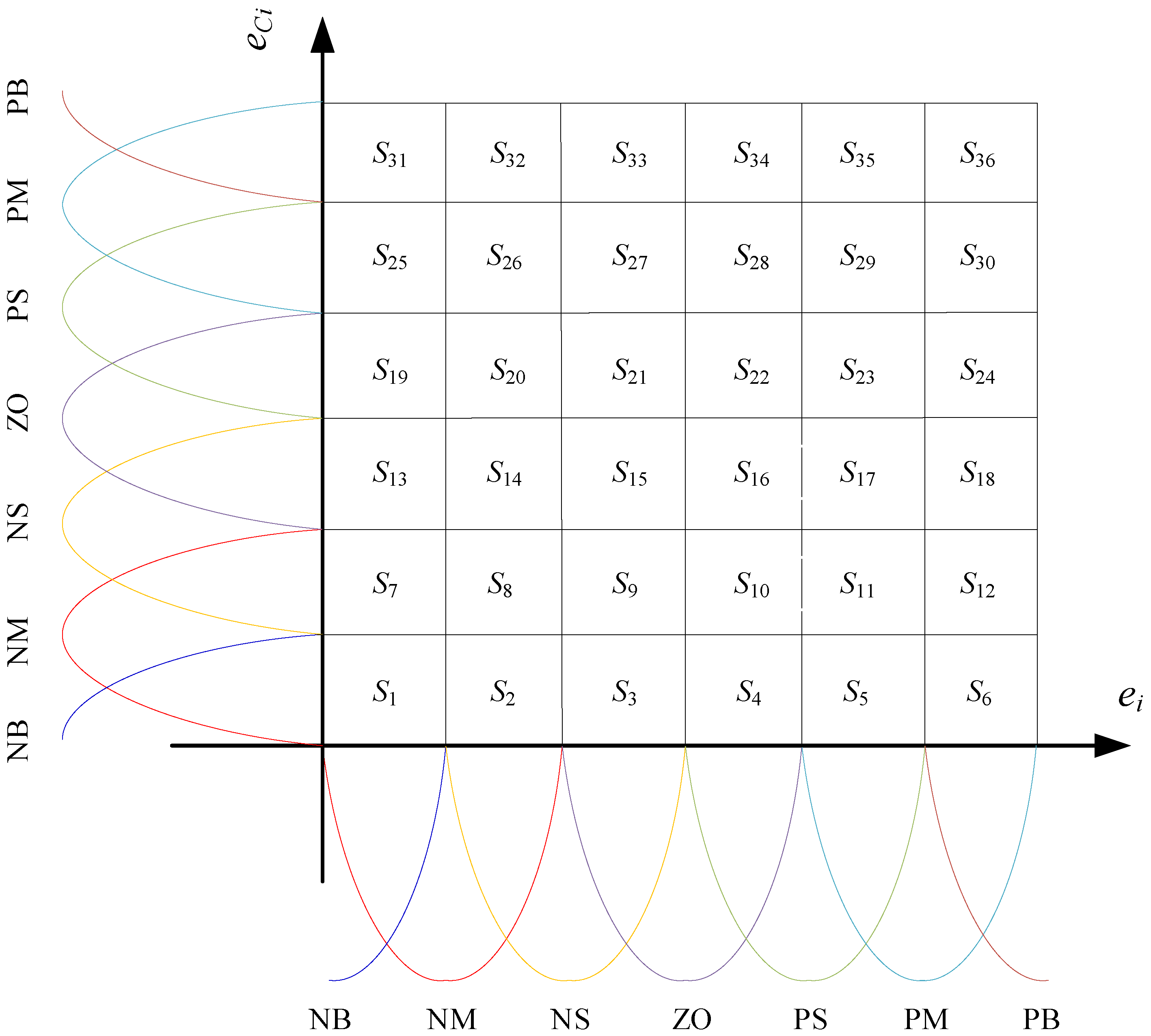
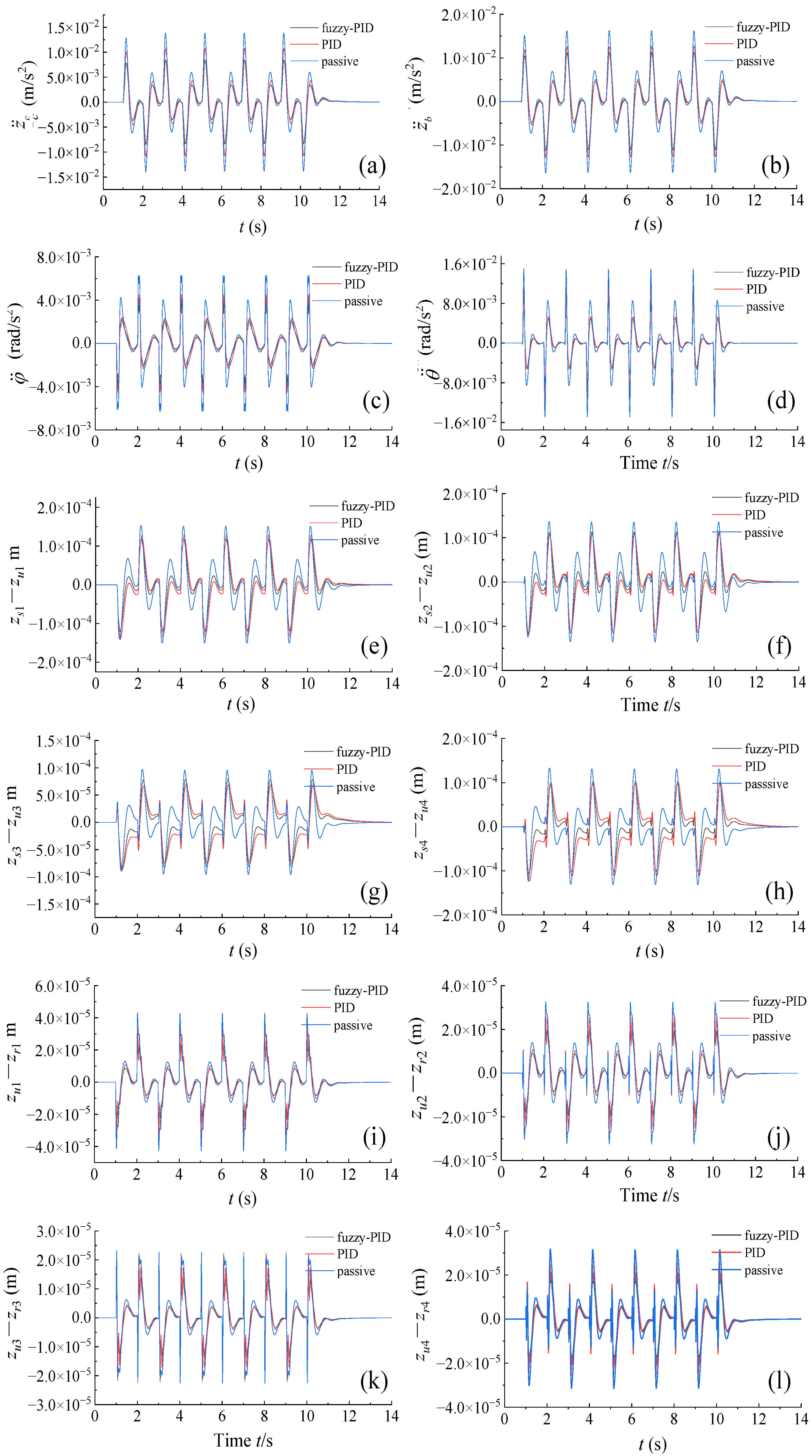
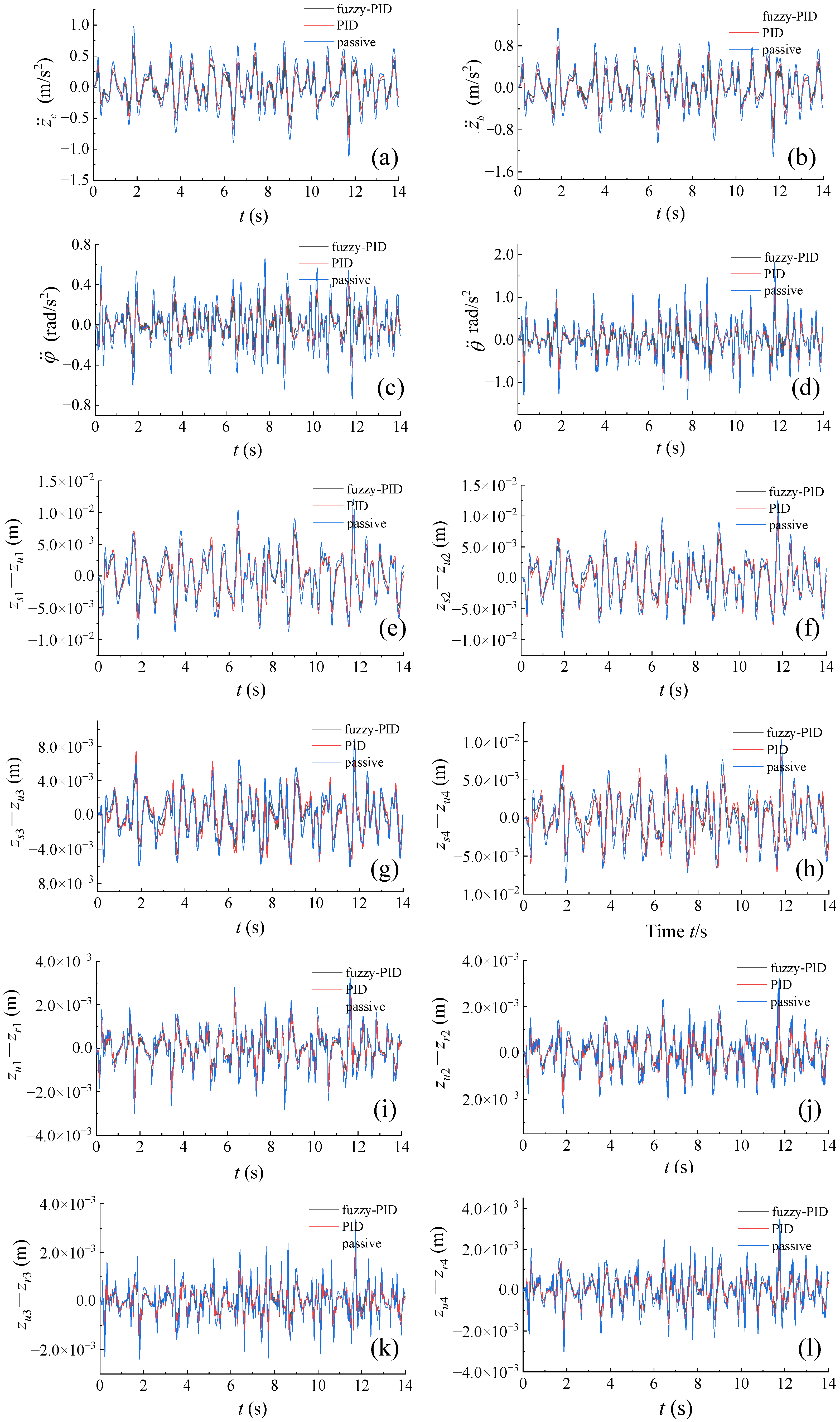
1. Introduction
Vehicles are one of the most prominent means of transportation in modern society, and the driving and riding experience of vehicles are receiving increasing attention. At present, vehicle suspension includes two types according to whether it has a control function: passive suspension and active suspension [
1,
2]. The parameters of each component of the passive suspension are determined, and it can only react passively to external forces based on its original design. The passive suspension cannot make timely changes according to the real-time conditions during the vehicle’s travel. The active suspension system and its control technology can address the limitation of the passive suspension system in adjusting to varying road conditions due to the rapid spread and development of electronics and intelligent control technology [
3,
4].
In classical fuel vehicles, the suspension is generally non-adjustable, so the comfort and sportiness of the vehicle are inherently contradictory. For this reason, air suspension systems [
5] or electromagnetic induction suspension systems [
6] have been added to advanced models of fuel vehicles to improve vehicle smoothness. Carbon neutrality and carbon peaking have accelerated the advent of the new energy vehicle era, which has been transformed to a great extent relative to classical fuel vehicles. Pure electric vehicles have mainly added an electric drive control system and eliminated the engine compared to classical fuel vehicles [
7]. Electronic applications have come a long way in pure electric vehicles. The electrified drive-by-wire chassis is more suitable for electric vehicle development. The wire-controlled system eliminates some of the bulky and less accurate pneumatic, hydraulic, and mechanical connections and replaces them with electric-signal-driven sensors, control units, and electromagnetic actuators, so it has the advantages of compact structure, good controllability, and fast response speed [
8]. The biggest advantage of the wire-controlled suspension system is that it can react according to different road conditions and driving status, which gives the car a better driving experience, and it is controlled by electric signals and is more intelligent. Advanced driver assistance systems (ADAS) are necessary to realize high-level autonomous driving for electric vehicles, so the wire-controlled chassis must be highly compatible with intelligent electric vehicles [
9]. Wire-controlled suspension is becoming an indispensable core technology in the new energy vehicle industry.
The control method of vehicle suspension systems has been widely studied, and more and more new methods have been applied to active suspension systems. Active suspension control can be divided into the classical control algorithm [
10], modern control algorithm [
11], and intelligent control method [
12]. Classical control methods include sky-hook control [
13] and classical PID control [
14]. Sky-hook control uses a negative feedback controller to generate a force proportional to the absolute speed of the controlled object, which can effectively suppress the resonance hump caused by the low-frequency vibration isolation mode without reducing the high-frequency vibration isolation capability. Ground-hook control [
15] and mixed sky-hook and ground-hook control [
16] are also derived based on sky-hook control. Classic PID control is a control algorithm that combines proportion, integration, and differentiation in a closed-loop system, which can automatically correct the control system accurately and quickly. Modern control algorithms include optimal control [
17], adaptive control [
18], robust control [
19], and sliding mode variable structure control [
20]. Optimal control is to find out the allowable control rule, make the dynamic system transfer from the initial state to a required terminal state, and ensure that a required performance index reaches the minimum (or large). It mainly includes linear quadratic form optimal control [
21] and the dynamic programming method [
22]. Adaptive control includes model reference adaptive control [
23] and self-tuning control [
24], and its main control idea is to modify the characteristics of the control object itself to adapt to changes in the dynamic characteristics of the object and disturbance. Robust control introduces some robust designs into the control system to make the system stable under the influence of uncertainties, mainly including the Kharitonov interval theory [
25], structural singular value theory (
μ theory) [
26], and H
∞ control theory [
27]. Sliding mode variable structure control can continuously change purposefully according to the current state of the system (such as deviation and its derivatives of each order) in the dynamic process, forcing the system to move according to the state track of the predetermined sliding mode, which includes single-mode sliding [
28], multi-mode sliding [
29], super-twisting sliding [
30], and adaptive sliding [
31]. Intelligent control methods include fuzzy control [
32], neural network control [
33], optimization control based on the genetic algorithm [
34], expert control [
35], and hierarchical intelligent control [
36]. Fuzzy control is an intelligent control method that imitates human fuzzy reasoning and decision-making processes. Neural network control can perform neural network model identification on complex nonlinear objects that are difficult to accurately model. The optimization control based on a genetic algorithm simulates biological evolution processes such as natural selection, heredity, and mutation. Expert control combines the theory and technology of expert systems with control theory, methods, and technologies, imitating the experience of experts in unknown environments. Based on adaptive control and self-organizing control, hierarchical intelligent control is divided into the organizational level, coordination level, and execution level according to the level of intelligent control, and these three levels follow the principle of intelligent descending and increasing accuracy.
Numerous scholars have consistently investigated the research area of active suspension technology to enhance the overall performance of vehicles. The control algorithm is the core of active suspension research, which is an effective means to enable active suspension to achieve ideal vibration damping. The research focus on intelligent control has gradually shifted to the fusion of classical or modern control methods and intelligent control methods, which utilize the adaptive ability of intelligent control methods to further improve the performance of the classical controller. Senthilkumar and Sivakumar [
37] introduced fuzzy control to the continuously damped automotive suspension system and solved the multi-variable dynamic characteristics of the active suspension system. Bozorgvar and Zahrai [
38] designed the suspension fuzzy logic controller and optimized the control rules with an enhanced genetic algorithm. Kaldas et al. [
39] developed a semi-active suspension system controller using fuzzy control theories together with the Kalman filter. Chen et al. [
40] integrated a neuro-fuzzy (NF) adaptive controller with a modeling neural network (MNN). An optimal adaptive fuzzy controller was presented by Mahmoodabadi and Javanbakht [
41], which utilized the gravitational search algorithm (GSA) to identify the optimal controller parameters. Zhi et al. [
42] proposed a variable-domain fuzzy control method to optimize the suspension parameters. Soleymani et al. [
43] designed two independent fuzzy controllers for the front and rear suspensions using an 8-DoF (degree of freedom) full-vehicle model and used a multi-objective Pareto optimal solution to tune the parameters of the fuzzy controller. Eltantawie [
44] designed a decentralized neuro-fuzzy controller using a magnetorheological damper as a semi-active control device. Ahmed et al. [
45] proposed a fuzzy DE-PID controller based on an improved DE (differential evolution) algorithm to enhance the control gain. Kumar et al. [
46] designed a fuzzy logic controller whose input data are the velocity and acceleration of front and rear wheels. Na et al. [
47] incorporated prescribed performance functions into the control implementation, which preserves transition and steady-state suspension performance. Fang and Bai [
48] investigated adaptive fuzzy fault-tolerant control through a sensor fault compensation approach. Li et al. [
49] considered the sampled Takagi-Sugeno (T-S) fuzzy semi-vehicle active suspension system to establish a continuous system with input delay. The online self-tuning output of the proportional coefficients of the fuzzy sliding mode controller was achieved by Hsiao and Wang [
50] through the use of a fuzzy control approach. Jia et al. [
51] tackled the fixed time control problem of suspension systems by using an event-triggered adaptive fuzzy control method. Hu and Yang [
52] proposed an improved fuzzy-PID-integrated control strategy. Moaaz et al. [
53] compared the jump vibration performance of magnetorheological semi-active suspension, passive suspension, and optimized passive suspension.
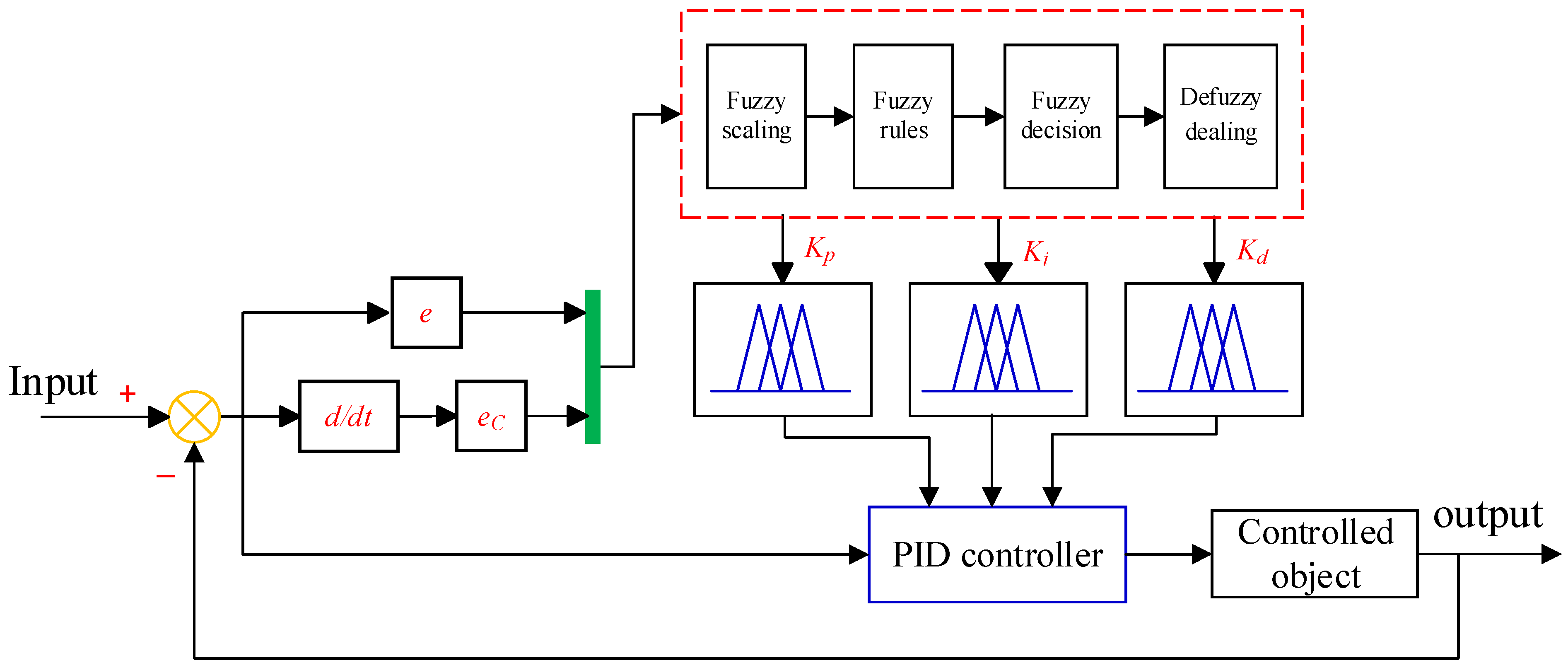
By isolating the vehicle body from road disturbances, the suspension system enhances passenger comfort, safety, and road handling. In the PID controller, the control quality is less sensitive to the change of the controlled object. The PID controller is linear, and it may not perform well in practice due to the nonlinearity of most controlled objects, resulting in decreased accuracy. The offline design of the PID algorithm is inadequate for handling the unexpected vibrations that occur when driving a vehicle under different road conditions. Therefore, a fuzzy-PID controller is proposed in this paper, which can further improve the performance of the active suspension system according to the fuzzy control rules. An 8-DoF model of full-vehicle active suspension is established, and the fuzzy-PID controller is designed by automatically adjusting the parameters of the PID controller. A suspension simulation model is established in the MATLAB/Simulink environment, and the vibration characteristics of the passive, PID control, and fuzzy-PID control suspensions are compared under the continuous crossing road hump model and C-level road model as control inputs.
2. Mathematical Model of Suspension
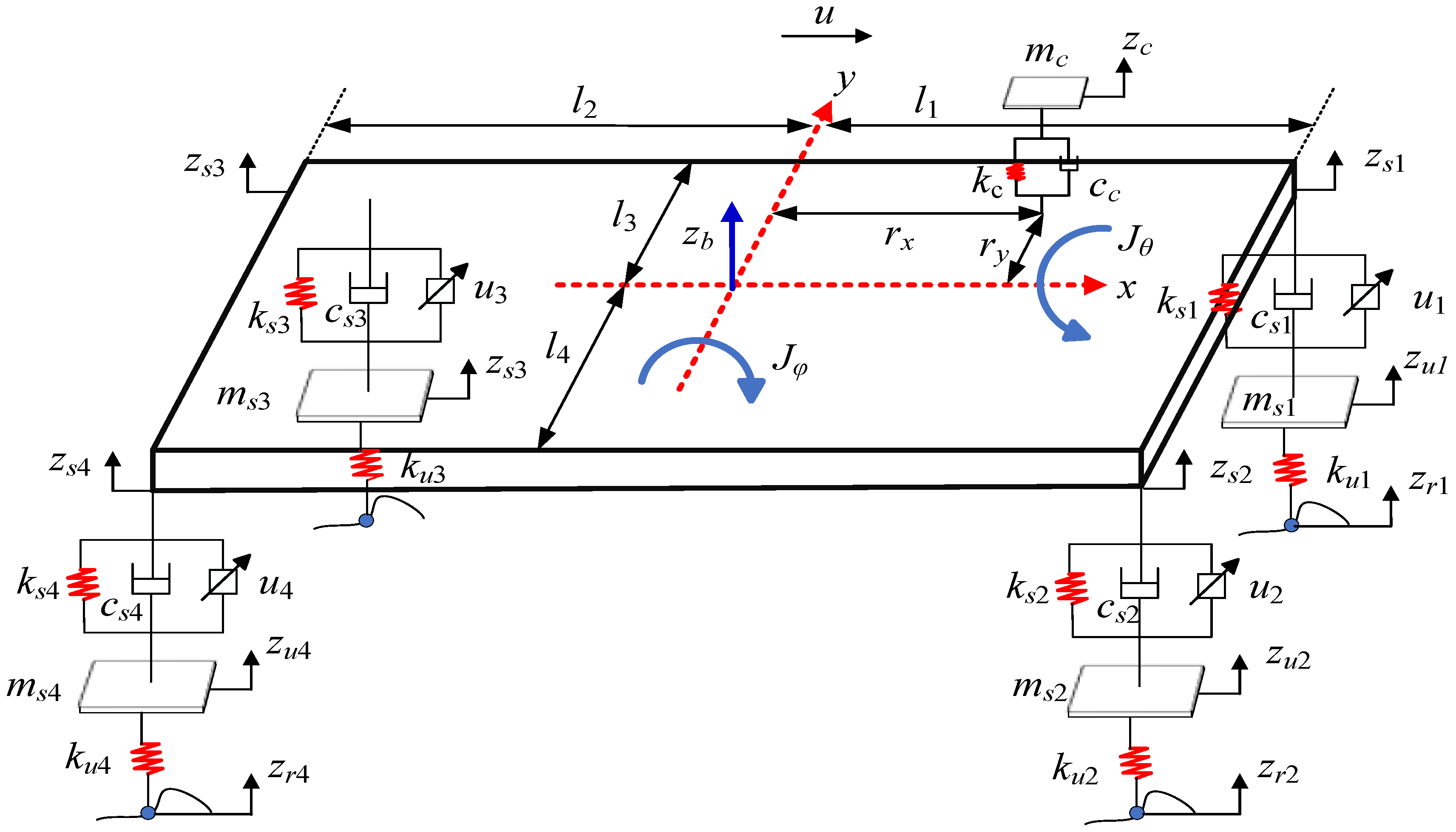
The 8-DOF dynamic model of the full vehicle comprehensively considers the effects of vertical, pitch, and roll motions. To reduce and suppress the vibration and impact caused by uneven road surfaces, the active suspension system is employed. The dynamic features of the vehicle’s suspension are fully represented by the active suspension, which actively controls the vibration that is transmitted to the human body. Based on the above analysis, the simplified physical model is shown in
Figure 1, and the corresponding mathematical model is established. Due to the longitudinal motion of the vehicle, when the pitch angle
θ and roll angle
φ change in a small range of change, the approximate kinematics between the vertical displacement
zsi of the suspension and the vertical displacement
zxy of the seat system position are as follows:
The equations below are derived from the kinematics and dynamics theory of the 8-DOF full-vehicle model:
- (1)
Equation for the motion of the center of mass of the human-chair system:
- (2)
Equation for the motion of the center of mass of the suspension body:
- (3)
Differential equation for suspension pitch rotation:
- (4)
Differential equation for suspension roll rotation:
- (5)
Equations for the movement of four unsprung masses:
where
zc is the vertical displacement of the human,
zb represents the vertical displacement of the center of mass of the vehicle,
zsi denotes the vertical displacement of the suspension,
zui is the vertical displacement of the tire,
θ means the pitch angle,
φ is the roll angle,
zxy is the vertical displacement of the human-chair system,
zri represents the vertical displacement excited by the road surface, and
ui is the suspension control input. The left-front wheel, right-front wheel, left-rear wheel, and right-rear wheel correspond to subscripts 1, 2, 3, and 4, respectively.
Table 1 provides parameters for the inherent characteristics of the full vehicle.
For simplicity, Equations (1)–(10) are written in matrix form:
where state variables
X = [
zc,
zb,
θ,
φ,
zu1,
zu2,
zu3,
zu4]
T, control variables
U = [
u1,
u2,
u3,
u4]
T, and excitation variables
Z = [
zr1,
zr2,
zr3,
zr4]
T. The mass matrix
M, damping matrix
C, stiffness matrix
K, control matrix
B, and excitation matrix
W are denoted as follows:
where
in which (since the itemization of damping matrix
C is almost the same as that of stiffness matrix
K, the itemization of stiffness matrix
K is omitted)
Let
be the state vector, the system dynamics Equation (11) can be converted into first-order dynamics as follows:
where
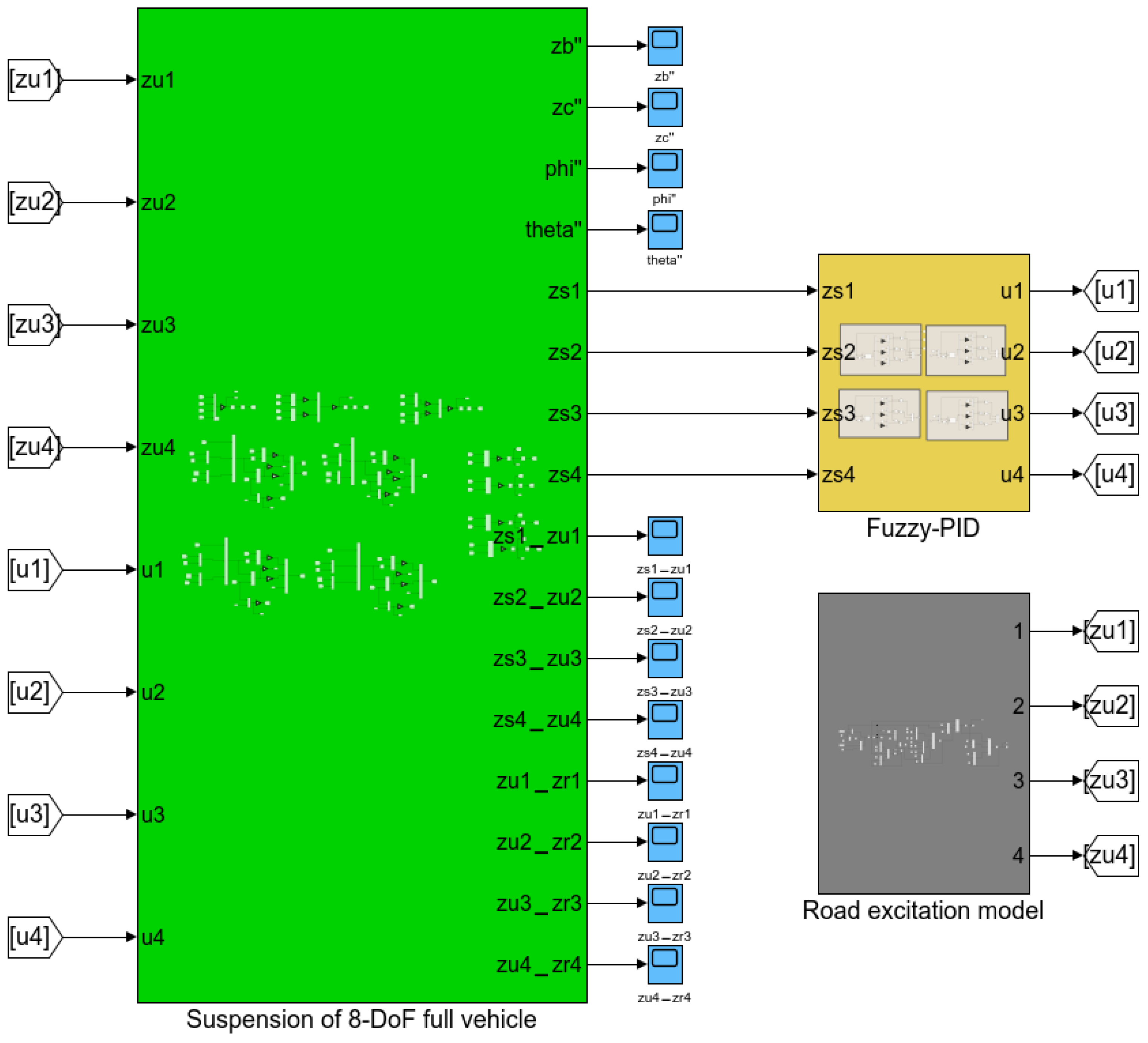
The mathematical model of the active suspension of the 8-DOF full vehicle is established using MATLAB/Simulink, as displayed in
Figure 2.