Effects of Crosswind on Pantograph–Catenary Wear Using Nonlinear Multibody System Dynamic Algorithms
Abstract
:1. Introduction
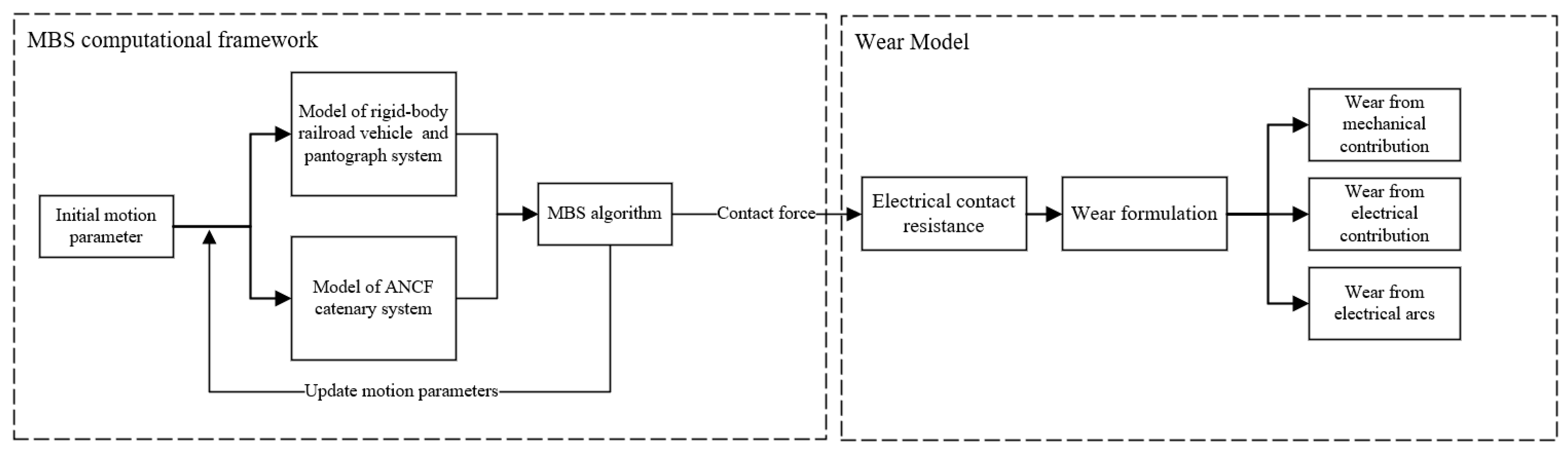
2. Wear Model
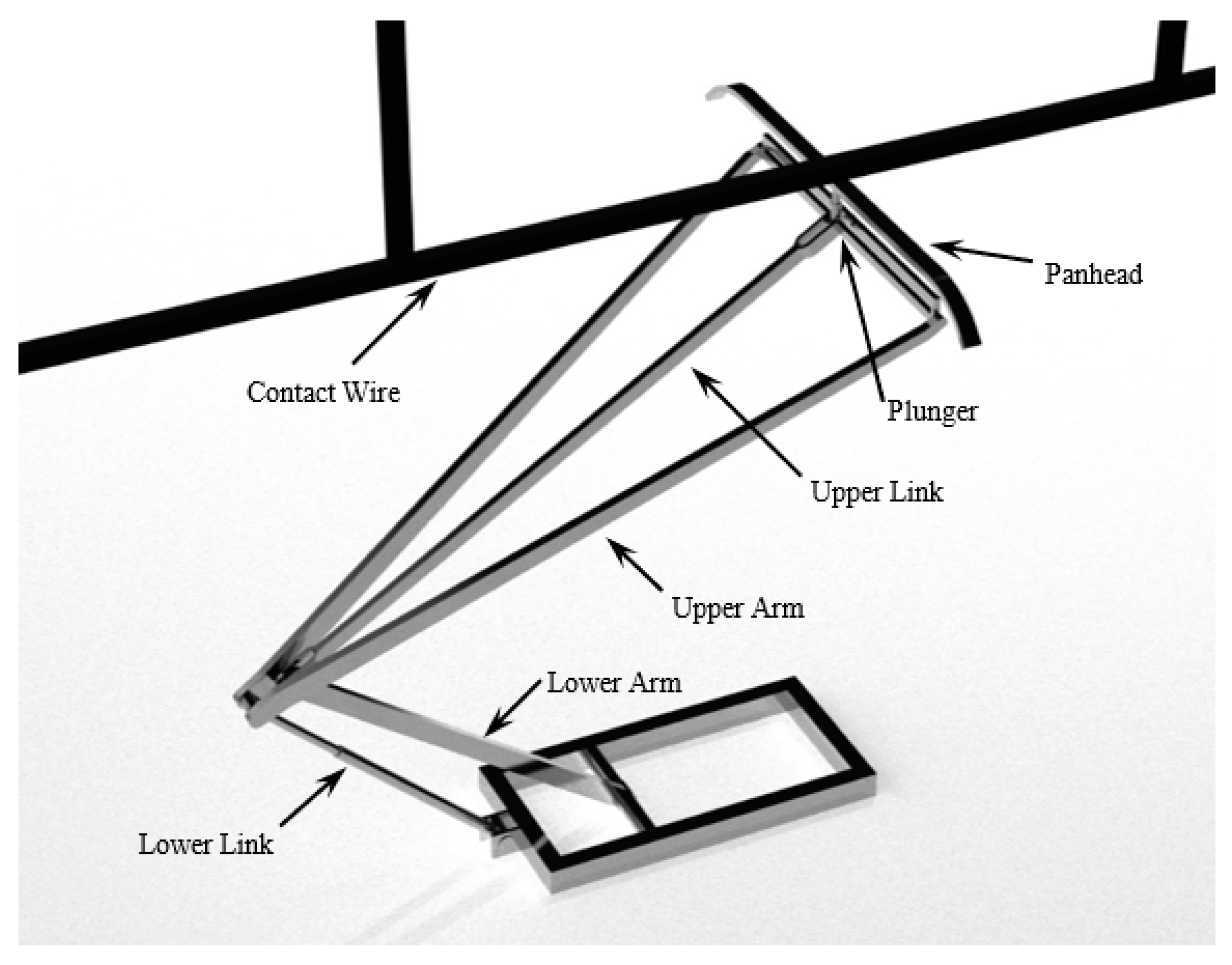
3. Pantograph–Catenary Contact Force Formulation
3.1. Contact Point and Contact Frame
3.2. Contact Forces
4. Pantograph–Catenary Aerodynamic Force Formulation
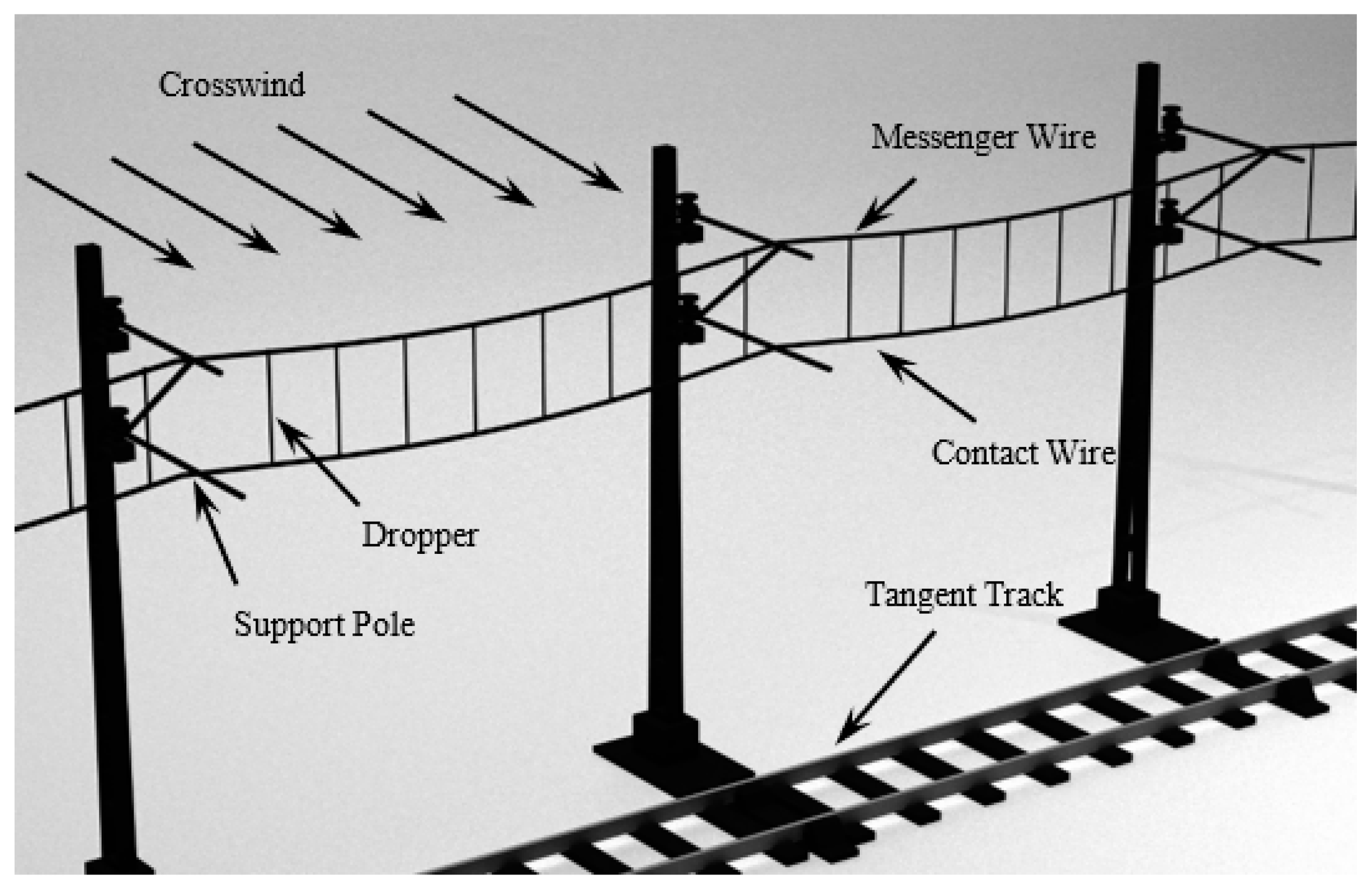
5. The ANCF Catenary System Model
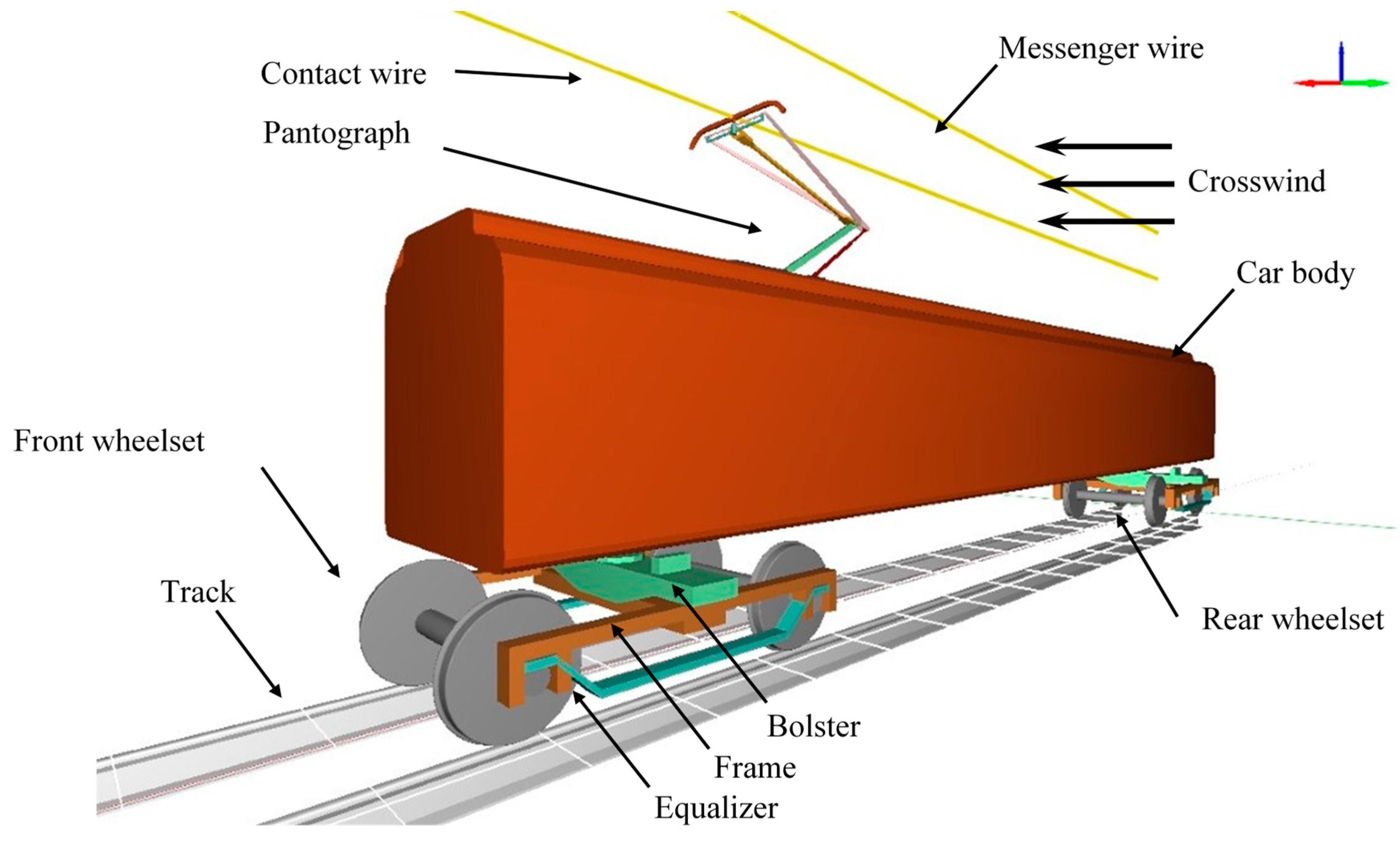
6. MBS Model and Equations of Motion
6.1. Railroad Vehicle and Pantograph MBS Models
6.2. Wheel–Rail Contact Kinematics
6.3. MBS Equations of Motion
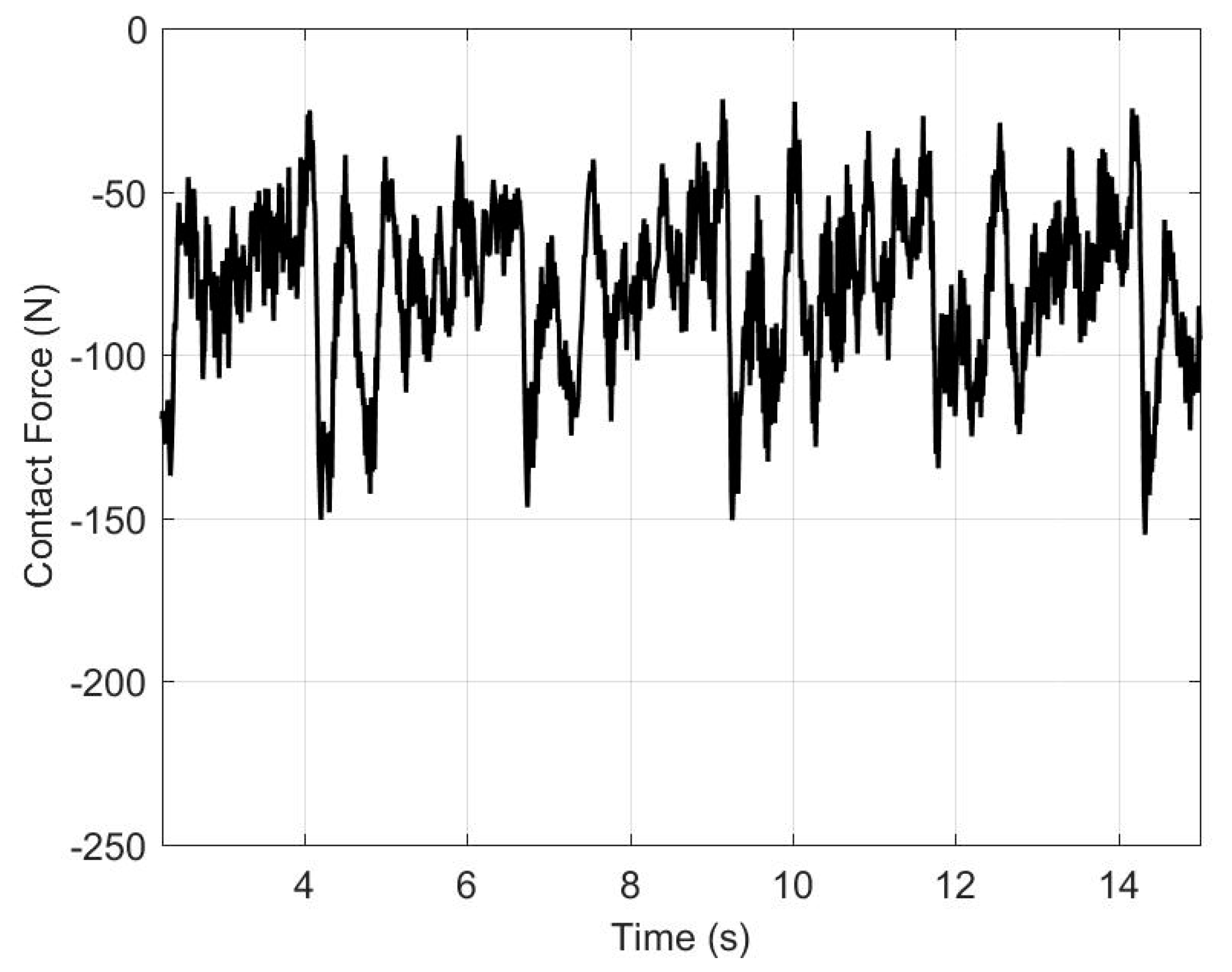
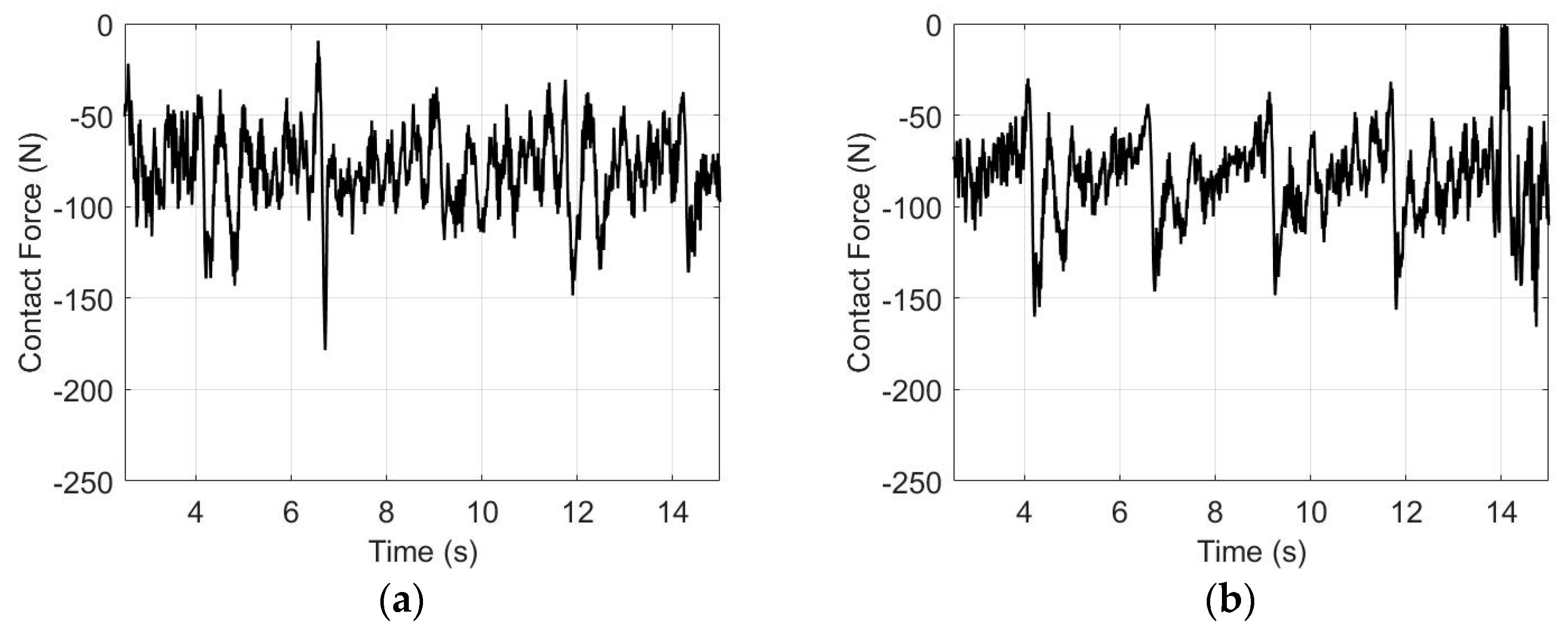
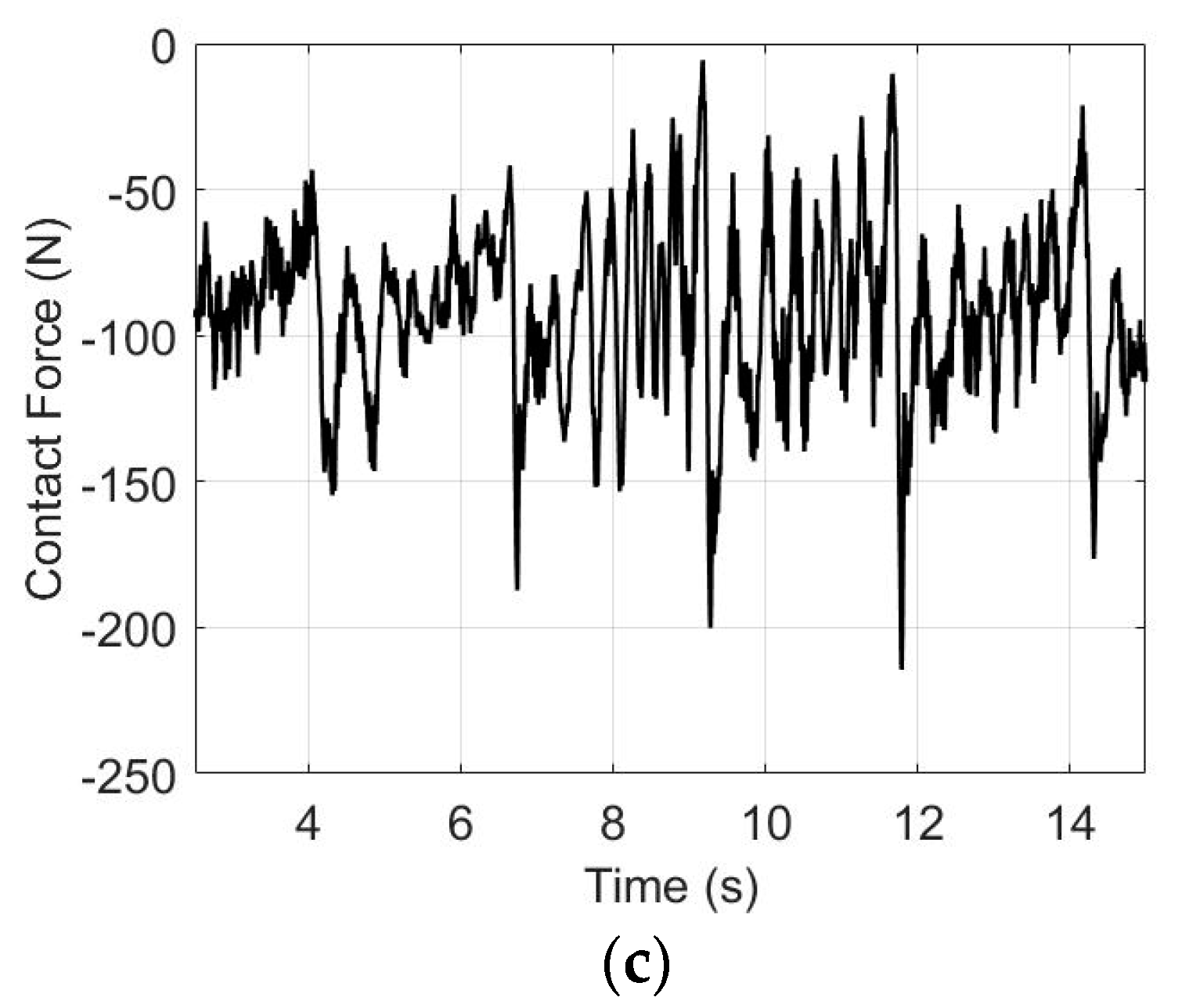
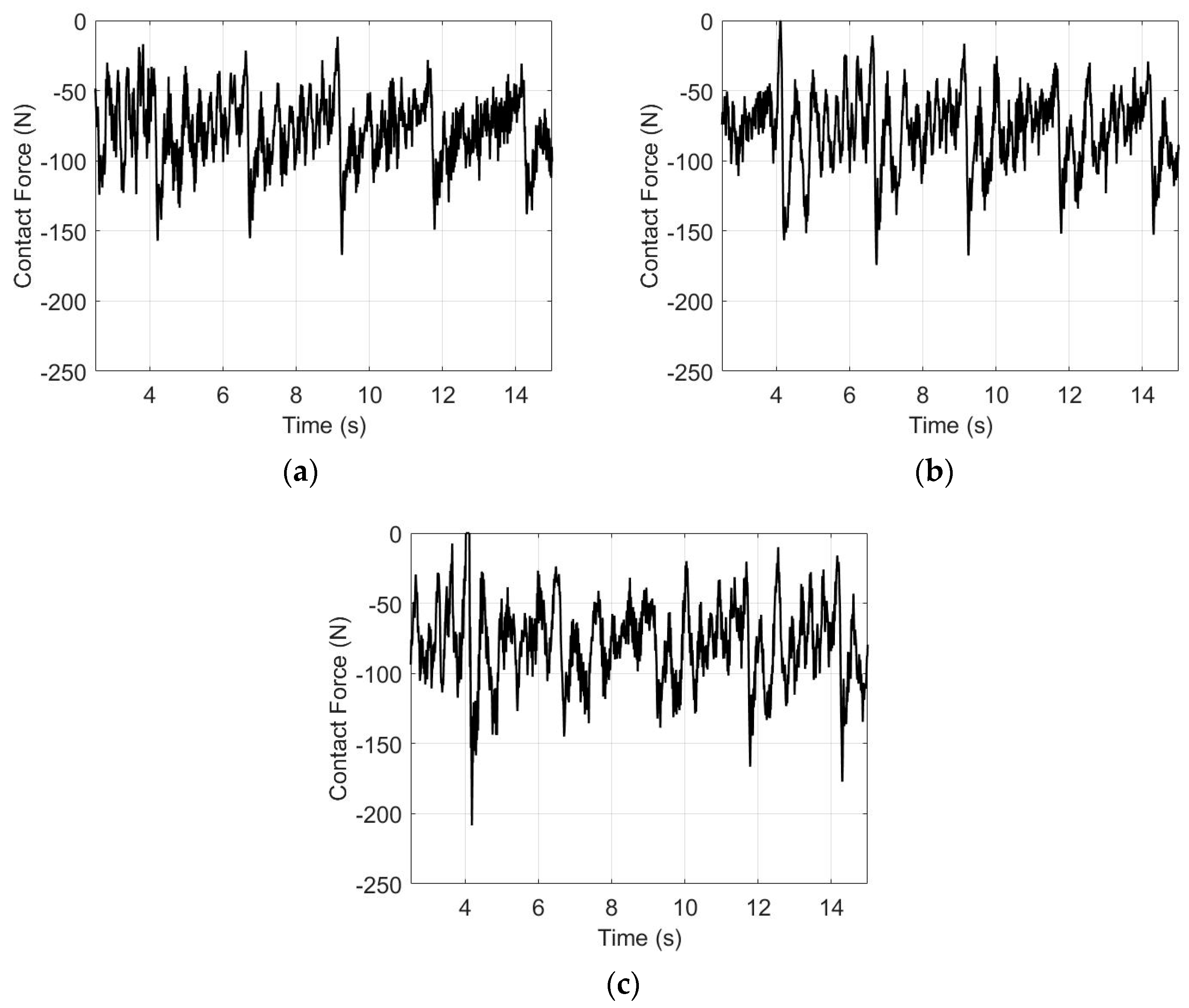
7. Numerical Results and Discussion
8. Conclusions
- The total NWR caused by the contact wire vibration during the crosswind excitation: for the pantograph and catenary with the aerodynamic design, the steady crosswind load increases the NWR of the contact wire from the mechanical contribution because of the increase in the contact force between the pantograph and catenary. The contact force fluctuation increases with the increase in the crosswind velocity. The NWR of the contact wire from the electrical contribution increases nonlinearly. Therefore, the total NWR is insignificant for the low-velocity crosswind and increases significantly for the high-velocity crosswind.
- The total NWR caused by the contact wire vibration after the crosswind excitation: the results show an increase in the SD of the contact force. The NWR from the electrical contribution and the percentage of contact loss increase significantly, whereas the mean contact force and NWR of the mechanical contribution remain almost unchanged. The total NWR increases significantly for the high-velocity crosswind.
- After the excitation of the high-velocity crosswind, a significant dispersion of the pantograph–catenary interaction and contact loss of the pantograph–catenary can occur because of severe vibration. The large uplift force in the pantograph head is necessary to suppress vibration. Therefore, a higher mean contact force causes higher wear, whereas a low mean contact force can reduce the reliability of the pantograph–catenary system.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pappalardo, C.M.; Patel, M.D.; Tinsley, B.; Shabana, A.A. Contact force control in multibody pantograph/catenary systems. Proc. Inst. Mech. Eng. Part K J. Multi Body Dyn. 2016, 230, 307–328. [Google Scholar] [CrossRef]
- Kulkarni, S.; Pappalardo, C.M.; Shabana, A.A. Pantograph/catenary contact formulations. J. Vib. Acoust. 2017, 139, 011010. [Google Scholar] [CrossRef]
- Seo, J.H.; Sugiyama, H.; Shabana, A.A. Three-dimensional large deformation analysis of the multibody pantograph/catenary systems. Nonlinear Dyn. 2005, 42, 199–215. [Google Scholar] [CrossRef]
- Seo, J.H.; Kim, S.W.; Jung, I.H.; Park, T.W.; Mok, J.Y.; Kim, Y.G.; Chai, J.B. Dynamic analysis of a pantograph–catenary system using absolute nodal coordinates. Veh. Syst. Dyn. 2006, 44, 615–630. [Google Scholar] [CrossRef]
- Daocharoenporn, S.; Mongkolwongrojn, M.; Kulkarni, S.; Shabana, A.A. Prediction of the pantograph/catenary wear using nonlinear multibody system dynamic algorithms. J. Tribol. 2019, 141, 051603. [Google Scholar] [CrossRef]
- Gere, J.M.; Weaver, W. Analysis of Framed Structures; Van Nostrand: New York, NY, USA, 1965. [Google Scholar]
- Shabana, A.A. Dynamics of Multibody Systems, 4th ed.; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Otsuka, K.; Makihara, K.; Sugiyama, H. Recent advances in the absolute nodal coordinate Formulation: Literature review from 2012 to 2020. J. Comput. Nonlinear Dyn. 2022, 17, 080803. [Google Scholar] [CrossRef]
- Peng, C.; Yang, C.; Xue, J.; Gong, Y.; Zhang, W. An adaptive variable-length cable element method for form-finding analysis of railway catenaries in an absolute nodal coordinate formulation. Eur. J. Mech. 2022, 93, 104545. [Google Scholar] [CrossRef]
- Bocciolone, M.; Resta, F.; Rocchi, D.; Tosi, A.; Collina, A. Pantograph aerodynamic effects on the pantograph–catenary interaction. Veh. Syst. Dyn. 2006, 44 (Suppl. S1), 560–570. [Google Scholar] [CrossRef]
- Carnevale, M.; Facchinetti, A.; Maggiori, L.; Rocchi, D. Computational fluid dynamics as a means of assessing the influence of aerodynamic forces on the mean contact force acting on a pantograph. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2016, 230, 1698–1713. [Google Scholar] [CrossRef]
- Song, Y.; Liu, Z.; Wang, H.; Lu, X.; Zhang, J. Nonlinear analysis of wind-induced vibration of high-speed railway catenary and its influence on pantograph–catenary interaction. Veh. Syst. Dyn. 2016, 54, 723–747. [Google Scholar] [CrossRef]
- Yao, Y.; Zou, D.; Zhou, N.; Mei, G.; Wang, J.; Zhang, W. A study on the mechanism of vehicle body vibration affecting the dynamic interaction in the pantograph–catenary system. Veh. Syst. Dyn. 2021, 59, 1335–1354. [Google Scholar] [CrossRef]
- Dai, Z.; Li, T.; Zhou, N.; Zhang, J.; Zhang, W. Numerical simulation and optimization of aerodynamic uplift force of a high-speed pantograph. Railw. Eng. Sci. 2021, 30, 117–128. [Google Scholar] [CrossRef]
- Song, Y.; Liu, Z.; Duan, F.; Lu, X.; Wang, H. Study on wind-induced vibration behaviour of railway catenary in spatial stochastic wind field based on nonlinear finite element procedure. J. Vib. Acoust. 2018, 140, 011010. [Google Scholar] [CrossRef]
- Shi, H.; Chen, G.; Yang, Y. A comparative study on pantograph-catenary models and effect of parameters on pantograph-catenary dynamics under crosswind. J. Wind. Eng. Ind. Aerodyn. 2021, 211, 104587. [Google Scholar] [CrossRef]
- Song, Y.; Jiang, T.; Nåvik, P.; Rønnquist, A. Geometry deviation effects of railway catenaries on pantograph–catenary interaction: A case study in Norwegian railway system. Railw. Eng. Sci. 2021, 29, 350–361. [Google Scholar] [CrossRef]
- Song, Y.; Rønnquist, A.; Jiang, T.; Nåvik, P. Identification of short-wavelength contact wire irregularities in electrified railway pantograph–catenary system. Mech. Mach. Theory 2021, 162, 104338. [Google Scholar] [CrossRef]
- Song, Y.; Wang, Z.; Liu, Z.; Wang, R. A spatial coupling model to study dynamic performance of pantograph-catenary with vehicle-track excitation. Mech. Syst. Signal Process. 2021, 151, 107336. [Google Scholar] [CrossRef]
- Bucca, G.; Collina, A. Electromechanical interaction between carbon-based pantograph strip and copper contact wire: A heuristic wear model. Tribol. Int. 2015, 92, 47–56. [Google Scholar] [CrossRef]
- Bucca, G.; Collina, A.; Manigrasso, R.; Mapelli, F.; Tarsitano, D. Analysis of electrical interferences related to the current collection quality in pantograph–catenary interaction. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2011, 225, 483–500. [Google Scholar] [CrossRef]
- Bucca, G.; Collina, A. A procedure for the wear prediction of collector strip and contact wire in pantograph–catenary system. Wear 2009, 266, 46–59. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, C.; Pang, X.; Song, C.; Ni, F.; Zhang, Y. Evolution processes of the tribological properties in pantograph/catenary system affected by dynamic contact force during current-carrying sliding. Wear 2021, 477, 203809. [Google Scholar] [CrossRef]
- EN 50318; Railway Applications—Current Collection Systems—Validation of Simulation of the Dynamic Interaction between Pantograph and Overhead Contact Line. European Standards (EN): Brussels, Belgium, 2002.
- Huan, R.H.; Pan, G.F.; Zhu, W.Q. Dynamics of pantograph-catenary system considering local singularities of contact wire with critical wavelengths. In Proceedings of the 1st International Workshop on High-Speed and Intercity Railways, Shenzhen and Hong Kong SAR, China, 19–22 July 2011; Lecture Notes in Electrical Engineering. Springer: Berlin/Heidelberg, Germany, 2012; pp. 319–333. [Google Scholar] [CrossRef]
- Tur, M.; García, E.; Baeza, L.; Fuenmayor, F.J. A 3D absolute nodal coordinate finite element model to compute the initial configuration of a railway catenary. Eng. Struct. 2014, 71, 234–243. [Google Scholar] [CrossRef]
- Bruni, S.; Ambrosio, J.; Carnicero, A.; Cho, Y.H.; Finner, L.; Ikeda, M.; Kwon, S.Y.; Massat, J.P.; Stichel, S.; Tur, M.; et al. The results of the pantograph–catenary interaction benchmark. Veh. Syst. Dyn. 2015, 53, 412–435. [Google Scholar] [CrossRef]
- Gerstmayr, J.; Shabana, A.A. Analysis of thin beams and cables using the absolute nodal co-ordinate formulation. Nonlinear Dyn. 2006, 45, 109–130. [Google Scholar] [CrossRef]
- Pombo, J.; Ambrósio, J.; Pereira, M.; Rauter, F.; Collina, A.; Facchinetti, A. Influence of the aerodynamic forces on the pantograph–catenary system for high-speed trains. Veh. Syst. Dyn. 2009, 47, 1327–1347. [Google Scholar] [CrossRef]
- Shabana, A.A.; Zaazaa, K.E.; Sugiyama, H. Railroad Vehicle Dynamics: A Computational Approach; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Aboubakr, A.K.; Shabana, A.A. Efficient and robust implementation of the TLISMNI method. J. Sound Vib. 2015, 353, 220–242. [Google Scholar] [CrossRef]

| Symbol | Meaning |
|---|---|
| Mean value of the contact force (N) | |
| Nominal electrical current during tests (A) | |
| Sliding speed (m/s) | |
| Decimal fraction value of percentage of contact loss | |
| Global position vector | |
| Shape function matrix of the ANCF element | |
| Transformation matrix | |
| Vector of element nodal coordinates | |
| Drag force vector | |
| Lift force vector | |
| Density | |
| Drag force coefficients | |
| Lift force coefficients | |
| Area where the aerodynamic force is exerted | |
| Cross-sectional area | |
| Relative velocity vector on the frame to the wind | |
| Unit vector of the drag force | |
| Unit vector of the lift force | |
| Jacobian matrix of the position field: rigid body , ANCF body | |
| Matrix that relates the angular velocity vector | |
| Skew symmetric matrix associated with the vector | |
| Location of the point with respect to the coordinate system of the body | |
| Modulus of elasticity | |
| Second moment of inertia | |
| Geometrically exact curvature from the Serret–Frenet formulas | |
| Axial normal strain | |
| Two tangent vectors to the surface | |
| Normal vector to the surface | |
| Vector of generalized coordinates | |
| Vector of nongeneralized coordinates or surface parameters | |
| Vector of Lagrange multipliers | |
| Mass matrix | |
| Jacobian constraint matrices | |
| External forces | |
| Quadratic velocity vector [7] |
| Mean Contact Force (N) | SD (N) | MNWR (mm3/km) | ENWR (mm3/km) | TNWR (mm3/km) | Percentage of Contact Loss | |
|---|---|---|---|---|---|---|
| Without wind | 79.0544 | 25.5508 | 2.5514 | 2.4552 | 5.0067 | 0 |
| Steady wind (10 m/s) | 80.9416 | 23.8995 | 2.6307 | 2.3721 | 5.0028 | 0 |
| Steady wind (20 m/s) | 85.3727 | 25.8908 | 2.9396 | 2.4647 | 5.4044 | 0.08 |
| Steady wind (30 m/s) | 92.1626 | 28.9224 | 3.9078 | 2.4055 | 6.3133 | 0 |
| Mean Contact Force(N) | SD (N) | MNWR (mm3/km) | ENWR (mm3/km) | TNWR (mm3/km) | Percentage of Contact Loss | |
|---|---|---|---|---|---|---|
| Without wind | 118.2223 | 22.2572 | 6.7288 | 2.1616 | 8.8904 | 0 |
| Steady wind (10 m/s) | 120.1296 | 21.1782 | 6.9961 | 2.1594 | 9.1555 | 0 |
| Steady wind (20 m/s) | 124.0970 | 20.8028 | 7.6066 | 2.1596 | 9.7662 | 0 |
| Steady wind (30 m/s) | 130.9205 | 24.6741 | 8.9854 | 2.1626 | 11.1480 | 0 |
| Mean Contact Force (N) | SD (N) | MNWR (mm3/km) | ENWR (mm3/km) | TNWR (mm3/km) | Percentage of Contact Loss | |
|---|---|---|---|---|---|---|
| Without wind | 79.0544 | 25.5508 | 2.5514 | 2.4552 | 5.0067 | 0 |
| Steady wind (10 m/s) | 79.3732 | 25.5514 | 2.5531 | 2.5580 | 5.1111 | 0 |
| Steady wind (20 m/s) | 79.6138 | 27.1695 | 2.6672 | 2.5930 | 5.2602 | 0.09 |
| Steady wind (30 m/s) | 80.0312 | 29.2231 | 2.7840 | 2.9855 | 5.7695 | 0.65 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Daocharoenporn, S.; Mongkolwongrojn, M. Effects of Crosswind on Pantograph–Catenary Wear Using Nonlinear Multibody System Dynamic Algorithms. World Electr. Veh. J. 2023, 14, 250. https://doi.org/10.3390/wevj14090250
Daocharoenporn S, Mongkolwongrojn M. Effects of Crosswind on Pantograph–Catenary Wear Using Nonlinear Multibody System Dynamic Algorithms. World Electric Vehicle Journal. 2023; 14(9):250. https://doi.org/10.3390/wevj14090250
Chicago/Turabian StyleDaocharoenporn, Siripong, and Mongkol Mongkolwongrojn. 2023. "Effects of Crosswind on Pantograph–Catenary Wear Using Nonlinear Multibody System Dynamic Algorithms" World Electric Vehicle Journal 14, no. 9: 250. https://doi.org/10.3390/wevj14090250
APA StyleDaocharoenporn, S., & Mongkolwongrojn, M. (2023). Effects of Crosswind on Pantograph–Catenary Wear Using Nonlinear Multibody System Dynamic Algorithms. World Electric Vehicle Journal, 14(9), 250. https://doi.org/10.3390/wevj14090250





