Abstract
The charging and discharging process of batteries generates a significant amount of heat, which can adversely affect their lifespan and safety. This study aims to enhance the performance of a lithium-ion battery (LIB) pack with a high discharge rate (5C) by proposing a combined battery thermal management system (BTMS) consisting of improved phase change materials (paraffin/aluminum composite) and forced-air convection. Battery thermal performance is simulated using computational fluid dynamics (CFD) to study the effects of heat transfer and flow parameters. To evaluate the impact of essential parameters on the thermal performance of the battery module, temperature uniformity and maximum temperature in the cells are evaluated. For the proposed cooling system, an ambient temperature of 24.5 °C and the application of a 3 mm thick paraffin/aluminum composite showed the best cooling effect. In addition, a 2 m/s inlet velocity with 25 mm cell spacing provided the best cooling performance, thus reducing the maximum temperature. The paraffin can effectively manage thermal parameters maintaining battery temperature stability and uniformity. Simulation results demonstrated that the proposed cooling system combined with forced-air convection, paraffin, and metal foam effectively reduced the maximum temperature and temperature difference in the battery by 308 K and 2.0 K, respectively.
1. Introduction
Due to their high energy density, safety, and long life, LIBs are becoming popular in electric vehicles [1,2,3]. Lithium-ion batteries generate a lot of heat after a long period of operation, and this heat accumulation may damage battery life and performance [4]. It may cause the battery to overheat or have a non-uniform temperature distribution, thus compromising its safety [5]. On the other hand, the low temperature of the environment reduces the energy density and power of the battery. For the safe operation of battery-based electric vehicles, it is essential to introduce a suitable BTMS [6]. A BTMS is the way to ensure the safety and performance of the battery module, extend the battery’s lifespan, and prevent thermal runaway. Consequently, necessary efforts are needed to develop a BTMS that maintains the battery’s temperature within an optimal operating range of 20–35 °C and provides enhanced temperature uniformity. The heat transfer environment, power consumption, and contact between the coolant and the battery surface are the main factors in the classification of BTMSs.
Nowadays, various strategies for thermal management of batteries have been developed. Cooling of batteries is conventionally carried out by liquid cooling, air cooling, and phase change materials (PCMs) [7]. In the active method, energy is spent on cooling, like in air- and water-cooling thermal management systems. In the passive method, cooling is done without expending energy, such as by using materials with high thermal storage capacity (i.e., PCM). The first requirement of air cooling is an appropriately designed configuration to maintain the temperature uniformity and temperature range of the battery pack. In BTMSs, maximum temperature (Tmax) refers to the highest temperature the battery achieves, while maximum temperature difference (ΔTmax) represents the temperature variation between batteries. Recent studies on air-cooling systems have focused on improving traditional structures and suggesting new designs. Airpath design, cell spacing, and pack arrangement are parameters for battery module optimization [8,9]. The key objectives for air-cooling designs are decreased energy consumption and temperature uniformity [10].
Wu et al. [11] investigated the battery thermal efficiency utilizing natural convection and forced air. They showed that forced convection reduced the maximum temperature from 47 °C to 30 °C. Wang et al. [12] researched the efficiency of air cooling considering various ambient temperatures. They concluded that ambient temperatures below 20 °C at 3C do not require forced-air cooling, but that forced-air cooling is needed if the ambient temperature exceeds 35 °C. Chen et al. [13] introduced a Z-type flow and flexible cell distance to reduce ΔTmax by approximately 60%. In another study, Fan et al. [14] examined air-cooling performance for parallel and crossed battery modules. They discovered that the aligned configuration had the maximum cooling efficiency and temperature uniformity, and the temperature difference was decreased by 12% compared to the crossed configuration. Kirad et al. [15] concluded that the cell distance between the batteries affects the temperature uniformity, and that the transverse distance impacts the cooling performance. Hasan et al. [16] designed a BTMS for electric vehicles using air cooling to reduce operating temperatures and prevent thermal runaway. The simulation results demonstrated that raising the Reynolds number (Re) and the cell spacing can significantly impact the thermal performance and cooling capacity of LIBs. With an Re of 30,000 and cell spacing of 6 mm, the optimal configuration provided improved electrical properties and extended battery life. Rabiei et al. [17] proposed a novel liquid cold plate for the thermal management of prismatic Li-ion batteries. They used wavy microchannels and metal-foam-embedded microchannels to reduce the maximum temperature by 4–6 °C and 14 °C, respectively, compared to straight microchannels. The anode is a critical component of batteries, and its material selection significantly impacts battery safety, charging efficiency, capacity, and overall lifespan [18]. Sha et al. [19] worked to improve the electrochemical performance of Li4Ti5O12 (LTO) anode material for lithium-ion batteries. Their results demonstrated that LTO composites are a promising anode material for lithium-ion batteries with a high discharge capacity, stability, and tap density.
Generally, BTMSs are subjected to PCM cooling due to its simplicity, low cost, and high efficiency. As a result of these materials’ high latent heat, cooling systems can absorb heat generated by LIBs, which can significantly decrease the temperature [20]. Kizilel et al. [21,22] investigated the cooling efficiency of the system, looking at PCM with air cooling to prevent heat diffusion among battery cells. They explained that air cooling at high velocity leads to non-uniformity of temperature distribution, observed above 3 °C in the cells. Nevertheless, PCM in the module significantly improved the temperature uniformity, with temperature variations of less than 0.2 °C. Ling et al. [23] studied 18,650 LIB pack thermal performance using a forced-air convection integrated PCM hybrid cooling system. They found that the ΔTmax and Tmax are below 3 °C and 50 °C, respectively, at rates less than 2C. A numerical analysis was conducted by Verma et al. [24] using capric acid and paraffin wax as the PCM. Their results showed that using PCM reduced battery temperatures by 9 K compared to before. Zhang et al. [25] studied the effect of PCM dosage on battery temperature control in PCM-based BTMSs. They introduced the “Heat ratio” to analyze dosage. The results showed a lower temperature by increasing PCM heat ratio and thermal conductivity. Iasiello et al. [26] conducted a numerical and experimental study on PCM with aluminum foam. Their study showed that porosity significantly impacts the melting process, more than pores per inch (PPI), and foam orientation. Javani et al. [27] recommended a 3D LIB model; the results indicated that battery temperature was reduced by 3 K for a PCM thickness of 12 mm. Also, the temperature distribution for Li-ion cells was enhanced by almost 10% when a 3 mm thick PCM was employed, which was a significant result for the TMS (thermal management system). In another study by Lamrani et al. [28], PCM was investigated as a TMS for LIBs. Results indicated that PCM reduced maximum battery temperatures by up to 3 °C. The simplified model provides a practical tool for battery pack designers to enhance thermal management systems. Bais et al. [29] studied RT-42 to determine the minimum PCM thickness for Li-ion cells to stay below 323 K at 3C. They found a required thickness of 3 mm. Combining air cooling and PCM significantly improved temperature control and maximum temperature in hybrid systems. In hybrid systems based on PCM, the sensible and latent heat capacities play an essential role, while in active systems, they participate in cooling the PCM [30]. Kermani et al. [31] analyzed the thermal efficiency of a battery module, looking at PCM with copper foam and an air-cooling system for prismatic lithium-ion batteries. Compared to natural convection, Tmax using the passive, active, and hybrid systems was reduced by 11 °C, 13 °C, and 24 °C, respectively. For the hybrid power train, Yoongi et al. [32] examined the effect of the melting fraction of PCM and flow rate on the thermal performance of an air-cooled and PCM LIB. The proposed BTMS was designed to maintain maximum temperature after the complete melting of the PCM. They could maintain Tmax below 49.2 °C at 4C discharge without consuming additional energy. Limited studies have optimized hybrid cooling systems, focusing only on passive or active ones. Under dynamic cycling, Peng Qin et al. [33] proposed a cooling system using air cooling and PCM. They recommended a 5 mm thickness of PCM for optimal cooling, effectively decreasing Tmax and ΔTmax at a high charge/discharge rate of 4C.
According to a review of the literature, various methods have been investigated to enhance the cooling system. Due to the limitation of using the forced-air cooling system, PCM, and metal foam in a single method, the combination of forced air, PCM, and metal foam has become a major subject of interest for researchers [34]. To the best of the authors’ knowledge, evaluating the performance of the BTMS using forced air and paraffin/aluminum composite together is necessary, and this is the main objective of this study (Table 1). In this way, both active and passive cooling methods can work together and in parallel to improve performance, prevent the melted PCM from becoming a thermal barrier, and reduce the risk of system failure. Based on the heat produced and heat transfer models, the thermal performance during the 5C discharge process until 720 s is analyzed. The results of this study signify a step towards developing a BTMS with better controllability. The following statements summarize the main aims of this work:
- To Analyze the performance of the BTMS using active and passive cooling techniques under forced air and paraffin/aluminum composite.
- To assess the effect of PCM on the BTMS heat dissipation performance, the thickness of PCM is proposed. A more reasonable optimal PCM for the BTMS is also suggested.
- To prevent thermal runaway, the distance between the cells and the airflow has been studied as factors that contribute to maintaining a uniform temperature distribution in the cells.
- PCM thermal conductivity and phase transition temperature are investigated in detail for paraffin and paraffin/Al foams to determine the battery temperature and PCM utilization.

Table 1.
Comparison between the current study and recent studies on hybrid cooling in lithium-ion batteries.
Table 1.
Comparison between the current study and recent studies on hybrid cooling in lithium-ion batteries.
| Research | Ref. | Year | Elements of Cooling System | Battery Type | C-Rate | ||
|---|---|---|---|---|---|---|---|
| Yoongi et al. | [32] | 2017 | PCM + Forced air | Prismatic | 4C | 322.3 | 3.2 |
| Qin et al. | [33] | 2019 | PCM + Forced air | Cylindrical | 3C | 289.1 | 1.2 |
| Kermani et al. | [31] | 2019 | PCM + Copper foam | Pouchy | 5C | 308.9 | 4.6 |
| Zhang et al. | [25] | 2021 | PCM | Prismatic | 5C | 314.5 | 2.5 |
| Lamrani et al. | [28] | 2021 | PCM | Cylindrical | 3C | 305.1 | - |
| Yang et al. | [34] | 2022 | Forced air | Prismatic | 4C | 324.8 | 2.8 |
| Current study | - | - | PCM + Aluminum foam + Forced air | Cylindrical | 5C | 308.1 | 2 |
2. Materials and Methods
As shown in Figure 1, the battery module is assumed to be a rectangular cube with dimensions of 108 mm × 30 mm × 65 mm. The thickness of the casing walls is 0.5 mm and they are made of glass. The battery used in this study is an LIB, commonly used in most commercial electric vehicles worldwide. The thermodynamic and physical properties of the battery cell are shown in Table 2. As shown in Figure 1, this module consists of four lithium-ion battery cells, and a PCM with variable thickness is embedded between each pair of battery cells. In this study, three paraffin thicknesses, four air velocities, three different cell distances, five different cooling fluid temperatures, and the effect of porosity were considered, in order to achieve the best possible state for the battery module. The PCM used in this study is RT-27; its relevant properties are indicated in Table 3.

Figure 1.
(a) Geometry and (b) schematic of LIB pack with the phase change material cooling system and cooling fan.

Table 2.
Physical and thermodynamic properties of battery cells [35,36].

Table 3.
Thermophysical properties of aluminum, air, PCM RT27, and PCM RT27 composite.
2.1. Modelling and Governing Equations
In order to investigate the efficiency of the TMS, the CFD method has been used. The governing equations of continuity, momentum, and energy are defined in two domains, including the cells and the cooling fluid (PCM and air). The following assumptions are made before simulation:
- The fluid flow is incompressible, and the flow regime is laminar and turbulent for different fluid velocities.
- Radiative heat transfer is neglected.
- The Boussinesq approximation estimates natural convection due to buoyancy.
- The metal foam is assumed to be isotropic and homogeneous.
- Volume expansion is neglected.
2.1.1. Battery
The first requirement in a BTMS performance investigation is to estimate the heat generation rate inside the battery cell. Bernardi’s [39] model is the most used equation among other thermal models to calculate heat generated. During the charge/discharge process, reversible/irreversible heat generation inside the battery cell cause a temperature increase. Reaction heat, joule heat, etc., are different types of heat generation inside the battery cell. Bernardi [39] proposed a correlation for heat generation inside a battery cell as follows:
is the total heat generated, is the irreversibly generated heat, is the reversible heat production, is the cell charge/discharge current, is the cell temperature, is the open-circuit voltage, is the battery voltage, and is the temperature coefficient of open-circuit voltage; these are all critical factors. During the discharge process, the battery voltage is expressed as follows:
is equivalent to internal resistance. By substituting Equation (1) into Equation (2), we get:
Because the battery cell is made of various materials, the density, specific heat capacity, and equivalent thermal conductivity must be used in the simulation and can be calculated as follows:
To simulate the produced heat rate during the discharge process, a user-defined function (UDF) is used based on the empirical study of Lai et al. [40], which considers the open circuit voltage temperature coefficient and the equivalent internal resistance. Table 4 shows the polynomial fit for the equivalent internal resistance at different temperatures.

Table 4.
Polynomial modeling of equivalent internal resistance (R) at different temperatures [40].
Moreover, can be expressed as follows:
The state of charge (SOC) measures the amount of energy available in a battery at a specific point in time expressed as a percentage [41]. SOC was defined as:
In the case of a battery cell, the energy conservation equation is as follows, where , , and are thermal conductivity, specific heat capacity, and density, respectively:
2.1.2. Coolant
This study defines the Reynolds number as . where , , L, and V are, respectively, the density, dynamic viscosity, characteristic length, and inlet velocity of air. Given that the Re exceeds 3000, the airflow is classified as turbulent flow. Consequently, this study adopts the standard k-ε model with an enhanced wall treatment to analyze the turbulent airflow. Also, the air can be treated as an incompressible fluid due to its relatively low velocity compared to the acoustic velocity. The governing equations for the analysis are presented as follows [42]:
Continuity equation:
Energy conservation equation:
Momentum conservation equation:
In the momentum equation, parameters , , , , , , and represent the mass density, thermal conductivity, velocity vector, static pressure, specific heat, temperature, and dynamic viscosity of the air, respectively.
Turbulence kinetic equation:
Turbulent kinetic energy dissipation equation:
, , , , , and are the turbulent kinetic energy, dissipation rate, molecular dynamic viscosity coefficient, turbulent viscosity coefficient, empirical parameters, and inverse effective Prandtl numbers of and , respectively. Equation (16) is employed to calculate the turbulent viscosity (), while Equation (17) is utilized to determine the turbulence production () [43].
The predetermined reference values for all model constants in equations are , , , [44].
2.1.3. Phase Change Material
The method of enthalpy-porosity is utilized for the phase change of liquid/solid during the melting process. The energy equation in the phase change process is as follows:
,, and represent the heat source, total enthalpy, and temperature, respectively. is specific heat that changes between solid and liquid phases, and is the sensible enthalpy. , , , and represent the enthalpy at standard temperature, specific heat capacity at constant pressure, melting point, and solidus point of the PCM, respectively.
2.2. Boundary and Initial Conditions
In this study, the following boundary conditions were used:
- The battery cells are fully charged.
- Initially, all module components have a temperature equal to the ambient temperature (24.5 °C).
- The cell heat generated is considered at 5C.
- The convective heat transfer coefficient between the battery and the environment equals 5 (W/m·K).
- The bottom wall of the battery module is thermally insulated.
- This study investigates five different cooling air temperatures (10, 15, 20, 24.5, and 30 °C) to dissipate heat and create suitable working conditions.
3. Numerical Method and Mesh Independency
A grid independence test is necessary for CFD simulations to ensure that the mesh size does not affect the results. A mesh discretizes the physical domain into a finite number of cells. The smaller the mesh size, the more accurate the simulation results will be. However, a smaller mesh size also means a higher computational cost. Therefore, adopting a mesh size that is small enough to achieve accurate results without being too computationally expensive is essential. The geometry and mesh were created using the ANSYS Workbench 2020 software environment. The grid distribution of the computing domain and the module components is shown in Figure 2. It can be observed that hexa and prism elements are applied to the domain for the current study. A transient model was used to simulate the BTMS due to unsteady heat generation. The turbulent flow was assumed for a Reynolds number greater than 3000, and a 3D battery module was simulated under the k-ε turbulence model in this paper. The battery module was exposed to an ambient temperature of 297.65 K at 5C. A constant velocity of 2 m/s provided air cooling. The simulation was performed with a time step of 0.1 s and 25 iterations per time step, with convergence residuals of 10−6, 10−6, and 10−9 for the continuity, velocity, and energy equations, respectively. The results of a mesh independence study for the average battery temperature distribution are shown in Figure 3. Meshes with varying numbers of elements, i.e., 93, 160, 175, 800, 251, 200, 359, 070, and 462,125, were selected for comparison. The differences between the average temperature values at the designated point is obtained when the mesh elements number was 251,200(less than 1%). Therefore, it was decided that the optimum mesh element number was 251,200, which was sufficient to achieve the desired accuracy while saving computational time. Consequently, this study selected an optimal mesh size for all cases.

Figure 2.
Mesh distribution across the battery and fluid domains: (a) battery grid, (b) PCM module grid, (c) BTMS grid.
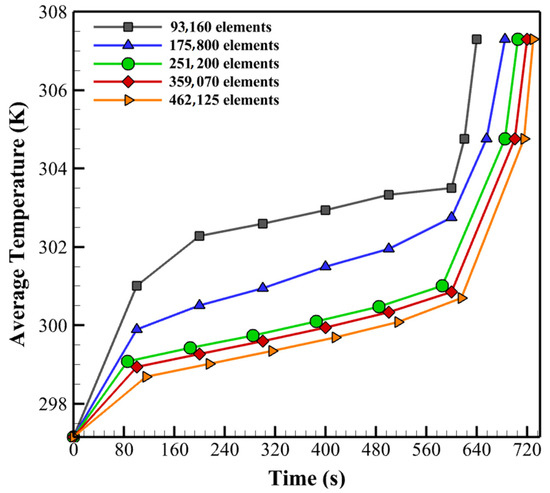
Figure 3.
Average temperature comparison to study mesh independency.
4. Validation of Numerical Model
To verify the battery thermal modelling, the numerical results of this study are compared with the experimental results of Lai et al. [40]. A 18,650 LIB with a capacity of 3 Ah is considered a sample, with an ambient temperature of 300 K and an SOC of 100%. The cell is under conditions where it is fully charged and insulated with a cover to reduce heat loss and is discharged at 5C. The validation was performed by ANSYS Fluent 2020 software. Figure 4a shows that the deviation between experimental data and numerical results is less than 1.1%, indicating good agreement. Figure 4b shows the fraction of PCM melting over 18 min, and the experimental and numerical results reported by Shmueli et al. [38] are compared with this study. The finite volume method was used for the discretization of the governing equations. Since the change in material density during a phase change is negligible, the continuity and momentum equations were solved using a pressure-based solver. A PCM model with a mushy zone value of 105 was employed [45,46]. The PCM initially starts to melt at a temperature of 22 °C and under conditions where adjacent walls are above the melting point of the fluid at a temperature of 30 °C. During the simulation process, under-relaxation coefficients of 0.3, 0.5, and 0.9 are applied to the pressure, momentum, and liquid fraction relation equations, respectively. Also, validation was conducted with a time step of 0.01 s and 20 iterations per time step. According to Figure 4b, with a maximum deviation of less than 5% from the experimental data, the numerical results of this study are acceptable.
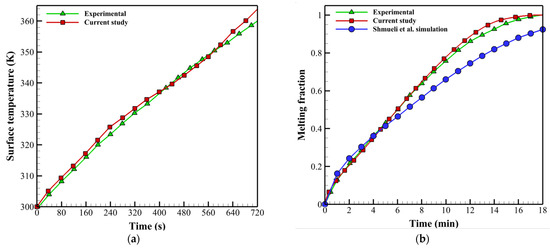
Figure 4.
(a) Surface temperature comparison between the numerical and the experimental results of Lai et al. [40]. (b) Melting fraction comparison between the numerical and the experimental results of Shmueli et al. [38].
5. Results and Discussion
In this section, the simulation results are presented. The performance of the combined cooling system is investigated by examining the inlet velocity, PCM thickness, cell spacing, metallic foam, and inlet temperature for a four-cell LIB pack. The results are compared in the 5C discharge process until 720 s.
5.1. Effect of Air Inlet Velocity
This section investigates the efficiency of the proposed BTMS by varying the fan speed under a 5C discharge rate and an inlet air temperature of 24.5 °C. Based on this assumption, the inlet velocities are presented in Table 5 in terms of Reynolds number. The flow regime type is determined based on the Reynolds number. Figure 5a displays the behavior of maximum temperature over time and the comparison of temperature uniformity of the module under different air velocities. When the velocity of the inlet increases, the maximum temperature of the discharge process gradually decreases, which is clearly evident after the first 20 s. However, in terms of temperature difference, increasing velocity gradually increases the battery’s temperature uniformity (Figure 5b). In the initial stages of discharge, the inlet air velocity has a negligible effect on reducing the temperature rise due to the paraffin melting before this stage. Thus, the inlet velocity increases, decreasing the battery’s temperature, and increasing the uniform temperature distribution. For inlet velocities of 2, 1, 0.5, and 0 m/s, the maximum temperatures were obtained as 308 K, 310.12 K, 313.47 K, and 323.20 K, respectively. Therefore, the average Reynolds number of 5613.6, which corresponds to 2 m/s inlet velocity, was selected for further analysis.

Table 5.
Air inlet velocity values in terms of Reynolds number.
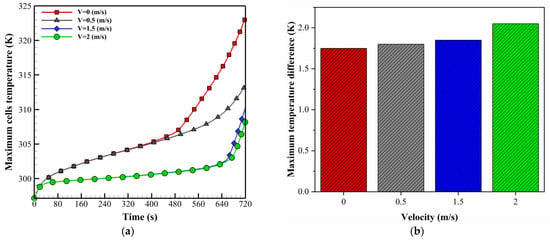
Figure 5.
(a) Influence of inlet velocity on Tmax. (b) Comparison of ΔTmax at different inlet velocities.
5.2. The Effect of PCM Thickness
Analysis of PCM at different thicknesses was performed to determine the optimal efficiency of the battery module. As a result, selecting the desired thickness could enhance the battery’s thermal performance. The battery pack had a composite paraffin/aluminum PCM with 4.49 W/m·K thermal conductivity and an initial thickness of 1 mm. To better demonstrate the thermal efficiency, the thickness of the PCM was adjusted to 1, 2, and 3 mm, while other parameters remained unchanged. The maximum temperature and temperature difference in the battery pack at the 5C discharge rate were compared (Figure 6). For a thickness of 1 mm, the maximum temperature and temperature difference were 319.70 K and 4.17 K, respectively. With an increase in thickness from 1 mm to 2 mm, the maximum values decreased to 315.69 K and 2.86 K, respectively. Following the heat transfer theory, increasing the thickness increases the thermal resistance. With the continued increase in thickness, the effects on the temperature uniformity and maximum temperature decreased to 0.2 and 308 K, respectively, from a thickness of 2 mm to 3 mm. Finally, when the PCM completely melts, its heat transfer capacity is reduced because of its low liquid thermal conductivity. Therefore, adopting the appropriate thickness can lead to a significant improvement in energy efficiency and cost savings.
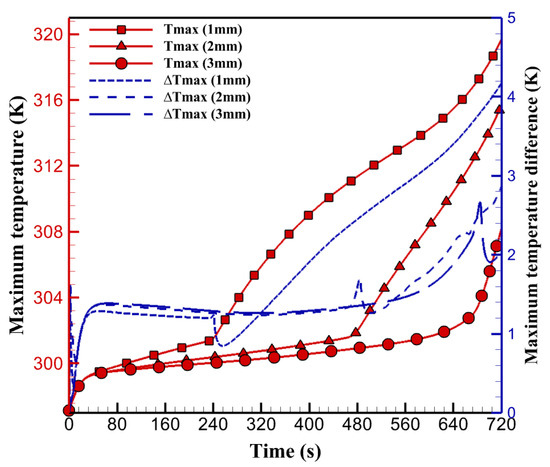
Figure 6.
Tmax and ΔTmax at different thicknesses of PCM.
5.3. Effect of Cell Distance
Temperature distributions are shown in Figure 7 for different cell spacings. It is obvious that the temperature decreases with an increase distance. Battery module thermal performance with a cell spacing of 21 mm is very poor, and the temperature quickly increases. The temperature growth with a cell spacing of 25 mm is slower than with 23 mm, indicating an improvement in the system’s thermal performance with an increase in cell distance. Regarding temperature uniformity, as shown in Figure 8, the cell with a 21 mm distance has the highest temperature rate and highest temperature difference at different cell distances. The cell with a 25 mm spacing has the lowest temperature difference, providing better temperature distribution than the other distances. The temperature difference between these two distances decreases by 2.04 °C when the spacing increases from 23 mm to 25 mm, which is attributed to the fast discharge rate.
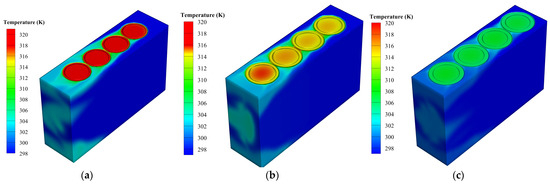
Figure 7.
Temperature distribution contour at various cell spacings: (a) 21 mm spacing, (b) 23 mm spacing, (c) 25 mm spacing.
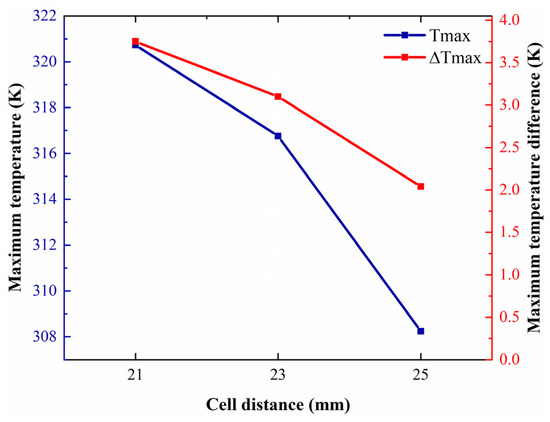
Figure 8.
Effect of cell spacing on Tmax and ΔTmax.
5.4. Impact of Metal Foam
Considering paraffin’s low thermal conductivity, the thermal management efficiency of the battery pack using paraffin and paraffin/aluminum composites under various conditions has been evaluated. Table 3 presents the thermophysical characteristics of the composite and paraffin. To discuss the effect of metallic foam, the average temperature of paraffin and paraffin/aluminum composites is compared as a first step. A moderate temperature profile of the battery pack is shown in Figure 9 under conditions that end at 720 s under the 5C discharge rate. At the end of the discharge process, observations indicate that the cooling achieved by the composite is less than that of paraffin. The average temperature for paraffin and composite was 312.70 K and 307.32 K, respectively. Regarding paraffin cooling, from 20 to 650 s, the temperature growth increases much faster than with the paraffin/aluminum composite, reaching 312.70 K at 720 s, exceeding the optimal operating temperature range. In addition, from 20 to 675 s, for cooling with the composite, the temperature growth is relatively smaller than that of pure paraffin. From 675 s to 720 s, the slope of temperature increase for the composite increases compared to paraffin. Compared to paraffin alone, the battery package temperature increases slower when using the paraffin/aluminum composite and is observed to discharge more slowly. The maximum battery pack temperature is 308.1 K and 313.42 K for paraffin/aluminum composite and pure paraffin coolants, respectively.
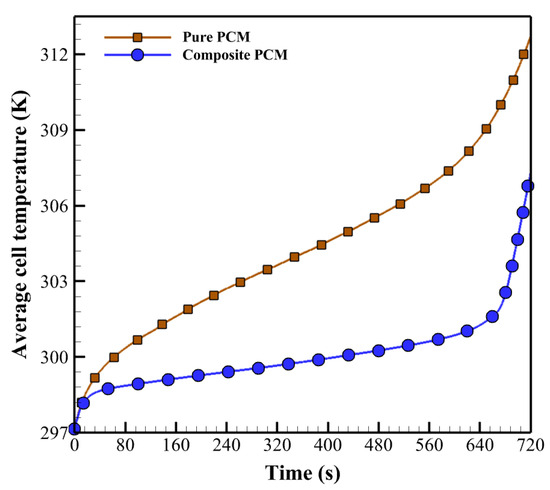
Figure 9.
Effect of metallic foam on the average battery temperature.
Figure 10 shows the temperature contours of paraffin and paraffin/aluminum composite, which have been cooled at the end of the discharge process. It is evident that the temperature contour of the paraffin/aluminum composite is more uniform than that of pure paraffin. This is because pure paraffin’s low thermal conductivity prevents the generated heat from being easily moved from the battery center to the paraffin, resulting in heat accumulation in the battery center. In contrast, the composite’s high thermal conductivity allows the heat produced by the battery to be transferred to the PCM and then to the environment. Furthermore, as seen in Figure 10 and Figure 11, the use of a paraffin/aluminum composite provides better temperature control than pure paraffin by presenting a more uniform distribution of liquid volume fraction. When cooling with paraffin alone, the PCM only melts near the cell due to the paraffin’s low thermal conductivity, which means it cannot transfer the heat generated by the cell. Conversely, due to its higher thermal conductivity, the composite paraffin melts the PCM farther from the cell. Although paraffin has a higher heat capacity than composite paraffin, its high thermal resistance, resulting from low thermal conductivity during the transfer process, causes its latent heat to be less effective.
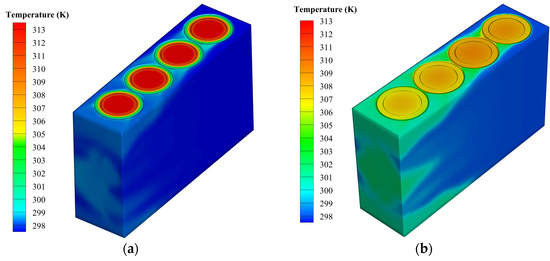
Figure 10.
Contour plot of cooled battery pack temperature distribution by the PCM: (a) Paraffin, (b) paraffin/aluminum composite.
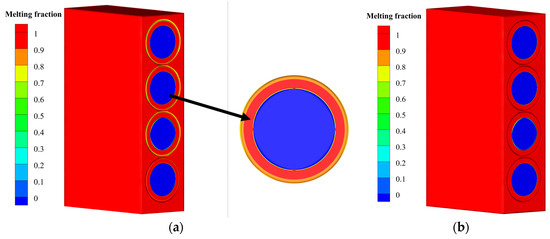
Figure 11.
Contour plot of the melting fraction of phase change material up to 700 s: (a) Paraffin, (b) paraffin/aluminum composite.
5.5. Effect of Air Inlet Temperature
Different ambient temperatures are examined to obtain the cooling performance of the proposed TMS when other simulation parameters are constant. Figure 12 shows changes in the maximum temperature and temperature uniformity. As can be seen, an increase in ambient temperature leads to a rise in temperature; in contrast, temperature uniformity exhibits the opposite behavior. At ambient temperatures of 10, 15, 20, 24.5, and 30 °C, the maximum temperature is 302.80, 303.30, 303.90, 308, and 315.7 K, respectively.
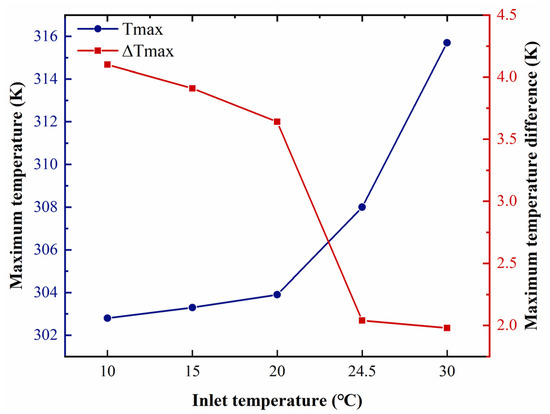
Figure 12.
Tmax and ΔTmax under different inlet temperatures.
6. Conclusions
This study proposed a BTMS for a cylindrical 18,650 battery module, including an air-cooling system and a PCM, to improve the thermal management controllability. Three different methods were investigated to improve thermal performance, including forced-air convection, PCM, and a combination of PCM (paraffin/aluminum composite) and air cooling. The combined cooling performance of air and paraffin at a discharge rate of 5C indicated that the combined strategy could effectively maintain and improve temperature uniformity within the optimal range compared to the other methods. Factors such as the influence of inlet air velocity, PCM thickness, cell distance, metallic foam, and cooling ambient temperature were discussed to investigate their effects on the battery’s thermal performance. The study’s results are summarized as follows:
- The paraffin/aluminum composite provides better thermal performance than paraffin alone for battery packs, since the high thermal conductivity of paraffin can transfer the heat produced by the batteries to the PCM and surrounding environment. As a result, the temperature distribution becomes more uniform, and the temperature decreases.
- With an increased air temperature, the temperature increases, followed by a decrease in the temperature difference. The proposed system can maintain the uniformity of temperature and the temperature in the optimal range for the battery under a cooling temperature of 10 to 24.5 °C.
- Increasing the thickness of paraffin can affect the efficiency of the BTMS. The proposed system is a paraffin/aluminum composite with a thickness of 3 mm. Increasing the thickness and combining aluminum foam with paraffin improves the capacity for temperature control in the thermal management system and maintains the cell temperature at 35 °C.
- Increasing the inlet air velocity improves temperature control, but the uniformity of the battery pack temperature worsens. Under a discharge rate of 5C and an environment temperature of 24.5 °C, with an inlet speed of 2 m/s, the proposed system can maintain the temperature difference and maximum temperature at 2.04 K and 308 K, respectively.
Author Contributions
Data curation, Investigation, Writing-original draft, S.S.; Conceptualization, Data curation, Investigation, Validation, Writing—review & editing, A.G.; Writing-original draft, Investigation, J.A.S.; Supervision, Methodology, Resources, Validation, Writing-review & editing, A.M.A.; Supervision, Writing—review & editing, M.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data available on request due to privacy.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| C: | Discharge rate (C) |
| H: | |
| : | |
| : | |
| : | |
| : | |
| : | |
| S: | Heat source |
| k: | Thermal conductivity (W/m·K) |
| : | Air thermal conductivity (W/m·K) |
| K: | Turbulent kinetic energy (m2/s2) |
| : | Turbulence production |
| : | Empirical parameters |
| : | Parameters of the turbulence model |
| R: | |
| : | Temperature coefficient of open-circuit voltage (V/K) |
| : | Open-circuit voltage (V) |
| : | Battery voltage (V) |
| I: | Cell charge/discharge current (A) |
| m: | Mass (kg) |
| : | Battery mass (kg) |
| L: | Characteristic length |
| : | Volume (m3) |
| : | Battery volume (m3) |
| : | Specific heat capacity (J/kg·K) |
| : | Battery specific heat capacity (J/kg·K) |
| : | Air specific heat capacity (J/kg·K) |
| T: | Temperature (K) |
| : | Air temperature (K) |
| : | Melting temperature (K) |
| : | Solidus temperature (K) |
| : | Maximum temperature (K) |
| : | Maximum temperature difference (K) |
| t: | Time (s) |
| V: | Velocity (m/s) |
| Re: | Reynolds number |
| Greek symbols | |
| : | Melting fraction of phase change material |
| : | |
| : | ) |
| : | ) |
| : | ) |
| : | Viscosity (kg·m/S) |
| : | Air viscosity (kg·m/S) |
| : | Turbulent viscosity coefficient |
| ε: | Turbulent dissipation rate |
| : | |
| Abbreviations | |
| BTMS: | Battery thermal management system |
| PCM: | Phase change materials |
| SOC: | State of charge |
| PPI: | Pores per inch |
| LIB: | Lithium-ion battery |
| TMS: | Thermal management system |
| CFD: | Computational fluid dynamics |
| UDF: | User-defined function |
References
- Han, X.; Ouyang, M.; Lu, L.; Li, J.; Zheng, Y.; Li, Z. A Comparative Study of Commercial Lithium-Ion Battery Cycle Life in Electrical Vehicle: Aging Mechanism Identification. J. Power Sources 2014, 251, 38–54. [Google Scholar] [CrossRef]
- Liu, X.; Li, K.; Wu, J.; He, Y.; Liu, X. An Extended Kalman Filter Based Data-Driven Method for State of Charge Estimation of Li-Ion Batteries. J. Energy Storage 2021, 40, 102655. [Google Scholar] [CrossRef]
- Lin, M.; Zeng, X.; Wu, J. State of Health Estimation of Lithium-Ion Battery Based on an Adaptive Tunable Hybrid Radial Basis Function Network. J. Power Source 2021, 504, 230063. [Google Scholar] [CrossRef]
- Ravdel, B.; Abraham, K.M.; Gitzendanner, R.; DiCarlo, J.; Lucht, B.; Campion, C. Thermal Stability of Lithium-Ion Battery Electrolytes. J. Power Source 2003, 119–121, 805–810. [Google Scholar] [CrossRef]
- Zhang, S.S.; Xu, K.; Jow, T.R. The Low Temperature Performance of Li-Ion Batteries. J. Power Source 2003, 115, 137–140. [Google Scholar] [CrossRef]
- Mehrenjani, J.R.; Gharehghani, A.; Nasrabadi, A.M.; Moghimi, M. Design, Modeling and Optimization of a Renewable-Based System for Power Generation and Hydrogen Production. Int. J. Hydrogen Energy 2022, 47, 14225–14242. [Google Scholar] [CrossRef]
- Ali, H.M. Thermal Management Systems for Batteries in Electric Vehicles: A Recent Review. Energy Rep. 2023, 9, 5545–5565. [Google Scholar] [CrossRef]
- Moradi, J.; Gharehghani, A.; Mirsalim, M. Numerical Comparison of Combustion Characteristics and Cost between Hydrogen, Oxygen and Their Combinations Addition on Natural Gas Fueled HCCI Engine. Energy Convers. Manag. 2020, 222, 113254. [Google Scholar] [CrossRef]
- Moradi, J.; Gharehghani, A.; Mirsalim, M. Numerical Investigation on the Effect of Oxygen in Combustion Characteristics and to Extend Low Load Operating Range of a Natural-Gas HCCI Engine. Appl. Energy 2020, 276, 115516. [Google Scholar] [CrossRef]
- Jiang, Z.Y.; Li, H.B.; Qu, Z.G.; Zhang, J.F. Recent Progress in Lithium-Ion Battery Thermal Management for a Wide Range of Temperature and Abuse Conditions. Int. J. Hydrogen Energy 2022, 47, 9428–9459. [Google Scholar] [CrossRef]
- Wu, M.S.; Liu, K.H.; Wang, Y.Y.; Wan, C.C. Heat Dissipation Design for Lithium-Ion Batteries. J. Power Source 2002, 109, 160–166. [Google Scholar] [CrossRef]
- Wang, T.; Tseng, K.J.; Zhao, J. Development of Efficient Air-Cooling Strategies for Lithium-Ion Battery Module Based on Empirical Heat Source Model. Appl. Therm. Eng. 2015, 90, 521–529. [Google Scholar] [CrossRef]
- Chen, K.; Chen, Y.; Li, Z.; Yuan, F.; Wang, S. Design of the Cell Spacings of Battery Pack in Parallel Air-Cooled Battery Thermal Management System. Int. J. Heat Mass Transf. 2018, 127, 393–401. [Google Scholar] [CrossRef]
- Fan, Y.; Bao, Y.; Ling, C.; Chu, Y.; Tan, X.; Yang, S. Experimental Study on the Thermal Management Performance of Air Cooling for High Energy Density Cylindrical Lithium-Ion Batteries. Appl. Therm. Eng. 2019, 155, 96–109. [Google Scholar] [CrossRef]
- Kirad, K.; Chaudhari, M. Design of Cell Spacing in Lithium-Ion Battery Module for Improvement in Cooling Performance of the Battery Thermal Management System. J. Power Source 2021, 481, 229016. [Google Scholar] [CrossRef]
- Abdulrasool Hasan, H.; Togun, H.; Abed, A.M.; Mohammed, H.I.; Biswas, N. A Novel Air-Cooled Li-Ion Battery (LIB) Array Thermal Management System–a Numerical Analysis. Int. J. Therm. Sci. 2023, 190, 108327. [Google Scholar] [CrossRef]
- Rabiei, M.; Gharehghani, A.; Andwari, A.M. Enhancement of Battery Thermal Management System Using a Novel Structure of Hybrid Liquid Cold Plate. Appl. Therm. Eng. 2023, 232, 121051. [Google Scholar] [CrossRef]
- Liu, Z.; Gao, Y.; Chen, H.; Wang, C.; Sun, Y.; Yan, P. Thermal Performance of Lithium Titanate Oxide Anode Based Battery Module under High Discharge Rates. World Electr. Veh. J. 2021, 12, 158. [Google Scholar] [CrossRef]
- Sha, Y.; Zhang, Z.; Chen, Y.; Lin, Q.; Zhong, Y.; Xu, X.; Shao, Z. One-Pot Combustion Synthesis of Li3VO4-Li4Ti5O12 Nanocomposite as Anode Material of Lithium-Ion Batteries with Improved Performance. Electrochim. Acta 2016, 222, 587–595. [Google Scholar] [CrossRef]
- Kshetrimayum, K.S.; Yoon, Y.G.; Gye, H.R.; Lee, C.J. Preventing Heat Propagation and Thermal Runaway in Electric Vehicle Battery Modules Using Integrated PCM and Micro-Channel Plate Cooling System. Appl. Therm. Eng. 2019, 159, 113797. [Google Scholar] [CrossRef]
- Kizilel, R.; Lateef, A.; Sabbah, R.; Farid, M.M.; Selman, J.R.; Al-Hallaj, S. Passive Control of Temperature Excursion and Uniformity in High-Energy Li-Ion Battery Packs at High Current and Ambient Temperature. J. Power Source 2008, 183, 370–375. [Google Scholar] [CrossRef]
- Kizilel, R.; Sabbah, R.; Selman, J.R.; Al-Hallaj, S. An Alternative Cooling System to Enhance the Safety of Li-Ion Battery Packs. J. Power Source 2009, 194, 1105–1112. [Google Scholar] [CrossRef]
- Ling, Z.; Wang, F.; Fang, X.; Gao, X.; Zhang, Z. A Hybrid Thermal Management System for Lithium-Ion Batteries Combining Phase Change Materials with Forced-Air Cooling. Appl. Energy 2015, 148, 403–409. [Google Scholar] [CrossRef]
- Verma, A.; Shashidhara, S.; Rakshit, D. A Comparative Study on Battery Thermal Management Using Phase Change Material (PCM). Therm. Sci. Eng. Prog. 2019, 11, 74–83. [Google Scholar] [CrossRef]
- Zhang, W.; Liang, Z.; Ling, G.; Huang, L. Influence of Phase Change Material Dosage on the Heat Dissipation Performance of the Battery Thermal Management System. J. Energy Storage 2021, 41, 102849. [Google Scholar] [CrossRef]
- Iasiello, M.; Mameli, M.; Filippeschi, S.; Bianco, N. Metal Foam/PCM Melting Evolution Analysis: Orientation and Morphology Effects. Appl. Therm. Eng. 2021, 187, 116572. [Google Scholar] [CrossRef]
- Javani, N.; Dincer, I.; Naterer, G.F.; Yilbas, B.S. Heat Transfer and Thermal Management with PCMs in a Li-Ion Battery Cell for Electric Vehicles. Int. J. Heat Mass Transf. 2014, 72, 690–703. [Google Scholar] [CrossRef]
- Lamrani, B.; Lebrouhi, B.E.; Khattari, Y.; Kousksou, T. A Simplified Thermal Model for a Lithium-Ion Battery Pack with Phase Change Material Thermal Management System. J. Energy Storage 2021, 44, 103377. [Google Scholar] [CrossRef]
- Bais, A.R.; Subhedhar, D.G.; Joshi, N.C.; Panchal, S. Numerical Investigation on Thermal Management System for Lithium Ion Battery Using Phase Change Material. Mater. Today Proc. 2022, 66, 1726–1733. [Google Scholar] [CrossRef]
- Karimi, D.; Behi, H.; Van Mierlo, J.; Berecibar, M. Novel Hybrid Thermal Management System for High-Power Lithium-Ion Module for Electric Vehicles: Fast Charging Applications. World Electr. Veh. J. 2022, 13, 86. [Google Scholar] [CrossRef]
- Mehrabi-Kermani, M.; Houshfar, E.; Ashjaee, M. A Novel Hybrid Thermal Management for Li-Ion Batteries Using Phase Change Materials Embedded in Copper Foams Combined with Forced-Air Convection. Int. J. Therm. Sci. 2019, 141, 47–61. [Google Scholar] [CrossRef]
- Xie, Y.; Tang, J.; Shi, S.; Xing, Y.; Wu, H.; Hu, Z.; Wen, D. Experimental and Numerical Investigation on Integrated Thermal Management for Lithium-Ion Battery Pack with Composite Phase Change Materials. Energy Convers. Manag. 2017, 154, 562–575. [Google Scholar] [CrossRef]
- Qin, P.; Liao, M.; Zhang, D.; Liu, Y.; Sun, J.; Wang, Q. Experimental and Numerical Study on a Novel Hybrid Battery Thermal Management System Integrated Forced-Air Convection and Phase Change Material. Energy Convers. Manag. 2019, 195, 1371–1381. [Google Scholar] [CrossRef]
- Yang, R.; Wang, M.; Xi, H. Thermal Investigation and Forced Air-Cooling Strategy of Battery Thermal Management System Considering Temperature Non-Uniformity of Battery Pack. Appl. Therm. Eng. 2023, 219, 119566. [Google Scholar] [CrossRef]
- Cicconi, P.; Kumar, P.; Varshney, P. A Support Approach for the Modular Design of Li-Ion Batteries: A Test Case with PCM. J. Energy Storage 2020, 31, 101684. [Google Scholar] [CrossRef]
- EIIdi, M.M.M.; Karkri, M.; Andwari, M.; Vincent, S. Hybrid Cooling Based Battery Thermal Management Using Composite Phase Change Materials and Forced Convection. J. Energy Storage 2021, 41, 102946. [Google Scholar] [CrossRef]
- Gharehghani, A.; Kakoee, A.; Andwari, A.M.; Megaritis, T.; Pesyridis, A. Numerical investigation of an RCCI engine fueled with natural gas/dimethyl-ether in various injection strategies. Energies 2021, 14, 1638. [Google Scholar] [CrossRef]
- Shmueli, H.; Ziskind, G.; Letan, R. Melting in a Vertical Cylindrical Tube: Numerical Investigation and Comparison with Experiments. Int. J. Heat Mass Transf. 2010, 53, 4082–4091. [Google Scholar] [CrossRef]
- Severino, B.; Gana, F.; Palma-Behnke, R.; Estévez, P.A.; Calderón-Muñoz, W.R.; Orchard, M.E.; Reyes, J.; Cortés, M. Multi-Objective Optimal Design of Lithium-Ion Battery Packs Based on Evolutionary Algorithms. J. Power Source 2014, 267, 288–299. [Google Scholar] [CrossRef]
- Lai, Y.; Wu, W.; Chen, K.; Wang, S.; Xin, C. A Compact and Lightweight Liquid-Cooled Thermal Management Solution for Cylindrical Lithium-Ion Power Battery Pack. Int. J. Heat Mass Transf. 2019, 144, 118581. [Google Scholar] [CrossRef]
- Zhang, B.; Ren, G. Li-Ion Battery State of Charge Prediction for Electric Vehicles Based on Improved Regularized Extreme Learning Machine. World Electr. Veh. J. 2023, 14, 202. [Google Scholar] [CrossRef]
- Li, W.; Xiao, M.; Peng, X.; Garg, A.; Gao, L. A Surrogate Thermal Modeling and Parametric Optimization of Battery Pack with Air Cooling for EVs. Appl. Therm. Eng. 2019, 147, 90–100. [Google Scholar] [CrossRef]
- Sahin, R.C.; Gocmen, S.; Cetkin, E. Thermal Management System for Air-Cooled Battery Packs with Flow-Disturbing Structures. J. Power Source 2022, 551, 232214. [Google Scholar] [CrossRef]
- Jefford, C.W.; Kabengele, T.; Kovacs, J.; Burger, U. Additions of fluorocarbenes to norbornadiene by linear cheletropic reaction. Tetrahedron Lett. 1974, 3, 257–260. [Google Scholar] [CrossRef]
- Jones, B.J.; Sun, D.; Krishnan, S.; Garimella, S.V. Experimental and Numerical Study of Melting in a Cylinder. Int. J. Heat Mass Transf. 2006, 49, 2724–2738. [Google Scholar] [CrossRef]
- Fadl, M.; Eames, P. A Numerical Investigation into the Heat Transfer and Melting Process of Lauric Acid in a Rectangular Enclosure with Three Values of Wall Heat Flu. Energy Procedia 2019, 158, 4502–4509. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).