Li-Ion Battery State of Charge Prediction for Electric Vehicles Based on Improved Regularized Extreme Learning Machine

Abstract

Battery state of charge prediction is one of the most essential state quantities of a battery management system. It is a prerequisite for the operation of a battery management system, but it becomes difficult to make an exact prediction of its state due to its characteristics, which cannot be measured directly. For the exact assessment of the Li-ion battery state of charge, the research proposes an extreme learning machine algorithm based on the alternating factor multiplier method with improved regularization. This method constructs a suitable online Li-ion battery state of charge prediction model using the alternating factor multiplier method in gradient form. The experiment demonstrates that the algorithm in the study has a reduction in the number of nodes in the implicit layer relative to the traditional extreme learning machine algorithm. The error fluctuations of the algorithm under two different excitation functions range from [−0.005, 0.005] and [0.082, 0.265]; The root mean square error of the data set in which the algorithm performs well is 1.9516 and 0.6157, respectively. The real simulation scenario created the predicted values of the state of charge in the realistic simulation scenario that fit the real value curve by 99.99%. The average and maximum errors of the proposed state of charge prediction model are the smallest compared to the long and short-term memory networks and gated cyclic units, 0.58% and 2.97%, respectively. The experiment demonstrates that the presented algorithm can reduce the computational burden while guaranteeing the state of charge model prediction.

1. Introduction

Automotive power comes from automotive batteries, which can be divided into traditional petroleum vehicles and new energy vehicles based on their different characteristics. Lithium batteries have a higher energy density, a lighter weight, and a longer operating life compared to conventional batteries, making them often used as batteries for new energy-efficient vehicles. With the widespread use of new energy electric vehicles, the capacity, safety, health status, and range of electric vehicle batteries have attracted widespread attention. An accurate state of charge prediction can effectively avoid overcharging or discharging, ensuring that the battery will not suffer irreversible damage. However, because the state of charge of lithium batteries cannot be directly measured, precise measuring instruments cannot be used to determine the value. How to accurately estimate the state of charge of lithium batteries has become a focus of research. Currently, the commonly used methods for estimating the state of charge are mainly split into three categories: traditional methods, model-based methods, and intelligent algorithms [1,2,3]. Intelligent algorithms are further split into three categories: neural networks, pattern logic control, and machine learning. Extreme learning machines are a kind of machine learning method. Because of its simple structure, fast running speed, and lack of need to adjust its advantages, it is widely used in various fields, and can simplify the setting of learning parameters to improve learning efficiency. Because the state of charge of a lithium battery cannot be directly predicted, the research is based on an extreme learning machine that directly generates model parameters in the prediction process of a lithium battery to estimate the state of charge. The entire process requires finding the optimal number of hidden layer nodes to achieve high accuracy. The extreme learning process has the problem of insufficient or overtraining training data in the practical operation process, as well as the related computational complexity and operation involved. Based on this, a regularization extreme learning machine learning algorithm based on the alternating direction multiplier methodis proposed. By regularization, the corresponding parameters are limited, and additional information is introduced to prevent the data from overfitting. The research is divided into five parts. The first part is the introduction; The second part is to discuss the related work in recent years; The third part is to build a sparse supervised learning neural network model by combining the regularization algorithm with the recursive alternating direction multiplier method; The fourth part evaluates the proposed algorithm model and the fifth part draws research conclusions.

2. Related Work

The use of neural networks to estimate the state of charge of batteries has achieved excellent performance. Li et al., proposed a new multi-step prediction method for battery SOC (State of Charge) systems based on gated recurrent neural networks to more accurately test the battery state of charge of electric vehicles and verified the effectiveness of their proposed method through experiments [4]. Oyewole et al., proposed a controlled transfer learning network for SOC prediction in the initial stages of degradation to solve the problem of deep learning models ignoring the dynamic changes of batteries, and experimentally proved the effectiveness of the algorithm [5]. Cheng et al., proposed a ML (Machine Learning)-based method for battery health evaluation by fusing relevant models with a personalized prediction scheme and experimentally verifying the performance of the algorithm [6]. Tian et al., proposed an Extreme Learning Machine (ETLM) method with special embedding and clustering for solving the difficult data aggregation in non-specific class domains, implementing feature learning and clustering in the same dataset [7]. Zhou et al., suggested an ETLM method based on ML for addressing the singularity and overfitting issues exhibited when the training samples’ quantity was below the hidden layer neurons (LN). For solving the singularity and overfitting issues when the training samples were below the implicit LN, Zhou et al., proposed a special incremental ETLM algorithm in view of stochastic reductions and verified the effectiveness of their algorithm through comparative experiments [8]. Guo et al., proposed an ETLM with elastic regularization for finding the minimum of the system optimization function and demonstrated experimentally that the algorithm required less training time and had higher recognition accuracy than a multilayer perceptron [9]. Chernozhukov et al., suggested an algorithm that used regularization techniques to keep all variables constant, reducing the possibility of overfitting a particular dataset, and verified the soundness of their algorithm experimentally [10]. Yang et al., proposed an ETLM algorithm with a smoothing regularizer for improving the compactness of the network and confirmed experimentally that the proposed algorithm possessed better functions in prediction and network sparsity [11]. Fan et al., suggested a new efficient limit learning ML algorithm with smooth L-0 regularization and experimentally demonstrated that the proposed algorithm had fewer hidden nodes and better generalization performance [12]. Zhang et al., proposed a directional algorithm for convex nonlinear second-order conic programming. The parallel inexact alternating direction method was used for addressing the multi-block separable CQSOCP (Command Query Second Order Cone Programming)subproblem, and the effectiveness of the proposed algorithm was demonstrated experimentally [13]. Silva et al., proposed a GOR-ETLM (Generalized Outlier Robustness-Extreme Learning Machine)algorithm and extended it for dealing with multi-objective regression issues using the error l (2, 1) norm and elastic net theory to produce a sparser network [14]. Zheng et al., proposed a new idea from the error analysis of SOC prediction in measurements, models, algorithms, and state parameters [15]. Niu et al., provided a new approach for overcoming the problem of convergence to local minima in traditional learning machines, and the proposed algorithm was tested through experiments [16]. Yan et al., proposed an algorithm combining images by Gaussian derivative models with ETLM for classification applications, and the effectiveness of the algorithm was confirmed based on experimental results [17]. Zhou et al., proposed a special particle swarm optimization-kernel ETLM method for landslide prediction, and the experiment indicated that the proposed algorithm outperformed other similar algorithms [18]. Wang et al., proposed a hybrid generalized maximum entropy criterion to replace the MSE algorithm in ETLM, considering the problem of non-noise interference, and established a novel robust ETLM model for improving the SOC prediction. It was experimentally demonstrated that the proposed algorithmic model could reach better predictions under various evaluation indexes relative to the traditional ETLM [19].

In conclusion, when estimating the state of charge of the battery, the extreme learning machine has good performance and is easy to operate. However, the traditional Extreme learning machine still has some shortcomings when applied to some specific fields. The SOC algorithm proposed by Oyewole et al., has effectiveness in charging prediction performance, but it still has overfitting issues [5]. The GOR-ETLM model proposed by Silva et al., has advantages over other ETLM techniques in the statistical analysis of outlier pollution data, but there is no improvement in other aspects of performance [14]. The feasible direction algorithm proposed by Zhang et al., for Barzilai and Borwein regularization can sparse the network structure and have better generalization performance [13]. However, the network structure of this algorithm inevitably increases the model size and testing time. The algorithm studied in this article utilizes the improvement work of extreme learning machines in predicting charge states and analyzes the performance of sparse neural networks and regularization in extreme learning machines. Finally, the regularization algorithm is combined with sparse neural networks to reduce the computational burden to a certain extent while ensuring the accuracy of the state of charge model estimation. In order to better adapt to the online prediction of the state of charge of lithium batteries, an improved regularized extreme learning machine algorithm is proposed to make up for the blank in the online prediction of the state of charge of lithium batteries.

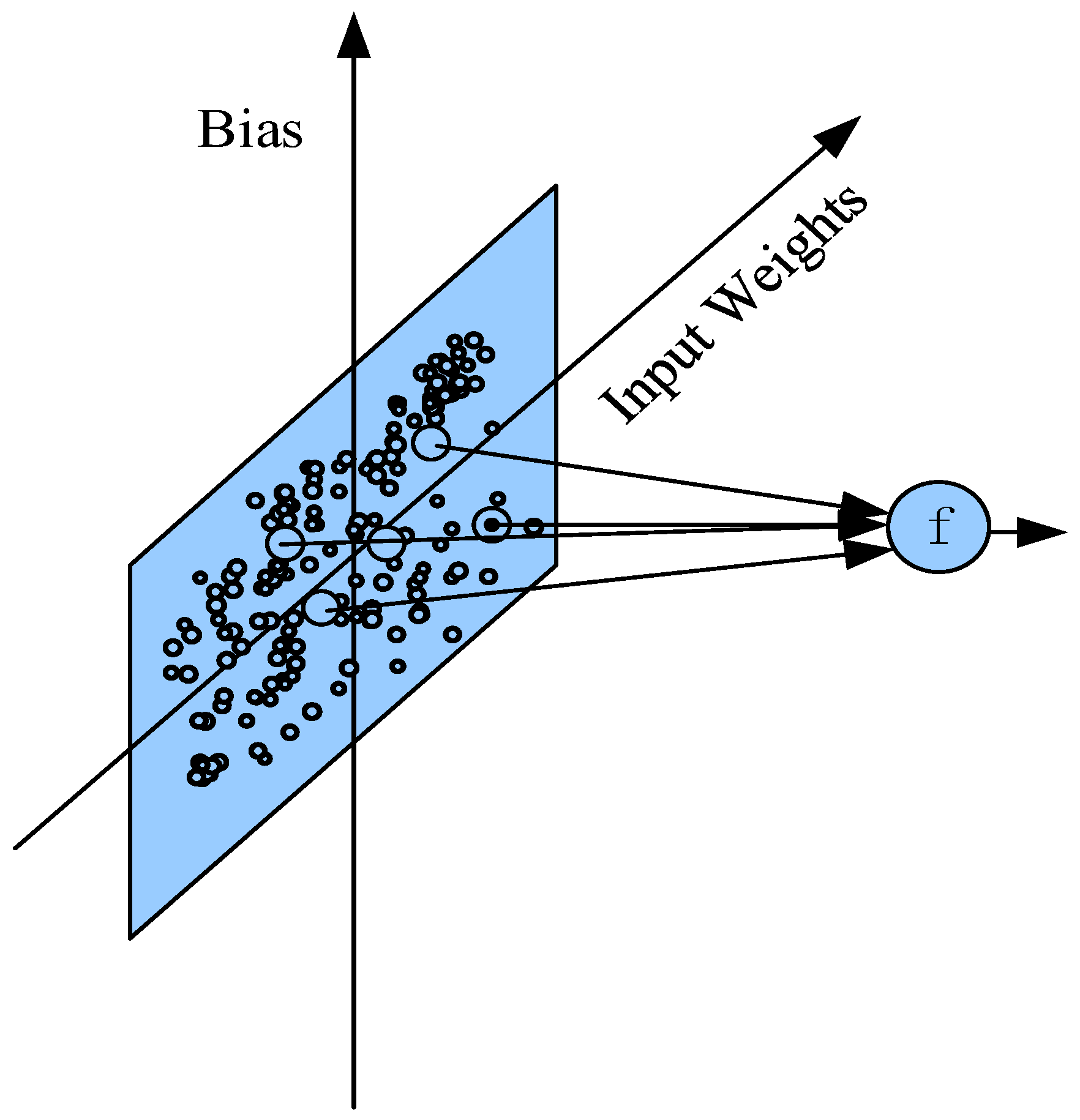
3. Battery State of Charge Prediction Based on Extreme Learning Machine Algorithm

This study focuses on constructing an improved regularized extreme learning ML algorithm for battery SOC prediction. In this method, a sparse supervised neural network is constructed to estimate the state of charge (LBSC) of lithium-ion batteries using the recursive form of the alternating factor multiplier method.

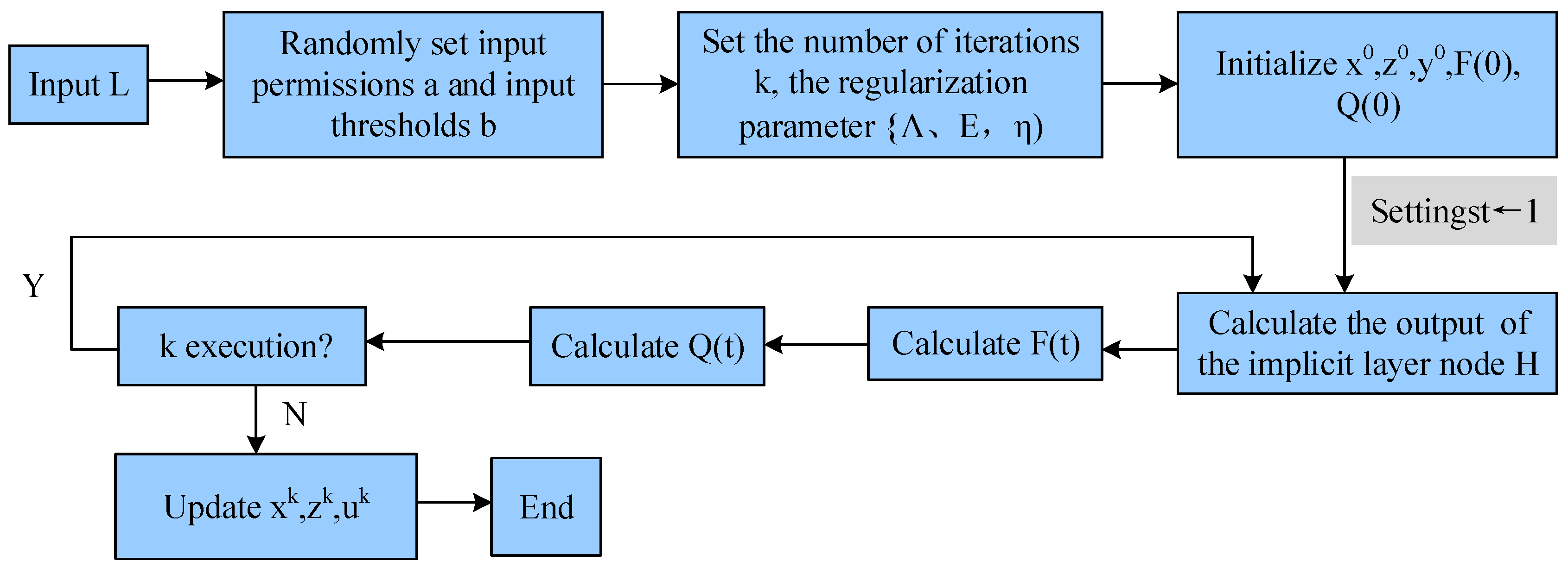
3.1. Learning Algorithm for Regularized Extreme Learning Machine Based on Alternating Direction Multiplier Method

In 2004, Huang et al., presented the ETLM method at the IEEE International Conference on Interaction. ETLM improves the learning efficiency by improving the backpropagation algorithm and simplifying the learning parameter settings [19]. ETLM is a class of feedforward neural networks based on Feedforward Neuron Networks, which is applicable to both supervised and unsupervised learning issues. The network structure of the ETLM is shown in Figure 1.

ETLM is utilized in various fields because of its simple structure and fast operation without the need for tuning. However, in practice, there is a problem of insufficient training data or overtraining. The regularization method introduces additional information in the original to prevent overfitting of the data and improve the generalization of the model [20]. This leads to the introduction of a regularized extreme learning machine approach, which reduces the risk of structural generalization of the model by restricting certain parameters through regularization. A common regularization method is usually to set the parameter $l_1,l_2$. In the regression model, the introduced parameter $l_1$ is called Lasso regression, which belongs to the non-integrable convex function (CF). The expression is showcased in Equation (1).

$$l_1=J_0+\lambda \left|\right|w|{|}_1$$

(1)

In Equation (1), $J_0$ serves as the root mean square error (RMSE) of the original loss function; $\lambda$ serves as the regularization penalty factor; $w$ is the model parameter. Parameter $l_2$ regularization, also known as Ridge Regression (RR), is a continuously derivable CF that prevents overfitting and decreases the computational burden by constraining the parameter parametrization, thus enhancing the generalization ability. The functional expression of the parameter $l_2$ is shown in Equation (2).

$$l_2=J_0+\lambda \left|\right|w|{|}_2$$

(2)

Alternate Direction Method of Multipliers (ADMM) is a computational framework for solving convex optimization with separability, which is a combination of the pairwise decomposition method and the generalized Lagrange multiplier method. It has good decomposition, good convergence, and a fast-processing speed. Distributed convex optimization problems, mainly applied in the case of large solution space sizes, can be solved in blocks, and the absolute accuracy of the solution is required to be reasonable.

In the pairwise decomposition method, the expression of the Lagrangian function (Lagrangian; L) that optimizes is demonstrated in Equation (3).

$$L(x,y)=f(x)+y^T(Ax-b)$$

(3)

In Equation (3), $y$ denotes the Lagrange multiplier; $T$ is the transpose matrix of the matrix $m\ast n$; $x$ is the variable and $x\in R^n$; $R$ serves as the set of real numbers; $A$ is the matrix and $A\in R^{n\ast m}$. The pairwise form of $L(x,y)$ is shown in Equation (4).

$$g(y)=\underset{x}{\inf }L(x,y)=-f*(-A^{T}y)-b^{T}y$$

(4)

In Equation (4), $y\in R^m$ serves as the parameter of the dual problem (DP); $f*()$ serves as the conjugate CF of $f()$. If the strong duality holds, the optimal solution (OS) of the original function and the OS function of the dual function are shown in Equation (5).

$$x*=\underset{x}{\arg }\min L(x,y*)$$

(5)

Assuming that $g(y)$ is continuously differentiable, then $\nabla g(y)=A\tilde{x}-b$. The gradient ascent method is used for solving the pairwise issue, and the pairwise ascent algorithm is iteratively updated as shown in Equation (6).

$$\left\{\begin{array}{l}{x}^{k+1}=\underset{x}{\arg }\min L(x,y^k)\\ y^{k+1}=y^k+{\alpha }^k(A{x}^{k+1}-b)\end{array}\right.$$

(6)

In Equation (6), ${\alpha }^k$ is the iteration step, and ${\alpha }^k$ > 0; $k$ is the iterations’ quantity. Reaching the OS requires ensuring the initial conditions and achieving pairwise feasibility. The related functional expression is shown in Equation (7).

$$Ax*-b=0,\nabla f(x*)+A^{T}y*=0$$

(7)

Since the number of implied nodes in ETLM needs to be measured repeatedly to be obtained, and the requirement for the number of implied nodes is stricter, too much or too little number is not conducive to the accuracy of the ETLM model. To address the issue that the number of ETLM implied nodes is difficult to determine, the study proposes an alternating direction method of multipliers based ETLM (ADMM-regularized ETLM, ADMM-ETLM), which is in view of the alternating direction multipliers method. The generalization of the network is enhanced by diminishing the parametric quantity of output parameters, which in turn produces a sparse model with stable performance. The functional expression of ADMM-ETLM is shown in Equation (8).

$$\underset{\beta }{\min }\frac{1}{2}||H\beta -h|{|}_2^2+\lambda ||\beta |{|}_1$$

(8)

In Equation (8), $H$ serves as the output matrix of the implied node; $\beta$ serves as the output authority; $\lambda$ serves as the regularization penalty factor of $l_1$. Generally, the value of $\lambda$ is small because the larger the $\lambda$ is, the stronger the regularization sparsity of $l_1$. For the desired output, the OS expression for the output authority is shown in Equation (9).

$$\stackrel{\wedge }{\beta }=\arg \underset{\beta }{\min }\{\frac{1}{2}||H\beta -h|{|}_2^2+\lambda ||\beta |{|}_1\}$$

(9)

Using AMDD to solve the constructed (9) regularized integrability problem, the obtained augmented Lagrangian function is shown in Equation (10).

$$l_{\epsilon }(x,z,u)=f(x)+g(z)+u^T(x-u)+\frac{\epsilon }{2}||x-z|{|}_2^2$$

(10)

In Equation (10), $u$ is a proportional pairwise function; $\epsilon$ is a penalty factor and $\epsilon$ > 0. $x$ and $z$ are the decomposition terms of the output authority $\beta$, which satisfies $x+z=\beta$, $f(x)$ and $g(z)$ are CF. The expression of the function to solve the convex rule using ADMM is shown in Equation (11).

$$\left\{\begin{array}{l}{x}^{k+1}=\arg \underset{x}{\min }{l}_{\epsilon }(x,z^k,u^k)\\ z^{k+1}=\arg \underset{z}{\min }{l}_{\epsilon }(x^{k+1},z,u^k)\\ u^{k+1}=u^k+\epsilon (x^{k+1}-z^{k+1})\end{array}\right.$$

(11)

In Equation (11), $k$ serves as the iterations’ quantity, and the values of $z^k$ and $x^k$ gradually converge with the increase of $k$. The above Equation (11) can solve the OS of $z$ and $x$; While the iterative update of $u$ ensures the further convergence of the OS of $z$ and $x$. The ADMM proximity algorithm is used to solve the $\arg \min L_{\epsilon }(.)$ function to obtain the corresponding $x,z,u$ function, as shown in Equation (12).

$$\left\{\begin{array}{l}{x}^{k+1}=pro{x}_{{}^{\eta f}}(z^k-u^k)\\ z^{k+1}=pro{x}_{{}^{\lambda g}}(x^{k+1}+u^k)\\ u^{k+1}=u^k+x^{k+1}-z^{k+1}\end{array}\right.$$

(12)

3.2. Recursive ADMM-Based Sparse Simple Learning Model for State of Charge Prediction

The SOC of lithium batteries indicates a state after some time of use or after a long time of remaining capacity to its fully charged state, commonly used as a percentage SOC in the range of [0, 1]. As SOC = 0, it depicts the battery as completely discharged; As SOC = 1, it depicts the battery as fully charged. Since the cycle life of lithium batteries is affected by various factors such as positive and negative electrode materials, battery design, and battery production, the model established by conventional experiments cannot be used as a general battery SOC prediction model. The current state of charge assessment models built by ML algorithms is generally based on offline mode, and then there is a possibility that real-time parameter changes cannot be accurately captured, thus reducing the prediction model’s precision. Based on this, the study considers the construction of a sparse supervised model for online real-time data processing to solve the above problem. Based on the regularized extreme learning machine method constructed in the previous paper, combined with the ADMM algorithm transformed into recursive form, the convergence of regularization is optimized and the computational complexity of input data in the algorithm model is reduced, so as to better serve the online SOC prediction of lithium batteries. FNN (Feedforward Neuron Network) embodies a brief structure and is extensively utilized, which can fit any continuous function with arbitrary accuracy and a square productable function. From the perspective of the system point, the feedforward network is a static nonlinear mapping. The complex nonlinear processing capability can be obtained through the relevant mapping. From the perspective of the computational point, it shortens rich dynamical behavior. Most feedforward networks’ classification and recognition generally exceed those of feedback networks. Since ETLM is an improvement of FNN and its back propagation algorithm, it can be regarded as a special kind of FNN. Figure 2 indicates the sparse role of regularization in FNN.

The expression of the OS of the objective function after adding regularization to the forward neural network is shown in Equation (13).

$$\underset{\beta }{\stackrel{\wedge }{\beta }=\arg \min }\{\frac{1}{2}||H\ast \beta -h|{|}_2^2+\lambda ||\beta |{|}_1\}$$

(13)

The output of the implicit layer node $H$ is adjusted, and the corresponding function expression is shown in Equation (14).

$${\left(\begin{array}{ccc}G(a_1,b_1,x_1)& \cdots & G(a_1,b_1,x_1)\\ ⋮& \cdots & ⋮\\ G(a_1,b_1,x_1)& \cdots & G(a_1,b_1,x_1)\end{array}\right)}_{N\ast L}$$

(14)

In Equation (14), $x$ serves as the input data; $a$ is the input authority and $a\in (-1,1)$; $b$ is the input threshold; and $b\in (0,1)$; $G(x)$ serves as the excitation function. As the excitation function is Gaussian, the function expression is shown in Equation (15).

$$G(a,b,x)=\exp \{-b||x-a|{|}_2^2\}$$

(15)

When the excitation function is Sigmoid, the expression of the function is shown in Equation (16).

$$G(a,b,x)=\frac{1}{1+\exp \{-a^{T}x+b\}}$$

(16)

The relevant expression for the objective function is Equation (17).

$$L_{\epsilon }(x,z,u)=f(x)+g(z)+u^T(x-z)+\frac{\epsilon }{2}||x-z|{|}^2$$

(17)

In Equation (17), $u$ is the pairwise variable for scaling. The rest of the parameters have the same meaning as above.

The corresponding OS of $x,z,u$ is obtained and expressed using Equation (18).

$$\left\{\begin{array}{l}{x}^{k+1}=\underset{x}{\arg \min }{L}_{\epsilon }(x,z^k,u^k)\\ z^{k+1}=\underset{z}{\arg \min }{L}_{\epsilon }(x^{k+1},z,u^k)\\ u^{k+1}=u^k+\epsilon (x^{k+1}-z^{k+1})\end{array}\right.$$

(18)

Using the $pro{x}_{{}^{\eta f}}(x)$ function for solving the $\arg \min L_{\epsilon }(x)$ function, the function expression of $pro{x}_{{}^{\eta f}}(x)$ is obtained as shown in Equation (19).

$$pro{x}_{{}^{\eta f}}(x)=\frac{1}{(H^{T}H+\epsilon I)}(H^{T}Y+\epsilon x^k)$$

(19)

Similarly, for the results obtained $pro{x}_{{}^{\lambda g}}(z)$ as shown in Equation (20).

$${(pro{x}_{{}^{\lambda g}}(z))}_i=\left\{\begin{array}{l}{z}_i-\lambda ,z_i\ge \lambda \\ 0,\left|z_i\right|\le \lambda \\ z_i+\lambda ,z_i\le -\lambda \end{array}\right.$$

(20)

The sparse model and the sparse output weights obtained by the improved regularized learning machine method can be used to build a certain SOC model. But the corresponding algorithm complexity is set to $O(n^3)$ due to the existence of matrix inversion in the iterative formula of the input data $x$. The algorithm complexity can be reduced to $O(n^2)$ when solving the regularization problem using the recursive form of ADMM, thus satisfying the need for online learning of the evaluation model. The purpose of learning only the newly added training data without relearning all the training data is achieved. The flow of the involved neural network sparse supervised learning algorithm is shown in Figure 3.

Figure 3 showcases the algorithm, which first needs to input the quantity of nodes in the hidden layer (HL), set $t\leftarrow 1$ by initializing the $x^0,z^0,u^0$ parameter, and cycle through the corresponding $Q(t),F(t)$ values. Set the regularization parameters of the model to 10⁻⁹, wherein the number of hidden nodes L is set to 50; The value of iteration number k is 1000; F(t) is the new hidden layer output of input data under the number of t; and Q(t) is the Convex function solution function under the Identity matrix I. The functional expressions for F(t) and Q(t) are given in Equation (21).

$$\left\{\begin{array}{l}F(t)=H_t^T{Y}_t\\ Q(t)=(H_t^T{H}_t+\epsilon I)-1\end{array}\right.$$

(21)

In Equation (21), $H$ is the output of the hidden node; $Y$ is the expected value, and the range of expected values set in the study is [0.4, 1.4].

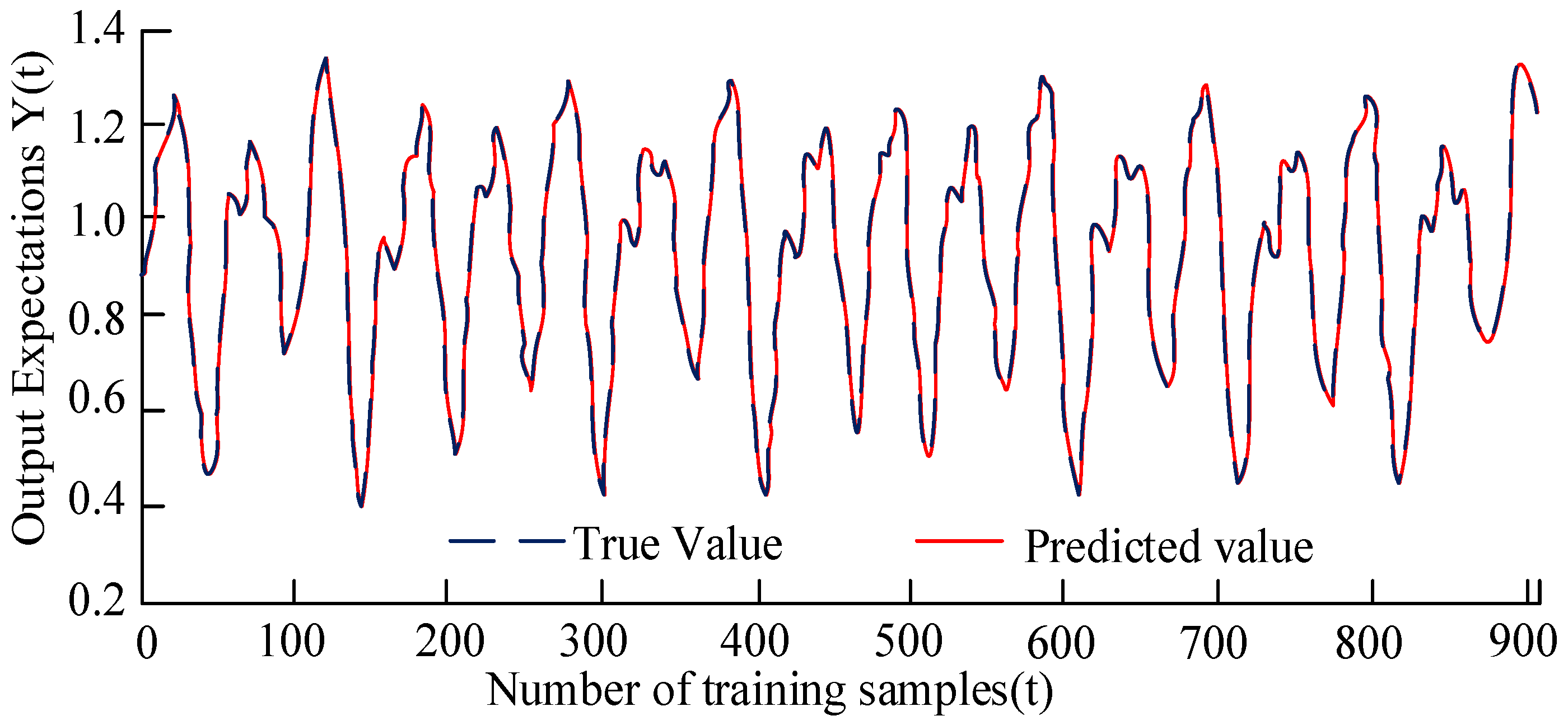
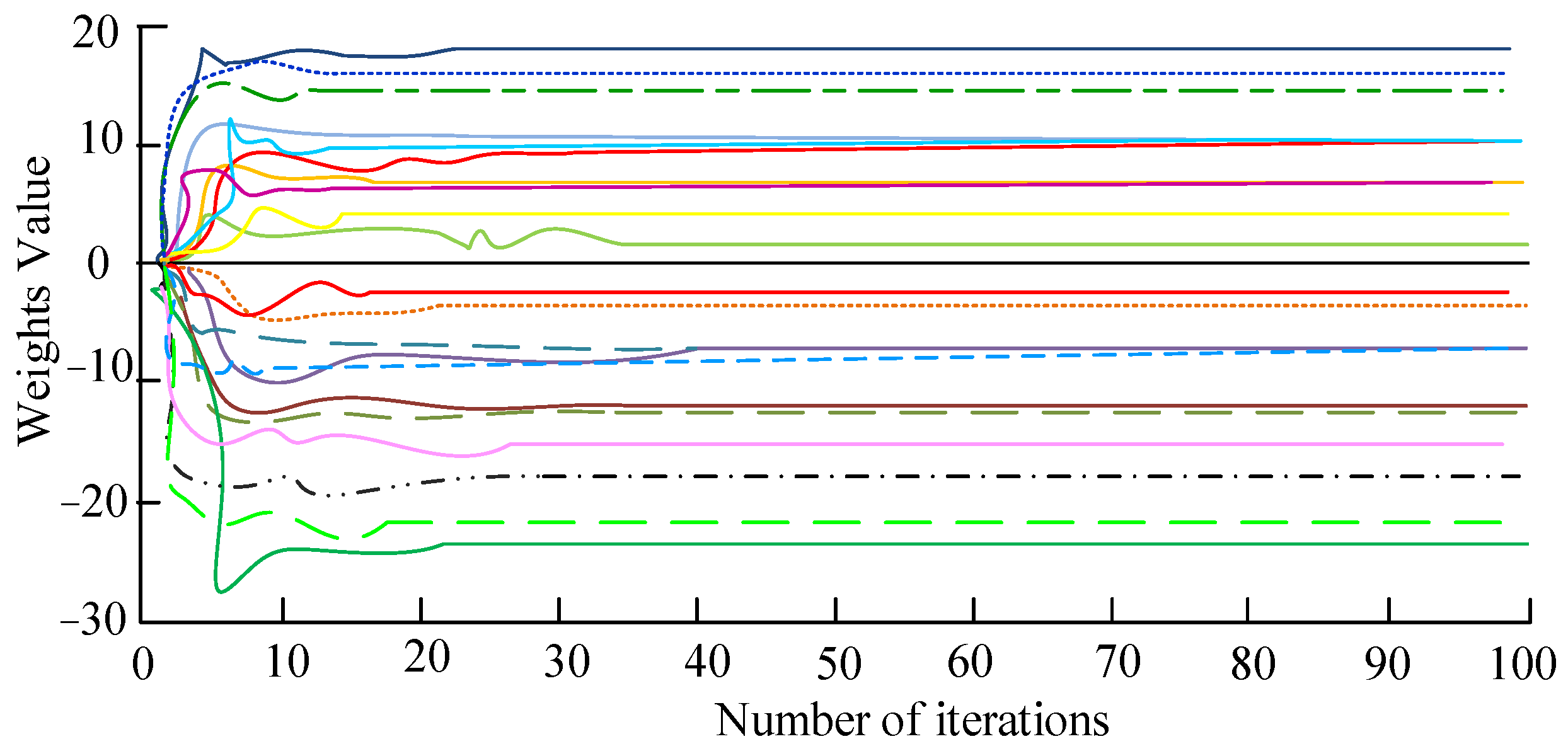
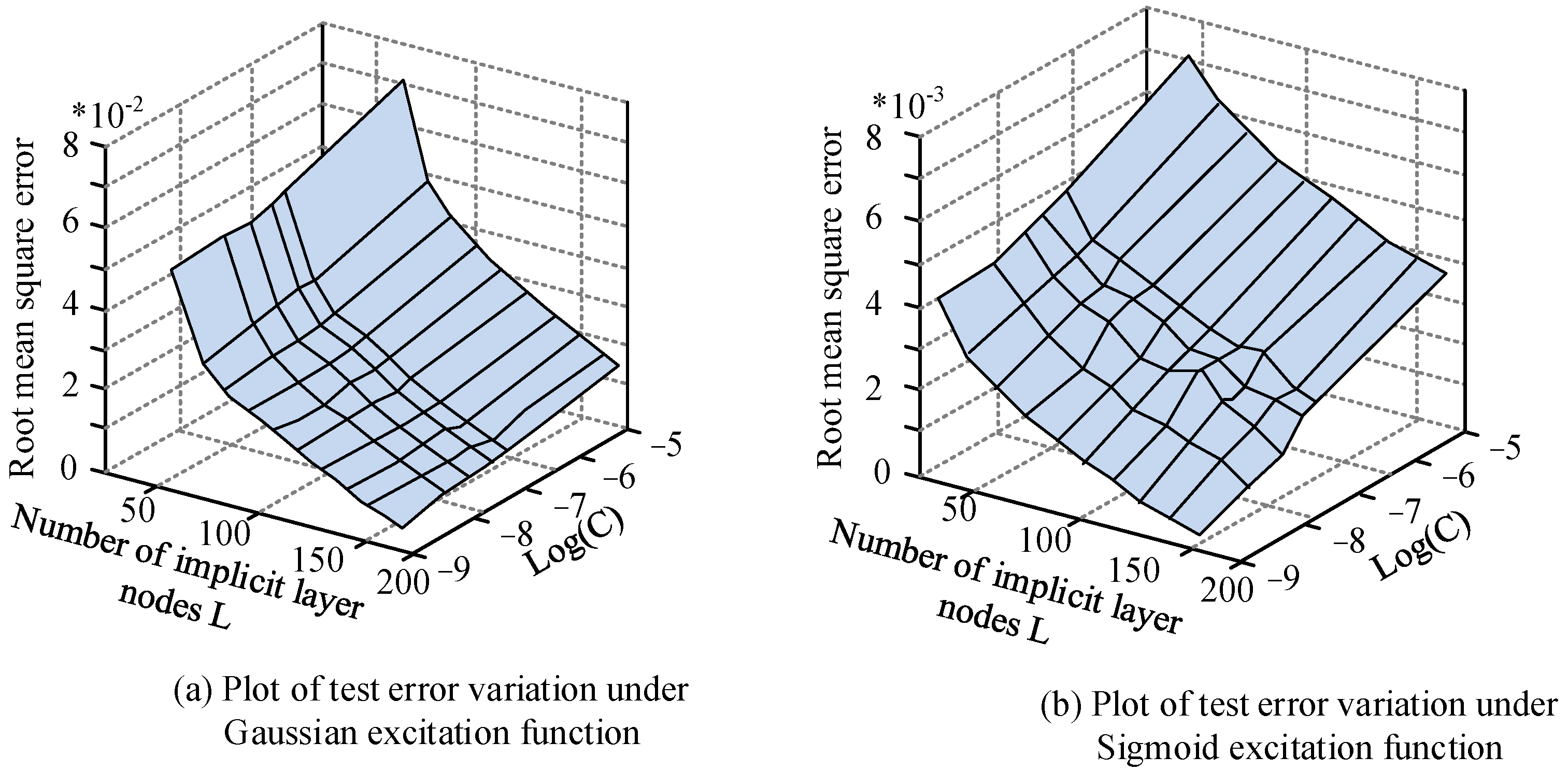
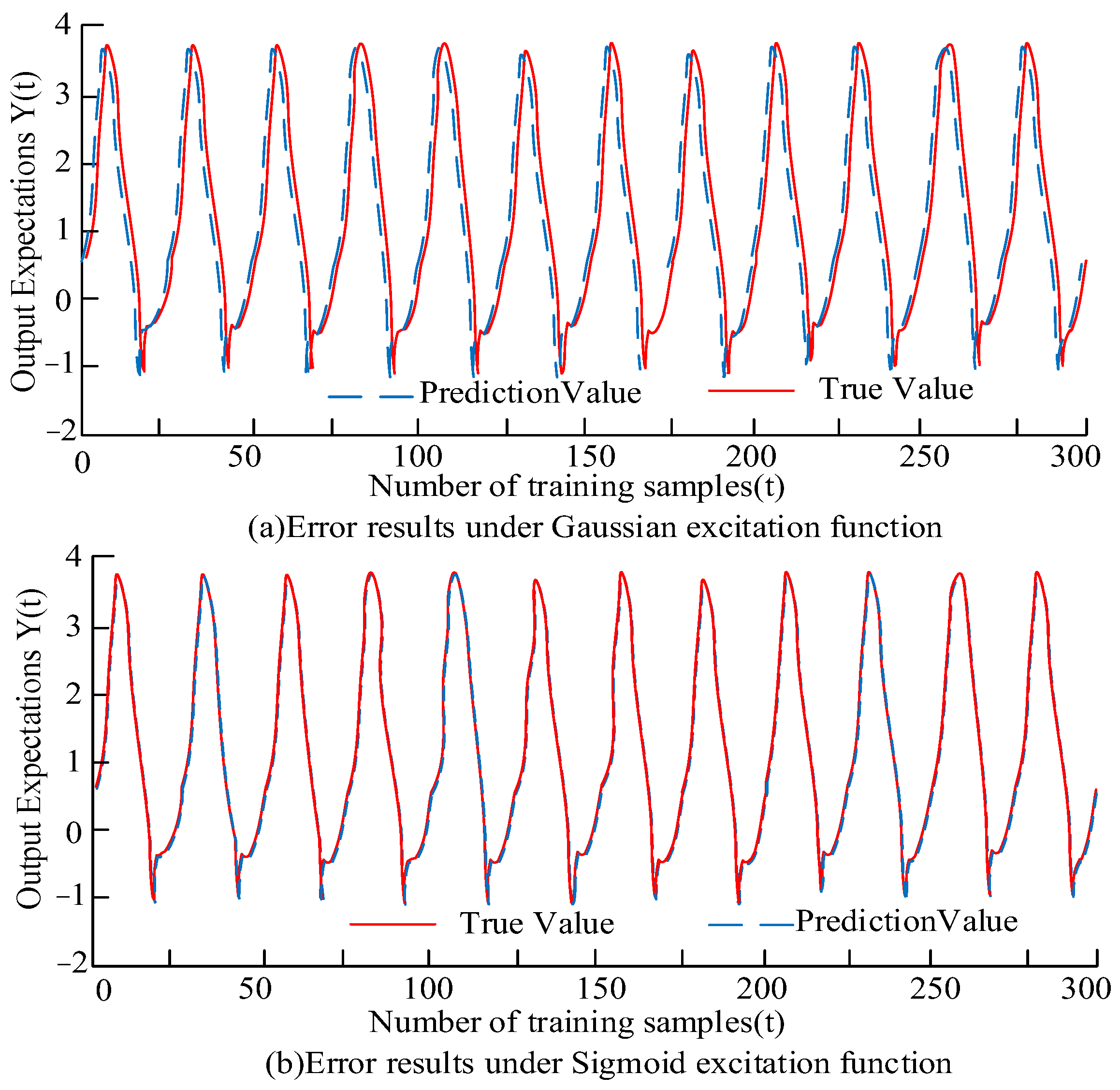
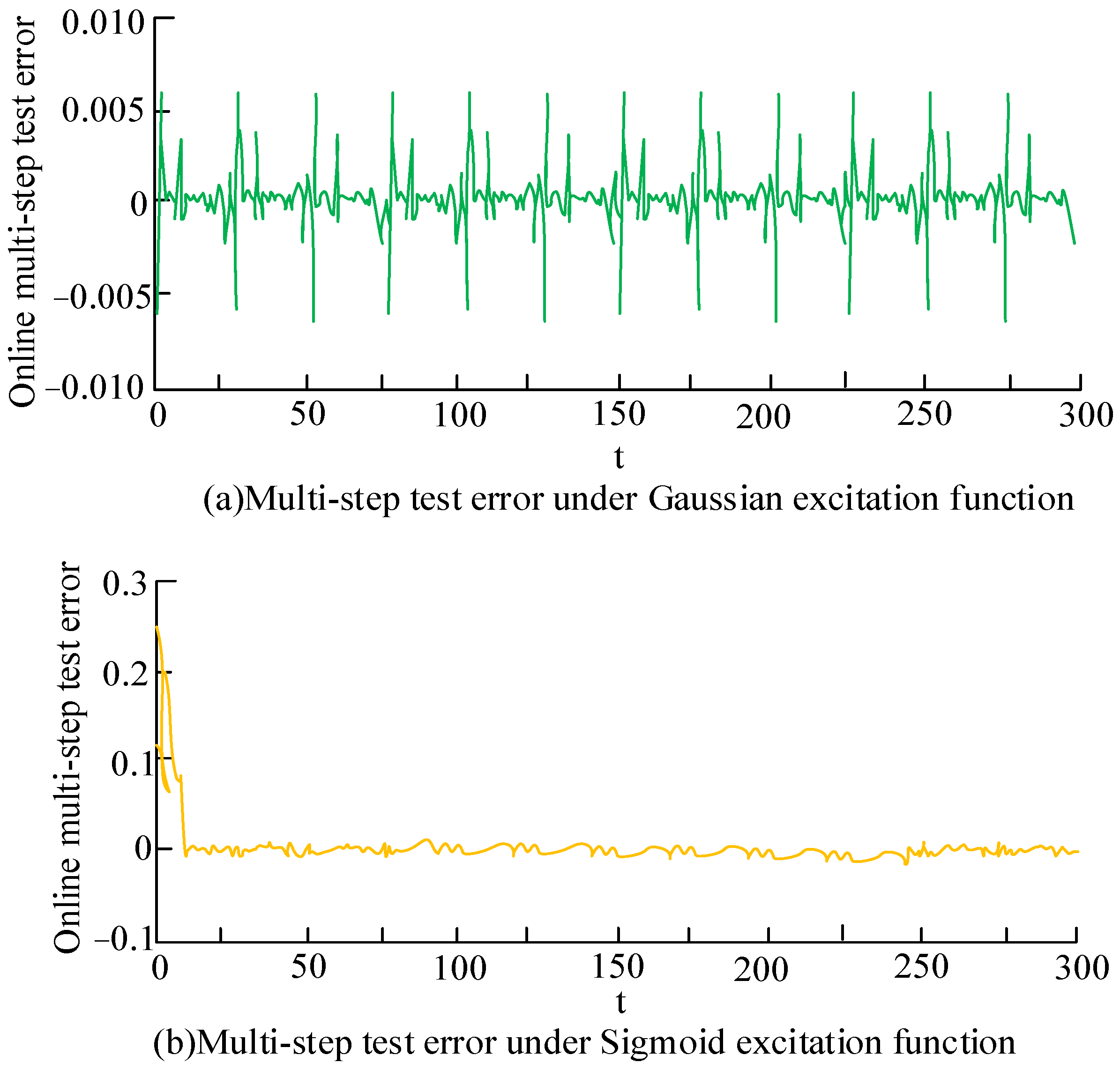
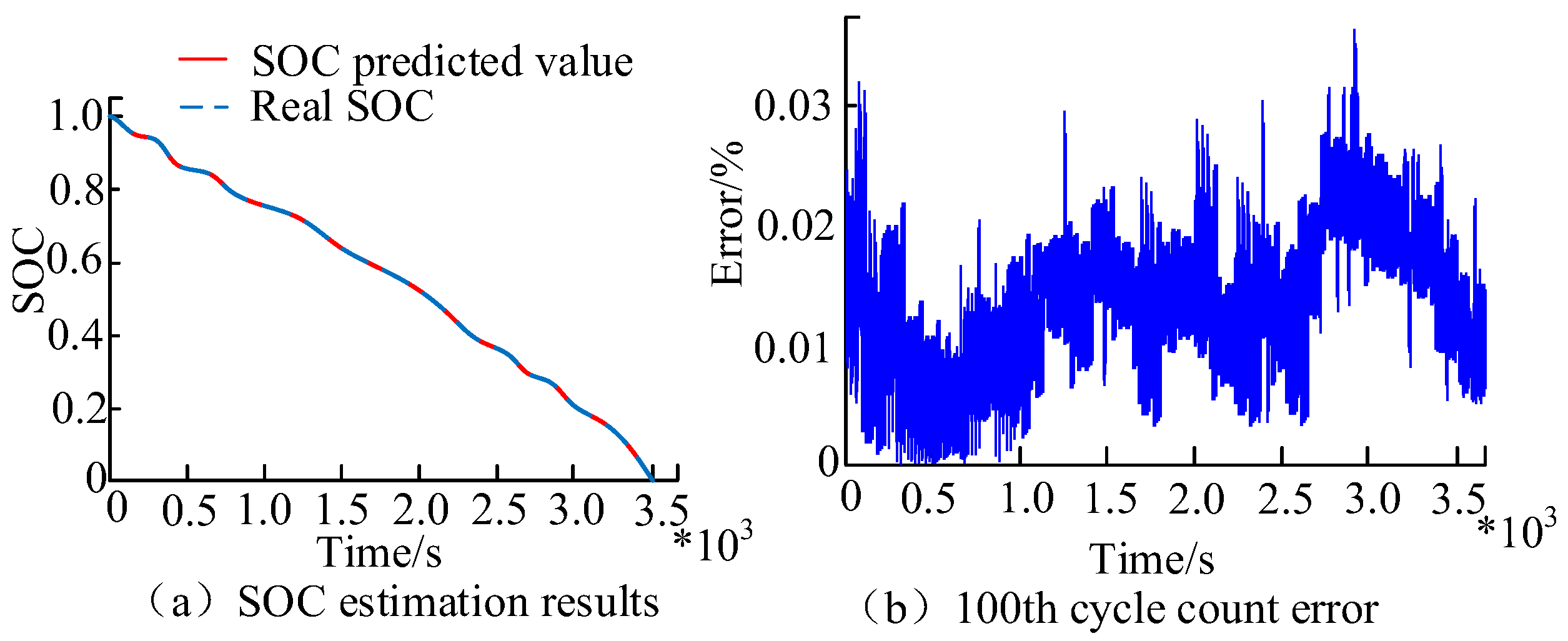
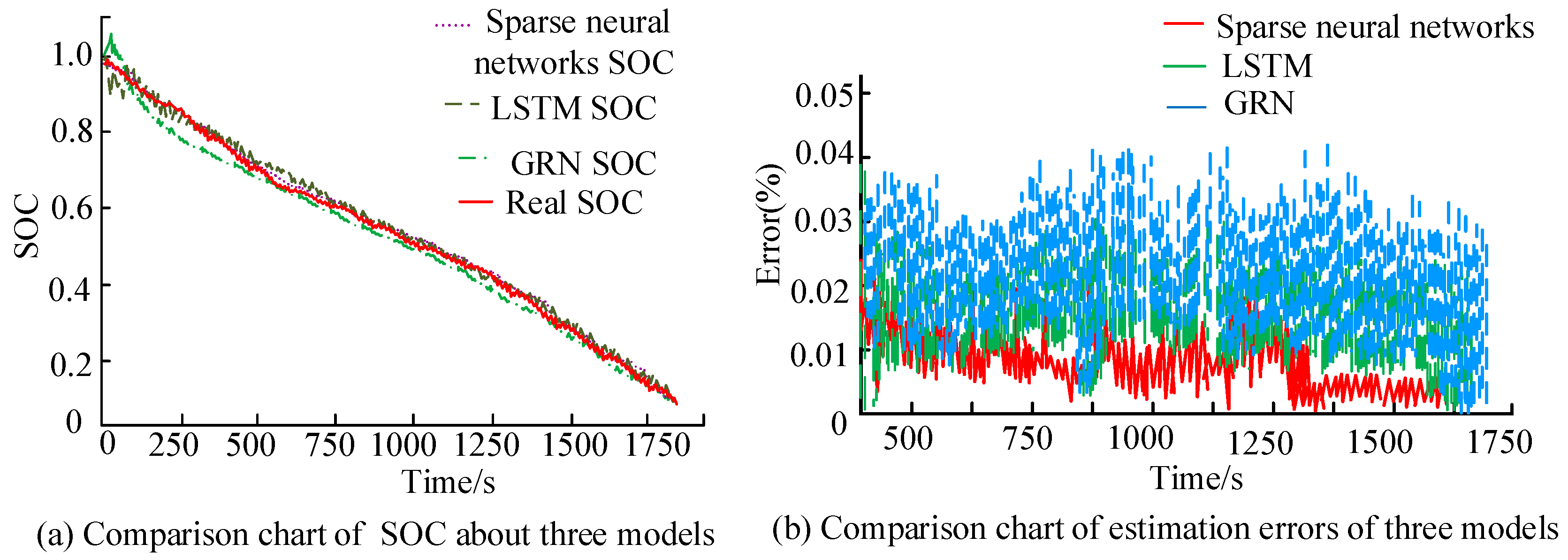
4. ADMM-ETLM Performance and Results Analysis of Sparse Neural Networks in Lithium Battery SOC Prediction

For testing the proposed algorithm, experiments were designed to perform simulation analysis on the Mackey-Glass time series system (the simulation experiment software package used is MackeyGlass_ T17). The Benchmark database was selected. 1902 sets of sample data were randomly selected to train the test network, of which 1000 sets were utilized to train and the remaining 902 sets were utilized to test, and the outcomes are depicted in Figure 4.

The figure showcases that the predicted output value (POV) changes with time. The POV and the actual output value curves can fit well. Both the predicted and actual output values show fluctuations across a wide range with time, and the fluctuation value range takes the value of [0.4, 1.38]. Setting the nodes’ quantity in the implied layer to 50, the useful weight output obtained under the same time series system is shown in Figure 5.

Figure 5 demonstrates that the useful output values tend to stabilize as the number of nodes in the HL increases. The number of nodes that are not zero is 23 in total, which is a decrease of 17 compared to the original nodes’ quantity set in the HL, greatly reducing the computational burden. Also in the figure, when the number of iterations is updated by 10 steps, it produces a value that converges to a constant and is stable, indicating that the study of the regularization mentioned above has a certain degree of convergence. The algorithm proposed in the study also achieves a stable result and maintains a small computational effort when setting a small value for the iterations’ quantity, further indicating the validity of the algorithm for regularization. For validating the sparse neural network (SNN) model in the study, the selection of the UCI (University of California, Irvine) database as the regression experimental test dataset and online regression experimental analysis experiments are designed to test the algorithm model.

A randomly selected UCI dataset aggregated 998 sets of sample data, of which 700 sets were used for the training of the neural network, and the remaining 298 sets were utilized as test data. The relationship between the SNN model in the study and the nodes’ quantity in the HL L and the 2-regularization penalty factor is experimentally verified, and Figure 6 indicates the results.

Figure 6a represents the relation between the regularization penalty factor and the RMSE of the test under the Gaussian excitation function. From Figure 6a, it can be seen that with the same logarithm of the regularization penalty factor, the RMSE shows an overall decreasing trend as the nodes’ quantity in the HL increases. The largest decrease is log(C) = −5, and the RMSE decreases from 0.0433 to 0.008; the smallest decrease is log(C) = −8, and the RMSE decreases from 0.0218 to 0.003. When the nodes’ quantity in the HL is certain, with the increase of log(C), the RMSE shows an increasing trend. The rise ranges from [0.003, 0.0008] to [0.0218, 0.0433]. Figure 6b represents the relationship between the regularization penalty factor and the RMSE of the test under the Sigmoid excitation function. Compared with Figure 6a, the fluctuation of the relationship between the quantity of implied nodes and RMSE shows an obvious “rising before falling” small steep slope for a certain logarithm of the positive penalty factor. From Figure 6b, the overall RMSE increases with the growth of the regularization penalty factor, ranging from [0.0025, 0.0039] to [0.0058, 0.0074]. The RMSE decreases with the growth of the nodes’ quantity in the HL, ranging from [0.0025, 0.0039] to [0.0039, 0.0074]. Figure 6 illustrates that the quantity of HL and the positive penalty factor have some influence on RMSE within a certain range, but the magnitude of their influence does not show an order of magnitude change. According to the figure, the optimal combination of parameters (C, L) for different functions can be selected, indicating the effective sparse effect of the SNN model presented in the study. The performance of the online ADMM neural network sparse supervised learning algorithm was tested using a multi-step prediction method. Experiments were designed with 286 steps of prediction, and the prediction results and the test errors corresponding to each step are shown in Figure 7 and Figure 8.

From Figure 7a, under the Gaussian excitation function, the output expected value curves of the predicted results and the true values show a consistent trend, and there is a good fitting effect between the two predicted curves. In Figure 7b, the predicted result curve obtained from the s-type excitation function is completely consistent with the true value prediction curve.

In Figure 8a, the online multi-step test error shows a regular fluctuation with the increase in test time in the range of [−0.005, 0.005] under the Gaussian excitation function. Under the Sigmoid excitation function, the online multi-step error tends to decrease with time. In addition to the initial 20 s, when the test error is larger in the range of [0.082, 0.265], after which the test error is basically 0. This indicates that the online learning method proposed in the study has good stability, and it further indicates that the sparse supervised learning algorithm of the neural network constructed in the study is well nonlinear. The dynamic prediction performance is good. Four sets of regression data originated from the real world in the UCI database were downloaded, including four types of data names, the quantity of data features, the quantity of training data samples, and the quantity of test data, as shown in

Table 1. Details of the data downloaded from the UCI dataset.

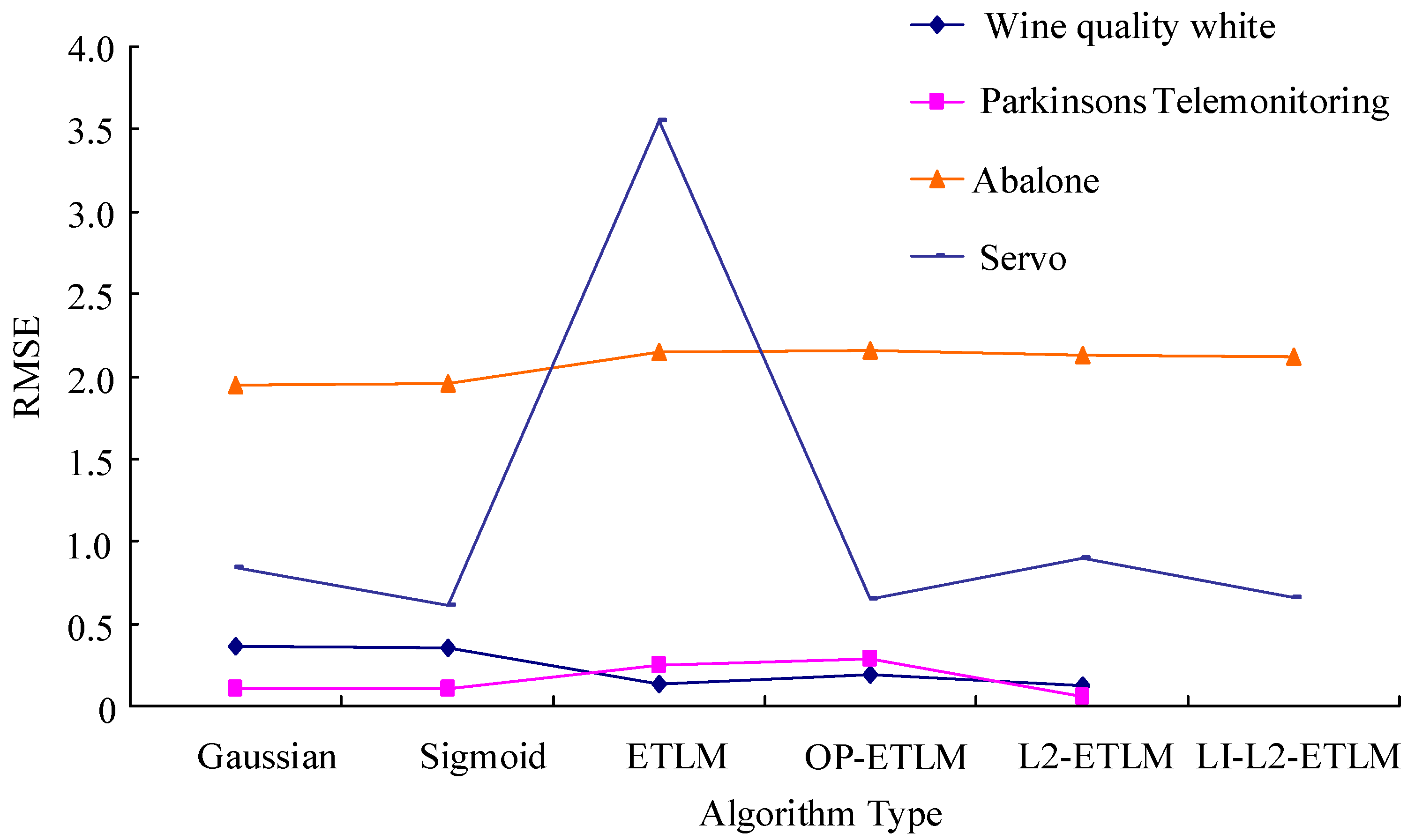
Name	Feature Data	Number of Training Samples	Test Data Sample Size
Wine quality white	11	3000	1898
Parkinsons Telemonitoring	22	2875	3000
Abalone	8	2784	1393
Servo	4	110	57

.

The experiments are designed to compare the presented algorithms with ETLM, Optimally Pruned ETLM (OP-ETLM), Ridge Regression Pruned ETLM (RRETLM), and Lasso Ridge Regression Pruned ETLM (L1-L2-ETLM) in regression analysis experiments. Learning Machine (L2-ETLM) and Lasso Ridge Regression Pruned ETLM (L1-L2-ETLM) in regression analysis experiments, and the performance metrics are expressed as the RMSE of the test set. Figure 9 showcases the outcomes.

Figure 9 indicates the L2-ETLM algorithm performs best in the Wine Quality White and Parkinson’s Telemonitoring datasets, with RMSEs of 0.1241 and 0.0564, respectively. The ADMM-LI-ETLM algorithm performs best in the Abalone and Servo datasets. The difference in the square root of ADMM-LI-ETLM under different excitation functions is small, ranging from 0.00669 to 0.225. There is no difference in the order of magnitude, indicating that the prediction values of ADMM-LI-ETLM with different excitation functions are less different and the performance is stable.

After testing the presented algorithm and the online evaluation model, the next step is the practical testing of the model applied to lithium batteries. The study uses a Sony VCT4 model 18650 battery as the experimental object. The algorithm is verified for the real-case Li-ion battery SOC prediction. The prediction results with errors at the 100th cycle are scaled up, and the outcomes are demonstrated in Figure 10.

Figure 10a showcases that the SOC prediction reduces as the cycle’s quantity increases, which is in line with reality. The curves of the actual SOC value and the forecasting SOC value fit well, and the curve of the predicted SOC value will be a little below the real SOC value at some moments. It can be considered that it is possible to make an accurate prediction of the SOC state of the Li-ion battery in the real situation and at the same time play a certain protective role. The error results for the 100th cycle are showcased in Figure 10b, which shows that the error value fluctuates with time from 0 to 0.037. The average error (AE) in the 100th cycle is 0.67%, indicating that the SOC evaluation model proposed in the study is good. For validating the model, the Sony VCT4 18650 battery was also used as the experimental object. Compared with the commonly used battery SOC prediction models with good performance, like the Long Short-Term Memory (LSTM) and Gated Recurrent Neural (GRN), the outcomes are demonstrated in Figure 11.

In Figure 11a, all three algorithms are able to fit the real SOC prediction curve well and present a realistic response to the SOC prediction with time change. Comparing the SOC prediction errors of the three SOC prediction models, Figure 11b indicates that the relative errors of the SOC prediction models proposed in the study are all below the LSTM and GRN. For the AE, the SNN model is 0.58%, the LSTM is 0.87%, and the GRN is 1.05%. The maximum error is 2.97% for the SNN model, 4.93% for the LSTM, and 4.08% for the GRU. The experiment demonstrates that the improved SNN SOC evaluation model of the study has better stability and accuracy compared with the single neural network SOC prediction model.

5. Conclusions

To achieve online prediction of the SOC of lithium batteries and guarantee the corresponding prediction accuracy, the study proposes an L1 regularized extreme learning machine method based on the alternating factor multiplier method. In this paper, some parameters are restricted by regularization to enhance generalization, and an online LBSC prediction model is constructed by converting the alternating factor multiplier method into recursive form. Experiments are conducted to verify the ADMM-LI-ETLM in the study. The nodes’ quantity of the implied layer obtained is 23, which decreases by 17 compared with the nodes’ quantity of the implied layer in the original setup. The multi-step prediction method is used for verifying the sparse supervised learning model proposed in the study, and the number of experimental steps is 286. The results show that the prediction results and the true values are identical under both Gaussian and Sigmoid excitation functions, and the fit between the prediction curve and the original curve is perfect. The test error is [−0.005, 0.005] for the Gaussian excitation function and [0.082, 0.265] for the Sigmoid excitation function. Comparing the performance of ADMM-L1-ETLM and LSM, L2-ETLM, and LI-L2-ETLM in regression experiments, the outcomes showcase that the RMSE values of ADMM-L1-ETLM fluctuate from 0.3599 to 1.9517. The Sony VCT4 model 18650 battery is applied as the experimental object to simulate the SOC prediction of Li-ion batteries in real-world situations. The outcomes indicate that the AE of the SOC prediction for the 100th cycle was 0.67%. The function of the sparse neural model and the LSTM and GRN models on the SOC prediction of Li-battery is compared under the same experimental environment and object. The results show that all three algorithm models can fit the real SOC curve well: the sparse neural model has the smallest SOC error, the AE is 0.58%, and the maximum error is 2.97%. The above outcomes showcase that the ADMM-L1-ETLM proposed in the study can reduce the computational burden, and the SNN model has better prediction accuracy and smoothness. It can further achieve online, real-time evaluation of the nuclear power status of new energy vehicles equipped with lithium-ion batteries, effectively extending battery life. Since the neural network used in the research is anextreme learning machine, the performance of online algorithms in other neural networks has not been taken into account. At the same time, the research only predicted the online state of charge of lithium batteries. Later, the performance of online algorithms proposed by the research will be considered on more experimental objects. Finally, from the comprehensive performance of the experimental results, it can be seen that the online algorithm proposed by the research has a good performance in high-dimensional data classification, which can be applied to speech recognition, image classification, and natural language processing. However, the data selected in the study are difficult to cover in various fields in the real world, and there is still room for improvement.