Abstract
During wireless charging of the traction battery of electrically powered vehicles, the active area between the ground and vehicle assemblies must be monitored for inductive power transfer. If metallic foreign objects enter this area, they interact with the magnetic field and can heat up strongly, and thus become a potential source of hazard. To detect such foreign objects, measurements based on passive inductive sensors have already been carried out in advance. However, a large number of factors influence the detectability of metallic foreign objects, such as the characteristics of the magnetic field of the ground assembly coil, the size, shape, position, orientation, and material composition of the foreign objects, or the design of the sensor coils. The related practical testing effort can be reduced if the characteristics of the charging system and the foreign object detection system can be simulated. Therefore, simulation models were developed within the scope of this work and validated with the help of practical measurements. These models were used in the next step to analyze new test arrangements that had not yet been investigated by measurement. In the simulations described here, precision in the range of 1 mV could be achieved. Cumulatively, many influencing factors can be easily investigated, and results can be generated in a largely automated manner and typically in a wider variety than with practical measurements.
1. Introduction
For wireless charging systems, inductive power transmission is currently favored by standards organizations [1,2,3,4]. The ground assembly coil located outside the vehicle and the vehicle assembly coil form an ironless transformer in this case. The magnetic field of this transformer also interacts with metallic objects that are not part of the charging system but are located in the active area between the ground assembly and the vehicle assembly. Such objects may be parts of the vehicle, but also undesired metal objects such as coins, metal foils, nails, etc. Metallic objects can become very hot in the magnetic field, mainly due to eddy current and hysteresis losses. Such a heated object is a potential safety hazard:
- If the object has a temperature at which it is dangerous to touch;
- If the object damages the surface on which it lies and, as a result, causes an electrical thermal issue;
- If flammable materials with which the object is in contact with ignite.
According to the SAE J2954 [1] and DIN EN IEC 61980-1 [2] standards, such hazards should be avoided by an appropriate design of the ground assembly coil or by using a subsystem for detecting metallic foreign objects.
In addition to the acquisition of the properties of electrical systems by measurement, the simulation of the behavior of such systems is becoming increasingly important in the automotive sector. With respect to the increasing automation, this is motivated, for example, by the test effort, which increases very rapidly with the increasing number and complexity of the electrical subsystems used in the vehicle. That is why, for example, European projects such as ArchitectECA2030 [5] or AI4CSM [6] are concerned with the virtual development and validation of electrical components in the vehicle. The work on the detection of metallic foreign objects in the ArchitectECA2030 project is organized into two main parts—the measurements on a real wireless charging system and the simulation of this system. The results of the practical measurements were published in [7]. In this paper, simulations related to foreign object detection are presented.The simulations were performed using the COMSOL Multiphysics® software including the AC/DC module [8]. By using the magnetic field interface, Maxwell’s equations are formulated based on the magnetic vector potential. The equations are solved in the simulations using the finite element method in the frequency domain. The developed simulation models are validated by the already published measurements on the real charging system. Finally, it is shown by an example that the validated models can be used to analyze new scenarios.
Section 2 of the paper presents the basic structure of the simulation environment. This represents the measurement setup, which was described in detail in [7]. Subsequently, in Section 3, the results of the simulation of the magnetic field of the ground assembly coil of the charging system are shown and compared with the values determined by measurement. This primary magnetic field determines the design of the sensor coils for the detection of metallic foreign objects. In Section 4, key aspects of the modeling of the foreign objects and sensor coils used in the simulations are discussed. Section 4.1 mainly focuses on the structure, size, shape, and material of the foreign objects and their effects on the parameters of the simulation. Section 4.2 describes the implementation of the sensor coils in the simulation and verifies it using measurement and simulation results obtained without a foreign object in the system. Based on this, Section 5 addresses the detection of metallic foreign objects. In Section 5.1, the simulation models and their interaction in the simulated charging system are validated by comparing the simulation and measurement results. The results of further extended simulations are shown in Section 5.2. The final Section 6 contains the conclusions drawn from the simulations.
2. Basic Simulation Setup
The simulation of the charging systems ground assembly focuses on the two main components of the magnetic circuit—the ground assembly coil and the ferrites arranged below it. The two components are simulated within a defined volume of air—a sphere with a radius of 1 m (Figure 1).
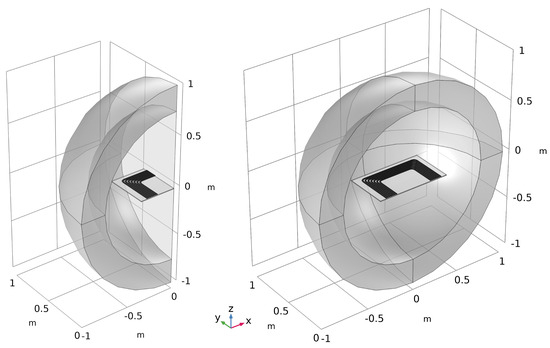
Figure 1.
Basic simulation setups. (Left) One quarter of the components and air volume; (right) half of the components and air volume.
To simplify the simulation environment and reduce simulation time, it was assumed that the simulated components are completely symmetrical in their geometric dimensions with respect to the medians of the sides of the rectangular ground assembly coil. Based on this assumption, for the simulations of the magnetic field of the ground assembly coil, the area to be simulated was reduced to a quarter of the components and the air volume (Figure 1 left). In subsequent simulations, where objects were moved to different positions, half of the coil, ferrites, and air volume were simulated to avoid objects protruding beyond the outer edges of the simulation model (Figure 1, right). The medians of the sides of the ground assembly coil are also the axes of the coordinate system used, whose origin coincides with the point of intersection of the medians.
The ground assembly coil is a single-layer flat coil consisting of seven turns of three parallel stranded wires NELC840/38SPSGB (type 2 litz wire, 5 × 4 × 42 AWG 38, ⌀4.2 mm) [9] with a width of 600 mm outside and 360 mm inside in the x-direction; in the y-direction, the width is 750 mm outside and 510 mm inside. The ferrites are 6 mm thick plates [10]. Their top sides form a surface of 720 mm in the x-direction and 840 mm in the y-direction, located 4 mm below () and centered on the coil. In the practical experiments, a carrier plate with a width of 768 mm was used to hold the sensor coils and the test objects. The plate was symmetrically arranged in the x-direction with respect to the coordinate origin and extended 444 mm in the y-direction into the area of the charging system ground assembly simulated here. The simulated sensor coils also cover a width of 384 mm on each side of the y-axis.
At the outer edge of the air volume, a quarter of the radius was defined as an infinite element domain. With the default values used for the parameters “Physical width”, “Pole distance,” and “dGeomChar”, a characteristic geometry dimension, the outer edge of the air volume is stretched in this way during the simulation up to a distance of about 2450 m, and is thus far away from the magnetic circuit of the ground assembly.
The cross-sectional area of the litz wires of the coil is simulated with a triangular mesh with a minimum element size of 2 mm. Over the length of the litz wire, this mesh is extruded with a maximum element size of 6 mm. In this way, the round cross-section of the strand is simulated by an equilateral octagon and the thickness remains the same over the entire length. The ferrites and the air volume were simulated with a tetrahedral mesh, allowing a minimum element size of 0.4 mm.
The material properties of the coil and air volume were simulated with the program-internal materials, copper and air. The material of the ferrites (BFM8) was simulated with information from the manufacturer’s data sheet [11]. A linear magnetization characteristic using the initial permeability of the material was used.
The conductor model used for the coil was the numerical homogenized multi-turn option, which modulates a bundle of thin wires, each separated by an electrical insulator. The effective cross-section of the stranded wire was specified as 6.7 mm2, based on 840 wires of type AWG 38; the number of turns was specified as seven. The three parallel stranded wires of the ground assembly coil were modeled as individual subcoils and supplied with a configurable current.
During the simulation, the coil geometry and the magnetic field of the current-carrying coil were analyzed at a frequency of 80 kHz. This way, the simulation results are comparable to the measurements from [7], where a switching frequency of 80 kHz was also used. The results of the coil geometry analysis are shown for the three parallel subcoils and the entire ground assembly coil in Table 1.

Table 1.
Results of the coil geometry analysis.
The simulation model provides approximately the same value for the inductance of the coil as the measurement, but only about one third of the measured value for the AC resistance. This is mainly due to the skin and proximity effects, which lead to higher AC resistance in practical measurements and are neglected in the simulation of the coil. However, this is not expected to have an effect on the further simulations, since the simulated current flowing through the subcoils is independent of the AC resistance.
3. The Magnetic Field of the Ground Assembly Coil
The characteristic of the magnetic field of the ground assembly coil is the basis for all functionalities and properties investigated here in the context of foreign object detection. Therefore, this was simulated separately in the first step and validated with the values determined during practical measurements. The magnetic field probe used in [7] for the measurements on the ground assembly of the charging system has a nearly square housing (height: 27 mm) and was moved over the coil at a height of . Therefore, the magnetic flux density was extracted from the simulation at three different heights: (bottom of the probe), (center of the probe), and (top of the probe). Since the measured values correlate well with the simulation results of the magnetic flux density at a height of , these values were also extracted from the simulation. The results of the simulations and measurements can be seen in the Figure 2 and Figure 3, as well as in Table 2. The scale divisions of the x- and y-axes were chosen to reflect the 24 mm grid of the grooves on the carrier plate used in the measurement.
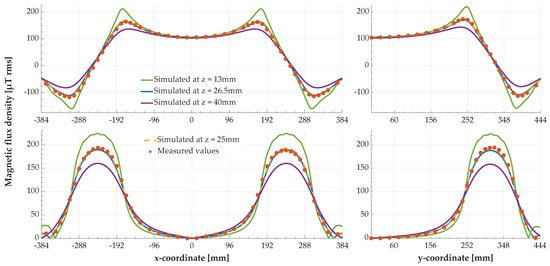
Figure 2.
Magnetic flux density of the magnetic field of the ground assembly coil at a current of 4 A rms. (Top) z-component; (bottom) component in the xy-plane; (left) along the x-axis of the coordinate system at ; (right) along the the y-axis of the coordinate system at .
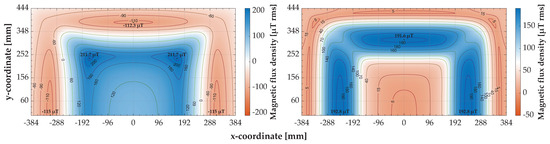
Figure 3.
Magnetic flux density of the magnetic field of the ground assembly coil simulated at and a current of 4 A rms. (Left) z-component; (right) component in the xy-plane.

Table 2.
Maximum values of the magnetic flux density of the charging system.
In analogy to the measurements in [7], an xy-component and the z-component of the simulated magnetic flux density were also presented in the evaluation of the simulation results. The component in the xy-plane is composed of the x and y components of the magnetic flux density. Its magnitude is determined as:
4. Modeling of the Foreign Objects and Sensor Coils
When modeling the foreign objects and the sensor coils, various parameters have to be taken into account in order to obtain correct results in the simulation and to keep the computational effort required for the simulation low. These include:
- The frequency of the current flowing through the ground assembly coil, which generates the magnetic field of the charging system. It determines how deeply the magnetic field penetrates electrically conductive materials;
- The spatial characteristic of the magnetic field surrounding the ground assembly coil;
- The parameters of the materials involved. They primarily determine whether the material is electrically and/or magnetically conductive, and thus, the behavior of the material in the magnetic field;
- The geometry and structure of the foreign objects. They define, for example, how big the object is, how it is shaped, what materials it is made of, and how thick the individual material layers are;
- The geometry and location of sensor coils. They determine which magnetic influences induce voltages and how high they are;
- The position and orientation of the foreign objects in relation to the magnetic field of the ground assembly coil and the sensor coils. These parameters determine how the foreign objects and the sensor coils are stimulated by the magnetic field;
- The relative sizes of the components involved. They determine how finely the simulation model must be meshed, and thus, how complex the simulation will be.
In this section, only a subset of these parameters is considered. However, dependencies between different parameters are also discussed.
4.1. Foreign Objects
In order to be able to validate the results of the simulations for the detection of foreign objects with the measurement results published in [7], models for the 0.05€ coin and the steel nail (Table 3) are created, since the most measurement data were captured for these objects. Furthermore, the two examples are common in daily life, show different behavior in the magnetic field, and show the influence of different parameters on the simulation.

Table 3.
Test objects used as metallic foreign objects for the simulation.
4.1.1. Meshing of the Foreign Objects
The definition of the simulation models for the foreign objects started with a comparison of different meshing variants for the different materials. In order to be able to show the influence of the materials, objects which consist fully of one material were used in the first step. The materials chosen were copper and iron, which are already available in the COMSOL software. The geometry of a 0.05€ coin was used for the objects.
One parameter for describing the influence of materials is the penetration depth of an external magnetic field into a metallic object. This can be estimated approximately as follows at medium frequencies:
where is the electrical resistivity and is the absolute permeability of the material under consideration. is the angular frequency.
The two materials studied differ mainly in their electrical conductivity and relative permeability (see Table 4). The electrical conductivity of iron is about a factor of 5.4 lower than that of copper. However, the relative permeability of iron in the simulation is greater than that of copper by a factor of 4000. According to Equation (2), this results in a penetration depth for iron that is about a factor of 27, smaller than for copper. This different penetration depth must be taken into account in the simulation in the meshing of the models.

Table 4.
Materials used for the simulations and their main simulation parameters.
To investigate the influence of the meshing of the object model for different materials, four variants were tested: a coarser but rather uniform mesh and a finer mesh with thin boundary layers—both as volume and surface meshes, respectively. The coarser mesh consists of elements with a minimum size of 0.4 mm and a maximum size of 1 mm. For the volume mesh, tetrahedral elements are used—for the surface mesh, triangular ones. In the case of the finer mesh, a triangular mesh with eight thin boundary layers is created on the round surface of the object. The boundary layers have a stretch factor of 1.2. In the case of the volume mesh, the structure of the surface is extruded in the direction of the thickness of the object with ten layers with a thickness ratio of four, where the boundary layers are also thinner than the central area. In the surface mesh, the same lateral structure is created on the side of the object. In addition, when using the surface meshes, an impedance condition is defined for the surface of the foreign object, which ensures that induced currents flow only on its surface and the inner region of the object is not part of the model and the simulation. The statistical data and the illustration of the meshes are shown in Table 5. In order to determine the number of mesh elements for the foreign object, the simulation model was manually meshed step-by-step. The difference between the number of mesh elements with and without the foreign object model results in the given number of mesh elements for the foreign object.

Table 5.
Influence of different meshes of the model of a foreign object on the simulations.
Figure 4 shows the influence of the different mesh structures on the magnetic flux density as a function of the material. The simulation results were taken from an edge located 2 mm below () and centered on the object in the y-direction ().
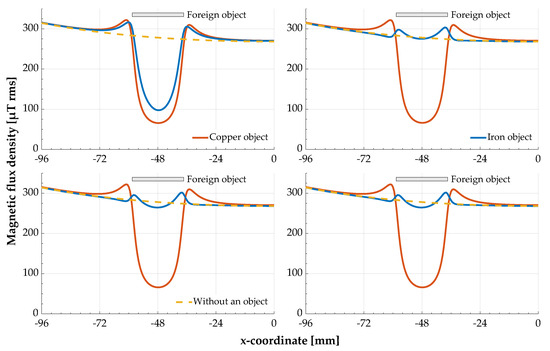
Figure 4.
Results of the simulations with different meshes of the foreign object models. The cross section of the foreign object represents its position and dimension with respect to the x-coordinate. (Top) Volume meshes; (bottom) surface meshes; (left) coarser but rather uniform meshes; (right) finer meshes with thin boundary layers.
In the case of copper, the simulation results show no visible differences and the differences in computational effort are negligible. The most efficient variant here is the coarser volume mesh. In the case of iron, the differences are partly very clear. With the coarser volume mesh, the simulation results are similar to those of copper and are thus wrong, since with a ferromagnetic material an amplification of the magnetic field is to be expected in contrast to the observed attenuation. With the other three mesh variants, this amplification of the magnetic field can be seen in the edge region of the object—in the center of the object, the magnetic field is slightly damped. This damping is somewhat more pronounced with the surface meshes than with the finer volume mesh. When using the surface meshes, however, the simulation effort increases significantly, since the solver needs more iterations to calculate the results—with the finer surface mesh, this is also noticeable due to the longer simulation time. In terms of the simulation result and the simulation effort, the fine volume mesh is the best variant here.
The results for the finer volume mesh and for the coarser surface mesh differ only slightly. One advantage of the surface mesh is its simple and uniform structure. It can be generated with only one instruction in the software, even for more complex object geometries. Therefore, the coarser surface mesh was used for the steel nail in the simulation instead of the finer volume mesh.
4.1.2. Materials for the Foreign Objects
The second important point regarding the simulation models for the foreign objects was the choice of materials and material parameters. For validation with the measurements from [7], a 0.05€ coin and a steel nail have to be modeled. According to the European Central Bank and the Council of the European Union, the 0.05€ coin is made of copper covered steel [12,13]—but an exact material composition is not given. Since the composition of the coin was also not analyzed in more detail, another simulation was carried out with an object made of copper covered iron, and the results were compared with those of the object made of copper (Figure 5). In this simulation, a thickness of 40 μm was assumed for the copper layer. The iron core and the copper covering were simulated with a coarser and a finer volume mesh, following the mesh structures of the previous section. The two regions were meshed separately so that a clear assignment of volume elements and material is possible in the simulation.
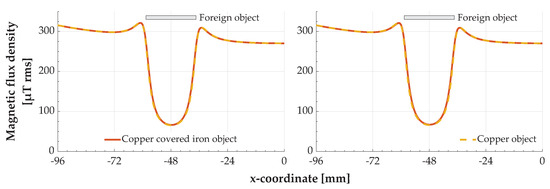
Figure 5.
Magnetic flux density below an object made of copper covered iron compared to an object made of copper. The cross section of the foreign object represents its position and dimension with respect to the x-coordinate. (Left) Coarser volume mesh; (right) finer volume mesh.
As can be seen from Figure 5, the magnetic flux density below the objects is only marginally affected by the different structure of the objects. This means that the steel core of the coin does not have to be modeled separately. Therefore, only copper was used for the final simulation model of the coin. For the material of the nail, the iron available in COMSOL can basically be used. However, an adjustment of the relative permeability is necessary (see Table 4). Since this value is subject to a very large variation in the case of steel, it was set to 200 by comparing the measured values from [7] and the simulation results.
Figure 6 shows the simulated magnetic flux density 2 mm below the two foreign objects ()—coin and nail—at a y-position of 24 mm. The steel nail amplifies the magnetic field of the ground assembly coil at both positions over its entire length, independent of the spatial characteristics of the field. The copper coin attenuates the magnetic field underneath at both positions and slightly amplifies it outside its edges.
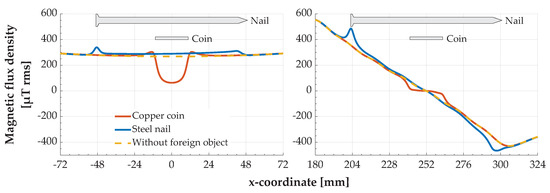
Figure 6.
Simulated magnetic flux density 2 mm below the two foreign objects at different x-positions (). The cross sections of the foreign objects represent their position and dimension in relation to the x-coordinate. (Left) At position ; (right) at position .
4.2. Sensor Coils
In the context of the practical measurements, several different geometries for the design of the sensor coils were investigated. In general, all variants are differential coils. If the sensor coil is designed in such a way that it is symmetrically stimulated by the magnetic field of the ground assembly coil, then its influences are faded out. As long as the feedback effects of the metallic foreign objects lead to an asymmetrical stimulation of the sensor coil, their influences can be measured. Ideally, this approach makes it possible to capture the influences of the relatively weak feedback effects of the foreign objects without disturbing influences from the comparatively strong magnetic field of the ground assembly coil. Within the scope of the simulations, the best measured conventional coil design from the perspective of foreign object detection, as proposed in [14,15,16], and the improved coil design based on it and presented in [7] will be modeled and investigated (Figure 7). In the improved coil design, the orientation of the conductor loops of the sensor coil changes at the points where the component of the magnetic field relevant for the induction of a voltage has a value of zero. This ideally prevents the voltage induced in the sensor coil from crossing the zero line (see also Figure 3 left). This means that foreign objects can also be detected at these points. The simulation model of the sensor coil, like the model of the ground assembly coil, exploits the symmetry properties and therefore consists only of the upper half of the real differential coil shown in Figure 7.
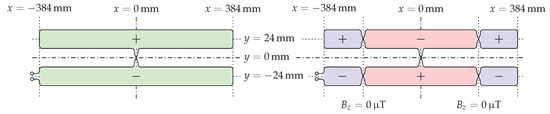
Figure 7.
Schematics of the sensor coil—the signs represent the orientation of the conductor loops, the colors indicate the induced voltage. (Left) Conventional version; (right) improved version.
4.2.1. Modeling of the Sensor Coils
For the measurements in [7], copper wire with a diameter of 0.3 mm was used for the sensor coils. If the sensor coils were modeled in the same way as the ground assembly coil of the charging system, mesh elements with a minimum size of about 140 μm would have to be used for the sensor coils. This in turn requires similarly small mesh elements in the adjacent air volume. Thus, a simulation with sensor coils would require significantly more simulation capacities than one without. For this reason, the voltages induced in the sensor coils were determined numerically. Following this approach, this can be done for a sensor coil of area A using the law of induction (Maxwell–Faraday equation) as follows:
where is the electric field in the sensor coil, is the contour line of the area A, is a path element of this contour, is the magnetic flux density that penetrates area A, and describes an element of area A.
For the calculation of the induced voltage using the electric field in the sensor coil, a circumferential vector must be defined in each conductor loop of the sensor coil. For such cases, COMSOL provides an boundary system consisting of two tangential vector variables and a normal vector, which are assigned to each surface. If several conductor loops of a sensor coil meet each other at an edge, then the tangential vector defined by COMSOL for these edges has the same direction for both conductor loops involved (Figure 8). Therefore, in such a case, the tangential vectors of the contour lines of the partial surfaces do not result in a circumferential vector for all the conductor loops. As a result, the direction of the tangential vector must be checked for each conductor loop and the calculation of the induced voltage must be adjusted manually if necessary. This method of calculation is therefore generally error-prone.

Figure 8.
Direction of the tangential vectors of the sensor coil plane calculated by COMSOL for a sensor coil with three different sections.
For this reason, the voltage induced in the sensor coils was determined based on the change in magnetic flux density over time. This calculation method uses the normal vector of the area in which the sensor coil is located. For all involved conductor loops, it is perpendicular to each partial surface enclosed by the sensor coil. Since in all simulations performed here the sensor coils are located in an xy-plane of the coordinate system, the calculation can be further simplified because only the component of the magnetic flux density in the z-direction can induce a voltage in the sensor coils.
4.2.2. Meshing of the Sensor Coils
In order to achieve high precision of the simulation results, the geometry of the sensor coil area was defined and meshed with the other components before the simulation was started. As with the modeling of the foreign objects, the meshing of the model can also influence the simulation results in this case. Therefore, using the example of a sensor coil with a single conductor loop of size 24 mm × 24 mm, the simulation model was manually meshed by a triangular mesh with a maximum element size of 2 mm. Based on this, the size of the mesh elements was changed using a variable factor. In addition to the sensor coil, the ground assembly coil and the ferrites were also included in this test. Figure 9 shows the test results.
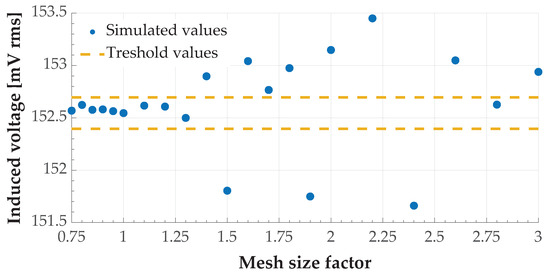
Figure 9.
Voltage induced in a sensor coil with size 24 mm × 24 mm as a function of the mesh size factor (, , ).
For an easier evaluation, arbitrary threshold values were chosen 0.15 mV below and above the reference value of the calculated voltage—the voltage at a mesh size factor of one. If a finer mesh is used (mesh size factor smaller than one), the value of the voltage induced in the sensor coil varies only slightly. If the mesh becomes coarser, the variation of the calculated voltage values increases significantly and exceeds one of the threshold values for the first time at a mesh size factor of 1.4. In general, however, the maximum variation remains within an acceptable range of about ±0.6%. The following simulations were performed with the mesh size used here as a reference.
4.2.3. Validation of the Simulation Model
The methods for simulating the voltage induced in a sensor coil were verified using the example of a coil with a single conductor loop of size 24 mm × 24 mm. In the case of a single conductor loop, the results show that the tangential vector generated by the software describes a closed loop in this conductor loop and the calculated voltage values are the same regardless of the calculation method selected from Equation (3). Figure 10 shows a comparison of the simulated voltage values and those measured in [7]. In general, there are only minor differences between the simulated and the measured voltage values.
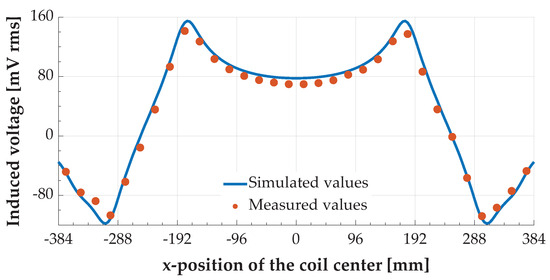
Figure 10.
Voltage induced in a sensor coil with size 24 mm × 24 mm as a function of its x-position (, ).
5. Detection of Metalic Foreign Objects
This section deals with the validation of the used simulation models based on the experimentally performed measurements and the simulation of arrangements not yet investigated by measurements. As for the measurements, for the simulations, the sensor coil was placed at a height of and the foreign objects at a height of . The sensor coils have an extension in x-direction of 768 mm and each conductor loop is 24 mm wide. The foreign objects are moved centrally above the sensor coil along its largest dimension. A current of 10 A rms flows through the ground assembly coil.
5.1. Validation of the Simulation Models
In the first step, the simulation models are validated by comparing the simulation results with the measured values. For this purpose, the influence on the sensor coil of both foreign objects—copper coin and steel nail—was simulated at different x-positions and with the same orientation as in the measurements (Figure 11). The sensor coil was divided into three subareas so that the induced voltages can be calculated from the simulation results for both a conventional design and for the improved design. During the measurements, the difference of the voltages induced in the subcoils of the real sensor coil was automatically generated due to the structure of the sensor coil. In contrast, in the simulation, only one half of the differential sensor coil is considered, since the second part is located symmetrically with respect to the ground assembly coil in the non-simulated part of the experimental setup. In order to be able to calculate the differential voltage in the sensor coil in the simulation with little effort, in addition to the simulations with a foreign object, one without a foreign object was also carried out. The result of this simulation is used as a reference for the simulations with a foreign object and is subtracted from them. The post-processing of the simulation results was done with MATLAB [17].

Figure 11.
Schematic of the simulation setup with sensor coil and foreign objects moving over it.
Figure 12 shows a comparison of the measured and simulated induced voltages in both the conventional and improved sensor coils for the 0.05€ coin and for the steel nail. The results of simulation and measurement match quite well. In the case of the improved sensor coil (Figure 12 right), deviations can be seen mainly in the areas where the z-component of the magnetic field of the ground assembly coil has the value zero. This is due to the fact that the individual conductor loops of the sensor coil should ideally end at these positions and indeed do so in the simulation. During the measurement, however, they could only be mapped quite inaccurately (with a difference of about 12 mm) due to the given grid of grooves in the carrier plate for placing the sensor coil. For both coil types, asymmetries of the measured values compared to the simulation results can be detected when comparing the values on both sides of the y-axis. This can be clearly seen in the case of the steel nail (Figure 12 bottom), where the induced voltage amplitudes are smaller than in the case of the 0.05€ coin. These symmetry deviations are related to the manual creation of the ground assembly coil and the sensor coils, as well as inaccuracies in the alignment of the carrier plate with respect to the ground assembly coil.
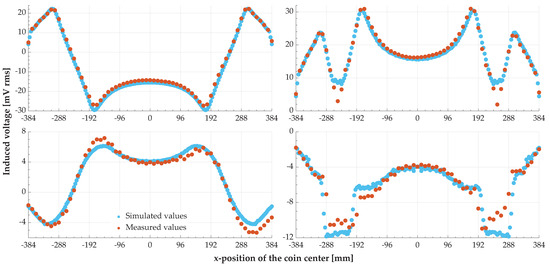
Figure 12.
Comparison of measurement and simulation results for different x-positions of the foreign objects. (Left) Conventional sensor coil; (right) improved sensor coil; (top) 0.05€ coin or copper coin; (bottom) steel nail.
5.2. Simulation of Non-Measured Arrangements
In the last simulation step, the dependence of the voltage induced in the sensor coils on the orientation of the foreign object was investigated. Since the steel nail, in contrast to the coin, does not have a rotationally symmetrical geometry in the xy-plane, these simulations were only carried out with the nail. The nail was rotated by 45° and by 90° for this purpose (Figure 13). In order to be able to rotate the steel nail by 90° and place it centrally above the sensor coil without it protruding from the simulation space, the center of the sensor coil was moved to the y-coordinate 60 mm. This also slightly changes the width of the three sections of the sensor coil, since the condition should still apply at the contact points of the individual conductor loops.
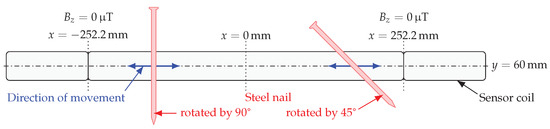
Figure 13.
Schematic of the simulation setup with sensor coil and rotated steel nail moving over it.
The results of the simulations can be seen in Figure 14. The further the nail is rotated, the smaller the part located above the sensor coil becomes, and thus, the smaller the influence on the magnetic field of the ground assembly coil that can be registered with the sensor coil. In a similar way, the effect of the improved shape of the sensor coil is affected. The further the nail is rotated, the less it protrudes into the two conductor loops of the sensor coil that abut at , and the smaller the achievable improvement in the simulated voltage amplitudes. If the voltage induced in the sensor coil reaches values smaller than 1 mV, the variation of the simulation results becomes comparatively very large.
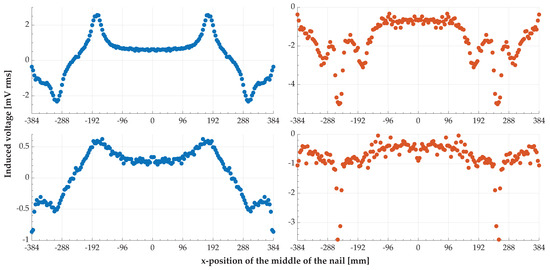
Figure 14.
Simulation results for the rotated steel nail. (Left) Conventional sensor coil; (right) improved sensor coil; (top) rotated by 45°; (bottom) rotated by 90°.
5.3. Precision of the Simulation Results
Especially when the values of the simulation results are close to zero, it can be seen very clearly that the simulation results vary slightly (see also Figure 14). To investigate this issue, voltage values from the simulations with a foreign object were analyzed, which are induced in a part of the sensor coil that is not influenced by the foreign object—one of the narrow conductor loops located at the edge of the sensor coil (see also Figure 11 and Figure 13). Again, the simulation without a foreign object was used as a reference. To calculate the simulated difference values, the reference value of the induced partial voltage was subtracted from the voltage values obtained in the presence of a foreign object in the system. The deviations of the calculated values from the expected value zero are shown in Figure 15.
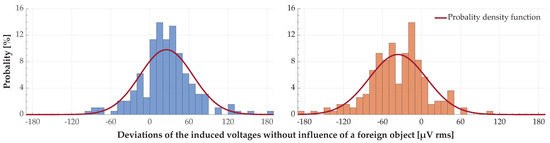
Figure 15.
Deviations of the induced voltage values in a part of the sensor coil for a total of 194 different simulations for each case. (Left) Sensor coil at position ; (right) sensor coil at position .
If the shown deviations of the simulated values of the induced voltages are approximated with a normal distribution for each case (see Figure 15), the parameters in Table 6 are obtained for them. The mean value of the normal distribution is a measure of the deviation of the result of the individual simulation without a foreign object from the mean value of the 194 simulations with a foreign object.

Table 6.
Parameters of the normal distributions approximated to the deviations of the simulated voltage values.
If a confidence interval of 99% is used as the basis, the simulation results vary by a value of about , which is about 104.75 μV and 113.16 μV, respectively. From Figure 14 it can be seen that there are significantly smaller deviations in the results for the conventional sensor coil than for the improved sensor coil. This indicates that the effective deviation with respect to the entire sensor coil depends mainly on the different calculation of the total voltage from the induced partial voltages. This means that the visible deviations are mainly influenced by the areas on both sides of the edges where the conductor loops get in touch. This results in a precision of the induced voltage of about ±0.42 mV to ±0.45 mV for the entire sensor coil. Whereby the deviations attributable to the individual subcoils are mostly compensated in the case of the conventional sensor coil due to its sign and maximized in the case of the improved variant.
Possible reasons for the deviations in the simulation results are the numerical accuracy of the calculations or slightly different meshings of the simulation model for different positions of the foreign object. However, a closer investigation is not part of this work.
5.4. Discussion of the Results of the Foreign Object Detection
In [7], an improvement of the sensor coils was proposed which allows to detect test objects even in areas where the relevant component of the magnetic field of the ground assembly coil has the value zero. During the simulations, the advantage of the improved design of the sensors became even more apparent, since the sensor coils could be modeled more accurately in terms of their size than it was the case during the practical measurements. This becomes especially apparent with foreign objects that either protrude only slightly into the involved conductor loops at the contact point of the sensor coil’s conductor loops, like the nail turned by 90° (Figure 14 bottom right), or which have only small dimensions with respect to the deviations from the optimal sensor coil design in the practical measurements, like the 0.05€ coin (Figure 12 top right).
Furthermore, the simulation results also show that the detectability of foreign objects, such as the steel nail, can still deteriorate compared to the practical measurements done in [7] if they have a different orientation relative to the sensor coil. In the practical realization of foreign object detection, this problem can be solved in at least two ways, and the listed points can also be combined:
- The measurements are performed only at the nominal operating currents of the charging system, which are about five to ten times higher for the system studied here than the value currently used in the simulation. This also increases the magnetic flux density and the voltage induced in the sensor coils;
- Additional sensor coils are used, which are located on a second level and are rotated by 90° compared to the sensor coil investigated here. With respect to the additional sensor coils, the steel nail rotated by 90° would again be aligned in parallel and thus induce a higher voltage.
The precision presented for the simulation results can possibly be further improved, e.g., by choosing a finer mesh or by lowering the tolerance limit of the solver. However, both measures are also associated with an increase in the simulation effort. Due to technical constraints, however, the precision of neither the practical measurements nor the simulations can be improved ad infinitum. In the practical measurements, for example, external interference signals and the inherent noise of the measurement hardware limit the achievable precision—in the simulations, the numerical accuracy of the calculations and the accuracy of the number format used have a limiting effect.
6. Conclusions
From the perspective of a wireless inductive charging system, the detection of metallic foreign objects represents a safety-relevant subfunction [1]. Within the ArchitectECA2030 project [5], the subcomponent of the charging system for metallic foreign object detection based on passive inductive sensors was investigated in more detail by measurements and simulations. In this paper, the results of the simulations are presented. For this purpose, the relevant subcomponents of a real charging system and two test objects were modeled. The main focus of the modeling was mainly on the interactions between magnetic field, metallic objects and voltages induced in the sensor coils. The simulations do not focus on the underlying operating principle of the sensor technology, as it is the case e.g., in [15,16,18], but concentrate on the practicality of the presented sensor technology. In this context, the influences of practical boundary conditions are considered, such as:
- Inhomogeneities of the magnetic field of the ground assembly coil;
- Influence of different material parameters;
- Effect of different material layers;
- Position of the foreign objects with respect to the ground assembly coil and the sensor coils;
- Orientation of the foreign objects with respect to the sensor coil.
In contrast, the simulations did not take into account:
- Other effects of the interaction of the magnetic field and the metallic foreign object, such as the heating of the foreign objects;
- The combination of different sensors for the detection of metallic and living objects and their possible mutual influence;
- The influence of aging effects, such as:
- −
- The contamination of surfaces;
- −
- The reduction of layer thicknesses due to wear.
- Weather influences, such as rain, snow or ice.
As with the practical measurements, only one test object was used at a time for each simulation. The results presented in Section 5 show that the simulation models created can be used to simulate the real electromagnetic influences of metallic foreign objects in the magnetic field on the sensor coils. Thus, the basic principle of virtual development based on already validated simulation models has been successfully demonstrated.
In future practical and simulative work, the sensors and the acquisition of measurement signals can be further improved. The presented results can also be used to compare the properties of the investigated sensors with sensors of other functional principles.
Author Contributions
Conceptualization, methodology, software, validation, formal analysis, investigation, data curation, writing—original draft preparation, visualization, U.H.; writing—review and editing, M.H. and A.W.; supervision, A.W. and N.M.; resources, project administration, funding acquisition, N.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research is part of ArchitectECA2030 and AI4CSM projects that have received funding from the ECSEL Joint Undertaking (JU) under grant agreement No 877539 and 101007326. The JU receives support from the European Union’s Horizon 2020 research and innovation programme and Germany, Austria, Belgium, Czech Republic, Italy, Netherlands, Lithuania, Latvia, France, Sweden, Norway. The projects on which this report is based was also funded by the German Federal Ministry of Education and Research under grant number 16MEE0109 and 16MEE0173. The content of this publication does not reflect the official opinion of the Joint Undertaking ECSEL or the German Federal Ministry of Education and Research. Responsibility for the information and views expressed therein lies entirely with the authors.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- SAE J2954:2020-10-20; Wireless Power Transfer for Light-Duty Plug-In/Electric Vehicles and Alignment Methodology. SAE International: Warrendale, PA, USA, 2020. [CrossRef]
- DIN EN IEC 61980-1:2021-09 VDE 0122-10-1:2021-09; Electric Vehicle Wireless Power Transfer (WPT) Systems—Part 1: General Requirements (IEC 61980-1:2020); German Version EN IEC 61980-1:2021. VDE: Offenbach am Main, Germany; DIN: Berlin, Germany, 2021.
- DIN CLC IEC/TS 61980-3:2021-10 VDE V 0122-10-3:2021-10; Electric Vehicle Wireless Power Transfer (WPT) Systems—Part 3: Specific Requirements for the Magnetic Field Wireless Power Transfer Systems (IEC/TS 61980-3:2019); German Version CLC IEC/TS 61980-3:2020. VDE: Offenbach am Main, Germany; DIN: Berlin, Germany, 2021.
- DIN EN ISO 19363:2021-02; Electrically Propelled Road Vehicles—Magnetic Field Wireless Power Transfer—Safety and Interoperability Requirements (ISO 19363:2020); English Version prEN ISO 19363:2020. DIN: Berlin, Germany, 2021.
- ArchitectECA2030. Trustable Architectures with Acceptable Residual Risk for the Electric, Connected and Automated Cars. Available online: https://architect-eca2030.eu/ (accessed on 15 March 2023).
- AI4CSM. Automotive Intelligence 4 Connected Shared Mobility. Available online: https://ai4csm.eu/ (accessed on 15 March 2023).
- Hentschel, U.; Labitzke, F.; Helwig, M.; Winkler, A.; Modler, N. Aspects of Foreign Object Detection in a Wireless Charging System for Electric Vehicles Using Passive Inductive Sensors. World Electr. Veh. J. 2022, 13, 241. [Google Scholar] [CrossRef]
- COMSOL Group. COMSOL Multiphysics® Simulation Software. Available online: https://www.comsol.com/comsol-multiphysics/ (accessed on 15 March 2023).
- New England Wire Technologies. Litz Wire Types and Constructions. Available online: https://www.newenglandwire.com/product/litz-wire-types-and-constructions/ (accessed on 15 March 2023).
- Blinzinger Electronik GmbH. Ferrites—Soft-Magnetic Ferrite Cores (MnZn). Available online: https://www.blinzinger-elektronik.de/en/ferrites/ferrite-blocks-ferrite-plates-ferrite-tiles-in-one-piece/ (accessed on 15 March 2023).
- Blinzinger Electronik GmbH. Data Sheet Ferrite Plate 120 × 40 × 6. Available online: https://www.blinzinger-elektronik.de/fileadmin/Daten/PDF/Ferritkerne/Datenblatt-Ferritplatte-120x40x6.pdf (accessed on 15 March 2023).
- European Central Bank. Common Sides. Available online: https://www.ecb.europa.eu/euro/coins/common/html/index.en.html (accessed on 15 March 2023).
- The Council of the European Union. COUNCIL REGULATION (EU) No 729/2014 of 24 June 2014 on Denominations and Technical Specifications of Euro Coins Intended for Circulation (Recast). Available online: https://https://eur-lex.europa.eu/legal-content/DE/TXT/?uri=CELEX:32014R0729 (accessed on 15 March 2023).
- Xiang, L.; Zhu, Z.; Tian, J.; Tian, Y. Foreign Object Detection in a Wireless Power Transfer System Using Symmetrical Coil Sets. IEEE Access 2019, 7, 44622–44631. [Google Scholar] [CrossRef]
- Thai, V.X.; Park, J.H.; Jeong, S.Y.; Rim, C.T.; Kim, Y.S. Equivalent-Circuit-Based Design of Symmetric Sensing Coil for Self-Inductance-Based Metal Object Detection. IEEE Access 2020, 8, 94190–94203. [Google Scholar] [CrossRef]
- Thai, V.X.; Jang, G.C.; Jeong, S.Y.; Park, J.H.; Kim, Y.S.; Rim, C.T. Symmetric Sensing Coil Design for the Blind-Zone Free Metal Object Detection of a Stationary Wireless Electric Vehicles Charger. IEEE Trans. Power Electron. 2020, 35, 3466–3477. [Google Scholar] [CrossRef]
- The MathWorks, Inc. Math. Graphics. Programming. Available online: https://www.mathworks.com/products/matlab.html (accessed on 15 March 2023).
- Meng, T.; Tan, L.; Zhong, R.; Xie, H.; Huang, X. Research on Metal Foreign Object Detection of Electric Vehicle Wireless Charging System Based on Detection Coil. World Electr. Veh. J. 2021, 12, 203. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).