Simplified Python Models for Photovoltaic-Based Charging Stations for Electric Vehicles Considering Technical, Economic, and Environmental Aspects
Abstract
1. Introduction
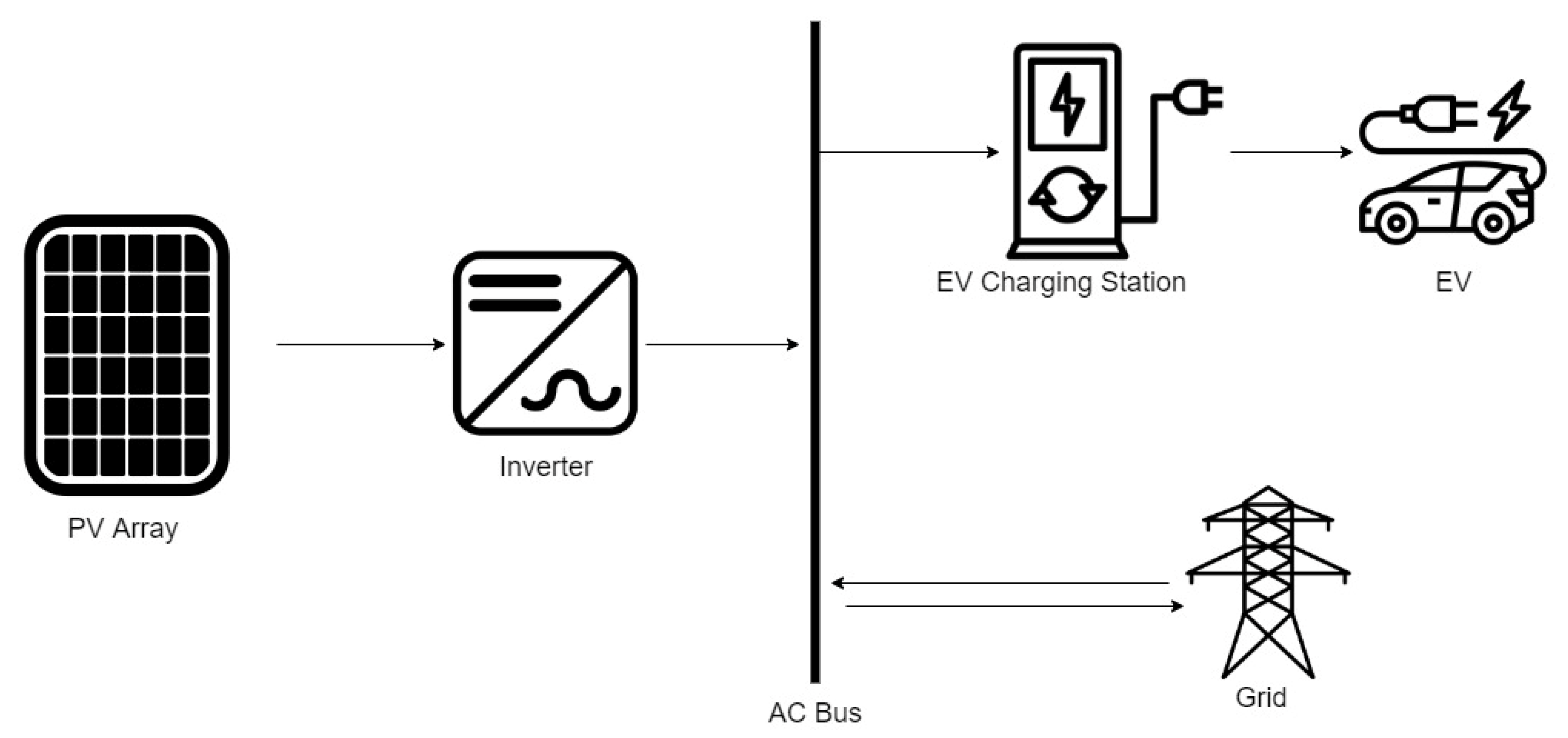
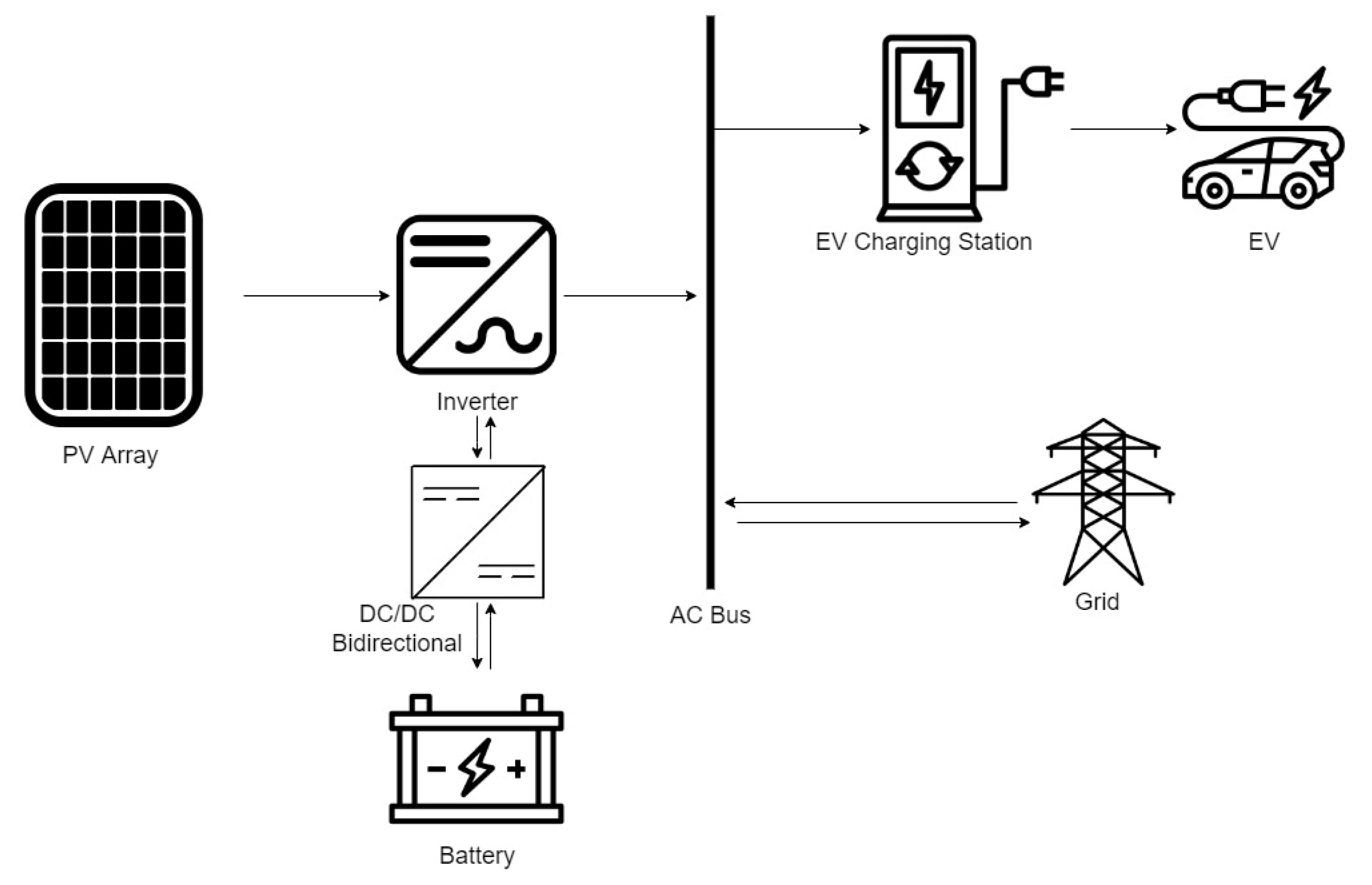
2. Modeling of EV Charging/Discharging System with Renewable Energy Resources
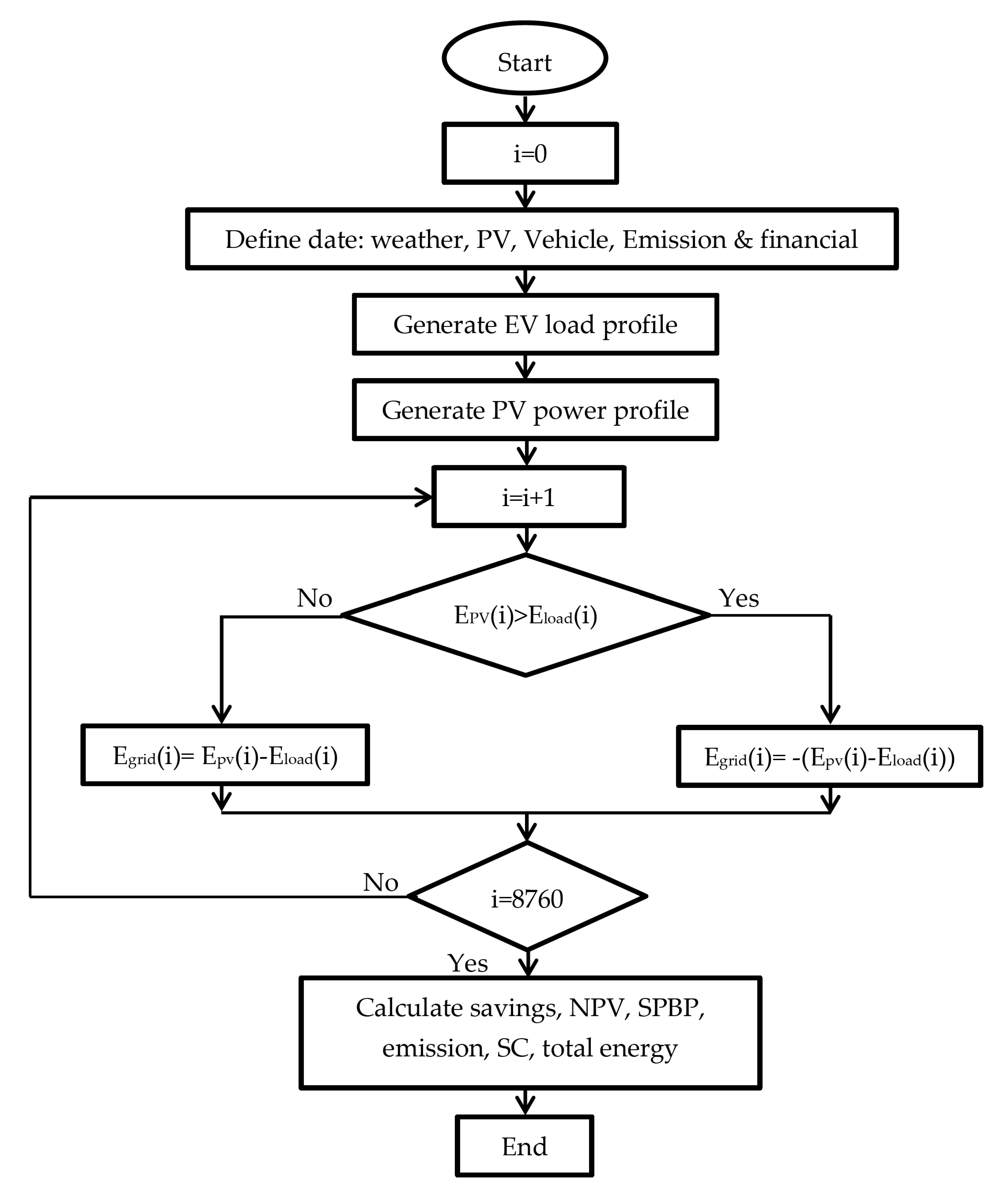
2.1. EV-Load Profile Generation
2.2. PV System Design
2.3. EV Charging Station Energy Models
2.4. Environmental Impact Modeling
2.5. Financial Parameters
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. (Python Codes)
Appendix A.1. PV/Grid Charging Station Code
Appendix A.2. PV/Grid/Battery Charging Station Code
References
- Adnan, N.; Nordin, S.M.; Rahman, I.; Vasant, P.; Noor, M.A. An Integrative Approach to Study on Consumer Behavior towards Plug-In Hybrid Electric Vehicles Revolution: Consumer Behavior towards Plug-In Hybrid Electric Vehicles. In Applied Behavioral Economics Research and Trends; IGI Global: Hershey, PA, USA, 2017. [Google Scholar]
- Parker, N.; Breetz, H.L.; Salon, D.; Conway, M.W.; Williams, J.; Patterson, M. Who saves money buying electric vehicles? Heterogeneity in total cost of ownership. Transp. Res. Part D Transp. Environ. 2021, 96, 102893. [Google Scholar] [CrossRef]
- Ahmad, F.; Iqbal, A.; Ashraf, I.; Marzband, M.; Khan, I. Optimal location of electric vehicle charging station and its impact on distribution network: A review. Energy Rep. 2022, 8, 2314–2333. [Google Scholar] [CrossRef]
- Zeb, M.Z.; Imran, K.; Khattak, A.; Janjua, A.K.; Pal, A.; Nadeem, M.; Zhang, J.; Khan, S. Optimal Placement of Electric Vehicle Charging Stations in the Active Distribution Network. IEEE Access 2020, 8, 68124–68134. [Google Scholar] [CrossRef]
- Torres, S.; Durán, I.; Marulanda, A.; Pavas, A.; Quirós-Tortós, J. Electric vehicles and power quality in low voltage networks: Real data analysis and modeling. Appl. Energy 2021, 305, 117718. [Google Scholar] [CrossRef]
- Tuan, L.A. Impacts of fast charging of electric buses on electrical distribution systems. CIRED Open Access Proc. J. 2017, 2017, 2350–2353. Available online: https://digital-library.theiet.org/content/journals/10.1049/oap-cired.2017.0802 (accessed on 1 October 2022).
- Mohsenzadeh, A.; Pazouki, S.; Ardalan, S.; Haghifam, M.-R. Optimal placing and sizing of parking lots including different levels of charging stations in electric distribution networks. Int. J. Ambient. Energy 2018, 39, 743–750. [Google Scholar] [CrossRef]
- Awasthi, A.; Venkitusamy, K.; Padmanaban, S.; Selvamuthukumaran, R.; Blaabjerg, F.; Singh, A.K. Optimal planning of electric vehicle charging station at the distribution system using hybrid optimization algorithm. Energy 2017, 133, 70–78. [Google Scholar] [CrossRef]
- Liu, Z.; Wen, F.; Ledwich, G. Optimal Planning of Electric-Vehicle Charging Stations in Distribution Systems. IEEE Trans. Power Deliv. 2013, 28, 102–110. [Google Scholar] [CrossRef]
- Zhu, Z.-H.; Gao, Z.-Y.; Zheng, J.-F.; Du, H.-M. Charging station location problem of plug-in electric vehicles. J. Transp. Geogr. 2016, 52, 11–22. [Google Scholar] [CrossRef]
- Battapothula, G.; Yammani, C.; Maheswarapu, S. Multi-objective simultaneous optimal planning of electrical vehicle fast charging stations and DGs in distribution system. J. Mod. Power Syst. Clean Energy 2019, 7, 923–934. [Google Scholar] [CrossRef]
- Moradi, M.H.; Abedini, M.; Tousi, S.R.; Hosseinian, S.M. Optimal siting and sizing of renewable energy sources and charging stations simultaneously based on Differential Evolution algorithm. Int. J. Electr. Power Energy Syst. 2015, 73, 1015–1024. [Google Scholar] [CrossRef]
- Islam, M.M.; Shareef, H.; Mohamed, A. Optimal location and sizing of fast charging stations for electric vehicles by incorporating traffic and power networks. IET Intell. Transp. Syst. 2018, 12, 947–957. [Google Scholar] [CrossRef]
- Falcão, E.A.M.; Teixeira, A.C.R.; Sodre, J.R. Analysis of CO2 emissions and techno-economic feasibility of an electric commercial vehicle. Appl. Energy 2017, 193, 297–307. [Google Scholar] [CrossRef]
- Laurischkat, K.; Jandt, D. Techno-economic analysis of sustainable mobility and energy solutions consisting of electric vehicles, photovoltaic systems and battery storages. J. Clean. Prod. 2018, 179, 642–661. [Google Scholar] [CrossRef]
- Kobashi, T.; Yarime, M. Techno-economic assessment of the residential photovoltaic systems integrated with electric vehicles: A case study of Japanese households towards 2030. Energy Procedia 2019, 158, 3802–3807. [Google Scholar] [CrossRef]
- Verma, A.; Raj, R.; Kumar, M.; Ghandehariun, S.; Kumar, A. Assessment of renewable energy technologies for charging electric vehicles in Canada. Energy 2015, 86, 548–559. [Google Scholar] [CrossRef]
- Fachrizal, R.; Shepero, M.; Åberg, M.; Munkhammar, J. Optimal PV-EV sizing at solar powered workplace charging stations with smart charging schemes considering self-consumption and self-sufficiency balance. Appl. Energy 2021, 307, 118139. [Google Scholar] [CrossRef]
- Han, X.; Garrison, J.; Hug, G. Techno-economic analysis of PV-battery systems in Switzerland. Renew. Sustain. Energy Rev. 2022, 158, 112028. [Google Scholar] [CrossRef]
- Kumar, V.; Teja, V.R.; Singh, M.; Mishra, S. PV Based Off-Grid Charging Station for Electric Vehicle. IFAC-PapersOnLine 2019, 52, 276–281. [Google Scholar] [CrossRef]
- Roselli, C.; Sasso, M. Integration between electric vehicle charging and PV system to increase self-consumption of an office application. Energy Convers. Manag. 2016, 130, 130–140. [Google Scholar] [CrossRef]
- Martin, H.; Buffat, R.; Bucher, D.; Hamper, J.; Raubal, M. Using rooftop photovoltaic generation to cover individual electric vehicle demand—A detailed case study. Renew. Sustain. Energy Rev. 2022, 157, 111969. [Google Scholar] [CrossRef]
- Deshmukh, S.S.; Pearce, J.M. Electric vehicle charging potential from retail parking lot solar photovoltaic awnings. Renew. Energy 2021, 169, 608–617. [Google Scholar] [CrossRef]
- Singh, A.; Shaha, S.S.; Nikhil, P.G.; Sekhar, Y.R.; Saboor, S.; Ghosh, A. Design and Analysis of a Solar-Powered Electric Vehicle Charging Station for Indian Cities. World Electr. Veh. J. 2021, 12, 132. [Google Scholar] [CrossRef]
- Chandra, G.R.; Bauer, P.; Zeman, M. System design for a solar powered electric vehicle charging station for workplaces. Appl. Energy 2016, 168, 434–443. [Google Scholar] [CrossRef]
- Tulpule, P.J.; Marano, V.; Yurkovich, S.; Rizzoni, G. Economic and environmental impacts of a PV powered workplace parking garage charging station. Appl. Energy 2013, 108, 323–332. [Google Scholar] [CrossRef]
- Good, C.; Shepero, M.; Munkhammar, J.; Boström, T. Scenario-based modelling of the potential for solar energy charging of electric vehicles in two Scandinavian cities. Energy 2019, 168, 111–125. [Google Scholar] [CrossRef]
- Li, C.; Shan, Y.; Zhang, L.; Zhang, L.; Fu, R. Techno-economic evaluation of electric vehicle charging stations based on hybrid renewable energy in China. Energy Strat. Rev. 2022, 41, 100850. [Google Scholar] [CrossRef]
- Bhatti, A.R.; Salam, Z.; Aziz, M.J.A.; Yee, K.P.; Ashique, R. Electric vehicles charging using photovoltaic: Status and technological review. Renew. Sustain. Energy Rev. 2016, 54, 34–47. [Google Scholar] [CrossRef]
- Brenna, M.; Foiadelli, F.; Leone, C.; Longo, M. Electric Vehicles Charging Technology Review and Optimal Size Estimation. J. Electr. Eng. Technol. 2020, 15, 2539–2552. [Google Scholar] [CrossRef]
- Sanguesa, J.A.; Torres-Sanz, V.; Garrido, P.; Martinez, F.J.; Marquez-Barja, J.M. A Review on Electric Vehicles: Technologies and Challenges. Smart Cities 2021, 4, 372–404. [Google Scholar] [CrossRef]
- Ciocia, A.; Amato, A.; Di Leo, P.; Fichera, S.; Malgaroli, G.; Spertino, F.; Tzanova, S. Self-Consumption and Self-Sufficiency in Photovoltaic Systems: Effect of Grid Limitation and Storage Installation. Energies 2021, 14, 1591. [Google Scholar] [CrossRef]
- Molina, M.B.T.; Prodanovic, M. Profitability assessment for self-sufficiency improvement in grid-connected non-residential buildings with on-site PV installations. In Proceedings of the 2013 International Conference on Clean Electrical Power (ICCEP), Alghero, Italy, 11–13 June 2013; pp. 353–360. [Google Scholar] [CrossRef]


| Power Level | Charger Location | Typical Use | Typical Power | Charging Time |
|---|---|---|---|---|
| Level 1 | On-board | Home | 1.3–2.4 kW | 40–50 h |
| Level 2 | On-board | Home, Workplace, and Public | 6.6–22 kW | 4–8 h |
| Level 3 | Off-board | Public DC Fast Station | 50–350 kW | <1 h |
| Vehicle Model | Number of Vehicles | Maximum Charging Power (kW) | Average Charging Duration (min) | kWh per Kilometer |
|---|---|---|---|---|
| Tesla Model 3 | 50 | 11 | 240 | 0.15 |
| Nissan Leaf | 50 | 6.6 | 240 | 0.18 |
| Hyundai IONIQ Electric | 50 | 7.2 | 240 | 0.16 |
| Input Voltage | 100 V/250 V/380 V (Three Phase) |
|---|---|
| Input frequency | 47~63 Hz |
| Max. output power | 7.6 kW/22 kW (Three Phase) |
| Max. output current | 32 A |
| Charging interface type | IEC 62196-2, SAE J1772 |
| Environment temperature | −40 °C~+80 °C |
| Protection degree | IP66 |
| Standby power consumption | <8 W |
| Number of Chargers | Assumed Session per Day | Actual Sessions per Day | Missed Sessions per Day |
|---|---|---|---|
| 5 | 20 | 12.4 | 7.6 |
| 10 | 20 | 18.5 | 1.5 |
| 15 | 20 | 19.9 | 0.1 |
| 20 | 20 | 19.9 | 0.1 |
| Month | EV Avg Monthly Load (kWh) | EV Avg Daily Load (kWh) |
|---|---|---|
| January | 17,161 | 554 |
| February | 15,970 | 570 |
| March | 19,000 | 613 |
| April | 16,803 | 560 |
| May | 16,926 | 546 |
| June | 17,208 | 574 |
| July | 16,724 | 539 |
| August | 19,263 | 621 |
| Sepeptember | 16,931 | 564 |
| October | 17,200 | 555 |
| November | 17,103 | 570 |
| December | 16,922 | 546 |
| Total | 207,211 | 567 |
| Month | Daily Average Irradiance (kWh/m2/day) | POA Irradiance (kWh/m2) | Daily Average Temperature (°C) |
|---|---|---|---|
| January | 4.20522 | 130.362 | 8.69 |
| February | 4.10834 | 115.034 | 10.55 |
| March | 6.03906 | 187.211 | 10.31 |
| April | 6.32847 | 189.854 | 15.3 |
| May | 7.64967 | 237.14 | 18.72 |
| June | 7.7606 | 232.818 | 20.37 |
| July | 7.89418 | 244.72 | 23.57 |
| August | 7.67325 | 237.871 | 23.18 |
| September | 6.96279 | 208.884 | 22.25 |
| October | 5.78391 | 179.301 | 20.35 |
| November | 4.19166 | 125.75 | 15.17 |
| December | 3.70693 | 114.915 | 10.03 |
| PV Net-Metering | PV Zero-Export | |||||
|---|---|---|---|---|---|---|
| System Capacity (kW) | 90 | 120 | 140 | 90 | 120 | 140 |
| Total PV Generation (kWh) | 149,633 | 199,506 | 232,752 | 97,190 | 103,389 | 105,788 |
| PV Energy Consumed locally (kWh) | 97,190 | 103,389 | 105,788 | 97,190 | 103,389 | 105,788 |
| Egrid exported (kWh) | 52,442 | 96,117 | 126,964 | 0 | 0 | 0 |
| Egrid Imported (kWh) | 110,020 | 103,821 | 101,422 | 110,020 | 103,821 | 101,422 |
| Self-Consumption Ratio (%) | 64.95 | 51.82 | 45.45 | 100% | 100% | 100% |
| Self-Sufficiency Ratio (%) | 46.90 | 49.89 | 51.05 | 46.90 | 49.89 | 51.05 |
| Payback Period (year) | 4.47 | 4.07 | 3.9 | 7.18 | 9.27 | 10.8 |
| Levelized Cost of Energy ($/kWh) | 0.057 | 0.056 | 0.055 | 0.088 | 0.108 | 0.122 |
| Total CO2 Saving (tCO2) | 240.34 | 275.25 | 298.53 | 203.63 | 207.97 | 209.65 |
| PV/Battery Net-Metering | PV/Battery Zero-Export | |||||
|---|---|---|---|---|---|---|
| System Capacity (kW) | 90 | 120 | 140 | 90 | 120 | 140 |
| Total PV Generation (kWh) | 149,633 | 199,506 | 232,752 | 137,099 | 152,385 | 156,623 |
| PV Energy Consumed locally (kWh) | 137,099 | 152,385 | 156,623 | 137,099 | 152,385 | 156,623 |
| Battery Energy (kWh) | 39,905 | 48,993 | 50,832 | 39,905 | 48,993 | 50,832 |
| Egrid exported (kWh) | 12,536 | 47,123 | 76,132 | 0 | 0 | 0 |
| Egrid Imported (kWh) | 70,111 | 54,825 | 50,587 | 70,111 | 54,825 | 50,587 |
| Self-Consumption Ratio (%) | 91.62% | 76.38 | 67.29 | 100% | 100% | 100% |
| Self-Sufficiency Ratio (%) | 66.16 | 73.54 | 75.58 | 66.16 | 73.54 | 75.58 |
| Payback Period (Year) | 6.75 | 6.14 | 5.90 | 7.37 | 8.07 | 8.85 |
| Levelized Cost of Energy ($/kWh) | 0.096 | 0.085 | 0.080 | 0.104 | 0.111 | 0.119 |
| CO2 Saving (tCO2) | 240.34 | 275.25 | 298.53 | 231.57 | 242.27 | 245.24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Direya, R.; Khatib, T. Simplified Python Models for Photovoltaic-Based Charging Stations for Electric Vehicles Considering Technical, Economic, and Environmental Aspects. World Electr. Veh. J. 2023, 14, 103. https://doi.org/10.3390/wevj14040103
Direya R, Khatib T. Simplified Python Models for Photovoltaic-Based Charging Stations for Electric Vehicles Considering Technical, Economic, and Environmental Aspects. World Electric Vehicle Journal. 2023; 14(4):103. https://doi.org/10.3390/wevj14040103
Chicago/Turabian StyleDireya, Rezeq, and Tamer Khatib. 2023. "Simplified Python Models for Photovoltaic-Based Charging Stations for Electric Vehicles Considering Technical, Economic, and Environmental Aspects" World Electric Vehicle Journal 14, no. 4: 103. https://doi.org/10.3390/wevj14040103
APA StyleDireya, R., & Khatib, T. (2023). Simplified Python Models for Photovoltaic-Based Charging Stations for Electric Vehicles Considering Technical, Economic, and Environmental Aspects. World Electric Vehicle Journal, 14(4), 103. https://doi.org/10.3390/wevj14040103







