Abstract
To enhance the speed stability and anti-interference performance of the interior permanent magnet synchronous motor (IPMSM) in electric vehicles, a composite control strategy, incorporating sliding mode control (SMC) and extended state observer (ESO), was implemented to regulate the IPMSM’s speed. Firstly, three simulation analysis models of the IPMSM were established based on its electrical parameters. The current-loop regulator was a PI regulator, while the speed-loop regulators consisted of a basic SMC regulator, a linear SMC–ESO regulator, and a nonlinear SMC–ESO regulator. The simulation analysis results demonstrated that all three speed-loop regulators effectively ensured the speed stability of the IPMSM. However, the nonlinear SMC–ESO regulator exhibited superior performance in terms of enhancing the IPMSM’s resistance to disturbances. Secondly, a hardware testing platform was constructed to validate the simulation analysis findings. The hardware testing results, when compared to the simulation analysis results, revealed the need for optimization of the PI regulator’s control parameters to maintain the speed stability of the IPMSM. Moreover, contrary to the simulation analysis results, the hardware testing results indicated minimal difference in the anti-disturbance performance of the IPMSM between the linear SMC–ESO regulator and the nonlinear SMC–ESO regulator. Finally, the differences between the simulation analysis results and the hardware testing results are thoroughly discussed and analyzed, providing valuable insights for the practical implementation of IPMSM in electric vehicle drive systems.
1. Introduction
Currently, the permanent magnet synchronous motor (PMSM) for electric vehicles has garnered attention from both scholars and manufacturers [1,2]. The operational stability and safety of electric vehicles rely heavily on the speed regulation (specifically, speed stability) and anti-disturbance performance of the PMSM. Therefore, a comprehensive study into the speed regulation of the PMSM is necessary to enhance the driving stability of electric vehicles. Simultaneously, the anti-disturbance performance of the PMSM plays a pivotal role in ensuring rapid response capability and stability of electric vehicles [3]. Building upon the development of nonlinear control theory, various approaches such as adaptive control, fuzzy neural network control and predictive control have been employed to address the speed regulation and anti-disturbance performance of the PMSM [4,5,6,7]. However, the implementation of the nonlinear control theory through computer programs necessitates high-speed computing performance from the hardware controller. Despite these efforts, the speed fluctuation of the PMSM persists due to the inherent nature of nonlinear control theory. Hence, further exploration and research are required to advance the speed stability and anti-disturbance performance of the PMSM.
The Active Disturbances Rejection Control (ADRC) strategy has been widely employed in the enhancement of speed control and anti-disturbance performance of PMSM. By utilizing an ADRC system comprising an Expansion State Observer (ESO) and a Sliding Mode Control (SMC) model, the ESO can effectively observe the speed error and load error of the PMSM, while the SMC model ensures rapid convergence of these errors. It is worth noting that the ADRC system can also incorporate various other types of observers and control models. In recent years, several ADRC strategies have been proposed and studied. For instance, Yang et al. introduced a novel ADRC strategy featuring a double degree-of-freedom (DOF) control model and an extended Kalman filter (EKF). This strategy aims to achieve fast dynamic response and robust anti-interference capability for PMSMs. The effectiveness of this proposed strategy was validated through comprehensive simulations and experimental analyses [8]. In addition, Gabbi et al. proposed a discrete-time SMC model that leverages disturbance observers and discrete digital time delay to mitigate speed fluctuations (caused by load variations) in PMSMs. The simulation and experimental results substantiated the efficacy of this method [9].
However, the insufficiency of accurate PMSM modeling poses a challenge to the effectiveness of the traditional ADRC strategy, particularly in low-speed conditions and for unconventional PMSM structures such as IPMSM, switched reluctance motor (SRM) and multiple-phase PMSM [10,11,12]. In addition, while the ADRC strategy primarily focuses on speed-loop regulation in PMSM, theoretical analysis indicates that current-loop regulation significantly impacts speed stability and anti-disturbance performance in PMSM [13,14]. Therefore, this study delves into the composite control of speed-loop and current-loop in IPMSM, with a specific emphasis on assessing and comparing three control models for the speed-loop. Notably, the IPMSM distinguishes itself from traditional PMSM through the inclusion of permanent magnets embedded in the rotor, resulting in high power density and a superior torque/inertia ratio [15,16,17].
This paper appraises a composite control strategy for improving the speed stability and anti-interference performance of IPMSM of electric vehicles. The primary objectives of this research are outlined as follows. Firstly, analysis and presentation of the theoretical model for the composite control strategy of the IPMSM are conducted. The current-loop regulator was implemented as a PI regulator, while the speed-loop regulators consisted of the basic SMC regulator, the linear SMC–ESO regulator and the nonlinear SMC–ESO regulator. Secondly, a comparative analysis of the theoretical simulation results was performed among the speed-loop regulators, namely, the basic SMC, linear SMC–ESO and nonlinear SMC–ESO, using the same parameter settings as the PI regulator. The findings of the theoretical simulation analysis demonstrated that the nonlinear SMC–ESO regulator exhibited the most effective performance in enhancing the anti-interference capabilities of the IPMSM. Thirdly, the theoretical simulation analysis results were validated through hardware experimental testing. The verification results indicated that both the linear SMC–ESO and nonlinear SMC–ESO regulators yielded similar effects in maintaining the anti-interference performance of the IPMSM. Finally, a comprehensive discussion and analysis are conducted to explicate the differences between the theoretical simulation analysis results and the hardware experimental testing results.
2. Mathematical Model and Regulator Design of IPMSM
2.1. Mathematical Model of IPMSM
The mechanical motion equation of IPMSM can be written as
where represents the rotational inertia, denotes the mechanical angular velocity, indicates the electromagnetic torque, signifies the load torque and expresses the damping coefficient [18]. Additionally, in terms of a dq two-phase synchronous rotating coordinate system, if the d-axis current is assumed as , then the electromagnetic torque can be expressed as
where represents the number of pole pairs, denotes the excitation flux (excitation flux linkage of permanent magnets) and signifies the q-axis current.
2.2. Current-Loop Regulator Design of IPMSM
In some references of PMSM and IPMSM, the current-loop was also named as the inner-loop [19]. This paper adopts a PI regulator as the current-loop regulator of IPMSM. In terms of a dq two-phase synchronous rotating coordinate system, the PI regulator of IPMSM can be expressed as
where the subscript symbols and represent the d-axis and q-axis, respectively, and denote the voltages, and signify the proportional coefficient, and depict the integral coefficient, and express the set value of current, and convey the feedback value of current, and stand for the inductances and refers to the electric angular velocity [20].
After theoretical analysis, the regulating parameters of the PI regulator for the d-axis current-loop and q-axis current-loop of IPMSM can be written as
where and is the resistance of stator phase winding.
The purpose of the current-loop regulator design was to swiftly provide the desired values for the d-axis current and q-axis current of IPMSM. However, the specific magnitude of the desired values for the d-axis current and q-axis current was determined by the speed-loop regulator of the IPMSM.
2.3. Speed-Loop Regulator Design of IPMSM
This paper introduces three speed-loop regulators, namely, the basic SMC regulator, the linear SMC–ESO regulator and the nonlinear SMC–ESO regulator, to investigate the speed stability and anti-interference performance of the IPMSM.
- (1)
- Basic SMC regulator design
In the d-axis current term , the q-axis current and mechanical angular speed of the IPMSM can be written as a new equation system [21]:
Define parameter as the error between mechanical angular speed’ constant value and feedback value :
where the symbol ‘’ signifies a derivation. Adopt the basic sliding mode surface and derive its expression as
Then, the q-axis current in Equation (7) can be expressed as
where represents the design parameters, denotes the constant velocity approach rate, signifies the symbolic function and indicates the exponential approach rate.
Equation (8) indicates that the error between mechanical angular speed’ constant value and feedback value can be converted to the q-axis current and the q-axis current is the input value of current-loop of IPMSM (see Equation (3)). Therefore, Equation (8) signifies the basic SMC regulator of IPMSM.
- (2)
- Linear SMC–ESO regulator design
ESO can also be applied in various fields such as mechanical processing, robotics motion control and unmanned aerial vehicle systems, etc. In this study, the load interference and speed fluctuation of the IPMSM were considered as new parameters by the ESO. The load interference refers to external interference, while the speed fluctuation pertains to internal interference.
According to the Equation (1) of IPMSM mathematical model, the linear second-order ESO can be written as
where represents the speed fluctuation observer of IPMSM, denotes the load interference observer of IPMSM and indicates the pole of linear second-order ESO [22,23].
Figure 1 shows the basic structure of linear second-order ESO (corresponding to Equation (1)). In Figure 1, the transfer function from to can be written as
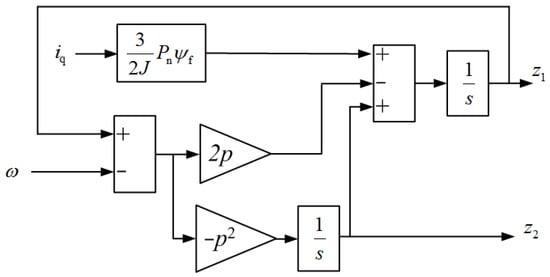
Figure 1.
The basic structure of linear second-order ESO.
If the q-axis current , then Equation (10) can be simplified as
Equation (11) indicates that the speed fluctuation observer is the low pass filter of IPMSM’s speed .
In the same way, the transfer function from to can be written as
Equation (12) shows that the load interference observer is the second-order low pass filter of IPMSM’s q-axis current .
According to the ESO theory, the pole decides the performance of linear second-order ESO. The more distance between pole and the imaginary axis, the better anti-disturbance and response performance of load interference observer . However, the more distance between pole , the more the imaginary axis can distort the filter effect of speed fluctuation observer , which may even result in system instability of IPMSM. Therefore, the value of pole should be selected based on the actual situation of IPMSM, especially in the condition of imprecise mathematical model of IPMSM.
After making a transformation on the load interference observer of a linear second-order ESO, and subsequently transmitting it to the input variable of the current loop of an IPMSM, a speed-loop regulator for the IPMSM was achieved, which was named as the linear SMC–ESO regulator.
- (3)
- Nonlinear SMC–ESO regulator design
Based on Equation (9)’s linear second-order ESO, a nonlinear second-order ESO was proposed in this paper, and its mathematical expression can be written as
where represents the design parameter, denotes the filter factor and the nonlinear function can be written as
In Equations (13) and (14), the design parameter represents a constant between 0 and 1. Under normal circumstances, the value range of filter factor is from to , where denotes the sample time. The larger filter factor , the better the filter effect of nonlinear second-order ESO and nonlinear function .
In addition, the smaller design parameter , the better target tracking ability of nonlinear second-order ESO and nonlinear function . However, it should be noted that the smaller design parameter reduces the filter effect of nonlinear second-order ESO and nonlinear function . Therefore, before the design parameter is decided, comprehensive experimental testing and analysis should be carried out between the design parameter and filter factor .
By incorporating the Equation (13) form of the nonlinear second-order ESO into the linear SMC–ESO regulator, an enhanced SMC–ESO regulator, referred to as the nonlinear SMC–ESO regulator, was devised.
3. Simulation Analysis
To verify the effectiveness of the aforementioned current-loop regulator and speed-loop regulators, the simulation models of the IPMSM were established, and the basic structure of IPMSM was shown in reference [21]. Figure 2 illustrates the system framework of the IPMSM simulation model.
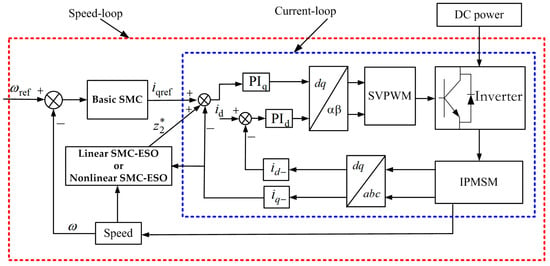
Figure 2.
System frame of simulation model of IPMSM.
In Figure 2, the d-axis current-loop regulator and q-axis current-loop regulator of IPMSM were the PI regulator. The speed-loop regulators of IPMSM were the basic SMC regulator, linear SMC–ESO regulator and nonlinear SMC–ESO regulator. During the simulation process, the input value of d-axis current-loop remained zero, and the regulating parameters of d-axis current-loop regulator and q-axis current-loop regulator of IPMSM were decided by the Equation (4), which tested and compared the performance differences among the above three speed-loop regulators.
The main electrical parameters of IPMSM are shown in Table 1.

Table 1.
Electrical parameters of IPMSM.
The other basic parameters parameter settings of simulation process of IPMSM are presented as follows:
- (1)
- d-axis current-loop regulator: , , ;
- (2)
- q-axis current-loop regulator: , , ;
- (3)
- Speed-loop regulator (basic SMC regulator): , , .
In Figure 3, the start-up response of IPMSM in the absence of any external load is depicted. The pole of ESO was set at 500, while the design parameter and filter factor of the nonlinear function were assigned values of 0.001 and 10, respectively. Based on the observations made from Figure 3a, it can be deduced that the overshoot and stabilization time of the speed response of the IPMSM remain nearly identical across the three speed-loop regulators (basic SMC regulator, linear SMC–ESO regulator and nonlinear SMC–ESO regulator). Furthermore, in the steady-state speed of the IPMSM, the steady-state value of the input q-axis current (i.e., the sum of q-axis current and ESO’s observed current , as shown in Figure 2) obtained from the three speed-loop regulators also exhibited identical characteristics. Therefore, Figure 3 provides evidence that both the linear SMC–ESO regulator and the nonlinear SMC–ESO regulator did not exhibit superiority over the basic SMC regulator during the start-up process and steady-state speed of the IPMSM.
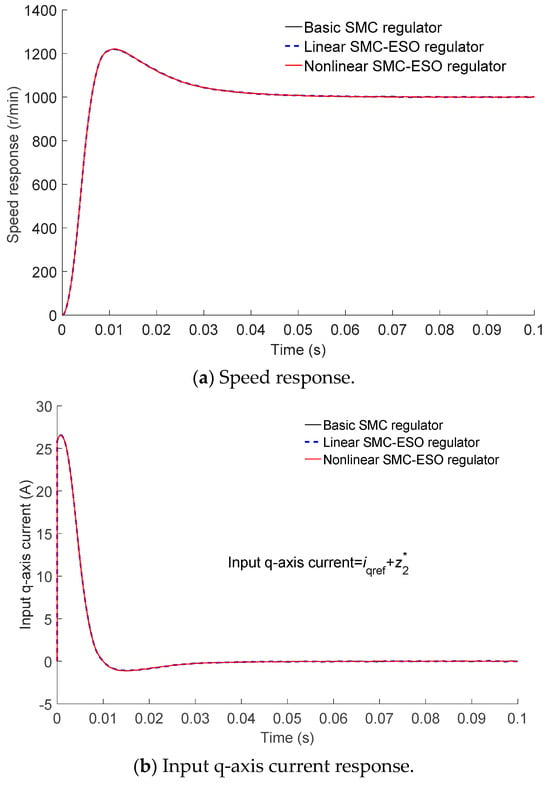
Figure 3.
Start-up response of IPMSM with no-load.
At 0.2 s, a step load of 5 N·m was applied to the rotor of the IPMSM. The subsequent anti-disturbance performance of the IPMSM, including the speed response and input q-axis current response, is depicted in Figure 4. In Figure 4a, the speed of the IPMSM decreases to 891 r/min when employing the fundamental SMC regulator. Conversely, the speed reductions for the linear SMC–ESO regulator and the nonlinear SMC–ESO regulator are 926 r/min and 947 r/min, respectively. Notably, the steady-state speed recovery time of the IPMSM using the nonlinear SMC–ESO regulator was shorter compared to that of both the fundamental SMC regulator and the linear SMC–ESO regulator. Therefore, Figure 4a demonstrates that the nonlinear SMC–ESO regulator minimized the speed fluctuation of the IPMSM and served as the optimal speed-loop regulator for enhancing the anti-disturbance performance of the IPMSM. Figure 4b illustrates the input q-axis current response corresponding to the speed response in Figure 4a. In Figure 4b, the response times for these three regulators were 5.17 ms, 2.72 ms and 0.64 ms, respectively. This phenomenon indicated that the nonlinear SMC–ESO regulator exhibited a faster response and superior anti-disturbance performance. Moreover, the nonlinear SMC–ESO regulator improved the steady-state speed recovery of the IPMSM by minimizing the largest overshoot and secondary fluctuation of the input q-axis current.
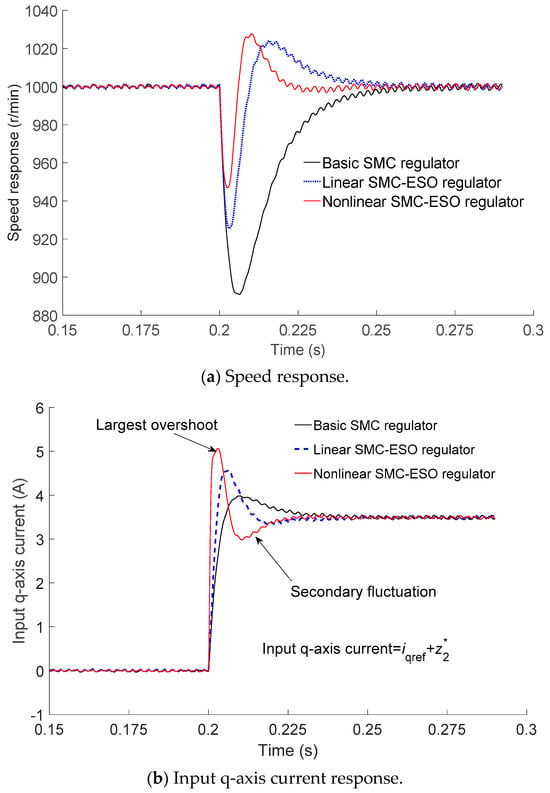
Figure 4.
Anti-disturbance performance of IPMSM with step load.
The q-axis current response of IPMSM under step load conditions is depicted in Figure 5. The step load magnitude was 5 N·m. A comparative analysis between Figure 5 and Figure 4b serves to further substantiate the superior performance and enhanced disturbance rejection capabilities of the nonlinear SMC–ESO regulator.
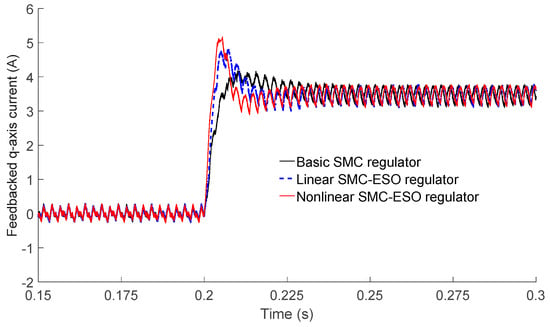
Figure 5.
Feedback q-axis current of IPMSM step load.
4. Experimental Test and Improvement
4.1. Experimental Setup
The experimental setup of the IPMSM system is illustrated in Figure 6. It comprised a PC, an IPMSM, an encoder (installed in the back end part of IPMSM), a DC power source, an inverter, a controller, three current sensors, a magnetic particle brake and a power meter. The PC-controller data communication facilitated real-time and visual control of the IPMSM, which was commonly referred to as the real-time control system in the relevant literature. Throughout the experimental testing process, the software program sampled at a frequency of 0.001 s, while the inverter operated at a switching frequency of 1000 Hz. In addition, the electrical parameters of the IPMSM aligned with those specified in Table 1 of the simulation analysis section.

Figure 6.
Experimental setup of the IPMSM system.
4.2. Speed Stability Test and Improvement
It should be acknowledged that differences often arise between the theoretical model of the IPMSM and its hardware implementation. These differences are due to the inherent limitations of theoretical models in accurately capturing the intricacies of the hardware system. Factors such as the damping coefficient, rotor inertia, phase resistance and inductance of the IPMSM are subject to variations induced by the winding temperature, rotor speed and load conditions. Therefore, the experimental testing process started up with a focus on assessing and enhancing the speed stability of the IPMSM.
Figure 7 depicts the comparison of speed stability for IPMSM. The parameters for the speed-loop regulator (basic SMC regulator) were maintained as , and . The original Proportional–Integral (PI) parameters and the improved PI parameters for the current-loop regulators are presented in Table 2. The speed fluctuation rate of the IPMSM, calculated using Equation (4) with the original PI parameters from Table 2, amounted to 18.2% ((maximum value − minimum value)/set value). However, considering the switching frequency of the inverter and based on comparative test results, the improved PI parameters were determined through an exploratory method (test results comparison). Accordingly, the speed fluctuation rate of the IPMSM was reduced to 3.8%.
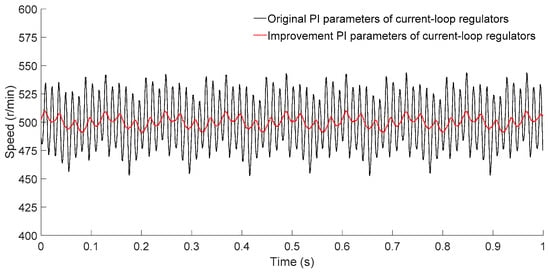
Figure 7.
Speed stability comparison of IPMSM (measured by the current sensor and collected by the software system of PC, see Figure 6a,b).

Table 2.
PI parameters of d-axis current-loop regulator and q-axis current-loop regulator.
Moreover, to ensure the comparability of speed test results and avoid the influence of high-order harmonics from the oscilloscope, the speed data of the IPMSM/s, as shown in Figure 7, were measured using a current sensor and collected by a PC-based software system. During the experimental test process, the self-protection mechanism of the inverter caused frequent shutdowns when the speed set value of the IPMSM was 1000 r/min. Therefore, a speed set value of 500 r/min was employed for all hardware tests conducted on the IPMSM system.
Moreover, the comparison of speed stability results, based on the linear SMC–ESO regulator and the nonlinear SMC–ESO regulator for the speed-loop regulator, indicated that the improved PI parameters for the current-loop regulators could effectively reduce the speed fluctuation rate of the IPMSM. Therefore, in the subsequent sections concerning the start-up response test and anti-disturbance performance test, the improved PI parameters from Table 2 were adopted for the d-axis current-loop regulator and q-axis current-loop regulator of the IPMSM.
4.3. Start-Up Response Test
Premised on the enhanced PI parameters of the d-axis current-loop regulator and q-axis current-loop regulator, the start-up response of IPMSM was assessed and compared using the aforementioned three speed-loop regulators, as depicted in Figure 8. Figure 8 shows that the start-up speed of the IPMSM was measured by the power meter and displayed by the oscilloscope (Figure 6b), and the target constant-speed was 500 r/min.
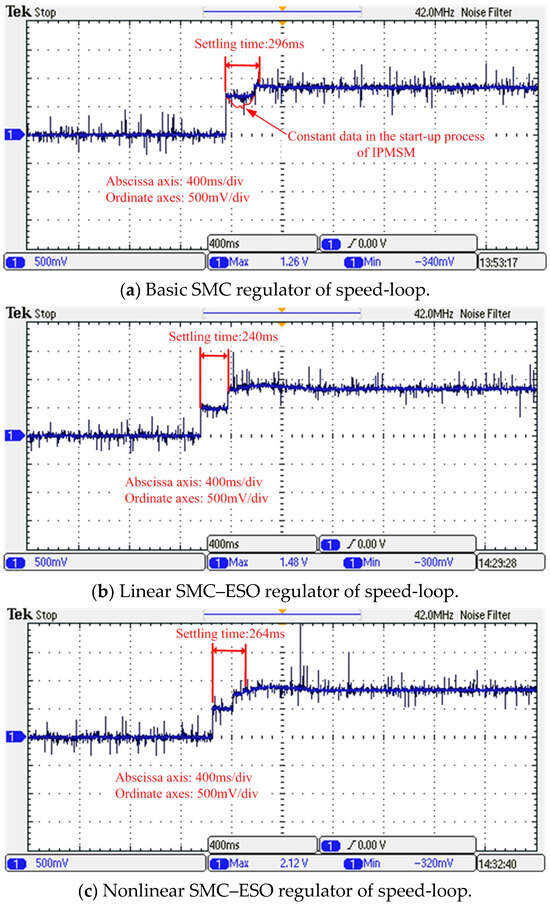
Figure 8.
Start-up response test of IPMSM (measured by the power meter and displayed by the oscilloscope).
For the basic SMC regulator in the speed-loop, the settling time of the IPMSM’s start-up speed was measured to be 296 ms. Conversely, for the linear SMC–ESO regulator and the nonlinear SMC–ESO regulator in the speed-loop, the settling times of the IPMSM’s start-up speed were determined to be 240 ms and 264 ms, respectively. In summary, Figure 8 demonstrates that the settling time of the IPMSM’s start-up speed remained nearly identical across the three aforementioned speed-loop regulators.
Comparing the tested average settling time of the IPMSM with the simulation analysis results presented in Figure 3a, it was evident that the former was smaller. This discrepancy can be attributed to the improved PI parameters of the d-axis current-loop regulator and q-axis current-loop regulator. Additionally, the start-up process of the IPMSM exhibited anomalous constant data phenomena (constant data in the start-up process of IPMSM of Figure 8a) due to the low output resolution of speed measurement for the power meter.
4.4. Anti-Disturbance Performance Test
To assess the anti-disturbance performance of the three speed-loop regulators, Figure 9 presents the response of IPMSM to a step load, with a constant speed of 500 r/min and a step load of 1.5 N·m. When the step load was applied to the rotor of the IPMSM, the settling time and speed fluctuation of the basic SMC regulator were approximately 760 ms and 147 r/min, respectively. However, when considering the linear SMC–ESO regulator and the nonlinear SMC–ESO regulator, the settling times were approximately 368 ms and 320 ms, respectively, with corresponding speed reductions of 94 r/min and 88 r/min. Therefore, it was evident that the anti-disturbance performances of both the linear SMC–ESO regulator and the nonlinear SMC–ESO regulator surpass that of the basic SMC regulator.
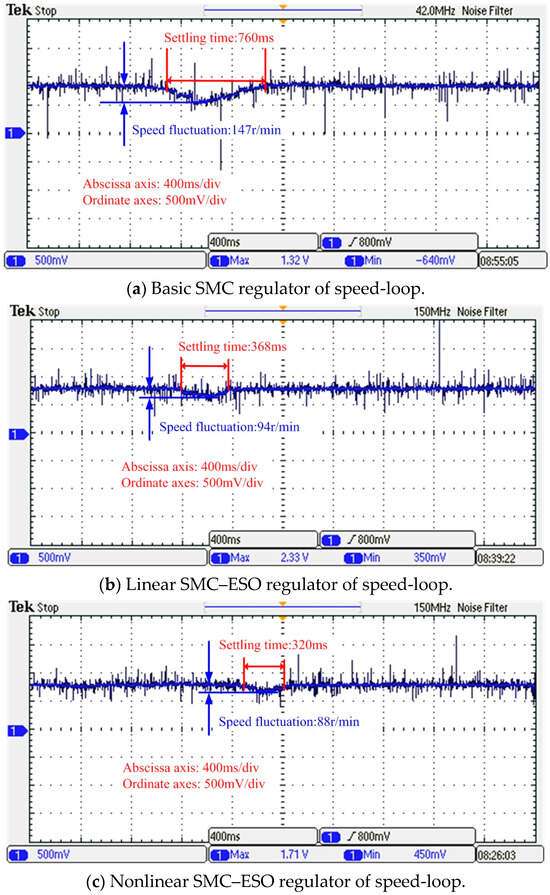
Figure 9.
Anti-disturbance performance test of IPMSM.
Additionally, throughout the multiple tests conducted to evaluate the anti-disturbance performance of the IPMSM, the disparity in settling time and speed fluctuation between the linear SMC–ESO regulator and the nonlinear SMC–ESO regulator was not pronounced (in comparison to the simulation results depicted in Figure 4a). This phenomenon can be attributed to the following factors:
- (1)
- The sampling frequency of the utilized software program was relatively low, resulting in a slower and less accurate transmission of the speed signal from the encoder to the controller;
- (2)
- The output resolution of speed measurement for the power meter was insufficient, thereby impeding the timely collection of the differences in settling time and speed fluctuation between the linear SMC–ESO regulator and the nonlinear SMC–ESO regulator by the oscilloscope.
5. Discussion
In the speed stability test, the speed fluctuation rate of IPMSM was reduced from 18.2% to 3.8% through the implementation of improved PI parameters in the current-loop regulator (Figure 7 of Section 4.2). However, when the same improved PI parameters of the current-loop regulator in the hardware system were applied to the simulation model of the IPMSM and the parameters of the speed-loop regulator (basic SMC regulator) were kept consistent with those of the hardware system, the speed fluctuation rate of the simulation results for the IPMSM increased, as depicted in Figure 10.
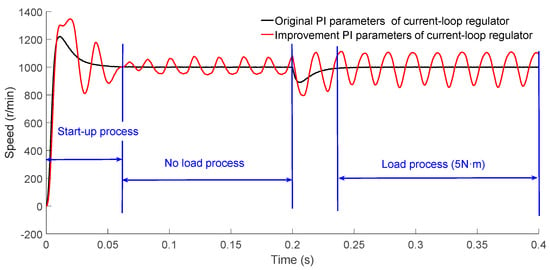
Figure 10.
The simulation results of current-loop regulator with original and improved PI parameters.
From the analysis presented in Figure 10, it can be deduced that the implementation of the improved PI parameters in the current-loop regulator led to a higher-speed fluctuation rate for the IPMSM throughout its operational processes. Specifically, the settling time of the start-up process was approximately 0.6 s, the speed fluctuation rate during the no-load process was approximately 13.2% and the speed fluctuation rate during the load process was approximately 25.3%. The corresponding reasons are as follows:
- (1)
- Discrepancies arose between the damping coefficient employed in the hardware testing phase and that utilized in the simulation analysis. In the former, the enhanced PI parameters were derived based on the actual damping coefficient of IPMSM. However, due to the challenge of evaluating the damping coefficient of IPMSM, it was assumed to be zero during the simulation analysis;
- (2)
- The simulation model of IPMSM did not precisely correspond to the features of its hardware system, resulting in inaccuracies pertaining to the flux linkage, rotor inertia and dq-axis inductances;
- (3)
- Throughout the hardware testing phase, the actual power quality of the inverter, the accuracy of the encoder and current sensors and the execution process of the software program exerted a significant influence on the selection of optimal PI parameters.
Therefore, the comparison between the results obtained from simulation analysis and hardware testing may provide valuable insights for the practical application of IPMSM in electric vehicle drive systems.
6. Conclusions
This paper adopts three speed-loop regulators to investigate the stability and anti-interference performance of IPMSM. Firstly, following theoretical analysis and modeling, the simulation results indicated that the three speed-loop regulators possessed the same functionality in ensuring the speed stability of IPMSM. However, the nonlinear SMC–ESO regulator emerged as the optimal speed-loop regulator for enhancing the anti-interference performance of IPMSM. Secondly, based on the simulation results, the PI parameters of the current-loop regulator of IPMSM were refined during the experimental testing phase, with the objective of improving the speed stability of the IPMSM system. Thirdly, leveraging the improved PI parameters of the current-loop regulator, the anti-interference performance of IPMSM was assessed. The test results demonstrated that both the linear SMC–ESO regulator and the nonlinear SMC–ESO regulator outperformed the basic SMC regulator. However, due to limitations inherent in the software and hardware systems, such as the sampling frequency, power meter and actual physical model, the linear SMC–ESO and nonlinear SMC–ESO regulators exhibited similar effects in maintaining the anti-interference performance of IPMSM, which deviated from the simulation results. Finally, the discussion section of this paper analyzes the difference between the simulation results and the hardware experimental testing results. The simulation calculations, hardware experimental tests and difference analysis of the speed-loop regulators may contribute to the practical application of IPMSM in electric vehicle drive systems.
Author Contributions
Conceptualization, Z.C. and X.D.; methodology, Z.C.; software, X.D. and M.F.; validation, Z.C.; writing—original draft preparation, Z.C.; writing—review and editing, X.D. All authors have read and agreed to the published version of the manuscript.
Funding
This work was financially supported by the Scientific and Technological Project in Henan Province under Grant No. 232102241024.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Badini, S.S.; Verma, V. Parameter independent speed estimation technique for PMSM drive in electric vehicle. Int. Trans. Electr. Energy Syst. 2021, 31, 13071. [Google Scholar] [CrossRef]
- Sepulchre, L.; Fadel, M.; Pietrzak-David, M.; Porte, G. MTPV flux-weakening strategy for PMSM high speed drive. IEEE Trans. Ind. Appl. 2018, 54, 6081–6089. [Google Scholar] [CrossRef]
- Wang, J.; Wang, X.; Luo, Z.; Assadian, F. Active disturbance rejection control of differential drive assist steering for electric vehicles. Energies 2020, 13, 2647. [Google Scholar] [CrossRef]
- Fan, S.; Zhang, Y.; Jin, J.; Wang, X.; Tong, C. Deadbeat predictive current control of PMSM drives with an adaptive flux-weakening controller. IET Power Electron. 2022, 15, 653–753. [Google Scholar] [CrossRef]
- Krishnamoorthy, S.; Sanjeevikumar, P.; Holm-Nielsen, J.B. Torque ripple minimization of PMSM using an adaptive Elman neural network-controlled feedback linearization-based direct torque control strategy. Int. Trans. Electr. Energy Syst. 2021, 31, 12685. [Google Scholar]
- Gmati, B.; Jlassi, I.; Khojet El Khil, S.; Marques Cardoso, A.J. Open-switch fault diagnosis in voltage source inverters of PMSM drives using predictive current errors and fuzzy logic approach. IET Power Electron. 2021, 14, 1059–1072. [Google Scholar] [CrossRef]
- Zhou, Z.; Xia, C.; Shi, T.; Geng, Q. Model predictive direct duty-cycle control for PMSM drive systems with variable control-Set. IEEE Trans. Ind. Electron. 2021, 68, 2976–2987. [Google Scholar] [CrossRef]
- Yang, Z.; Yan, Z.; Lu, Y.; Wang, W.; Yu, L.; Geng, Y. Double DOF strategy for continuous-wave pulse generator based on extended Kalman Filter and adaptive linear active disturbance rejection control. IEEE Trans. Power Electron. 2022, 37, 1382–1393. [Google Scholar] [CrossRef]
- Gabbi, T.S.; Hilton, A.G.; Vieira, R.P. Discrete-time sliding mode control based on disturbance observer applied to current control of permanent magnet synchronous motor. IET Power Electron. 2021, 14, 875–887. [Google Scholar] [CrossRef]
- Wang, P.; Xu, Y.; Ding, R.; Liu, W.; Shu, S.; Yang, X. Multi-Kernel neural network sliding mode control for permanent magnet linear synchronous motors. IEEE Access 2021, 9, 57385–57392. [Google Scholar] [CrossRef]
- Apte, A.; Thakar, U.; Joshi, V. Disturbance observer based speed control of PMSM using fractional order PI controller. IEEE/CAA J. Autom. Sin. 2019, 6, 316–326. [Google Scholar] [CrossRef]
- Lamichhane, A.; Zhou, L.; Yao, G.; Luqman, M. Modeling, control and power management of six-phase PMSM based shipboard MVDC distribution System. Energies 2020, 13, 4229. [Google Scholar] [CrossRef]
- Nakayama, Y.D.S. Design of band elimination filter for PMSM vector control operable in overmodulation region of inverter. Electr. Eng. Jpn. 2019, 207, 45–56. [Google Scholar] [CrossRef]
- Lascu, C.; Andreescu, G.D. PLL position and speed observer with integrated current observer for sensorless PMSM drives. IEEE Trans. Ind. Electron. 2020, 67, 5990–5999. [Google Scholar] [CrossRef]
- Makaino, Y.; Doki, S. Position sensorless control for IPMSM of spatial inductance distribution with nonsinusoidal inductance waveform based on pattern matching method. Electr. Eng. Jpn. 2017, 201, 35–42. [Google Scholar] [CrossRef]
- Liu, J.; Gong, C.; Han, Z.; Yu, H. IPMSM model predictive control in flux-weakening operation using an improved algorithm. IEEE Trans. Ind. Electron. 2018, 65, 9378–9387. [Google Scholar] [CrossRef]
- Uddin, M.N.; Rahman, M.M. Online torque-flux estimation-based nonlinear torque and flux control scheme of IPMSM drive for reduced torque ripples. IEEE Trans. Power Electron. 2019, 34, 636–645. [Google Scholar] [CrossRef]
- Schmid, H.C.; Schroedl, M.; Heyden, M.V. Design space analysis including experimental verification for an electrical machine based on a parametric and functional IPMSM model. IEEE Trans. Ind. Electron. 2021, 68, 7863–7873. [Google Scholar] [CrossRef]
- Chen, B.; Shen, A.; Li, P.; Luo, X.; Xu, S.; Xu, J. Restart strategy for sensorless PMSM drive system based on zero-voltage vector. IET Electr. Power Appl. 2020, 14, 2362–2369. [Google Scholar] [CrossRef]
- Yuan, L.; Hu, B.X.; Wei, K.Y.; Chen, S. The Control Principle and MATLAB Simulation of Modern Permanent Magnet Synchronous Motor; Beijing University of Aeronautics and Astronautics Press: Beijing, China, 2016. [Google Scholar]
- Wei, Y.; Sun, L.; Chen, Z. An improved sliding mode control method to increase the speed stability of permanent magnet synchronous motors. Energies 2022, 15, 6313. [Google Scholar] [CrossRef]
- Bouguenna, I.F.; Azaiz, A.; Tahour, A.; Larbaoui, A. Robust neuro-fuzzy sliding mode control with extended state observer for an electric drive system. Energy 2019, 169, 1054–1063. [Google Scholar] [CrossRef]
- Humaidi, A.J.; Ibraheem, I.K. Speed control of permanent magnet DC motor with friction and measurement noise using novel nonlinear extended state observer-based anti-disturbance control. Energies 2019, 12, 1651. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).