High-Reliability Rotor Position Detection Method for Sensorless Control of Synchronous Condenser
Abstract
:1. Introduction
2. Dual Rotor Initial Position Detection Method
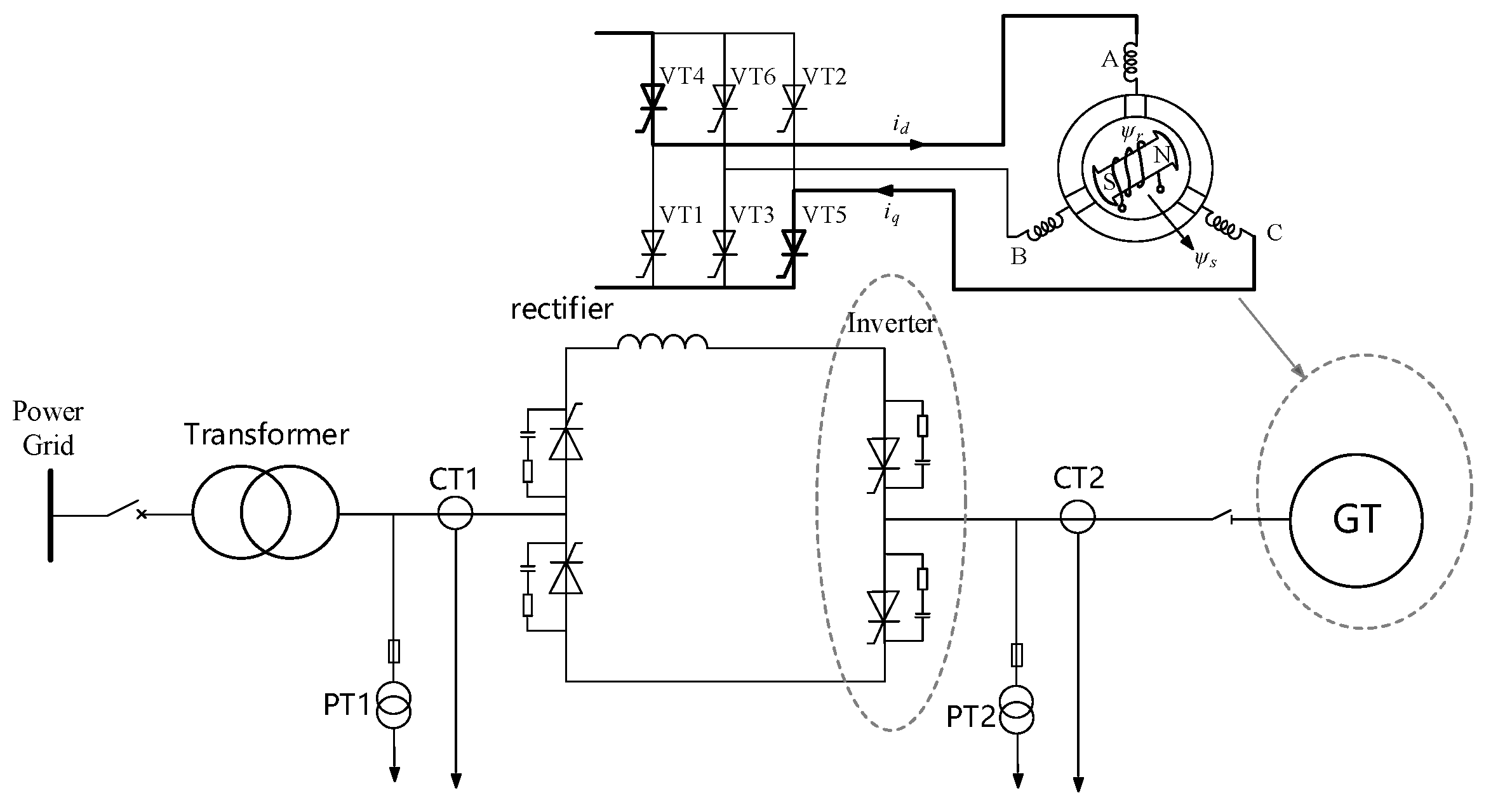
2.1. Start up Analysis of SFC
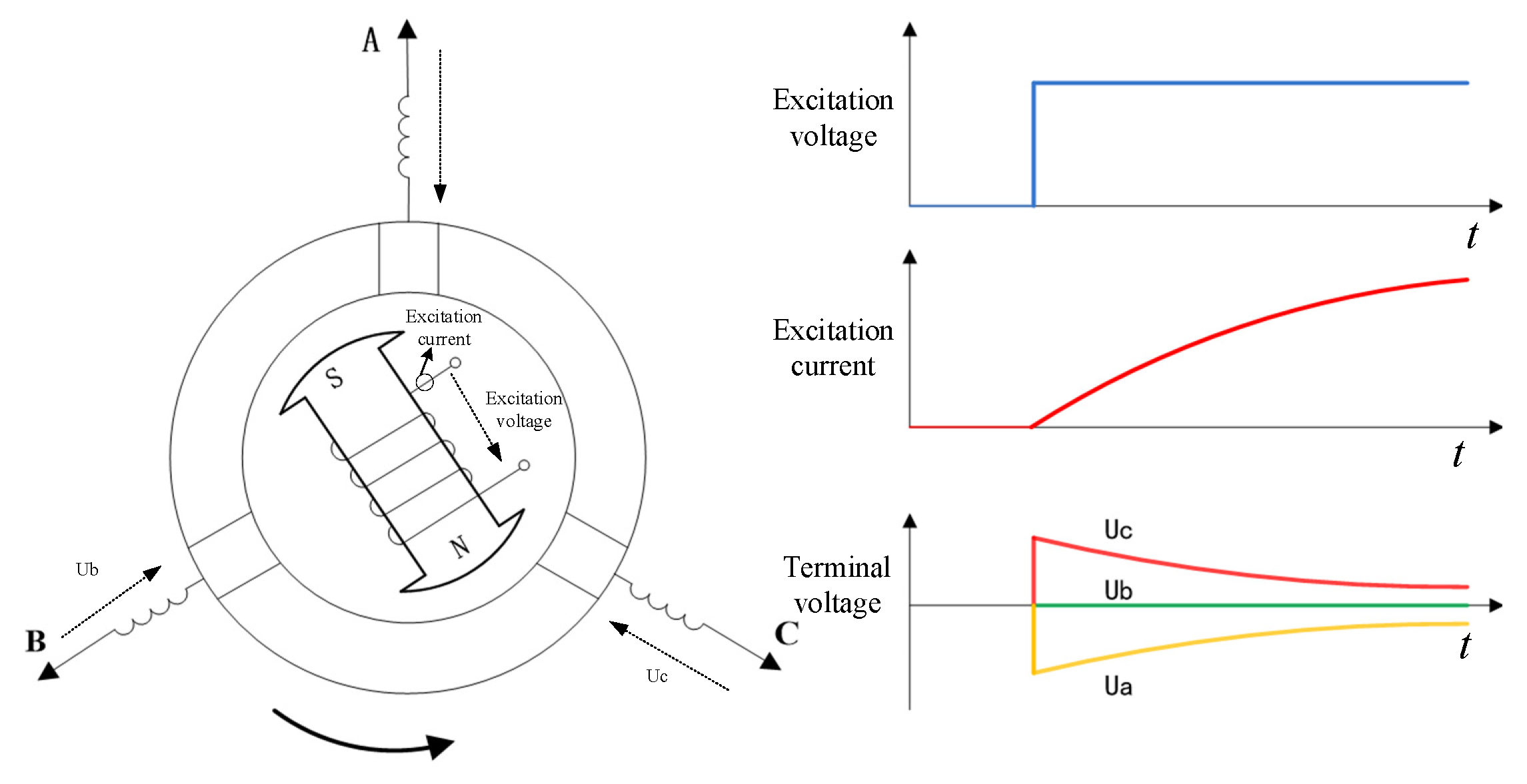
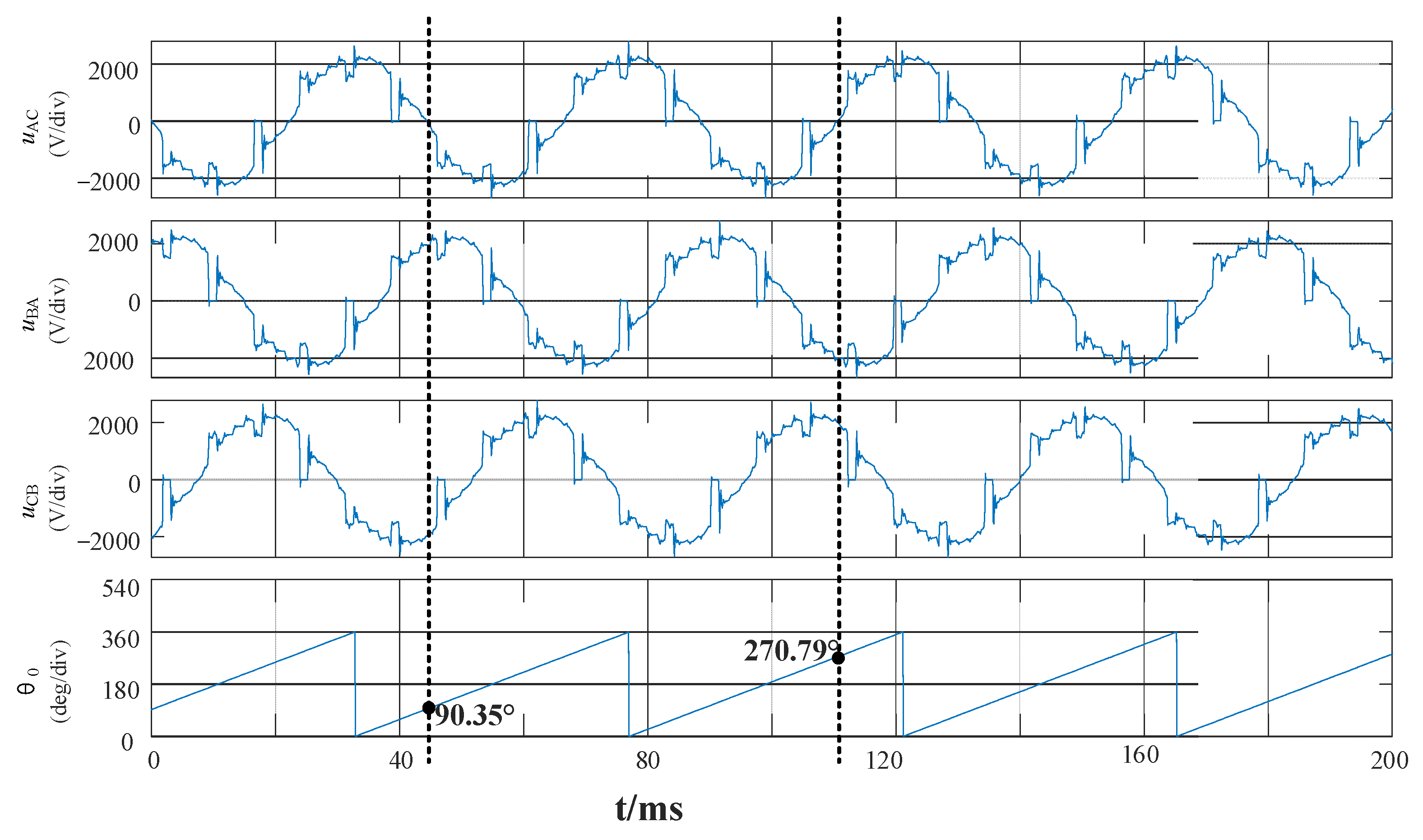
2.2. Voltage Detection Method
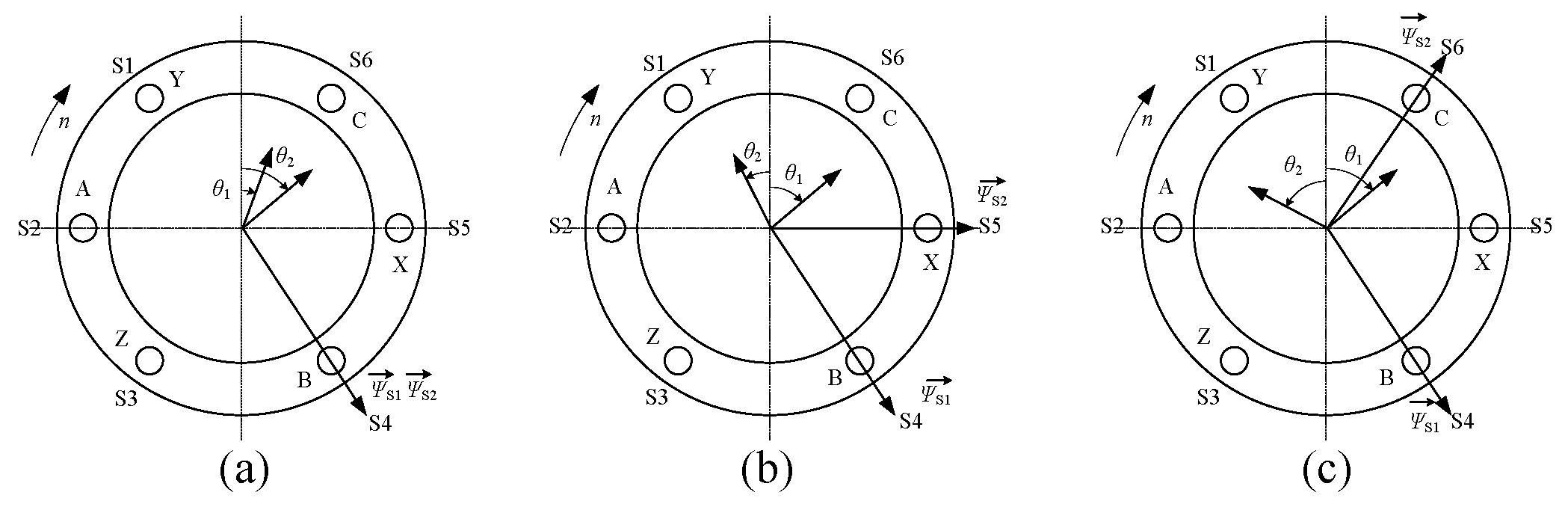
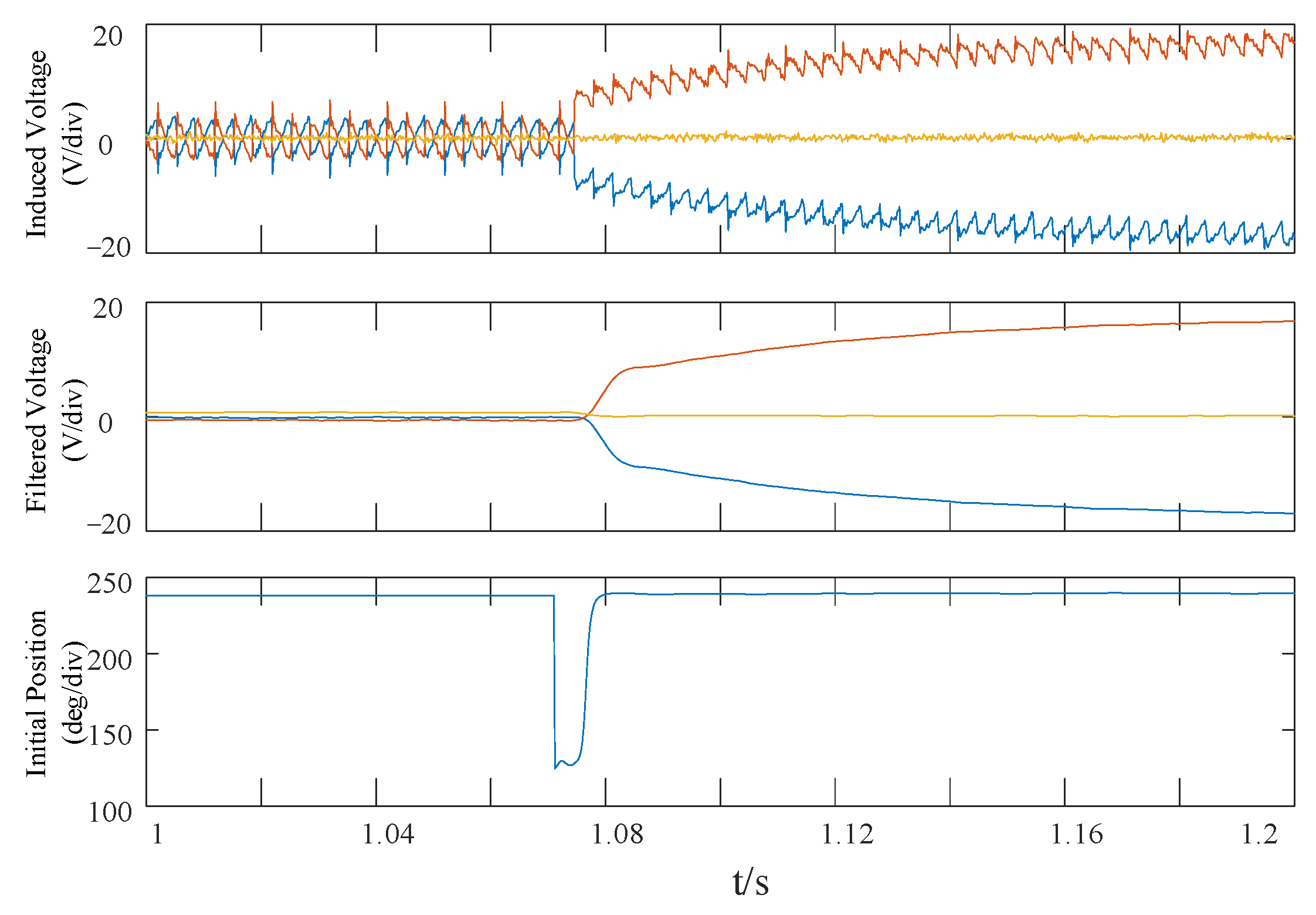
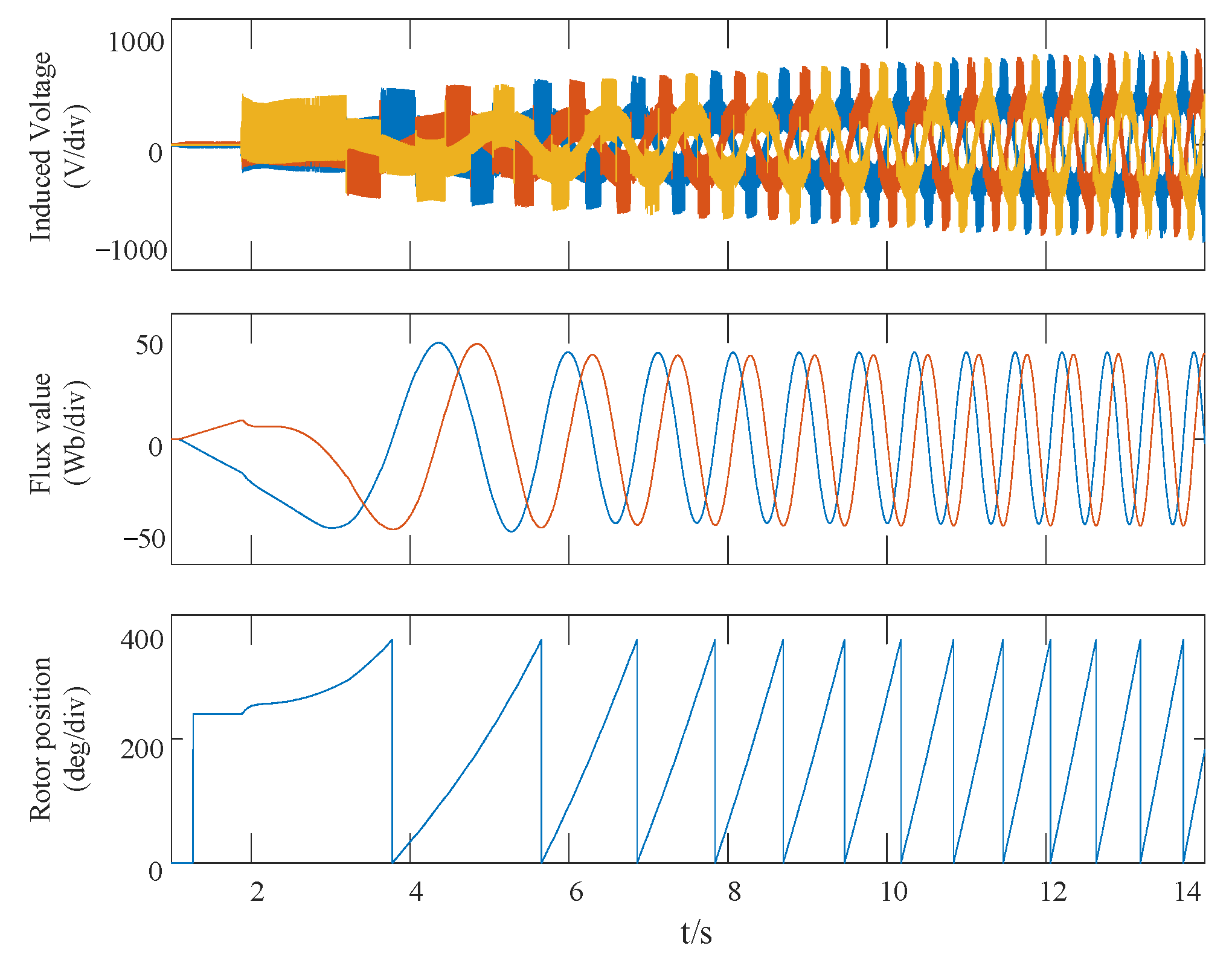
2.3. Magnetic Flux Detection Method
3. Method for Detecting Rotor Position during Operation
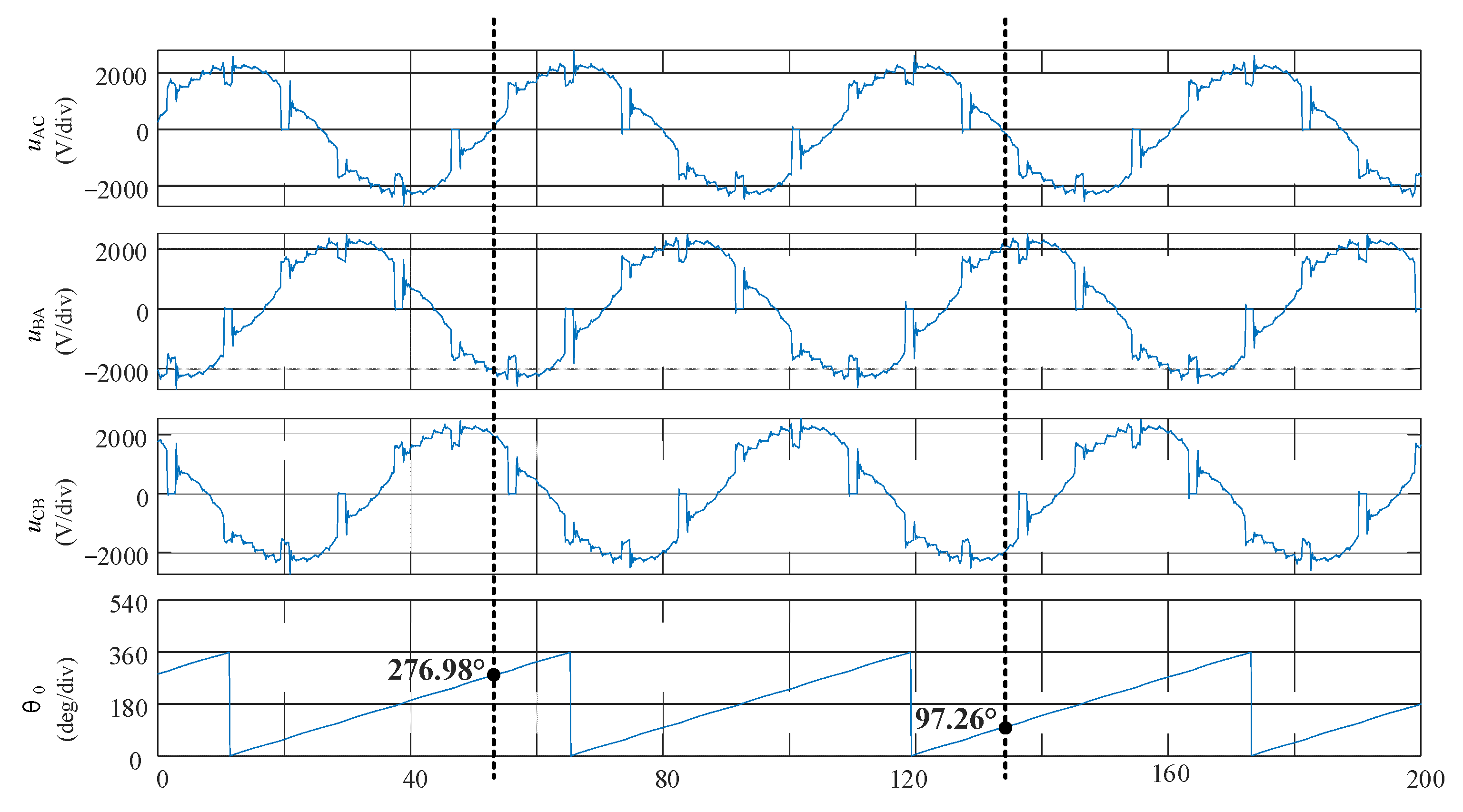
3.1. Synchronous Phase Compensation
- (1)
- Waveform distortion is significantly reduced and symmetrical.
- (2)
- The zero-crossing time is the same as that of the original signal without a phase offset.
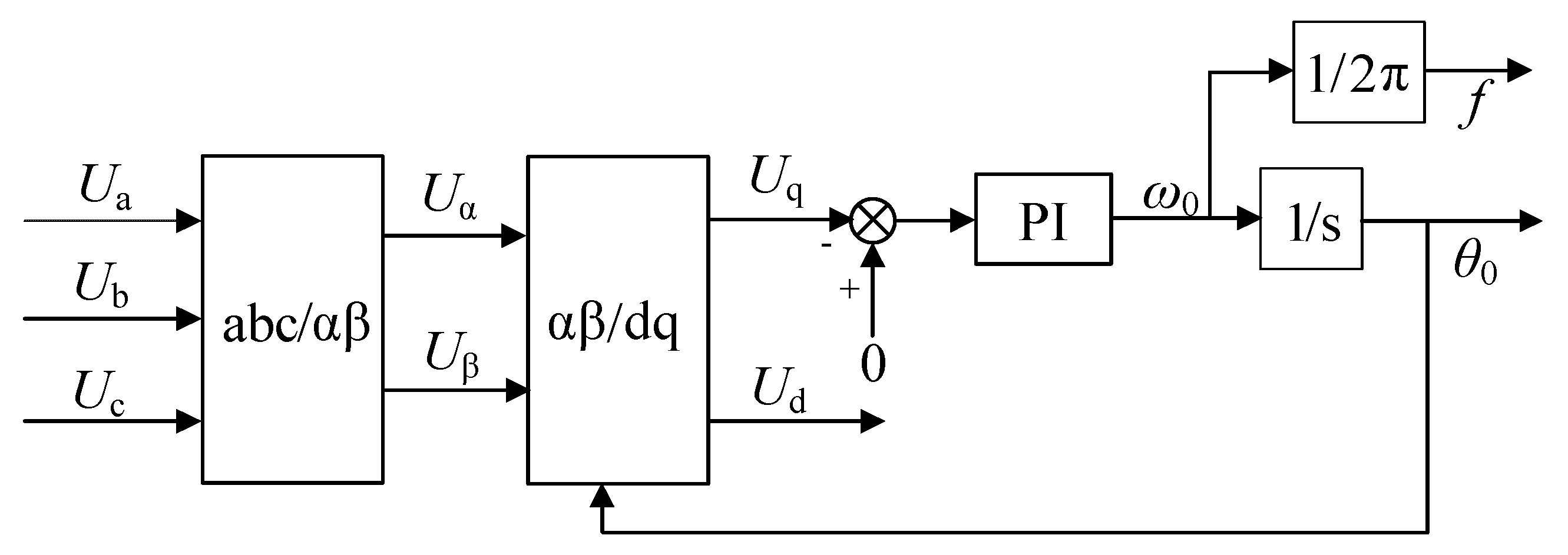
3.2. Software Phase-Locked Loop Based on Rotating Coordinate System
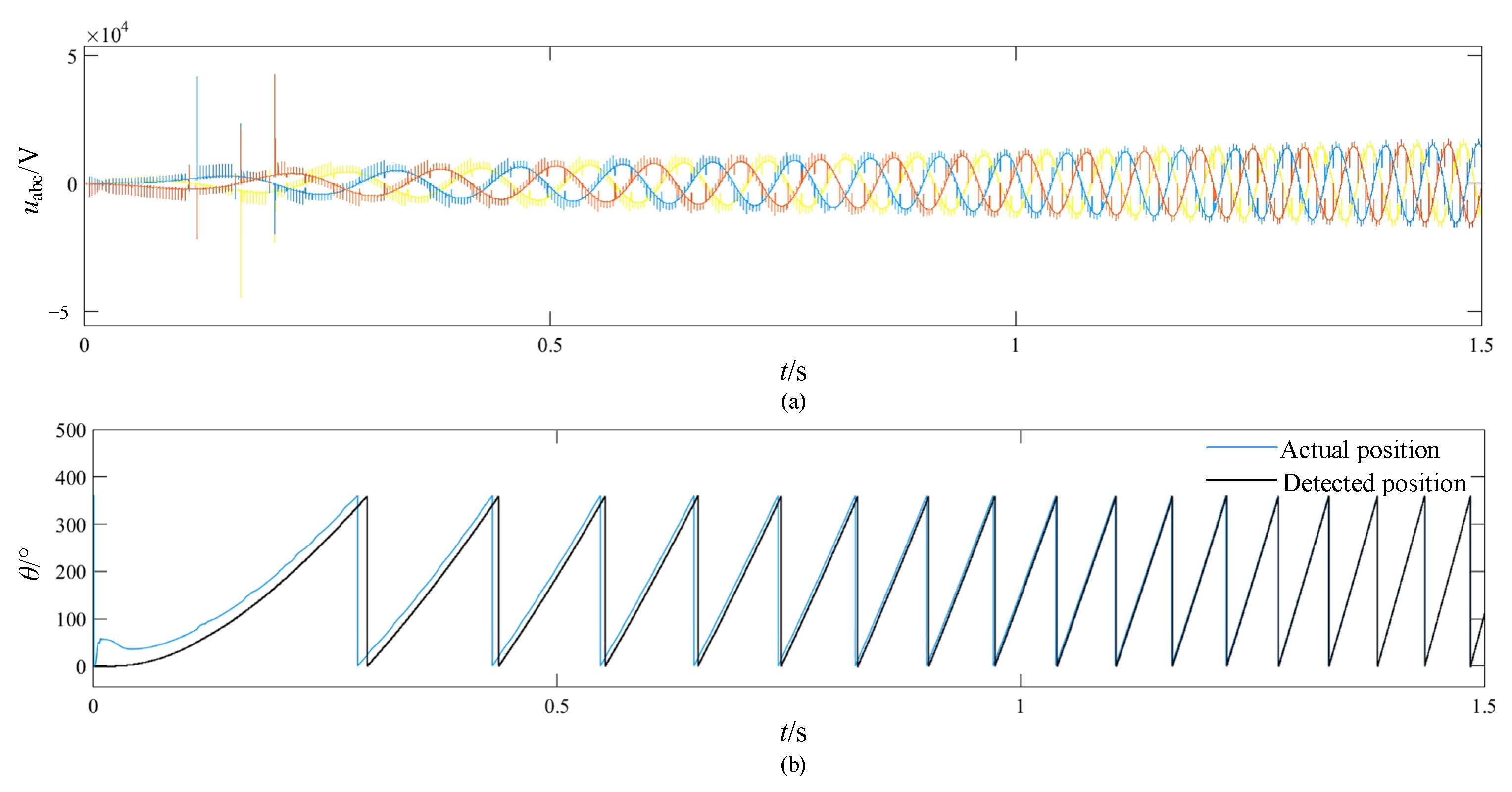
4. RTDS Verification
5. Conclusions
- Two position detection methods are used to check each other, which can effectively avoid reverse rotation when the unit starts and improve the safety of large synchronous motors.
- Synchronous phase compensation can effectively reduce the influence of a distorted waveform on detection accuracy and improve phase detection accuracy to within 1%, thus providing technical support for the high-performance control of SFCS.
- The algorithm does not need additional hardware circuits, has few parameters, and can be easily applied in engineering.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ramachandra Sekhar, K.; Vinoth Kumar, N.; Harada, Y. Impact of renewable energy control center on voltage stability and transmission network efficiency in wind farm integrated grid. In Proceedings of the 2014 IEEE International Conference on Power Electronics, Drives and Energy Systems, Mumbai, India, 16–19 December 2014; pp. 1–6. [Google Scholar]
- Teleke, S.; Abdulahovic, T.; Thiringer, T.; Svensson, J. Dynamic Performance Comparison of Synchronous Condenser and SVC. IEEE Trans. Power Deliv. 2008, 23, 1606–1612. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, L.; Jiang, Q. Impact of Synchronous Condenser on Sub/Super-Synchronous Oscillations in Wind Farms. IEEE Trans. Power Deliv. 2021, 36, 2075–2084. [Google Scholar] [CrossRef]
- Wang, P.; Mou, Q.; Liu, X.; Gu, W.; Chen, X. Start-Up Control of a Synchronous Condenser Integrated HVDC System With Power Electronics Based Static Frequency Converter. IEEE Access 2019, 7, 146914–146921. [Google Scholar] [CrossRef]
- Tan, J.; Xue, R.; Tan, H.; Zhang, T.; Zhao, Y.; Zhao, B.; Wu, S.; Zhai, Y.; Dang, H. Design and Experimental Investigations on the Helium Circulating Cooling System Operating at Around 20 K for a 300-kvar Class HTS Dynamic Synchronous Condenser. IEEE Trans. Appl. Supercond. 2022, 32, 5400405. [Google Scholar] [CrossRef]
- Hadavi, S.; Rathnayake, D.B.; Jayasinghe, G.; Mehrizi-Sani, A.; Bahrani, B. A Robust Exciter Controller Design for Synchronous Condensers in Weak Grids. IEEE Trans. Power Syst. 2022, 37, 1857–1867. [Google Scholar] [CrossRef]
- Hadavi, S.; Mansour, M.Z.; Bahrani, B. Optimal Allocation and Sizing of Synchronous Condensers in Weak Grids With Increased Penetration of Wind and Solar Farms. IEEE J. Emerg. Sel. Top. Circuits Syst. 2021, 11, 199–209. [Google Scholar] [CrossRef]
- Hadavi, S.; Saunderson, J.; Mehrizi-Sani, A.; Bahrani, B. A Planning Method for Synchronous Condensers in Weak Grids Using Semi-Definite Optimization. IEEE Trans. Power Syst. 2023, 38, 1632–1641. [Google Scholar] [CrossRef]
- Magsaysay, G.; Schuette, T.; Fostiak, R.J. Use of a static frequency converter for rapid load response in pumped-storage plants. IEEE Trans. Energy Convers. 1995, 10, 694–699. [Google Scholar] [CrossRef]
- Ryu, H.; Kim, B.; Lee, J.; Lim, I. A Study of Synchronous Motor Drive using Static Frequency Converter. In Proceedings of the 2006 12th International Power Electronics and Motion Control Conference, Portoroz, Slovenia, 30 August–1 September 2006; pp. 1496–1499. [Google Scholar]
- Liu, T.-H.; Lin, C.-Y.; Yang, J.-S.; Chang, W.-Y. Modeling and harmonics elimination for a static frequency converter driving a 300 MVA synchronous machine. In Proceedings of the IEEE International Symposium on Industrial Electronics, Warsaw, Poland, 17–20 June 1996; Volume 2, pp. 602–607. [Google Scholar]
- Meghana, R.; Singh, R.R. Sensorless Start-Up Control for BLDC Motor using Initial Position Detection Technique. In Proceedings of the 2020 IEEE International Conference on Power Electronics, Smart Grid and Renewable Energy (PESGRE2020), Cochin, India, 2–4 January 2020; pp. 1–6. [Google Scholar]
- Song, X.; Han, B.; Zheng, S.; Chen, S. A Novel Sensorless Rotor Position Detection Method for High-Speed Surface PM Motors in a Wide Speed Range. IEEE Trans. Power Electron. 2018, 33, 7083–7093. [Google Scholar] [CrossRef]
- Yeh, H.-C.; Yang, S.-M. Phase Inductance and Rotor Position Estimation for Sensorless Permanent Magnet Synchronous Machine Drives at Standstill. IEEE Access 2021, 9, 32897–32907. [Google Scholar] [CrossRef]
- Wang, Z.; Yao, B.; Guo, L.; Jin, X.; Li, X.; Wang, H. Initial Rotor Position Detection for Permanent Magnet Synchronous Motor Based on High-Frequency Voltage Injection without Filter. World Electr. Veh. J. 2020, 11, 71. [Google Scholar] [CrossRef]
- Iturra, R.G.; Thiemann, P. Sensorless Rotor Position detection of Synchronous Machine using Direct Flux Control—Comparative evaluation of rotor position estimation methods. In Proceedings of the 2021 XVIII International Scientific Technical Conference Alternating Current Electric Drives (ACED), Ekaterinburg, Russia, 24–27 May 2021; pp. 1–6. [Google Scholar]
- Martin, F.; Leibfried, T. An universal high voltage source based on a static frequency converter. In Proceedings of the Conference Record of the 2006 IEEE International Symposium on Electrical Insulation, Toronto, ON, Canada, 11–14 June 2006; pp. 420–423. [Google Scholar]


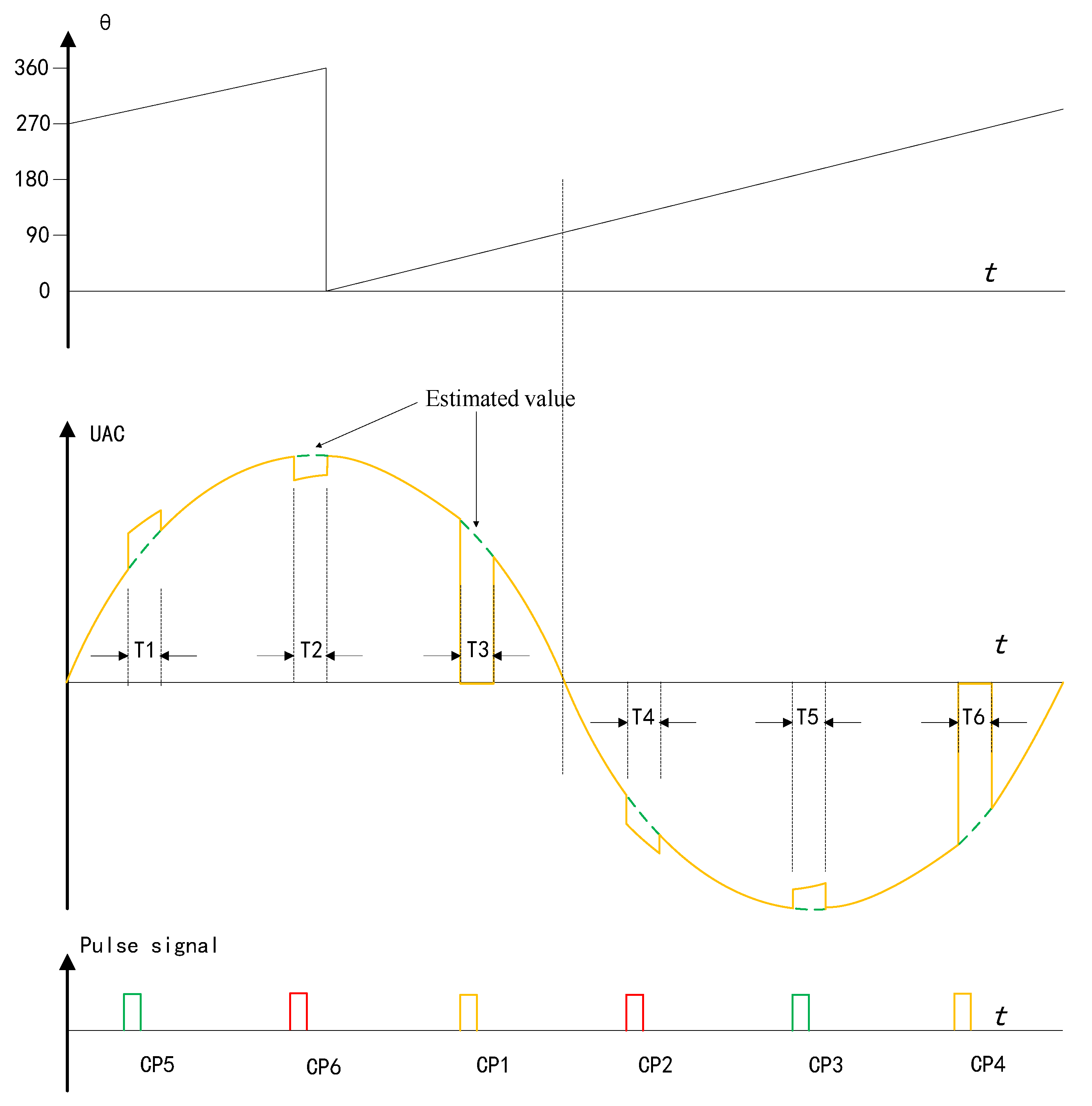


| Parameter | Value |
|---|---|
| Transformer turn ratio | 10 kV/0.9 kV/0.9 kV |
| Direct current reactor | 2.4 mH |
| Voltage of power grid | 500 kV |
| Rated power of Synchronous Condensers | 300 MVar |
| Rated voltage of Synchronous Condensers | 20 kV |
| Rated current of Synchronous Condensers | 8660 A |
| Rated speed of Synchronous Condensers | 3000 r/min |
| Parameter | Value |
|---|---|
| G1(z) | (0.000375 + 0.000750∙z−1 + 0.000375∙z−2)/(1 − 1.9445∙z−1 − 0.9460∙z−2) |
| G2(z) | 200∙z − 194 |
| KP | 5.0 |
| KI | 20.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, X.; Liu, T.; Mu, W.; Zhao, J. High-Reliability Rotor Position Detection Method for Sensorless Control of Synchronous Condenser. World Electr. Veh. J. 2023, 14, 299. https://doi.org/10.3390/wevj14100299
Shi X, Liu T, Mu W, Zhao J. High-Reliability Rotor Position Detection Method for Sensorless Control of Synchronous Condenser. World Electric Vehicle Journal. 2023; 14(10):299. https://doi.org/10.3390/wevj14100299
Chicago/Turabian StyleShi, Xiangjian, Teng Liu, Wei Mu, and Jianfeng Zhao. 2023. "High-Reliability Rotor Position Detection Method for Sensorless Control of Synchronous Condenser" World Electric Vehicle Journal 14, no. 10: 299. https://doi.org/10.3390/wevj14100299
APA StyleShi, X., Liu, T., Mu, W., & Zhao, J. (2023). High-Reliability Rotor Position Detection Method for Sensorless Control of Synchronous Condenser. World Electric Vehicle Journal, 14(10), 299. https://doi.org/10.3390/wevj14100299





