Multi-Objective Optimization with Mayfly Algorithm for Periodic Charging in Wireless Rechargeable Sensor Networks
Abstract
:1. Introduction
- We find a solution to the problem of wireless energy transfer (WET) by researching the mobile charging demand method, which involves the introduction of two sets of energy variables: emin, which refers to the calculated minimum or lowest energy, and ethresh, which refers to the threshold energy in the node. In addition to this, we present the multi-objective functions as a potential solution to this problem.
- As far as we know, this is the first time the mayfly algorithm has been used in sensor node charging. Optimizing multiple objectives, including minimizing the total energy consumption of sensor nodes, minimizing the total distance traveled by MC, and maximizing vacation time for the mobile charger, is formulated in this work as an optimal problem. Using seven other good performance algorithms, we assessed MA’s efficiency in reducing sensor node energy consumption, mobile charging distance, and vacation time.
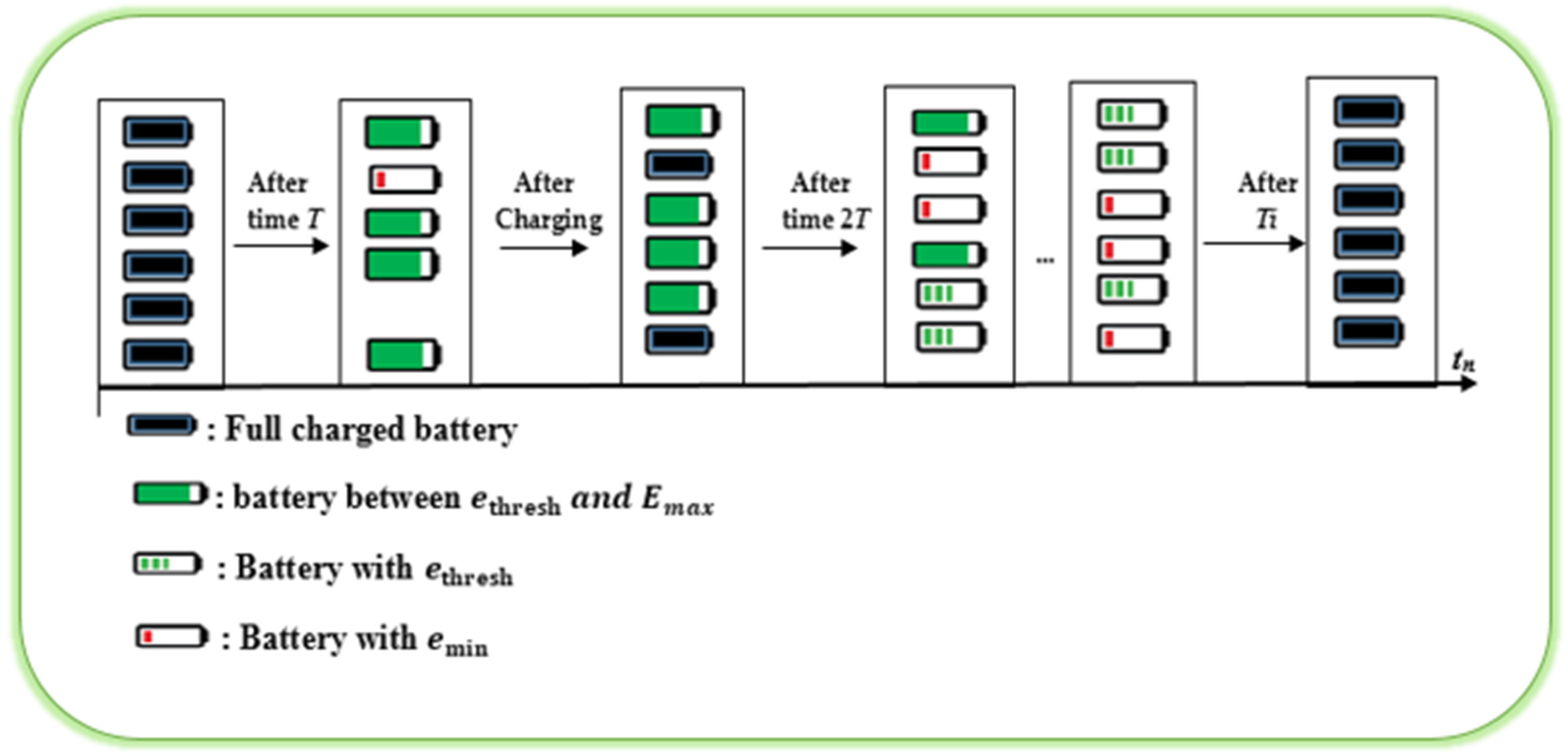
- Introduces the concept of a renewable energy cycle in which the remaining energy level of a sensor node’s battery exhibits periodicity over time. We present both the necessary and sufficient conditions for a renewable energy cycle and demonstrate that feasible solutions that meet these requirements can provide renewable energy cycles and, consequently, a long lifetime for sensor networks.
2. Literature Review
3. Methods
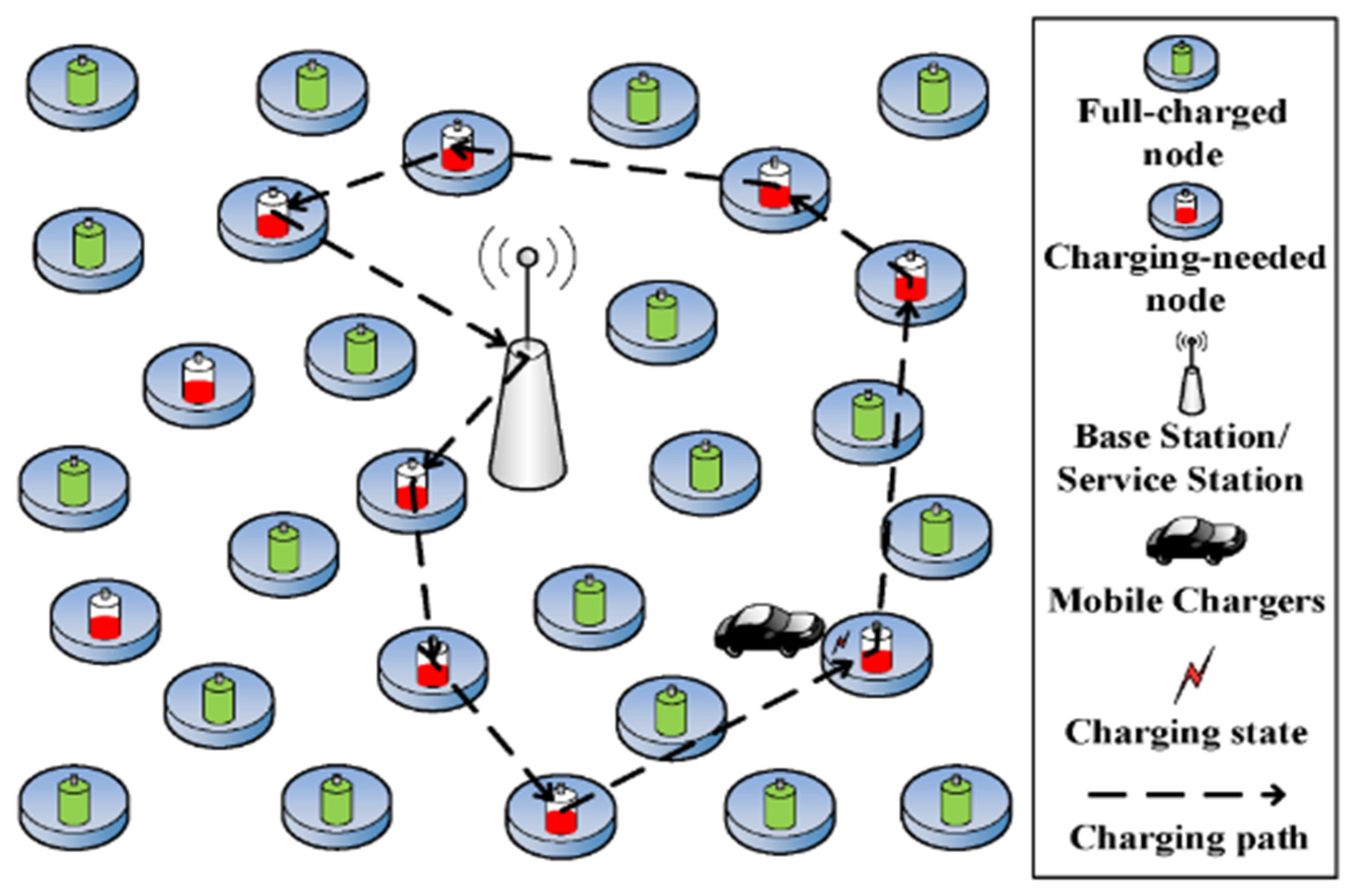
3.1. MC and Travel Path
3.2. Control Methodology
4. Total Energy Consumption Analysis
5. Proposed Strategy
5.1. Optimization with Flowing Rate and Data Routing
5.2. The Procedure of Joint Design
5.2.1. Step 1
5.2.2. Step 2
5.2.3. Step 3
| Algorithm 1 |
| Define the value of T and the number of the visits set |
| Initialize Pmax and Pmin |
| Initialize emin and ethresh |
| Set g |
| Set the recharging period of node i, Ti and classify Zk |
| Define Z1, Z2, …, Zg |
| For i = 1,2 3,…, n do |
| a= |
| i Za |
| End for |
| Set the visiting nodes and traveling path of T |
| For j = 1, 2, 3,…, |
| If j is odd, then |
| = |
| else |
| write as |
| = |
| End if |
| For ∀ ∈ Fj do |
| Charge nodes to Emax |
| End for |
| End for |
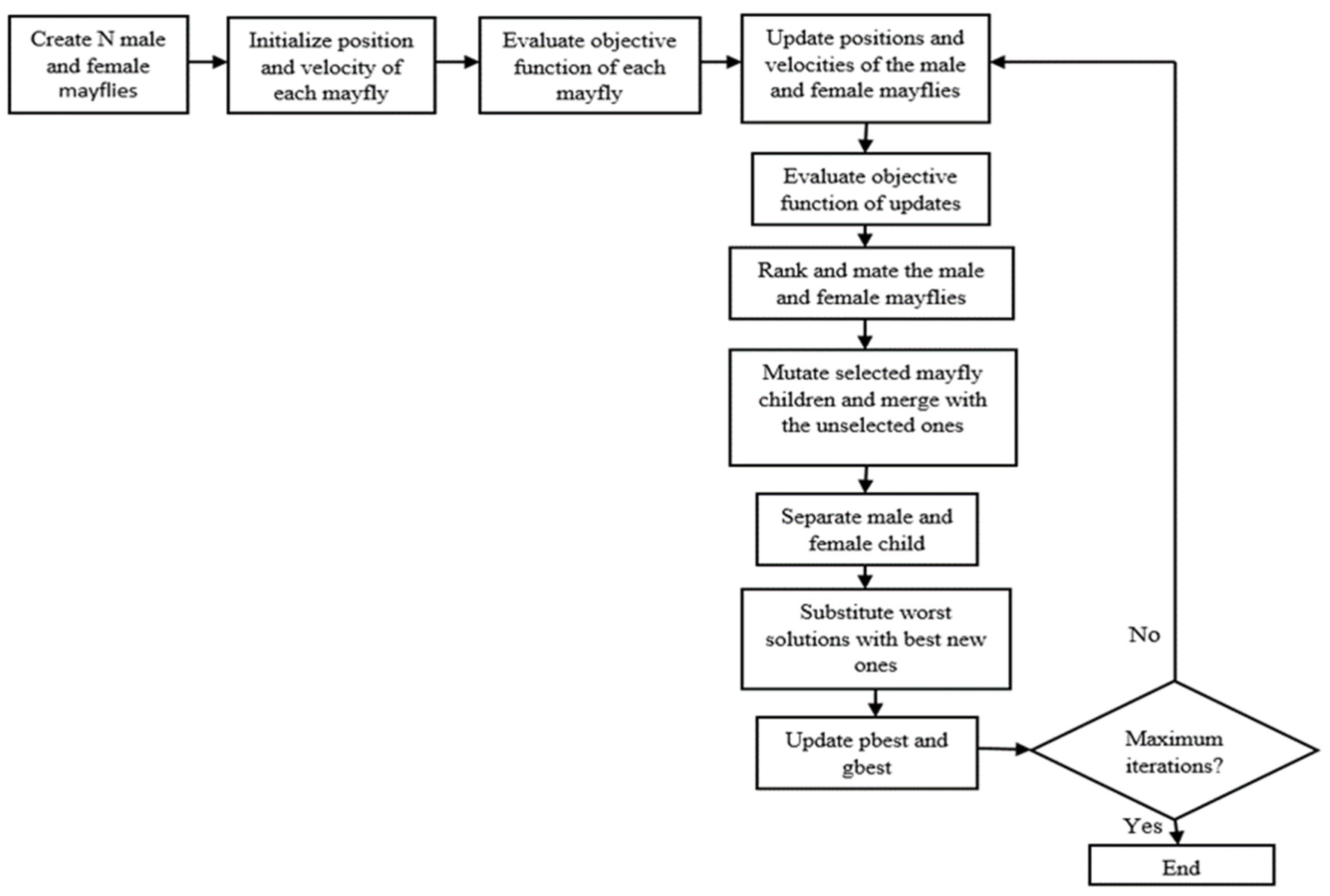
5.3. Mayfly Algorithm
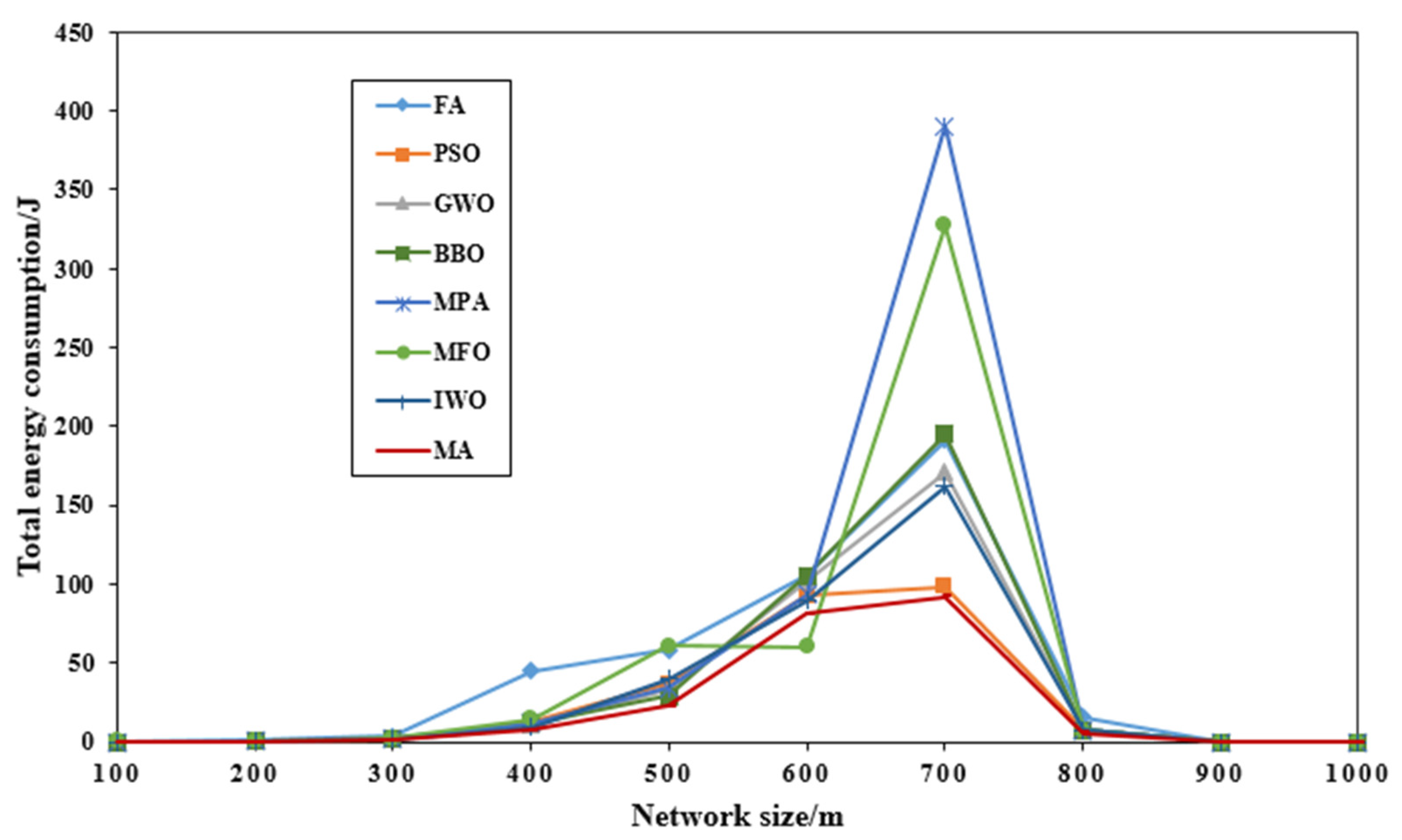
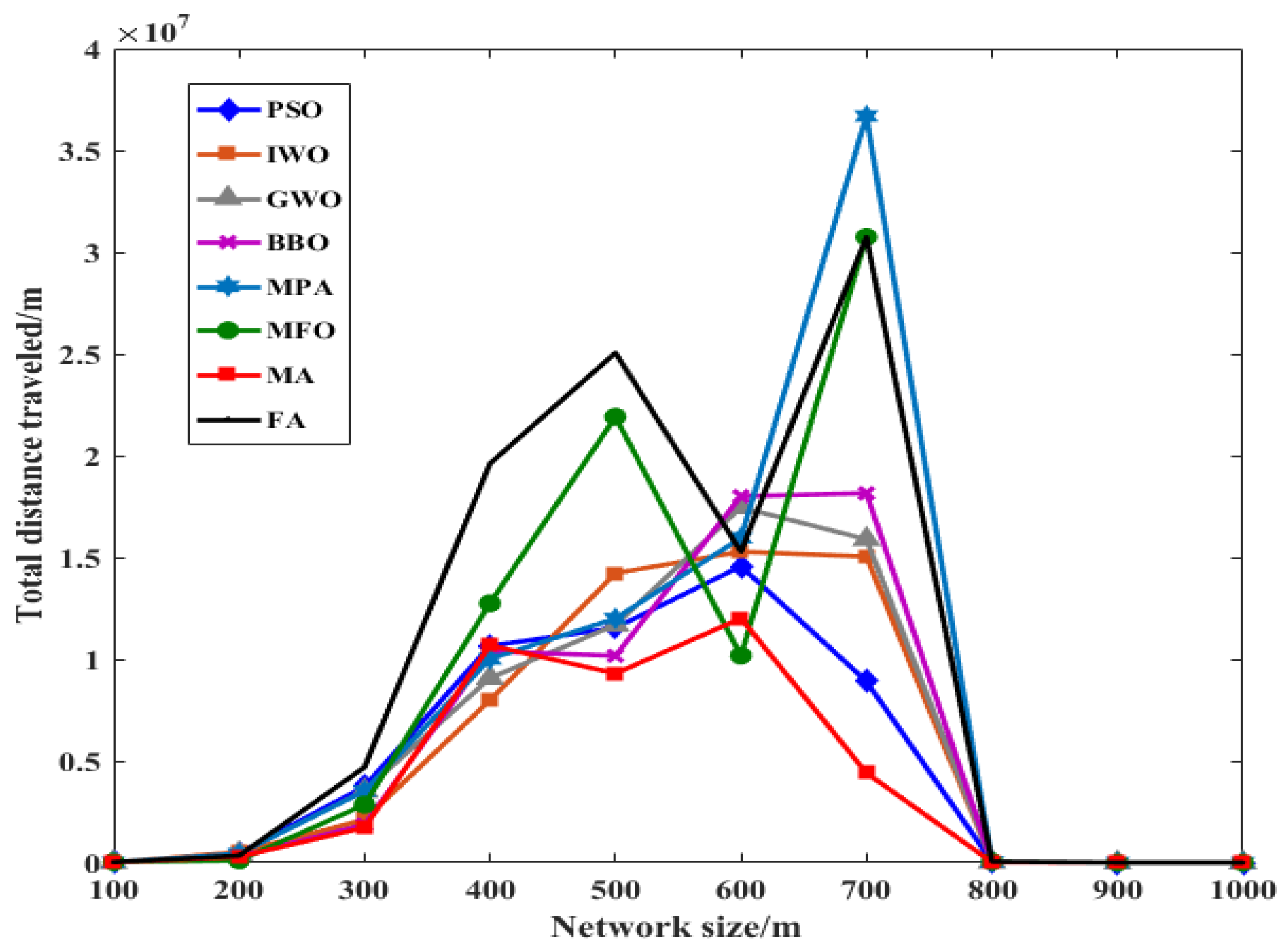
6. Results and Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviations | Description |
| λ | The efficiency of non-radiative energy transfer |
| T | MC periodic trip cycle |
| Hn | Set of nodes that must be visited during the Cth cycle |
| Emin | General minimum energy in the node |
| Emax | Maximum energy in the node |
| emin | Proposed minimum energy |
| ethresh | Proposed threshold energy |
| N | Number of sensor nodes |
| RS | Rest station |
| BS | Base station |
| Ri | Node i data rate |
| pi | Energy consumption rate at sensor node i |
| MC | Mobile charger |
| Pk | Traveling path of MC |
| Dn | Distance of Pk |
| tn | Time spent traveling Pk |
| Vacation time of MC at the rest station | |
| µvac | MC vacation time ratio |
| WSN | Wireless sensor network |
| WET | Wireless energy transfer |
| TSP | Traveling salesman problem |
| ti | Charging duration of node i |
| Ptotal | System total energy consumption |
| Dtotal | Total distance traveled over all cycles |
| Ttotal | Total time spent overall cycles |
| Wij, WiB | Flow rate coefficient from node i to node j (or base station) |
| Vij, ViB | Energy consumption for transmitting a unit of data from node i to node j or base station |
| ρ | Constant coefficient |
| α | Path loss index |
| dij | Distance between sensor i and sensor j (or base station B) |
| β1 and β2 | Constant coefficients in transmission energy modeling |
| (XB, YB) | Coordinates of the base station |
| V | Traveling speed of MCV |
| U | Energy transfer rate of MCV |
| g | The number of sets needing to be classified |
| Zk | The defined set that needs to be classified |
| Fj | The set of nodes that should be visited during the jth cycle |
References
- Mukase, S.; Xia, K.; Umar, A. Optimal Base Station Location for Network Lifetime Maximization in Wireless Sensor Network. Electronics 2021, 10, 2760. [Google Scholar] [CrossRef]
- Dong, M.; Ota, K.; Yang, L.T.; Chang, S.; Zhu, H.; Zhou, Z. Mobile agent-based energy-aware and user-centric data collection in wireless sensor networks. Comput. Netw. 2014, 74, 58–70. [Google Scholar] [CrossRef]
- He, S.; Chen, J.; Jiang, F.; Yau, D.K.Y.; Xing, G.; Sun, Y.J.I. Transactions on mobile computing Energy provisioning in wireless rechargeable sensor networks. IEEE Trans. Mob. Comput. 2012, 12, 1931–1942. [Google Scholar] [CrossRef]
- Li, Y.; Fu, L.; Chen, M.; Chi, K.; Zhu, Y. RF-based charger placement for duty cycle guarantee in battery-free sensor networks. IEEE Commun. Lett. 2015, 19, 1802–1805. [Google Scholar] [CrossRef] [Green Version]
- Fu, L.; Cheng, P.; Gu, Y.; Chen, J.; He, T. Minimizing charging delay in wireless rechargeable sensor networks. In Proceedings of the 2013 Proceedings IEEE INFOCOM, Turin, Italy, 14–19 April 2013; pp. 2922–2930. [Google Scholar]
- Chen, T.-S.; Chen, J.-J.; Gao, X.-Y.; Chen, T.-C. Mobile Charging Strategy for Wireless Rechargeable Sensor Networks. Sensors 2022, 22, 359. [Google Scholar] [CrossRef]
- Mysorewala, M.F.; Cheded, L.; Aliyu, A. Review of energy harvesting techniques in wireless sensor-based pipeline monitoring networks. Renew. Sustain. Energy Rev. 2022, 157, 112046. [Google Scholar]
- Jiang, S.; Song, Z. A review on the state of health estimation methods of lead-acid batteries. J. Power Sources 2022, 517, 230710. [Google Scholar] [CrossRef]
- Prauzek, M.; Konecny, J.; Borova, M.; Janosova, K.; Hlavica, J.; Musilek, P. Energy harvesting sources, storage devices and system topologies for environmental wireless sensor networks: A review. Sensors 2018, 18, 2446. [Google Scholar] [CrossRef] [Green Version]
- Jia, J.; Chen, J.; Deng, Y.; Wang, X.; Aghvami, A.-H. Joint power charging and routing in wireless rechargeable sensor networks. Sensors 2017, 17, 2290. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, T.N.; Liu, B.-H.; Chu, S.-I.; Do, D.-T.; Nguyen, T.D. WRSNs: Toward an efficient scheduling for mobile chargers. IEEE Sens. J. 2020, 20, 6753–6761. [Google Scholar] [CrossRef]
- Lin, C.; Han, D.; Deng, J.; Wu, G. P2S: A Primary and Passer-By Scheduling Algorithm for On-Demand Charging Architecture in Wireless Rechargeable Sensor Networks. IEEE Trans. Veh. Technol. 2017, 66, 8047–8058. [Google Scholar] [CrossRef]
- Ye, X.; Liang, W. Charging utility maximization in wireless rechargeable sensor networks. Wirel. Netw. 2017, 23, 2069–2081. [Google Scholar] [CrossRef]
- Yang, C.-M.; Shih, K.-P.; Chang, S.-H. A priority-based energy replenishment scheme for wireless rechargeable sensor networks. In Proceedings of the 2017 31st International Conference on Advanced Information Networking and Applications Workshops (WAINA), Taipei, Taiwan, 27–29 March 2017; pp. 547–552. [Google Scholar]
- Liu, T.; Wu, B.; Xu, W.; Cao, X.; Peng, J.; Wu, H. Learning an effective charging scheme for mobile devices. In Proceedings of the 2020 IEEE International Parallel and Distributed Processing Symposium (IPDPS), New Orleans, LA, USA, 18–22 May 2020; pp. 202–211. [Google Scholar]
- Lin, C.; Zhou, J.; Guo, C.; Song, H.; Wu, G.; Obaidat, M.S. TSCA: A temporal-spatial real-time charging scheduling algorithm for on-demand architecture in wireless rechargeable sensor networks. IEEE Trans. Mob. Comput. 2017, 17, 211–224. [Google Scholar] [CrossRef]
- Sangare, F.; Xiao, Y.; Niyato, D.; Han, Z. Mobile charging in wireless-powered sensor networks: Optimal scheduling and experimental implementation. IEEE Trans. Veh. Technol. 2017, 66, 7400–7410. [Google Scholar] [CrossRef]
- Xu, W.; Xu, Z.; Peng, J.; Liang, W.; Liu, T.; Jia, X.; Das, S.K. Approximation algorithms for the team orienteering problem. In Proceedings of the IEEE INFOCOM 2020-IEEE Conference on Computer Communications, Toronto, ON, Canada, 6–9 July 2020; pp. 1389–1398. [Google Scholar]
- Mukase, S.; Xia, K.; Umar, A.; Owoola, E.O. On-Demand Charging Management Model and Its Optimization for Wireless Renewable Sensor Networks. Sensors 2022, 22, 384. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Wu, B.; Wu, H.; Peng, J. Low-cost collaborative mobile charging for large-scale wireless sensor networks. IEEE Trans. Mob. Comput. 2016, 16, 2213–2227. [Google Scholar] [CrossRef]
- Liang, W.; Xu, Z.; Xu, W.; Shi, J.; Mao, G.; Das, S.K. Approximation algorithms for charging reward maximization in rechargeable sensor networks via a mobile charger. IEEE/ACM Trans. Netw. 2017, 25, 3161–3174. [Google Scholar] [CrossRef]
- Ma, Y.; Liang, W.; Xu, W. Charging utility maximization in wireless rechargeable sensor networks by charging multiple sensors simultaneously. IEEE/ACM Trans. Netw. 2018, 26, 1591–1604. [Google Scholar] [CrossRef]
- Latif, K.; Javaid, N.; Ahmad, A.; Khan, Z.A.; Alrajeh, N.; Khan, M.I. On energy hole and coverage hole avoidance in underwater wireless sensor networks. IEEE Sens. J. 2016, 16, 4431–4442. [Google Scholar] [CrossRef]
- Jha, S.K.; Eyong, E.M. An energy optimization in wireless sensor networks by using a genetic algorithm. Telecommun. Syst. 2018, 67, 113–121. [Google Scholar] [CrossRef]
- Abbas, M.; Otayf, N. A novel methodology for optimum energy consumption in wireless sensor networks. Front. Eng. Built Environ. 2021, 1, 25–31. [Google Scholar] [CrossRef]
- Norouzi, A.; Zaim, A.H. Genetic algorithm application in optimization of wireless sensor networks. Sci. World J. 2014, 2014, 286575. [Google Scholar] [CrossRef] [PubMed]
- Vimalarani, C.; Subramanian, R.; Sivanandam, S.N. An enhanced PSO-based clustering energy optimization algorithm for wireless sensor network. Sci. World J. 2016, 2016, 8658760. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sahoo, B.M.; Amgoth, T.; Pandey, H.M. Particle swarm optimization based energy efficient clustering and sink mobility in heterogeneous wireless sensor network. Ad Hoc Netw. 2020, 106, 102237. [Google Scholar] [CrossRef]
- Sachidhanandam, P.; Balasubramanie, P. Elevated Ensemble Dynamic Energy-Aware Routing Optimization Based Energy Management and Network Lifetime Improvement in WSN. Wirel. Pers. Commun. 2021, 1–13. [Google Scholar] [CrossRef]
- Chowdhury, A.; De, D. Energy-efficient coverage optimization in wireless sensor networks based on Voronoi-Glowworm Swarm Optimization-K-means algorithm. Ad Hoc Netw. 2021, 122, 102660. [Google Scholar] [CrossRef]
- Singh, J. Enhancement of Lifetime of Wireless Sensor Network Based on Energy-Efficient Circular LEACH Algorithm. In International Conference on Innovative Computing and Communications; Springer: Singapore, 2022; pp. 537–551. [Google Scholar]
- Kaur, J.; Rani, P.; Dahiya, B.P. Hybrid artificial bee colony and glow worm algorithm for energy efficient cluster head selection in wireless sensor networks. World J. Eng. 2021, 19, 147–156. [Google Scholar] [CrossRef]
- Dwivedi, A.K.; Sharma, A.K. I-FBECS: Improved fuzzy based energy efficient clustering using biogeography based optimization in wireless sensor network. Trans. Emerg. Telecommun. Technol. 2021, 32, e4205. [Google Scholar] [CrossRef]
- Srinivas, M.; Amgoth, T. EE-hHHSS: Energy-efficient wireless sensor network with mobile sink strategy using hybrid Harris hawk-salp swarm optimization algorithm. Int. J. Commun. Syst. 2020, 33, e4569. [Google Scholar] [CrossRef]
- Loganathan, G.B.; Salih, I.H.; Karthikayen, A.; Kumar, N.S.; Durairaj, U. EERP: Intelligent Cluster based Energy Enhanced Routing Protocol Design over Wireless Sensor Network Environment. Int. J. Mod. Agric. 2021, 10, 1725–1736. [Google Scholar]
- Zervoudakis, K.; Tsafarakis, S. A mayfly optimization algorithm. Comput. Ind. Eng. 2020, 145, 106559. [Google Scholar] [CrossRef]
- Owoola, E.O.; Xia, K.; Wang, T.; Umar, A.; Akindele, R.G. Pattern Synthesis of Uniform and Sparse Linear Antenna Array Using Mayfly Algorithm. IEEE Access 2021, 9, 77954–77975. [Google Scholar] [CrossRef]
- Valdez, F.; Castillo, O.; Melin, P. Bio-Inspired Algorithms and Its Applications for Optimization in Fuzzy Clustering. Algorithms 2021, 14, 122. [Google Scholar] [CrossRef]
- Xie, L.; Shi, Y.; Hou, Y.T.; Lou, W.; Sherali, H.D.; Midkiff, S.F. On renewable sensor networks with wireless energy transfer: The multi-node case. In Proceedings of the 2012 9th Annual IEEE Communications Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks (SECON), Seoul, Korea, 18–21 June 2012; pp. 10–18. [Google Scholar]
- Xie, L.; Shi, Y.; Hou, Y.T.; Lou, W.; Sherali, H.D.; Midkiff, S.F. Multi-node wireless energy charging in sensor networks. IEEE/ACM Trans. Netw. 2014, 23, 437–450. [Google Scholar] [CrossRef]
- Fu, L.; Cheng, P.; Gu, Y.; Chen, J.; He, T. Optimal charging in wireless rechargeable sensor networks. IEEE Trans. Veh. Technol. 2015, 65, 278–291. [Google Scholar] [CrossRef]
- Liu, C.; Chau, K.T.; Zhang, Z.; Qiu, C.; Lin, F.; Ching, T.W. Multiple-receptor wireless power transfer for magnetic sensors charging on Mars via magnetic resonant coupling. J. Appl. Phys. 2015, 117, 17A743. [Google Scholar] [CrossRef] [Green Version]
- Lu, X.; Niyato, D.; Wang, P.; Kim, D.I.; Han, Z. Wireless charger networking for mobile devices: Fundamentals, standards, and applications. IEEE Wirel. Commun. 2015, 22, 126–135. [Google Scholar] [CrossRef] [Green Version]
- Kumar, N.; Dash, D.; Kumar, M. An efficient on-demand charging schedule method in rechargeable sensor networks. J. Ambient Intell. Humaniz. Comput. 2021, 12, 8041–8058. [Google Scholar] [CrossRef]
- Chawra, V.K.; Gupta, G.P. Hybrid meta-heuristic techniques based efficient charging scheduling scheme for multiple Mobile wireless chargers based wireless rechargeable sensor networks. Peer-to-Peer Netw. Appl. 2021, 14, 1303–1315. [Google Scholar] [CrossRef]
- Ouyang, W.; Obaidat, M.S.; Liu, X.; Long, X.; Xu, W.; Liu, T. Importance-Different Charging Scheduling Based on Matroid Theory for Wireless Rechargeable Sensor Networks. IEEE Trans. Wirel. Commun. 2021, 20, 3284–3294. [Google Scholar] [CrossRef]
- Lyu, Z.; Wei, Z.; Pan, J.; Chen, H.; Xia, C.; Han, J.; Shi, L. Periodic charging planning for a mobile WCE in wireless rechargeable sensor networks based on hybrid PSO and GA algorithm. Appl. Soft Comput. 2019, 75, 388–403. [Google Scholar] [CrossRef]
- Yang, M.; Wang, A.; Sun, G.; Zhang, Y. Deploying charging nodes in wireless rechargeable sensor networks based on improved firefly algorithm. Comput. Electr. Eng. 2018, 72, 719–731. [Google Scholar] [CrossRef]
- Chaaf, A.; Saleh Ali Muthanna, M.; Muthanna, A.; Alhelaly, S.; Elgendy, I.A.; Iliyasu, A.M.; El-Latif, A.; Ahmed, A. Energy-efficient relay-based void hole prevention and repair in clustered multi-AUV underwater wireless sensor network. Secur. Commun. Netw. 2021, 2021, 9969605. [Google Scholar] [CrossRef]
- Lizy, P.J.; Indra, N.C. Metaheuristic energy efficient protocol for heterogeneous WSN. Mater. Today Proc. 2021. [Google Scholar] [CrossRef]
- Xie, L.; Shi, Y.; Hou, Y.T.; Lou, W.; Sherali, H.D.; Zhou, H.; Midkiff, S.F. A mobile platform for wireless charging and data collection in sensor networks. IEEE J. Sel. Areas Commun. 2015, 33, 1521–1533. [Google Scholar] [CrossRef]
- Dai, H.; Liu, Y.; Chen, G.; Wu, X.; He, T.; Liu, A.X.; Ma, H. Safe charging for wireless power transfer. IEEE/ACM Trans. Netw. 2017, 25, 3531–3544. [Google Scholar] [CrossRef]
- Roxin, A.; Abdou, W.; Derigent, W. Interoperable Digital Building Twins Through Communicating Materials and Semantic BIM. SN Comput. Sci. 2022, 3, 23. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. IEEE, Particle swarm optimization. In Proceedings of the 1995 IEEE International Conference on Neural Networks Proceedings, Perth, Australia, 27 November–1 December 1995. [Google Scholar]
- Goldberg, D.E. Genetic Algorithms in Search Optimization and Machine Learning; Addion Wesley: Boston, MA, USA, 1989; Volume 1989, p. 36. [Google Scholar]
- Yang, X.-S. Nature-Inspired Metaheuristic Algorithms; Luniver Press: Beckington, UK, 2010; ISBN 1905986289. [Google Scholar]
- Brown, G.E.; Rive, A.C.; Ferrari, M.C.O.; Chivers, D.P. The dynamic nature of antipredator behavior: Prey fish integrate threat-sensitive antipredator responses within background levels of predation risk. Behav. Ecol. Sociobiol. 2006, 61, 9–16. [Google Scholar] [CrossRef]


| Simulation Parameters | Description of the Abbreviation |
|---|---|
| Nodes | 50 |
| Area length and width | 100–1000 m |
| RS, BS | center |
| U | 5 W |
| V | 7 m/s |
| λ | 0.85 |
| Emax | 10.8 kJ |
| Emin | 0.05 × Emax |
| Data rate Ri | [1, 10] kb/s |
| β1 | 50 nJ/b |
| β2 | 0.0013 pJ/b/m4 |
| α | 4 |
| ρ | 50 nJ/b |
| Number of parameters | 20 |
| Maximum iterations | 50 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mukase, S.; Xia, K. Multi-Objective Optimization with Mayfly Algorithm for Periodic Charging in Wireless Rechargeable Sensor Networks. World Electr. Veh. J. 2022, 13, 120. https://doi.org/10.3390/wevj13070120
Mukase S, Xia K. Multi-Objective Optimization with Mayfly Algorithm for Periodic Charging in Wireless Rechargeable Sensor Networks. World Electric Vehicle Journal. 2022; 13(7):120. https://doi.org/10.3390/wevj13070120
Chicago/Turabian StyleMukase, Sandrine, and Kewen Xia. 2022. "Multi-Objective Optimization with Mayfly Algorithm for Periodic Charging in Wireless Rechargeable Sensor Networks" World Electric Vehicle Journal 13, no. 7: 120. https://doi.org/10.3390/wevj13070120
APA StyleMukase, S., & Xia, K. (2022). Multi-Objective Optimization with Mayfly Algorithm for Periodic Charging in Wireless Rechargeable Sensor Networks. World Electric Vehicle Journal, 13(7), 120. https://doi.org/10.3390/wevj13070120







