A New Hybrid Ant Colony Optimization Based PID of the Direct Torque Control for a Doubly Fed Induction Motor
Abstract
:1. Introduction
- −
- Optimization of speed and torque tracking in terms of overshoot, rejection time, and response time.
- −
- Reduction of torque and fluxes ripples.
- −
- Minimization of the stator and rotor currents THDs (Total Harmonic Distortion).
- −
- Minimization of the system execution time according to the optimal gains.
2. Model in Alpha-Beta Frame of the DFIM
- Stator Electric equations:
- Rotor Electric equations:
- Stator Magnetic equations:
- Rotor Magnetic equations:
- Mechanical equations
3. Analytical Study of DTC
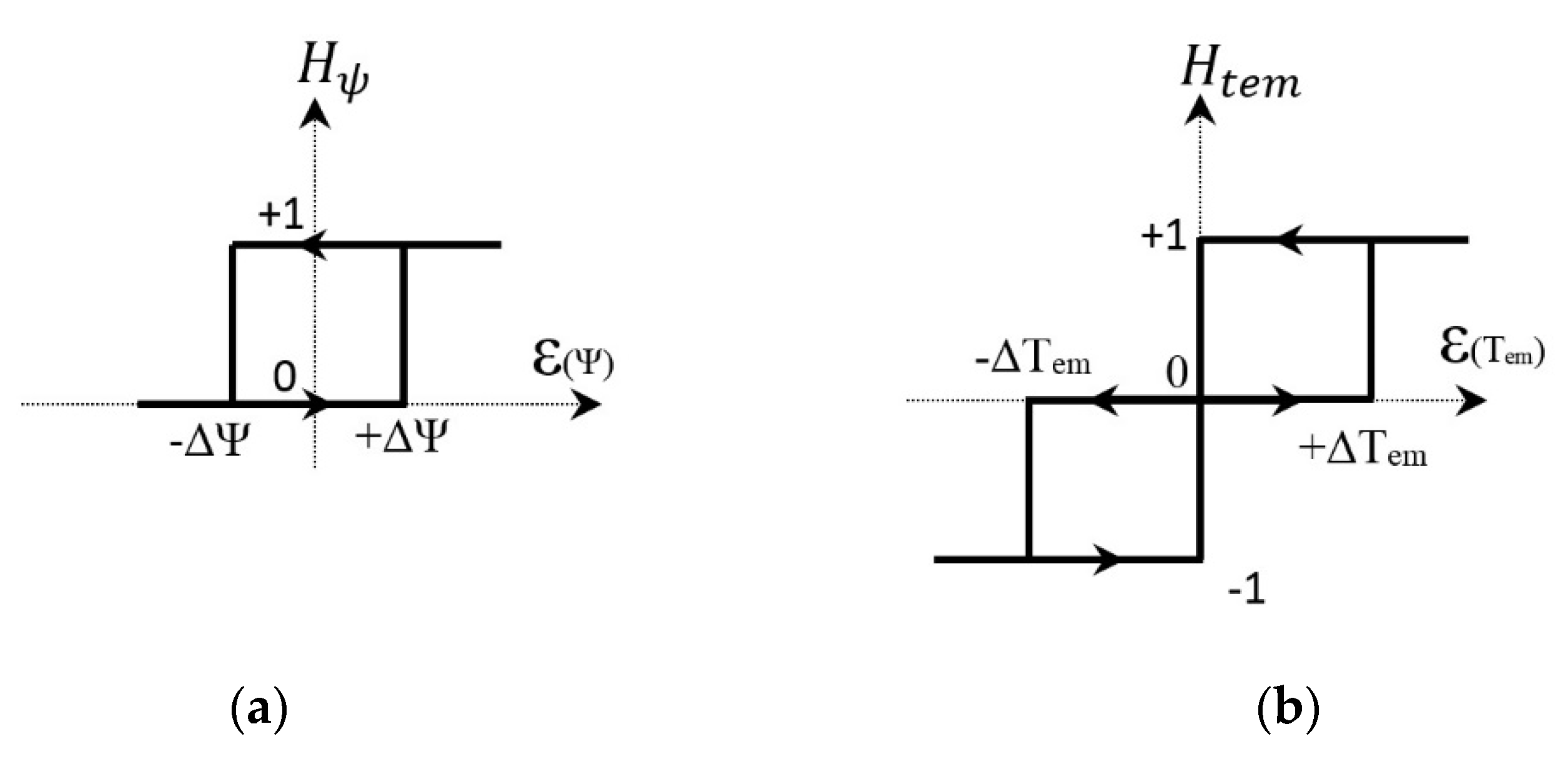
3.1. Flux and Torque Correctors
3.2. Establishment of a Switching Table
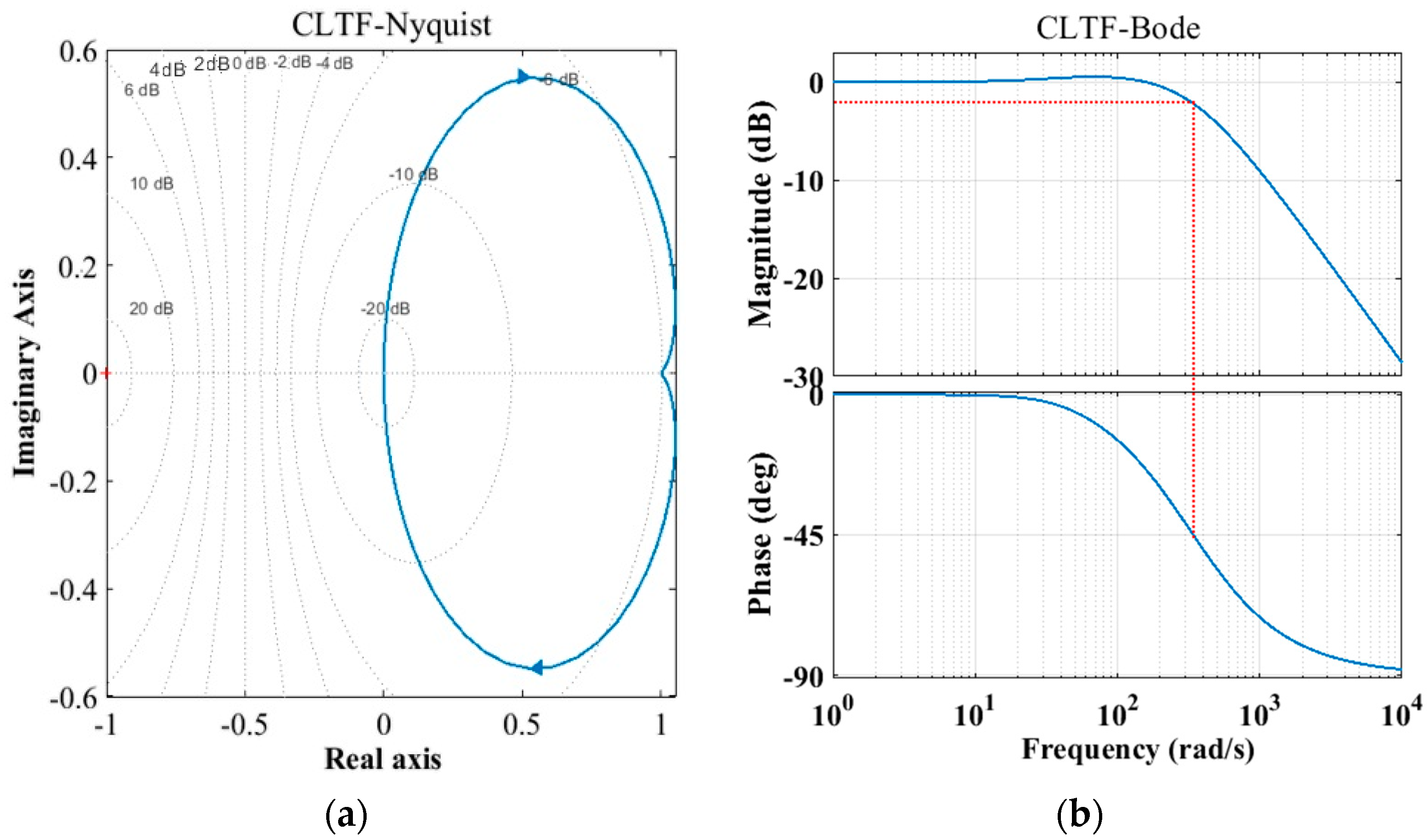
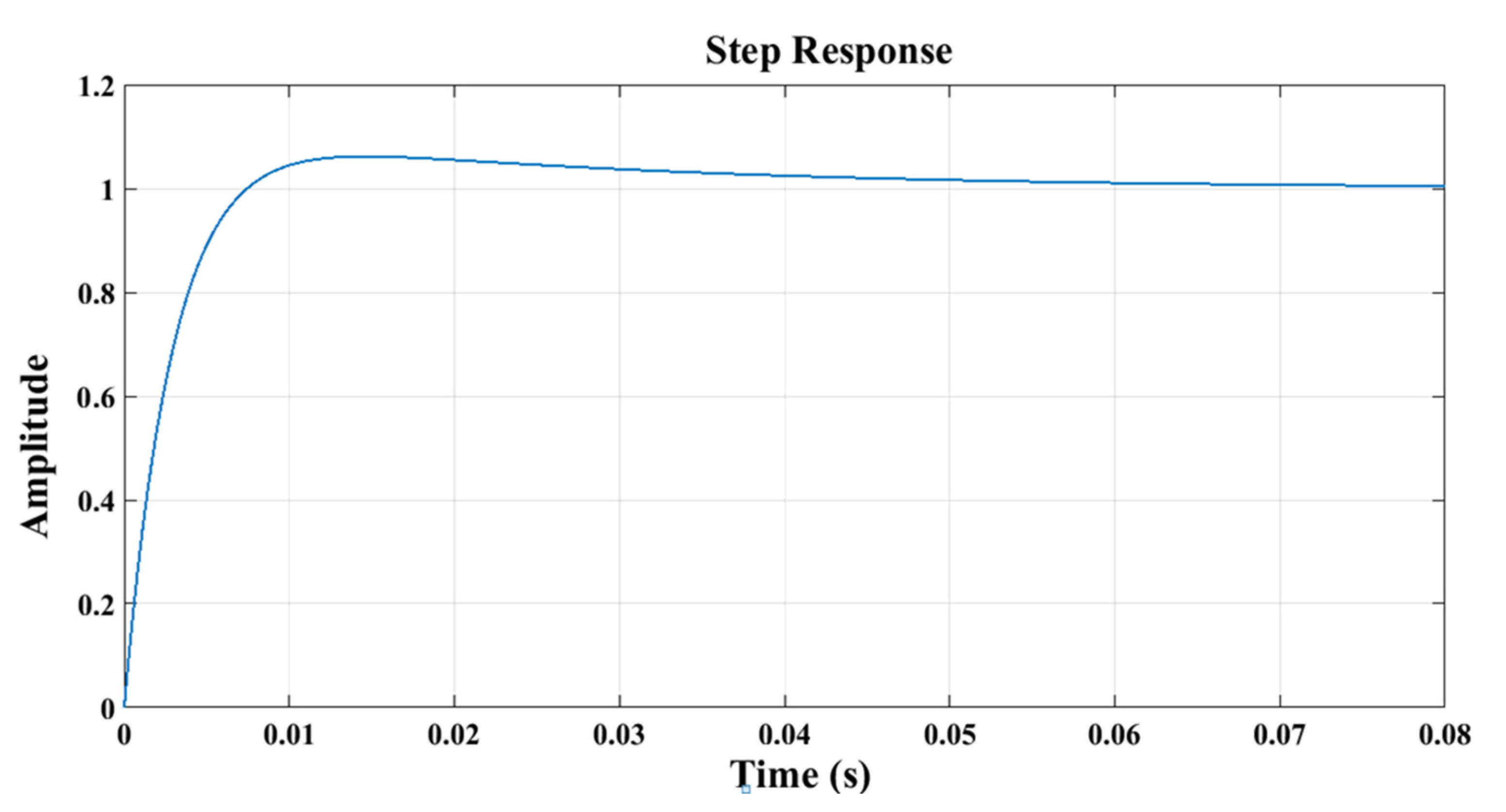
3.3. Syntheses Technique to Calculate the Speed PI Parameters
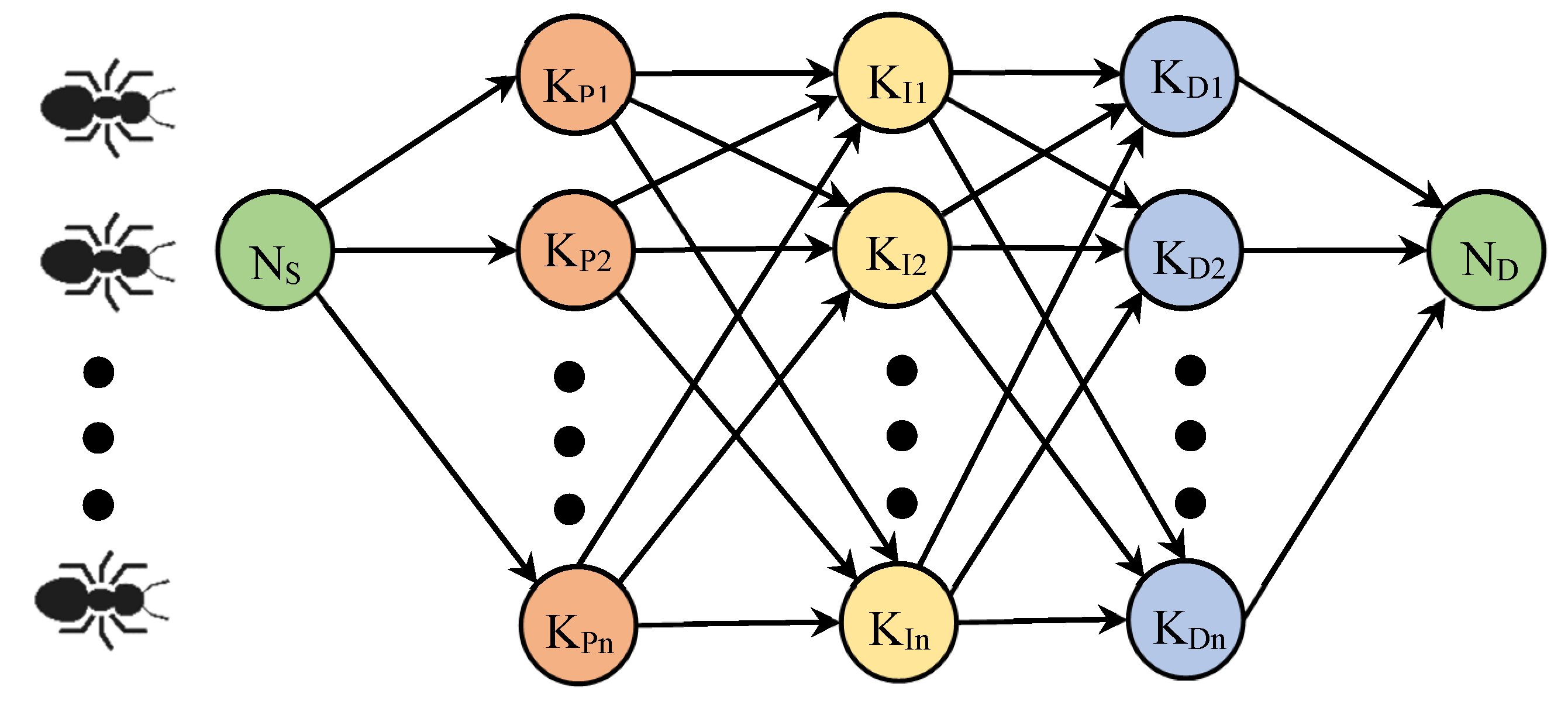
4. Ant Colony Optimization Algorithm
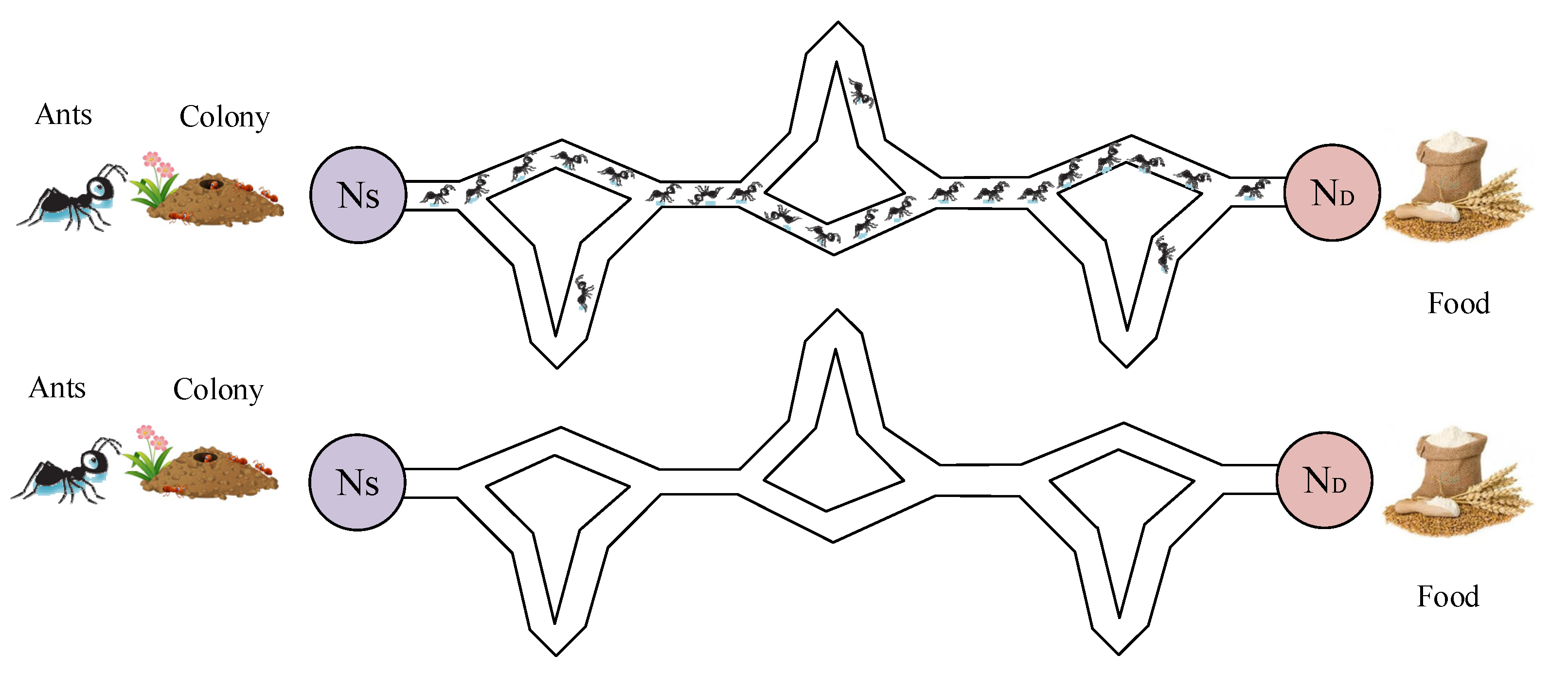
4.1. Working Principal
- The visibility factor, also known as the gluttonous force, is denoted by the letter , where represents the decision that needs to be taken.
- It is possible to calculate the trace factor as , where is the decision being made and the bigger this value is, the more fascinating it has been in the past to make this decision.
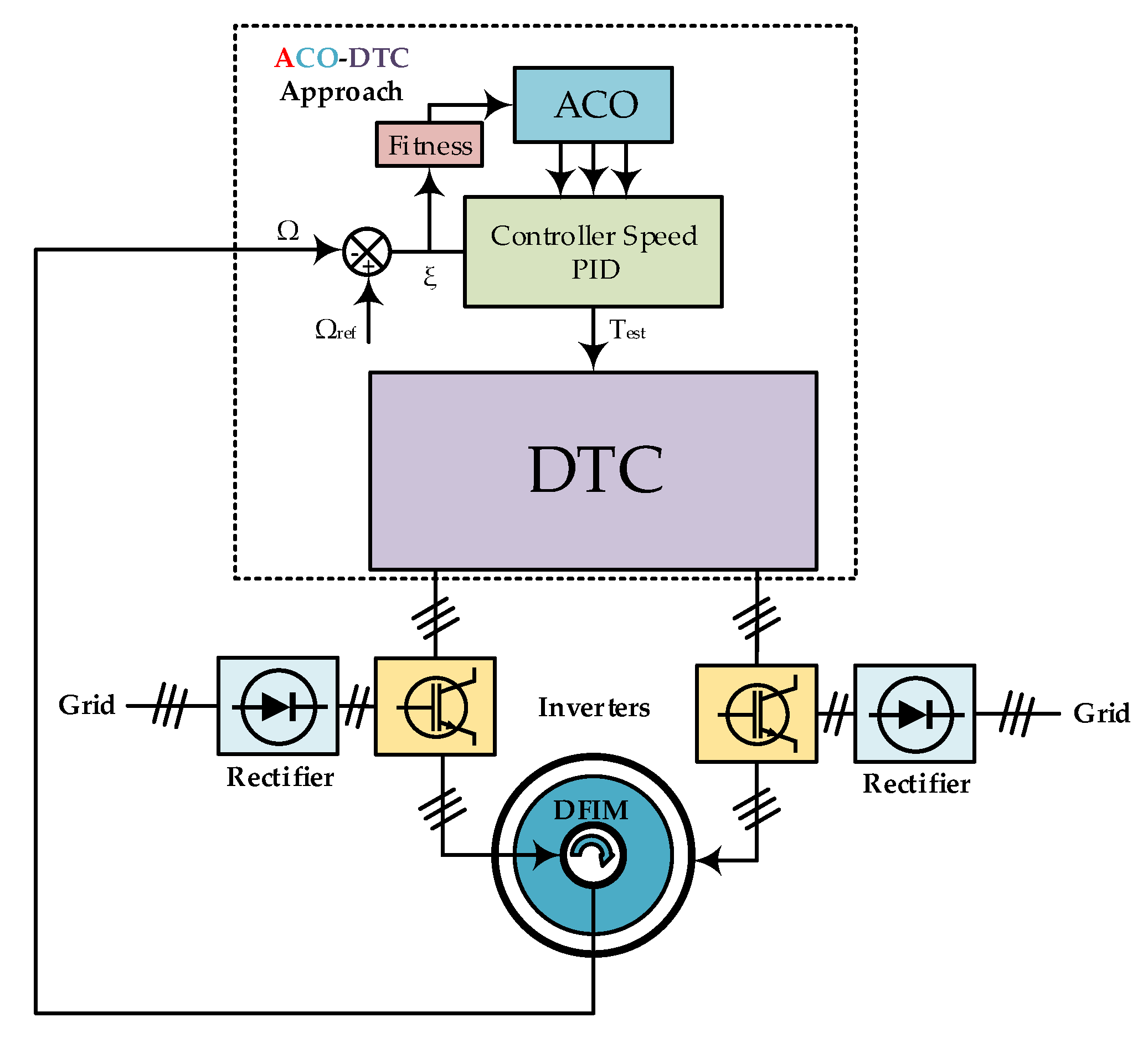
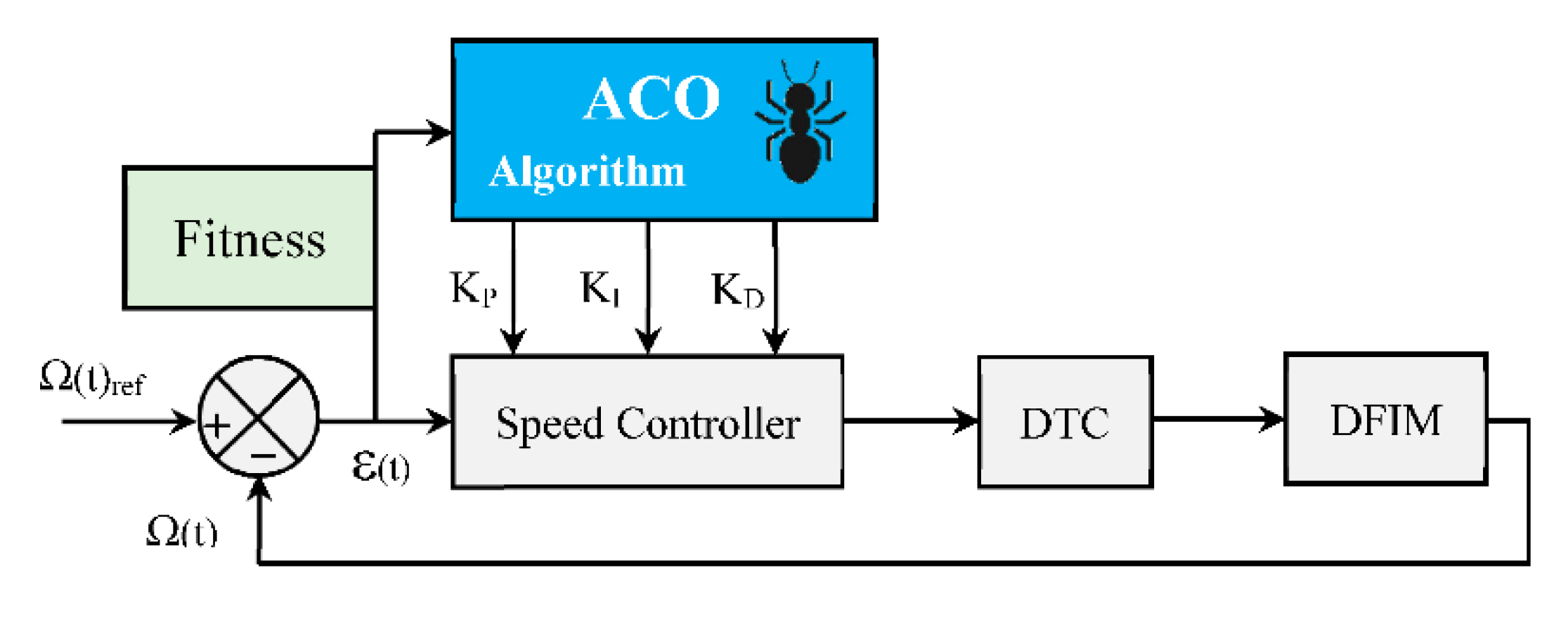
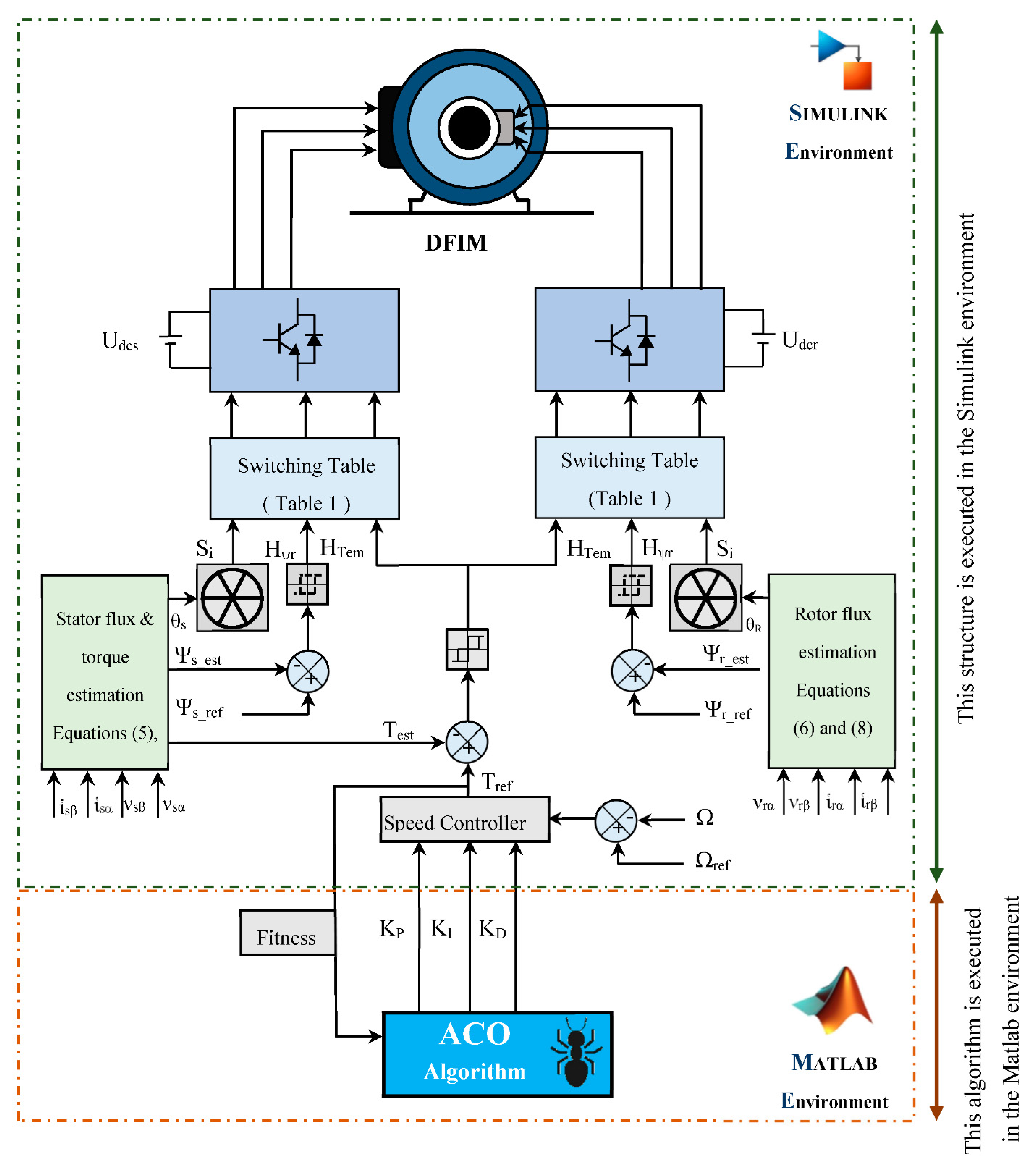
4.2. Design of the Combined ACO with PID Controller
5. Fitness
6. ACO Parameters
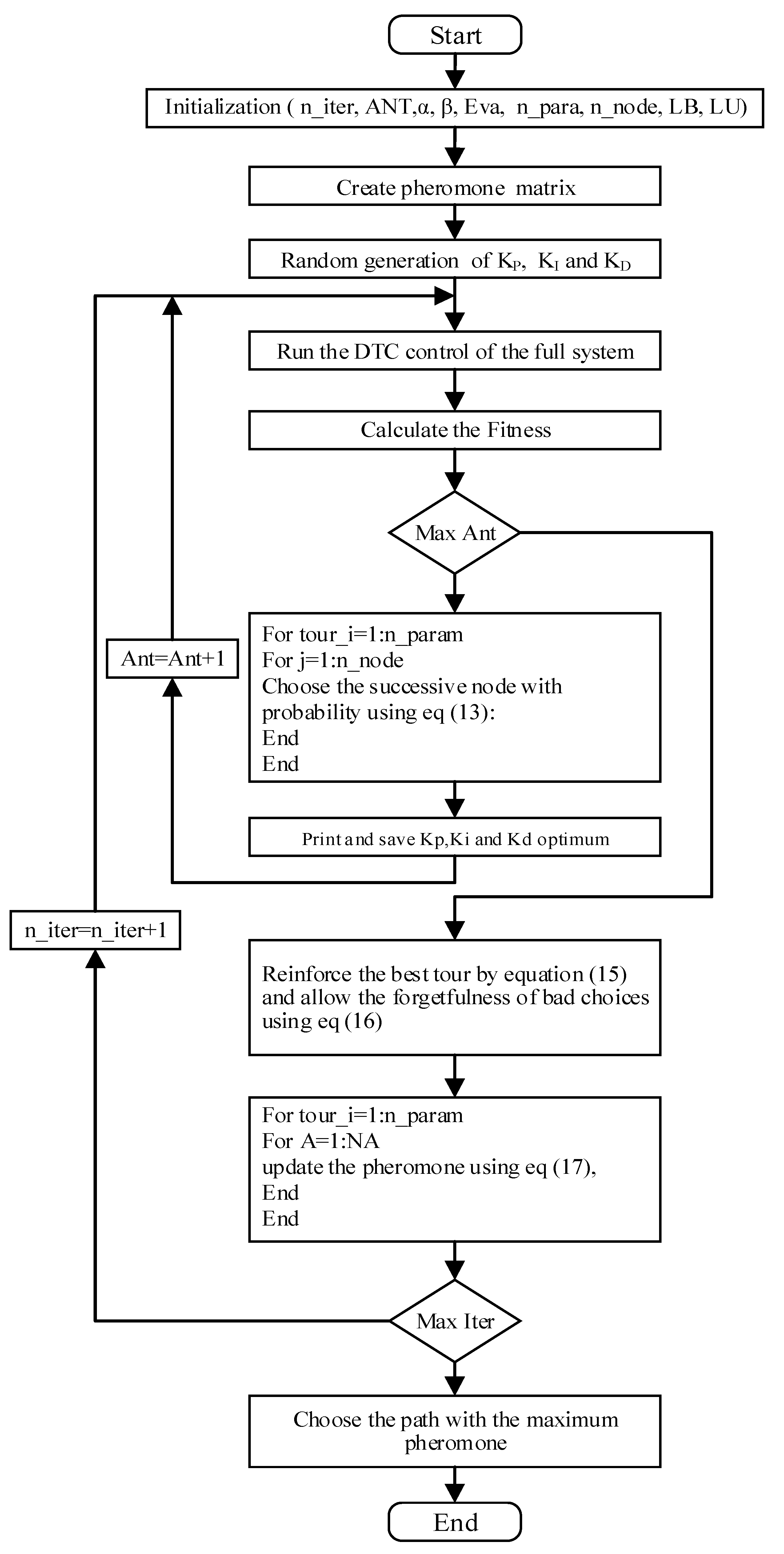
| Algorithm 1. Algorithm of ACO |
| Begin Step 1. Initialization of the ACO algorithm parameters (, α, β, Eva, n_para, n_node, LB, LU). Create a pheromone matrix and initialize probale solutions to the parameters at random intervals (, , ) by employing a uniform distribution. Step 2. Start the DTC and obtain the fitness by using the combined cost functions based on their weights. Step 3. Identify the node that has the greatest chance of succeeding with probability. using Equation (13). Step 4. Print the optimal parameters values of the speed PID regulator (, , ). The step 2 should be repeated until the maximum number of ants is attained. Step 5. Make use of the pheromone evaporation calculated by this equation (15), to reinforce the best road and by using Equation (16), we may be able to allow for the forgetfulness of bad decisions. Step 6. Equation (17) should be used to update the pheromone globally in accordance with the optimal solutions established in Step 5.Step 2 should be repeated as many times as necessary until the maximum number of iterations has been achieved. Step 7. Choose the best road expressed by the optimal PID gains which is can be concentrated by the maximum pheromone. End |
7. Simulation Procedure and Interpretation
- The speed reference starts with a step of 78.5 rad/s lasting 0.5 s.
- The reference speed abruptly drops to the nominal speed of 157 rad/s, the equivalent of 1500 rpm, which lasts for 1 s.
- The reference speed drops progressively with a slope of −157 rad/s until the rotation comes to a complete stop. This phase lasts 0.25 s.
- After the complete stop of rotation, the machine changes the direction of rotation, which is indicated by the negative values of speed.
- A progressive increase in the reverse direction of a slope of −157 rad/s until reaching the speed of −157 rad/s. This speed remains constant between 2.5 s and 3.5 s.
- After 157 rad/s, the speed suddenly drops to −78.5 rad/s from 3.5 s to 4 s and the test cycle is completed.
- In parallel with the reference speed, a variable load torque is applied at instants of 0.75 s and 2.75 s.
- A load torque of 10 Nm, which implies a nominal load of a 1.5 Kw machine, is applied between 0.75 s and 1.25 s.
- A nominal load torque of −10 Nm is applied between 2.75 s and 3.25 s. The choice of this negative value is made to follow the direction of rotation of the machine in the reverse direction.
- The sampling frequency: fs = 10 kHz.
- Hysteresis bands widths: ΔTem = ±0.01 Nm, ΔΨs = ΔΨr = ±0.001 Wb.
- Application of a nominal loads TL = 10 Nm and TL = −10 Nm at t = 0.75 s. and at t = 2.75 s respectively.
Results and Interpretation
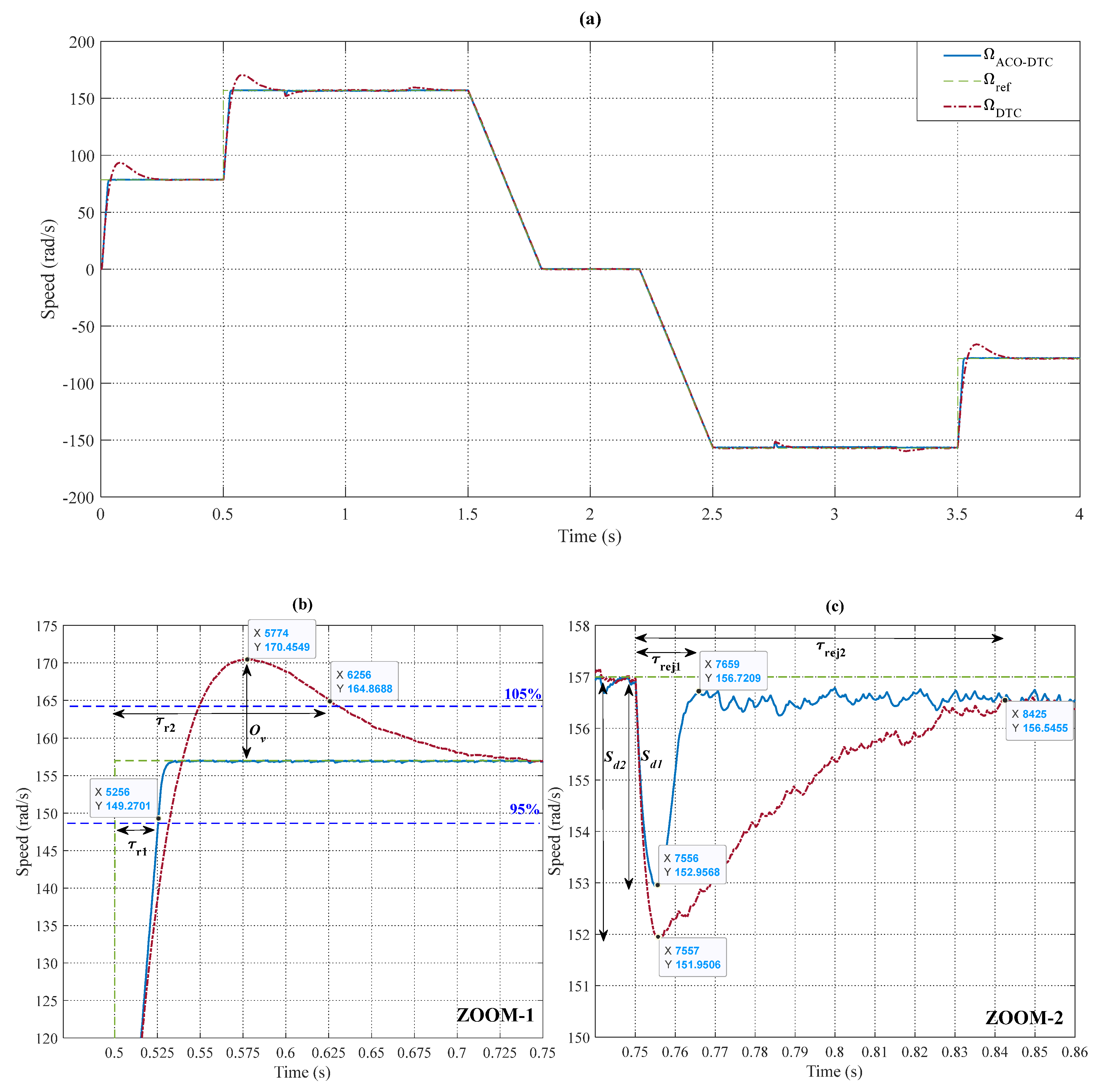
- Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 represent the performances of the DFIM, when the DFIM functions at a speed step of 78.5 rad/s and then instantaneously increases to 157 rad/s and then along a linear slope the speed decreases to −157 rad/s and then instantaneously increases to −78 rad/s, the motor during its functioning according to the speed characteristic i is subjected to torques of 10 Nm and −10 Nm applied at time t = 0.75 s and time t = 2.75 s.
- It is illustrated in Figure 11a–c that the motor has a smooth response to changes in load, even when the load changes suddenly. After 0.75 s, the motor rotates at speeds of 78.5 rad/s and 157 rad/s with a starting load of 0 Nm and an increase in load to 10 Nm after 0.75 s, the motor is considered to be in operation. The responses of the two controls show a complete tracking of the speed reference, showing remarkable differences. This response shows the improvement of the speed characteristic by the intelligent ACO-DTC approach compared to classic DTC, the overshoot is globally removed in the case of using ACO-DTC, the classic DTC presents 13.45 rad/s giving an improvement by 100%, for the response time of the ACO-DTC given ms 25.6 ms and 50.7 ms for the classic DTC, showing 49.5% as an improvement, The rejection time of the ACO-DTC is 15.9 ms, whereas the standard DTC is 92.5 ms, indicating an improvement of 82.81% over the classic DTC. Undershoot of the ACO-DTC given ms was 4.0432 rad/s and 5.0494 rad/s for the classic DTC, indicating a 19.92% improvement.
- The motor torque responses for different strategies are illustrated in Figure 12, From this figure, it is remarked that the response of torque of the proposed ACO-DTC strategy contains fewer ripples compared to the conventional DTC which are presented by 21.88% improvement rates for ACO-DTC compared to DTC (2.445 Nm for DTC and 1.95 Nm for ACO-DTC), the DFIM torque is controlled smoothly, it also has fewer undershoot when there is a sudden load change at 0.75 s and 2.75 s for different strategies.
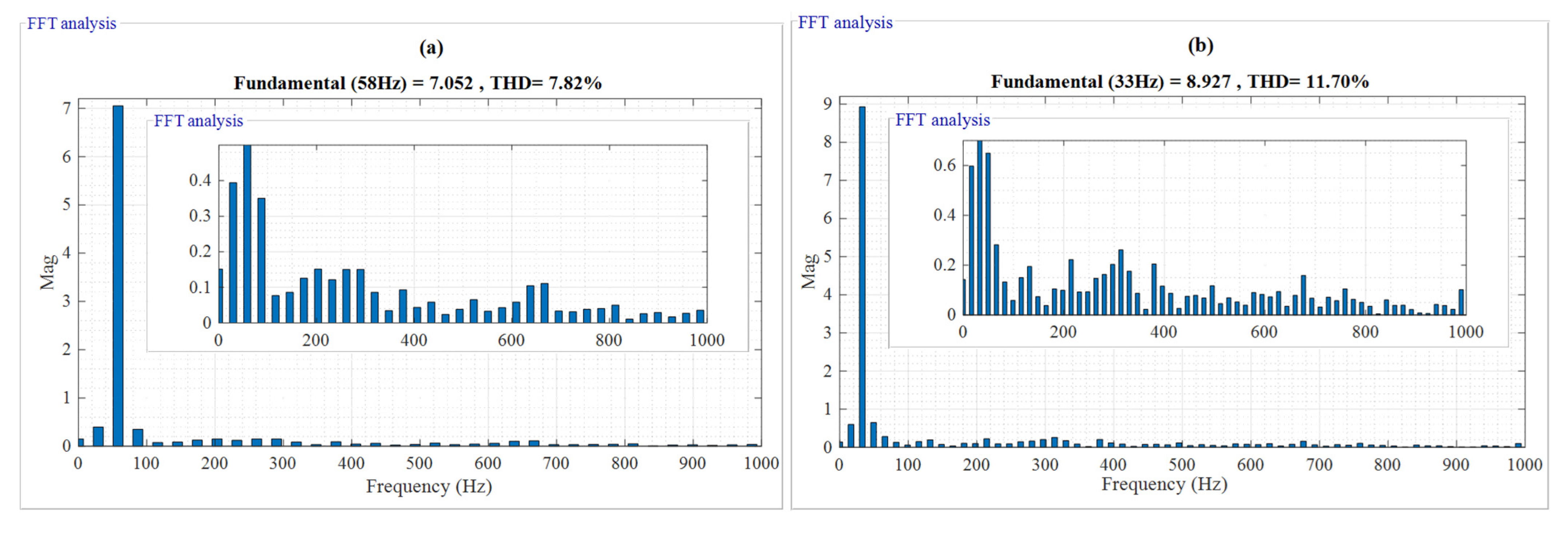
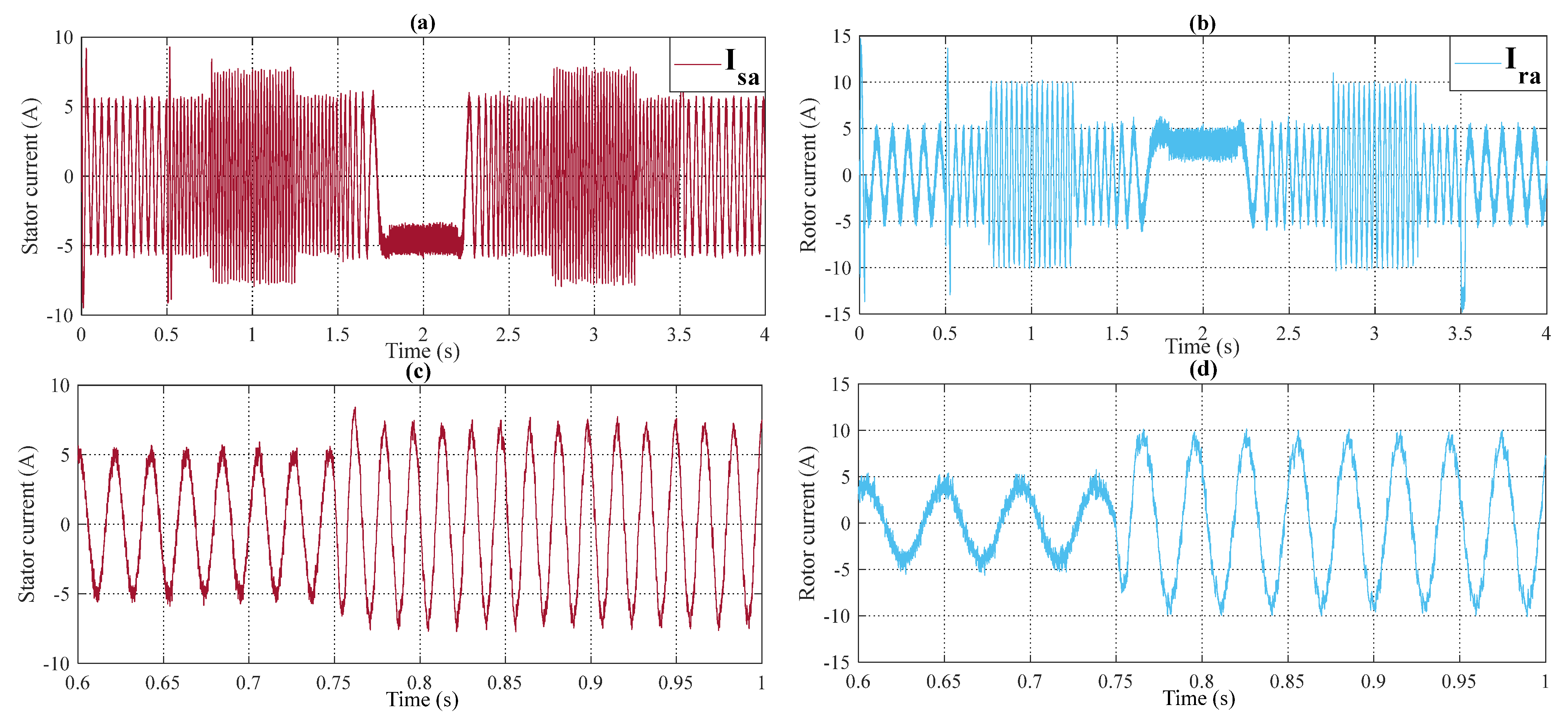
- Figure 13 and Figure 14 show the currents characteristics of the stator and rotor DFIM and their THDs. From these figures, it can be seen that the form of the stator and rotor currents deviates from their ideal form expressed by a THD of 7.82% and 11.7%, respectively, which makes the amount of harmonic rich by ripples causing torque ripples of 2.445 Nm for the conventional DTC.
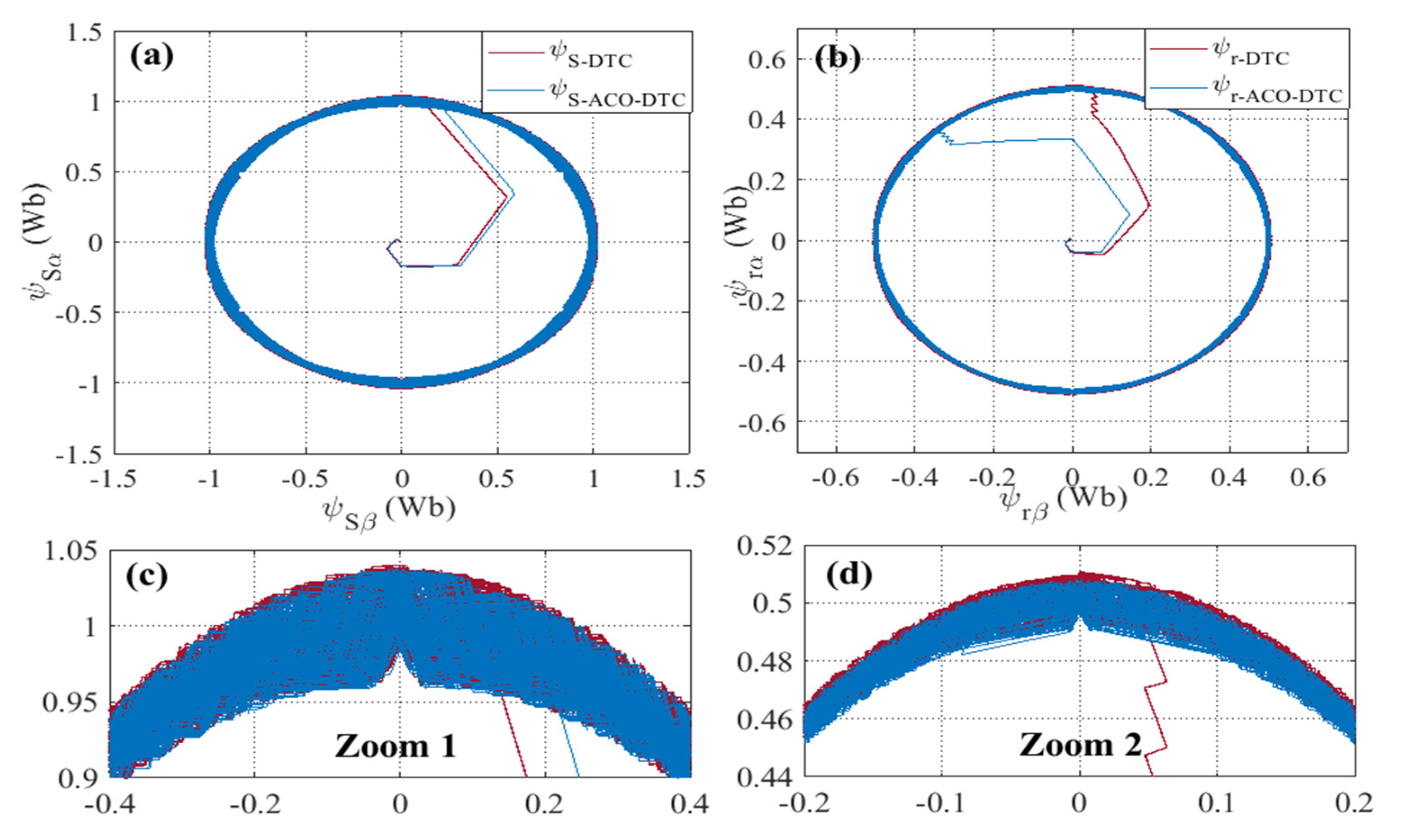
- Figure 17 illustrates the flux responses of the stator and rotor of the classical DTC and ACO-DTC which show improvement in flux amplitudes by 26.66% and 19.45%, respectively.
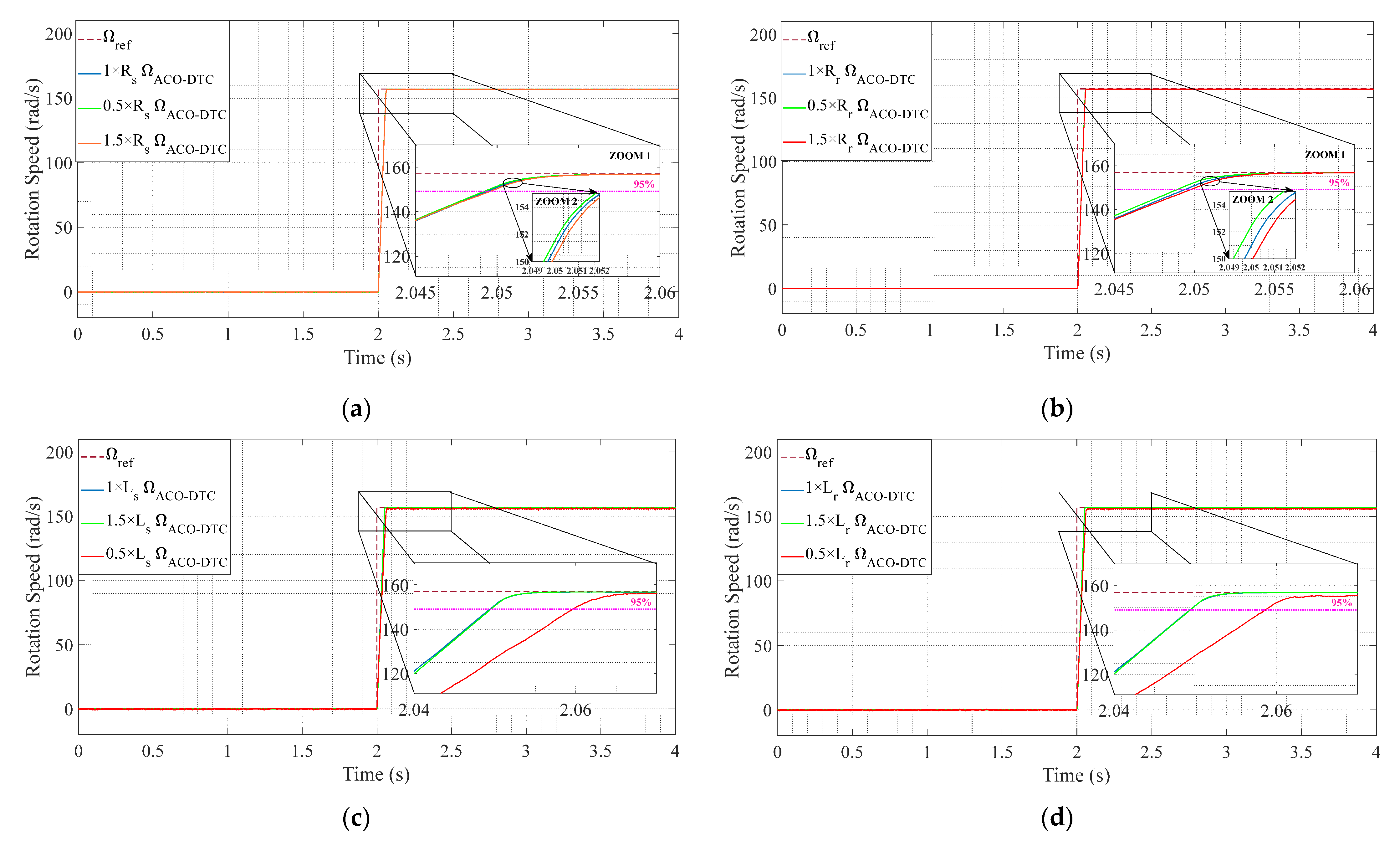
8. Robustness Test of the ACO-DTC
9. Discussion and Comparison of the Proposed ACO-DTC with Some Works Recently Published
10. Conclusions
- −
- The response time, rejection time, and overshoot are improved by 49.5%, 82.81%, and 100%, respectively.
- −
- The amplitude of the torque ripples is minimized by 21.88%.
- −
- The current THDs are reduced by 38.21% and 32.05%, respectively.
- −
- The following points are the topics on which the scientific community has chosen to concentrate its efforts:
- −
- Performance improvement of DTC control of a DFIM by artificial neuron networks.
- −
- Reduction of the effect of the hysteresis comparators by using the ANN controller.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| List of symbols | |
| , | Stator and rotor voltages in (α, β) plan |
| Stator and rotor directs voltages | |
| , | Stator and rotor currents in (α, β) plan |
| Stator and rotor fluxes in (α, β) plan | |
| Stator and rotor resistors | |
| Stator and rotor inductors | |
| Mutual Inductance | |
| Number of pairs of poles | |
| Rotor angular speed | |
| Stator angular speed | |
| and | Stator and Rotor Fluxes position |
| Electromagnetic Torque Hysterisis Output | |
| and | Stator and Rotor Fluxes Hysterisis Output |
| Inverters Sectors | |
| and | PID gains |
| Ω | Rotation speed |
| Speed reference | |
| Speed error | |
| Time constant | |
| Electromagnetic torque | |
| Resistant torque | |
| Viscous friction coefficient | |
| Moment of inertia | |
| List of Abbreviations | |
| DFIM | Doubly Fed Induction Motor |
| DTC | Direct Torque Control |
| GA-DTC | Genetic Algorithm Direct Torque Control |
| ACO-DTC | Ant Colony Optimization Direct Torque Control |
| GA | Genetic Algorithm |
| ACO | Ant Colony Optimzation |
| PSO | Particle Swarm Optimization |
| EP | Evolutionary Programming |
| FSA | Future Search Algorithm |
| PID | Proportional Integrator Derivator |
| DTFC | Direct Torque Fuzzy Control |
| DTNC | Direct Torque Neural Control |
| DTNFC | Direct Torque Neural-Fuzzy Control |
| ANFIS | Adaptive Neuro-Fuzzy Inference System |
| IAE | Integral Absolute Error |
| ISE | Integrale square Error |
| ITAE | Integral Time Absolute Error |
| THD | Total Harmonic Distortion |
| n_eter | Iteration Number |
| n_ant | Ants Number |
| Eva | Evaporation rate |
| n_node | Nodes Number |
| n_par | Parameters Number |
Appendix A
| Symbols | Value |
|---|---|
| n_eter | 300 |
| n_ANT | 30 |
| α | 0.8 |
| β | 0.2 |
| Eva | 0.9 |
| n_par | 3 |
| n_node | 5000 |
| Symbols | Values (Unit) |
|---|---|
| Pn | 1.5 Kw |
| Vs | 400 v |
| Vr | 130 v |
| P | 2 |
| f | 50 Hz |
| Rs | 1.75 Ω |
| Rr | 1.68 Ω |
| Ls | 0.295 H |
| Lr | 0.104 H |
| M | 0.165 H |
| f | 0.0027 kg·m2/s |
| J | 0.001 kg·m2 |
References
- El Ouanjli, N.; Derouich, A.; El Ghzizal, A.; Chebabhi, A.; Taoussi, M.; Bossoufi, B. Direct Torque Control Strategy Based on Fuzzy Logic Controller for a Doubly Fed Induction Motor. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2018; Volume 161, p. 12004. [Google Scholar]
- Mossa, M.A.; Echeikh, H.; Iqbal, A. Enhanced control technique for a sensor-less wind driven doubly fed induction generator for energy conversion purpose. Energy Rep. 2021, 7, 5815–5833. [Google Scholar] [CrossRef]
- Mossa, M.A.; Al-Sumaiti, A.S.; Do, T.D.; Diab, A.A.Z. Cost-Effective Predictive Flux Control for a Sensorless Doubly Fed Induction Generator. IEEE Access 2019, 7, 172606–172627. [Google Scholar] [CrossRef]
- Mahfoud, S.; Derouich, A.; El Ouanjli, N.; Mohammed, T.; Hanafi, A. Field Oriented Control of Doubly Fed Induction Motor using Speed Sliding Mode Controller. In E3S Web of Conferences; EDP Sciences: Les Ulis, France, 2021; Volume 229, p. 1061. [Google Scholar]
- Mossa, M.A.; Bolognani, S. Effective model predictive direct torque control for an induction motor drive. In Proceedings of the IEEE 2016 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Capri, Italy, 22–24 June 2016; pp. 746–754. [Google Scholar] [CrossRef]
- Rahman, M.F.; Patterson, D.; Cheok, A.; Betz, R. 30: Motor Drives. In Power Electronics Handbook, 4th ed.; Rashid, M.H., Ed.; Butterworth-Heinemann: Oxford, UK, 2018; pp. 945–1021. [Google Scholar]
- Mossa, M.A.; Bolognani, S. Predictive Control for an Induction Motor Drive Based on a Quasi-Linear Model. In Proceedings of the 2018 Twentieth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 18–20 December 2018; pp. 242–248. [Google Scholar]
- Mossa, M.A.; Bolognani, S. Effective sensorless model predictive direct torque control for a doubly fed induction machine. In Proceedings of the 2017 Nineteenth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 19–21 December 2017; pp. 1201–1207. [Google Scholar]
- Hassan, A.; Mohamed, Y.S.; El-Sawy, A.; Mossa, M.A. Control of a Wind Driven DFIG Connected to the Grid Based on Field Orientation. Wind Eng. 2011, 35, 127–143. [Google Scholar] [CrossRef]
- Mahfoud, S.; Derouich, A.; El Ouanjli, N.; El Mahfoud, M. Enhancement of the Direct Torque Control by using Artificial Neuron Network for a Doubly Fed Induction Motor. Intell. Syst. Appl. 2022, 13, 200060. [Google Scholar] [CrossRef]
- Hmidet, A.; Boubaker, O. Real-Time Low-Cost Speed Monitoring and Control of Three-Phase Induction Motor via a Voltage/Frequency Control Approach. Math. Probl. Eng. 2020, 2020, 6913813. [Google Scholar] [CrossRef]
- El Ouanjli, N.; Derouich, A.; El Ghzizal, A.; Chebabhi, A.; Taoussi, M. A comparative study between FOC and DTC control of the Doubly Fed Induction Motor (DFIM). In Proceedings of the 2017 International Conference on Electrical and Information Technologies (ICEIT), Rabat, Morocco, 15–18 November 2017; pp. 1–6. [Google Scholar]
- Mossa, M.A.; Mohamed, Y.S. Novel Scheme for Improving the Performance of a Wind Driven Doubly Fed Induction Generator during Grid Fault. Wind Eng. 2012, 36, 305–334. [Google Scholar] [CrossRef]
- Mossa, M.A.; Echeikh, H.; Quynh, N.V. A Novel Sensorless Predictive Voltage Control for an Induction Motor Drive Based on a Back-Stepping Observer-Experimental Validation. IEEE Access 2021, 9, 11921–11942. [Google Scholar] [CrossRef]
- Jayachitra, A.; Vinodha, R. Genetic Algorithm Based PID Controller Tuning Approach for Continuous Stirred Tank Reactor. Adv. Artif. Intell. 2014, 2014, 791230. [Google Scholar] [CrossRef]
- Ye, Y.; Yin, C.-B.; Gong, Y.; Zhou, J.-J. Position control of nonlinear hydraulic system using an improved PSO based PID controller. Mech. Syst. Signal Proc. 2017, 83, 241–259. [Google Scholar] [CrossRef]
- Feng, H.; Yin, C.-B.; Weng, W.-W.; Ma, W.; Zhou, J.-J.; Jia, W.-H.; Zhang, Z.-L. Robotic excavator trajectory control using an improved GA based PID controller. Mech. Syst. Signal Process. 2018, 105, 153–168. [Google Scholar] [CrossRef]
- Mahfoud, S.; Derouich, A.; Iqbal, A.; El Ouanjli, N. ANT-colony optimization-direct torque control for a doubly fed induction motor: An experimental validation. Energy Rep. 2022, 8, 81–98. [Google Scholar] [CrossRef]
- Elsisi, M.; Soliman, M.; Aboelela, M.A.S.; Mansour, W. GSA-based design of dual proportional integral load frequency controllers for nonlinear hydrothermal power system. Int. J. Electr. Comput. Energetic Electron. Commun. Eng. 2015, 9, 928–934. [Google Scholar]
- Wang, Y.; Jin, Q.; Zhang, R. Improved fuzzy PID controller design using predictive functional control structure. ISA Trans. 2017, 71, 354–363. [Google Scholar] [CrossRef]
- Abdo, M.M.; Vali, A.R.; Toloei, A.R.; Arvan, M.R. Stabilization loop of a two axes gimbal system using self-tuning PID type fuzzy controller. ISA Trans. 2014, 53, 591–602. [Google Scholar] [CrossRef]
- Hou, Y.-Y. Design and implementation of EP-based PID controller for chaos synchronization of Rikitake circuit systems. ISA Trans. 2017, 70, 260–268. [Google Scholar] [CrossRef] [PubMed]
- Elsisi, M.; Soliman, M. Optimal design of robust resilient automatic voltage regulators. ISA Trans. 2021, 108, 257–268. [Google Scholar] [CrossRef] [PubMed]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Parpinelli, R.S.; Lopes, H.; Freitas, A. Data mining with an ant colony optimization algorithm. IEEE Trans. Evol. Comput. 2002, 6, 321–332. [Google Scholar] [CrossRef] [Green Version]
- Twomey, C.; Stützle, T.; Dorigo, M.; Manfrin, M.; Birattari, M. An analysis of communication policies for homogeneous multi-colony ACO algorithms. Inf. Sci. 2010, 180, 2390–2404. [Google Scholar] [CrossRef] [Green Version]
- Echevarría, L.C.; de Campos Velho, H.F.; Becceneri, J.C.; da Silva Neto, A.J.; Santiago, O.L. The fault diagnosis inverse problem with Ant Colony Optimization and Ant Colony Optimization with dispersion. Appl. Math. Comput. 2014, 227, 687–700. [Google Scholar] [CrossRef]
- Sakthivel, A.; Vijayakumar, P.; Senthilkumar, A.; Lakshminarasimman, L.; Paramasivam, S. Experimental investigations on Ant Colony Optimized PI control algorithm for Shunt Active Power Filter to improve Power Quality. Control Eng. Pract. 2015, 42, 153–169. [Google Scholar] [CrossRef]
- Rajasekar, N.; Sundaram, K.M. Feedback controller design for variable voltage variable speed induction motor drive via Ant Colony Optimization. Appl. Soft Comput. 2012, 12, 2132–2136. [Google Scholar] [CrossRef]
- Ünal, M.; Erdal, H.; Topuz, V. Trajectory tracking performance comparison between genetic algorithm and ant colony optimization for PID controller tuning on pressure process. Comput. Appl. Eng. Educ. 2012, 20, 518–528. [Google Scholar] [CrossRef]
- dos Santos Coelho, L.; de Andrade Bernert, D.L. A modified ant colony optimization algorithm based on differential evolution for chaotic synchronization. Expert Syst. Appl. 2010, 37, 4198–4203. [Google Scholar] [CrossRef]
- Zemmit, A.; Messalti, S.; Harrag, A.E. A new improved DTC of doubly fed induction machine using GA-based PI controller. Ain Shams Eng. J. 2018, 9, 1877–1885. [Google Scholar] [CrossRef]
- Mahfoud, S.; Derouich, A.; El Ouanjli, N.; El Mahfoud, M.; Taoussi, M. A New Strategy-Based PID Controller Optimized by Genetic Algorithm for DTC of the Doubly Fed Induction Motor. Systems 2021, 9, 37. [Google Scholar] [CrossRef]
- Chiha, I.; Liouane, N.; Borne, P. Tuning PID controller using multi-objective ant colony optimization. Appl. Comput. Intell. Soft Comput. 2012, 2012, 11. [Google Scholar]
- Varol, H.; Bingul, Z. A new PID tuning technique using ant algorithm. In Proceedings of the 2004 American Control Conference, Boston, MA, USA, 30 June–2 July 2004; Volume 3, pp. 2154–2159. [Google Scholar]
- Yunus, A.M.S.; Abu-Siada, A.; Mosaad, M.I.; Albalawi, H.; Aljohani, M.; Jin, J.X. Application of SMES Technology in Improving the Performance of a DFIG-WECS Connected to a Weak Grid. IEEE Access 2021, 9, 124541–124548. [Google Scholar] [CrossRef]
- Mosaad, M.I.; Abu-Siada, A.; Ismaiel, M.M.; Albalawi, H.; Fahmy, A. Enhancing the Fault Ride-through Capability of a DFIG-WECS Using a High-Temperature Superconducting Coil. Energies 2021, 14, 6319. [Google Scholar] [CrossRef]
- Falehi, A.D. Optimal Design and Analysis of NIOFPID-Based Direct Power Control to Strengthen DFIG Power Control. J. Dyn. Syst. Meas. Control 2018, 140, 91001. [Google Scholar] [CrossRef]
- Falehi, A.D. Optimal Fractional Order BELBIC to Ameliorate Small Signal Stability of Interconnected Hybrid Power System. Environ. Prog. Sustain. Energy 2019, 38, 13208. [Google Scholar] [CrossRef]
- Falehi, A.D. An innovative optimal RPO-FOSMC based on multi-objective grasshopper optimization algorithm for DFIG-based wind turbine to augment MPPT and FRT capabilities. Chaos Solitons Fractals 2020, 130, 109407. [Google Scholar] [CrossRef]
- Falehi, A.D. Optimal Power Tracking of DFIG-Based Wind Turbine Using MOGWO-Based Fractional-Order Sliding Mode Controller. J. Sol. Energy Eng. 2019, 142, 31004. [Google Scholar] [CrossRef]
- Abderazak, S.; Farid, N. Comparative study between Sliding mode controller and Fuzzy Sliding mode controller in a speed control for doubly fed induction motor. In Proceedings of the 2016 4th International Conference on Control Engineering & Information Technology (CEIT), Hammamet, Tunisia, 16–18 December 2016; pp. 1–6. [Google Scholar]





| Sector Si | |||||||
|---|---|---|---|---|---|---|---|
| S1 | S2 | S3 | S4 | S5 | S6 | ||
| 1 | 1 | v2(110) | v3(010) | v4(011) | v5(001) | v6(101) | v1(100) |
| 0 | v7(111) | v0(000) | v7(111) | v0(000) | v7(111) | v0(000) | |
| −1 | v6(101) | v1(100) | v2(110) | v3(010) | v4(011) | v5(001) | |
| 0 | 1 | v3(010) | v4(011) | v5(001) | v6(101) | v1(100) | v2(110) |
| 0 | v0(000) | v7(111) | v0(000) | v7(111) | v0(000) | v7(111) | |
| −1 | v5(001) | v6(101) | v1(100) | v2(110) | v3(010) | v4(011) | |
| PID Parameters | KP | KI | KD |
|---|---|---|---|
| Maximum Value | 100 | 5 | 1 |
| Minimum Value | 0 | 0 | 0 |
| Controller Parameters | Classic DTC | ACO-DTC |
|---|---|---|
| KP | 0.776 | 46.5947 |
| KI | 28.74 | 3.54094 |
| KD | 0 | 0.076549 |
| Performances | Characteristics | DTC | ACO-DTC | Improvements % |
|---|---|---|---|---|
| Response Time (ms) | 50.7 | 25.6 | 49.5 | |
| Overshoot (rad/s) | 13.4549 | 0 | 100 | |
| Rejection Time (ms) | 92.5 | 15.9 | 82.81 | |
| Undershoot (rad/s) | 5.0494 | 4.0432 | 19.92 | |
| Ripples (Nm) | 2.445 | 1.91 | 21.88 | |
| Ripples (wb) | 0.05855 | 0.04294 | 26.66 | |
| Ripples (wb) | 0.0122 | 0.00983 | 19.45 | |
| THD (%) | 7.82 | 4.82 | 38.21 | |
| THD (%) | 11.7 | 7.98 | 32.05 |
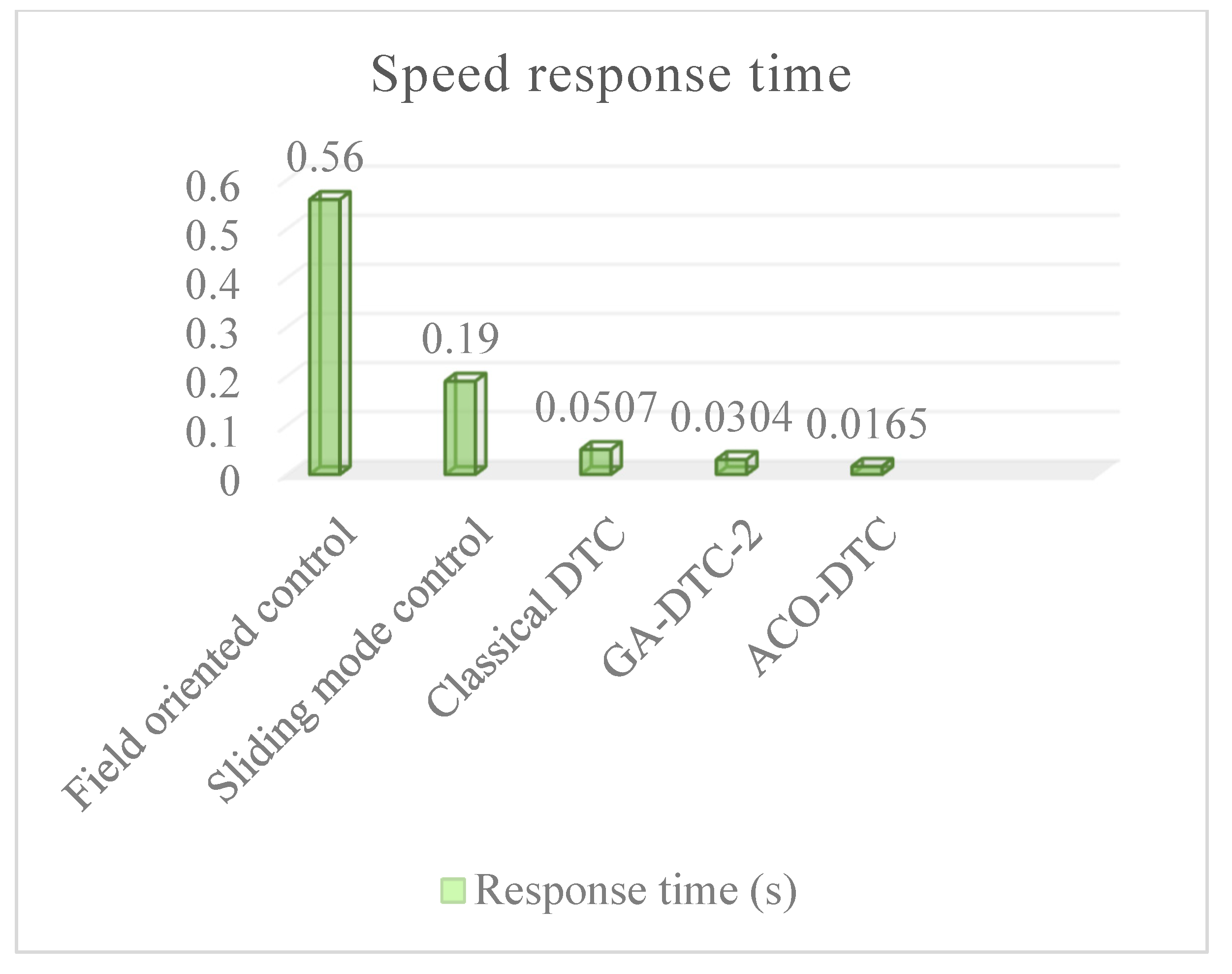
| References of Publications | Techniques | Speed Response Time (s) | Torque Ripples Amplitude (Nm) | Robustness of Techniques |
|---|---|---|---|---|
| [12] | FOC | 0.56 | 2.5 | Not robust |
| [42] | SMC | 0.19 | 2.4 | Not robust |
| - | Classical DTC | 0.0507 | 2.445 | Robust |
| [32] | GA-DTC-1 | 0.18 | 0.16 | Robust |
| [33] | GA-DTC-2 | 0.0304 | 2.05 | Robust |
| Proposed technique | ACO-DTC | 0.0256 | 1.91 | Robust |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahfoud, S.; Derouich, A.; El Ouanjli, N.; Quynh, N.V.; Mossa, M.A. A New Hybrid Ant Colony Optimization Based PID of the Direct Torque Control for a Doubly Fed Induction Motor. World Electr. Veh. J. 2022, 13, 78. https://doi.org/10.3390/wevj13050078
Mahfoud S, Derouich A, El Ouanjli N, Quynh NV, Mossa MA. A New Hybrid Ant Colony Optimization Based PID of the Direct Torque Control for a Doubly Fed Induction Motor. World Electric Vehicle Journal. 2022; 13(5):78. https://doi.org/10.3390/wevj13050078
Chicago/Turabian StyleMahfoud, Said, Aziz Derouich, Najib El Ouanjli, Nguyen Vu Quynh, and Mahmoud A. Mossa. 2022. "A New Hybrid Ant Colony Optimization Based PID of the Direct Torque Control for a Doubly Fed Induction Motor" World Electric Vehicle Journal 13, no. 5: 78. https://doi.org/10.3390/wevj13050078
APA StyleMahfoud, S., Derouich, A., El Ouanjli, N., Quynh, N. V., & Mossa, M. A. (2022). A New Hybrid Ant Colony Optimization Based PID of the Direct Torque Control for a Doubly Fed Induction Motor. World Electric Vehicle Journal, 13(5), 78. https://doi.org/10.3390/wevj13050078









