Modification of Cycle Life Model for Normal Aging Trajectory Prediction of Lithium-Ion Batteries at Different Temperatures and Discharge Current Rates
Abstract
:1. Introduction
2. Cycle Life Experiments and Results
2.1. Cycle Life Test
2.2. Cycle Life Test Results
3. Normal Aging Trajectory Acquisition Based on Wavelet Transform
3.1. Wavelet Transform Method
3.2. Normal Aging Trajectory Acquisition Results
4. Modified Life Model for Normal Aging Trajectory Prediction
4.1. Introduction of the Empirical Models
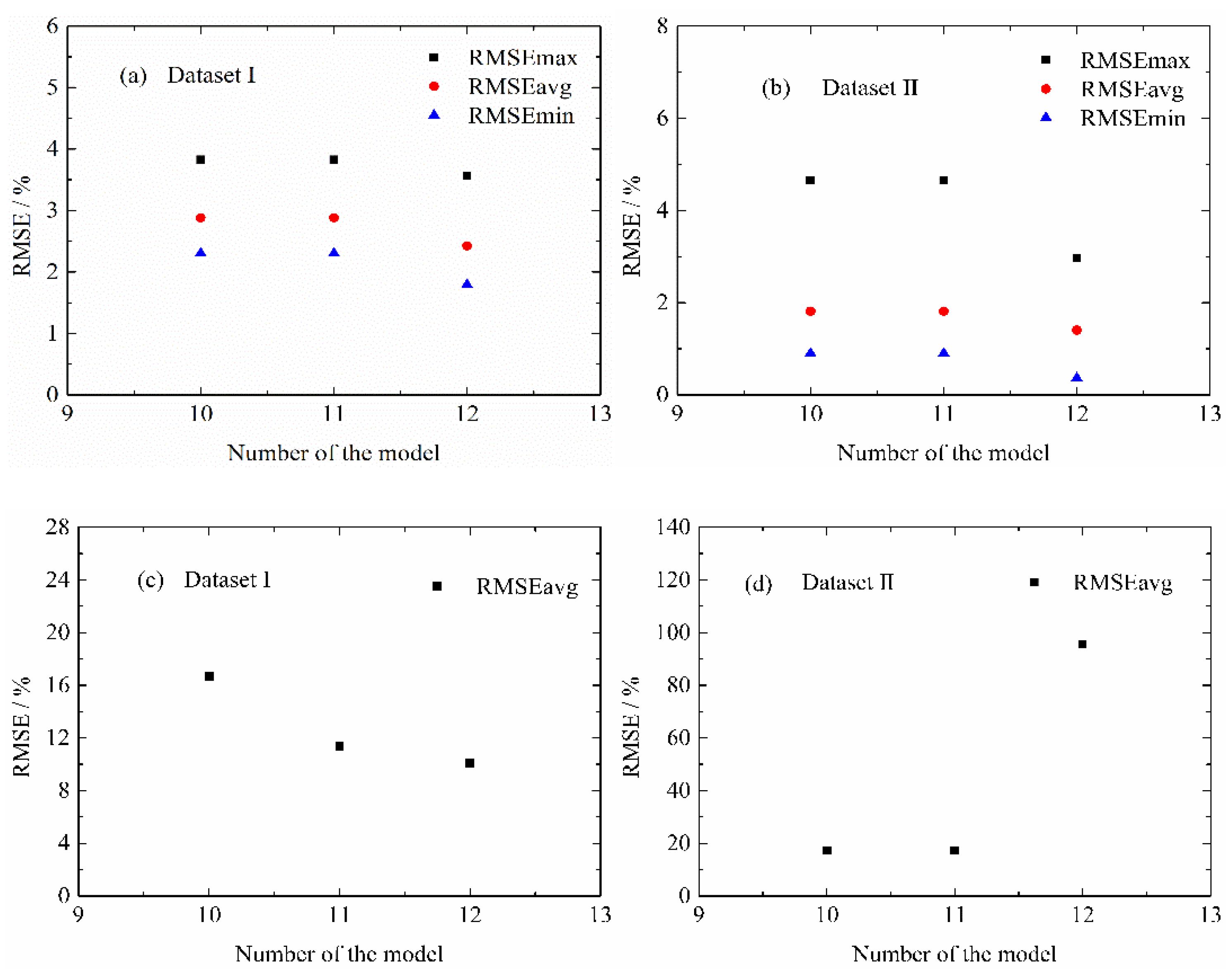
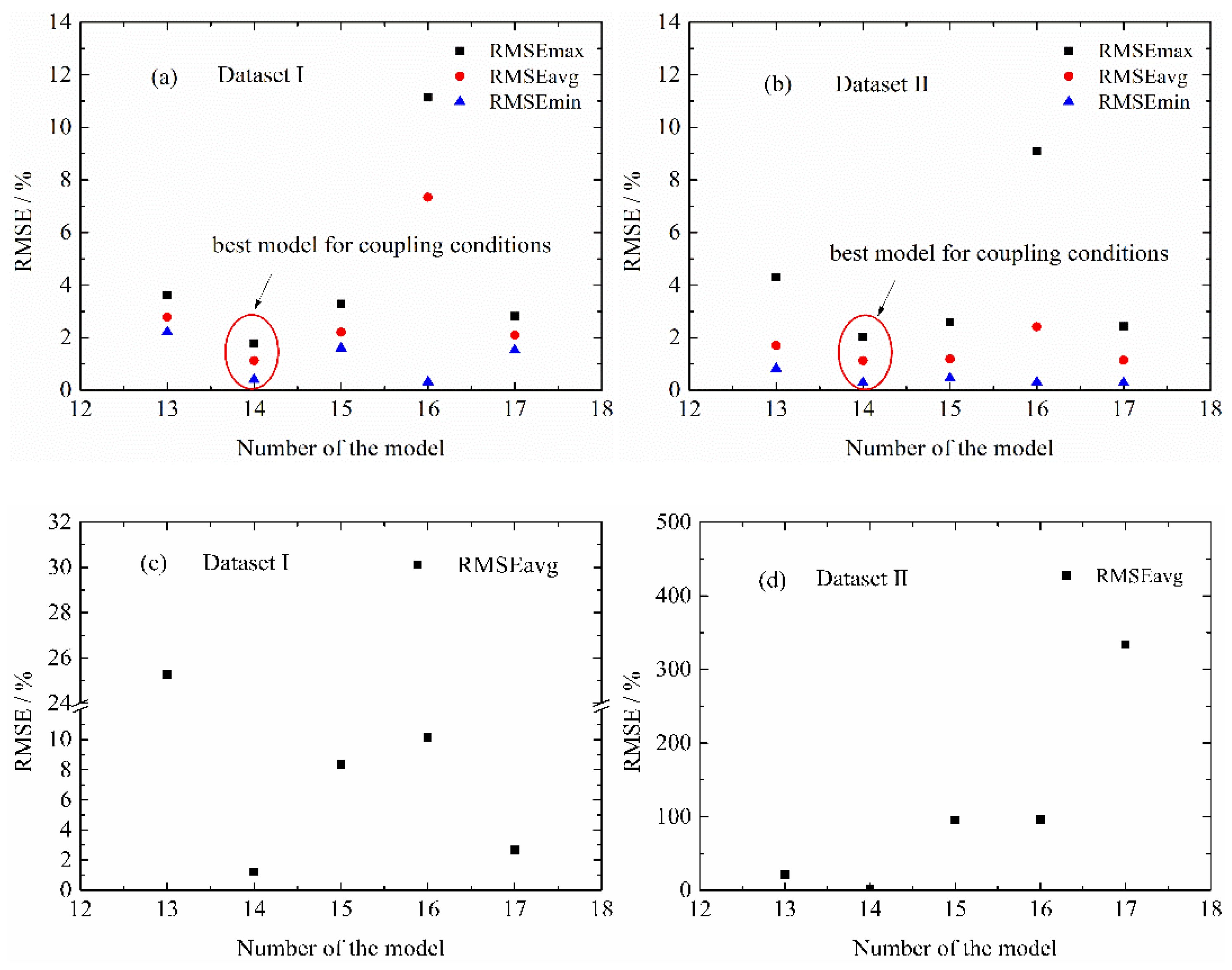
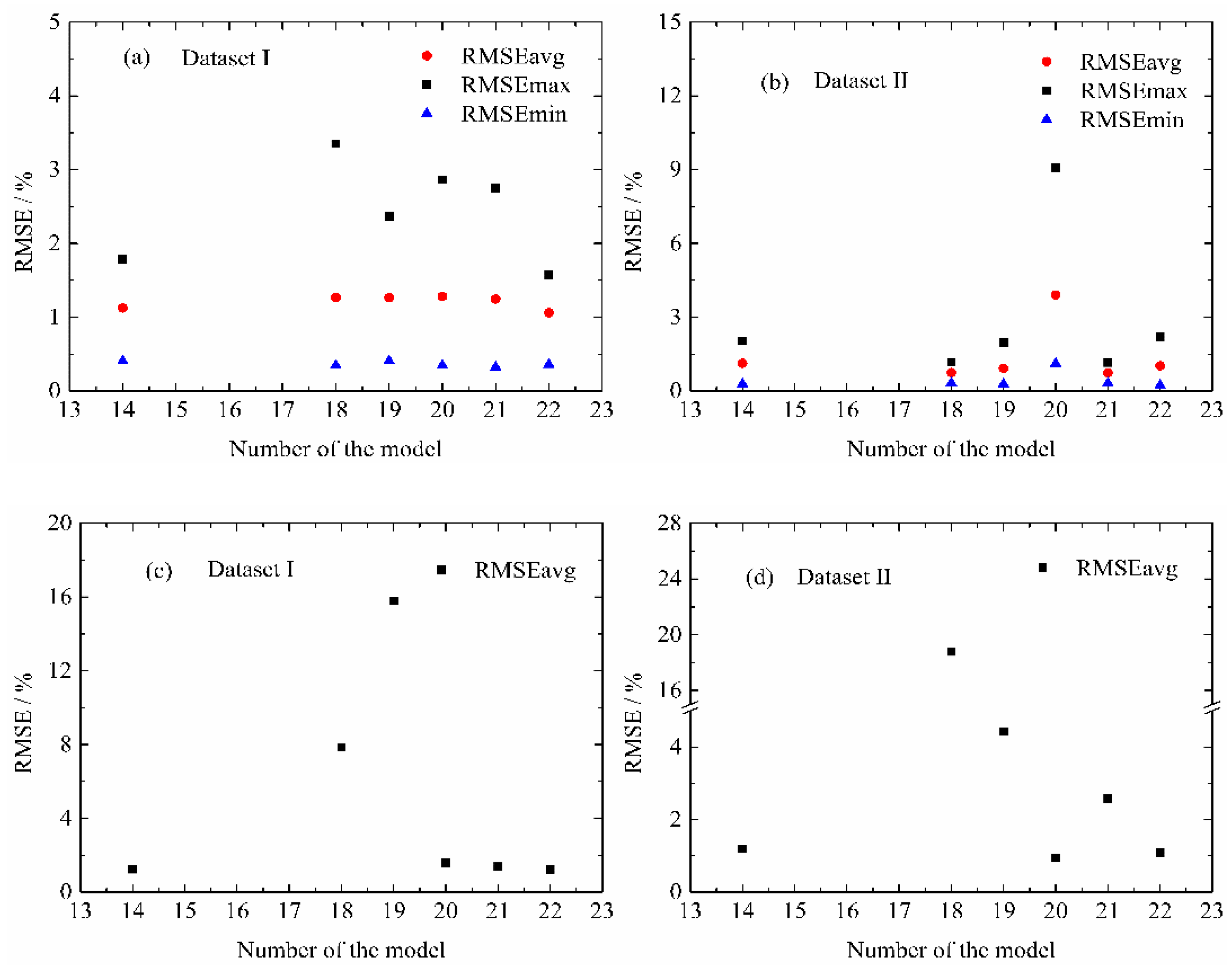
4.2. Influence of Life Model Structure on the Normal Aging Trajectory Prediction
4.3. Sensitivity Analysis of the Life Model Parameters for Normal Aging Trajectory Prediction
4.3.1. Sensitivity Analysis Method
- Set an appropriate variation range of the model parameter. The common values of the model parameters are calculated by the PSO algorithm. The variation range is set to be ±20% of the common values.
- Generate 700 numbers with the uniform distribution within the variation range for each parameter.
- Calculate the common output capacity retention series using the empirical model with the common parameter values, where i is the condition number in the dataset. Then, calculate the distribution output capacity retention series using the same model with the generated parameter values, where n is the generated number. Then, the relative sensitivity criteria under different operating conditions of each model parameter can be calculated using Equation (17):
- Obtain the overall parameter sensitivity under all conditions. The parameter sensitivity index value can be defined as the sum of the relative sensitivity criteria at various battery operating conditions, k is the parameter number and m is the number of the conditions in the Dataset I.
4.3.2. MPSA Analysis Results and Discussion
4.4. Modified Life Model for Normal Aging Trajectory Prediction
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Model | Model Parameter |
|---|---|
| ) | n is the cycle number; a1, a2 are the model parameters. |
| n is the cycle number; a1 is the model parameter. | |
| n is the cycle number; a1, a2 are the model parameters. | |
| n is the cycle number; a1, a2, a3 are the model parameters. | |
| n is the cycle number; a1, a2, a3, N0 are the model parameters. | |
| n is the cycle number; a1, a2, a3, a4 are the model parameters. | |
| n is the cycle number; a1, a2 are the model parameters. | |
| ) | n is the cycle number; a1, a2, a3, a4 are the model parameters. |
| n is the cycle number; A, t1, y0 are the model parameters. | |
| n is the cycle number; B and z are the model parameters; T is the absolute temperature; Ea is the active energy; and R is the universal gas constant. | |
| Ah is the cumulative discharge capacity; B and z are the model parameters; T is the absolute temperature; Ea is the active energy; and R is the universal gas constant. | |
| are model parameters; T is absolute temperature; and the Tref is 40 °C in literature. | |
| are the model parameters. | |
| is the discharge current rate. | |
| is the discharge current rate. | |
| T is the absolute temperature; n is the cycle number; Irate is the discharge current rate; and a, b, c, d, e are the model parameters. | |
| I is the discharge current rate; R is the universal gas constant; T is the absolute temperature; Ah is the cumulative discharge capacity; and a, b, c, d, e, f are model parameters. | |
| C is the discharge current rate; R is the universal gas constant; T is the absolute temperature; Ah is the cumulative discharge capacity; a1, a2, a3, a4 are the model parameters; -a2 represents the active energy; | |
| R is the universal gas constant; T is the absolute temperature; Ah is the cumulative discharge capacity; and a1, a2, a3, a4, a5 are the model parameters. | |
| C is the discharge current rate; R is the universal gas constant; T is the absolute temperature; Ah is the cumulative discharge capacity; and a1, a2, a3, a4, a5, a6, a7,a8 are the model parameters. | |
| C is the discharge current rate; R is the universal gas constant; T is the absolute temperature; Ah is the cumulative discharge capacity; a1, a2, a3, β are the model parameters; -a2 represents the active energy; | |
| C is the discharge current rate; R is the universal gas constant; T is the absolute temperature; Ah is the cumulative discharge capacity; and a1, a2, a3, a4, a5, β are the model parameters. | |
| C is the discharge current rate; R is the universal gas constant; T is the absolute temperature; Ah is the cumulative discharge capacity; and a1, a2, a3, a4, a5 are the model parameters. -a3 represents the active energy |
References
- Gao, Y.; Jiang, J.; Zhang, C.; Zhang, W.; Jiang, Y. Aging Mechanisms Under Different State-Of-Charge Ranges and the Multi-Indicators System of State-Of-Health for Lithium-Ion Battery with Li(NiMnCo)O2 Cathode. J. Power Sources 2018, 400, 641–651. [Google Scholar] [CrossRef]
- Han, X.; Meng, Q.; Sun, T.; Sun, J. Preparation and Electrochemical Characterization of Single-Crystalline Spherical LiNi1/3Co1/3Mn1/3O2 Powders Cathode Material for Li-ion Batteries. J. Power Sources 2010, 195, 3047–3052. [Google Scholar] [CrossRef]
- Barré, A.; Deguilhem, B.; Grolleau, S.; Gérard, M.; Suard, F.; Riu, D. A Review on Lithium-Ion Battery Aging Mechanisms and Estimations for Automotive Applications. J. Power Sources 2013, 241, 680–689. [Google Scholar] [CrossRef] [Green Version]
- Han, X.; Lu, L.; Zheng, Y.; Feng, X.; Li, Z.; Li, J.; Ouyang, M. A Review on the Key Issues of the Lithium Ion Battery Degradation Among the Whole Life Cycle. eTransportation 2019, 1, 100005. [Google Scholar] [CrossRef]
- Jalkanen, K.; Karppinen, J.; Skogström, L.; Laurila, T.; Nisula, M.; Vuorilehto, K. Cycle Aging of Commercial NMC/graphite Pouch Cells at Different Temperatures. Appl. Energy 2015, 154, 160–172. [Google Scholar] [CrossRef]
- Bitzerand, B.; Gruhle, A. A New Method for Detecting Lithium Plating by Measuring the Cell Thickness. J. Power Sources 2014, 262, 297–302. [Google Scholar] [CrossRef]
- Sarasketa-Zabala, E.; Gandiaga, I.; Martinez-Laserna, E.; Rodriguez-Martinez, L.M.; Villarreal, I. Cycle Aging Analysis of a LiFePO4/graphite Cell with Dynamic Model Validations: Towards Realistic Lifetime Predictions. J. Power Sources 2015, 275, 573–587. [Google Scholar] [CrossRef]
- Wu, L.; Fuand, X.; Guan, Y. Review of the Remaining Useful Life Prognostics of Vehicle Lithium-Ion Batteries Using Data-Driven Methodologies. Appl. Sci. 2016, 6, 166. [Google Scholar] [CrossRef] [Green Version]
- Jafari, M.; Khan, K.; Gauchia, L. Deterministic Models of Li-ion Battery Aging: It is a Matter of Scale. J. Energy Storage 2018, 20, 67–77. [Google Scholar] [CrossRef]
- Ahmadian, A.; Sedghi, M.; Elkamel, A.; Fowler, M.; Golkar, M.A. Plug-In Electric Vehicle Batteries Degradation Modeling for Smart Grid Studies: Review, Assessment and Conceptual Framework. Renew. Sustain. Energy Rev. 2018, 81, 2609–2624. [Google Scholar] [CrossRef]
- Nuhic, A.; Terzimehic, T.; Soczka-Guth, T.; Buchholz, M.; Dietmayer, K. Health Diagnosis and Remaining Useful Life Prognostics of Lithium-Ion Batteries Using Data-Driven Methods. J. Power Sources 2013, 239, 680–688. [Google Scholar] [CrossRef]
- Hu, X.; Jiang, J.; Cao, D.; Egardt, B. Battery Health Prognosis for Electric Vehicles Using Sample Entropy and Sparse Bayesian Predictive Modeling. IEEE Trans. Ind. Electron. 2015, 63, 2645–2656. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiong, R.; He, H.; Pecht, M.G. Long Short-Term Memory Recurrent Neural Network for Remaining Useful Life Prediction of Lithium-Ion Batteries. IEEE Trans. Veh. Technol. 2018, 67, 5695–5705. [Google Scholar] [CrossRef]
- Severson, K.A.; Attia, P.M.; Jin, N.; Perkins, N.; Jiang, B.; Yang, Z.; Chen, M.H.; Aykol, M.; Herring, P.K.; Fraggedakis, D.; et al. Data-Driven Prediction of Battery Cycle Life Before Capacity Degradation. Nat. Energy 2019, 4, 383–391. [Google Scholar] [CrossRef] [Green Version]
- Hu, C.; Jain, G.; Tamirisa, P.; Gorka, T. Method for Estimating Capacity and Predicting Remaining Useful Life of Lithium-Ion Battery. Appl. Energy 2014, 126, 182–189. [Google Scholar] [CrossRef]
- Bloom, I.; Cole, B.W.; Sohn, J.J.; Jones, S.A.; Polzin, E.G.; Battaglia, V.S.; Henriksen, G.L.; Motloch, C.; Richardson, R.; Unkelhaeuser, T.; et al. An Accelerated Calendar and Cycle Life Study of Li-ion Cells. J. Power Sources 2001, 101, 238–247. [Google Scholar] [CrossRef]
- Käbitz, S.; Gerschler, J.B.; Ecker, M.; Yurdagel, Y.; Emmermacher, B.; André, D.; Mitschand, T.; Sauer, D.U. Cycle and Calendar Life Study of a Graphite|LiNi1/3Mn1/3Co1/3O2 Li-ion High Energy System. Part a: Full Cell Characterization. J. Power Sources 2013, 239, 572–583. [Google Scholar] [CrossRef]
- Lee, Y.J.; Choi, H.Y.; Ha, C.W.; Yu, J.H.; Hwang, M.J.; Doh, C.H.; Choi, J.H. Cycle Life Modeling and the Capacity Fading Mechanisms in a graphite/LiNi0.6Co0.2Mn0.2O2 Cell. J. Appl. Electrochem. 2015, 45, 419–426. [Google Scholar] [CrossRef]
- He, W.; Williard, N.; Osterman, M.; Pecht, M. Prognostics of Lithium-Ion Batteries Based On Dempster–Shafer Theory and the Bayesian Monte Carlo Method. J. Power Sources 2011, 196, 10314–10321. [Google Scholar] [CrossRef]
- Unoand, M.; Tanaka, K. Accelerated Charge–Discharge Cycling Test and Cycle Life Prediction Model for Supercapacitors in Alternative Battery Applications. IEEE Trans. Ind. Electron. 2012, 59, 4704–4712. [Google Scholar]
- Cordoba-Arenas, A.; Onori, S.; Guezennec, Y.; Rizzoni, G. Capacity and Power Fade Cycle-Life Model for Plug-In Hybrid Electric Vehicle Lithium-Ion Battery Cells Containing Blended Spinel and Layered-Oxide Positive Electrodes. J. Power Sources 2015, 278, 473–483. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Purewal, J.; Liu, P.; Hicks-Garner, J.; Soukazian, S.; Sherman, E.; Sorenson, A.; Vu, L.; Tataria, H.; Verbrugge, M.W. Degradation of Lithium Ion Batteries Employing Graphite Negatives and Nickel–Cobalt–Manganese Oxide + Spinel Manganese Oxide Positives: Part 1, Aging Mechanisms and Life Estimation. J. Power Sources 2014, 269, 937–948. [Google Scholar] [CrossRef]
- Schmalstieg, J.; Käbitz, S.; Ecker, M.; Sauer, D.U. A Holistic Aging Model for Li(NiMnCo)O2 Based 18650 Lithium-Ion Batteries. J. Power Sources 2014, 257, 325–334. [Google Scholar] [CrossRef]
- Diao, W.; Saxenaand, S.; Pecht, M. Accelerated Cycle Life Testing and Capacity Degradation Modeling of LiCoO2-graphite Cells. J. Power Sources 2019, 435, 226830. [Google Scholar] [CrossRef]
- Cong, X.; Zhang, C.; Jiang, J.; Zhang, W.; Jiang, Y. A Hybrid Method for the Prediction of the Remaining Useful Life of Lithium-Ion Batteries with Accelerated Capacity Degradation. IEEE Trans. Veh. Technol. 2020, 69, 12775–12785. [Google Scholar] [CrossRef]
- Tröltzsch, U.; Kanoun, O.; Tränkler, H.R. Characterizing Aging Effects of Lithium Ion Batteries by Impedance Spectroscopy. Electrochim. Acta 2006, 51, 1664–1672. [Google Scholar] [CrossRef]
- Zhangand, Q.; White, R.E. Capacity Fade Analysis of a Lithium Ion Cell. J. Power Sources 2008, 179, 793–798. [Google Scholar] [CrossRef]
- Burns, J.C.; Jain, G.; Smith, A.J.; Eberman, K.W.; Scott, E.; Gardner, J.P.; Dahn, J.R. Dahn Evaluation of Effects of Additives in Wound Li-Ion Cells through High Precision Coulometry. J. Electrochem. Soc. 2011, 158, A255. [Google Scholar] [CrossRef]
- Yang, X.G.; Leng, Y.; Zhang, G.; Ge, S.; Wang, C.Y. Modeling of Lithium Plating Induced Aging of Lithium-Ion Batteries: Transition from Linear to Nonlinear Aging. J. Power Sources 2017, 360, 28–40. [Google Scholar] [CrossRef]
- Burrell, R.M.; Zulke, A.A.; Keil, P.; Hoster, H. Communication—Identifying and Managing Reversible Capacity Losses that Falsify Cycle Aging Tests of Lithium-Ion Cells. J. Electrochem. Soc. 2020, 167, 130544. [Google Scholar] [CrossRef]
- Konishi, H.; Yoshikawa, M.; Hirano, T.; Hidaka, K. Evaluation of Thermal Stability in Li0.2NixMn(1−x)/2Co(1−x)/2O2 (X = 1/3, 0.6, and 0.8) through X-ray Absorption Fine Structure. J. Power Sources 2014, 254, 338–344. [Google Scholar] [CrossRef]
- Noh, H.J.; Youn, S.; Yoon, C.S.; Sun, Y.K. Comparison of the Structural and Electrochemical Properties of Layered Li[NixCoyMnz]O2 (X = 1/3, 0.5, 0.6, 0.7, 0.8 and 0.85) Cathode Material for Lithium-Ion Batteries. J. Power Sources 2013, 233, 121–130. [Google Scholar] [CrossRef]
- Huang, Z.D.; Liu, X.M.; Zhang, B.; Oh, S.W.; Ma, P.C.; Kim, J.K. LiNi1/3Co1/3Mn1/3O2 with a Novel One-Dimensional Porous Structure: A High-Power Cathode Material for Rechargeable Li-ion Batteries. Scr. Mater. 2011, 64, 122–125. [Google Scholar] [CrossRef]
- Eddahech, A.; Briatand, O.; Vinassa, J. Lithium-Ion Battery Performance Improvement Based On Capacity Recovery Exploitation. Electrochim. Acta 2013, 114, 750–757. [Google Scholar] [CrossRef]
- Zhou, D.; Zhang, K.; Ravey, A.; Gao, F.; Miraoui, A. Parameter Sensitivity Analysis for Fractional-Order Modeling of Lithium-Ion Batteries. Energies 2016, 9, 123. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Si, X.; Huand, C.; Pecht, M.G. A Prognostic Model for Stochastic Degrading Systems with State Recovery: Application to Li-Ion Batteries. IEEE Trans. Reliab. 2017, 66, 1293–1308. [Google Scholar] [CrossRef]
- Wang, F.; Fan, B.; Liu, S.; Qian, G.; Huang, X.; Han, S. Attenuation Test and Duplication of Power Battery’s Cycle Life. J. Automot. Saf. Energy 2012, 3, 71–76. [Google Scholar]
- Wei, S. Research on Lifespan Factors and Test Methods of Traction Lithium-Ion Batteries; Beijing Jiaotong University: Beijing, China, 2014. [Google Scholar]
- Yafei, L. Study on Life Estimation and Optimization of Lithium-Ion Power Battery for Extended Range Electric Vehicle; South China University of Technology: Guangzhou, China, 2015. [Google Scholar]
- Lifuand, L.; Dongyu, Z. Cycle Life Prediction Method of Lithium Batteries Basedon Morphology and Properties. J. South China Univ. Technol. 2018, 4, 7–13. [Google Scholar]
- Li, H.L.; Su, J.R. Cycle-Life Prediction Model Studies of Lithium-Ion Batteries. Chin. J. Power Sources 2008, 32, 242–246. [Google Scholar]
- Wang, J.; Liu, P.; Hicks-Garner, J.; Sherman, E.; Soukiazian, S.; Verbrugge, M.; Tataria, H.; Musser, J.; Finamore, P. Cycle-Life Model for graphite-LiFePO4 Cells. J. Power Sources 2011, 196, 3942–3948. [Google Scholar] [CrossRef]
- Yutao, L.; Feng, W.; Hao, Y.; Xiutian, L. A Study on the Driving-cycle-based Life Model for LiFePO4 Battery. Automot. Eng. 2015, 37, 881–885. [Google Scholar]





| Item | Battery I | Battery II |
|---|---|---|
| Cathode material | Li[Ni0.5Co0.2Mn0.3]O2 | Li[Ni0.6Co0.2Mn0.2]O2 |
| Anode material | Graphite | Graphite |
| Nominal capacity | 114 Ah | 36 Ah |
| Charging cut-off voltage | 4.25 V | 4.15 V |
| Discharging cut-off voltage | 2.8 V | 2.5 V |
| Shape | prismatic | pouch |
| Condition Number | Cycle Temperature | Discharge Current Rate |
|---|---|---|
| 1 | 25 °C | 1 C |
| 2 | 35 °C | 1 C |
| 3 | 45 °C | 1 C |
| 4 | 50 °C | 1 C |
| 5 | 55 °C | 1 C |
| 6 | 25 °C | 0.5 C |
| 7 | 25 °C | 1 C |
| 8 | 25 °C | 1.5 C |
| 9 | 25 °C | 2 C |
| Condition Number | Cycle Temperature | Discharge Current Rate |
|---|---|---|
| 10 | 25 °C | 1 C |
| 11 | 35 °C | 1 C |
| 12 | 45 °C | 1 C |
| 13 | 25 °C | 1 C |
| 14 | 25 °C | 1.5 C |
| 15 | 25 °C | 2 C |
| 16 | 35 °C | 1.5 C |
| 17 | 35 °C | 2 C |
| Wavelet Function | Decomposed Number | Denoising Method | Threshold Estimation Method | |
|---|---|---|---|---|
| Haar | 3 | s | minimaxi | 58–78% |
| Haar | 3 | h | minimaxi | 52–77% |
| Haar | 4 | s | minimaxi | 68–87% |
| db4 | 3 | s | minimaxi | 54–70% |
| db4 | 4 | s | minimaxi | 66–87% |
| db4 | 3 | s | heursure | 43–70% |
| db4 | 4 | s | heursure | 43–87% |
| db4 | 4 | h | heursure | 11–86% |
| db4 | 5 | s | heursure | 48–89% |
| db4 | 5 | h | heursure | 20–84% |
| sym4 | 4 | s | heursure | 44–87% |
| sym4 | 3 | s | sqtwolog | 65–80% |
| Model | Model Parameter |
|---|---|
| ) | n is the cycle number; a1, a2 are the model parameters. |
| n is the cycle number; a1 is the model parameter. | |
| n is the cycle number; a1, a2 are the model parameters. | |
| n is the cycle number; a1, a2, a3 are the model parameters. | |
| n is the cycle number; a1, a2, a3, N0 are the model parameters. | |
| n is the cycle number; a1, a2, a3, a4 are the model parameters. | |
| n is the cycle number; a1, a2 are the model parameters. | |
| ) | n is the cycle number; a1, a2, a3, a4 are the model parameters. |
| n is the cycle number; A, t1, y0 are the model parameters. | |
| n is the cycle number; B and z are the model parameters; T is the absolute temperature; Ea is the active energy; and R is the universal gas constant. | |
| Ah is the cumulative discharge capacity; B and z are the model parameters; T is the absolute temperature; Ea is the active energy; and R is the universal gas constant. | |
| Tref is the reference temperature; n is the cycle number; dTref and α are model parameters; T is absolute temperature; and the Tref is 40 °C in literature. | |
| are the model parameters. | |
| is the discharge current rate. | |
| is the discharge current rate. | |
| T is the absolute temperature; n is the cycle number; Irate is the discharge current rate; and a, b, c, d, e are the model parameters. | |
| I is the discharge current rate; R is the universal gas constant; T is the absolute temperature; Ah is the cumulative discharge capacity; and a, b, c, d, e, f are model parameters. |
| Model | Highly Sensitive Parameters |
|---|---|
| ) | |
| none | |
| none | |
| none | |
| none | |
| ) | |
| η | |
| a | |
| e | |
| b |
| Improved Models |
|---|
| Model | Dataset I | Dataset II | ||
|---|---|---|---|---|
| Train Dataset | Test Dataset | Train Dataset | Test Dataset | |
| Model 14 | 1.12% | 1.22% | 1.12% | 1.19% |
| Model 23 | 1.06% | 1.21% | 1.02% | 1.09% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, X.; Zhang, C.; Wang, L.; Zhang, W.; Zhang, L. Modification of Cycle Life Model for Normal Aging Trajectory Prediction of Lithium-Ion Batteries at Different Temperatures and Discharge Current Rates. World Electr. Veh. J. 2022, 13, 59. https://doi.org/10.3390/wevj13040059
Jia X, Zhang C, Wang L, Zhang W, Zhang L. Modification of Cycle Life Model for Normal Aging Trajectory Prediction of Lithium-Ion Batteries at Different Temperatures and Discharge Current Rates. World Electric Vehicle Journal. 2022; 13(4):59. https://doi.org/10.3390/wevj13040059
Chicago/Turabian StyleJia, Xinyu, Caiping Zhang, Leyi Wang, Weige Zhang, and Linjing Zhang. 2022. "Modification of Cycle Life Model for Normal Aging Trajectory Prediction of Lithium-Ion Batteries at Different Temperatures and Discharge Current Rates" World Electric Vehicle Journal 13, no. 4: 59. https://doi.org/10.3390/wevj13040059
APA StyleJia, X., Zhang, C., Wang, L., Zhang, W., & Zhang, L. (2022). Modification of Cycle Life Model for Normal Aging Trajectory Prediction of Lithium-Ion Batteries at Different Temperatures and Discharge Current Rates. World Electric Vehicle Journal, 13(4), 59. https://doi.org/10.3390/wevj13040059







