A Structure Optimized Method Based on AFSA for Soft Magnetic Strips of Inner Double-Layer Shield for Wireless Power Transmission of EV

Abstract

A structure optimized method based on the artificial fish swarm algorithm (AFSA) for the soft magnetic strips of the inner double-layer shield is proposed in this paper and applied to the coupler of the wireless power transfer (WPT) system of an electrical vehicle (EV). Some structure parameters including length, height, width and distances of the strips are selected to fit their relationships with the coupling coefficient, which directly effects the transfer efficiency of the coupler by the linear fitting method. Based on these relationships, a group of parameters is obtained by the AFSA with the largest coupling coefficient and suitable volume to achieve optimal transfer efficiency without lots of repetitive results of the finite element analysis. The effectiveness of the proposed method is demonstrated quantitatively according to the outcomes and comparisons among different structure parameters and algorithms.

1. Introduction

With the development of the electrical vehicle (EV), the requirements of the supporting facilities of the EV are increasing, such as enough parking areas and charging piles. However, these necessary facilities are hard to realize in densely populated urban areas due to the requirement for a lot of space and cables. Since the wireless power transfer (WPT) system converts the power into the high-frequency magnet field and sends this into the EV from a distance, the required cables, chargers and amount of space of the traditional charging piles are not needed, and the security of charging facilities is improved [1]. The charging process can even be directly applied to the operating EV to realize quasi-dynamic WPT with temporary parking [2] and dynamic WPT without any stops [3]. The coupler is the key for the WPT system, and it has four parts, including the primary coil, primary shield, secondary coil and secondary shield. The transfer efficiency of the coupler is a serious problem as it limits the application of the WPT [4]. To solve this problem, some improvements to the shapes of the coils are presented, such as double D-type (DD) [5], double D-type quadrature (DDQ) [6], Taichi [7], bipolar pad (BP) [8], tripolar pad (TQ) [9] and quadruple pad (QP) [10], where the DDQ has a more stable charging process and better anti-offset performance than the quadrature coil, and the latter three types have less leakage in the magnetic field from the additional pads which require a larger covered space. Some new-style three-dimensional coils have been produced in recent years, such as the solenoid coil in [11], cylinder-shaped coils in [12] and rotation coils in [13], and these are presented to further decrease the leaked magnetic field of the coils with the developing covered spaces.

In order to further improve the transfer efficiency, two magnet shields should be inserted at the outside of the coils, and the transfer efficiency is also affected by the adopted shape, structure and material of the shield [14]. For the shape of the shield, this needs to be adjusted according to the shape of the coil, such as the DD coils with ferrite strips or bars in [15] and the cylindrical or pad shield for the circle coil in [16]; these shields effectively gather the leakage from the magnetic field and improve the transfer efficiency of the coupler. An improved circle shield with an extended part is installed on the secondary shield in [17] to reduce the influence of the fringe effect due to the soft magnetic material, but the adopted structure parameters of the shield are obtained by a large amount of results taken from multiple repetitive application of finite element analyses.

For the structure and material of the shield, aluminum foil [18] and ferrite [19] are two typical materials for the hard and soft magnetic material to produce a single-layer shield with one kind of material, but a single material only has a fixed shielded range of magnetic field frequency. Some new soft magnetic materials have been presented in recent years to obtain a larger frequency range of the magnet field, such as the nanocrystalline material in [20] and the hybrid high-temperature superconductor/ferromagnetic material in [21]. Since different materials have different characters and shielded ranges for the magnetic field frequencies, two materials can be combined as a double-layer shield to prolong the range, such as the combination of ferrite and aluminum [22]. By that analogy, three or more materials can be combined as a multi-layer shield to obtain a longer frequency range to cover most frequencies of the magnet field [23].

An optimal structure parameter selection method for the inner layer strip using the soft magnetic material is proposed in this paper to realize the best coupling coefficient and transfer efficiency of the coupler of the WPT system. The relationships among the coupling coefficient and some structure parameters including the length, width, height and distance of the strips are obtained by the linear fitting method and analyzed by the correlation method. Since these relationships are multiple objective problems, a group of the optimal structure parameters is achieved using the artificial fish swarm algorithm (AFSA) without several repetitive works. Compared with some typical groups of parameters and algorithms, the advantages of the coupling coefficient and the estimated error of the proposed method are verified by the optimized results and finite element analyses.

This paper is organized as follows: In Section 2, the basic structure of the shield is introduced. In Section 3, the structure parameters and their relationships with the coupling coefficient are obtained. In Section 4, the optimized shield structure is obtained by the AFSA and verified by the finite element analysis. A discussion of the possibility of the proposed method for different shapes of the shield and a conclusion for this paper are summarized in Section 5 and Section 6, respectively.

2. Structure of Shield

The shields are covered on the outside of the coils to make the magnet field gather between them. For the secondary shield using the soft magnetic material, this can be seen as a double-layer shield since this shield is combined with the chassis, which is always made from a hard magnetic material such as the aluminum alloy. The basic structure of the WPT system is shown in Figure 1.

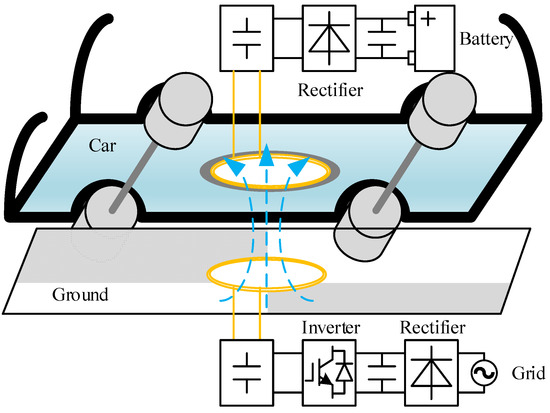
Figure 1. Basic structure of the WPT system.

Compared with the secondary side of the coupler, the chassis is large enough to set up the secondary side. The transfer efficiency is mainly affected by the structure of the inner layer of soft magnetic material. Considering the limited cost and space under the chassis, the ferrite strips are always adopted as the inner layer. The magnetic field strength curves at the outside of the 5 mm secondary shield are shown in Figure 2, and the basic parameters of the adopted materials are listed in Table 1. The Mn-Zn ferrite is a soft magnetic material compared with aluminum due to its larger permeability, and these two materials have different main working frequency ranges to shield the magnetic field with different frequencies. Most of the magnet fields are gathered between the shields, but some leaking magnetic fields enter the outer space through the gaps among the strips. The structure of these strips has a strong relationship with the transfer efficiency.

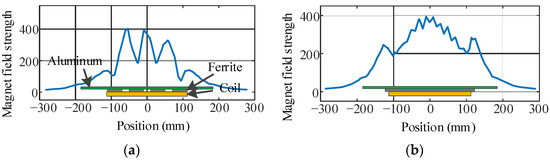
Figure 2. Magnet field strength curves for different directions of the inner soft magnetic strips. (a) x-axis. (b) y-axis.

Table 1. Basic parameters of the adopted materials.

	Permeability	Resistivity	Saturation Magnetic Flux Density	Working Frequency Range
Aluminum	0 H/m	26.55 nΩ	-	>100 kHz
Mn-Zn Ferrite	2500 H/m	∞	0.5 T	1 kHz~10 MHz

3. Structure Parameter Analysis

The structure of the secondary side of the coupler is shown in Figure 3, and a coil and a double-layer shield are combined as the secondary side. The structure variables including distance d, length l, width w and height h of the strips of the inner layer of the shield shown in Figure 4, and the following condition should be satisfied by the number of the strips N to cover most areas of the coil.

min(N(w + d)) ≥ 2 r

(1)

where r is the outer radius of the coil.

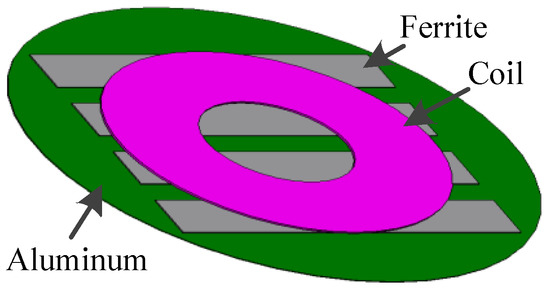
Figure 3. Structure of the secondary side.

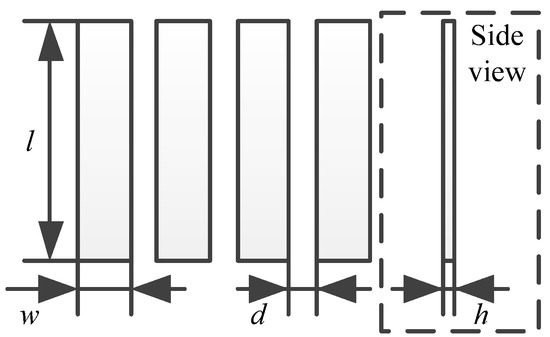
Figure 4. Structure of the strips of the inner layer of the shield.

These variables are selected to test the relationship of the coupling coefficient k and find an optimal structure with the largest transfer efficiency η.

3.1. Distances between Strips d

Finite element analysis is a kind of mathematical simulation method to estimate real physical systems by some simple and related units. The distance between the strips is selected as being from 10 mm to 30 mm, and their magnet field strength on the x-axis and y-axis are shown in Figure 5, respectively. According to these waves by the finite element analysis software, the magnet fields overflow and enter the outer space by the gaps between the strips. The waveform of the coupling coefficient k is shown in Figure 6. It can be seen that the maximum magnetic field strength by the overflowed field is increased and the coupling coefficient is decreased with the increment in the distance.

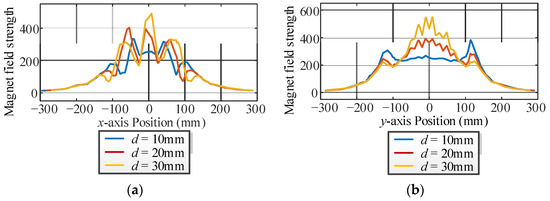
Figure 5. Magnet field strength waveforms with different distances. (a) x-axis. (b) y-axis.

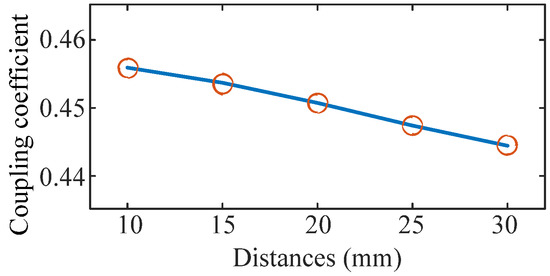
Figure 6. Coupling coefficient waveform with different distances.

The linear fitting method is adopted to obtain the relationship between the distance and coupling coefficient, and the fitting result is

$$k={\displaystyle \sum _{i=0}^j{a}_{di}{d}^{j-i}}$$

(2)

where a_di are the coefficients for the polynomial and j is the order of the linear fitting method.

A three-order linear fitting method, which is expressed as follows, is applied, and the fitting results are shown in Figure 7. As shown in this figure, all of the sampled points are located in the confidence interval, and this curve can be used to reflect the relationship.

$$k=a_{d0}{d}^3+a_{d1}{d}^2+a_{d2}d+a_{d3},$$

(3)

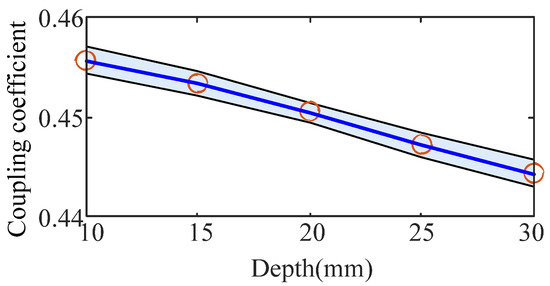
Figure 7. Fitting curve with different distances.

3.2. Length of Strips l

The length of the strips is tested from 120 mm to 320 mm. The waveforms of the magnet field strength and the coupling coefficient are shown in Figure 8 and Figure 9, respectively. According to these waveforms, the maximum magnetic field strength of the overflowed magnet field is decreased and the coupling coefficient is increased with the increment in the length.

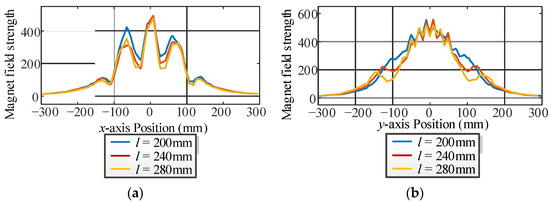
Figure 8. Magnet field strength waveforms with different lengths. (a) x-axis. (b) y-axis.

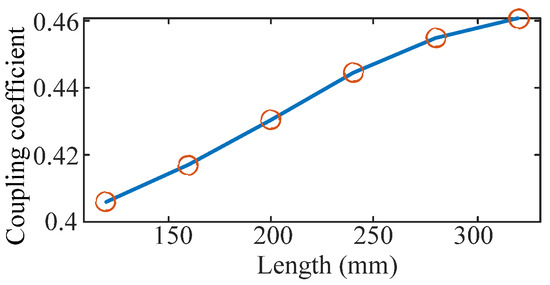
Figure 9. Coupling coefficient waveform with different lengths.

A four-order linear fitting method is applied, and the fitting results are shown in Figure 10. As shown in this figure, all of the sampled points are also located in the confidence interval, and this curve can be used to reflect the relationship.

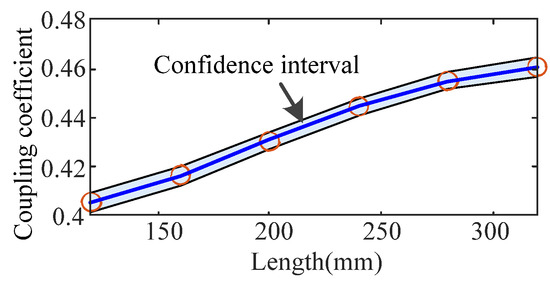
Figure 10. Fitting curve with different lengths.

3.3. Width of Strips w

The width of the strips is tested from 20 mm to 70 mm. The waveforms of the magnet field strength and the coupling coefficient are shown in Figure 11 and Figure 12, respectively, where N = 6 when the width equals 20 mm and 30 mm according to Equation (1). The maximum magnetic field strength of the overflowed magnet field is decreased and the coupling coefficient is increased with the increment in the width. Moreover, the coupling coefficient has an obvious decrement when N equals 6, and the transfer efficiency is influenced by the value of N.

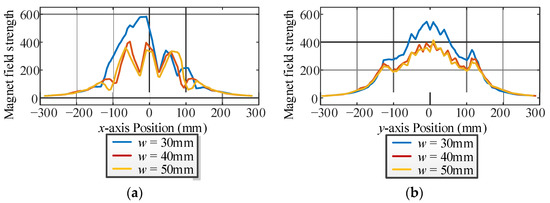
Figure 11. Magnet field strength waveforms with different widths. (a) x-axis. (b) y-axis.

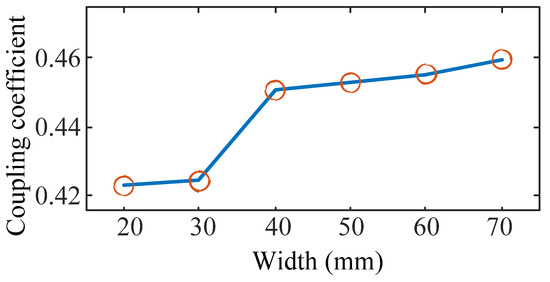
Figure 12. Coupling coefficient waveform with different widths.

Similarly, a four-order linear fitting method is applied, and the fitting results are shown in Figure 13. As shown in this figure, all of the sampled points are also located in the confidence interval, and this curve can be used to reflect the relationship.

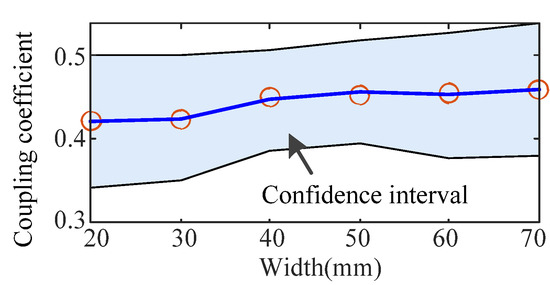
Figure 13. Fitting curve with different widths.

3.4. Height of Strips h

The length of the strips is tested from 0.5 mm to 3 mm. The waveforms of the magnet field strength and the coupling coefficient are shown in Figure 14 and Figure 15, respectively. According to these waveforms, the maximum magnetic field strength of the overflowed magnet field is weakly decreased and the coupling coefficient is increased with the increment in the height.

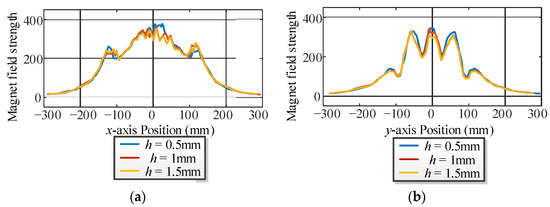
Figure 14. Magnet field strength waveforms with different heights. (a) x-axis. (b) y-axis.

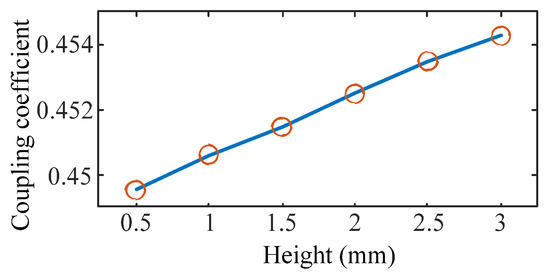
Figure 15. Coupling coefficient waveform with different heights.

A four-order linear fitting method is applied, and the fitting results are shown in Figure 16. As shown in this figure, all of the sampled points are also located in the confidence interval, and this curve can be used to reflect the relationship.

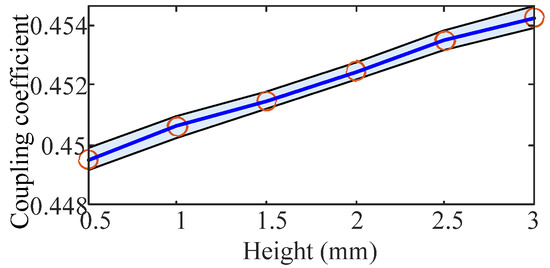
Figure 16. Fitting curve with different heights.

4. Optimized Method of Shield Structure

4.1. Correlation Analysis

Based on the above-mentioned fitting curves, all of the obtained coefficients are summarized in Table 2, where a_dx, a_lx, a_wx and a_hx (x = 1, 2, …) are the coefficients for the depth, length, width and height of the strips, respectively.

Table 2. Coefficients for the shield structure.

Coefficients	Values	Coefficients	Values
ad1	6.267 × 10−7	aw1	1.063 × 10−7
ad2	−4.23 × 10−5	aw2	−1.953 × 10−5
ad3	3.11 × 10−4	aw3	0.0013
ad4	0.456	aw4	−0.0324
al1	1.101 × 10−11	aw5	0.7049
al2	−1.695 × 10−8	ah1	−2.084 × 10−4
al3	7.431 × 10−6	ah2	0.0014
al4	−9.299 × 10−4	ah3	−0.0034
al5	0.437	ah4	0.0051
		ah5	0.4477

The correlation results by the Pearson are listed in Table 3. According to the data, these parameters reach statistical significance, and are valuable for finding the optimal values to obtain better transfer efficiency.

Table 3. Correlation results by the Pearson.

	Distances	Length	Width	Height
Pearson correlation	0.993	0.998	0.928	0.999
Pearson significance	0.000	0.000	0.008	0.000

4.2. AFSA-Optimized Structure Method

4.2.1. Basic Principle of AFSA

The AFSA has four behaviors including prey, swarm, follow and random to simulate the vision and predation processes of fish. An artificial fish on a two-dimensional space is selected as an example, as shown in Figure 17; the fish moves to X_v within a step if the food concentration at X_v is larger than X, which is the current location. If the fish obtains more food concentrations within the visual range, more suitable judgments can be obtained. This process is expressed as [23]:

$$\begin{array}{cc}{x}_{vi}=x_i+visual\cdot r& i=1,2,\cdots ,n\end{array}$$

(4)

$$X_{next}=\frac{X_v-X}{\Vert X_v-X\Vert }\cdot Step\cdot r$$

(5)

where X = (x₁,x₂,…,x_n), X_v = (x_v1,x_v2,…,x_vn), r is a random value within (−1, 1), n is the number of variables. Under the conditions of structure optimization, n is the same as the number of parameters. The flowchart of the AFSA is shown in Figure 18, where MAXGEN is the maximum number of iterations.

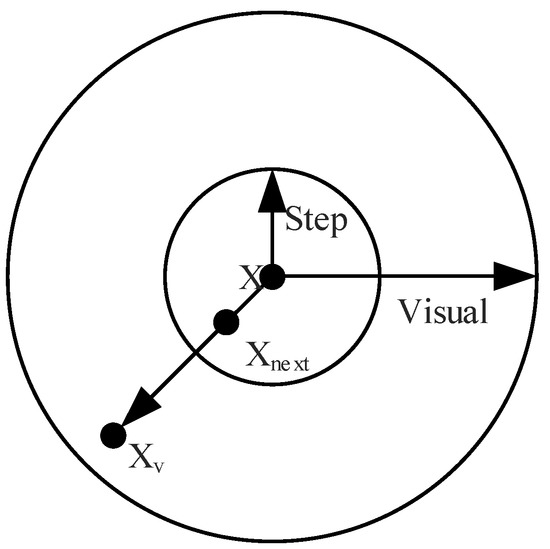
Figure 17. Sketch of visual and step of the artificial fish.

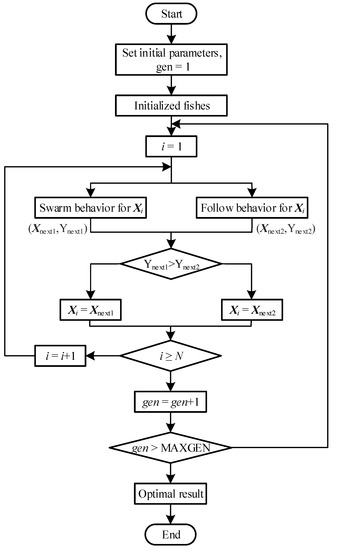
Figure 18. Flowchart of the AFSA.

4.2.2. Optimization Process

Based on the curves in Figure 6, Figure 9, Figure 12 and Figure 15, the coupling coefficient k can be changed to k(d, l, w, h), and the volume V of the shield is also affected by these parameters and can be changed to V(d, l, w, h). There are two objectives that should be considered in the AFSA. The first one is the maximum transfer efficiency, which can be reflected by the coupling coefficient k. The second one is the minimum volume of the shield. Following this, a cost function is used to realize the objectives

$$\max f\left[V\left(d,l,w,h\right),k\left(d,l,w,h\right)\right]=k\left(d,l,w,h\right)+\frac{1}{V\left(d,l,w,h\right)}$$

(6)

where

$$\begin{array}{ccc}\{\begin{array}{c}V=lh\left[Nw+\left(N-1\right)d\right]\\ k={\displaystyle \sum \left(\frac{{\lambda }_x}{{\displaystyle \sum {\lambda }_x}}{k}_x\right)}\end{array}& s.t.& N\in {\mathbb{Z}}^{+},x\in \left[\begin{array}{cccc}l& h& w& d\end{array}\right]\end{array}$$

(7)

and λ_x and k_x are the Pearson correlation values from Table 3 and the coupling coefficient from the results of Table 2 for the structure parameters, respectively.

The first term and second term of the cost function are applied to achieve the two objectives, respectively.

With N equal to 2, 4, 6, 8 and 10, the curves of the cost function value are shown in Figure 19, and the optimal results are summarized in Table 4, where all of the results are satisfied with the condition in Equation (1). According to these curves and points, the cost functions are converged as constants within the iterations.

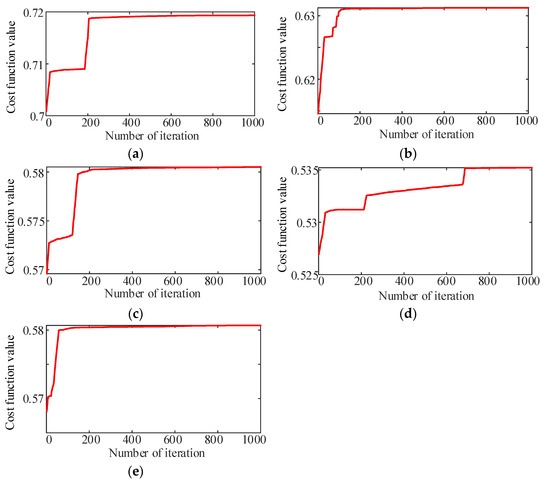
Figure 19. Curves of the cost function value. (a) N = 2, (b) N = 4, (c) N = 6, (d) N = 8, (e) N = 10.

Table 4. Parameters for the AFSA.

Labels	Value	Labels	Value
Number of fishes	100	Visual distance	1
Maximum iteration	1000	Congestion factor	0.618
Maximum probe	100	Step	0.1

According to the data in Table 5, the increasing volume and decreasing coupling coefficient are obtained with the increment in the number of strips. According to the current trends continuing, the volume and coupling coefficient have the best performance if N equals 1, i.e., the ferrite covers the secondary side coil fully.

Table 5. Results of the optimization.

	Length	Height	Width	Distances	Volume	Coupling Coefficient
N = 2	337.01 mm	3.01 mm	100.0 mm	5.02 mm	2.08 × 105 mm3	0.6474
N = 4	326.52 mm	3.01 mm	86.54 mm	5.00 mm	3.55 × 105 mm3	0.5716
N = 6	317.17 mm	2.99 mm	87.78 mm	5.00 mm	5.24 × 105 mm3	0.5225
N = 8	341.73 mm	3.00 mm	80.02 mm	5.00 mm	6.92 × 105 mm3	0.5152
N = 10	333.46 mm	3.00 mm	73.21 mm	5.00 mm	7.78 × 105 mm3	0.5123

4.3. Validations by the Finite Element Analysis

The distributions and x-axis curves of the finite element analysis are shown in Figure 20 and Figure 21, respectively, where the x-axis passes through the center of the strip and perpendicular to the length of the strip. The shields with the optimal structure parameters fully cover the secondary coil if N is larger than 4, and the magnetic field strengths at the edges of the shield are decreased. Since the volume is increased on the x-axis mainly, and the total of the leakage magnet fields is increased with the increasing number of strips, a better coupling coefficient is achieved with the limited number of strips.

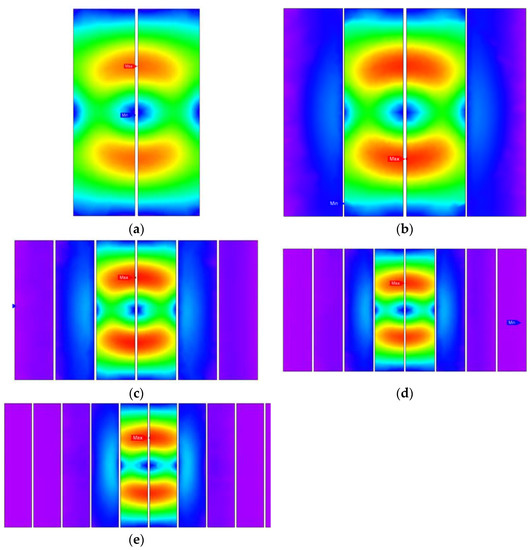
Figure 20. Distributions of the magnet field strength. (a) N = 2, (b) N = 4, (c) N = 6, (d) N = 8, (e) N = 10.

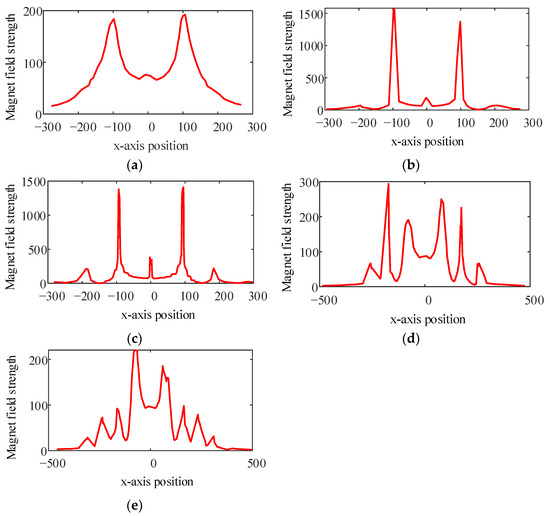
Figure 21. Curves of the magnet field strength on the x-axis. (a) N = 2, (b) N = 4, (c) N = 6, (d) N = 8, (e) N = 10.

According to Figure 21, an interesting phenomenon appears in that the strength that enters the outer space through the gaps among the strips (excepting the center gap) becomes a major problem if N belongs to (4,6). However, this problem is gradually eliminated with the further increasing number of strips.

The finite element results are summarized in Table 5, and the comparison of the coupling coefficients between the optimized results and finite element results are shown in Figure 22. According to the results in the figures and table, the coupling coefficient is decreased with the decrement in the number of strips, which basically confirms the trend in Table 4. These coefficients are the largest values comparing the curves in Figure 6, Figure 9, Figure 13 and Figure 15, and an optimal structure is found to improve the efficiency. The decreasing trend of the coupling coefficient of the finite element analyses is slower than the trend in Table 6. The reason for this phenomenon is that the accuracies of the optimal parameters are limited because these predicted parameters are located out of the tested ranges. The limitation of the accuracy can be improved if the selected testing ranges of the parameters in Section 3 are enlarged and the number of testing points is increased.

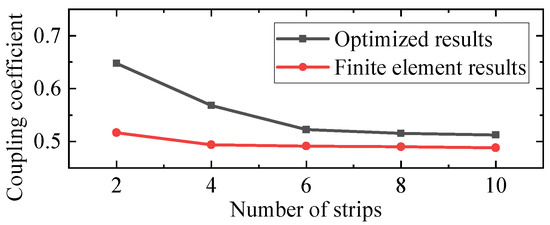
Figure 22. Comparison between the optimized and finite element results.

Table 6. Results of the finite element analyses.

	Primary Coil Inductance	Secondary Coil Inductance	Mutual Inductance	Coupling Coefficient
N = 2	92.222 μH	76.827 μH	43.558 μH	0.517
N = 4	92.503 μH	76.338 μH	41.505 μH	0.494
N = 6	91.754 μH	75.292 μH	40.812 μH	0.491
N = 8	91.571 μH	74.717 μH	40.576 μH	0.490
N = 10	90.764 μH	73.641 μH	39.901 μH	0.488

4.4. Performance Comparisons

Under the same initial conditions and limitations, the typical nondominated sorting genetic algorithm II (NSGA-II) and particle swarm optimization (PSO) algorithms are tested to find the optimal structure, and their results are listed in Table 7 where the estimated error at the last row is the error value between the optimized results and finite element results. This shows that the largest coupling coefficient with the limited volume and best accuracy is obtained by the AFSA. However, the achieved calculation time is the largest compared with the other two algorithms.

Table 7. Performance comparison for different optimization methods.

	AFSA	NSGA-II	PSO
Length	326.52 mm	330.69 mm	334.52 mm
Height	3.01 mm	3.00 mm	2.99 mm
Width	86.54 mm	73.21 mm	75.19 mm
Distance	5.00 mm	5.00 mm	5.00 mm
Volume	3.55 × 105 mm3	3.09 × 105 mm3	3.17 × 105 mm3
Coupling coefficient	0.5716	0.5123	0.5178
Calculation time	8.2541 s	7.7048 s	8.2207 s
Estimated error	13.576%	14.651%	14.843%

Under the same conditions, two groups of structure parameters of ferrite strip shield in [24,25] were tested to compare the optimal structure, and the comparison result is listed in Table 8. This shows that the coupling coefficient is increased by about 7.085% with the 10.994% increased volume. Some of the magnetic fields that entered external space are covered by the larger volume to increase transfer efficiency, and a balance between the transfer efficiency and volume is reached.

Table 8. Performance comparison for different structure shields.

	Optimal Structure	Structure in [24]	Structure in [25]
Volume	3.82 × 105 mm3	1.5 × 105 mm3	3.4 × 105 mm3
Coupling coefficient	0.494	0.399	0.459

5. Some Discussions

Excepting the ferrite strips of the inner layer, the proposed method has large flexibility and can also be used to tune the structure of the shield with different shapes, such as the cylinder and cuboid, which are shown in Figure 23. For the previous shape, the thickness and radius can be selected as parameters to obtain the optimal structure, and the length, width and height can be selected as parameters for the latter one.

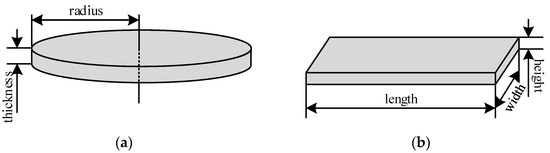
Figure 23. Structure of the shield with different shapes. (a) cylinder, (b) cuboid.

However, the proposed method is hard to directly apply to some special shields with more difficult structures, such as the octagon and sectors shields in Figure 24; these structure parameters are hard to determine and to find an optimal structure. Some approximate method should be used for these shields. For example, optimizing can be performed by approximating the sectors in Figure 23b as a whole circle.

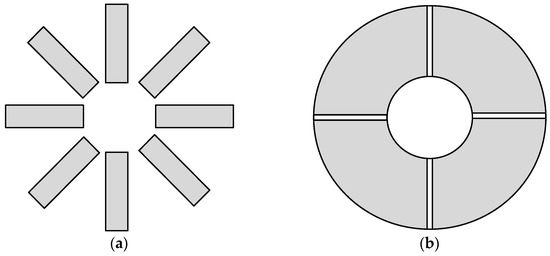
Figure 24. Special structures of the shield. (a) octagon, (b) sectors.

6. Conclusions

A selection method for the structure parameters of the inner layer of the secondary shield using soft magnetic strips is proposed in this paper and applied to the coupler of an EV to obtain the optimal transfer efficiency. The coupling coefficient curves with different structure parameters of the strips are fitted using the linear fitting method and a group of the optimal structure parameters is obtained using the AFSA. The advantages including optimal transfer efficiency and estimated error are demonstrated according to the comparisons among the different structure parameters from the other works of literature and algorithms, as well as the effectiveness of the proposed method.